Leveraging Land Cover Priors for Isoprene Emission Super-Resolution
Abstract
1. Introduction
- Land Cover-Informed SR: We propose a DL-based SR framework that incorporates LC information to enhance the spatial pattern of BVOC emissions, particularly isoprene.
- High-Resolution Satellite-Derived Inventory: We leverage an extremely recent high-resolution satellite-derived isoprene emission inventory to ensure accurate and up-to-date emission data for model training and evaluation.
- Recent Super-Resolution Network: We employ Hybrid Attention Transformer (HAT), a recent transformer-based SR network, to super-resolve isoprene emissions with improved accuracy and spatial detail.
- Climate-Aware Performance Evaluation: We evaluate the model’s performance across distinct climate classes by training the system on climate-specific conditions, analyzing robustness across diverse environmental settings.
- Generalization Across Unseen Regions: We investigate the model’s ability to generalize by super-resolving isoprene emissions in unseen climate conditions and geographical regions, identifying key challenges and potential improvements for robust performance.
2. Related Works
3. Materials
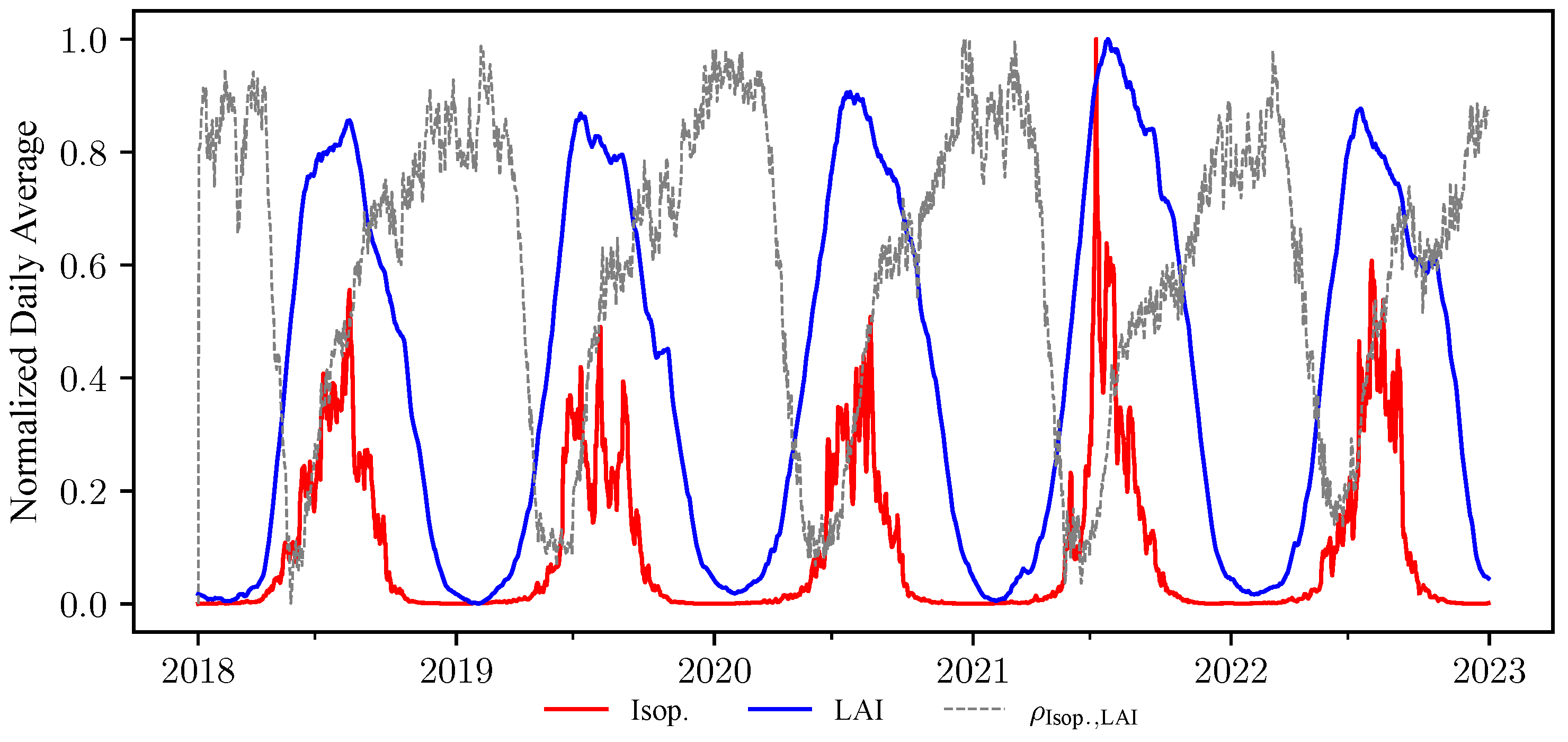
3.1. Isoprene Inventory
3.2. LAI Inventory
3.3. Land Cover Data
3.4. Climate Class Data
4. Methods
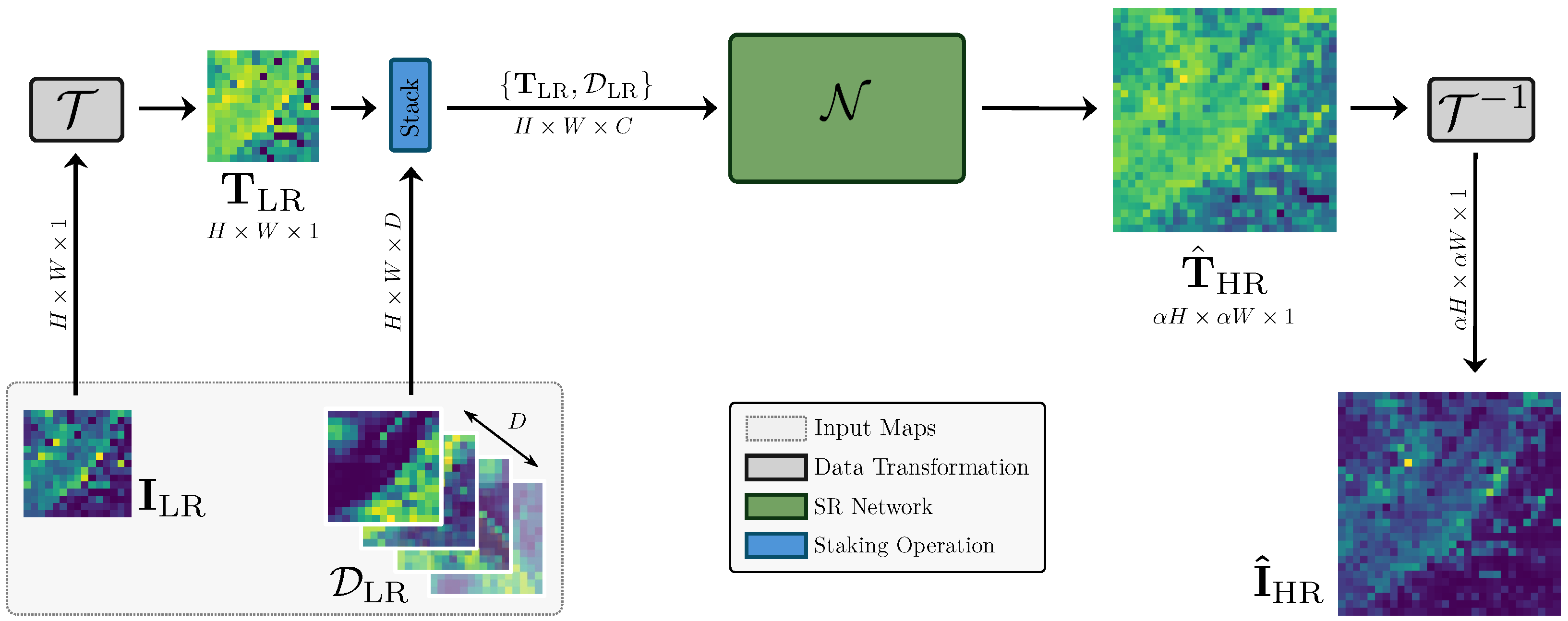
4.1. Leveraging Land Cover Priors for Isoprene Emission Super-Resolution
4.1.1. Isoprene Data Transformation
4.1.2. Super-Resolution Neural Networks
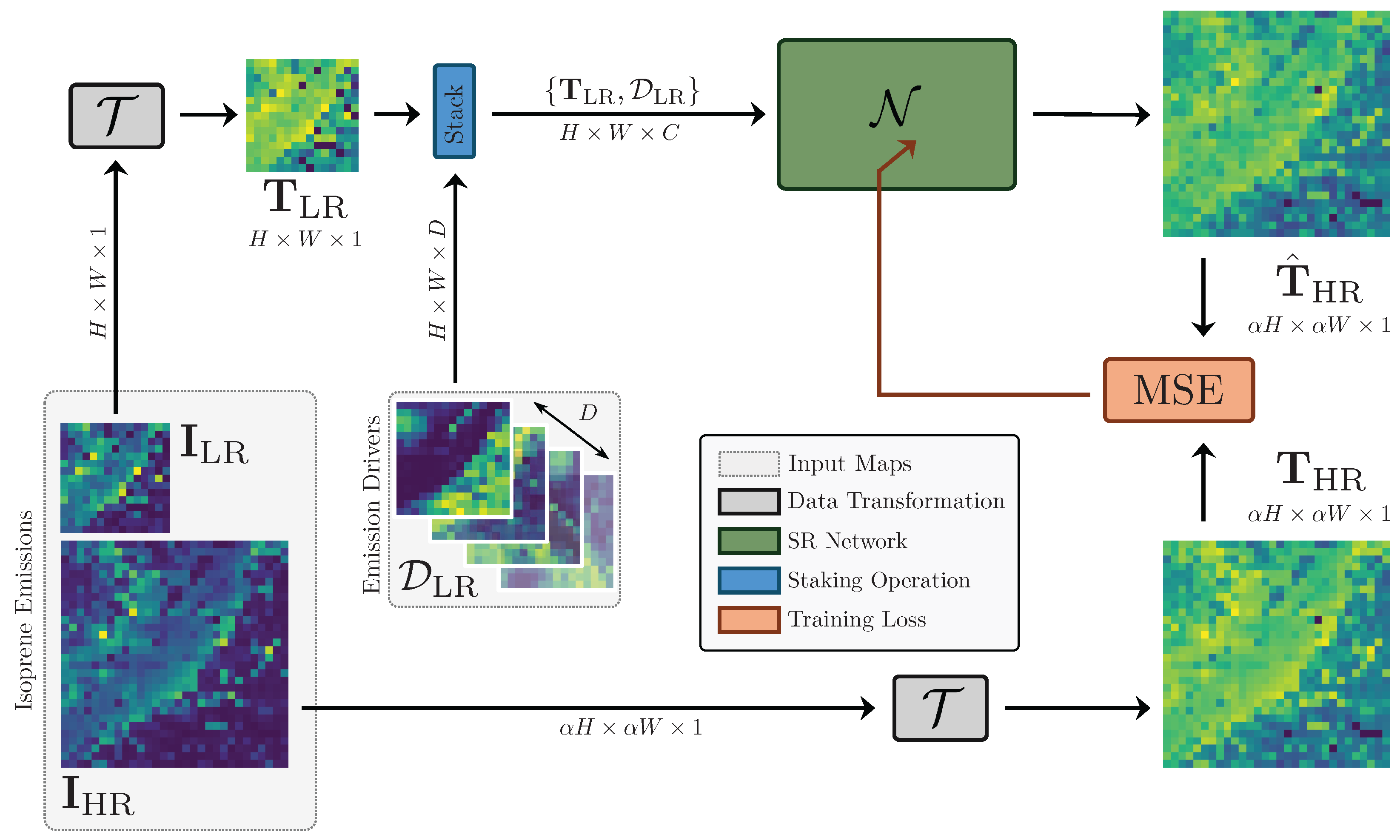
4.2. Training Pipeline
5. Experimental Dataset
5.1. Study Area
5.2. Pre-Processing Workflow
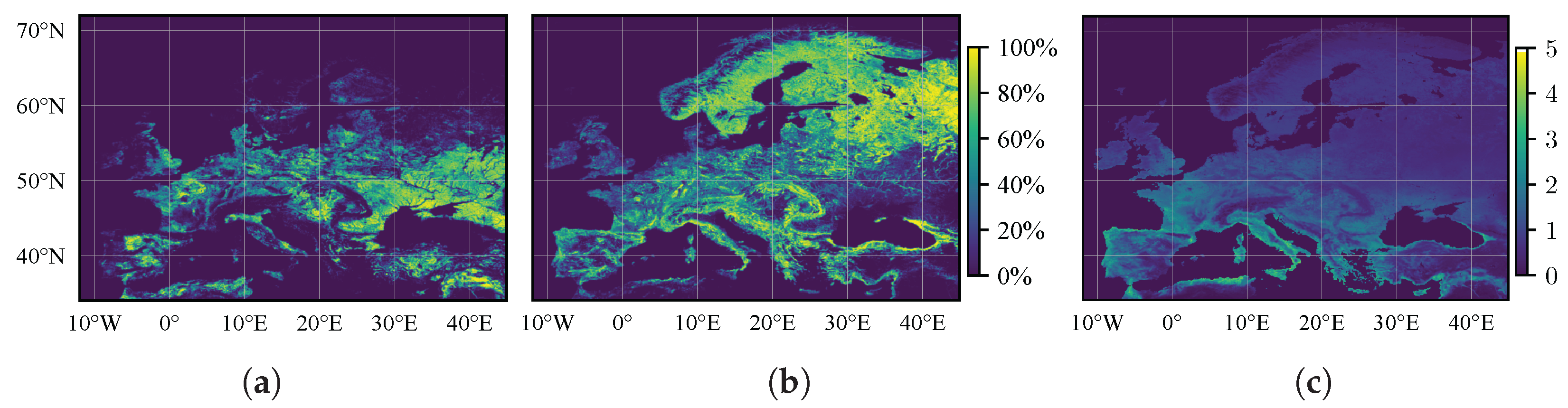
5.2.1. Land Cover Maps
5.2.2. Leaf Area Index Maps
5.2.3. Climate Class Maps
5.3. Patch Extraction
5.4. Climate-Specific Folding
5.5. Experimental Scenarios
- Standard scenario, where training and evaluation data are coherent in terms of climate zones and geographical areas.
- Unseen spatial areas scenario, in which we evaluate our method over geographical areas never seen in the training phase.
- Unseen climate zone scenario, where we test over climate zones never seen in the training phase.
5.5.1. Standard Scenario
5.5.2. Unseen Spatial Areas Scenario
5.5.3. Unseen Climate Zones Scenario
6. Experimental Setup
6.1. Training Settings
6.2. Evaluation Metrics
7. Results
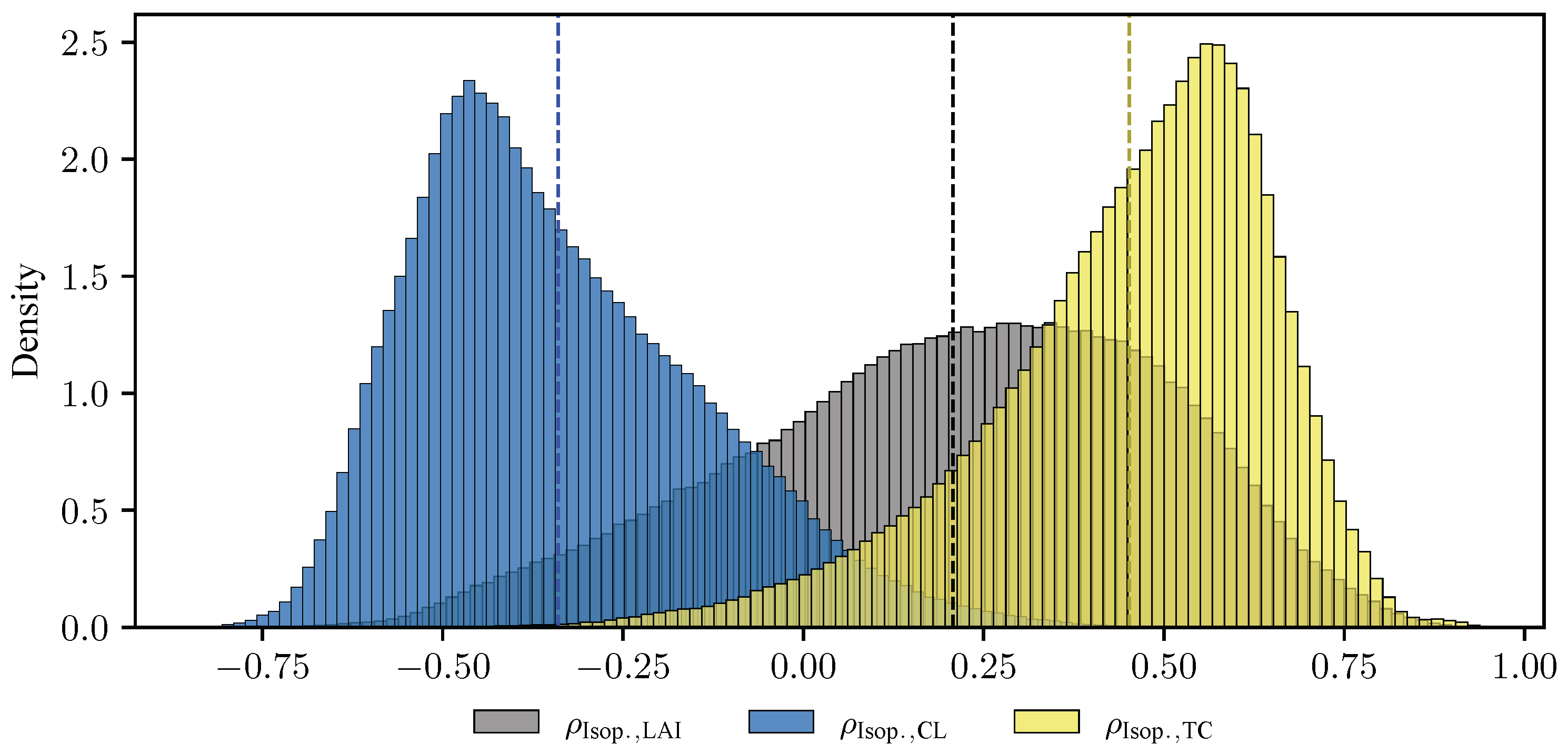
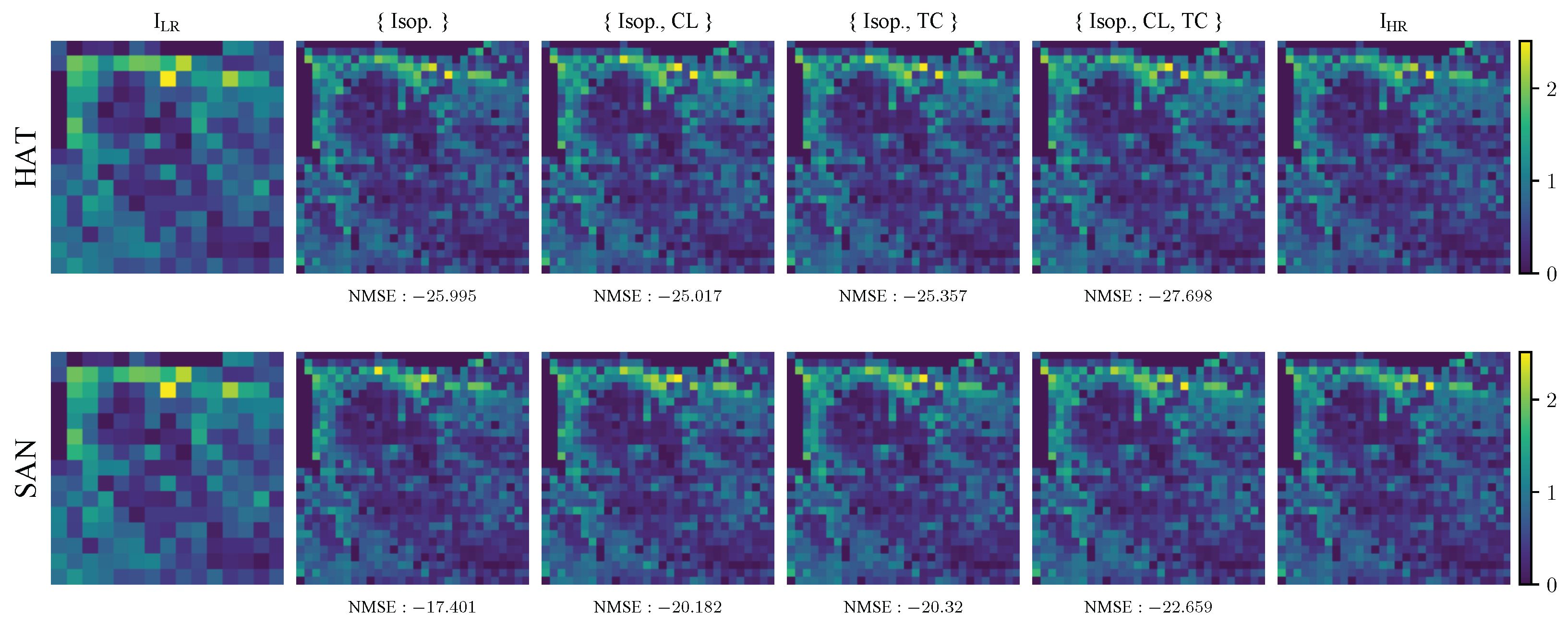
7.1. Selecting the Emission Drivers
7.2. Leveraging Semantic Priors
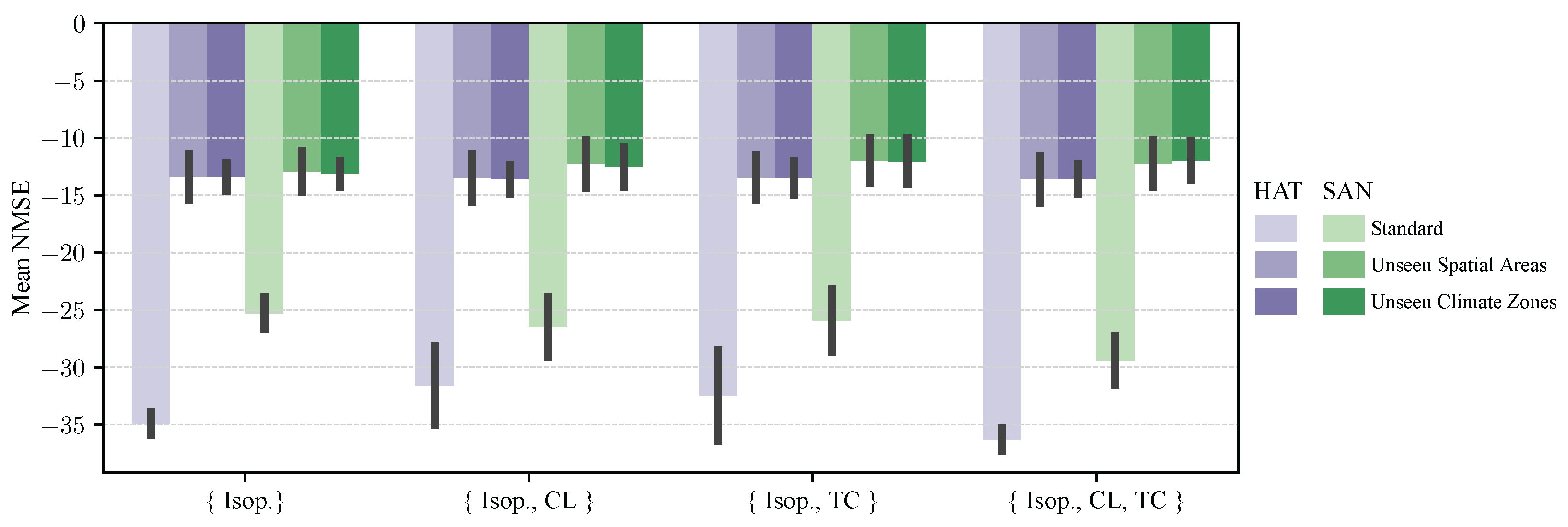
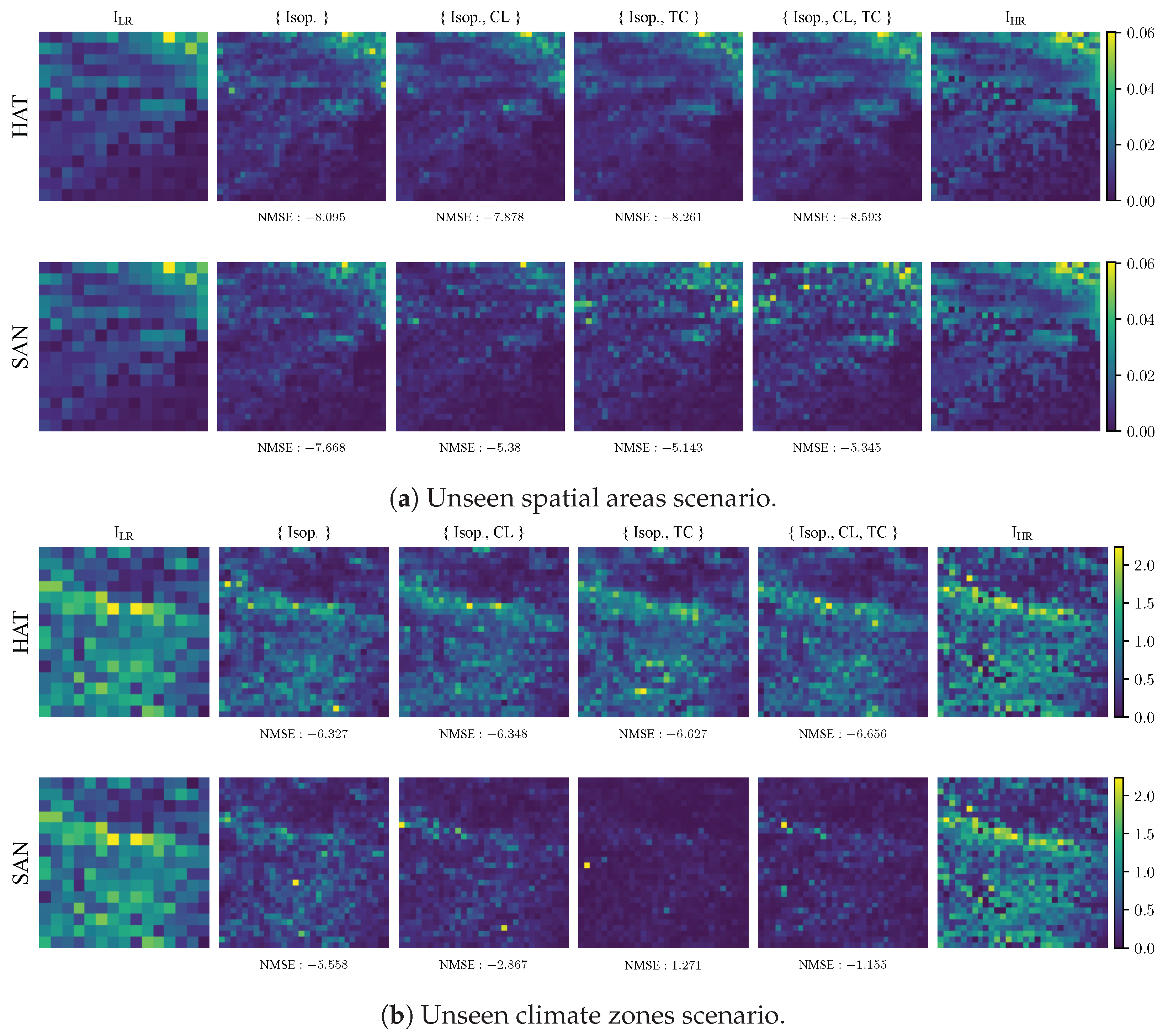
7.3. Generalization Studies
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, C.H. (Ed.) Signal and Image Processing for Remote Sensing, 3rd ed.; Signal and Image Processing of Earth Observations; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Tuia, D.; Schindler, K.; Demir, B.; Zhu, X.X.; Kochupillai, M.; Džeroski, S.; van Rijn, J.N.; Hoos, H.H.; Del Frate, F.; Datcu, M.; et al. Artificial Intelligence to Advance Earth Observation: A review of models, recent trends, and pathways forward. IEEE Geosci. Remote Sens. Mag. 2024, 2–25. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Sdraka, M.; Papoutsis, I.; Psomas, B.; Vlachos, K.; Ioannidis, K.; Karantzalos, K.; Gialampoukidis, I.; Vrochidis, S. Deep Learning for Downscaling Remote Sensing Images: Fusion and super-resolution. IEEE Geosci. Remote Sens. Mag. 2022, 10, 202–255. [Google Scholar] [CrossRef]
- Siddique, M.A.; Naseer, E.; Usama, M.; Basit, A. Estimation of Surface-Level NO2 Using Satellite Remote Sensing and Machine Learning: A review. IEEE Geosci. Remote Sens. Mag. 2024, 12, 8–34. [Google Scholar] [CrossRef]
- Hobeichi, S.; Nishant, N.; Shao, Y.; Abramowitz, G.; Pitman, A.; Sherwood, S.; Bishop, C.; Green, S. Using Machine Learning to Cut the Cost of Dynamical Downscaling. Earth’s Future 2023, 11, e2022EF003291. [Google Scholar] [CrossRef]
- Rampal, N.; Hobeichi, S.; Gibson, P.B.; Baño-Medina, J.; Abramowitz, G.; Beucler, T.; González-Abad, J.; Chapman, W.; Harder, P.; Gutiérrez, J.M. Enhancing Regional Climate Downscaling through Advances in Machine Learning. Artif. Intell. Earth Syst. 2024, 3, 230066. [Google Scholar] [CrossRef]
- Sokhi, R.S.; Moussiopoulos, N.; Baklanov, A.; Bartzis, J.; Coll, I.; Finardi, S.; Friedrich, R.; Geels, C.; Grönholm, T.; Halenka, T.; et al. Advances in air quality research—Current and emerging challenges. Atmos. Chem. Phys. 2022, 22, 4615–4703. [Google Scholar] [CrossRef]
- Park, S.; Singh, K.; Nellikkattil, A.; Zeller, E.; Mai, T.; Cha, M. Downscaling Earth System Models with Deep Learning. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 3733–3742. [Google Scholar]
- Baño Medina, J.; Manzanas, R.; Cimadevilla, E.; Fernández, J.; González-Abad, J.; Cofiño, A.S.; Gutiérrez, J.M. Downscaling multi-model climate projection ensembles with deep learning (DeepESD): Contribution to CORDEX EUR-44. Geosci. Model Dev. 2022, 15, 6747–6758. [Google Scholar] [CrossRef]
- Baño-Medina, J.; Iturbide, M.; Fernández, J.; Gutiérrez, J.M. Transferability and Explainability of Deep Learning Emulators for Regional Climate Model Projections: Perspectives for Future Applications. Artif. Intell. Earth Syst. 2024, 3, e230099. [Google Scholar] [CrossRef]
- Chiang, C.H.; Huang, Z.H.; Liu, L.; Liang, H.C.; Wang, Y.C.; Tseng, W.L.; Wang, C.; Chen, C.T.; Wang, K.C. Climate Downscaling: A Deep-Learning Based Super-resolution Model of Precipitation Data with Attention Block and Skip Connections; National Taiwan Normal University: Taiwan, China, 2023. [Google Scholar]
- Wang, M.; Franklin, M.; Li, L. Generating Fine-Scale Aerosol Data through Downscaling with an Artificial Neural Network Enhanced with Transfer Learning. Atmosphere 2022, 13, 255. [Google Scholar] [CrossRef]
- Yadav, N.; Sorek-Hamer, M.; Von Pohle, M.; Asanjan, A.A.; Sahasrabhojanee, A.; Suel, E.; Arku, R.E.; Lingenfelter, V.; Brauer, M.; Ezzati, M.; et al. Using deep transfer learning and satellite imagery to estimate urban air quality in data-poor regions. Environ. Pollut. 2024, 342, 122914. [Google Scholar] [CrossRef] [PubMed]
- Geiss, A.; Silva, S.J.; Hardin, J.C. Downscaling atmospheric chemistry simulations with physically consistent deep learning. Geosci. Model Dev. 2022, 15, 6677–6694. [Google Scholar] [CrossRef]
- Liu, Y.; Qiao, Y.; Hao, Y.; Wang, F.; Rashid, S.F. Single Image Super Resolution Techniques Based on Deep Learning: Status, Applications and Future Directions. J. Image Graph. 2021, 9, 74–86. [Google Scholar] [CrossRef]
- Eyring, V.; Collins, W.D.; Gentine, P.; Barnes, E.A.; Barreiro, M.; Beucler, T.; Bocquet, M.; Bretherton, C.S.; Christensen, H.M.; Dagon, K.; et al. Pushing the frontiers in climate modelling and analysis with machine learning. Nat. Clim. Change 2024, 14, 916–928. [Google Scholar] [CrossRef]
- Materia, S.; García, L.P.; van Straaten, C.; O, S.; Mamalakis, A.; Cavicchia, L.; Coumou, D.; de Luca, P.; Kretschmer, M.; Donat, M. Artificial intelligence for climate prediction of extremes: State of the art, challenges, and future perspectives. WIREs Clim. Change 2024, 15, e914. [Google Scholar] [CrossRef]
- Do, T.N.N.; Sudo, K.; Ito, A.; Emmons, L.; Naik, V.; Tsigaridis, K.; Seland, Ø.; Folberth, G.A.; Kelley, D.I. Historical Trends and Controlling Factors of Isoprene Emissions in CMIP6 Earth System Models. EGUsphere 2024, 2024, 1–49. [Google Scholar] [CrossRef]
- Weber, J.; Archer-Nicholls, S.; Abraham, N.L.; Shin, Y.M.; Griffiths, P.; Grosvenor, D.P.; Scott, C.E.; Archibald, A.T. Chemistry-driven changes strongly influence climate forcing from vegetation emissions. Nat. Commun. 2022, 13, 7202. [Google Scholar] [CrossRef] [PubMed]
- Tani, A.; Mochizuki, T. Review: Exchanges of volatile organic compounds between terrestrial ecosystems and the atmosphere. J. Agric. Meteorol. 2021, 77, 66–80. [Google Scholar] [CrossRef]
- Laothawornkitkul, J.; Taylor, J.E.; Paul, N.D.; Hewitt, C.N. Biogenic volatile organic compounds in the Earth system. New Phytol. 2009, 183, 27–51. [Google Scholar] [CrossRef]
- Mircea, M.; Borge, R.; Finardi, S.; Briganti, G.; Russo, F.; de la Paz, D.; D’Isidoro, M.; Cremona, G.; Villani, M.G.; Cappelletti, A.; et al. The Role of Vegetation on Urban Atmosphere of Three European Cities. Part 2: Evaluation of Vegetation Impact on Air Pollutant Concentrations and Depositions. Forests 2023, 14, 1255. [Google Scholar] [CrossRef]
- Bauwens, M.; Stavrakou, T.; Müller, J.F.; Van Schaeybroeck, B.; De Cruz, L.; De Troch, R.; Giot, O.; Hamdi, R.; Termonia, P.; Laffineur, Q.; et al. Recent past (1979–2014) and future (2070–2099) isoprene fluxes over Europe simulated with the MEGAN–MOHYCAN model. Biogeosciences 2018, 15, 3673–3690. [Google Scholar] [CrossRef]
- Ashworth, K.; Boissard, C.; Folberth, G.; Lathière, J.; Schurgers, G. Global Modelling of Volatile Organic Compound Emissions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 451–487. [Google Scholar]
- Cai, M.; An, C.; Guy, C. A scientometric analysis and review of biogenic volatile organic compound emissions: Research hotspots, new frontiers, and environmental implications. Renew. Sustain. Energy Rev. 2021, 149, 111317. [Google Scholar] [CrossRef]
- Guenther, A.; Hewitt, C.N.; Erickson, D.; Fall, R.; Geron, C.; Graedel, T.; Harley, P.; Klinger, L.; Lerdau, M.; Mckay, W.A.; et al. A global model of natural volatile organic compound emissions. J. Geophys. Res. 1995, 100, 8873. [Google Scholar] [CrossRef]
- Lai, C.Y.; Hassanzadeh, P.; Sheshadri, A.; Sonnewald, M.; Ferrari, R.; Balaji, V. Machine learning for climate physics and simulations. arXiv 2024, arXiv:2404.13227. [Google Scholar] [CrossRef]
- Giganti, A.; Mandelli, S.; Bestagini, P.; Marcon, M.; Tubaro, S. Multi-BVOC Super-Resolution Exploiting Compounds Inter-Connection. In Proceedings of the European Signal Processing Conference (EUSIPCO), Helsinki, Finland, 4–8 September 2023; pp. 1315–1319. [Google Scholar]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. DeepSD: Generating High Resolution Climate Change Projections through Single Image Super-Resolution. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar]
- Lloyd, D.T.; Abela, A.; Farrugia, R.A.; Galea, A.; Valentino, G. Optically Enhanced Super-Resolution of Sea Surface Temperature Using Deep Learning. IEEE Trans. Geosci. Remote Sens. (TGRS) 2022, 60, 5000814. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Foster, I.; Chang, W.; Kettimuthu, R.; Kotamarthi, V.R. Fast and accurate learned multiresolution dynamical downscaling for precipitation. Geosci. Model Dev. 2021, 14, 6355–6372. [Google Scholar] [CrossRef]
- Wu, X.; Cao, Z.H.; Huang, T.Z.; Deng, L.J.; Chanussot, J.; Vivone, G. Fully-Connected Transformer for Multi-Source Image Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 2071–2088. [Google Scholar] [CrossRef]
- Guenther, A.; Jiang, X.; Shah, T.; Huang, L.; Kemball-Cook, S.; Yarwood, G. Model of Emissions of Gases and Aerosol from Nature Version 3 (MEGAN3) for Estimating Biogenic Emissions. In Air Pollution Modeling and Its Application XXVI, Proceedings of the ITM, Ottawa, ON, Canada, 14–18 May 2018; Mensink, C., Gong, W., Hakami, A., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Silibello, C.; Finardi, S.; Pepe, N.; Baraldi, R.; Ciccioli, P.; Mircea, M.; Ciccioli, P. Modelling of Biogenic Volatile Organic Compounds Emissions Using a Detailed Vegetation Inventory Over a Southern Italy Region. In Air Pollution Modeling and Its Application XXVIII, Proceedings of the ITM, Virtual, 18–20 February 2021; Mensink, C., Jorba, O., Eds.; Springer: Cham, Switzerland, 2021; pp. 279–285. [Google Scholar]
- Ramacher, M.O.P.; Kakouri, A.; Speyer, O.; Feldner, J.; Karl, M.; Timmermans, R.; Denier van der Gon, H.; Kuenen, J.; Gerasopoulos, E.; Athanasopoulou, E. The UrbEm Hybrid Method to Derive High-Resolution Emissions for City-Scale Air Quality Modeling. Atmosphere 2021, 12, 1404. [Google Scholar] [CrossRef]
- Marongiu, A.; Distefano, G.G.; Moretti, M.; Petrosino, F.; Fossati, G.; Collalto, A.G.; Angelino, E. Machine Learning Approach for Local Atmospheric Emission Predictions. Air 2024, 2, 380–401. [Google Scholar] [CrossRef]
- Mu, Q.; Denby, B.R.; Wærsted, E.G.; Fagerli, H. Downscaling of air pollutants in Europe using uEMEP_v6. Geosci. Model Dev. 2022, 15, 449–465. [Google Scholar] [CrossRef]
- Nuterman, R.; Mahura, A.; Baklanov, A.; Amstrup, B.; Zakey, A. Downscaling system for modeling of atmospheric composition on regional, urban and street scales. Atmos. Chem. Phys. 2021, 21, 11099–11112. [Google Scholar] [CrossRef]
- Liu, N.; Ma, R.; Wang, Y.; Zhang, L. Inferring Fine-Grained Air Pollution Map via a Spatiotemporal Super-Resolution Scheme. In Proceedings of the ACM International Joint Conference on Pervasive and Ubiquitous Computing, London, UK, 9–13 September 2019; ACM Digital Library: New York, NY, USA, 2019; pp. 498–504. [Google Scholar]
- Quesada-Chacón, D.; Baño-Medina, J.; Barfus, K.; Bernhofer, C. Downscaling CORDEX Through Deep Learning to Daily 1 km Multivariate Ensemble in Complex Terrain. Earth’s Future 2023, 11, e2023EF003531. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Franklin, M.; Yin, Q.; Wu, J.; Camps-Valls, G.; Zhu, Z.; Wang, C.; Ge, Y.; Reichstein, M. Improving air quality assessment using physics-inspired deep graph learning. npj Clim. Atmos. Sci. 2023, 6, 152. [Google Scholar] [CrossRef]
- Brecht, R.; Bakels, L.; Bihlo, A.; Stohl, A. Improving trajectory calculations by FLEXPART 10.4+ using single-image super-resolution. Geosci. Model Dev. 2023, 16, 2181–2192. [Google Scholar] [CrossRef]
- Passarella, L.S.; Mahajan, S.; Pal, A.; Norman, M.R. Reconstructing High Resolution ESM Data Through a Novel Fast Super Resolution Convolutional Neural Network (FSRCNN). Geophys. Res. Lett. 2022, 49, e2021GL097571. [Google Scholar] [CrossRef]
- Baño Medina, J.; Manzanas, R.; Gutiérrez, J.M. Configuration and intercomparison of deep learning neural models for statistical downscaling. Geosci. Model Dev. 2020, 13, 2109–2124. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II; West, G.; Stull, R. Deep-Learning-Based Gridded Downscaling of Surface Meteorological Variables in Complex Terrain. Part II: Daily Precipitation. J. Appl. Meteorol. Climatol. 2020, 59, 2075–2092. [Google Scholar] [CrossRef]
- Nguyen, B.M.; Tian, G.; Vo, M.T.; Michel, A.; Corpetti, T.; Granero-Belinchon, C. Convolutional Neural Network Modelling for MODIS Land Surface Temperature Super-Resolution. In Proceedings of the European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 1806–1810. [Google Scholar]
- Yasuda, Y.; Onishi, R.; Hirokawa, Y.; Kolomenskiy, D.; Sugiyama, D. Super-resolution of near-surface temperature utilizing physical quantities for real-time prediction of urban micrometeorology. Build. Environ. 2022, 209, 108597. [Google Scholar] [CrossRef]
- Stengel, K.; Glaws, A.; Hettinger, D.; King, R.N. Adversarial super-resolution of climatological wind and solar data. Proc. Natl. Acad. Sci. USA 2020, 117, 16805–16815. [Google Scholar] [CrossRef]
- Giganti, A.; Mandelli, S.; Bestagini, P.; Marcon, M.; Tubaro, S. Super-Resolution of BVOC Maps by Adapting Deep Learning Methods. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023; pp. 1650–1654. [Google Scholar]
- An, T.; Zhang, X.; Huo, C.; Xue, B.; Wang, L.; Pan, C. TR-MISR: Multiimage Super-Resolution Based on Feature Fusion With Transformers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1373–1388. [Google Scholar] [CrossRef]
- Ibrahim, M.; Benavente, R.; Lumbreras, F.; Ponsa, D. 3DRRDB: Super Resolution of Multiple Remote Sensing Images using 3D Residual in Residual Dense Blocks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; IEEE: New York, NY, USA, 2022; Volume 6, pp. 322–331. [Google Scholar] [CrossRef]
- Aiello, E.; Agarla, M.; Valsesia, D.; Napoletano, P.; Bianchi, T.; Magli, E.; Schettini, R. Synthetic Data Pretraining for Hyperspectral Image Super-Resolution. IEEE Access 2024, 12, 65024–65031. [Google Scholar] [CrossRef]
- Miller, L.; Pelletier, C.; Webb, G.I. Deep Learning for Satellite Image Time-Series Analysis: A review. IEEE Geosci. Remote Sens. Mag. 2024, 12, 81–124. [Google Scholar] [CrossRef]
- Salvetti, F.; Mazzia, V.; Khaliq, A.; Chiaberge, M. Multi-Image Super Resolution of Remotely Sensed Images Using Residual Attention Deep Neural Networks. Remote Sens. 2020, 12, 2207. [Google Scholar] [CrossRef]
- Razzak, M.T.; Mateo-García, G.; Lecuyer, G.; Gómez-Chova, L.; Gal, Y.; Kalaitzis, F. Multi-spectral multi-image super-resolution of Sentinel-2 with radiometric consistency losses and its effect on building delineation. ISPRS J. Photogramm. Remote Sens. 2023, 195, 1–13. [Google Scholar] [CrossRef]
- Ping, B.; Su, F.; Han, X.; Meng, Y. Applications of Deep Learning-Based Super-Resolution for Sea Surface Temperature Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. (JSTAR) 2021, 14, 887–896. [Google Scholar] [CrossRef]
- Izumi, T.; Amagasaki, M.; Ishida, K.; Kiyama, M. Super-resolution of sea surface temperature with CNN and GAN-based methods. J. Water Clim. Change 2022, 13, 1673–1683. [Google Scholar] [CrossRef]
- Tian, T.; Cheng, L.; Wang, G.; Abraham, J.; Wei, W.; Ren, S.; Zhu, J.; Song, J.; Leng, H. Reconstructing ocean subsurface salinity at high resolution using a machine learning approach. Earth Syst. Sci. Data 2022, 14, 5037–5060. [Google Scholar] [CrossRef]
- Damiani, A.; Ishizaki, N.N.; Sasaki, H.; Feron, S.; Cordero, R.R. Exploring super-resolution spatial downscaling of several meteorological variables and potential applications for photovoltaic power. Sci. Rep. 2024, 14, 7254. [Google Scholar] [CrossRef]
- Oyama, N.; Ishizaki, N.N.; Koide, S.; Yoshida, H. Deep generative model super-resolves spatially correlated multiregional climate data. Sci. Rep. 2023, 13, 5992. [Google Scholar] [CrossRef]
- Kumar, B.; Atey, K.; Singh, B.B.; Chattopadhyay, R.; Acharya, N.; Singh, M.; Nanjundiah, R.S.; Rao, S.A. On the modern deep learning approaches for precipitation downscaling. Earth Sci. Inform. 2023, 16, 1459–1472. [Google Scholar] [CrossRef]
- Mardani, M.; Brenowitz, N.; Cohen, Y.; Pathak, J.; Chen, C.Y.; Liu, C.C.; Vahdat, A.; Nabian, M.A.; Ge, T.; Subramaniam, A.; et al. Residual Corrective Diffusion Modeling for Km-scale Atmospheric Downscaling. arXiv 2024, arXiv:2309.15214. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the NIPS ’20—34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Giganti, A.; Mandelli, S.; Bestagini, P.; Marcon, M.; Tubaro, S. Super-Resolution of Bvoc Emission Maps Via Domain Adaptation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Pasadena, CA, USA, 16–21 July 2023; pp. 738–741. [Google Scholar]
- Giganti, A.; Mandelli, S.; Bestagini, P.; Tubaro, S. Learn from Simulations, Adapt to Observations: Super-Resolution of Isoprene Emissions via Unpaired Domain Adaptation. Remote Sens. 2024, 16, 3963. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- BIRA-IASB. Top-Down Isoprene Emissions Inventory; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- SEEDS. SEEDS Summary of Achievements; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- Müller, J.F.; Stavrakou, T.; Peeters, J. Chemistry and deposition in the Model of Atmospheric composition at Global and Regional scales using Inversion Techniques for Trace gas Emissions (MAGRITTE v1.1)—Part 1: Chemical mechanism. Geosci. Model Dev. 2019, 12, 2307–2356. [Google Scholar] [CrossRef]
- CNRM. Leaf Area Index Inventory; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; Daems, D.; De Keersmaecker, W.; Brockmann, C.; Kirches, G.; Wevers, J.; Cartus, O.; Santoro, M.; Fritz, S.; et al. ESA WorldCover 10 m 2021 v200; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- Ciccioli, P.; Silibello, C.; Finardi, S.; Pepe, N.; Ciccioli, P.; Rapparini, F.; Neri, L.; Fares, S.; Brilli, F.; Mircea, M.; et al. The potential impact of biogenic volatile organic compounds (BVOCs) from terrestrial vegetation on a Mediterranean area using two different emission models. Agric. For. Meteorol. 2023, 328, 109255. [Google Scholar] [CrossRef]
- Opacka, B.; Müller, J.F.; Stavrakou, T.; Bauwens, M.; Sindelarova, K.; Markova, J.; Guenther, A.B. Global and regional impacts of land cover changes on isoprene emissions derived from spaceborne data and the MEGAN model. Atmos. Chem. Phys. 2021, 21, 8413–8436. [Google Scholar] [CrossRef]
- Beck, H.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Lutsko, N.J.; Dufour, A.; Zeng, Z.; Jiang, X.; van Dijk, A.I.; Miralles, D.G. High-resolution (1 km) Köppen-Geiger maps for 1901–2099 based on constrained CMIP6 projections. Sci. Data 2023, 10, 724. [Google Scholar] [CrossRef]
- Peñuelas, J.; Staudt, M. BVOCs and global change. Trends Plant Sci. 2010, 15, 133–144. [Google Scholar] [CrossRef]
- Stavrakou, T.; Müller, J.F.; Bauwens, M.; De Smedt, I.; Van Roozendael, M.; Guenther, A.; Wild, M.; Xia, X. IIsoprene emissions over Asia 1979–2012: Impact of climate and land-use changes. Atmos. Chem. Phys. 2014, 14, 4587–4605. [Google Scholar] [CrossRef]
- Zhang, S.; Lyu, Y.; Yang, X.; Yuan, L.; Wang, Y.; Wang, L.; Liang, Y.; Qiao, Y.; Wang, S. Modeling Biogenic Volatile Organic Compounds Emissions and Subsequent Impacts on Ozone Air Quality in the Sichuan Basin, Southwestern China. Front. Ecol. Evol. 2022, 10, 924944. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Wu, C.; Lin, G. Regional to global distributions, trends, and drivers of biogenic volatile organic compound emission from 2001 to 2020. Atmos. Chem. Phys. 2024, 24, 3309–3328. [Google Scholar] [CrossRef]
- Dramsch, J.S.; Kuglitsch, M.M.; Fernández-Torres, M.Á.; Toreti, A.; Albayrak, R.A.; Nava, L.; Ghaffarian, S.; Cheng, X.; Ma, J.; Samek, W.; et al. Explainability can foster trust in artificial intelligence in geoscience. Nat. Geosci. 2025, 18, 112–114. [Google Scholar] [CrossRef]
- Sindelarova, K.; Markova, J.; Simpson, D.; Huszar, P.; Karlicky, J.; Darras, S.; Granier, C. High-resolution biogenic global emission inventory for the time period 2000–2019 for air quality modelling. Earth Syst. Sci. Data 2022, 14, 251–270. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Peterson, R.A.; Cavanaugh, J.E. Ordered quantile normalization: A semiparametric transformation built for the cross-validation era. J. Appl. Stat. 2020, 47, 2312–2327. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhou, J.; Qiao, Y.; Dong, C. Activating More Pixels in Image Super-Resolution Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 22367–22377. [Google Scholar]
- Bishop, C.M.; Bishop, H. Deep Learning: Foundations and Concepts; Springer International Publishing: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-Order Attention Network for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Carbone, A.; Restaino, R.; Vivone, G.; Chanussot, J. Model-Based Super-Resolution for Sentinel-5P Data. IEEE Trans. Geosci. Remote Sens. (TGRS) 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Hoyer, S.; Hamman, J. xarray: N-D labeled arrays and datasets in Python. J. Open Res. Softw. 2017. [Google Scholar] [CrossRef]
- Li, X.; Dong, W.; Wu, J.; Li, L.; Shi, G. Superresolution Image Reconstruction: Selective milestones and open problems. IEEE Signal Process. Mag. 2023, 40, 54–66. [Google Scholar] [CrossRef]
- Donini, E.; Bruzzone, L.; Bovolo, F. Super-Resolution of Radargrams With a Generative Deep Learning Model. IEEE Trans. Geosci. Remote Sens. (TGRS) 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. (TIP) 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Alves, E.G.; Tóta, J.; Turnipseed, A.; Guenther, A.B.; Vega Bustillos, J.O.W.; Santana, R.A.; Cirino, G.G.; Tavares, J.V.; Lopes, A.P.; Nelson, B.W.; et al. Leaf phenology as one important driver of seasonal changes in isoprene emissions in central Amazonia. Biogeosciences 2018, 15, 4019–4032. [Google Scholar] [CrossRef]
- NILU-CNRM. Bottom Up Isoprene Emissions (Assimilated Data); Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]

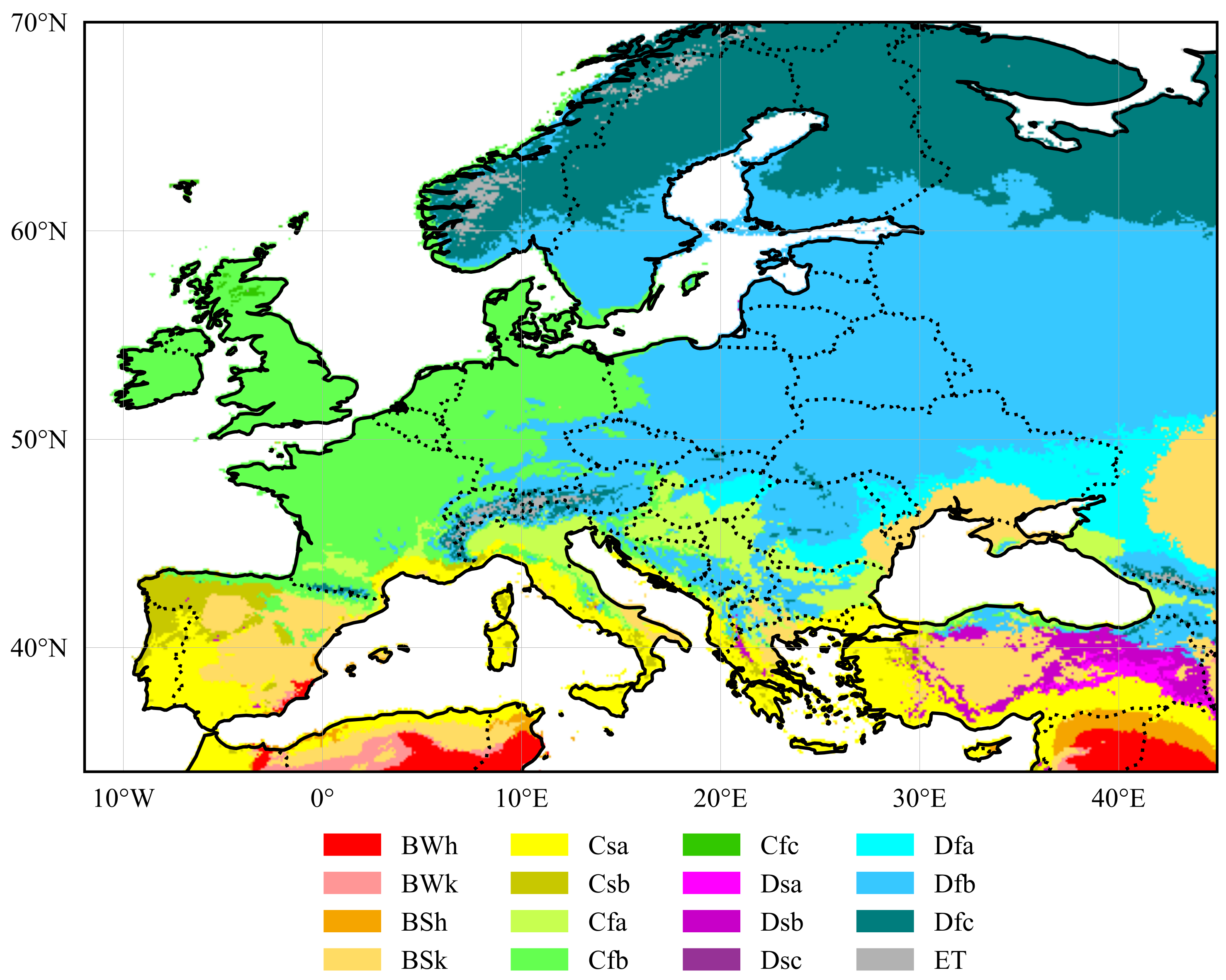
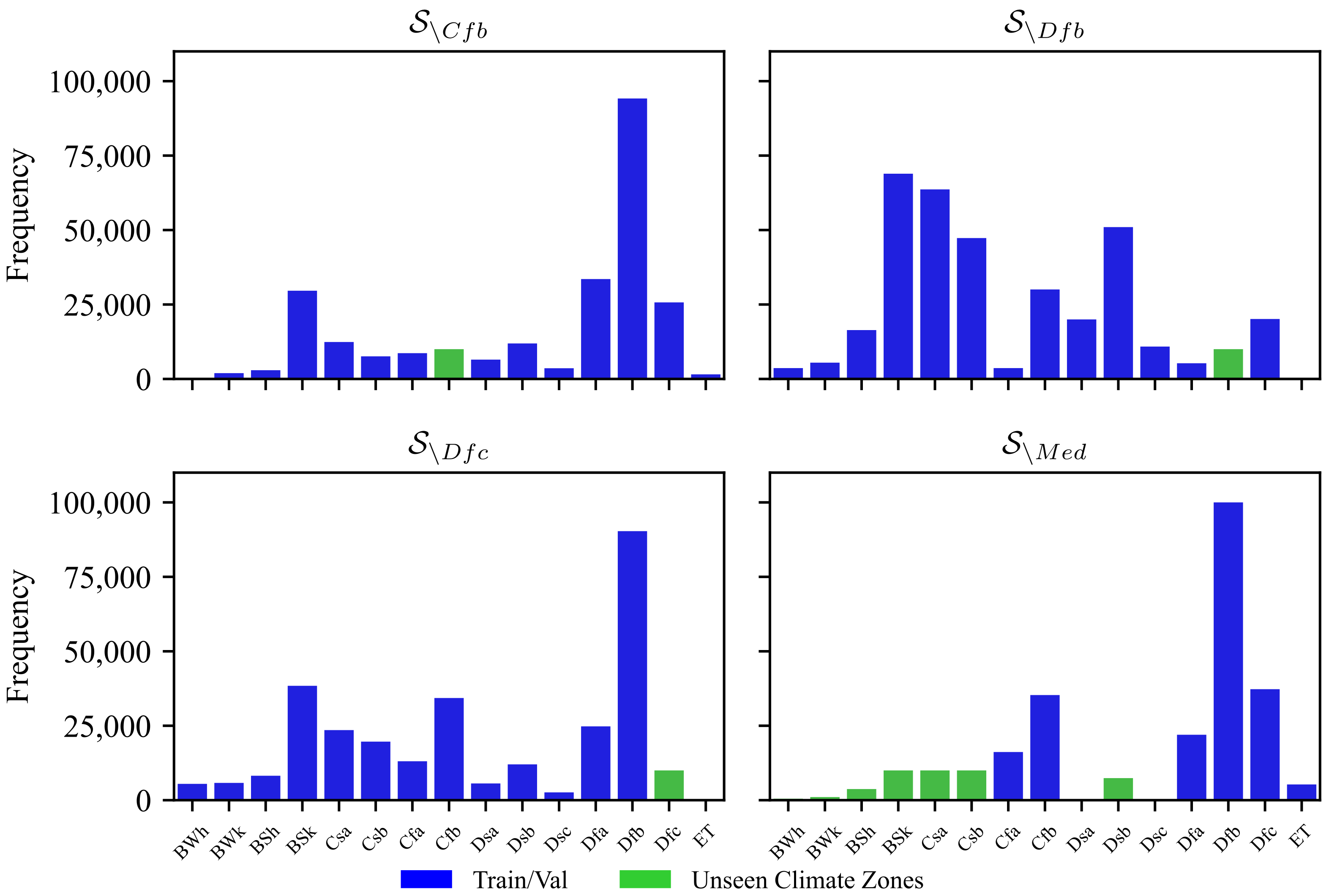





| Climate Class | Description |
|---|---|
| BWh | Arid, desert, hot |
| BWk | Arid, desert, cold |
| BSh | Arid, steppe, hot |
| BSk | Arid, steppe, cold |
| Csa | Temperate, dry summer, hot summer |
| Csb | Temperate, dry summer, warm summer |
| Cfa | Temperate, no dry season, hot summer |
| Cfb | Temperate, no dry season, warm summer |
| Cfc | Temperate, no dry season, cold summer |
| Dsa | Cold, dry summer, hot summer |
| Dsb | Cold, dry summer, warm summer |
| Dsc | Cold, dry summer, cold summer |
| Dfa | Cold, no dry season, hot summer |
| Dfb | Cold, no dry season, warm summer |
| Dfc | Cold, no dry season, cold summer |
| ET | Polar, tundra |
| Transformed Data Domain (Avg, Std) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Data Fold | Configuration | NMSE ↓ | SSIM ↑ | PSNR ↑ | MaxAE ↓ | UIQI ↑ | SCC ↑ |
| HAT | −35.04, 6.42 | 0.98, 0.05 | 38.11, 5.02 | 0.04, 0.04 | 0.97, 0.09 | 0.98, 0.06 | ||
| −27.79, 5.71 | 0.94, 0.08 | 30.86, 4.29 | 0.10, 0.06 | 0.94, 0.11 | 0.94, 0.09 | |||
| −30.14, 6.02 | 0.96, 0.07 | 33.21, 4.61 | 0.07, 0.05 | 0.96, 0.10 | 0.96, 0.07 | |||
| −36.69, 6.48 | 0.99, 0.04 | 39.76, 5.05 | 0.04, 0.04 | 0.98, 0.09 | 0.99, 0.04 | |||
| −36.23, 7.04 | 0.98, 0.06 | 39.69, 5.55 | 0.03, 0.02 | 0.98, 0.10 | 0.98, 0.06 | |||
| −35.43, 6.93 | 0.98, 0.07 | 38.89, 5.37 | 0.04, 0.03 | 0.97, 0.11 | 0.98, 0.07 | |||
| −35.21, 6.63 | 0.98, 0.06 | 38.67, 5.11 | 0.04, 0.03 | 0.97, 0.10 | 0.98, 0.06 | |||
| −37.42, 7.22 | 0.99, 0.05 | 40.89, 5.58 | 0.03, 0.02 | 0.98, 0.10 | 0.99, 0.05 | |||
| −34.68, 5.80 | 0.99, 0.04 | 37.88, 4.45 | 0.04, 0.04 | 0.98, 0.08 | 0.98, 0.05 | |||
| −33.39, 5.79 | 0.98, 0.04 | 36.6, 4.43 | 0.05, 0.04 | 0.98, 0.08 | 0.98, 0.05 | |||
| −28.16, 5.42 | 0.95, 0.07 | 31.36, 4.03 | 0.08, 0.06 | 0.95, 0.09 | 0.95, 0.07 | |||
| −36.12, 5.89 | 0.99, 0.03 | 39.32, 4.55 | 0.04, 0.03 | 0.98, 0.08 | 0.99, 0.04 | |||
| −33.81, 6.17 | 0.98, 0.04 | 36.84, 4.82 | 0.05, 0.04 | 0.97, 0.08 | 0.98, 0.05 | |||
| −29.85, 5.92 | 0.96, 0.06 | 32.89, 4.55 | 0.07, 0.05 | 0.96, 0.09 | 0.96, 0.07 | |||
| −36.28, 6.13 | 0.99, 0.03 | 39.31, 4.80 | 0.04, 0.03 | 0.98, 0.08 | 0.99, 0.03 | |||
| −35.10, 6.22 | 0.99, 0.04 | 38.14, 4.88 | 0.04, 0.04 | 0.98, 0.08 | 0.98, 0.04 | |||
| SAN | −24.93, 4.90 | 0.90, 0.11 | 28.00, 3.67 | 0.13, 0.09 | 0.89, 0.13 | 0.88, 0.13 | ||
| −25.80, 5.56 | 0.91, 0.11 | 28.87, 4.30 | 0.12, 0.08 | 0.91, 0.12 | 0.90, 0.11 | |||
| −24.52, 5.42 | 0.90, 0.11 | 27.59, 4.12 | 0.14, 0.10 | 0.90, 0.13 | 0.89, 0.11 | |||
| −28.07, 6.17 | 0.94, 0.09 | 31.14, 4.85 | 0.09, 0.06 | 0.94, 0.11 | 0.94, 0.09 | |||
| −26.84, 5.00 | 0.94, 0.10 | 30.30, 3.73 | 0.10, 0.08 | 0.94, 0.12 | 0.93, 0.12 | |||
| −29.99, 5.89 | 0.96, 0.09 | 33.45, 4.62 | 0.08, 0.07 | 0.96, 0.11 | 0.96, 0.09 | |||
| −29.96, 5.88 | 0.96, 0.09 | 33.42, 4.55 | 0.07, 0.07 | 0.96, 0.11 | 0.96, 0.08 | |||
| −32.13, 6.00 | 0.97, 0.07 | 35.59, 4.60 | 0.06, 0.06 | 0.97, 0.1 | 0.97, 0.07 | |||
| −23.62, 4.39 | 0.89, 0.10 | 26.83, 3.18 | 0.17, 0.12 | 0.89, 0.13 | 0.87, 0.13 | |||
| −23.71, 5.04 | 0.89, 0.11 | 26.92, 3.82 | 0.18, 0.12 | 0.90, 0.12 | 0.89, 0.11 | |||
| −25.37, 5.42 | 0.92, 0.10 | 28.57, 4.14 | 0.13, 0.09 | 0.92, 0.11 | 0.91, 0.1 | |||
| −30.01, 6.67 | 0.96, 0.08 | 33.21, 5.35 | 0.07, 0.06 | 0.95, 0.1 | 0.96, 0.07 | |||
| −25.76, 5.23 | 0.91, 0.10 | 28.79, 4.05 | 0.13, 0.09 | 0.91, 0.13 | 0.90, 0.13 | |||
| −26.33, 5.71 | 0.92, 0.10 | 29.37, 4.51 | 0.12, 0.09 | 0.92, 0.12 | 0.92, 0.11 | |||
| −23.81, 5.09 | 0.89, 0.11 | 26.84, 3.90 | 0.17, 0.11 | 0.90, 0.13 | 0.88, 0.11 | |||
| −27.44, 6.18 | 0.94, 0.10 | 30.48, 4.93 | 0.10, 0.07 | 0.93, 0.11 | 0.93, 0.09 | |||
| Isoprene Data Domain (Avg, Std) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Data Fold | Configuration | NMSE ↓ | SSIM ↑ | PSNR ↑ | MaxAE ↓ | UIQI ↑ | SCC ↑ |
| HAT | −17.35, 12.83 | 0.94, 0.15 | 29.85, 11.93 | 204.68, 555.71 | 0.70, 0.40 | 0.94, 0.11 | ||
| −9.17, 13.51 | 0.85, 0.21 | 21.67, 12.83 | 281.33, 643.93 | 0.62, 0.40 | 0.86, 0.14 | |||
| −11.83, 12.96 | 0.89, 0.19 | 24.33, 12.22 | 250.26, 610.56 | 0.66, 0.40 | 0.90, 0.12 | |||
| −19.42, 12.58 | 0.95, 0.14 | 31.92, 11.76 | 182.35, 526.54 | 0.71, 0.40 | 0.96, 0.10 | |||
| −17.80, 15.17 | 0.92, 0.18 | 30.03, 14.40 | 345.73, 706.11 | 0.84, 0.29 | 0.94, 0.13 | |||
| −17.07, 14.99 | 0.91, 0.18 | 29.30, 14.19 | 345.61, 706.91 | 0.83, 0.29 | 0.93, 0.14 | |||
| −16.80, 14.85 | 0.91, 0.18 | 29.03, 14.15 | 346.54, 707.77 | 0.83, 0.30 | 0.93, 0.13 | |||
| −19.47, 14.63 | 0.93, 0.15 | 31.70, 13.87 | 318.25, 679.18 | 0.85, 0.28 | 0.94, 0.13 | |||
| −16.93, 12.30 | 0.94, 0.15 | 29.82, 11.58 | 149.16, 386.15 | 0.70, 0.40 | 0.95, 0.10 | |||
| −15.47, 12.25 | 0.93, 0.17 | 28.36, 11.59 | 154.12, 392.45 | 0.69, 0.40 | 0.94, 0.10 | |||
| −9.04, 12.86 | 0.86, 0.22 | 21.93, 12.36 | 199.73, 442.25 | 0.63, 0.40 | 0.88, 0.13 | |||
| −18.76, 11.82 | 0.95, 0.14 | 31.65, 11.16 | 131.37, 363.45 | 0.71, 0.39 | 0.96, 0.09 | |||
| −15.72, 14.09 | 0.93, 0.17 | 27.54, 13.31 | 217.76, 577.69 | 0.67, 0.41 | 0.93, 0.12 | |||
| −10.95, 14.75 | 0.88, 0.21 | 22.77, 14.09 | 263.47, 629.47 | 0.63, 0.41 | 0.89, 0.14 | |||
| −18.98, 13.35 | 0.95, 0.14 | 30.79, 12.57 | 182.40, 531.77 | 0.69, 0.40 | 0.96, 0.10 | |||
| −17.52, 13.71 | 0.94, 0.16 | 29.33, 12.97 | 196.47, 550.80 | 0.68, 0.41 | 0.95, 0.11 | |||
| SAN | −5.34, 14.03 | 0.77, 0.24 | 17.84, 13.54 | 337.51, 695.52 | 0.55, 0.39 | 0.76, 0.19 | ||
| −6.47, 13.61 | 0.80, 0.23 | 18.97, 13.31 | 314.10, 675.29 | 0.59, 0.39 | 0.79, 0.18 | |||
| −5.17, 13.77 | 0.77, 0.24 | 17.67, 13.34 | 326.66, 686.39 | 0.56, 0.39 | 0.76, 0.17 | |||
| −8.86, 13.96 | 0.84, 0.24 | 21.37, 13.52 | 281.56, 644.70 | 0.62, 0.40 | 0.85, 0.15 | |||
| −7.54, 14.41 | 0.80, 0.26 | 19.77, 13.95 | 450.83, 793.87 | 0.72, 0.34 | 0.81, 0.18 | |||
| −11.54, 14.07 | 0.86, 0.22 | 23.77, 13.65 | 380.77, 739.76 | 0.78, 0.31 | 0.88, 0.16 | |||
| −11.90, 13.49 | 0.87, 0.21 | 24.13, 12.94 | 364.04, 726.35 | 0.79, 0.31 | 0.88, 0.15 | |||
| −14.21, 13.66 | 0.89, 0.19 | 26.44, 13.09 | 345.90, 708.96 | 0.81, 0.30 | 0.91, 0.14 | |||
| −4.18, 13.46 | 0.76, 0.25 | 17.07, 13.06 | 248.90, 485.88 | 0.53, 0.39 | 0.75, 0.18 | |||
| −4.05, 13.41 | 0.76, 0.25 | 16.94, 13.16 | 244.59, 481.94 | 0.56, 0.39 | 0.77, 0.17 | |||
| −6.25, 12.95 | 0.80, 0.24 | 19.14, 12.52 | 220.32, 462.37 | 0.59, 0.40 | 0.81, 0.16 | |||
| −11.44, 13.15 | 0.88, 0.22 | 24.32, 12.58 | 179.76, 423.17 | 0.66, 0.40 | 0.90, 0.13 | |||
| −5.40, 16.36 | 0.79, 0.26 | 17.21, 15.94 | 339.18, 699.78 | 0.55, 0.40 | 0.79, 0.19 | |||
| −6.68, 15.72 | 0.81, 0.26 | 18.50, 15.35 | 306.36, 671.01 | 0.57, 0.41 | 0.82, 0.17 | |||
| −3.21, 16.32 | 0.75, 0.27 | 15.02, 16.09 | 354.69, 711.83 | 0.53, 0.40 | 0.77, 0.17 | |||
| −8.18, 15.28 | 0.83, 0.25 | 19.99, 14.86 | 279.92, 646.75 | 0.60, 0.41 | 0.85, 0.16 | |||
| Training Runtimes | |||||
|---|---|---|---|---|---|
| HAT | SAN | ||||
| Data Fold | Configuration | Epochs | Time [min] | Epochs | Time [min] |
| 499 | 1847 | 72 | 452 | ||
| 75 | 280 | 69 | 452 | ||
| 88 | 322 | 66 | 430 | ||
| 307 | 1148 | 72 | 490 | ||
| 679 | 2561 | 67 | 440 | ||
| 729 | 2828 | 69 | 466 | ||
| 666 | 2634 | 69 | 467 | ||
| 614 | 2290 | 78 | 500 | ||
| 499 | 1843 | 69 | 436 | ||
| 499 | 1846 | 64 | 439 | ||
| 77 | 280 | 67 | 442 | ||
| 499 | 1840 | 149 | 1043 | ||
| 499 | 1859 | 72 | 487 | ||
| 85 | 311 | 69 | 466 | ||
| 483 | 1798 | 65 | 430 | ||
| 499 | 1854 | 69 | 438 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ummerle, C.; Giganti, A.; Mandelli, S.; Bestagini, P.; Tubaro, S. Leveraging Land Cover Priors for Isoprene Emission Super-Resolution. Remote Sens. 2025, 17, 1715. https://doi.org/10.3390/rs17101715
Ummerle C, Giganti A, Mandelli S, Bestagini P, Tubaro S. Leveraging Land Cover Priors for Isoprene Emission Super-Resolution. Remote Sensing. 2025; 17(10):1715. https://doi.org/10.3390/rs17101715
Chicago/Turabian StyleUmmerle, Christopher, Antonio Giganti, Sara Mandelli, Paolo Bestagini, and Stefano Tubaro. 2025. "Leveraging Land Cover Priors for Isoprene Emission Super-Resolution" Remote Sensing 17, no. 10: 1715. https://doi.org/10.3390/rs17101715
APA StyleUmmerle, C., Giganti, A., Mandelli, S., Bestagini, P., & Tubaro, S. (2025). Leveraging Land Cover Priors for Isoprene Emission Super-Resolution. Remote Sensing, 17(10), 1715. https://doi.org/10.3390/rs17101715







