Confidence-Aware Ship Classification Using Contour Features in SAR Images
Abstract
1. Introduction
Contributions
- Introduction of 13 novel handcrafted features based on ship contours for classification in SAR images.
- Application of the entropy to probabilistic SAR ship classification.
- Combination of classification models based on the entropy.
- Association of classification predictions with entropy-derived confidence levels.
2. Related Works
2.1. Handcrafted Features
2.2. Confidence Estimation
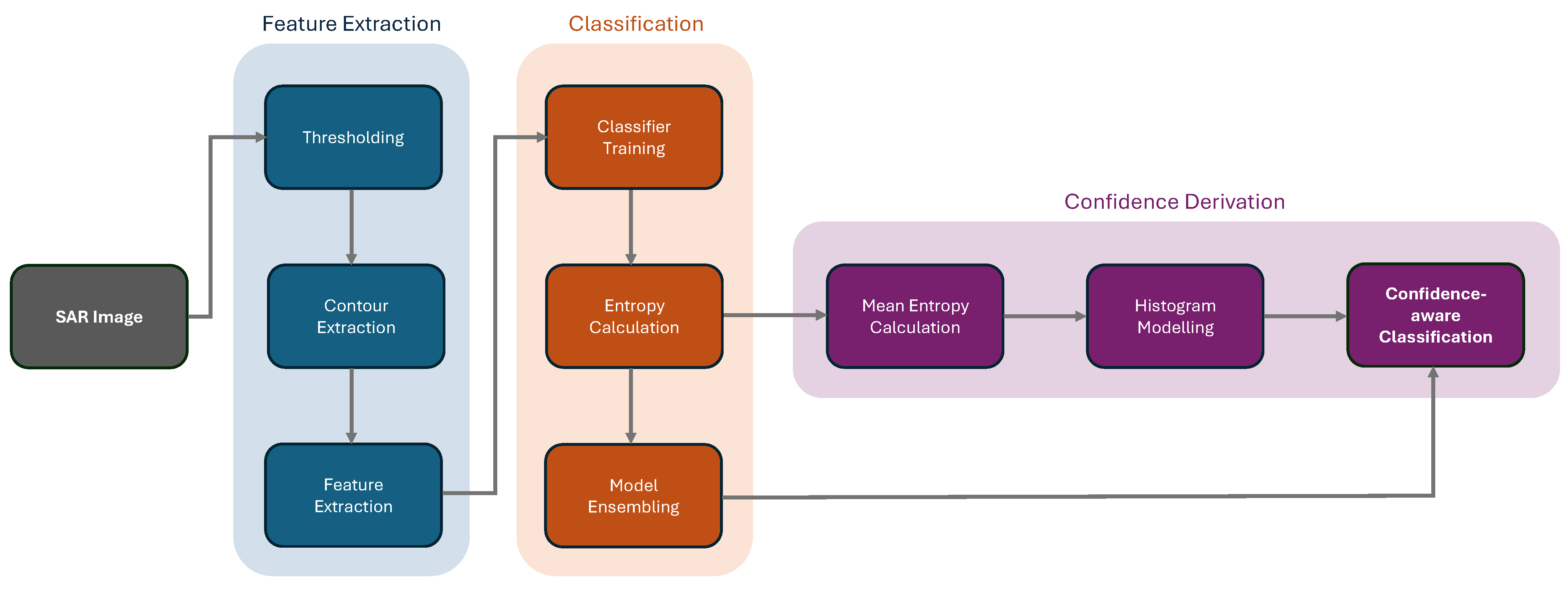
3. Methodology
3.1. Contour Extraction
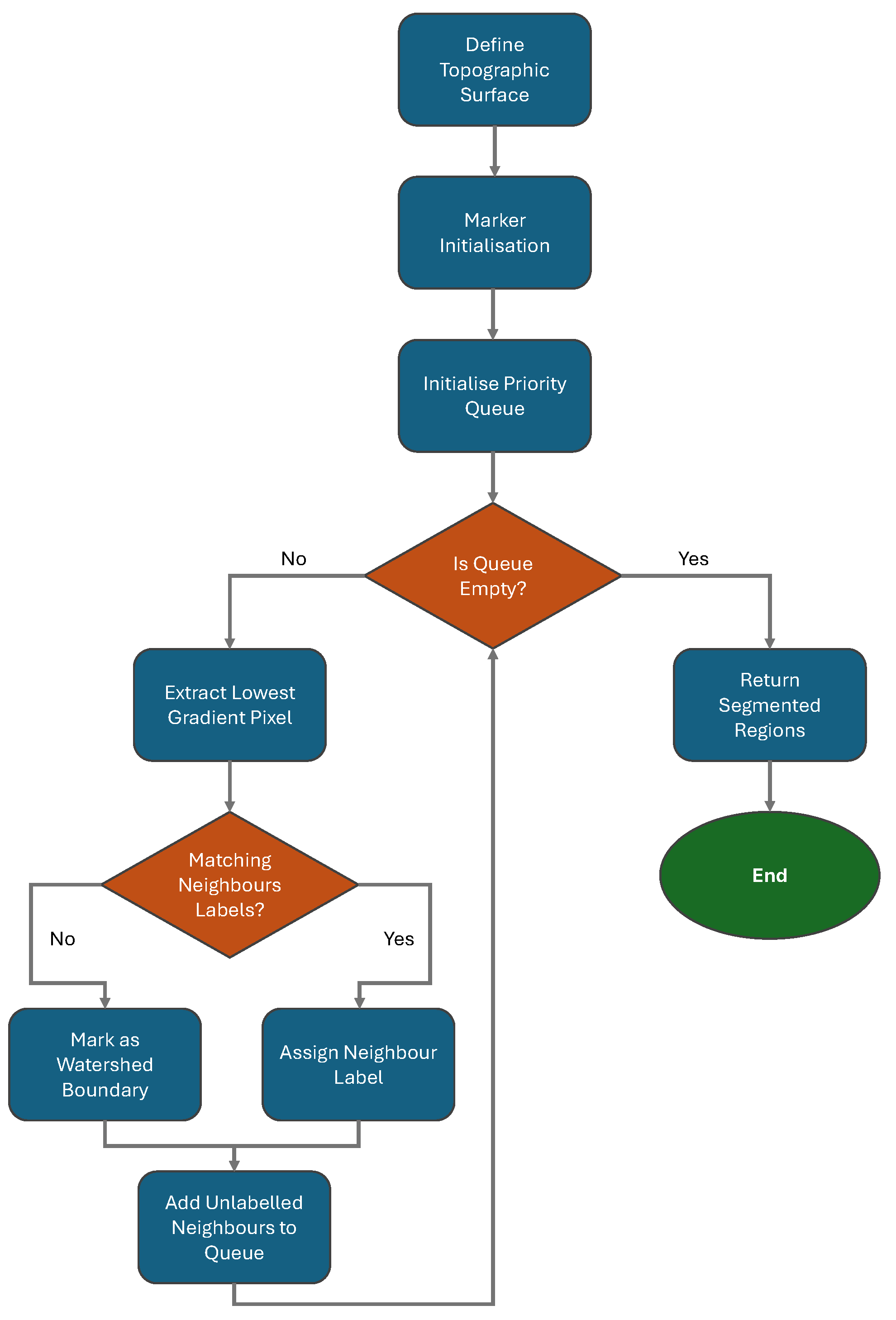
3.1.1. Watershed Segmentation
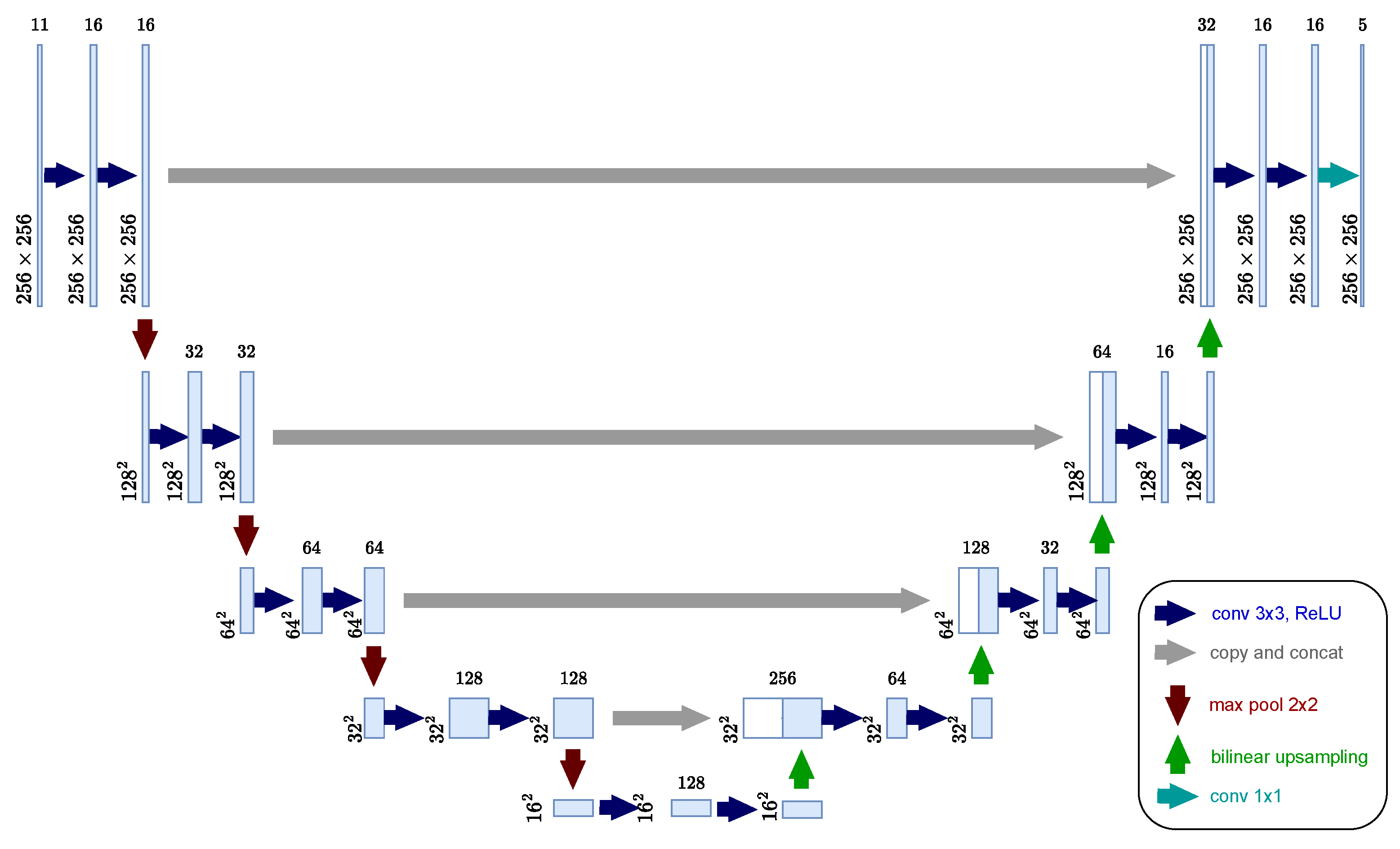
3.1.2. U-Net
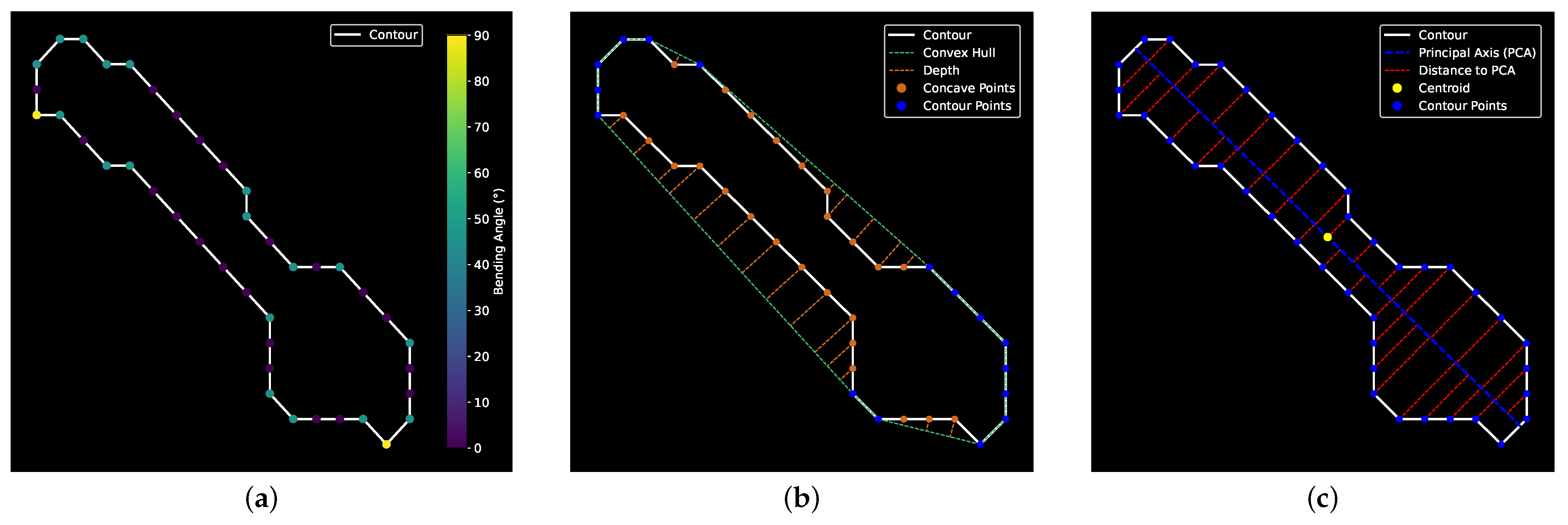
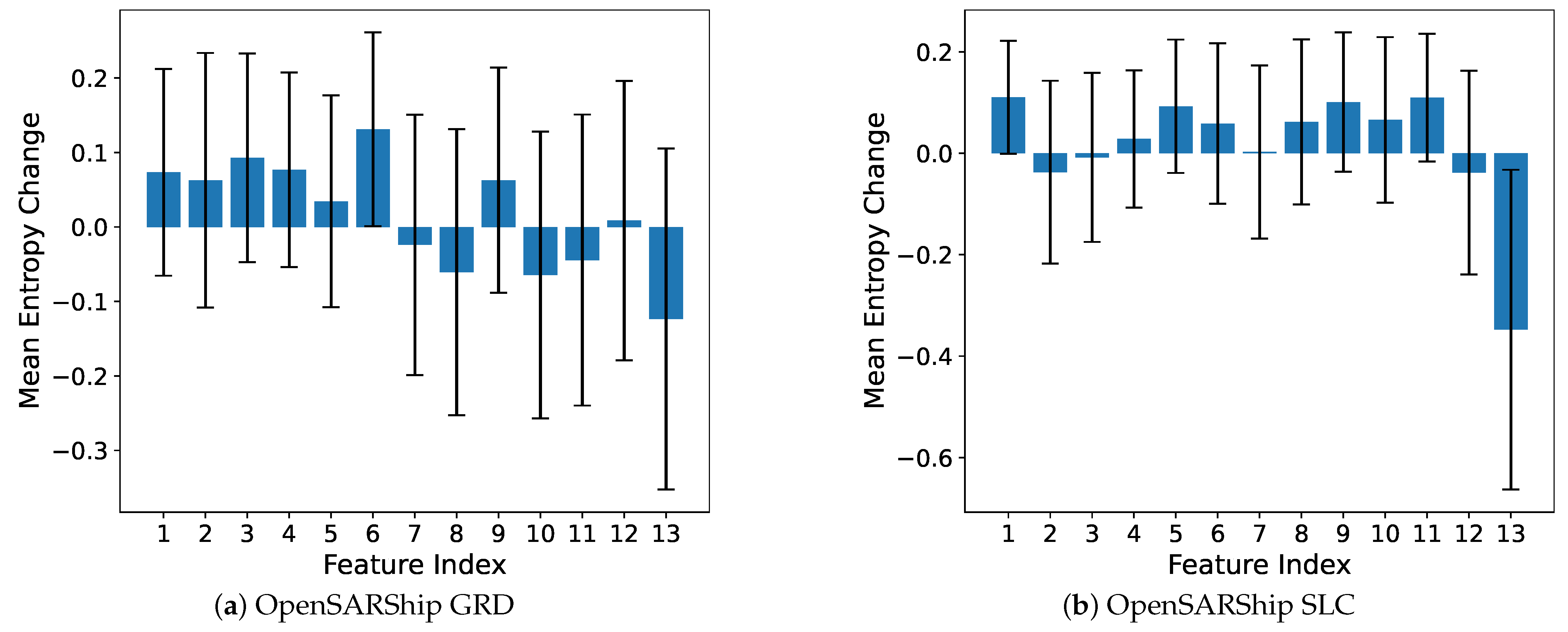
3.2. Proposed Features
- is the perimeter of the contour, calculated as the sum of the Euclidean distances between successive points along the contour:where is a vector , representing the coordinate of the contour point, represents the norm of vector , and is the total number of contour points. Please note that for a closed contour .
- represents the complexity of the contour, determined by the ratio of the contour’s perimeter to the square root of its area A:
- quantifies the bending energy, reflecting the curvature present along the contour. This is achieved by averaging the angles between consecutive edges:where · is the dot product of two vectors, and:
- , , and concentrate on the concave points of the contour, specifically the areas where the ship’s shape curves inward. The convex hull, which is the smallest convex shape that entirely encloses the contour, is first identified:where is the point on the convex hull represented as a vector , and M is the total number of convex hull points.The depth of a point on the contour is defined as the Euclidean distance to the nearest point on the convex hull:Concave points are defined as points on the contour where the depth is strictly greater than zero. is then defined as the count of these concave points:where denotes the cardinality, and:Accordingly, , , and are the mean, standard deviation, and the sum of their depths, respectively:
- , , and capture the major direction of variation of the contour by measuring the perpendicular distances to the principal component axis (PCA):where is the perpendicular distance of the ith contour point to the principal axis, is the principal axis unit vector derived from PCA, and is the vector to the centroid, calculated as:The perpendicular distances are then used to compute three features that capture the distribution of contour points relative to the principal axis: the mean () represents the average deviation of the points, the standard deviation () quantifies the variability of these deviations, and the sum () reflects the total deviation across all points:
- , , and are the radiometric features, defined as the mean, standard deviation, and sum, respectively, of the intensity of the pixels along the contour:where represents the intensity value of the pixel along the contour.
3.3. Entropy-Based Ensembling
- Feature Concatenation: This method involves combining all features across different thresholds for each sample:where ∪ represents the union of the sets, and is the feature set for the threshold:
- Expanded Samples: By considering each feature set from different thresholds for the same samples as distinct entities, the number of samples effectively increases, given by:where is the original number of samples and is the resulting number of expanded samples.
- Majority Voting: In this approach, each classifier contributes equally to the final decision, with the predicted class being determined by a simple majority vote among all classifiers:where is the majority vote prediction for the sample, and is an indicator function, defined as:
- Probability Averaging: This method averages the probabilities assigned to each class by the different classifiers, therefore consolidating the predictions into a single probabilistic outcome for each class:
- Minimum-Entropy Selection: This approach identifies the classifier with the lowest entropy in its predictions, , for each sample:The prediction of this classifier is selected as the final outcome:
3.4. Entropy-Based Confidence Levels
- Ensemble High Confidence, in which predictions present entropy values below one standard deviation from the mean:This threshold is chosen because samples in this range exhibit significantly lower uncertainty than average, indicating that the classifiers within the ensemble are highly certain about their predictions. Statistically, for a Gaussian distribution, approximately 68% of the data lies within one standard deviation of the mean. Thus, samples falling below the threshold defined in (32) are in the lower tail, highlighting particularly confident predictions.
- Ensemble Moderate Confidence, where predictions possess entropy values in the following range:This range is selected to capture samples that exhibit average or slightly below-average uncertainty. These samples represent predictions where the ensemble of classifiers is generally confident but not to the extent of those classified under high confidence. This classification acknowledges the natural variance in model certainty, categorizing predictions that are reasonably sure but not exceptionally so.
- Ensemble Low Confidence, in which predictions have entropy values exceeding the mean:Samples in this category have higher than average entropy, indicating a higher level of uncertainty in the ensemble’s predictions. This classification is critical for identifying instances where the model’s predictions are less reliable, possibly due to conflicting information among the classifiers or inherent complexity in the sample that challenges clear classification.
4. Experimental Setup
4.1. Datasets
4.1.1. OpenSARShip
4.1.2. FUSAR-Ship
4.1.3. HRSID
4.2. Implementation Details
4.2.1. Contour Extraction Process
4.2.2. Classification Process
4.2.3. Entropy Analysis
5. Results and Discussion
5.1. Contour Extraction Results
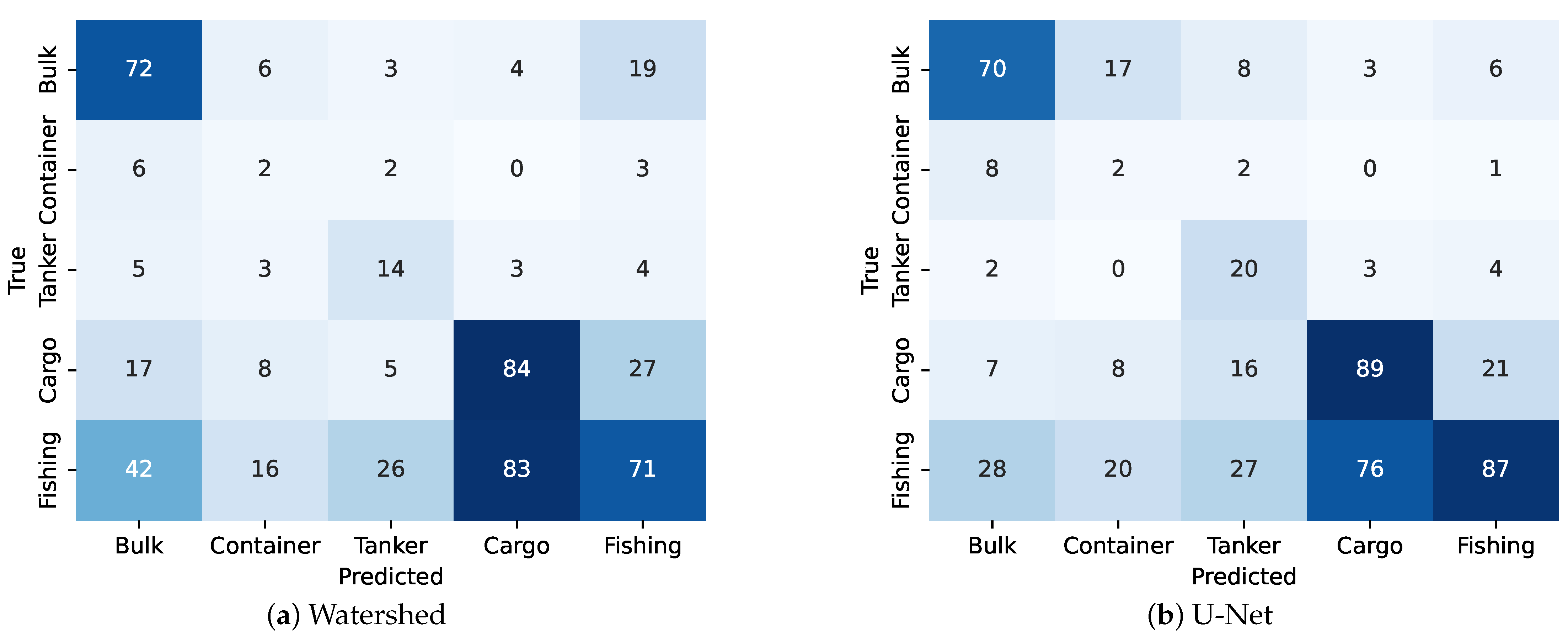
5.2. Classification Results
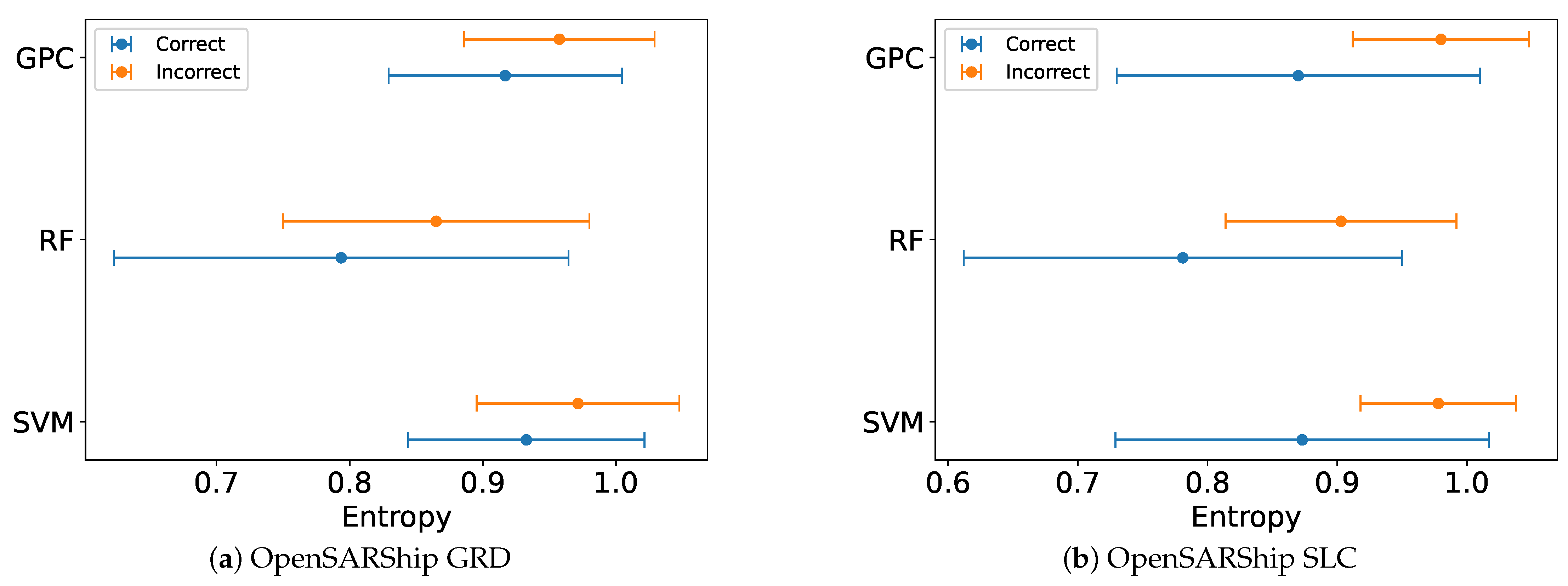
5.3. Entropy-Based Ensembling Results
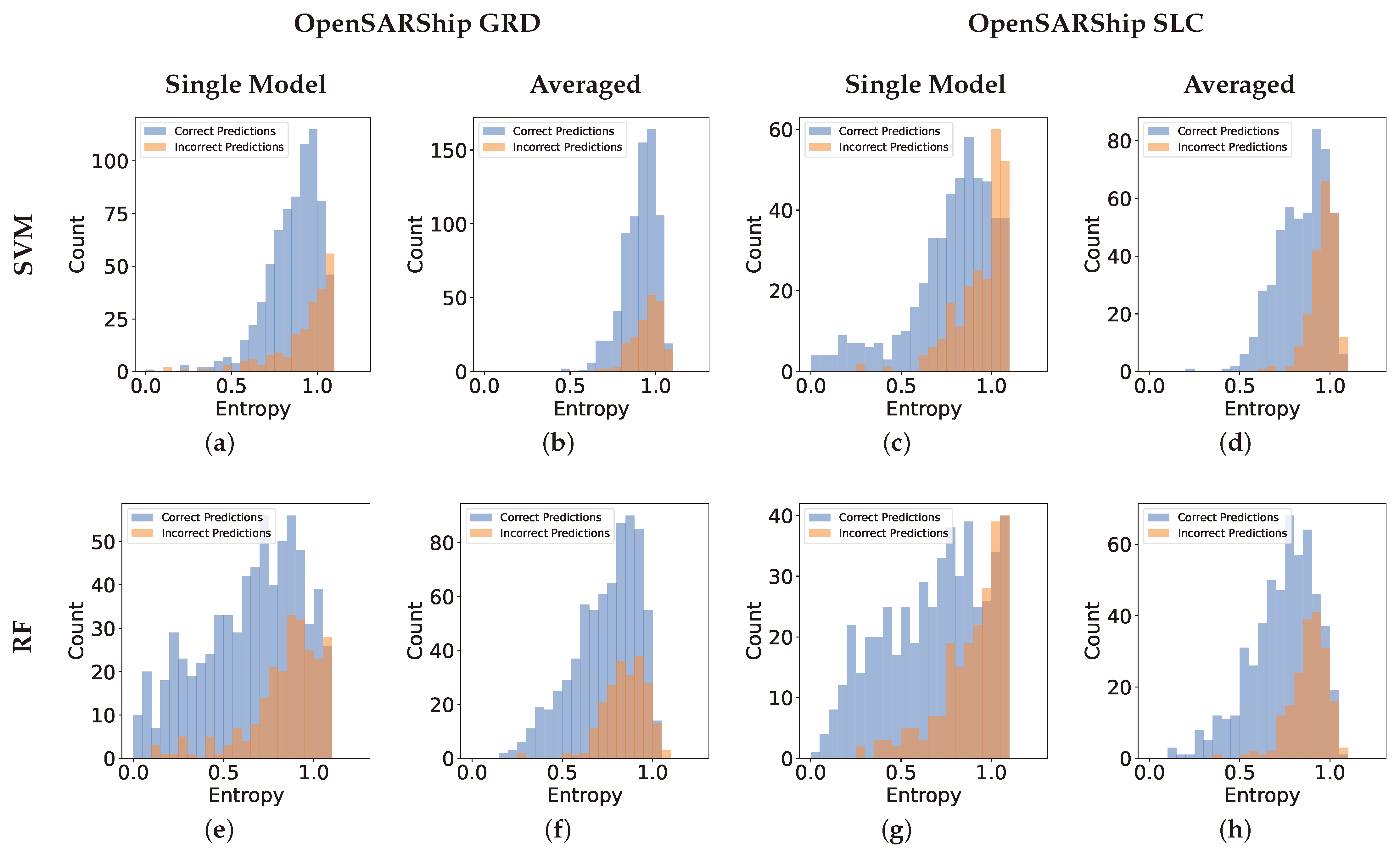
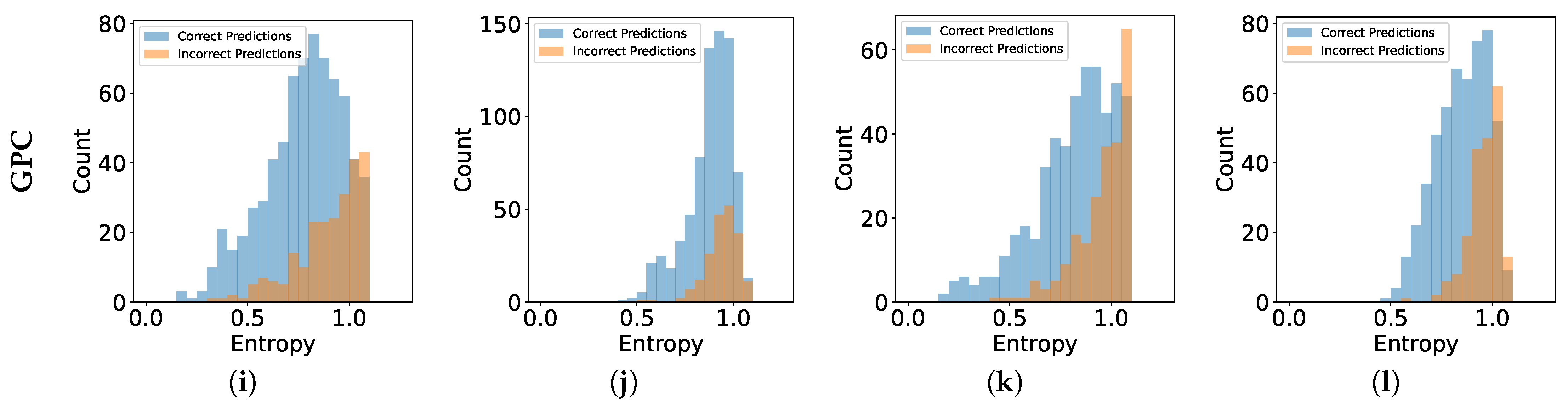
5.4. Confidence-Aware Classification Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Margarit, G.; Mallorqui, J.J.; Fabregas, X. Single-Pass Polarimetric SAR Interferometry for Vessel Classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3494–3502. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Liu, H. Ship Classification in Medium-Resolution SAR Images via Densely Connected Triplet CNNs Integrating Fisher Discrimination Regularized Metric Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3022–3039. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X.; Zhang, J.; Gao, G.; Dai, Y.; Liu, G.; Jia, Y.; Wang, X.; Zhang, Y.; Bao, M. Evaluation and Improvement of Generalization Performance of SAR Ship Recognition Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9311–9326. [Google Scholar] [CrossRef]
- Rodger, M.; Guida, R. Classification-Aided SAR and AIS Data Fusion for Space-Based Maritime Surveillance. Remote Sens. 2021, 13, 104. [Google Scholar] [CrossRef]
- Xu, Y.; Lang, H. Ship Classification in SAR Images with Geometric Transfer Metric Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6799–6813. [Google Scholar] [CrossRef]
- Snapir, B.; Waine, T.W.; Biermann, L. Maritime Vessel Classification to Monitor Fisheries with SAR: Demonstration in the North Sea. Remote Sens. 2019, 11, 353. [Google Scholar] [CrossRef]
- Bentes, C.; Velotto, D.; Tings, B. Ship Classification in TerraSAR-X Images with Convolutional Neural Networks. IEEE J. Ocean. Eng. 2018, 43, 258–266. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D.; et al. HOG-ShipCLSNet: A Novel Deep Learning Network with HOG Feature Fusion for SAR Ship Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. What, Where, and How to Transfer in SAR Target Recognition Based on Deep CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2324–2336. [Google Scholar] [CrossRef]
- Roscher, R.; Bohn, B.; Duarte, M.F.; Garcke, J. Explainable Machine Learning for Scientific Insights and Discoveries. IEEE Access 2020, 8, 42200–42216. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How. Remote Sens. 2021, 13, 2091. [Google Scholar] [CrossRef]
- McIver, D.; Friedl, M. Estimating pixel-scale land cover classification confidence using nonparametric machine learning methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1959–1968. [Google Scholar] [CrossRef]
- Beckler, B.; Pfau, A.; Orescanin, M.; Atchley, S.; Villemez, N.; Joseph, J.E.; Miller, C.W.; Margolina, T. Multilabel Classification of Heterogeneous Underwater Soundscapes with Bayesian Deep Learning. IEEE J. Ocean. Eng. 2022, 47, 1143–1154. [Google Scholar] [CrossRef]
- Mehrtash, A.; Wells, W.M.; Tempany, C.M.; Abolmaesumi, P.; Kapur, T. Confidence Calibration and Predictive Uncertainty Estimation for Deep Medical Image Segmentation. IEEE Trans. Med. Imaging 2020, 39, 3868–3878. [Google Scholar] [CrossRef]
- Wang, J. Uncertainty Estimation for CNN-based SAR Target Classification. In Proceedings of the 2023 8th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 21–23 April 2023; pp. 523–527. [Google Scholar] [CrossRef]
- Yang, G.; Li, H.C.; Yang, W.; Fu, K.; Sun, Y.J.; Emery, W.J. Unsupervised Change Detection of SAR Images Based on Variational Multivariate Gaussian Mixture Model and Shannon Entropy. IEEE Geosci. Remote Sens. Lett. 2019, 16, 826–830. [Google Scholar] [CrossRef]
- Margarit, G.; Tabasco, A. Ship Classification in Single-Pol SAR Images Based on Fuzzy Logic. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3129–3138. [Google Scholar] [CrossRef]
- Xing, X.; Ji, K.; Zou, H.; Chen, W.; Sun, J. Ship Classification in TerraSAR-X Images with Feature Space Based Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1562–1566. [Google Scholar] [CrossRef]
- Lang, H.; Zhang, J.; Zhang, X.; Meng, J. Ship Classification in SAR Image by Joint Feature and Classifier Selection. IEEE Geosci. Remote Sens. Lett. 2016, 13, 212–216. [Google Scholar] [CrossRef]
- Lang, H.; Wu, S. Ship Classification in Moderate-Resolution SAR Image by Naive Geometric Features-Combined Multiple Kernel Learning. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1765–1769. [Google Scholar] [CrossRef]
- Gray, R.M. Entropy and Information Theory; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Zhang, H.; Tian, X.; Wang, C.; Wu, F.; Zhang, B. Merchant Vessel Classification Based on Scattering Component Analysis for COSMO-SkyMed SAR Images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1275–1279. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Wu, F.; Jiang, S.; Zhang, B.; Tang, Y. A Novel Hierarchical Ship Classifier for COSMO-SkyMed SAR Data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 484–488. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Jiang, S.; Zhang, H.; Zhang, B. Classification of Vessels in Single-Pol COSMO-SkyMed Images Based on Statistical and Structural Features. Remote Sens. 2015, 7, 5511–5533. [Google Scholar] [CrossRef]
- Zhu, J.W.; Qiu, X.L.; Pan, Z.X.; Zhang, Y.T.; Lei, B. An Improved Shape Contexts Based Ship Classification in SAR Images. Remote Sens. 2017, 9, 145. [Google Scholar] [CrossRef]
- Lin, H.; Song, S.; Yang, J. Ship Classification Based on MSHOG Feature and Task-Driven Dictionary Learning with Structured Incoherent Constraints in SAR Images. Remote Sens. 2018, 10, 190. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, X.; Pan, Z.; Zhang, Y.; Lei, B. Projection Shape Template-Based Ship Target Recognition in TerraSAR-X Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 222–226. [Google Scholar] [CrossRef]
- Al Hinai, A.A.; Guida, R. Ship Classification Using Layover in Sentinel-1 Images. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 7495–7498. [Google Scholar] [CrossRef]
- Knapskog, A.O.; Brovoll, S.; Torvik, B. Characteristics of ships in harbour investigated in simultaneous images from TerraSAR-X and PicoSAR. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 422–427. [Google Scholar] [CrossRef]
- Iervolino, P.; Guida, R.; Whittaker, P. A Model for the Backscattering From a Canonical Ship in SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1163–1175. [Google Scholar] [CrossRef]
- Mena, J.; Pujol, O.; Vitrià, J. A Survey on Uncertainty Estimation in Deep Learning Classification Systems from a Bayesian Perspective. ACM Comput. Surv. 2021, 54, 193. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Arora, M.K.; Ghosh, S.K. Estimating and accommodating uncertainty through the soft classification of remote sensing data. Int. J. Remote Sens. 2005, 26, 2995–3007. [Google Scholar] [CrossRef]
- Giacco, F.; Thiel, C.; Pugliese, L.; Scarpetta, S.; Marinaro, M. Uncertainty Analysis for the Classification of Multispectral Satellite Images Using SVMs and SOMs. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3769–3779. [Google Scholar] [CrossRef]
- Loosvelt, L.; Peters, J.; Skriver, H.; Lievens, H.; Van Coillie, F.M.; De Baets, B.; Verhoest, N.E. Random Forests as a tool for estimating uncertainty at pixel-level in SAR image classification. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 173–184. [Google Scholar] [CrossRef]
- Dehghan, H.; Ghassemian, H. Measurement of uncertainty by the entropy: Application to the classification of MSS data. Int. J. Remote Sens. 2006, 27, 4005–4014. [Google Scholar] [CrossRef]
- Park, L.A.F.; Simoff, S. Using Entropy as a Measure of Acceptance for Multi-label Classification. In Proceedings of the Advances in Intelligent Data Analysis XIV, Saint Etienne, France, 22–24 October 2015; Fromont, E., De Bie, T., van Leeuwen, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 217–228. [Google Scholar]
- Tornetta, G.N. Entropy Methods for the Confidence Assessment of Probabilistic Classification Models. Statistica 2021, 81, 383–398. [Google Scholar] [CrossRef]
- Rennie, J.D.; Shih, L.; Teevan, J.; Karger, D.R. Tackling the poor assumptions of naive bayes text classifiers. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 616–623. [Google Scholar]
- Omati, M.; Sahebi, M.R. Change Detection of Polarimetric SAR Images Based on the Integration of Improved Watershed and MRF Segmentation Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4170–4179. [Google Scholar] [CrossRef]
- Bai, M.; Urtasun, R. Deep Watershed Transform for Instance Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2858–2866. [Google Scholar] [CrossRef]
- Dhage, P.; Phegade, M.R.; Shah, S.K. Watershed segmentation brain tumor detection. In Proceedings of the 2015 International Conference on Pervasive Computing (ICPC), Pune, India, 8–10 January 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Xue, Y.; Zhao, J.; Zhang, M. A Watershed-Segmentation-Based Improved Algorithm for Extracting Cultivated Land Boundaries. Remote Sens. 2021, 13, 939. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Ge, S.; Gu, H.; Su, W.; Praks, J.; Antropov, O. Improved Semisupervised UNet Deep Learning Model for Forest Height Mapping with Satellite SAR and Optical Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5776–5787. [Google Scholar] [CrossRef]
- Li, L.; Wang, C.; Zhang, H.; Zhang, B. Residual Unet for Urban Building Change Detection with Sentinel-1 SAR Data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1498–1501. [Google Scholar] [CrossRef]
- Li, J.; Guo, C.; Gou, S.; Chen, Y.; Wang, M.; Chen, J.W. Ship Segmentation on High-Resolution Sar Image by a 3D Dilated Multiscale U-Net. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2575–2578. [Google Scholar] [CrossRef]
- Leung, K. Neural-Network-Architecture-Diagrams. Available online: https://github.com/kennethleungty/Neural-Network-Architecture-Diagrams (accessed on 30 April 2024).
- Salerno, E. Using Low-Resolution SAR Scattering Features for Ship Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–4. [Google Scholar] [CrossRef]
- Bolourchi, P.; Moradi, M.; Demirel, H.; Uysal, S. Improved SAR target recognition by selecting moment methods based on Fisher score. Signal Image Video Process. 2020, 14, 39–47. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Böken, B. On the appropriateness of Platt scaling in classifier calibration. Inf. Syst. 2021, 95, 101641. [Google Scholar] [CrossRef]
- Chen, Z.; Lin, T.; Xia, X.; Xu, H.; Ding, S. A synthetic neighborhood generation based ensemble learning for the imbalanced data classification. Appl. Intell. 2018, 48, 2441–2457. [Google Scholar] [CrossRef]
- Huang, L.; Liu, B.; Li, B.; Guo, W.; Yu, W.; Zhang, Z.; Yu, W. OpenSARShip: A Dataset Dedicated to Sentinel-1 Ship Interpretation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 195–208. [Google Scholar] [CrossRef]
- Li, B.; Liu, B.; Huang, L.; Guo, W.; Zhang, Z.; Yu, W. OpenSARShip 2.0: A large-volume dataset for deeper interpretation of ship targets in Sentinel-1 imagery. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Al Hinai, A.A.; Guida, R. Investigating the Complex Signal Kurtosis for SAR Ship Classification. In Proceedings of the 2023 8th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Bali, Indonesia, 23–27 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Iervolino, P.; Guida, R. A Novel Ship Detector Based on the Generalized-Likelihood Ratio Test for SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3616–3630. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition. Sci. China Inf. Sci. 2020, 63, 1–19. [Google Scholar] [CrossRef]
- Wei, S.; Zeng, X.; Qu, Q.; Wang, M.; Su, H.; Shi, J. HRSID: A High-Resolution SAR Images Dataset for Ship Detection and Instance Segmentation. IEEE Access 2020, 8, 120234–120254. [Google Scholar] [CrossRef]
- Yu, F.; Sun, W.; Li, J.; Zhao, Y.; Zhang, Y.; Chen, G. An improved Otsu method for oil spill detection from SAR images. Oceanologia 2017, 59, 311–317. [Google Scholar] [CrossRef]
- Henry, C.; Azimi, S.M.; Merkle, N. Road Segmentation in SAR Satellite Images with Deep Fully Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1867–1871. [Google Scholar] [CrossRef]
- Feng, S.; Ji, K.; Ma, X.; Zhang, L.; Kuang, G. Target Region Segmentation in SAR Vehicle Chip Image with ACM Net. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- CVAT.ai Corporation. Computer Vision Annotation Tool (CVAT); Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Li, Y.; Lai, X.; Wang, M.; Zhang, X. C-SASO: A Clustering-Based Size-Adaptive Safer Oversampling Technique for Imbalanced SAR Ship Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]







| OpenSARShip | ||||
|---|---|---|---|---|
| GRD | SLC | |||
| Train | Test | Train | Test | |
| Bulk carrier | 154 | 663 | 233 | 100 |
| Container ship | 154 | 66 | 233 | 344 |
| Tanker | 154 | 206 | 233 | 281 |
| FUSAR-Ship | ||
|---|---|---|
| Train | Test | |
| Bulk carrier | 150 | 104 |
| Container ship | 150 | 13 |
| Tanker | 150 | 29 |
| Cargo | 150 | 141 |
| Fishing | 150 | 238 |
| Dataset | Model | IoU | Dice |
|---|---|---|---|
| HRSID | Watershed | 43.3% | 58.7% |
| U-Net | 79.8% | 88.4% | |
| OpenSARShip GRD | Watershed | 68.8% | 81.0% |
| U-Net | 61.5% | 73.1% | |
| OpenSARShip SLC | Watershed | 46.8% | 60.7% |
| U-Net | 59.9% | 73.1% | |
| FUSAR-Ship | Watershed | 61.4% | 75.2% |
| U-Net | 70.7% | 82.0% |
| OpenSARShip GRD | OpenSARShip SLC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Features | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | |
| NGFs | 58.0% | 56.7% | 59.0% | 52.1% | 56.8% | 53.3% | 53.5% | 50.7% | |
| LRCS | 75.5% | 61.7% | 68.7% | 64.2% | 64.4% | 57.9% | 57.9% | 57.0% | |
| Hu Moments | 47.8% | 42.1% | 48.7% | 40.2% | 45.1% | 44.8% | 44.3% | 42.2% | |
| Zernike Moments | 70.6% | 60.8% | 65.9% | 59.9% | 47.4% | 48.3% | 48.0% | 45.2% | |
| Watershed Segmentation | Geometric Contour | 70.1% | 59.1% | 64.8% | 58.8% | 53.2% | 51.0% | 52.6% | 49.4% |
| Radiometric Contour | 73.6% | 60.8% | 68.6% | 62.0% | 62.2% | 59.1% | 58.8% | 56.8% | |
| Combined Contour | 78.5% | 65.4% | 72.5% | 66.4% | 68.7% | 64.7% | 67.3% | 64.4% | |
| U-Net Segmentation | Geometric Contour | 65.8% | 59.3% | 62.9% | 56.5% | 65.2% | 63.9% | 65.7% | 61.6% |
| Radiometric Contour | 69.9% | 58.2% | 62.1% | 57.6% | 67.3% | 65.5% | 67.0% | 63.4% | |
| Combined Contour | 75.5% | 63.7% | 68.8% | 63.6% | 71.9% | 68.4% | 71.4% | 67.8% | |
| VGG-19 | 68.1% | 56.8% | 65.5% | 57.8% | 64.5% | 63.7% | 63.4% | 60.5% | |
| FUSAR-Ship 3-Categories | FUSAR-Ship 5-Categories | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Features | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | |
| NGFs | 73.3% | 62.4% | 73.8% | 65.6% | 39.0% | 37.3% | 47.5% | 34.9% | |
| LRCS | 75.3% | 62.8% | 71.7% | 65.6% | 34.7% | 35.5% | 49.1% | 31.8% | |
| Hu Moments | 56.8% | 58.7% | 58.0% | 54.2% | 36.8% | 32.7% | 42.7% | 33.9% | |
| Zernike Moments | 56.2% | 42.7% | 46.0% | 43.2% | 32.4% | 27.9% | 31.9% | 27.0% | |
| Watershed Segmentation | Geometric Contour | 65.8% | 56.2% | 56.9% | 54.3% | 41.0% | 39.9% | 43.0% | 35.9% |
| Radiometric Contour | 74.0% | 60.3% | 64.7% | 61.0% | 43.2% | 37.3% | 46.3% | 38.2% | |
| Combined Contour | 75.3% | 64.3% | 65.9% | 62.8% | 46.3% | 38.0% | 44.5% | 39.0% | |
| U-Net Segmentation | Geometric Contour | 64.4% | 51.5% | 53.7% | 51.3% | 47.0% | 39.9% | 43.0% | 38.9% |
| Radiometric Contour | 69.9% | 57.8% | 62.4% | 58.3% | 42.5% | 38.4% | 47.9% | 37.0% | |
| Combined Contour | 77.4% | 62.2% | 64.3% | 63.0% | 51.0% | 43.5% | 50.3% | 43.1% | |
| VGG-19 | 80.3% | 70.1% | 73.6% | 70.3% | 57.3% | 58.0% | 63.6% | 57.9% | |
| OpenSARShip GRD | OpenSARShip SLC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ensemble Method | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | |
| SVM | Optimal Single Model | 78.5% | 65.4% | 72.5% | 66.4% | 68.7% | 64.7% | 67.3% | 64.4% |
| Expanded Samples | 69.4% | 55.2% | 62.4% | 57.0% | 62.2% | 59.2% | 61.1% | 58.2% | |
| Feature Concatenation | 76.6% | 63.9% | 73.4% | 65.7% | 66.2% | 63.3% | 64.3% | 61.9% | |
| Majority Voting | 78.7% | 65.3% | 74.1% | 67.3% | 69.2% | 67.6% | 69.7% | 65.7% | |
| Minimum Entropy | 73.9% | 62.2% | 72.6% | 63.5% | 70.3% | 64.1% | 65.6% | 64.3% | |
| Probability Averaging | 79.6% | 66.3% | 74.9% | 68.1% | 71.2% | 68.1% | 70.5% | 67.0% | |
| Entropy-Weighted Probabilities | 80.7% | 68.0% | 74.4% | 69.1% | 71.2% | 67.3% | 69.6% | 66.6% | |
| RF | Optimal Single Model | 76.3% | 63.2% | 72.1% | 65.2% | 67.4% | 63.0% | 65.3% | 62.9% |
| Expanded Samples | 66.0% | 55.7% | 65.8% | 56.4% | 67.8% | 64.6% | 67.3% | 64.0% | |
| Feature Concatenation | 75.3% | 63.3% | 74.0% | 65.0% | 73.5% | 69.2% | 72.0% | 69.1% | |
| Majority Voting | 77.0% | 64.5% | 74.9% | 66.5% | 71.2% | 68.9% | 72.0% | 67.7% | |
| Minimum Entropy | 74.4% | 61.7% | 72.0% | 63.8% | 72.6% | 67.2% | 69.4% | 67.4% | |
| Probability Averaging | 77.5% | 65.1% | 74.3% | 66.5% | 74.3% | 69.9% | 72.8% | 69.8% | |
| Entropy-Weighted Probabilities | 79.6% | 66.3% | 74.2% | 67.9% | 74.1% | 69.1% | 71.7% | 69.2% | |
| GPC | Optimal Single Model | 76.9% | 63.9% | 72.6% | 65.9% | 69.2% | 64.5% | 66.9% | 64.7% |
| Expanded Samples | 67.5% | 54.7% | 63.2% | 56.2% | 63.5% | 60.0% | 61.9% | 59.3% | |
| Feature Concatenation | 73.4% | 61.8% | 73.1% | 63.7% | 67.9% | 63.8% | 65.7% | 63.2% | |
| Majority Voting | 79.0% | 66.1% | 75.1% | 67.8% | 70.9% | 67.4% | 69.5% | 66.5% | |
| Minimum Entropy | 74.1% | 62.5% | 73.1% | 63.7% | 72.4% | 66.7% | 68.7% | 67.1% | |
| Probability Averaging | 80.3% | 67.4% | 75.8% | 69.0% | 72.1% | 67.5% | 70.1% | 67.4% | |
| Entropy-Weighted Probabilities | 81.8% | 69.1% | 75.4% | 70.3% | 72.1% | 67.5% | 70.1% | 67.4% | |
| SVM RF GPC | Majority Voting | 79.0% | 65.4% | 73.8% | 67.5% | 69.8% | 64.9% | 67.0% | 65.0% |
| Minimum Entropy | 79.0% | 65.4% | 73.5% | 67.5% | 71.6% | 66.8% | 69.6% | 67.1% | |
| Probability Averaging | 78.9% | 65.2% | 73.4% | 67.3% | 70.6% | 66.0% | 68.6% | 66.1% | |
| Entropy-Weighted Probabilities | 79.2% | 65.8% | 73.5% | 67.7% | 71.6% | 67.0% | 69.8% | 67.2% | |
| OpenSARShip GRD | OpenSARShip SLC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Confidence Level | Accuracy | Precision | Recall | F1 Score | No. of Samples | Accuracy | Precision | Recall | F1 Score | No. of Samples |
| SVM Single | High | 81.4% | 77.7% | 81.0% | 78.7% | 129 | 95.7% | 63.2% | 62.1% | 62.6% | 93 |
| Moderate | 87.7% | 77.0% | 84.4% | 79.8% | 261 | 80.7% | 75.8% | 69.1% | 70.4% | 197 | |
| Low | 71.3% | 51.5% | 58.2% | 52.0% | 544 | 56.8% | 57.1% | 58.2% | 55.1% | 435 | |
| SVM Ensemble | High | 87.8% | 84.1% | 87.8% | 85.1% | 213 | 97.4% | 65.3% | 65.3% | 65.3% | 191 |
| Moderate | 81.2% | 64.0% | 77.0% | 65.5% | 292 | 74.5% | 67.0% | 68.4% | 67.4% | 243 | |
| Low | 72.5% | 46.7% | 50.6% | 47.1% | 429 | 51.2% | 56.7% | 54.5% | 51.4% | 291 | |
| RF Single | High | 91.3% | 86.6% | 91.7% | 88.5% | 173 | 93.8% | 86.9% | 87.2% | 87.0% | 145 |
| Moderate | 88.9% | 74.0% | 86.5% | 76.5% | 217 | 83.2% | 78.2% | 78.9% | 78.5% | 161 | |
| Low | 64.0% | 49.5% | 57.0% | 48.8% | 544 | 56.3% | 59.2% | 61.3% | 55.9% | 419 | |
| RF Ensemble | High | 96.6% | 95.6% | 97.4% | 96.4% | 233 | 95.5% | 86.7% | 87.1% | 86.9% | 176 |
| Moderate | 80.3% | 58.8% | 69.8% | 59.7% | 294 | 80.1% | 73.3% | 78.8% | 74.1% | 221 | |
| Low | 67.3% | 47.0% | 51.8% | 47.2% | 407 | 52.1% | 53.8% | 53.4% | 51.2% | 328 | |
| GPC Single | High | 88.5% | 82.1% | 85.5% | 82.4% | 156 | 90.9% | 88.3% | 82.7% | 85.0% | 110 |
| Moderate | 85.5% | 66.8% | 79.3% | 70.9% | 255 | 81.9% | 74.6% | 71.8% | 72.6% | 193 | |
| Low | 65.2% | 48.4% | 57.2% | 48.6% | 523 | 58.3% | 56.3% | 57.0% | 55.4% | 422 | |
| GPC Ensemble | High | 90.9% | 84.4% | 91.5% | 86.3% | 241 | 94.5% | 77.4% | 83.5% | 79.5% | 165 |
| Moderate | 83.7% | 59.5% | 74.1% | 63.8% | 282 | 75.3% | 69.4% | 72.1% | 70.0% | 299 | |
| Low | 68.1% | 46.5% | 50.4% | 46.5% | 411 | 51.7% | 55.8% | 54.3% | 51.4% | 261 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Hinai, A.A.; Guida, R. Confidence-Aware Ship Classification Using Contour Features in SAR Images. Remote Sens. 2025, 17, 127. https://doi.org/10.3390/rs17010127
Al Hinai AA, Guida R. Confidence-Aware Ship Classification Using Contour Features in SAR Images. Remote Sensing. 2025; 17(1):127. https://doi.org/10.3390/rs17010127
Chicago/Turabian StyleAl Hinai, Al Adil, and Raffaella Guida. 2025. "Confidence-Aware Ship Classification Using Contour Features in SAR Images" Remote Sensing 17, no. 1: 127. https://doi.org/10.3390/rs17010127
APA StyleAl Hinai, A. A., & Guida, R. (2025). Confidence-Aware Ship Classification Using Contour Features in SAR Images. Remote Sensing, 17(1), 127. https://doi.org/10.3390/rs17010127











