Application of Remote Sensing Floodplain Vegetation Data in a Dynamic Roughness Distributed Runoff Model
Abstract
1. Introduction
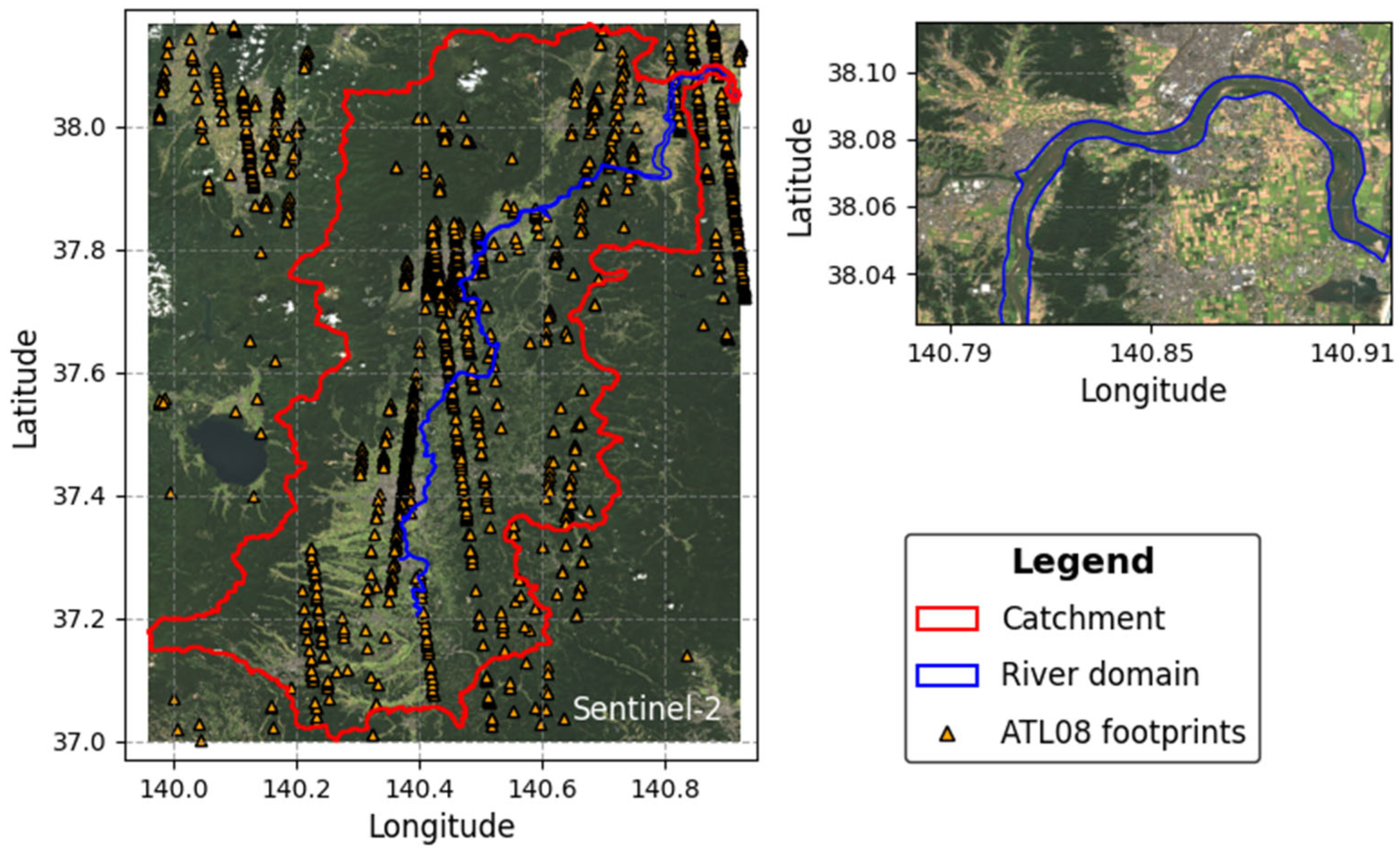
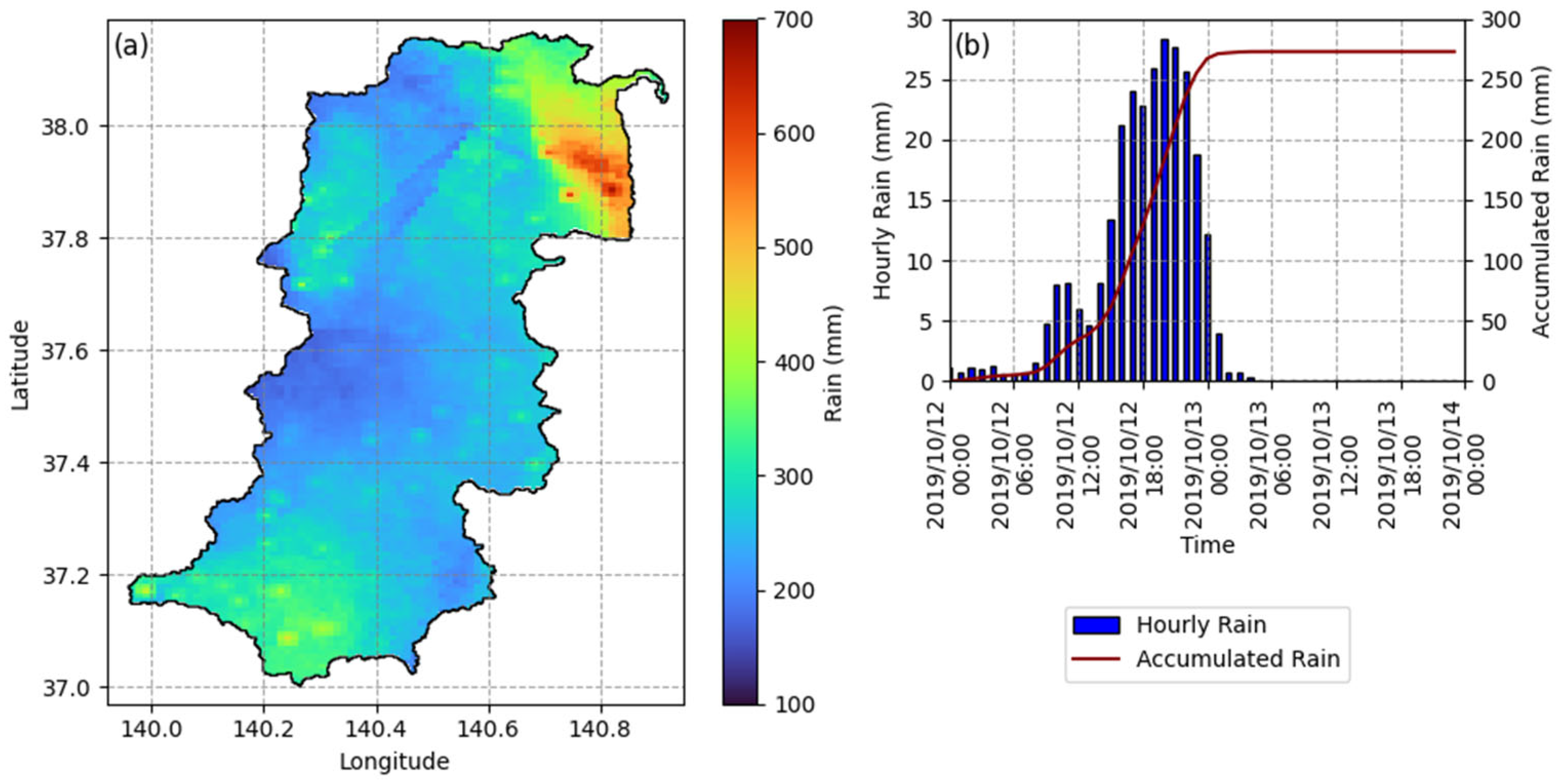
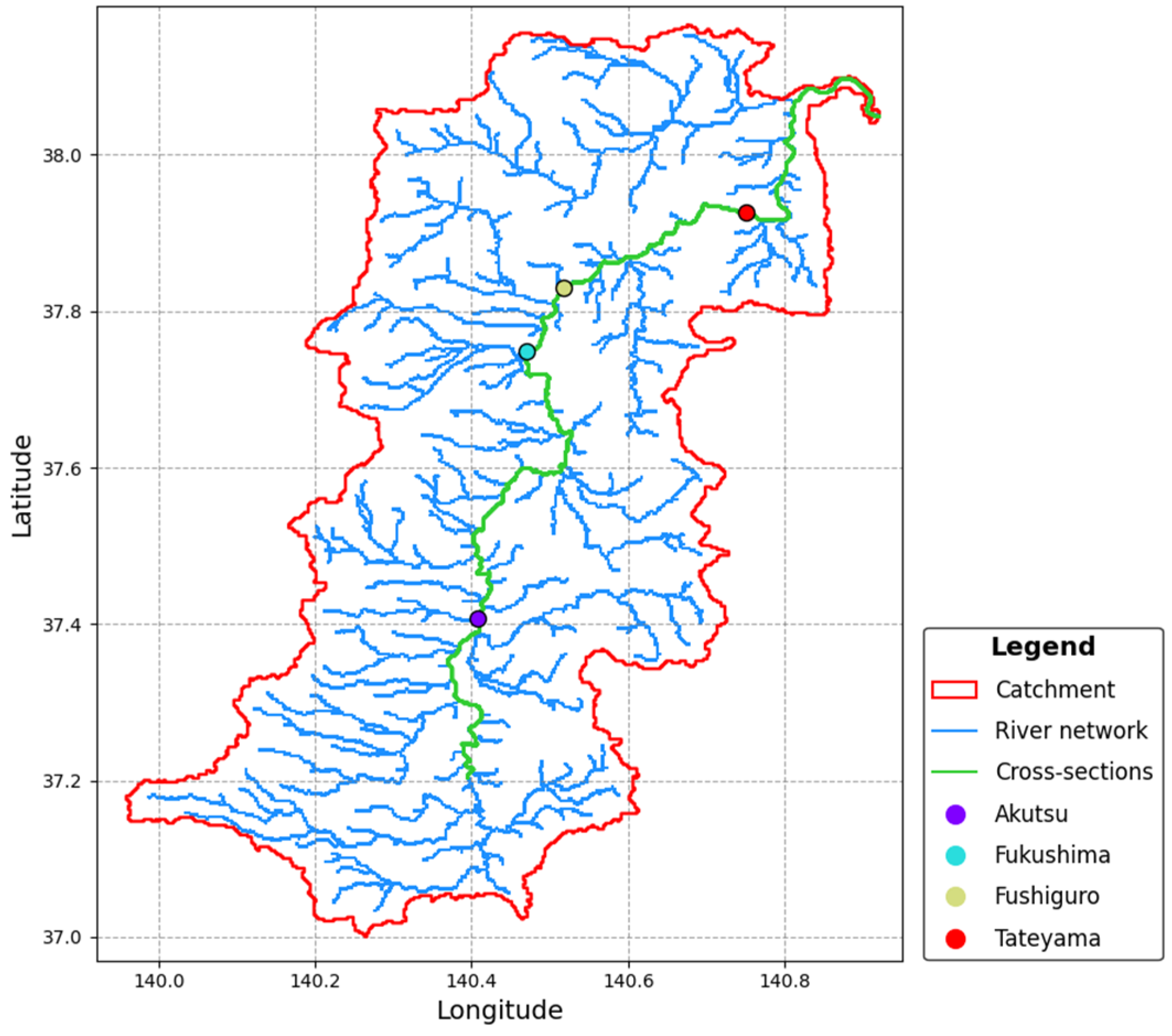
2. Study Area
3. Materials and Methods
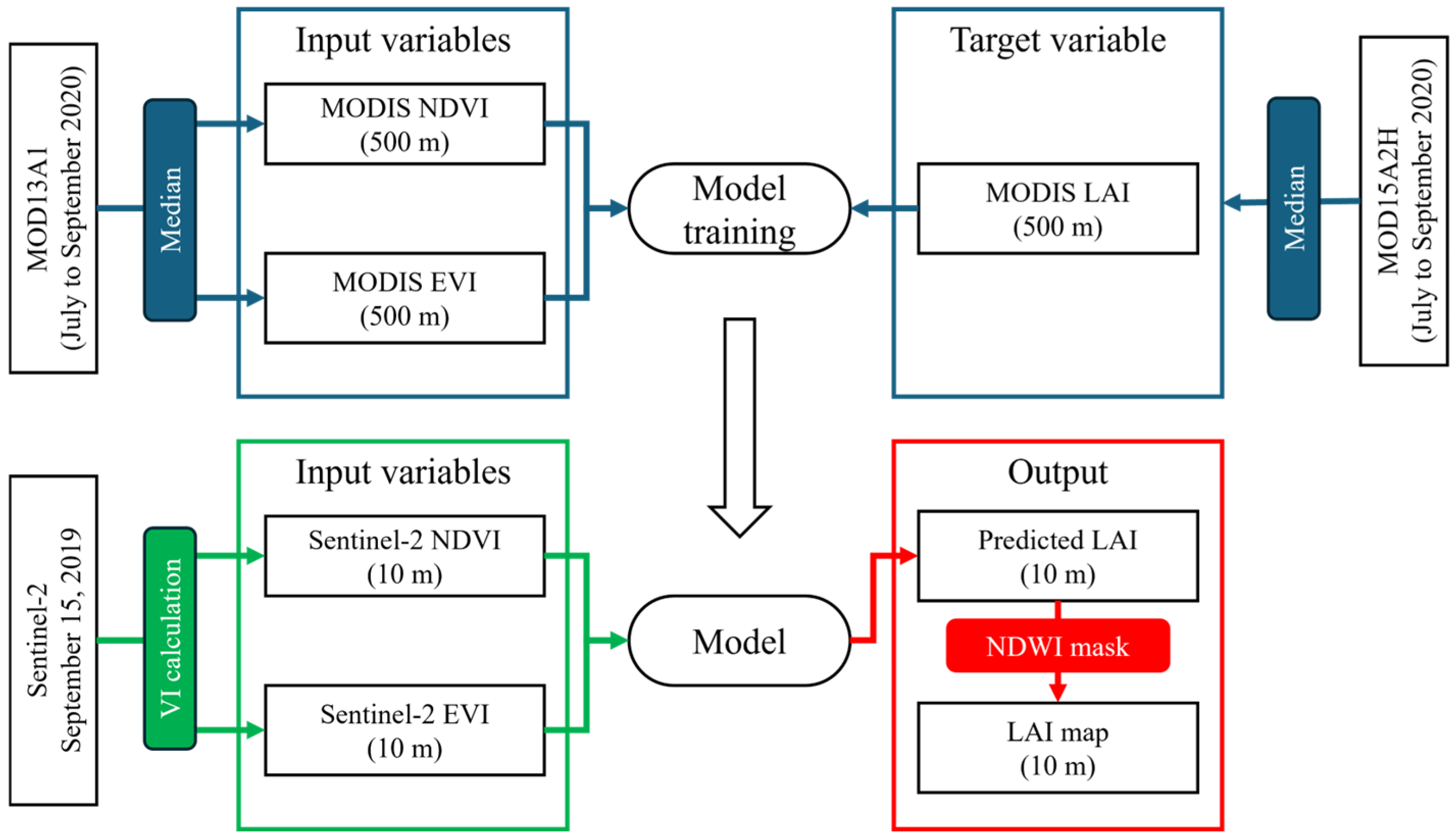
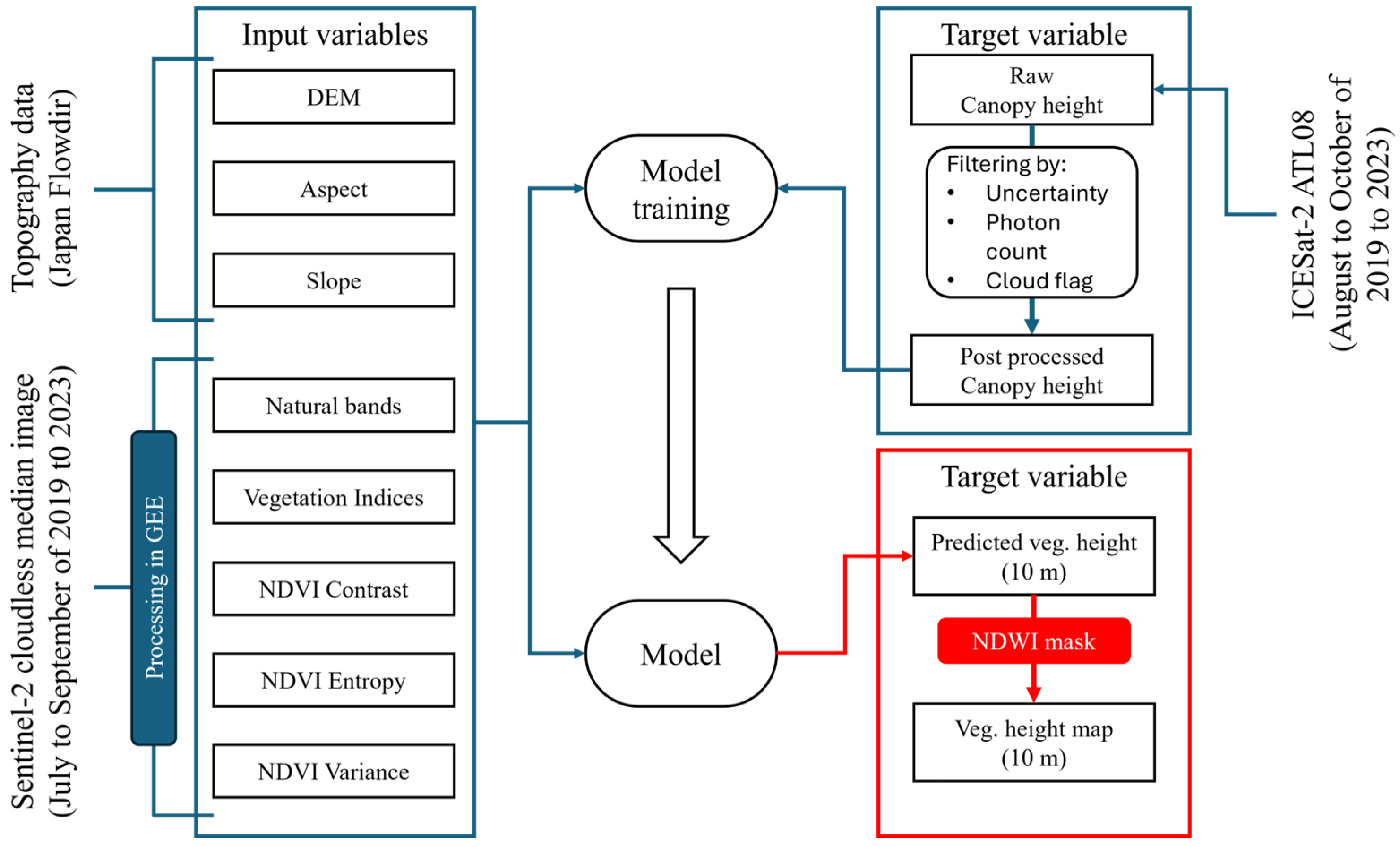
3.1. Mapping Vegetation Parameters
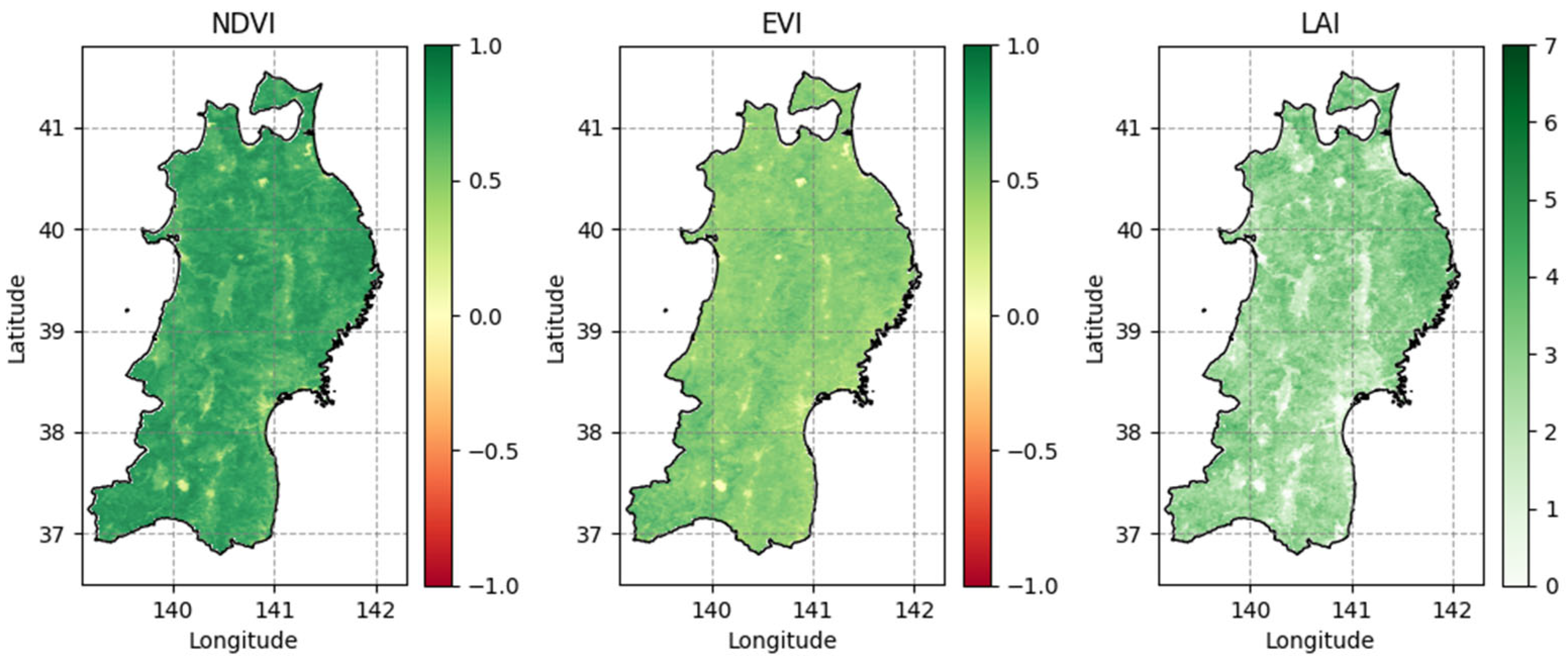
3.1.1. LAI Downscaling
3.1.2. Vegetation Height Extrapolation
3.2. RRI Model
3.2.1. Dynamic Roughness Routine
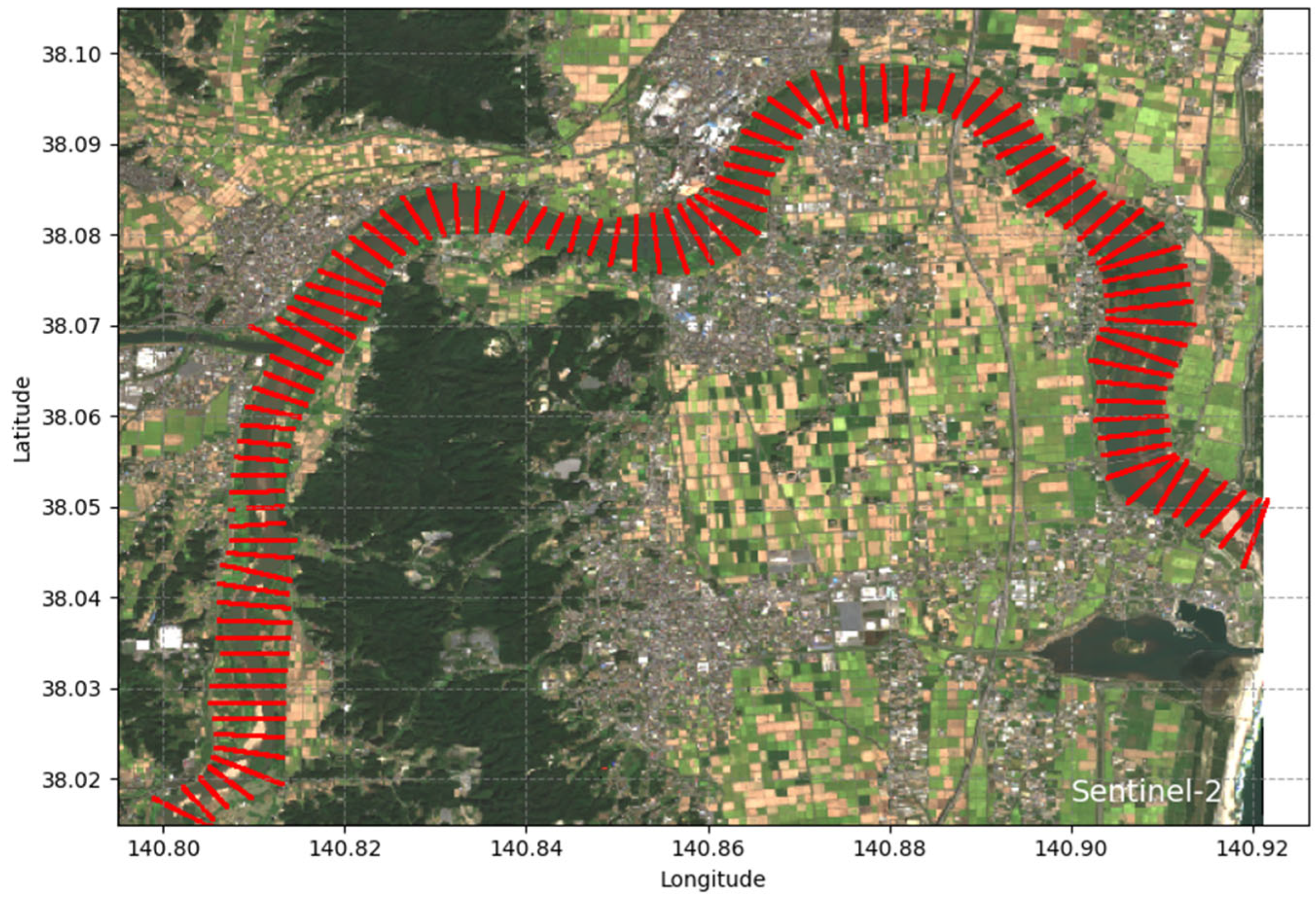
3.2.2. Cross-Sections Vegetation Parameters
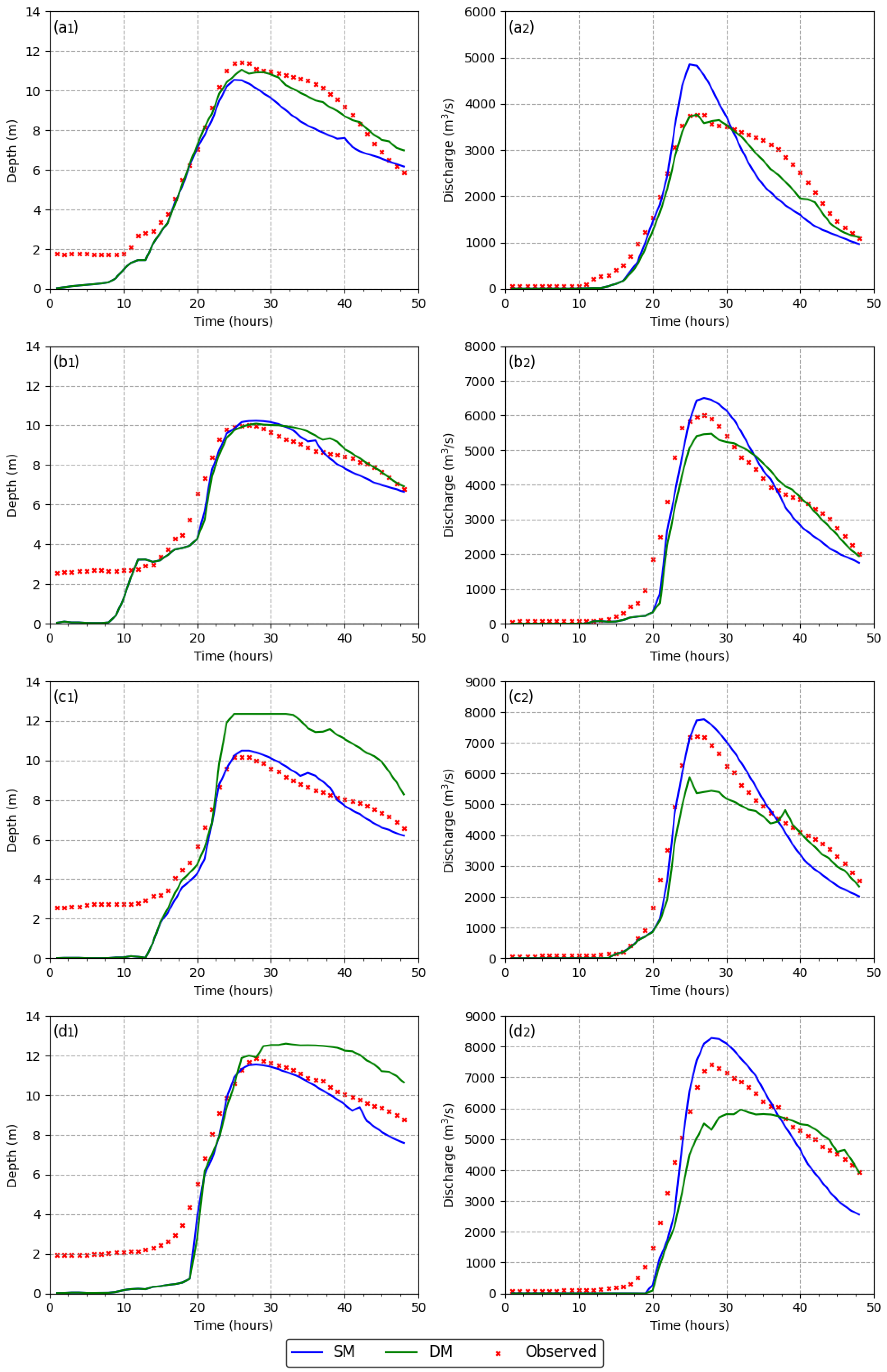
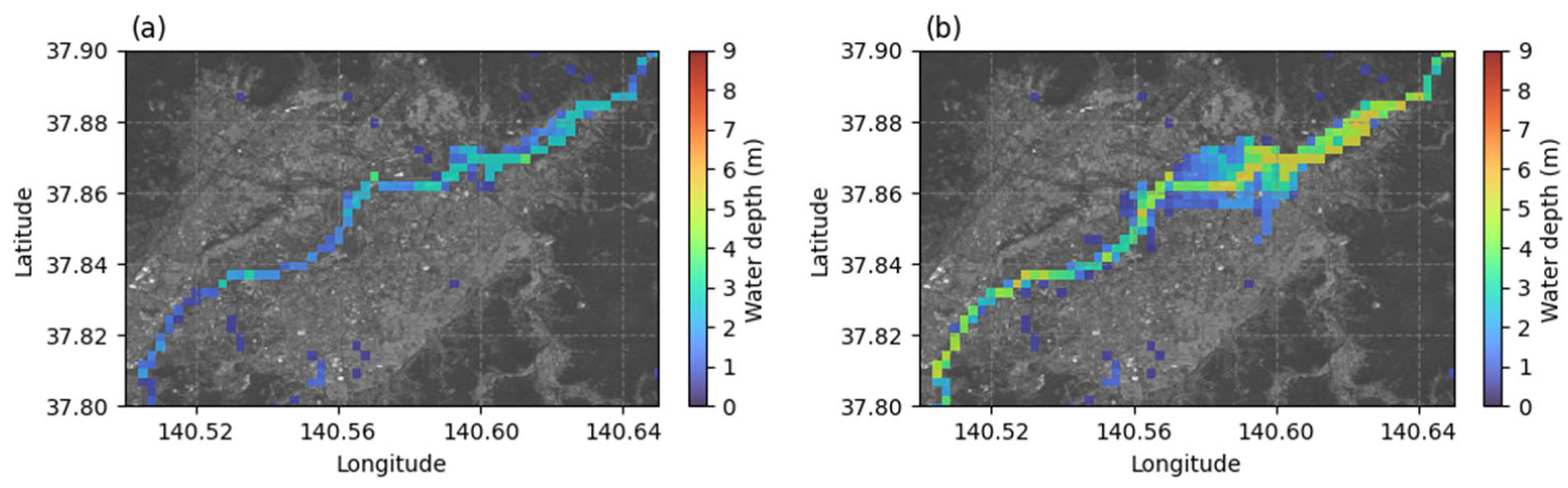
4. Results
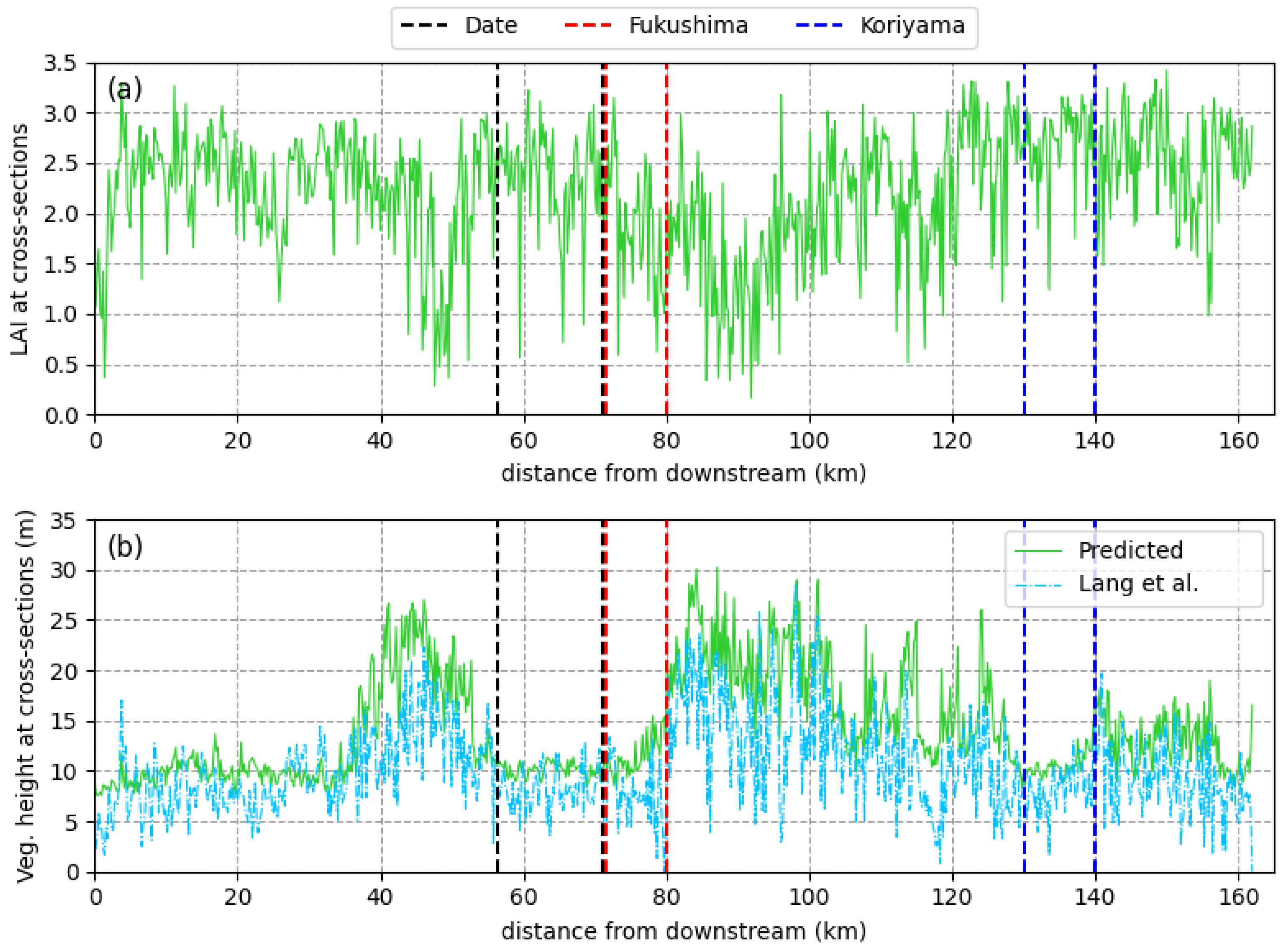
4.1. Vegetation Estimation Results
4.2. Simulation Results
5. Discussions
5.1. Vegetation Parameters in the Floodplains
5.2. Vegetation Effect
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bates, P.D. Remote Sensing and Flood Inundation Modelling. Hydrol. Process 2004, 18, 2593–2597. [Google Scholar] [CrossRef]
- Cowan, W.L. Estimating Hydraulic Roughness Coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Ebrahimi, N.G.; Fathi-Moghadam, M.; Kashefipour, S.M.; Saneie, M.; Ebrahimi, K. Effects of Flow and Vegetation States on River Roughness Coefficients. J. Appl. Sci. 2008, 8, 2118–2123. [Google Scholar] [CrossRef]
- Tabacchi, E.; Lambs, L.; Guilloy, H.; Planty-Tabacchi, A.-M.; Muller, E.; Décamps, H. Impacts of Riparian Vegetation on Hydrological Processes. Hydrol. Process 2000, 14, 2959–2976. [Google Scholar] [CrossRef]
- Järvelä, J. Determination of Flow Resistance Caused by Non-submerged Woody Vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow Resistance of Emergent Rigid and Flexible Floodplain Vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, Turbulence, and Diffusion in Flow through Emergent Vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J.; Aberle, J. Leaf Area Index as Vegetation Density Measure for Hydraulic Analyses. J. Hydraul. Eng. 2013, 139, 461–469. [Google Scholar] [CrossRef]
- Wu, F.-C.; Shen, H.W.; Chou, Y.-J. Variation of Roughness Coefficients for Unsubmerged and Submerged Vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Analytical Solution of the Depth-averaged Flow Velocity in Case of Submerged Rigid Cylindrical Vegetation. Water Resour. Res. 2007, 43, w06413. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M. Flow and Transport in Channels with Submerged Vegetation. Acta Geophys. 2008, 56, 753–777. [Google Scholar] [CrossRef]
- Devi, T.B.; Kumar, B. Experimentation on Submerged Flow over Flexible Vegetation Patches with Downward Seepage. Ecol. Eng. 2016, 91, 158–168. [Google Scholar] [CrossRef]
- Wang, P.; Wang, C.; Zhu, D.Z. Hydraulic Resistance of Submerged Vegetation Related to Effective Height. J. Hydrodyn. 2010, 22, 265–273. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E. Flow Resistance Models for Flexible Submerged Vegetation. J. Hydrol. 2007, 342, 213–222. [Google Scholar] [CrossRef]
- Nikora, V.; Larned, S.; Nikora, N.; Debnath, K.; Cooper, G.; Reid, M. Hydraulic Resistance Due to Aquatic Vegetation in Small Streams: Field Study. J. Hydraul. Eng. 2008, 134, 1326–1332. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.E.; Mynett, A.; Verwey, A. On Inducing Equations for Vegetation Resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid. Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An Analysis of the Influence of Riparian Vegetation on the Propagation of Flood Waves. Environ. Model. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Modeling the Flow Resistance of Woody Vegetation Using Physically Based Properties of the Foliage and Stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the Blade Scale to the Reach Scale: A Characterization of Aquatic Vegetative Drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J. Estimation of Drag Forces Caused by Natural Woody Vegetation of Different Scales. J. Hydrodyn. 2014, 26, 608–623. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow Resistance of Floodplain Vegetation Mixtures for Modelling River Flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- van Iersel, W.; Straatsma, M.; Addink, E.; Middelkoop, H. Monitoring Height and Greenness of Non-Woody Floodplain Vegetation with UAV Time Series. ISPRS J. Photogramm. Remote Sens. 2018, 141, 112–123. [Google Scholar] [CrossRef]
- Fortes, A.A.; Hashimoto, M.; Udo, K.; Ichikawa, K. Satellite and UAV Derived Seasonal Vegetative Roughness Estimation for Flood Analysis. Proc. IAHS 2024, 386, 203–208. [Google Scholar] [CrossRef]
- Fortes, A.A.; Hashimoto, M.; Udo, K.; Ichikawa, K.; Sato, S. Dynamic Roughness Modeling of Seasonal Vegetation Effect: Case Study of the Nanakita River. Water 2022, 14, 3649. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.; Liu, M. Landsat-Scale Regional Forest Canopy Height Mapping Using ICESat-2 Along-Track Heights: Case Study of Eastern Texas. Remote Sens. 2022, 15, 1. [Google Scholar] [CrossRef]
- Chang, Q.; Zwieback, S.; DeVries, B.; Berg, A. Application of L-Band SAR for Mapping Tundra Shrub Biomass, Leaf Area Index, and Rainfall Interception. Remote Sens. Environ. 2022, 268, 112747. [Google Scholar] [CrossRef]
- Lang, N.; Jetz, W.; Schindler, K.; Wegner, J.D. A High-Resolution Canopy Height Model of the Earth. Nat. Ecol. Evol. 2023, 7, 1778–1789. [Google Scholar] [CrossRef]
- Price, J.C. Estimating Leaf Area Index from Satellite Data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 727–734. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Green, E.P.; Mumby, P.J.; Edwards, A.J.; Clark, C.D.; Ellis, A.C. Estimating Leaf Area Index of Mangroves from Satellite Data. Aquat. Bot. 1997, 58, 11–19. [Google Scholar] [CrossRef]
- Gokool, S.; Kunz, R.P.; Toucher, M. Deriving Moderate Spatial Resolution Leaf Area Index Estimates from Coarser Spatial Resolution Satellite Products. Remote Sens. Appl. 2022, 26, 100743. [Google Scholar] [CrossRef]
- Colombo, R. Retrieval of Leaf Area Index in Different Vegetation Types Using High Resolution Satellite Data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Petrou, Z.I.; Tarantino, C.; Adamo, M.; Blonda, P.; Petrou, M. Estimation of Vegetation Height through Satellite Image Texture Analysis. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; Volume 39, p. B8. [Google Scholar]
- Petrou, Z.I.; Manakos, I.; Stathaki, T.; Mucher, C.A.; Adamo, M. Discrimination of Vegetation Height Categories With Passive Satellite Sensor Imagery Using Texture Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1442–1455. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the Relationship of NDVI with Leaf Area Index in a Deciduous Forest Site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Yoshida, K.; Maeno, S.; Ogawa, S.; Mano, K.; Nigo, S. Estimation of Distributed Flow Resistance in Vegetated Rivers Using Airborne Topo-bathymetric LiDAR and Its Application to Risk Management Tasks for Asahi River Flooding. J. Flood Risk Manag. 2020, 13, e12584. [Google Scholar] [CrossRef]
- Harada, S.; Ishikawa, T. Evaluation of the Effect of Hamao Detention Pond on Excess Runoff from the Abukuma River in 2019 and Simple Remodeling of the Pond to Increase Its Flood Control Function. Appl. Sci. 2022, 12, 729. [Google Scholar] [CrossRef]
- Konami, T.; Koga, H.; Kawatsura, A.; Matsuyoshi, K.; Ida, N. Research on Proper Flood Information Service Based on the Flood Caused by Typhoon Hagibis in 2019 in the Upper Abukuma River Basin. J. JSCE 2022, 10, 513–520. [Google Scholar] [CrossRef]
- Moriguchi, S.; Matsugi, H.; Ochiai, T.; Yoshikawa, S.; Inagaki, H.; Ueno, S.; Suzuki, M.; Tobita, Y.; Chida, T.; Takahashi, K.; et al. Survey Report on Damage Caused by 2019 Typhoon Hagibis in Marumori Town, Miyagi Prefecture, Japan. Soils Found. 2021, 61, 586–599. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Sun, R.; Zhou, H.; Zhang, H. A Model-Downscaling Method for Fine-Resolution LAI Estimation. Remote Sens. 2020, 12, 4147. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Ovakoglou, G.; Clevers, J.G.P.W. Relationship between MODIS EVI and LAI across Time and Space. Geocarto Int. 2020, 35, 1385–1399. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Neuenschwander, A.; Pitts, K. The ATL08 Land and Vegetation Product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Yamazaki, D.; Togashi, S.; Takeshima, A.; Sayama, T. High-Resolution Flow Direction Map of Japan. J. JSCE 2020, 8, 234–240. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Lourenço, R.B.; Kurz, W.A.; Snider, J. Spatially Continuous Mapping of Forest Canopy Height in Canada by Combining GEDI and ICESat-2 with PALSAR and Sentinel. Remote Sens. 2022, 14, 5158. [Google Scholar] [CrossRef]
- Sayama, T.; Tatebe, Y.; Iwami, Y.; Tanaka, S. Hydrologic Sensitivity of Flood Runoff and Inundation: 2011 Thailand Floods in the Chao Phraya River Basin. Nat. Hazards Earth Syst. Sci. 2015, 15, 1617–1630. [Google Scholar] [CrossRef]
- Sayama, T.; Tatebe, Y.; Tanaka, S. An Emergency Response-Type Rainfall-Runoff-Inundation Simulation for 2011 Thailand Floods. J. Flood Risk Manag. 2017, 10, 65–78. [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall–Runoff–Inundation Analysis of the 2010 Pakistan Flood in the Kabul River Basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; US Geological Survey: Denver, CO, USA, 1989.
- Ishizaki, H.; Matsuyama, H. Distribution of the Annual Precipitation Ratio of Radar/Raingauge-Analyzed Precipitation to AMeDAS across Japan. SOLA 2018, 14, 192–196. [Google Scholar] [CrossRef]




| Variable | Formula |
|---|---|
| Normalized difference vegetation index (NDVI) | |
| Enhanced vegetation index (EVI) | |
| Modified soil adjusted vegetation index (MSAVI2) | |
| Atmospheric resistant vegetation index (ARVI) | |
| Red-edge Chlorophyll index (RECI) | |
| Red-green vegetation index (RGVI) | |
| Red-edge normalized vegetation index a (ReNDVIa) | |
| Red-edge normalized vegetation index b (ReNDVIb) | |
| Visible atmospherically resistant index (VARI) |
| Land Class | Manning’s n | Soil Depth (m) | Porosity | Infiltration (m/s) | Unsat. Porosity |
|---|---|---|---|---|---|
| Forest | 0.16 | 0.5 | 0.501 | 0.1 | 0.03 |
| Small vegetation | 0.04 | 0.5 | 0.501 | 0.1 | 0.03 |
| Water bodies | 0.03 | 0.5 | 0.501 | 0.1 | 0.50 |
| Buildings | 0.15 | 0.5 | 0.501 | 0.1 | 0.10 |
| Metric | LAI | Veg. Height (m) |
|---|---|---|
| MAE | 0.36 | 4.2 |
| MSE | 0.27 | 30.3 |
| RMSE | 0.52 | 5.5 |
| R | 0.79 | 0.74 |
| R2 | 0.62 | 0.55 |
| Station | Nash–Sutcliffe | RMSE (m) | |
|---|---|---|---|
| Akutsu | SM | 0.87 | 1.31 |
| DM | 0.94 | 0.87 | |
| Fukushima | SM | 0.80 | 1.27 |
| DM | 0.79 | 1.29 | |
| Fushiguro | SM | 0.69 | 1.55 |
| DM | 0.22 | 2.46 | |
| Tateyama | SM | 0.86 | 1.49 |
| DM | 0.78 | 1.85 | |
| Station | Nash–Sutcliffe | RMSE (m3/s) | |
|---|---|---|---|
| Akutsu | SM | 0.84 | 555.79 |
| DM | 0.96 | 268.35 | |
| Fukushima | SM | 0.92 | 590.70 |
| DM | 0.93 | 565.00 | |
| Fushiguro | SM | 0.95 | 549.15 |
| DM | 0.91 | 712.13 | |
| Tateyama | SM | 0.92 | 798.38 |
| DM | 0.90 | 870.21 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fortes, A.A.; Hashimoto, M.; Udo, K. Application of Remote Sensing Floodplain Vegetation Data in a Dynamic Roughness Distributed Runoff Model. Remote Sens. 2025, 17, 1672. https://doi.org/10.3390/rs17101672
Fortes AA, Hashimoto M, Udo K. Application of Remote Sensing Floodplain Vegetation Data in a Dynamic Roughness Distributed Runoff Model. Remote Sensing. 2025; 17(10):1672. https://doi.org/10.3390/rs17101672
Chicago/Turabian StyleFortes, Andre A., Masakazu Hashimoto, and Keiko Udo. 2025. "Application of Remote Sensing Floodplain Vegetation Data in a Dynamic Roughness Distributed Runoff Model" Remote Sensing 17, no. 10: 1672. https://doi.org/10.3390/rs17101672
APA StyleFortes, A. A., Hashimoto, M., & Udo, K. (2025). Application of Remote Sensing Floodplain Vegetation Data in a Dynamic Roughness Distributed Runoff Model. Remote Sensing, 17(10), 1672. https://doi.org/10.3390/rs17101672







