Next Article in Journal
Cloud and Aerosol Impacts on the Radiation Budget over China from 2000 to 2023
Previous Article in Journal
Spatiotemporal Dynamics of Habitat Quality in Semi-Arid Regions: A Case Study of the West Songnen Plain, China
Previous Article in Special Issue
A Comparative Evaluation of Two Bias Correction Approaches for SST Forecasting: Data Assimilation Versus Deep Learning Strategies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 10
10.3390/rs17101665
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Automated Eddy Identification and Tracking in the Northwest Pacific Based on Conventional Altimeter and SWOT Data

by
Lan Zhang
1,2,
Cheinway Hwang
3,*,
Han-Yang Liu
3,
Emmy T. Y. Chang
4 and
Daocheng Yu
5
1
Institute of Earthquake Forecasting, China Earthquake Administration, No. 63, Fuxing Road, Beijing 100036, China
2
Institute of Geodesy and Geoinformation, University of Bonn, 53115 Bonn, Germany
3
Department of Civil Engineering, National Yang Ming Chiao Tung University, 1001 Ta Hsueh Road, Hsinchu 300, Taiwan
4
Institute of Oceanography, National Taiwan University, No. 1, Sec. 4, Roosevelt Road, Taipei 106, Taiwan
5
School of Geomatics, Liaoning Technical University, Fuxin 123000, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(10), 1665; https://doi.org/10.3390/rs17101665
Submission received: 22 February 2025 / Revised: 4 May 2025 / Accepted: 5 May 2025 / Published: 9 May 2025
(This article belongs to the Special Issue Satellite Remote Sensing for Ocean and Coastal Environment Monitoring)
Browse Figures
Review Reports Versions Notes

Abstract

:
Eddy identification and tracking are essential for understanding ocean dynamics. This study employed the elliptical Gaussian function (EGF) simulations and the py-eddy-tracker (PET) algorithm, validated by Surface Velocity Program (SVP) drifter data, to track eddies in the western North Pacific Ocean. The PET method effectively identified large- and mesoscale eddies but struggled with submesoscale features, indicating areas for improvement. Simulated satellite altimetry by EGF, mirroring Surface Water and Ocean Topography (SWOT)’s high-resolution observations, confirmed PET’s capability in processing fine-scale data, though accuracy declined for submesoscale eddies. Over 22 years, 1,188,649 eddies were identified, mainly concentrated east of Taiwan. Temporal analysis showed interannual variability, more cyclonic than anticyclonic eddies, and a seasonal peak in spring, likely influenced by marine conditions. Short-lived eddies were uniformly distributed, while long-lived ones followed major currents, validating PET’s robustness with SVP drifters. The launch of the SWOT satellite in 2022 has enhanced fine-scale ocean studies, enabling the detection of submesoscale eddies previously unresolved by conventional altimetry. SWOT observations reveal intricate eddy structures, including small cyclonic features in the northwestern Pacific, demonstrating its potential for improving eddy tracking. Future work should refine the PET algorithm for SWOT’s swath altimetry, addressing data gaps and unclosed contours. Integrating SWOT with in situ drifters, numerical models, and machine learning will further enhance eddy classification, benefiting ocean circulation studies and climate modeling.

1. Introduction

Oceanic eddies, rotating fluid structures prevalent in the ocean’s dynamic system, exhibit considerable variation across a broad spectrum of spatial and temporal scales. The spatial scales of the mesoscale eddies and submesoscale eddies are usually bounded by the Rossby deformation radius. The oceanic mesoscale can be characterized as consisting of variability with radius scales of 10–500 km [1]. Mesoscale eddies are primarily driven by geostrophic balance, significantly influencing large-scale ocean circulation and nutrient transport [2,3]. In contrast, submesoscale eddies are smaller (less than 10 km), transient (lasting days to weeks), and driven by frontal dynamics and mixed-layer instabilities, playing a crucial role in vertical exchanges of heat, momentum, and biogeochemical properties [3,4]. To more clearly delineate the scale range of eddies identified and tracked in this study, we classify oceanic eddies into three categories: large-scale eddies, with dimensions up to 100 km; mesoscale eddies, measuring between 10 and 100 km; and submesoscale or small-scale eddies, characterized by diameters less than 10 km. The small-scale eddies referred to in this study differ from those described by [1,2], whose work focused exclusively on mesoscale eddies with radii greater than approximately 40 km. The term ‘small-scale eddies’ in [1] refers to mesoscale eddies at the lower end of the mesoscale range, which still fall within the mesoscale regime. The temporal presence of these eddies can vary significantly, lasting from several days to multiple months, illustrating their dynamic nature [5,6].
The advent and subsequent advancement of satellite altimeter technology has made high-resolution altimeter satellites essential for studying ocean eddies. These satellites provide critical data on key oceanic parameters, such as sea level anomaly (SLA), absolute dynamic topography (ADT), and geostrophic currents, which are essential for robust identification, detection, and analysis of eddies. The formation and evolution of eddies have a substantial impact on ocean circulation, climate variability, marine biology, and other interconnected fields, underscoring the importance of their study [7,8,9,10,11,12]. The integration of data from multiple altimeter satellites for the identification and analysis of large-scale and mesoscale eddies has become a focal point in modern oceanographic research.
Despite these technological strides, the current literature reveals limitations in the comprehensive tracking and analysis of oceanic eddies, especially concerning mesoscale, submesoscale, and small-scaled formations. Early methods for using satellite altimeter data for eddy identification included manual visual analysis, which required researchers to identify oceanic eddies by visually analyzing SLA fields. This approach was inefficient and subjective, leading to inconsistent eddy identification and significant errors. The first automated procedure for detection and tracking of eddies in altimeter data were developed by [13], building upon techniques developed previously for turbulence studies from numerical model simulations [14,15,16]. The Okubo–Weiss threshold method often used simple thresholds to identify eddies, such as considering local maxima or minima on SLA images as eddy centers, requiring careful sensitivity analysis to avoid over-identification or under-identification of eddies [1]. Subsequent studies have fine-tuned the methodology to address various shortcomings [2,17,18]. The procedures for identifying eddies relate to geostrophic current velocity analysis [13,17,18,19], involving data smoothing and requiring the computation of SLA derivatives, which could reduce the resolution of the flow field and amplify any noise that is present in the SLA field [1,20]. These methods are mainly used for identifying large and mesoscale eddies.
The capacity to accurately detect and analyze submesoscale eddies remains a formidable challenge due to limitations in spatial resolution and the sensitivity of methodologies to inherent noise within satellite altimeter data. The nuanced dynamics of these submesoscale eddies are crucial for explaining the finer details and transient processes of ocean dynamics, especially in terms of vertical material exchange in the ocean [21,22], yet they are frequently underrepresented or insufficiently captured in existing studies [1,6,23]. Recent advancements, particularly the launch of the SWOT satellite in December 2022, have significantly enhanced the study of fine-scale oceanic features. SWOT offers new insights into ocean dynamics and the role of submesoscale eddies in climate processes (https://cnes.fr/en/press-releases/two-years-launch-exceptionally-precise-swot-data-reap-rewards-30-years-progress, accessed on 5 May 2025), providing an opportunity to overcome previous limitations in identifying submesoscale eddies [24]. For instance, SWOT has successfully captured submesoscale cyclonic eddies in the northwestern Pacific, providing unprecedented detail on these dynamic structures [25].
In response to these challenges and opportunities, this paper aims to address the identified limitations in existing methodologies for eddy detection and analysis, with particular emphasis on identifying and tracking eddies across varying scales. By employing the Py_Eddy_Tracking (PET) algorithm developed by [26,27,28] based on the theoretical framework in [1], this study attempts to reconstruct the 22-year spatiotemporal variability of mesoscale eddies in the northwest Pacific and to evaluate the robustness of eddy tracking methodologies. Additionally, this research explores the potential of Surface Water and Ocean Topography (SWOT) sea level measurements in detecting ocean eddies. Launched on 16 December 2022, SWOT represents a breakthrough in identifying fine-scaled variations in ocean surface water [29]. Through the improvement of eddy tracking methodologies and validation using in situ data, this paper seeks to contribute to the oceanographic community’s capacity to study and interpret the intricate and dynamic nature of oceanic eddies. We report on the short-term and long-term spatiotemporal evolution of ocean eddies in the northwest Pacific Ocean, validated by drifter data. For the first time, we demonstrate how SWOT altimeter data can be used in studying submesoscale eddies in the northwest Pacific Ocean and highlight SWOT’s current limitations.

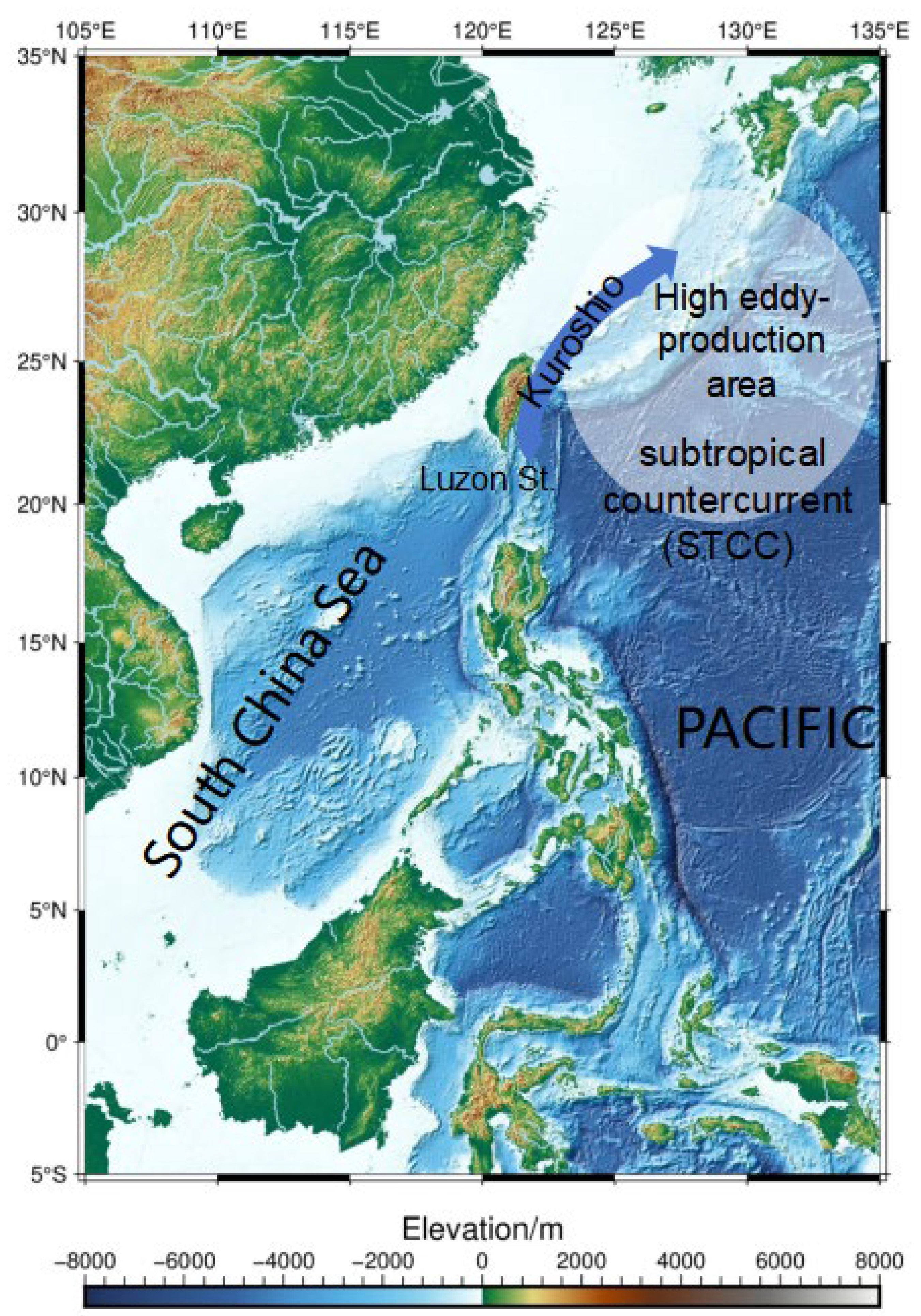
2. Study Area

The study area (Figure 1) is situated in the northwest Pacific Ocean, primarily south of Japan, encompassing the South China Sea (SCS), the waters off Taiwan, and the region east of Taiwan within the North Pacific subtropical countercurrent (STCC) zone. This region is characterized by dynamic oceanic conditions and complex circulatory patterns that play a critical role in the formation and behavior of ocean eddies.
The oceanography of this area is influenced by several major currents, most notably the Kuroshio Current, which flows northward along the eastern coast of Taiwan before turning eastward at the latitude of Japan. The interaction between the Kuroshio Current and the STCC creates a unique marine environment conducive to the generation of mesoscale and submesoscale eddies [30,31,32]. These eddies significantly influence heat, nutrient transport, and biological productivity across vast areas of the Pacific [7,33,34].
Furthermore, the Luzon Strait, situated south of Taiwan, acts as a key gateway for the exchange of water masses between the SCS and the Pacific Ocean. This strait is a region of intense eddy activity, influenced by the variable bathymetry and the interaction of the Kuroshio Current with local water masses [35,36]. The presence of these eddies contributes to complex circulation patterns that have significant implications for regional climate and marine ecosystems [37,38]. Recent studies highlight the prolific eddy activity in offshore eastern Taiwan, west of the STCC zone, where the convergence of different water masses and the influence of monsoonal winds exacerbate the conditions for eddy formation [39,40]. These eddies typically follow a west-northwestward trajectory, interacting with the Kuroshio and playing a crucial role in the lateral mixing of ocean waters and the distribution of biological and chemical constituents [12].
This study area was chosen due to its dynamic nature, providing an ideal setting for evaluating the capabilities of conventional nadir-looking altimeters and the wide-swath SWOT altimeter. The high-resolution data from these instruments enable a more detailed examination of mesoscale and submesoscale eddies, enhancing our understanding of their formation, evolution, and impacts on oceanic and atmospheric processes. The application of the PET algorithm and SWOT data in this region aims to address the current limitations in eddy detection and tracking, offering new insights into the intricate dynamics of ocean eddies.

3. Satellite Altimeter and In Situ Data

3.1. Altimeter Data

We use the daily global gridded SLA provided by the Copernicus Marine Environment Monitoring Service (CMEMS, marine.copernicus.eu), covering the period from 2000 to 2023. The SLA grids have a resolution of 0.25° × 0.25° and integrate observations from multiple altimetry satellites, including ERS-1/2, TOPEX/Poseidon (T/P), Jason-1/2/3, Cryosat-2, Saral/AltiKa, HY-2, and among others. SLA is calculated from the sea surface height (SSH) measured by satellite altimetry by subtracting the mean sea surface, which is the average SSH from 1993 to 2012 used in this study, and applying corrections for tides, atmospheric pressure, and electromagnetic biases. CMEMS datasets also provide geostrophic velocity components in eastward and northward directions, which are directly used in our tracking algorithm. In this paper, such SLA grids refer to grids from conventional altimetry.
The SWOT mission employs Ka-band Radar Interferometer (KaRIn), which makes measurements over a swath of 120 km (with a 20 km nadir gap that is sampled with coarse resolution along the centerline by a conventional altimeter), providing the first direct observations of ocean topography and land surface water in two dimensions [29]. One of its objectives is to measure SSH and terrestrial water heights. The KaRIn measurement technique reveals the cascading of ocean circulation processes from large scale to submesoscale, down to ~5 km in wavelength, using two synthetic aperture radar (SAR) antennas separated by a 10 m mast for interferometry in orbit [29]. We have used Level 3 expert products (L3_LR_SSH_Expert) from the SWOT mission, both in the CalVal orbit (pass 21 in the 1-day repeat/fast sampling orbit) from 29 March 2023 to 9 July 2023, and in the science orbit (21-day repeat; 4 cycles are used in this study) within the study area, from 7 September 2023, to 21 November 2023. The Level 3 products have employed a series of corrections (ocean tide from the FES22 model, solid earth tide, coherent internal tide, pole tide, and dynamic atmospheric corrections, removing spurious pixels) and mitigated random errors using an AI-based algorithm [41,42].

3.2. Drifter Data

To verify the eddy tracking results, we use drifter data from the Surface Velocity Program (SVP) [43]. A SVP drifter is a Lagrangian current-following device designed to track water currents at a depth of 15 m beneath the ocean surface. It is equipped with a buoy at the surface and a steel cable extending below, which holds multiple sensors. This setup allows the SVP drifter to collect data on ocean surface velocity by tracking the movement of the buoy and to gather temperature data via sensors on the cable. The collected information is transmitted to the surface buoy. This design allows effective measurement of the ocean’s surface velocity and temperature over extended periods and across wide areas. We used SVP drifter data from 1 January 2004 to 1 January 2005, and from 1 January 2018 to 1 January 2019. The drifter data were obtained from the Global Drifter Program website (https://www.aoml.noaa.gov/phod/gdp/index.php, accessed on 5 May 2025).

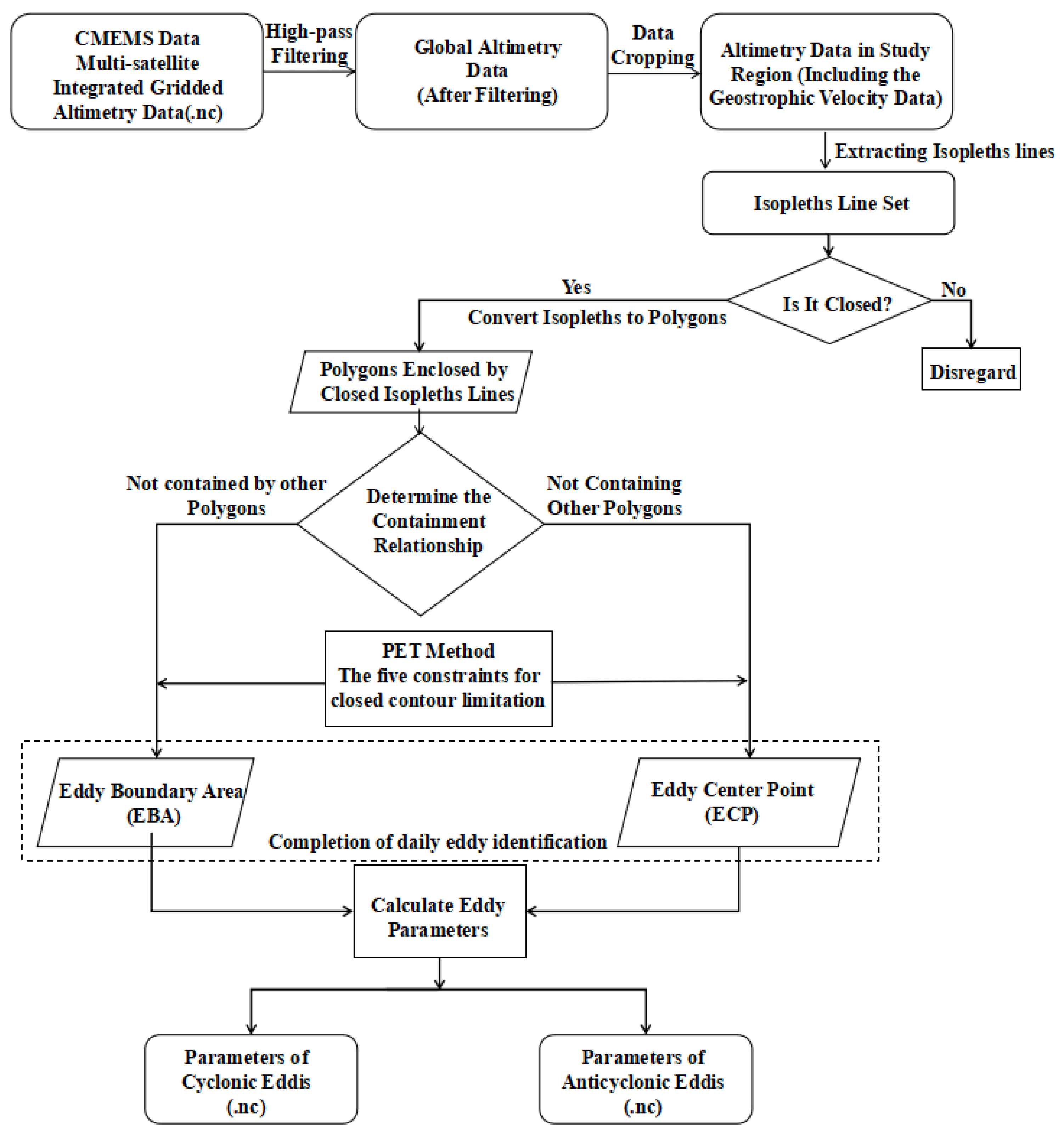
4. Methods for Automatic Identification and Tracking of Eddies

4.1. Automated Identification and Tracking

We identified and tracked eddies by analyzing local extremum values in SLA and the velocity vectors of the eddies (geostrophic velocity) using an automated algorithm, PET (https://py-eddy-tracker.readthedocs.io/en/stable/, accessed on 5 May 2025), as described by [1,25]. Figure 2 shows the workflow for eddy identification. The process starts by applying a high-pass filter with a radius of 300–500 km to the daily SLA maps to emphasize significant SLA signals. These filtered SLA maps are then analyzed to find closed contours (isopleths) ranging from −100 to 100 cm, with a minimum separation of 0.4 cm between them. Isopleths that are not closed are disregarded. The algorithm then evaluates the containment relationships among polygons formed by closed isopleths. Polygons not enclosed by others are identified as eddy boundaries, while those not enclosing others are marked as eddy centers. Based on five closed-contour constraints [26] (Appendix A), eddies are classified as anticyclonic (center point higher than surroundings) or cyclonic (center point lower than surroundings).
Eddy tracking maps the movement of an eddy’s center from formation to dissipation, conducted separately for anticyclonic and cyclonic types. The method identifies eddies that intersect across consecutive time steps. An eddy with no intersection is considered dissipated. If exactly two eddies intersect, they are treated as the same eddy. When more than two intersect, indicating potential merging or splitting, a cost function from [44] is applied to ensure continuity. Further details are provided in [26,44]. The five PET algorithm constraints for closed contours were also applied to higher-resolution altimeter datasets, such as SWOT SLA data. A minimum area of 8 pixels allows detection of the smallest submesoscale eddies, which typically exhibit SLA amplitudes of a few to several tens of centimeters. We use 0.4 cm contour intervals to meets the resolution needs for their identification. Details of the constraints are provided in Appendix A.

4.2. Validating PET Identification Using Simulated Eddies at Various Scales

Here, we validate eddy identification by the PET method using simulated eddies and explain the radii associated with eddy boundaries. We employ the elliptical Gaussian function (EGF) to simulate ocean eddies at the large, meso-, and sub-mesoscales to see how eddy sizes are related to identification errors. The expression for EGF is detailed in Appendix B. Ref. [45] noted that the most typical shape of an ocean eddy closely resembles that of a Gaussian curve. In this study, we simulated eddies on various spatial scales. The SLA values for these eddies are given on a 0.018° × 0.018° grid within the study area (Figure 1) to match the spatial resolution of SWOT. Table 1 shows the EGF parameters (Appendix B) for the simulated eddies.
Figure 3 illustrates the simulated SLA and the corresponding closed contours of different scales. The results identified using the PET algorithm by inputting these simulated SLA data are shown in Figure 4. The identification of anticyclonic eddies is clearly demonstrated in all three examples, as indicated by the red contours in Figure 4, which correspond to the size and position settings in Figure 3. The red dashed line represents the identified eddies with the Effective Radius (ER) of the eddy, while the solid red line indicates the eddies with the Speed-based Radius (SR). ER represents the spatial extent or the average radius of an eddy, serving as a measure of the eddy’s overall size. A larger effective radius suggests that an eddy can affect a more extensive area, potentially impacting a greater volume of water. Traditionally, the spatial extent of an eddy is determined by setting an SLA threshold, such as 2 mm [46]. In the PET algorithm, this could be adjusted based on the maximum pixel value. High-pass filtering tends to increase the area of the identified eddy. In our simulation, we assigned smaller maximum pixel values for eddies of various scales to reduce the size errors caused by filtering. The SR refers to the radius of a circle with the same area as that within the closed contours of the SLA, where the average geostrophic speed is maximized. SR helps in understanding the intensity and rotational dynamics of the eddy. Eddies with larger speed radii typically exhibit stronger rotational forces over a more extensive area. In the following sections, the closed contours corresponding to ER and SR are used to represent the shape and size of the identified eddy. We note from Figure 4c and Table 2 that for submesoscale eddies, the relative difference between ER and SR tends to decrease due to their compact structure and limited radial velocity gradient.
Table 2 shows the statistics for the parameters of identified eddies across various scales, including the ER, SR, the fitted circle radius (FCR, the squared root of the product of the set semi-major and semi-minor axes), and their associated errors. For eddies of all scales, the ER exceeds the FCR, a discrepancy attributed to high-pass filtering that enlarges the range of the eddies. With the spatial filtering applied in the objective analysis used to produce SLA gridded maps [1] (Appendix A), eddies having an amplitude weaker than ~1–2 cm or a radius smaller than ~40 km should probably be considered as noisy artifact structures on the daily SLA maps based on conventional altimeter data [44]. For large and mesoscale eddies, the ER closely matches the radii established in the simulated data, with relative errors for FCR of 5.2% and 10.2%, respectively; SR is only half of the ER. Ref. [26] pointed out that, compared to the CSS11 eddies datasets [1], where SR is about 70% of ER, the speed radius identified by the PET method is smaller. For submesoscale eddies, the relative error between ER and FCR significantly increases to 39%, and ER is the same size as SR. The results presented in Table 2 suggest that while the PET algorithm is effective, it can be further refined to improve the detection and characterization of submesoscale eddies.

5. Results and Discussions

5.1. Eddies from Conventional Altimeter Data

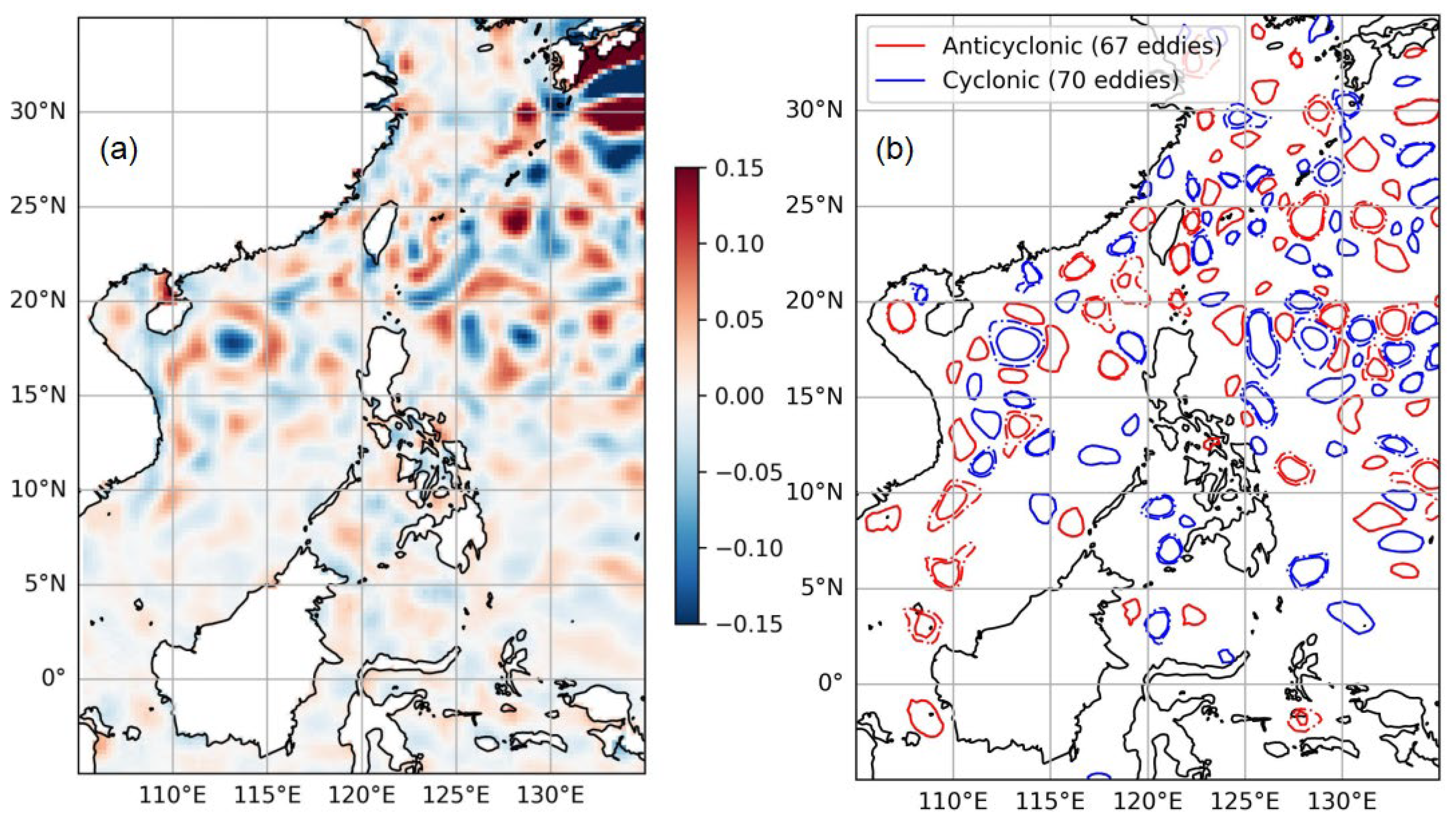
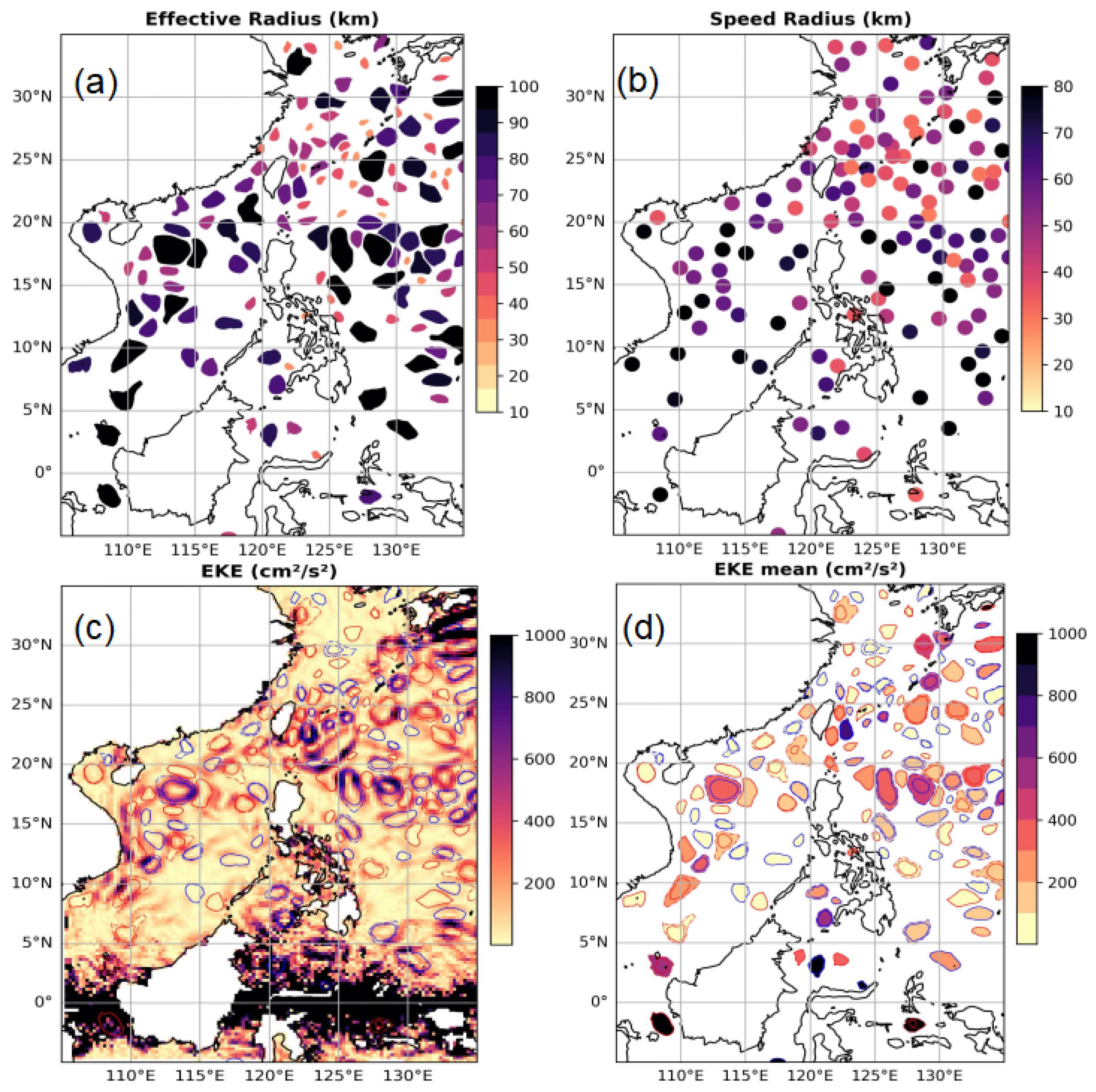
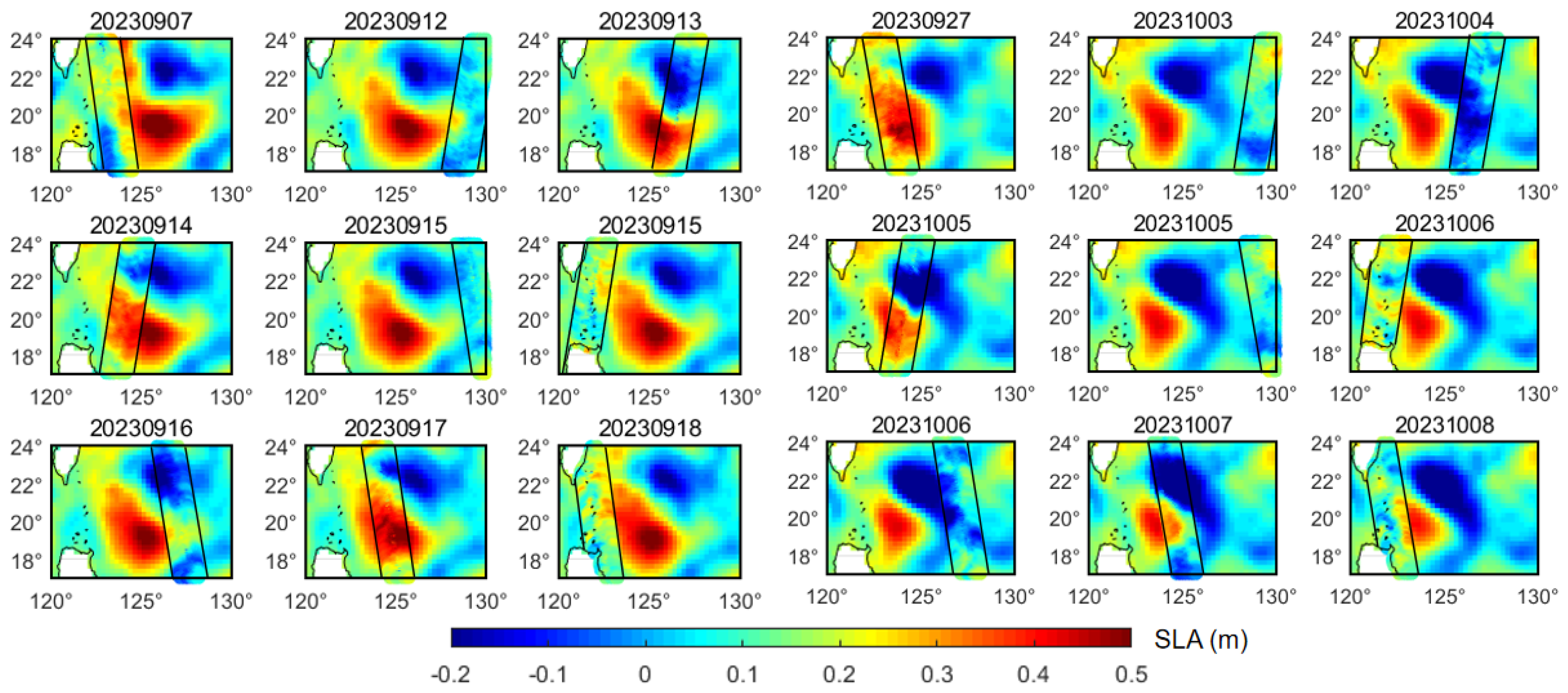
5.1.1. Snapshot of Ocean Eddies: A Case Study from 1 May 2023

As we transition into the results of our study, this section offers an analysis of the ocean eddies identified on a representative day in spring 2023. This initial exploration is important for understanding the complicated behaviors and characteristics of eddies within one day and for showing the capabilities of the PET algorithm in discerning subtle yet significant oceanic features for subsequent analyses.
We chose 1 May 2023 as the date for illustration. Figure 5a shows the spatial distribution of SLA following the application of a 500 km high-pass filter. Here, red denotes areas with higher SLA values, and blue signifies regions with lower SLA values, effectively highlighting large- to meso-scale sea surface height anomalies. The application of a high-pass filter helps to remove large-scale variability and emphasize mesoscale structures such as eddies. This method is particularly effective in regions with strong currents and complex topography [1]. Figure 5a shows noticeable eddy-like structures, particularly around the 20°N latitude.
Figure 5b shows that a total of 67 cyclonic and 70 anticyclonic eddies were identified from the analysis in Figure 5a and further refined through the PET algorithm using five contour constraints (Appendix A). The solid and dashed lines within Figure 5b delineate the effective and speed-related contours of these eddies, respectively. In the eastern region of Taiwan, there is a significant presence of highly active eddies originating from the distant Pacific Ocean, which are pivotal in influencing the Kuroshio Current east of Taiwan. PET identification in the area east of Taiwan shows three adjacent anticyclonic eddies, consistent with the ocean current patterns associated with the Kuroshio Current east of Taiwan. In this vicinity, the ocean currents on both the east and west flanks of the Kuroshio’s main stream are characterized by southward counterflows [37]. Furthermore, a considerable number of eddies are detected in the region spanning 15°S to 25°N and 105°E to 135°E, especially in the region east of the Luzon Strait. This area is known for its dynamic eddy activity, influenced by the interaction between the Kuroshio Current and the North Equatorial Current [47].
The interplay between eddy size, strength, and kinetic energy is vital for understanding ocean dynamics. Larger eddies with high eddy kinetic energy (EKE) can transport more energy and materials across long distances, influencing the ocean’s thermohaline circulation and impacting weather and climate patterns. EKE is the quadratic sum of two geostrophic velocity components, which can depict the intensity of the flow, rotational patterns, fluid diffusion, and convergence, as well as the deformation behavior of the fluid under various mechanical effects [48]. Figure 6a,b display the ERs and SRs of the identified eddies, respectively. It is observed that both ERs and SRs correlate strongly with the eddies’ size. In the region spanning 15°S to 20°N and 105°E to 130°E, particularly in the eastern part of Luzon Island, the area influenced by the eastward-flowing Kuroshio to the east of Japan, eddies exhibit larger ERs and VRs. The Kuroshio Current region is characterized by fast flow velocities and large flow rates, leading to an increase in energy. Under these conditions, larger eddies may be generated [49]. Eddies located near the coast are typically smaller, possibly because in the shallow waters near the coast, eddies cannot fully develop, resulting in smaller radii [11]. In Figure 6a,b, the ER of many eddies is observed to be much larger than the SR, consistent with our results in Section 4.2. The core of an eddy has high rotational speeds, represented by the SR, while the outer regions have lower speeds, contributing to a larger ER. Underwater topography, like continental shelves and ridges, can affect an eddy’s size and intensity. For instance, an eddy encountering a slope might spread out horizontally, increasing the ER, but still maintain a high-speed core, as indicated by the SR [50].
Figure 6c,d present the EKE and mean EKE within each identified eddy contour calculated from SLA data. Regions characterized by large and dense eddy formations exhibit higher EKE levels, especially on the east side of Taiwan Island and Japan. This is linked to the Kuroshio Extension. Ref. [51] pointed out that the Kuroshio leaves the east coast of Japan, forming an eastward unstable jet, making the Kuroshio Extension the most active eddy region and the peak area of eddy kinetic energy in the North Pacific. A higher mean EKE does not always correspond to a larger ER. For instance, an eddy located east of Taiwan shows a relatively small ER but has a high mean EKE, as indicated by the darker color within the eddy contour in Figure 6d. Both the underwater topography and different stages of the eddy’s lifespan could cause this situation. Notably, due to the Rossby parameter nearing zero in the region of 5°S~5°N, which results in an infinitely large geostrophic flow speed, the EKE values in this area should not be considered for reference because the equatorial region’s dynamics are dominated by other forces, such as wind-driven currents and equatorial waves, which are not accurately represented by geostrophic calculations [52].

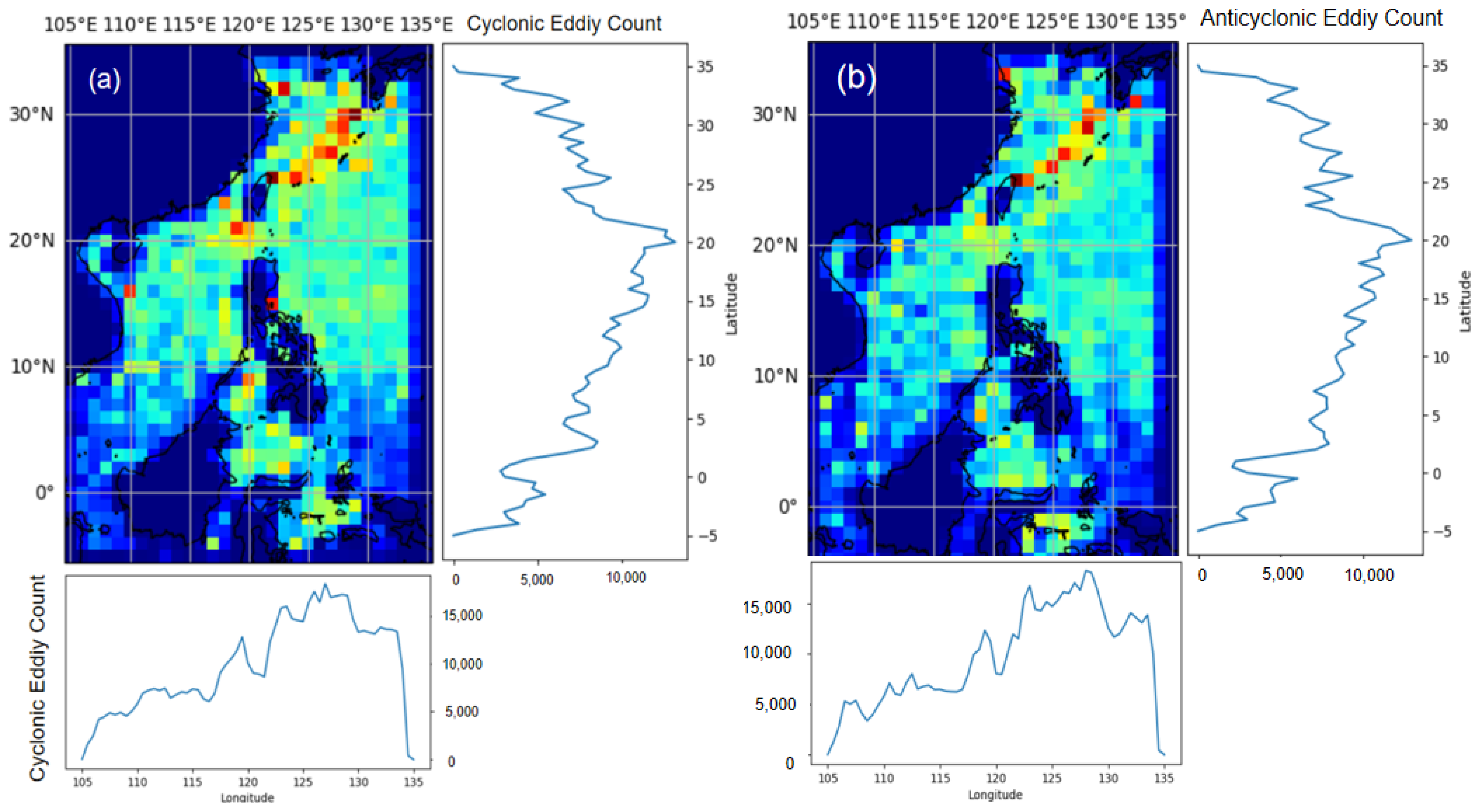
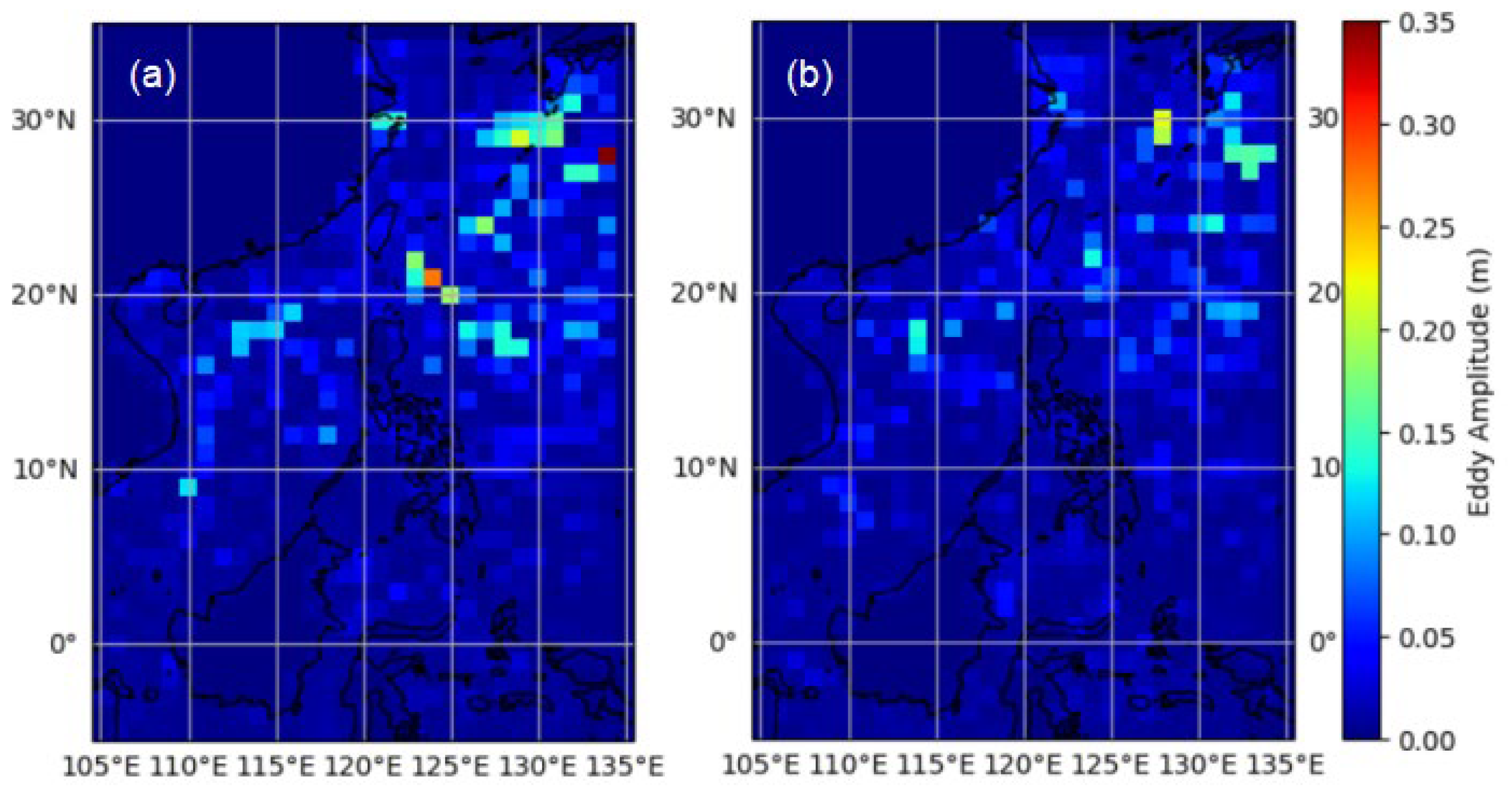
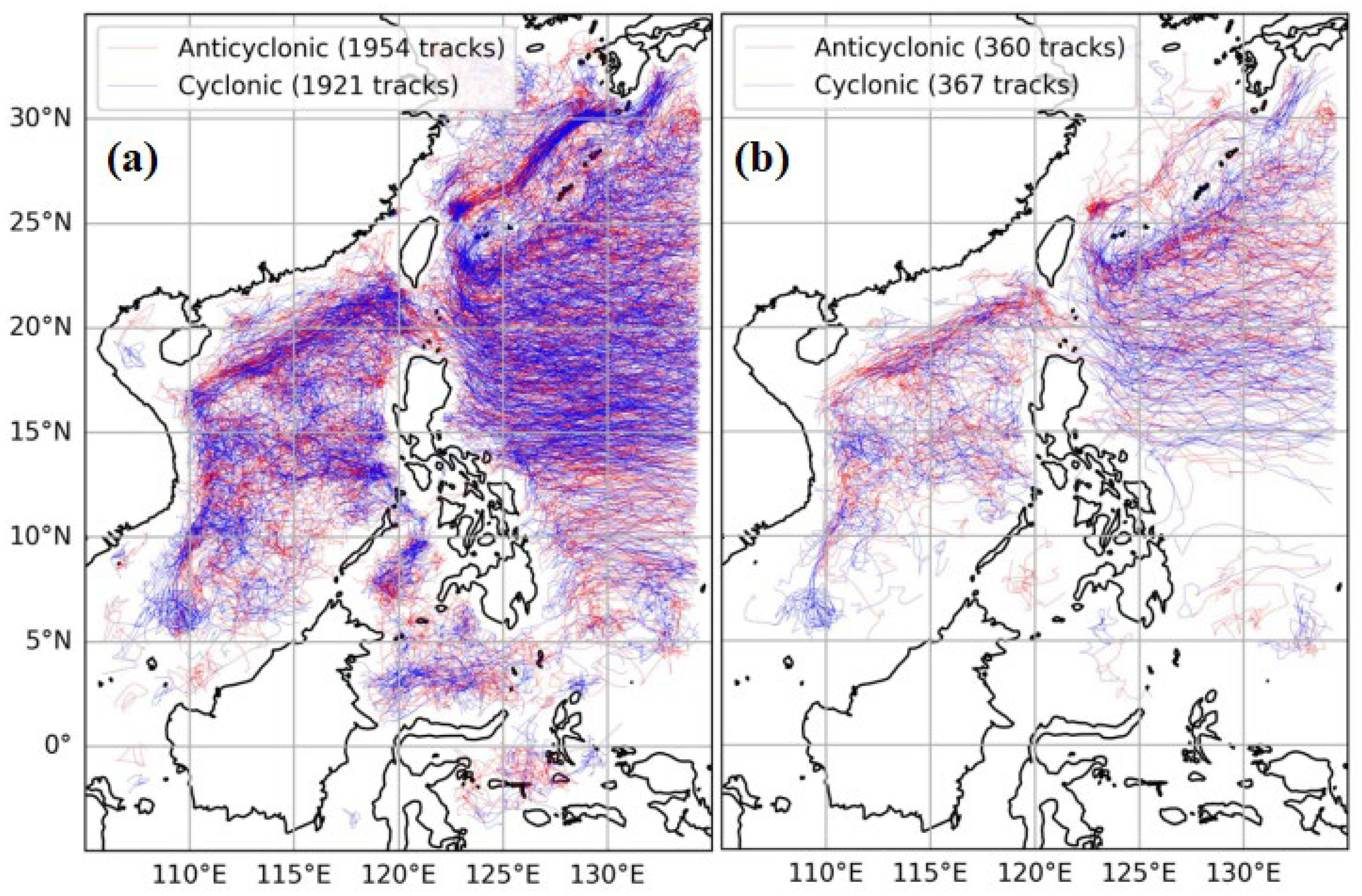
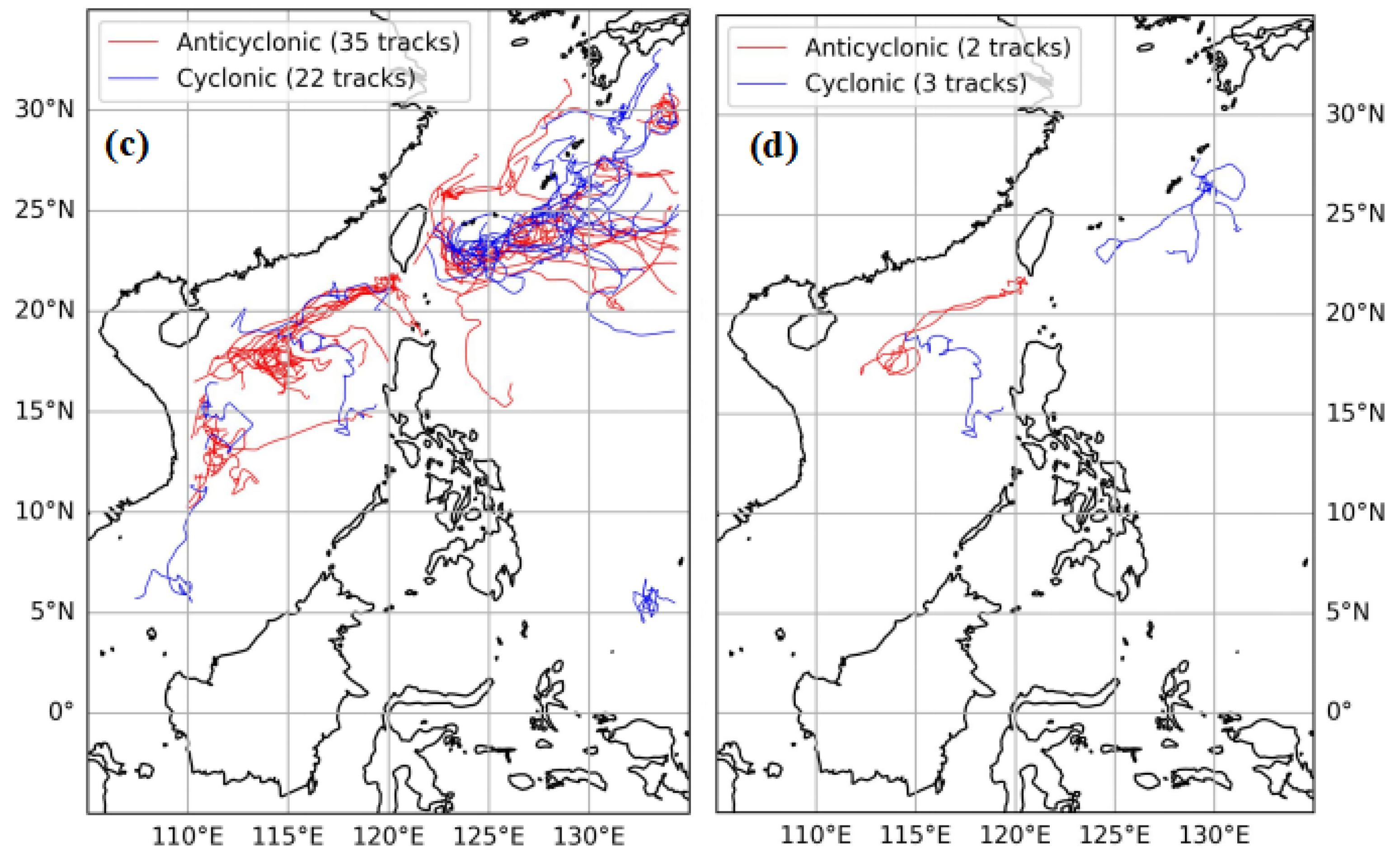
5.1.2. Long-Term Spatiotemporal Characteristics of the Detected Eddies

After examining the detailed characteristics of ocean eddies on a single spring day in 2023, we now situate these observations within longer-term trends. This section presents an analysis of the spatiotemporal patterns of eddy occurrences from 2000 to 2022, spanning more than two decades. Over the study period, the total occurrences of eddies identified using the PET method were aggregated. In our study area, a total of 1,188,649 eddies were identified during these 22 years, consisting of 600,398 cyclonic eddies and 588,251 anticyclonic eddies. This extensive dataset allows for a comprehensive analysis of eddy dynamics, providing insights into their spatial distribution and temporal variability, which are crucial for understanding oceanic processes and their impacts on climate and marine ecosystems.
Figure 7a shows the spatial distribution of all identified cyclonic eddies between 1 January 2000 and 31 December 2022 on a 1° × 1° grid. The occurrences of cyclonic and anticyclonic eddies have similar spatial distributions. Significant peaks in eddy occurrences are noted in the northern SCS, the northeastern region of Taiwan adjacent to the Kuroshio. These regions are known for their high eddy activity due to the interaction of various ocean currents and the complex topography [53,54]. The highest number of cyclonic and anticyclonic eddies in a single grid (1° × 1°) reached 2188 and 2380, respectively. To explore a detailed understanding of the distribution patterns and identify regions with significant eddy activity, we conducted a statistical analysis of cyclonic and anticyclonic eddy counts along both longitude and latitude, compiling counts at 0.5° intervals. The results are shown with line charts in Figure 7a,b.
The meridional analysis highlights a significant peak in eddy occurrences in the eastern region of Taiwan Island (123°E–130°E). Eddies in the ocean generally propagate westward due to the influence of the Coriolis force [55]. In the northwest Pacific, westward-propagating eddies are blocked by the Kuroshio, leading to the accumulation of eddy signals in the area east of Taiwan. This is reflected in Figure 7, where the number of eddies in this region is significantly greater than at other longitudes. The zonal eddies count statistics plot shows a notably higher count within the latitude range of approximately 15°N to 25°N compared to other latitude regions. This finding is consistent with the research by [7] which identified 18°N–25°N as a frequent eddy occurrence zone, and with the strong EKE observed in the 18°N–25°N, 125°E–140°E region in the 8-year satellite altimetry reanalysis by [56]. The higher eddy count in this latitude range can be attributed to the dynamic interactions between the North Equatorial Current, the Kuroshio, and the regional wind patterns, which create favorable conditions for eddy formation and propagation [49].
Figure 8 shows the mean amplitudes (peak SLA) of eddies within 1° × 1° grid cells during the period from 1 January 2000 to 31 December 2022. The amplitude of an eddy is a crucial parameter as it reflects the strength of the sea level anomaly associated with the eddy, which in turn indicates the eddy’s potential impact on oceanic mixing and nutrient transport [1]. Regions with higher amplitudes still appear in the northeastern waters of Taiwan and the northern region of the SCS, consistent with statistics on effective radius and velocity radius, indicating that larger eddies experience stronger amplitude variations in SLA. This consistency suggests a robust relationship between the size of the eddy and its amplitude, which can influence the energy transfer processes within the ocean [10].
The maximum amplitudes of cyclonic and anticyclonic eddies reach 0.036 m and 0.022 m, respectively. Cyclonic eddies, characterized by their counterclockwise rotation in the northern hemisphere, typically show higher amplitudes due to the upwelling of deeper, colder water to the surface, leading to greater sea level anomalies [57]. Compared to anticyclonic eddies, regions with higher amplitudes of cyclonic eddies show a wider range and relatively larger values. The broader range of cyclonic eddies may be attributed to the more dynamic and variable nature of these features, allowing them to propagate over larger distances and interact with various oceanic currents and topographical features [58]. Eddies with high amplitudes are generated southeast of Japan. In the spatial distribution of EKE on the same day, as shown in Figure 6c also exhibits extreme values in this area, indicating a correlation between the amplitude of eddy and locally oceanic hydrodynamics.
Figure 9a illustrates the interannual variations in the number of cyclonic and anticyclonic eddies from 2000 to 2022, indicating that the number of both cyclonic and anticyclonic eddies exhibits significant interannual variability without a clear long-term increasing or decreasing trend. The occurrence of eddies in this region is influenced by a combination of factors, including oceanic currents, wind patterns, and possibly climate phenomena such as El Niño and La Niña [1]. As shown in Figure 9a, among the nine moderate-to-strong La Niña events, seven corresponded to peaks in eddy counts, especially for anticyclonic eddies. Conversely, during the three moderate-to-strong El Niño events, the counts of both cyclonic and anticyclonic eddies reached their lowest values. This finding is consistent with the analysis by [59], who investigated the influence of El Niño–Southern Oscillation (ENSO) on eddy variability in the northwest Pacific Ocean and found that the total number of eddies tends to decrease during El Niño and increase during La Niña events. Ref. [60] investigated the variability of EKE in the South China Sea and found that the EKE levels were lower than normal during El Niño events but higher during La Niña events. They suggested that El Niño (La Niña) events induce anomalous anticyclonic (cyclonic) wind stress curl over the South China Sea, which weakens (strengthens) the background cyclonic circulation and consequently leads to suppressed (enhanced) eddy activity during El Niño (La Niña) periods. The number of cyclonic and anticyclonic eddies in the region exhibits similar interannual variability, but the peak number of cyclonic eddies surpasses that of anticyclonic eddies. This is consistent with the global statistics reported by [61] and the finding of [62] in the Southwestern Taiwan Strait.
Figure 9b shows a 22-year statistical analysis of cyclonic and anticyclonic eddy counts for each month, revealing a similar change pattern for both types of eddies. Both cyclonic and anticyclonic eddy counts peak around February and June, with a subpeak for cyclonic eddies occurring in August. The seasonal variation suggests that certain periods of the year are more conducive to eddy formation, possibly due to seasonal changes in wind patterns, ocean stratification, and the strength of the Kuroshio Current [49]. The sharp increase in eddy numbers from February to March can be attributed to seasonal variations in oceanic conditions, which is consistent with the findings of [63], who reported a notable peak in the number of cyclonic eddies between January and April in this region, such as changes in wind patterns and ocean currents, which significantly influence eddy formation and intensity [1,7,64]. The identified eddies show a relative decrease in their number during the second half of the year, particularly in October and November. This decrease could be linked to more stable oceanic conditions and dynamics that are less favorable for eddy formation during these months.

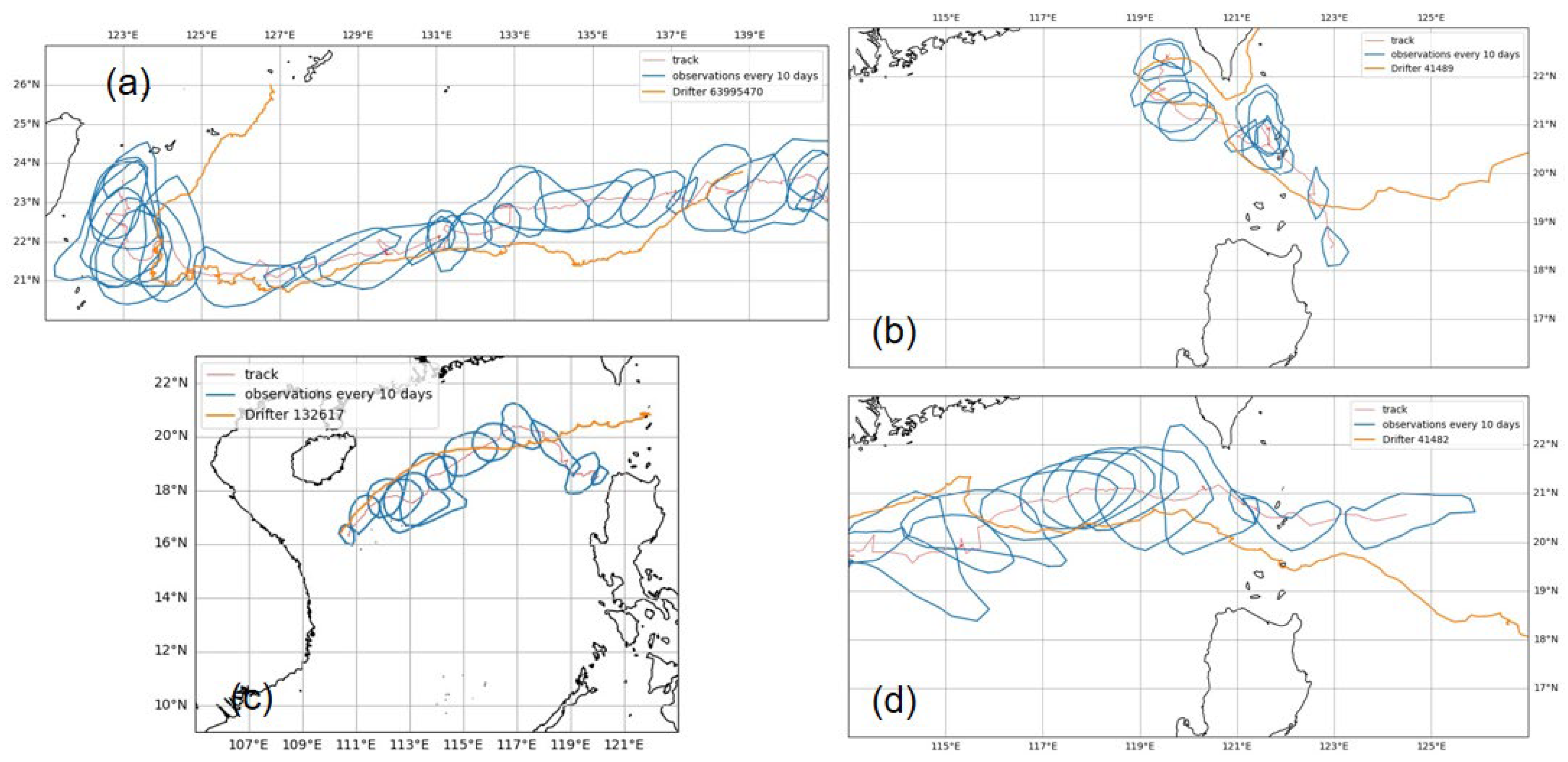
5.1.3. Eddy Validation Using SVP Drifters

We employed the PET method to track eddies within our study area. Figure 10 shows eddy trajectories with lifespans exceeding 8, 16, 32, and 48 weeks from 1 January 2000 to 5 June 2023, respectively. Figure 10a shows a total of 3875 trajectories, with roughly equal numbers of cyclones and anticyclones. Eddies with lifespans exceeding 8 weeks are widely distributed across the study area, displaying high density and complex, interwoven tracks. The region also exhibits frequent short-lived eddies, suggesting that shorter-lived eddies can form and dissipate in a variety of environments. This reflects the dynamic and variable nature of mesoscale oceanic processes [1]. Additionally, high-density eddy trajectories can be observed east and north of Taiwan and in the northern SCS regions, showing spatial characteristics consistent with the distribution of major ocean currents. Figure 10b shows the eddy trajectories exceeding 16 weeks, which are significantly fewer compared to those in Figure 10a. The number of trajectories shows that eddies with lifespans between 8 and 16 weeks account for 80% of eddies lasting longer than 8 weeks. The number of cyclonic trajectories slightly exceeds that of anticyclonic ones. Ref. [16] found that cyclones with lifespans greater than 16 weeks outnumber anticyclones by 6% globally. Tracks of eddies with lifespans over 16 weeks cover a wide area, with particularly high density in the Kuroshio region and the northern SCS. In contrast, there are almost no eddy trajectories along the coast and in enclosed sea areas formed by islands, suggesting that few eddies survive beyond 16 weeks in these regions. This is consistent with [11], who noted that eddies cannot fully develop in the shallow waters near the coast, resulting in shorter lifespans.
Figure 10c,d show the eddy trajectories with a lifespan longer than 32 weeks and 48 weeks tracked from 1 January 2000 to 5 June 2023, respectively. Only 35 anticyclonic and 22 cyclonic eddies exhibit lifespans longer than 32 weeks, indicating that while many eddies are generated, only a few persist for extended periods. This is consistent with [16], who found that globally, the eddies with the longest lifetimes and longest propagation distances are predominantly anticyclonic. It can be observed that eddies with lifespans exceeding 32 weeks are mainly concentrated in the northeastern waters of Taiwan and the northern part of the SCS, showing certain regularities and following major current systems closely in their movement. Around 25°N, eddies form within the shear zone between the eastward Subtropical Countercurrent (18–25°N) and the westward North Equatorial Current [7]. They propagate westward at several centimeters per second, evolve during transit, and eventually dissipate upon encountering the Kuroshio Current [64]. In the northern South China Sea, eddies typically form near strait exits and dissipate in shallow coastal waters. This concentration highlights the significant role of major current systems and regional topography in sustaining long-lived eddies [10]. Only five eddies exceed the lifespan of 48 weeks. Although their number is very small, they have a significant impact on SSH. According to [16], SSH is typically influenced by four to six eddies per year within eddy-rich regions.
These long-lived eddies can be categorized into two types of eddy trajectories based on their propagation paths. The first type propagates westward along the Kuroshio Current, reaching the eastern waters of Taiwan and dissipating after encountering the Ryukyu Islands of Japan. The second type originates near the northern Philippines in the Luzon Strait, extends into the SCS, and further stretches towards Hainan Island. This classification is consistent with the study by [65], who tracked eddy trajectories in southern and eastern Taiwan using ECCO2-SSEDG data from 2008 to 2015. The former trajectory type accounts for 96% of the total tracked trajectories, indicating a dominant pattern influenced by the strong, persistent flow of the Kuroshio Current.
Figure 11 shows the percentages of cyclonic eddies and anticyclonic eddies with various speed radii and amplitudes, categorized by the lifespan of the eddies from 1 January 2000 to 5 June 2023. The distribution patterns for both cyclonic eddies and anticyclonic eddies are similar, suggesting that the processes governing the formation, growth, and dissipation of these eddies are comparable. The majority of the total number of cyclonic eddies and anticyclonic eddies have lifespans ranging from 3 to 48 weeks, which are critical for mesoscale ocean dynamics and play a substantial role in energy transfer and material transport within the ocean [17].
Figure 11a,c show the percentage distribution of anticyclonic and cyclonic eddies by speed radius, grouped by different lifespans. Eddies with shorter lifespans (less than 3 weeks) tend to have smaller speed radii, indicating that these eddies are generally less stable and dissipate more quickly. In contrast, eddies with longer lifespans (over 48 weeks) exhibit a broader range of speed radii, suggesting that larger eddies are more stable and can persist for extended periods. This pattern corresponds with the understanding that larger eddies possess more energy and structural coherence, allowing them to maintain their integrity over longer durations [1].
Figure 11b,d show the percentage distribution of anticyclonic and cyclonic eddies by amplitude, categorized by different lifespans. Similarly to the speed radius distribution, shorter-lived eddies typically have lower amplitudes, reflecting their weaker intensity and shorter persistence. Longer-lived eddies, however, can have a wide range of amplitudes, with many showing higher values. Short-lived eddies are likely influenced by transient atmospheric conditions and local topographic features, while long-lived eddies are more affected by large-scale oceanic currents and climatic patterns [49].
For our analysis, we selected three distinct regions—offshore eastern Taiwan, the area encompassing southern Taiwan and the Luzon Strait, and the northern SCS region—to use SVP float data for validating the eddy trajectories identified in this study. Figure 12a presents the validation of an eddy trajectory in the eastern region of Taiwan using SVP float data from 2018 to 2019, specifically selecting the SVP float with ID 63995470. The blue contours in Figure 12 shows the closed contours of this eddy at 10-day intervals. By comparing the eddy trajectories with the float data based on their temporal and spatial alignment, we identified a cyclonic eddy characterized by clockwise rotation. The SVP floats’ trajectories closely follow the eddy contours, demonstrating a coincident path between the observed drifter paths and the identified eddy movements. This indicates the effectiveness of the eddy tracking method.
Figure 12b,d validate two eddy trajectories in the region south of Taiwan for the period 2004–2005, using SVP float trajectories with IDs 41489 and 41482. The ocean currents in this region are significantly influenced by monsoons, resulting in pronounced seasonal variations. During the winter, the northeast monsoon alters the flow dynamics, causing the main stream of the Kuroshio Current to split at the southernmost tip of Taiwan’s Hengchun Peninsula, forming a branch. This branch partly intrudes into the northern SCS and partly merges with cyclonic eddies southwest of Taiwan, aiding in the formation of the Loop Current [37]. The distinct differences between the two trajectories in the southern region, as shown in Figure 12b,c, are influenced by the Kuroshio Current, its branches, and the loop currents south of Taiwan [66]. This complex interaction highlights the dynamic nature of the region, where monsoonal winds and major ocean currents create varying eddy patterns and behaviors [49]. The consistency between the SVP float and the eddy contours indicates that the PET method can capture the complex movements of eddies in regions with strong currents and undulating topography.
The SCS region, as validated in Figure 12c, is known for its complex circulation patterns influenced by both the monsoon system and regional currents. Using the SVP float trajectory with ID 132617, we validated the eddy trajectories identified across all four regions. These trajectories are consistent with the motion of the SVP floats, providing evidence for the accuracy of our eddy tracking method. The consistency between the SVP drifters and the eddy contours over time shows the robustness of the PET method for tracking eddies.

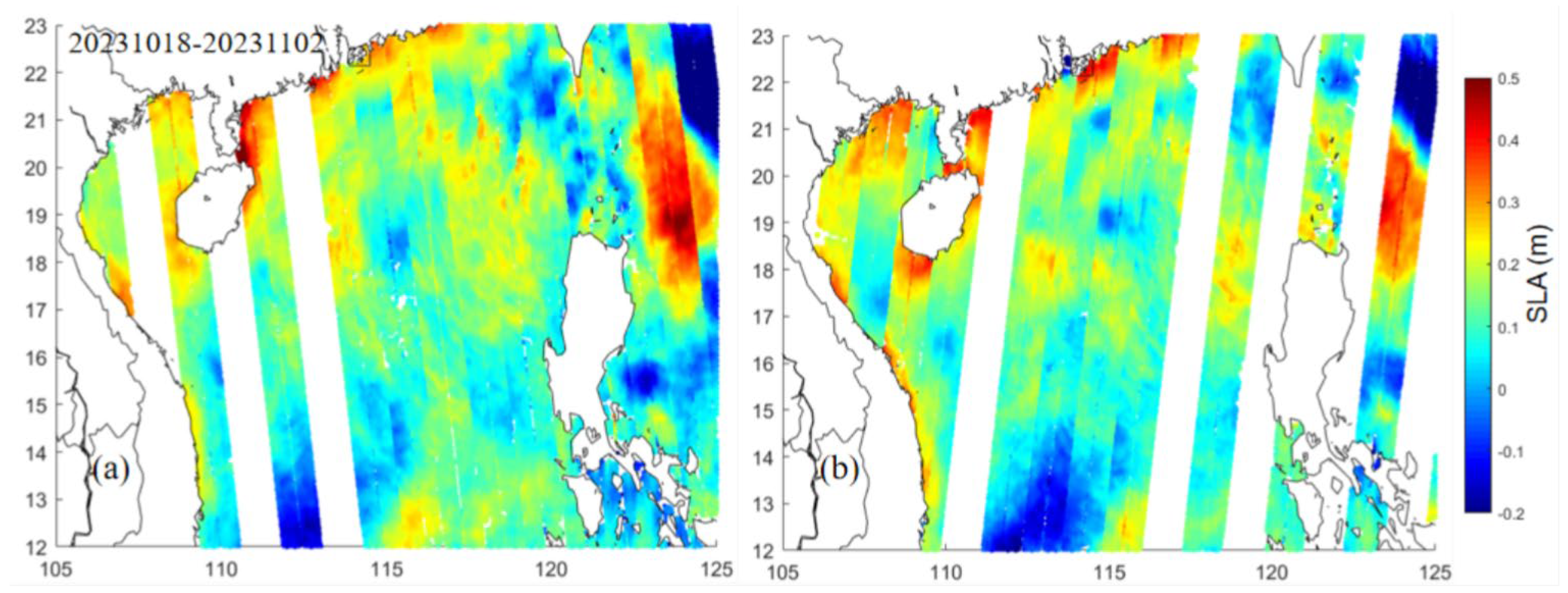
5.2. A Preliminary Assessment of SWOT Observations for Eddy Detection

Building on the results of mesoscale eddy detection and tracking using conventional altimeter data in Section 5.1, we further explore the potential of high-resolution satellite observations for identifying smaller-scale features. Given the limitations of traditional altimetry in resolving submesoscale dynamics, the newly available SWOT data provide an opportunity to examine submesoscale eddies with unprecedented spatial detail. The following section presents a preliminary investigation into the identification of submesoscale eddies based on SWOT observations.

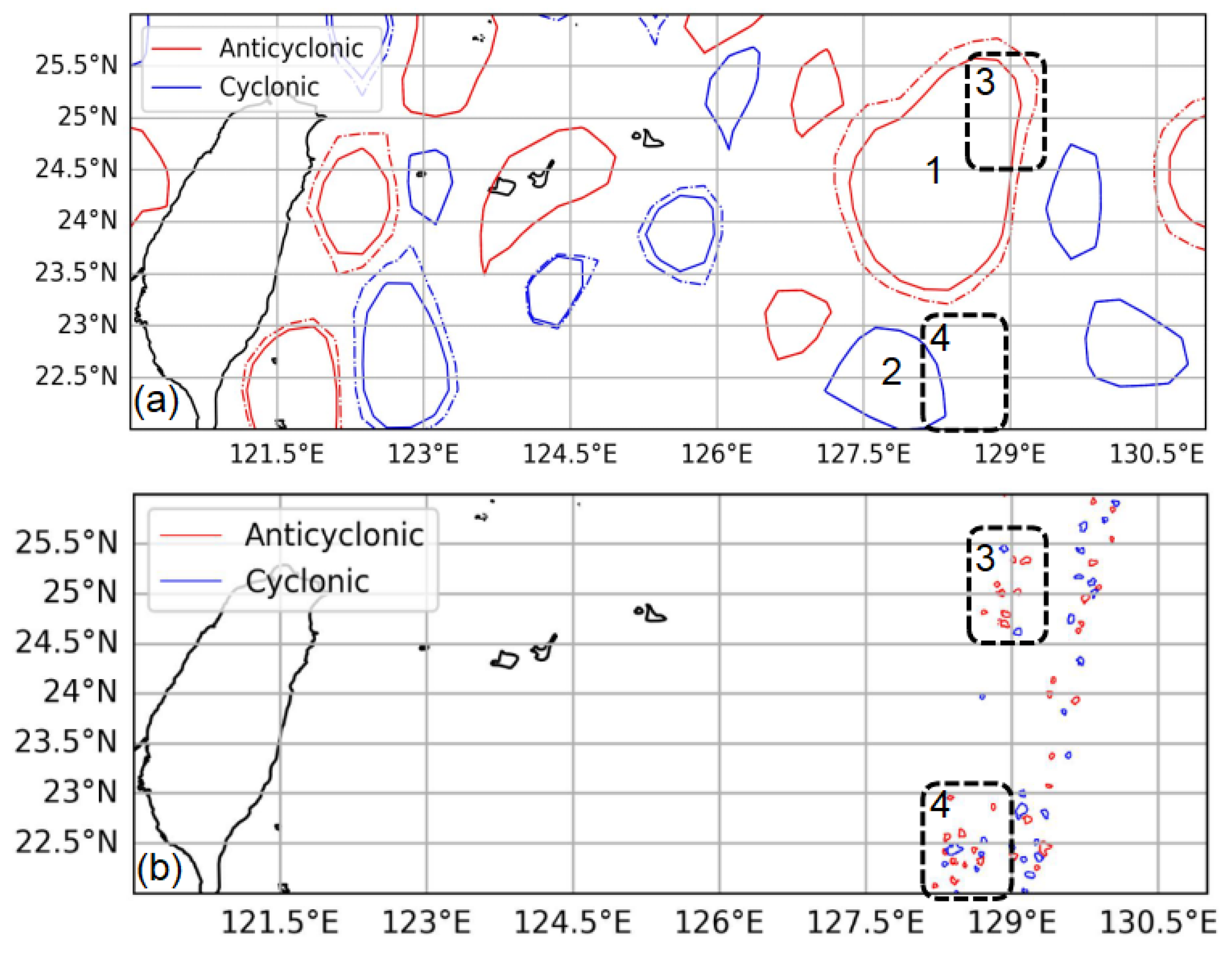
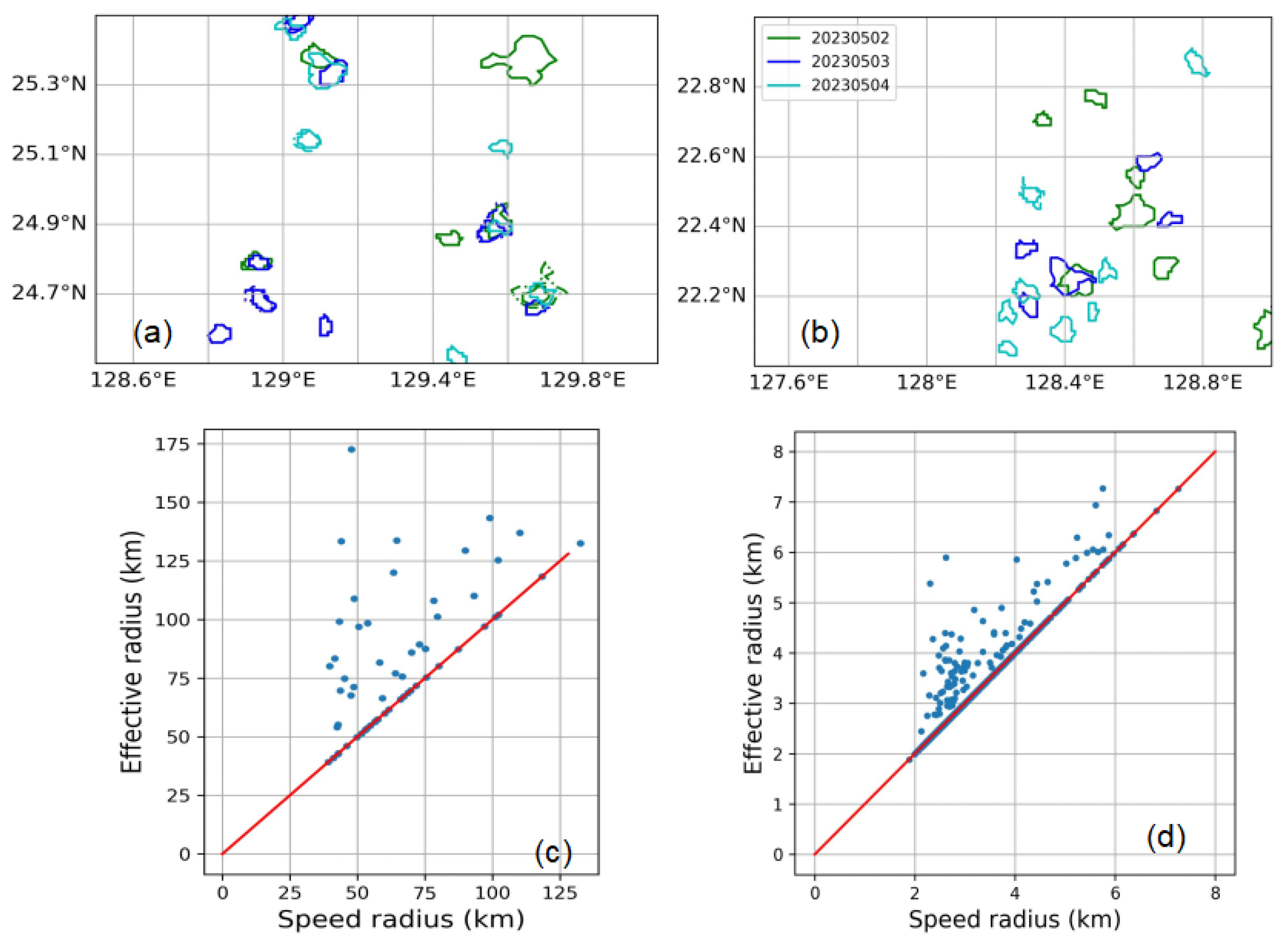
5.2.1. ‘Eddy’ Detection Using Observations from SWOT’s One-Day Orbit

Since early 2023, we have joined the SWOT CalVal team to collect sea surface height measurements by Global Navigation Satellite System (GNSS) on a research vessel from Taiwan in June 2023. This effort aims to validate the measurements of SWOT under Pass 21 of SWOT’s one-day repeat mission in the region shown in Figure 13. The GNSS validation result is still under investigation.
Figure 13 displays the SLA on 1 May 2023, obtained from conventional altimeter satellites and the SWOT satellite, both demonstrating the basic characteristics of an anticyclonic eddy. A comparison between SWOT and conventional AVISO altimeter observations indicates that SWOT and conventional altimeter data generally agree on the position and magnitudes of this anticyclonic eddy. Additionally, SWOT exhibits the capability to discern the frontal regions of eddies, as also noted by [29]. The detailed observation capabilities of SWOT, as shown in Figure 13, highlight its potential for revolutionizing our understanding of ocean surface topography. By providing higher spatial resolution data, SWOT may reveal the structure and dynamics of eddies with unprecedented clarity, which is essential for studying their role in ocean mixing, heat transport, and biogeochemical cycles [26,67].
Figure 14 compares the cyclonic and anticyclonic eddies identified using the PET method from conventional altimeter and small structures identified from SWOT data. It is noted that the PET algorithm did not identify the largest anticyclonic eddy with the SWOT data, which is shown in Figure 14a, with an effective radius of approximately 83 km. Instead, the algorithm detected dozens of submesoscale features in Figure 14b. It is observed that such features primarily occur within and around the peripheries of two large-scale eddies, labeled as 3 and 4. This suggests a complex interplay between mesoscale and submesoscale processes that could be influenced by the dynamics of larger eddies [6]. The edges of large-scale and mesoscale eddies intensify gradients at submesoscale, leading to mesoscale strain-induced frontogenesis. These fronts, with km-scale gradients, generate smaller-scale instabilities [68] (SWOT Science Team Meeting, 2024). These fine-scale features are recognized as a key structuring regime for biogeochemistry and ecology [69]. We cannot confirm whether the submesoscale features identified in Figure 14b around the large- and mesoscale eddies are submesoscale eddies, nor can we confirm their key structure and role in the dynamics. Further repeated measurements by SWOT may improve this understanding.
Figure 15 shows the submesoscale structures identified from three consecutive days of SWOT satellite observations in regions labeled 3 and 4 in Figure 14. We observed that these structures identified at the same location for two or three consecutive days are considered the same submesoscale features. The emergence and dissipation of these small-scale structures within the three-day period are apparent. Few structures persist for the entire duration of three days, except for the three eddies depicted in Figure 15a, which is located within the edge of the large-scale eddy labeled 1 in Figure 14a. It is hypothesized that the lifespan of these small-scale structures is correlated with their positions within large-scale eddies. Large-scale eddies can influence the formation and stability of smaller eddies, providing a favorable environment for their persistence [6]. Statistical analysis in Figure 15d reveals that the SRs and ERs of the identified submesoscale features fall within the range of 2 to 8 km. We also provided the SRs and ERs of large and mesoscale eddies identified in Figure 15c for comparison. The discrepancy between SR and ER in Figure 15c suggests that large-scale and mesoscale eddies have more pronounced structural differences. Compared to large and mesoscale eddies, the ERs and SRs of submesoscale features lie closer to the line of equality. This observation is consistent with our simulation result of the submesoscale eddies in Section 4.2. This highlights the capability of SWOT to capture finer details in smaller structures.

5.2.2. Eddy Detection Using Observations from SWOT’s 21-Day Orbit

Figure 16 compares the SLA values from conventional altimeter data and SWOT’s 21-day orbit data from 7 September 2023 to 21 September 2023, as well as the identified eddies over the study area. The SWOT 21-day orbit basically covers the entire study area, despite small gaps due to the inherent gap problem in the 21-day orbit data. Due to SWOT’s orbital revolution, the eddies observed in different swaths have shifted over time. However, large-scale eddies have lifespans of several months while undergoing slight changes in shapes and positions within two weeks. Therefore, in comparison with the SLA observed from conventional altimeter data, we found that SWOT can effectively capture large-scale and mesoscale eddies. The sizes and positions of these eddies from SWOT data are generally consistent with those from conventional altimeter observations, as shown in Figure 16a,b. Besides detailing the frontal edges of eddies, SWOT also reveals intricate details in non-eddy areas, which are regions where submesoscale eddies are generated.
Using the PET method, we also identified submesoscale features in SWOT’s 21-day data; the large-scale eddies cannot be identified solely through SWOT data because the boundaries of the swaths disrupt closed contour lines. The spatial distribution of these submesoscale features is widespread throughout the study area, with a higher density near large and medium-scale eddies and in the enclosed sea areas formed by numerous islands. The causes and spatial distribution of submesoscale eddies have not been fully studied yet. Ref. [70] noted that eddies smaller than 50 km in scale can be generated by several processes, such as interactions between large-scale ocean currents and bottom topography, islands, or headlands, atmospheric forcing, and barotropic or baroclinic instabilities in currents and fronts. Ref. [71] analyzed submesoscale eddy activity in the Baltic, Black, and Caspian Seas during 2009–2010, using over 2000 radar images from European Remote Satellites ERS-1, and ERS-2, and Envisat. This analysis identified more than 14,000 eddy structures with diameters ranging from 1 to 75 km, of which 95% were between 1 and 15 km. This indicates a widespread presence of submesoscale eddies, under 15 km, in these regions.
Figure 17 presents the SLA observations over the study area, obtained from two cycles of SWOT’s 21-day repeat orbit, effectively covering the entire marine region depicted in Figure 5. The SLA data reveals detailed spatial patterns, including prominent ripple-like features in the SCS region west of the Luzon Strait, which are shown in greater detail in Figure 18. These features suggest the presence of internal waves, which are typically undetectable by conventional altimetry. Internal waves, which oscillate within the ocean’s interior rather than on the surface, play a significant role in ocean mixing and energy transfer processes. Detecting these features is crucial for an improved understanding of ocean dynamics [72]. The study of internal waves is beyond the scope of this paper.
Figure 19 illustrates the temporal evolution of two large-scale eddies shown in Figure 16a. These datasets, obtained through the combination of conventional altimetry and SWOT’s KaRIn data, cover the period from 7 September to 8 October in 2023. Due to the temporal discontinuity of SWOT data, only snapshots of the SWOT orbit passing through this area are shown in the subfigures of Figure 19. The combination of data from conventional altimeters and the SWOT altimeter provides a more complete picture of these eddies’ formation, maturation, and dissipation, revealing the complex interactions between cyclonic and anticyclonic eddies.

6. Discussion

6.1. Errors Induced by High-Pass Filter

High-pass filtering introduces potential errors in eddy identification, as it tends to increase the detected size of eddies. As discussed in Section 4.2, applying a high-pass filter at different radii (20–300 km) resulted in significant variations in eddy count and spatial distribution. Ref. [28] pointed out that using ADT instead of SLA maps as input can improve eddy identification in regions with strong sea surface height (SSH) gradients. However, larger filter radii may cause signal leakage in strong gradient regions, leading to the loss of physical content after filtering. Therefore, we ultimately chose SLA maps as input and applied a 300 km high-pass filter. Comparing our results with the Mesoscale Eddy Trajectory Atlas Product (META3.1, [28]) from 1 January 2000 to 31 December 2020, META3.1 identified 448,912 cyclonic and 441,442 anticyclonic eddies in the study area, while our results show 516,747 and 505,112, respectively, surpassing META3.1 by over 100,000 eddies. The use of a deep learning-based approach, such as that proposed by [73,74], may optimize the choice of filter length. Other detection algorithms, such as TOEddies, do not require spatial filtering and operate directly on the ADT field. In global eddy tracking statistics, this approach yields approximately 2% more eddies compared to META3.2 [75].

6.2. Limitations of PET in Identifying Submesoscale Eddies

Submesoscale eddies may not strictly adhere to geostrophic balance [67] and may not always form closed structures [76]. As a result, it remains uncertain whether the small-scale features identified using SWOT data genuinely represent submesoscale eddies or are merely artifacts caused by data noise. Further verification is required to confirm the validity of these detected structures. Moreover, in our efforts to identify Submesoscale eddies, we utilized SLA data input while applying a smaller filtering radius and lower pixel threshold. This methodological choice, although intended to enhance the detection of finer-scale features, may have inadvertently introduced additional errors. Specifically, the reduced filtering radius can exaggerate noise, making it difficult to distinguish actual submesoscale eddies from transient fluctuations in the SLA field. Similarly, the lower pixel threshold may contribute to the over-identification of weak or short-lived eddies, many of which could be spurious.
Addressing these issues requires further refinement of the PET algorithm, particularly in terms of optimizing filter settings to strike a balance between detecting genuine submesoscale eddies and minimizing false detections. Incorporating complementary datasets, such as in situ drifter measurements and high-resolution ocean model outputs, may provide an additional means of verifying the existence and properties of these small-scale features. Future studies should focus on refining detection criteria and testing alternative filtering techniques to improve the reliability of submesoscale eddy identification.

7. Conclusions

In this study, we employed EGF simulations and the PET algorithm, validated by SVP drifter data, to identify and track eddies in the northwest Pacific Ocean. The PET method demonstrated high accuracy in detecting large- and mesoscale eddies, with the long-lived eddies associated with major currents, notably abundant around 20°N latitude, with peaks in EKE, eddy radius, and amplitude along the Kuroshio Current and northern South China Sea. Over 22 years, we identified 1,188,649 eddies, with a seasonal increase in spring linked to marine environmental factors. Simulated satellite altimetry data, mirroring SWOT’s high-resolution capabilities, confirmed the PET method’s effectiveness in processing detailed datasets, and revealed eddies as small as a few km in diameter, despite a noted decline in accuracy for submesoscale eddies. Future work should enhance the PET algorithm for SWOT’s swath altimetry, addressing data fragmentation and unclosed contours. Integrating SWOT with in situ drifters and models will refine eddy tracking, while machine learning can further improve classification, benefiting ocean circulation and climate studies.

Author Contributions

C.H., L.Z. and H.-Y.L. conceptualized the initial idea and experimental design. L.Z. and H.-Y.L. made all computations and wrote the first draft, with C.H. and L.Z. assessing the SWOT observations. E.T.Y.C. and D.Y. commented on the draft. All authors have read and agreed to the published version of the manuscript.

Funding

This study is supported by the National Science and Technology Council, Taiwan, under grant numbers 113-2611-M-A49-001 and 112-2221-E-A49-025-MY3. This study is also supported by the Central Public-interest Scientific Institution Basal Research Fund (CEAIEF20240305); the NNSFC (National Natural Science Foundation of China) (4230040788), and State Key Laboratory of Geodesy and Earth’s Dynamics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences (SKLGED2023-2-1).

Data Availability Statement

The SWOT_L3_SSH product, derived from the L2 SWOT KaRIn low-rate ocean data products (NASA/JPL and CNES), is produced and made freely available by AVISO and DUACS teams as part of the DESMOS Science Team project. AVISO/DUACS, 2023. SWOT Level 3 SSH Expert (v0.3). CNES, https://doi.org/10.24400/527896/A01-2023.018, accessed on 5 May 2025. The drifter data are provided by the Surface Velocity Program and available on the Global Drifter Program website (https://www.aoml.noaa.gov/phod/gdp/index.php, accessed on 5 May 2025). The code for the Py_Eddy_Tracking (PET) algorithm is provided by [26,27,28].

Acknowledgments

The PET eddy automatic identification method is based on [1,26,27,28].

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Five Constraints for Closed Polygons

The five constraints on the closed contours of eddies used in this study considered the recommendations of Mason et al., (2014) [26], but we also made some improvements. First, whereas the SLA interval used in their article was 1 cm, this study has adjusted it to 0.4 cm, meaning there is a contour for every 0.4 cm interval of SLA. This change was made because this study aims to capture small-scale oceanic dynamical phenomena more accurately. Second, this study has increased the shape error from the original 55% to 70%. The shape error is the difference in area between the outermost closed contour of the original eddy and its best-fit circle, as a proportion of the best-fit circle’s area. The reason for loosening the restriction to 70% is to ensure detection of elongated eddies, which are often seen in dynamically active regions [28]. The other constraints follow the recommendation of PET as follows:
  • An eddy’s closed contour includes only one eddy center SLA extremum, with anticyclonic eddies containing only one SLA maximum value and cyclonic eddies containing only one SLA minimum value, differing from the constraint of [1].
  • The area of the region enclosed by the closed SLA isopleth lines is between 8 pixels and 1000 pixels. For submesoscale eddies, which are generally smaller than 10 km in radius, an excessive number of pixels may fail to accurately capture their compact structure and can lead to an overestimation of their ER during detection. Therefore, we set the maximum pixel value to 150 pixels.
  • The eddy amplitude (Amplitude, A) is between 1 cm and 150 cm. A = |SLA_center—SLA_contour|, where SLA_center is the SLA at the center of the eddy within the closed SLA isopleth, and SLA_contour is the average SLA on that closed isopleth.
  • For anticyclonic eddies, the formed eddy area only includes those pixels where the SLA value is greater than the current set SLA interval value; for cyclonic eddies, the formed eddy area only includes those pixels where the SLA value is less than the current set SLA interval value, with the interval value set at 0.4 cm in this study.
  • Passing the shape test with Error_Shape ≤ 70%, where Error_Shape = Area_deviation/Area_(p_eff), with Area_(p_eff) being the area of the green best-fit circle shown in Figure 3 and Figure 4, which has the same area as the red closed contour, and Area_deviation being the area enclosed outside the green best-fit circle and within the red closed contour.

Appendix B. Elliptical Gaussian Functions for Simulated Eddies

This paper uses the elliptical Gaussian function (EGF) to simulate the SLA values across an ocean eddy. With a simulated eddy, the SLA value is expressed as proposed by Nobach and Honkanen (https://en.wikipedia.org/wiki/Gaussian_function, accessed on 5 May 2025):
f x , y = A   exp ( − ( a ( x   −   x 0 ) 2 + 2 b x   −   x 0 y   −   y 0 + c ( y   −   y 0 ) 2 ) )
where
a   = c o s 2 θ 2 σ x 2 + s i n 2 θ 2 σ y 2
b   = − s i n 2 θ 4 σ x 2 + s i n 2 θ 4 σ y 2
c   = s i n 2 θ 2 σ x 2 + c o s 2 θ 2 σ y 2
where f x , y is SLA at a location x , y and x 0 , y 0 is the eddy center of the EGF with the maximum or minimum SLA value. σ x , σ y are the standard deviations along the x-axis (east) and y-axis (north), respectively, which determine the spread of the Gaussian function along these axes. A is the amplitude of the eddy, i.e., the height difference between the eddy center and the eddy edge. θ is the rotation angle of the ellipse relative to the x-axis, which indicates how the major and minor axes of the ellipse are oriented. In this paper, the semi-major axis and semi-minor axis of an EGF are related to σ x , σ y   as
σ x = R m a j o r 2
σ y = R m i n o r 2
Equations (A5) and (A6) imply that the spread of SLA within an eddy is smoother for larger major and minor axes compared to eddies with smaller axes. The choice in Equations (A5) and (A6) are realistic but not mandatory.

References

  1. Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
  2. Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
  3. Garabato, A.C.N.; Yu, X.; Callies, J.; Barkan, R.; Polzin, K.L.; Frajka-Williams, E.E.; Griffies, S.M. Kinetic energy transfers between mesoscale and submesoscale motions in the open ocean’s upper layers. J. Phys. Oceanogr. 2022, 52, 75–97. [Google Scholar] [CrossRef]
  4. Thomas, L.N.; Tandon, A.; Mahadevan, A. Submesoscale processes and dynamics. Ocean Model. Eddying Regime 2008, 177, 17–38. [Google Scholar]
  5. McWilliam, J.C. Fluid dynamics at the margin of rotational control. Environ. Fluid Mech. 2008, 8, 441–449. [Google Scholar] [CrossRef]
  6. McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef]
  7. Qiu, B. Seasonal eddy field modulation of the North Pacific Subtropical Countercurrent: TOPEX/Poseidon observations and theory. J. Phys. Oceanogr. 1999, 29, 2471–2486. [Google Scholar] [CrossRef]
  8. Moum, J.N.; Nash, J.D. Mixing measurements on an equatorial ocean mooring. J. Atmos. Oceanic Technol. 2009, 26, 317–336. [Google Scholar] [CrossRef]
  9. Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Thomas, M. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
  10. Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
  11. Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
  12. Mensah, V.; Jan, S.; Andres, M.; Chang, M.H. Response of the Kuroshio east of Taiwan to mesoscale eddies and upstream variations. J. Oceanogr. 2020, 76, 271–288. [Google Scholar] [CrossRef]
  13. Isern-Fontanet, J.; García-Ladona, E.; Font, J. Identification of marine eddies from altimetric maps. J. Atmos. Oceanic Technol. 2003, 20, 772–778. [Google Scholar] [CrossRef]
  14. Okubo, A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 445–454. [Google Scholar] [CrossRef]
  15. Weiss, J. The dynamics of entropy transfer in two-dimensional hydrodynamics. Phys. D Nonlinear Phenom. 1991, 48, 273–294. [Google Scholar] [CrossRef]
  16. Fu, L.L.; Chelton, D.B.; Le Traon, P.Y.; Morrow, R. Eddy dynamics from satellite altimetry. Oceanography 2010, 23, 14–25. [Google Scholar] [CrossRef]
  17. Morrow, R.; Birol, F.; Griffin, D.; Sudre, J. Divergent pathways of cyclonic and anticyclonic ocean eddies. Geophys. Res. Lett. 2004, 31, 24. [Google Scholar] [CrossRef]
  18. Chaigneau, S.; Gizolme, A.; Grados, C. Mesoscale eddies of Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
  19. Hwang, C.; Chen, S.A. Circulations and eddies over the South China Sea derived from TOPEX/Poseidon altimetry. J. Geophys. Res. Ocean. 2000, 105, 23943–23965. [Google Scholar] [CrossRef]
  20. Barabinot, Y.; Speich, S.; Carton, X. Defining mesoscale eddies boundaries from in-situ data and a theoretical framework. J. Geophys. Res. Ocean. 2024, 129, e2023JC020422. [Google Scholar] [CrossRef]
  21. Lapeyre, G.; Klein, P. Impact of the small-scale elongated filaments on the oceanic vertical pump. J. Mar. Res. 2006, 64, 835–851. [Google Scholar] [CrossRef]
  22. Hewitt, H.; Fox-Kemper, B.; Pearson, B. The small scales of the ocean may hold the key to surprises. Nat. Clim. Change 2022, 12, 496–499. [Google Scholar] [CrossRef]
  23. Qiu, B.; Chen, S.; Klein, P.; Sasaki, H.; Sasai, Y. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent. J. Phys. Oceanogr. 2014, 44, 3079–3098. [Google Scholar] [CrossRef]
  24. Michael, D.; Fu, L.L.; Lettenmaier, D.P.; Alsdorf, D.E.; Rodriguez, E.; Esteban-Fernandez, D. The Surface Water and Ocean Topography Mission: Observing Terrestrial Surface Water and Oceanic Submesoscale Eddies. Proc. IEEE 2010, 98, 766–779. [Google Scholar]
  25. Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale eddies detected by SWOT and moored observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
  26. Mason, E.; Pascual, A.; McWilliams, J.C. A new sea surface height–based code for oceanic mesoscale eddy tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
  27. Mason, E.; Pascual, A.; Gaube, P.; Ruiz, S.; Pelegrí, J.L.; Delepoulle, A. Subregional characterization of mesoscale eddies across the Brazil-Malvinas Confluence. J. Geophys. Res. Oceans 2017, 122, 3329–3357. [Google Scholar] [CrossRef]
  28. Pegliasco, C.; Delepoulle, A.; Mason, E.; Morrow, R.; Faugère, Y.; Dibarboure, G. META3.1exp: A new global mesoscale eddy trajectory atlas derived from altimetry. Earth Syst. Sci. Data 2022, 14, 1087–1107. [Google Scholar] [CrossRef]
  29. Fu, L.L.; Pavelsky, T.; Cretaux, J.F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Dibarboure, G. The Surface Water and Ocean Topography Mission: A breakthrough in radar remote sensing of the ocean and land surface water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
  30. Metzger, E.J.; Hurlburt, H.E. The nondeterministic nature of Kuroshio penetration and eddy shedding in the South China Sea. J. Phys. Oceanogr. 2001, 31, 1712–1732. [Google Scholar] [CrossRef]
  31. Yuan, D.; Han, W.; Hu, D. Anti-cyclonic eddies northwest of Luzon in summer-fall observed by satellite altimeters. Geophys. Res. Lett. 2007, 34, L13610. [Google Scholar] [CrossRef]
  32. Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the South China Sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. Ocean. 2011, 116, C06018. [Google Scholar] [CrossRef]
  33. Xiu, P.; Chai, F.; Shi, L.; Xue, H.; Chao, Y. A census of eddy activities in the South China Sea during 1993–2007. J. Geophys. Res. Oceans 2010, 115, C03012. [Google Scholar] [CrossRef]
  34. He, Y.; Xie, J.; Cai, S. Interannual variability of winter eddy patterns in the eastern South China Sea. Geophys. Res. Lett. 2016, 43, 5185–5193. [Google Scholar] [CrossRef]
  35. Yuan, D.; Han, W.; Hu, D. Surface Kuroshio path in the Luzon Strait area derived from satellite remote sensing data. J. Geophys. Res. Ocean. 2006, 111, C11007. [Google Scholar] [CrossRef]
  36. Caruso, M.J.; Gawarkiewicz, G.G.; Beardsley, R. Interannual variability of the Kuroshio intrusion in the South China Sea. J. Oceanogr. 2006, 62, 559–575. [Google Scholar] [CrossRef]
  37. Jan, S.; Mensah, V.; Andres, M.; Chang, M.H.; Yang, Y.J. Eddy-Kuroshio interactions: Local and remote effects. J. Geophys. Res. Ocean. 2017, 122, 9744–9764. [Google Scholar] [CrossRef]
  38. Jan, S.; Chern, C.S.; Wang, J.; Chiou, M.D. Generation and propagation of baroclinic tides modified by the Kuroshio in the Luzon Strait. J. Geophys. Res. Ocean. 2012, 117, C2. [Google Scholar] [CrossRef]
  39. Zhang, Y.; Zhang, Z.; Chen, D.; Qiu, B.; Wang, W. Strengthening of the Kuroshio current by intensifying tropical cyclones. Science 2020, 368, 988–993. [Google Scholar] [CrossRef]
  40. Ren, Q.; Yu, F.; Nan, F.; Li, Y.; Wang, J.; Liu, Y.; Chen, Z. Effects of mesoscale eddies on intraseasonal variability of intermediate water east of Taiwan. Sci. Rep. 2022, 12, 9182. [Google Scholar] [CrossRef]
  41. Gómez-Navarro, L.; Cosme, E.; Sommer, J.L.; Papadakis, N.; Pascual, A. Development of an image de-noising method in preparation for the Surface Water and Ocean Topography Satellite Mission. Remote Sens. 2020, 12, 734. [Google Scholar] [CrossRef]
  42. Tréboutte, A.; Carli, E.; Ballarotta, M.; Carpentier, B.; Faugère, Y.; Dibarboure, G. KaRIn noise reduction using a convolutional neural network for the SWOT Ocean Products. Remote Sens. 2023, 15, 2183. [Google Scholar] [CrossRef]
  43. Lumpkin, R.; Pazos, M. Measuring surface currents with Surface Velocity Program drifters: The instrument, its data, and some recent results. Lagrangian Anal. Predict. Coast. Ocean Dyn. 2007, 39, 67. [Google Scholar]
  44. Pegliasco, C.; Chaigneau, A.; Morrow, R. Main eddy vertical structures observed in the four major Eastern Boundary Upwelling Systems. J. Geophys. Res. Oceans 2015, 120, 6008–6033. [Google Scholar] [CrossRef]
  45. Wang, Z.; Li, Q.; Sun, L.; Li, S.; Yang, Y.; Liu, S. The most typical shape of oceanic mesoscale eddies from global satellite sea level observations. Front. Earth Sci. 2015, 9, 202–208. [Google Scholar] [CrossRef]
  46. Hwang, C.; Wu, C.R.; Kao, R. TOPEX/Poseidon observations of mesoscale eddies over the Subtropical Countercurrent: Kinematic characteristics of an anticyclonic eddy and a cyclonic eddy. J. Geophys. Res. Ocean. 2004, 109, C08013. [Google Scholar] [CrossRef]
  47. Qiu, B.; Lukas, R. Seasonal and interannual variability of the North Equatorial Current, the Mindanao Current, and the Kuroshio along the Pacific western boundary. J. Geophys. Res. Oceans 1996, 101, 12315–12330. [Google Scholar] [CrossRef]
  48. Ferrari, R.; Wunsch, C. The distribution of eddy kinetic and potential energies in the global ocean. Tellus A Dyn. Meteorol. Oceanogr. 2010, 62, 92–108. [Google Scholar] [CrossRef]
  49. Qiu, B.; Chen, S. Variability of the Kuroshio extension jet, recirculation gyre, and mesoscale eddies on decadal time scales. J. Phys. Oceanogr. 2005, 35, 2090–2103. [Google Scholar] [CrossRef]
  50. Kamenkovich, V.M.; Leonov, Y.P.; Nechaev, D.A.; Byrne, D.A.; Gordon, A.L. On the influence of bottom topography on the Agulhas eddy. J. Phys. Oceanogr. 1996, 26, 892–912. [Google Scholar] [CrossRef]
  51. Qiu, B. Encyclopedia of Ocean Sciences; Academic Press: Cambridge, MA, USA, 2001; pp. 1413–1426. [Google Scholar]
  52. Chelton, D.B.; Schlax, M.G. Global observations of oceanic Rossby Waves. Science 1996, 272, 234–238. [Google Scholar] [CrossRef]
  53. Zhang, Z.; Zhao, W.; Qiu, B.; Tian, J. Anticyclonic eddy sheddings from Kuroshio loop and the accompanying cyclonic eddy in the northeastern South China Sea. J. Phys. Oceanogr. 2017, 47, 1243–1259. [Google Scholar] [CrossRef]
  54. Shi, Y.; Liu, X.; Liu, T.; Chen, D. Characteristics of mesoscale eddies in the vicinity of the Kuroshio: Statistics from satellite altimeter observations and OFES model data. J. Mar. Sci. Eng. 2022, 10, 1975. [Google Scholar] [CrossRef]
  55. Kamenkovich, I.; Berloff, P.; Pedlosky, J. Role of eddy forcing in the dynamics of multiple zonal jets in a model of the North Atlantic. J. Phys. Oceanogr. 2009, 39, 1361–1379. [Google Scholar] [CrossRef]
  56. Lee, I.H.; Ko, D.S.; Wang, Y.H.; Centurioni, L.; Wang, D.P. The mesoscale eddies and Kuroshio transport in the western North Pacific east of Taiwan from 8-year (2003–2010) model reanalysis. Ocean Dyn. 2013, 63, 1027–1040. [Google Scholar] [CrossRef]
  57. Chow, C.H.; Shih, Y.Y.; Chien, Y.T.; Chen, J.Y.; Fan, N.; Wu, W.C.; Hung, C.C. The wind effect on biogeochemistry in eddy cores in the Northern South China Sea. Front. Mar. Sci. 2021, 8, 717576. [Google Scholar] [CrossRef]
  58. Chu, F.; Si, Z.; Yan, X.; Liu, Z.; Yu, J.; Pang, C. Physical structure and evolution of a cyclonic eddy in the Northern South China sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2022, 189, 103876. [Google Scholar] [CrossRef]
  59. Simanungkalit, Y.A.; Pranowo, W.; Purba, N.; Riyantini, I.; Nurrahman, Y. Influence of El Nino Southern Oscillation (ENSO) phenomena on eddies variability in the northwest Pacific Ocean. IOP Conf. Ser. Earth Environ. Sci. 2018, 176, 012002. [Google Scholar] [CrossRef]
  60. Cheng, X.; Qi, Y. Variations of eddy kinetic energy in the South China Sea. J. Oceanogr. 2010, 66, 85–94. [Google Scholar] [CrossRef]
  61. Zhao, H.; Yue, X.; Wang, L.; Wu, X.; Chen, Z. Submesoscale short-lived eddies in the southwestern Taiwan Strait observed by high-frequency surface-wave radars. Remote Sens. 2024, 16, 589. [Google Scholar] [CrossRef]
  62. Yin, Y.; Lin, X.; Hou, Y. Seasonality of the Kuroshio intensity east of Taiwan modulated by mesoscale eddies. J. Mar. Syst. 2019, 193, 84–93. [Google Scholar] [CrossRef]
  63. Jia, F.; Wu, L.; Qiu, B. Seasonal modulation of eddy kinetic energy and its formation mechanism in the southeast Indian Ocean. J. Phys. Oceanogr. 2011, 41, 657–665. [Google Scholar] [CrossRef]
  64. Qiu, B.; Chen, S. Eddy-mean flow interaction in the decadally-modulating Kuroshio Extension system. Deep Sea Res. II 2010, 57, 1098–1110. [Google Scholar] [CrossRef]
  65. Yang, S.; Xing, J.; Sheng, J.; Chen, S.; Chen, D. A process study of interactions between a warm eddy and the Kuroshio Current in Luzon Strait: The fate of eddies. J. Mar. Syst. 2019, 194, 66–80. [Google Scholar] [CrossRef]
  66. Chen, C.T.A.; Jan, S.; Huang, T.H.; Tseng, Y.H. Spring of no Kuroshio intrusion in the southern Taiwan Strait. J. Geophys. Res. Ocean. 2010, 115, C8. [Google Scholar] [CrossRef]
  67. Fu, L.L.; Ferrari, R. Observing oceanic submesoscale processes from space. Eos 2008, 89, 488. [Google Scholar] [CrossRef]
  68. Tom, F.; d’Ovidio, F.; Gerald, D. Ocean Finescale Dynamics—SWOT Science Team Meeting 2024. Available online: https://swot.jpl.nasa.gov/events/63/2024-swot-science-team-meeting/ (accessed on 5 May 2025).
  69. Lévy, M.; Franks, P.J.S.; Smith, K.S. The role of submesoscale currents in structuring marine ecosystems. Nat. Commun. 2018, 9, 4758. [Google Scholar] [CrossRef]
  70. Alpers, W.; Brandt, P.; Lazar, A.; Dagorne, D.; Sow, B.; Faye, S.; Hansen, M.W.; Rubino, A.; Poulain, P.M.; Brehmer, P. A small-scale oceanic eddy off the coast of West Africa studied by multi-sensor satellite and surface drifter data. Remote Sens. Environ. 2013, 129, 132–143. [Google Scholar] [CrossRef]
  71. Karimova, S. Spiral eddies in the Baltic, Black and Caspian seas as seen by satellite radar data. Adv. Space Res. 2012, 50, 1107–1124. [Google Scholar] [CrossRef]
  72. Whalen, C.B.; De Lavergne, C.; Naveira Garabato, A.C.; Klymak, J.M.; MacKinnon, J.A.; Sheen, K.L. Internal wave-driven mixing: Governing processes and consequences for climate. Nat. Rev. Earth Environ. 2020, 1, 606–621. [Google Scholar] [CrossRef]
  73. Duo, Z.; Wang, W.; Wang, H. Oceanic mesoscale eddy detection method based on deep learning. Remote Sens. 2019, 11, 1921. [Google Scholar] [CrossRef]
  74. Sun, H.; Li, H.; Xu, M.; Yang, F.; Zhao, Q.; Li, C. A lightweight deep learning model for ocean eddy detection. Front. Mar. Sci. 2023, 10, 1266452. [Google Scholar] [CrossRef]
  75. Ioannou, A.; Guez, L.; Laxenaire, R.; Speich, S. Global Assessment of Mesoscale Eddies with TOEddies: Comparison Between Multiple Datasets and Colocation with In Situ Measurements. Remote Sens. 2024, 16, 4336. [Google Scholar] [CrossRef]
  76. Ni, Q.; Zhai, X.; Wilson, C.; Chen, C.; Chen, D. Submesoscale eddies in the South China Sea. Geophys. Res. Lett. 2021, 48, e2020GL091555. [Google Scholar] [CrossRef]
Remotesensing 17 01665 g001
Figure 1. Seafloor and topographic map of the study area. The high-eddy-production area covers the North Pacific subtropical countercurrent (STCC). The bathymetric data from Generic Mapping Tools Version 6 @earth_relief are integrated from Shuttle Radar Topography Mission and other datasets.
Figure 1. Seafloor and topographic map of the study area. The high-eddy-production area covers the North Pacific subtropical countercurrent (STCC). The bathymetric data from Generic Mapping Tools Version 6 @earth_relief are integrated from Shuttle Radar Topography Mission and other datasets.
Remotesensing 17 01665 g001
Remotesensing 17 01665 g002
Figure 2. Workflow for eddy identification with PET.
Figure 2. Workflow for eddy identification with PET.
Remotesensing 17 01665 g002
Remotesensing 17 01665 g003
Figure 3. Simulated SLA with large-scale (a), mesoscale (b), and submesoscale (c) eddies. (d–f) are simulated close contours with the same scales as (a–c).
Figure 3. Simulated SLA with large-scale (a), mesoscale (b), and submesoscale (c) eddies. (d–f) are simulated close contours with the same scales as (a–c).
Remotesensing 17 01665 g003
Remotesensing 17 01665 g004
Figure 4. Identified eddies at (a) large-scale, (b) mesoscale, and (c) submesoscale using the PET method. The dashed red curves correspond to the eddy boundaries from ER, while the solid curves correspond to the eddy boundaries from SR.
Figure 4. Identified eddies at (a) large-scale, (b) mesoscale, and (c) submesoscale using the PET method. The dashed red curves correspond to the eddy boundaries from ER, while the solid curves correspond to the eddy boundaries from SR.
Remotesensing 17 01665 g004
Remotesensing 17 01665 g005
Figure 5. (a) SLA on 1 May 2023 by applying a 500 km high-pass filter; unit is m. (b) Identified CE (blue) and AE (red) obtained based on the contours extracted from Figure 5a and screened using the five contour constraints. The solid line and the dashed line represent the speed-based contour and the effective contour of the eddy, respectively.
Figure 5. (a) SLA on 1 May 2023 by applying a 500 km high-pass filter; unit is m. (b) Identified CE (blue) and AE (red) obtained based on the contours extracted from Figure 5a and screened using the five contour constraints. The solid line and the dashed line represent the speed-based contour and the effective contour of the eddy, respectively.
Remotesensing 17 01665 g005
Remotesensing 17 01665 g006
Figure 6. (a) ER, (b) SR, (c) EKE, and (d) EKE mean of identified eddies on 1 May 2023. The EKE mean refers to the filling of EKE within each identified eddy contour.
Figure 6. (a) ER, (b) SR, (c) EKE, and (d) EKE mean of identified eddies on 1 May 2023. The EKE mean refers to the filling of EKE within each identified eddy contour.
Remotesensing 17 01665 g006
Remotesensing 17 01665 g007
Figure 7. (a) The spatial distribution of identified cyclonic eddies by the PET method from 1 January 2000 to 31 December 2022 on a 1° × 1° grid. The curves on the right and bottom represent the eddy counts along longitude and latitude, respectively. (b) Same as (a) but for anticyclonic eddies.
Figure 7. (a) The spatial distribution of identified cyclonic eddies by the PET method from 1 January 2000 to 31 December 2022 on a 1° × 1° grid. The curves on the right and bottom represent the eddy counts along longitude and latitude, respectively. (b) Same as (a) but for anticyclonic eddies.
Remotesensing 17 01665 g007
Remotesensing 17 01665 g008
Figure 8. The spatial distribution of amplitudes of cyclonic (a) and anticyclonic (b) eddy was identified from 1 January 2000 to 31 December 2022 on a 1° × 1° grid.
Figure 8. The spatial distribution of amplitudes of cyclonic (a) and anticyclonic (b) eddy was identified from 1 January 2000 to 31 December 2022 on a 1° × 1° grid.
Remotesensing 17 01665 g008
Remotesensing 17 01665 g009
Figure 9. (a) Statistical analysis of cyclonic and anticyclonic eddy counts for each month in the northwest Pacific Ocean, south of Japan, with a three-month moving average. ENSO events are highlighted whenever the ONI.v5 exceeds a threshold of 1 (moderate to strong El Niño, red) or −1 (moderate to strong La Niña, blue). (b) The climatologically monthly mean of the number of cyclonic and anticyclonic eddies during 2000–2022.
Figure 9. (a) Statistical analysis of cyclonic and anticyclonic eddy counts for each month in the northwest Pacific Ocean, south of Japan, with a three-month moving average. ENSO events are highlighted whenever the ONI.v5 exceeds a threshold of 1 (moderate to strong El Niño, red) or −1 (moderate to strong La Niña, blue). (b) The climatologically monthly mean of the number of cyclonic and anticyclonic eddies during 2000–2022.
Remotesensing 17 01665 g009
Remotesensing 17 01665 g010aRemotesensing 17 01665 g010b
Figure 10. (a) Eddy trajectories with a lifespan greater than 8 (a), 16 (b), 32 (c), and 48 (d) weeks tracked from 1 January 2000 to 5 June 2023. Here, the eddy lifetime refers to the duration of the eddy trajectories within the study area.
Figure 10. (a) Eddy trajectories with a lifespan greater than 8 (a), 16 (b), 32 (c), and 48 (d) weeks tracked from 1 January 2000 to 5 June 2023. Here, the eddy lifetime refers to the duration of the eddy trajectories within the study area.
Remotesensing 17 01665 g010aRemotesensing 17 01665 g010b
Remotesensing 17 01665 g011
Figure 11. (a,b) are statistics on the percentage of anticyclonic eddies by speed radius and amplitude, grouped by different lifespans; (c,d) are same as (a,b) but for cyclonic eddies.
Figure 11. (a,b) are statistics on the percentage of anticyclonic eddies by speed radius and amplitude, grouped by different lifespans; (c,d) are same as (a,b) but for cyclonic eddies.
Remotesensing 17 01665 g011
Remotesensing 17 01665 g012
Figure 12. Spatial overlay verification of cyclonic eddy trajectories (in red) and SVP floats (in orange). The blue contours represent the closed contours of the eddy with a 10-day interval. (a) Eastern region of Taiwan; (b,d) southern region of Taiwan; (c) SCS region. The arrows indicate the travel direction of the eddies. The dates are shown in the text.
Figure 12. Spatial overlay verification of cyclonic eddy trajectories (in red) and SVP floats (in orange). The blue contours represent the closed contours of the eddy with a 10-day interval. (a) Eastern region of Taiwan; (b,d) southern region of Taiwan; (c) SCS region. The arrows indicate the travel direction of the eddies. The dates are shown in the text.
Remotesensing 17 01665 g012
Remotesensing 17 01665 g013
Figure 13. (a) SLA observations from conventional altimetry and (b) SWOT’s one-day orbit on 1 May 2023.
Figure 13. (a) SLA observations from conventional altimetry and (b) SWOT’s one-day orbit on 1 May 2023.
Remotesensing 17 01665 g013
Remotesensing 17 01665 g014
Figure 14. (a) Cyclonic and anticyclonic submesoscale eddies detected from conventional altimetry, and (b) from SWOT’s one-day orbit on 1 May 2023. See the text for the numbers in the dashed rectangles.
Figure 14. (a) Cyclonic and anticyclonic submesoscale eddies detected from conventional altimetry, and (b) from SWOT’s one-day orbit on 1 May 2023. See the text for the numbers in the dashed rectangles.
Remotesensing 17 01665 g014
Remotesensing 17 01665 g015
Figure 15. (a,b) Submesoscale features identified from three-day observations of SWOT satellites in two sub-regions labeled 3 and 4 in Figure 14. (c,d) SRs and ERs based on data from conventional altimeter data (Figure 5b) and SWOT data (pass 21) on 1 May 2023.
Figure 15. (a,b) Submesoscale features identified from three-day observations of SWOT satellites in two sub-regions labeled 3 and 4 in Figure 14. (c,d) SRs and ERs based on data from conventional altimeter data (Figure 5b) and SWOT data (pass 21) on 1 May 2023.
Remotesensing 17 01665 g015
Remotesensing 17 01665 g016
Figure 16. (a) SLA from conventional altimetry, (b) from SWOT (one cycle of 21-day science orbit), (c) eddies identified from the SLA in (a), and (d) eddies identified the SLA in (b). In (d), only eddy centers (circles) are shown without contours like in (c).
Figure 16. (a) SLA from conventional altimetry, (b) from SWOT (one cycle of 21-day science orbit), (c) eddies identified from the SLA in (a), and (d) eddies identified the SLA in (b). In (d), only eddy centers (circles) are shown without contours like in (c).
Remotesensing 17 01665 g016
Remotesensing 17 01665 g017
Figure 17. (a,b) SLA observations from two cycles of ascending and descending SWOT’s 21-day orbit. The dates of the cycles are shown in the figures.
Figure 17. (a,b) SLA observations from two cycles of ascending and descending SWOT’s 21-day orbit. The dates of the cycles are shown in the figures.
Remotesensing 17 01665 g017
Remotesensing 17 01665 g018
Figure 18. (a,b) Ripple-like SLA features from one cycle of SWOT’s 21-day ascending and descending orbit on the west side of the Luzon Strait. The dates are shown in the figures.
Figure 18. (a,b) Ripple-like SLA features from one cycle of SWOT’s 21-day ascending and descending orbit on the west side of the Luzon Strait. The dates are shown in the figures.
Remotesensing 17 01665 g018
Remotesensing 17 01665 g019
Figure 19. Evolutions of two large-scale eddies shown in Figure 16a obtained by the combination of the radar altimeters and KaRIn in the days that SWOT orbit during the period from 7 September to 8 October 2023.
Figure 19. Evolutions of two large-scale eddies shown in Figure 16a obtained by the combination of the radar altimeters and KaRIn in the days that SWOT orbit during the period from 7 September to 8 October 2023.
Remotesensing 17 01665 g019
Table 1. EGF parameters for the simulated eddies (see also Appendix B).
Table 1. EGF parameters for the simulated eddies (see also Appendix B).
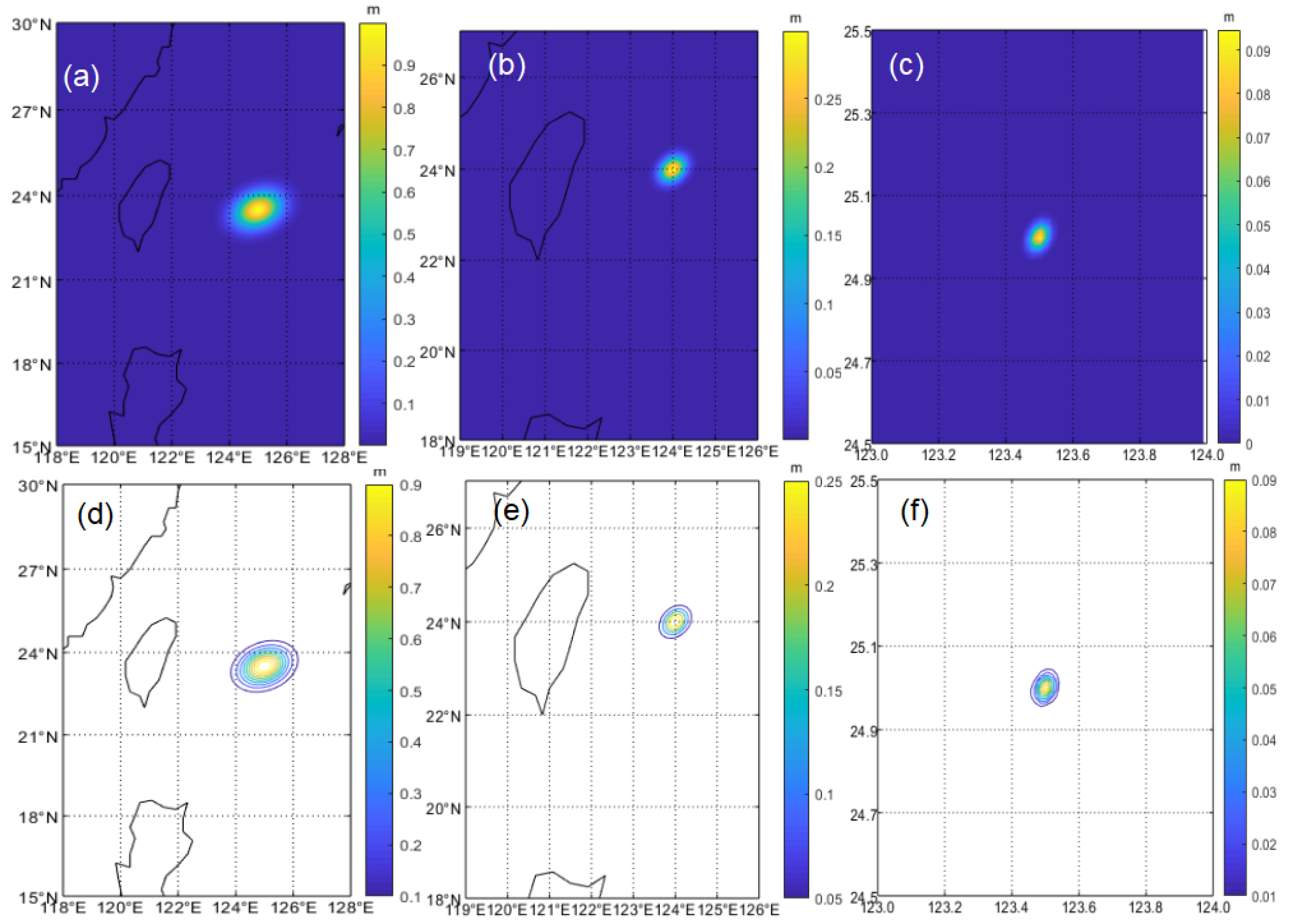
Eddy ScaleEddy CenterSemi-Major Axis (km)Semi-Minor Axis (km)Amplitude (m)Rotation Angle
Large-scale eddy(125°E, 23.5°N)12593.751.030°
Mesoscale eddy(124°E, 24°N)5037.50.345°
Submesoscale eddy(123.5°E, 25°N)53.750.160°
Table 2. Parameters of eddy identification at various scales.
Table 2. Parameters of eddy identification at various scales.
ER (km)SR (km)FCR (km)Relative Errors
Between ER and FCR
Large-scale eddy113.8950.63108.255.2%
Mesoscale eddy47.7327.5743.3010.2%
Submesoscale eddy6.026.024.3339.0%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, L.; Hwang, C.; Liu, H.-Y.; Chang, E.T.Y.; Yu, D. Automated Eddy Identification and Tracking in the Northwest Pacific Based on Conventional Altimeter and SWOT Data. Remote Sens. 2025, 17, 1665. https://doi.org/10.3390/rs17101665

AMA Style

Zhang L, Hwang C, Liu H-Y, Chang ETY, Yu D. Automated Eddy Identification and Tracking in the Northwest Pacific Based on Conventional Altimeter and SWOT Data. Remote Sensing. 2025; 17(10):1665. https://doi.org/10.3390/rs17101665

Chicago/Turabian Style

Zhang, Lan, Cheinway Hwang, Han-Yang Liu, Emmy T. Y. Chang, and Daocheng Yu. 2025. "Automated Eddy Identification and Tracking in the Northwest Pacific Based on Conventional Altimeter and SWOT Data" Remote Sensing 17, no. 10: 1665. https://doi.org/10.3390/rs17101665

APA Style

Zhang, L., Hwang, C., Liu, H.-Y., Chang, E. T. Y., & Yu, D. (2025). Automated Eddy Identification and Tracking in the Northwest Pacific Based on Conventional Altimeter and SWOT Data. Remote Sensing, 17(10), 1665. https://doi.org/10.3390/rs17101665

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop