Space Domain Awareness Observations Using the Buckland Park VHF Radar
Abstract
1. Introduction
2. Buckland Park VHF Radar RSO Observations
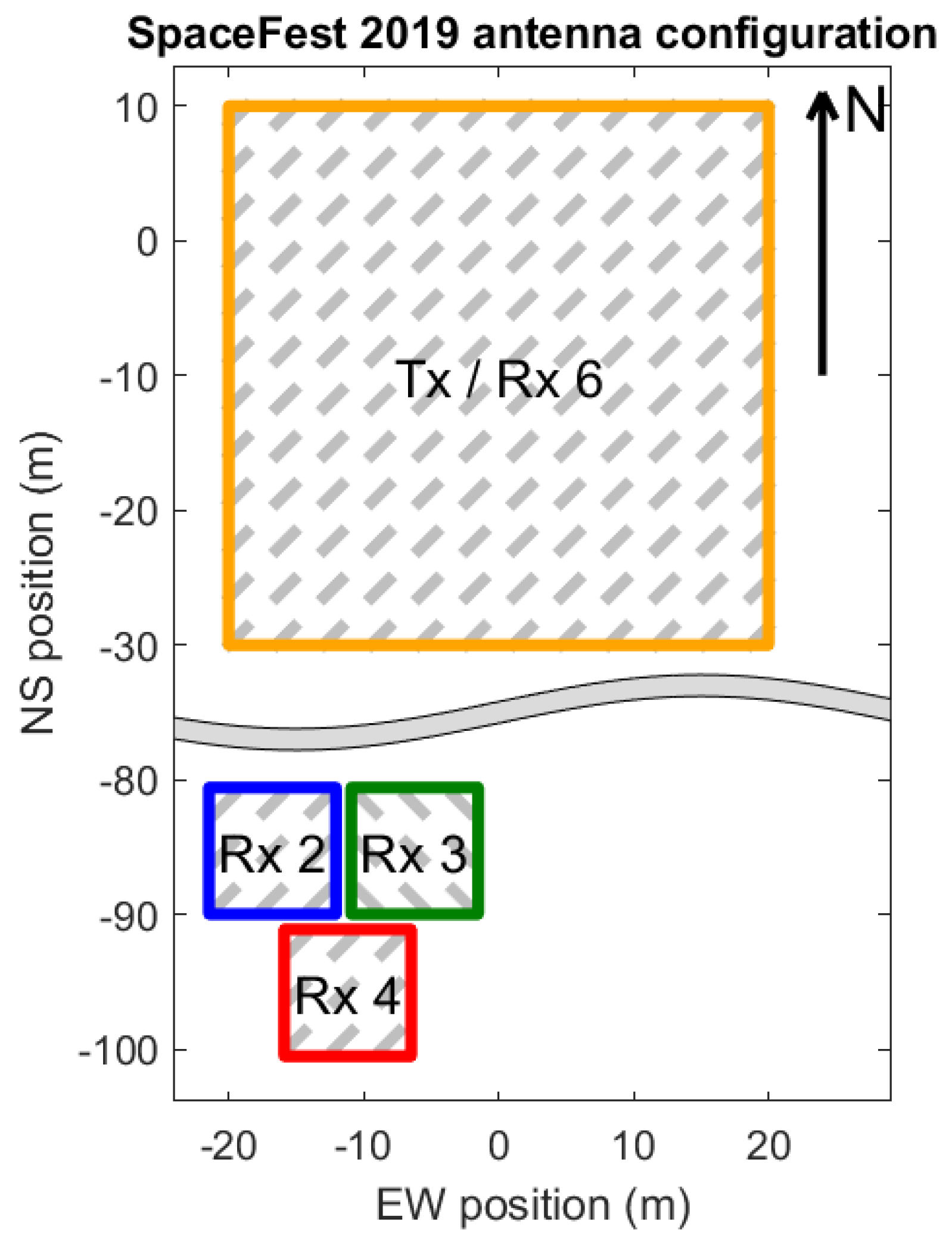
2.1. The Buckland Park VHF Radar
2.2. BPST RSO Observations
- Range migration is mitigated by dividing the RT data into overlapping coherent processing intervals (CPIs) of 4.096 s. Contiguous CPIs are spaced 0.512 s apart (i.e., an 8-times oversampling factor) to maintain acceptable temporal resolution;
- Doppler broadening is mitigated by applying acceleration processing [19] to compensate for RSO motion throughout the CPI. This is achieved by processing each CPI using a bank of radial acceleration hypotheses covering the expected range of LEO RSO radial accelerations (0 to 250 ms−2), yielding a three-dimensional range–time–radial acceleration (RTA) data-set .
- Detection mode (DM) uses radial acceleration processing to generate peaks over the entire RDA space. This allows matching with the RDA parameters obtained using either simplified generalised perturbation (SGP4) propagation of two-line elements (TLE) or Special Perturbations (SPs) data [20], both issued by SpaceTrack (https://www.space-track.org, accessed on 26 March 2024), in addition to the identification of objects that are not in the SpaceTrack catalogue;
- Catalogue maintenance mode (CMM) uses radial acceleration processing using a subset of RDA space around each TLE/SP propagation: i.e., range ±5 km, Doppler ±20 Hz, radial acceleration ±0.05 kms−1. This processing is consequently significantly less computationally intensive than detection mode but only allows the identification of catalogued objects and may miss objects with erroneous propagation state vectors.
3. New BPST Radar Capabilities Introduced for SpaceFest 2019
3.1. Revised Operating Parameters
3.2. Beam and PRF Scheduling
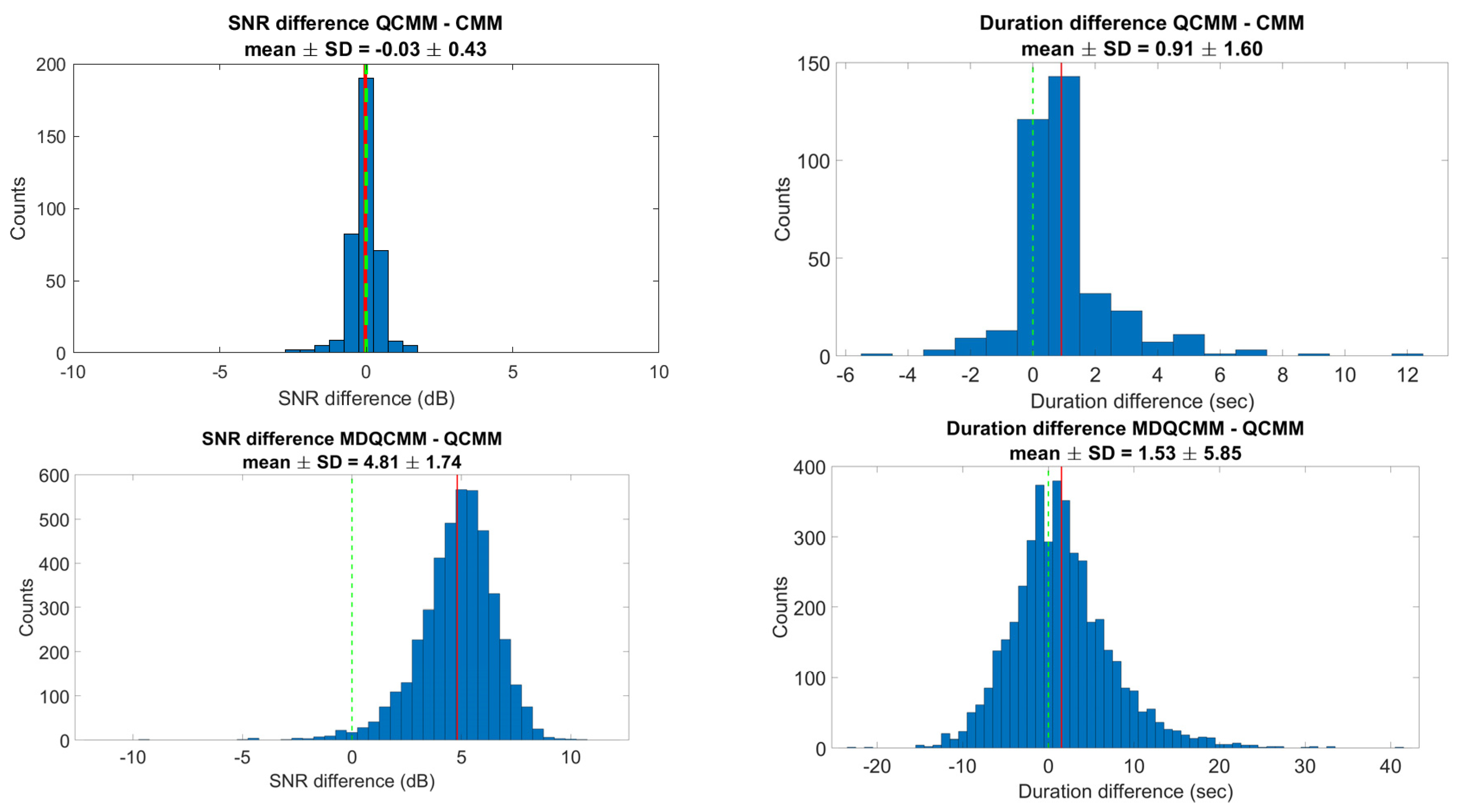
3.3. Quick Catalogue Maintenance Mode (QCMM) Processing
- Range migration correction: Use the propagated range to convert the range–time data to “range difference” ′) time data, This is achieved by interpolating across the range dimension or through a circular shift of the range–time data through the range dimension by samples, where represents the rounding-up operator and ∆r is the range resolution. The former option is applied in this paper, with the interpolation achieved using a simple Fourier method.where represents the fast Fourier transform and is the range ambiguity.
- Phase correction: The change in phase resulting from the change in the propagated range is corrected using the following:
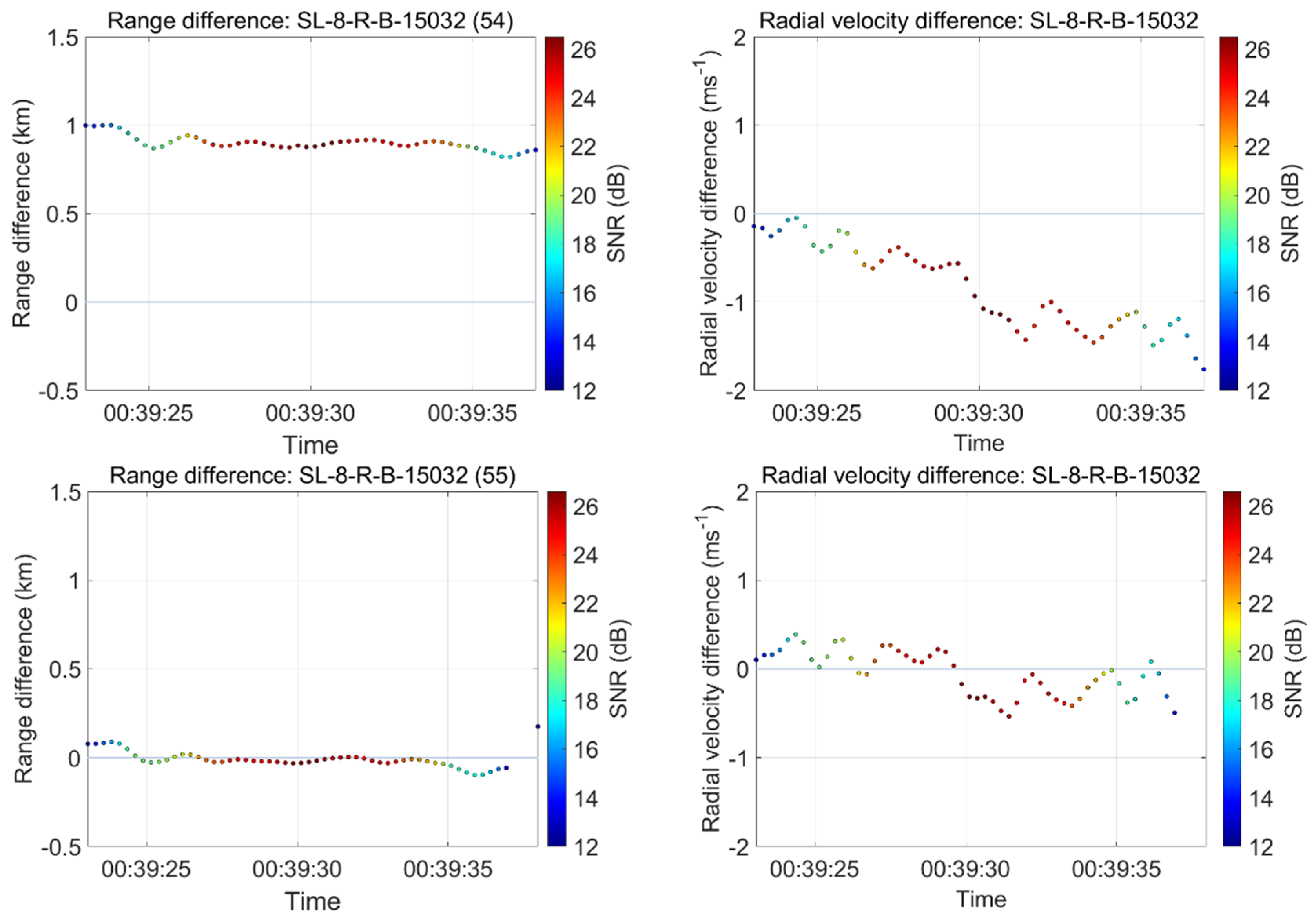
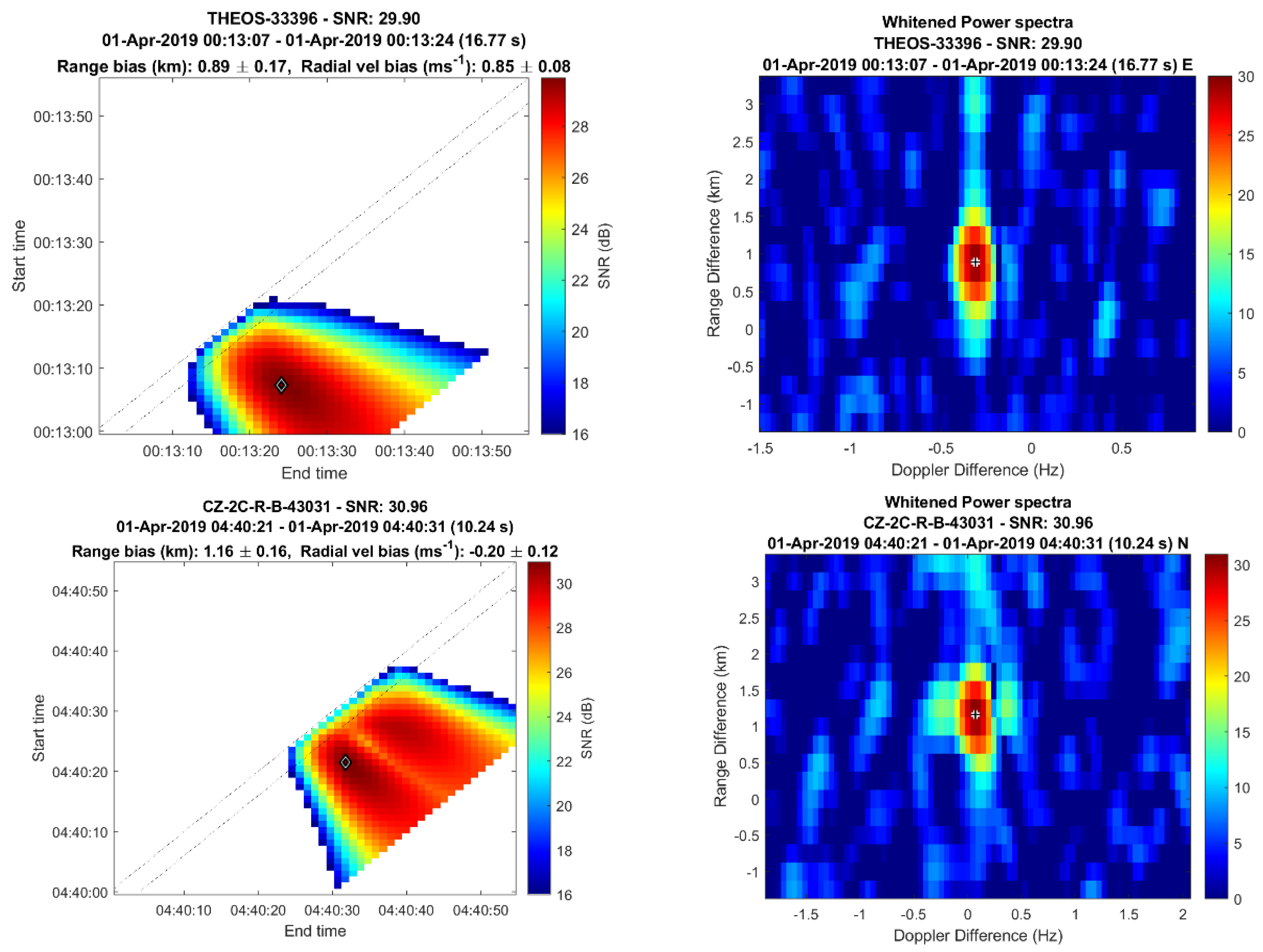
3.4. Matched Duration Quick Catalogue Maintenance Mode (MDQCMM) Processing
3.5. Ionospheric Correction
3.6. Use of Auxiliary Antennae Arrays
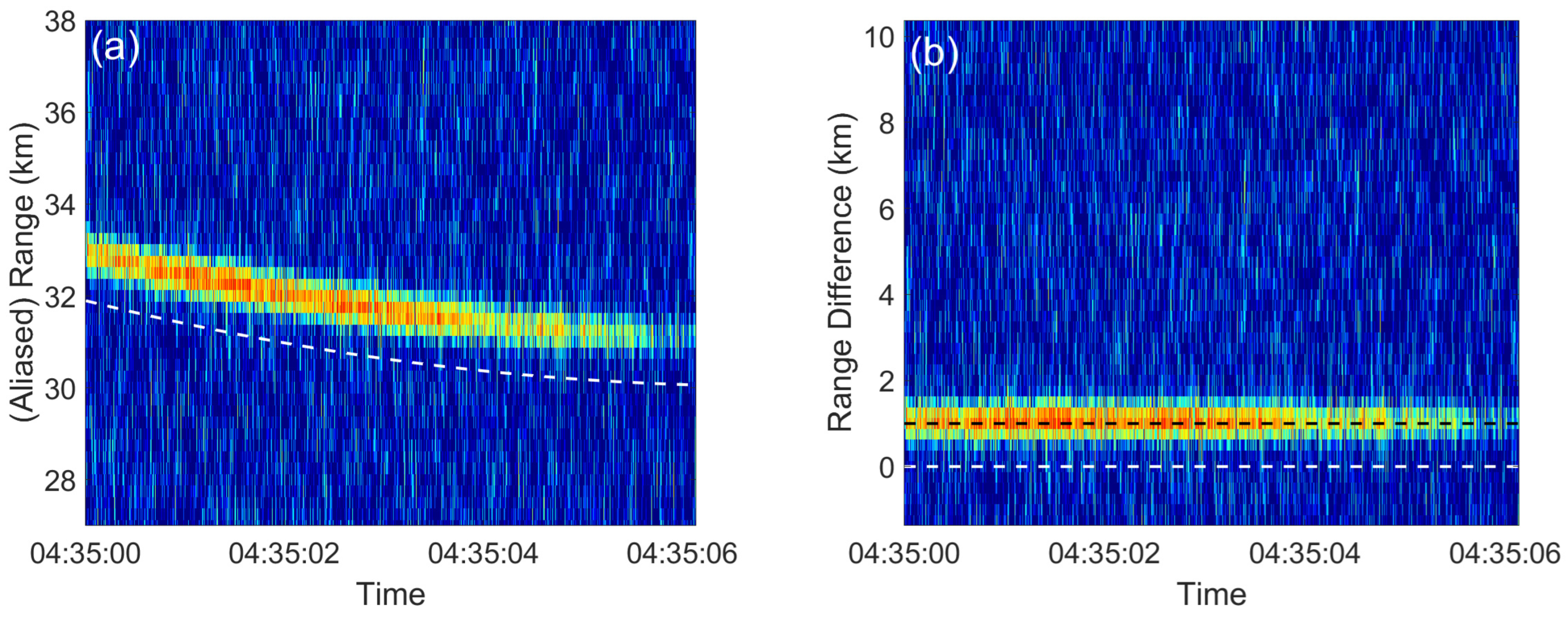
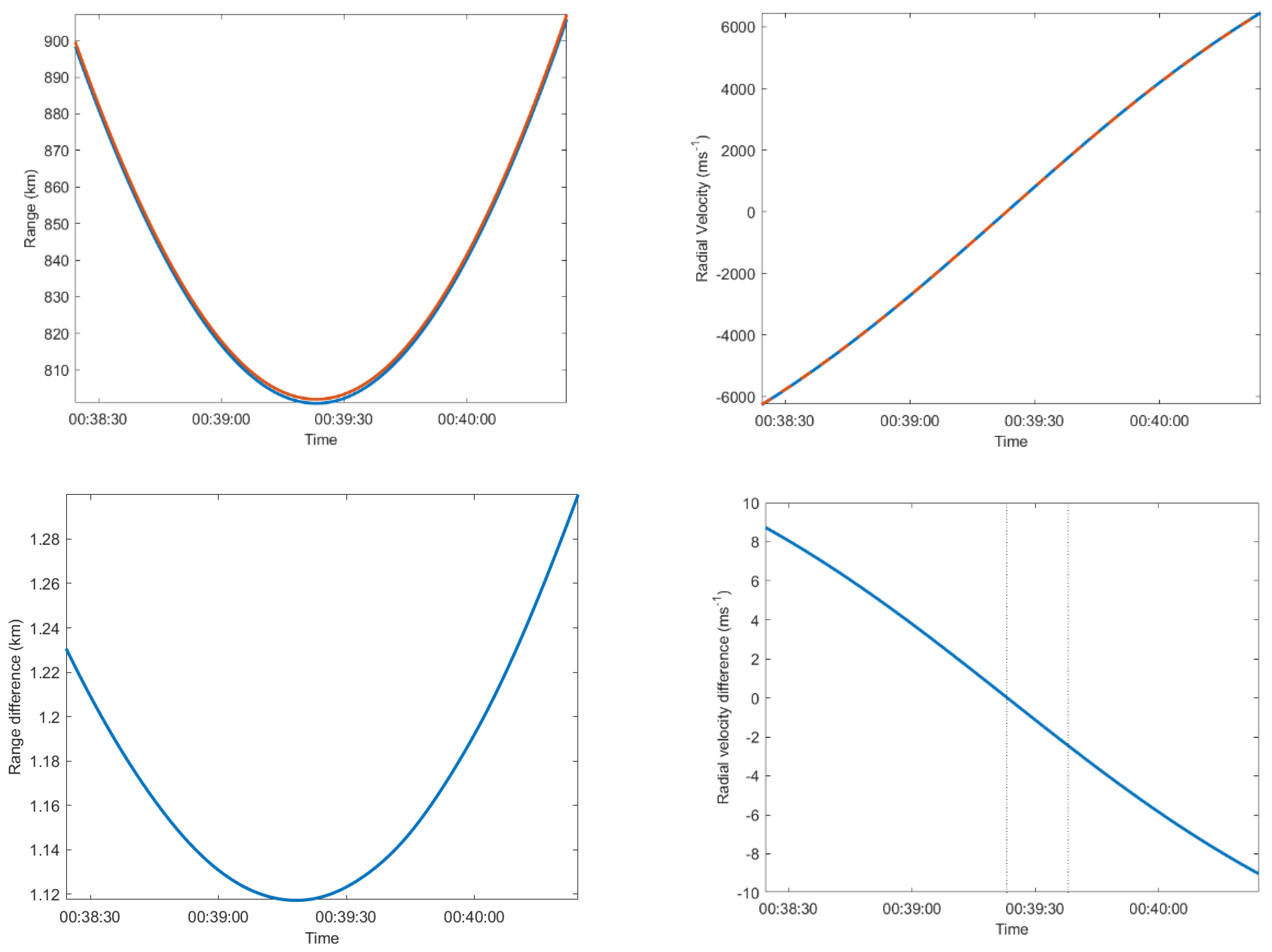
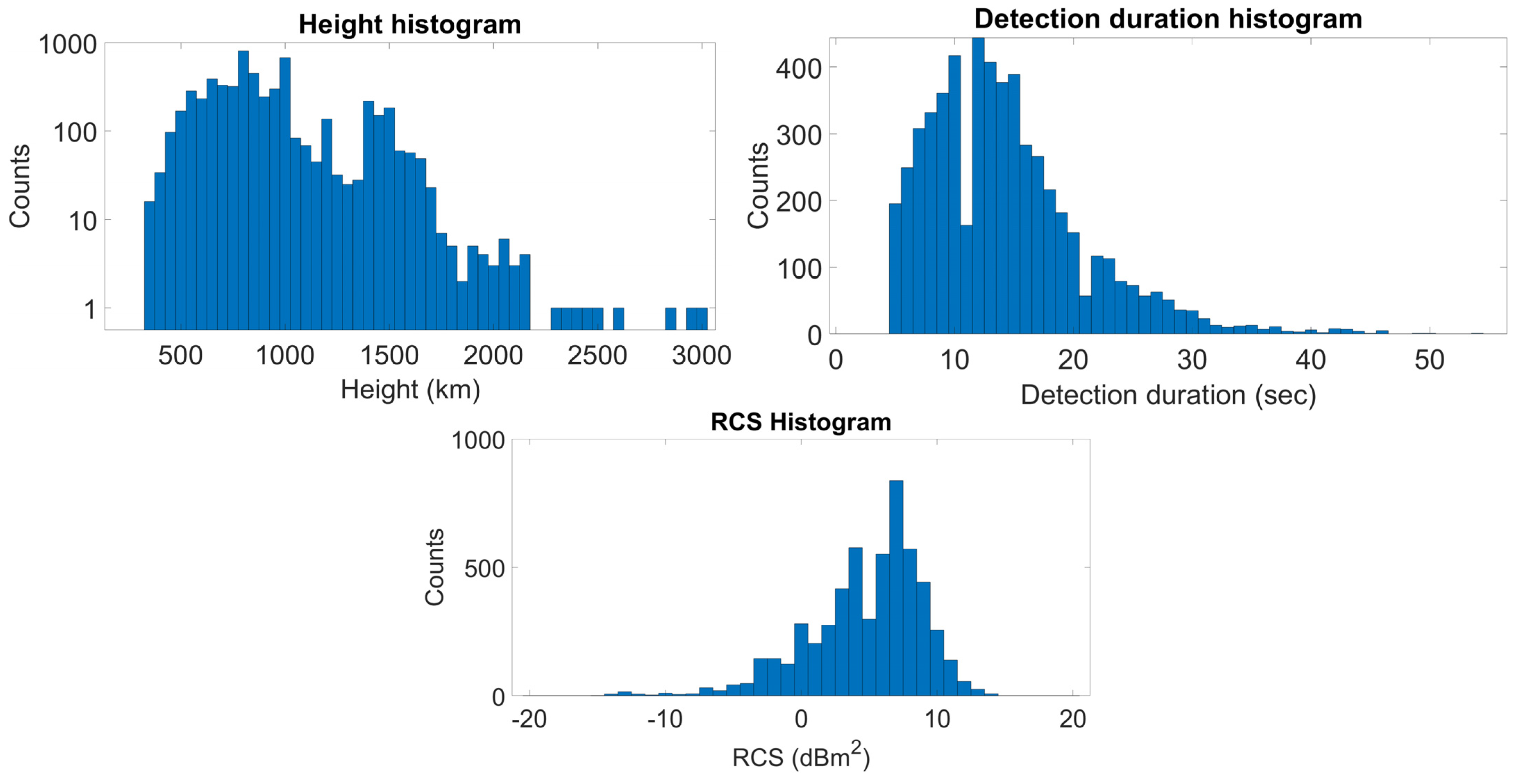
4. Standard Mode Results
4.1. Special Perturbation (SP) Data Comparisons
4.2. International Laser Ranging Service Data Comparisons
5. High-Range Resolution Mode Results
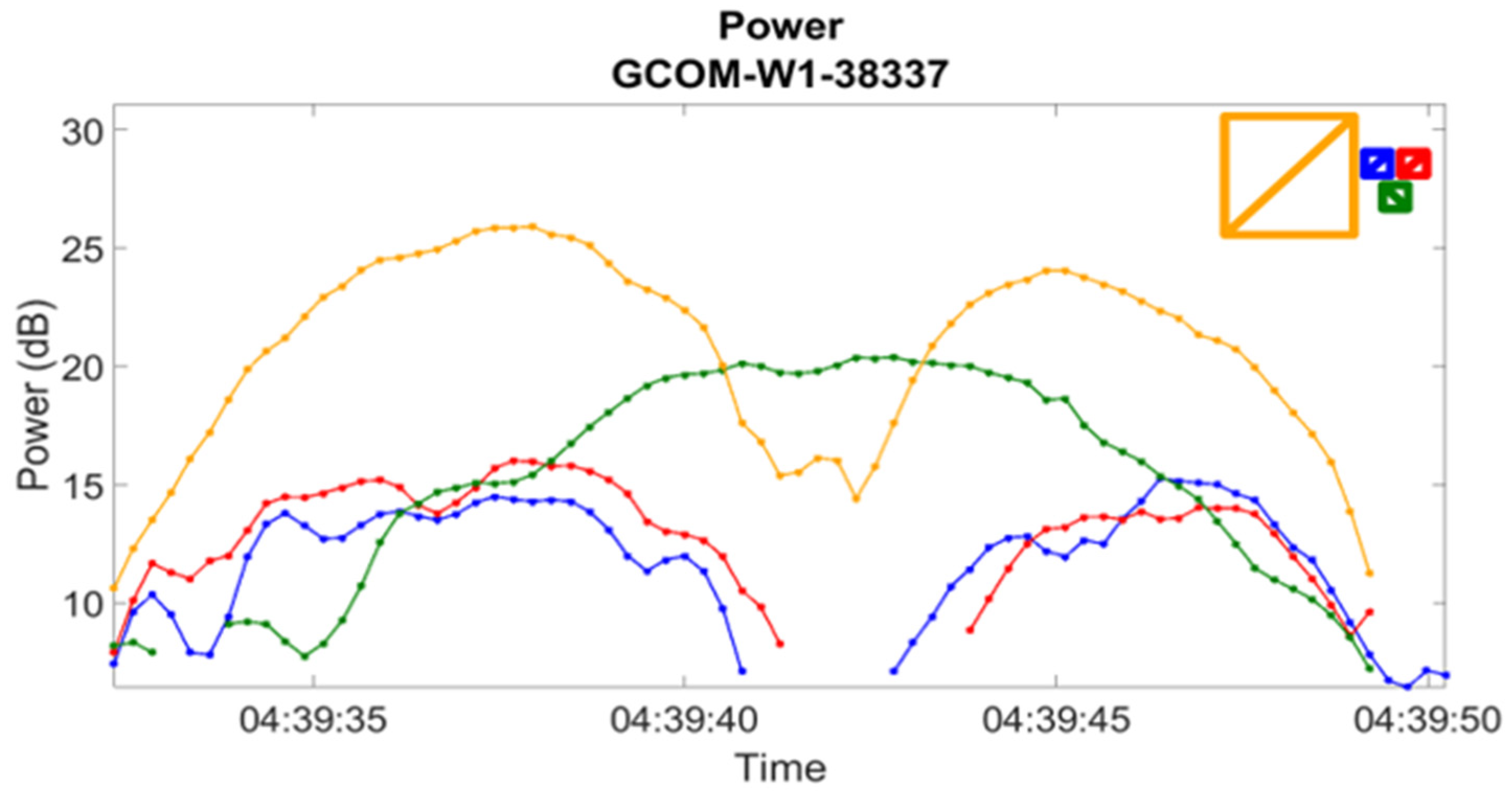
6. Spectrogram Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boley, A.C.; Byers, M. Satellite mega-constellations create risks in Low Earth Orbit, the atmosphere and on Earth. Sci. Rep. 2021, 11, 10642. [Google Scholar] [CrossRef] [PubMed]
- Mann, A. Starlink: SpaceX’s Satellite Internet Project. 2021. Available online: https://www.space.com/spacex-starlink-satellites.html (accessed on 26 March 2024).
- Patel, N.V. Averting space doom. IEEE Spectr. 2015, 52, 16–17. Available online: https://ieeexplore.ieee.org/abstract/document/7024495 (accessed on 26 March 2024).
- ESA. Spacecraft Dodges Large Constellation. Available online: https://www.esa.int/Safety_Security/ESA_spacecraft_dodges_large_constellation (accessed on 26 March 2024).
- Smith, C.H.; Greene, B.; Bold, M.; Drury, R. Development of a new SDA facility at Learmonth Australia. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 11–14 September 2018. [Google Scholar]
- Space Surveillance Telescope Declared Operational—Australian Defence Magazine. Available online: https://www.australiandefence.com.au/news/space-surveillance-telescope-declared-operational (accessed on 26 March 2024).
- LeoLabs Commits to WA for Next Space Radar. October 2021. Available online: https://www.wa.gov.au/government/announcements/leolabs-commits-wa-next-space-radar (accessed on 26 March 2024).
- Cohen, G.; Afshar, S.; van Schaik, A.; Wabnitz, A.; Bessell, T.; Rutten, M.; Morreale, B. Event-based sensing for space situational awareness. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 19–22 September 2017. [Google Scholar]
- Frazer, G.J.; Meehan, D.H.; Warne, G.M. Decametric measurements of the ISS using an experimental HF line-of-sight radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, SA, Australia, 9–12 September 2013. [Google Scholar]
- Frazer, G.J.; Rutten, M.; Cheung, B.; Cervera, M.A. Orbit determination using a decametric line-of-site radar. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 9–12 September 2014. [Google Scholar]
- Palmer, J.E.; Hennessy, B.; Rutten, M.; Merrett, D.; Tingay, S.; Kaplan, D.; Tremblay, S.; Ord, S.M.; Morgan, J.; Wayth, R.B. Surveillance of Space using passive radar and the Murchison Widefield Array. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017; pp. 1715–1720. [Google Scholar]
- Hennessy, B.; Rutten, M.; Young, R.; Tingay, S.; Summers, A.; Gustainis, D.; Crosse, B.; Sokolowski, M. Establishing the Capabilities of the Murchison Widefield Array as a Passive Radar for the Surveillance of Space. Remote Sens. 2022, 14, 2571. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Spargo, A.J.; Reid, I.M.; Adami, C. Low Earth Orbit Object Observations Using the Buckland Park VHF Radar. Radio Sci. 2020, 55, 2019RS006873. [Google Scholar] [CrossRef]
- Hall, T.D.; Duff, G.F.; Maciel, L.J. The Space Mission at Kwajalein. Linc. Lab. J. 2012, 19, 48–63. [Google Scholar]
- Dolman, B.K.; Reid, I.M.; Tingwell, C. Stratospheric tropospheric wind profiling radars in the Australian network. Earth Planets Space 2018, 70, 170. [Google Scholar] [CrossRef]
- Morris, R.J.; Murphy, D.J.; Vincent, R.A.; Holdsworth, D.A.; Klekociuk, A.R.; Reid, I.M. Characteristics of the wind, temperature and PMSE field above Davis, Antarctica. J. Atmos. Sol.-Terr. Phys. 2006, 68, 418–435. [Google Scholar] [CrossRef]
- Morris, R.J.; Klekociuk, A.R.; Holdsworth, D.A. First observations of Southern Hemisphere polar mesosphere winter echoes including conjugate occurrences at∼69 S latitude. Geophys. Res. Lett. 2011. [Google Scholar] [CrossRef]
- Spargo, A.J.; Reid, I.M.; MacKinnon, A.D. Multistatic meteor radar observations of gravity-wave–tidal interaction over southern Australia. Atmos. Meas. Tech. 2019, 12, 4791–4812. [Google Scholar] [CrossRef]
- McGeogh, J.; Jensen, J. Acceleration and Velocity Processing of HF Radar Signals; Technical Report; Naval Research Laboratory: Washington, DC, USA, 1967. [Google Scholar]
- Bird, D. Sharing Space Situational Awareness Data. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 14–17 September 2010. [Google Scholar]
- Davies, K. Ionospheric Radio; IET: London, UK, 1990. [Google Scholar]
- Holdsworth, D.A.; Reid, I.M. Preliminary Count Rate Maximisation of the Buckland Park Interferometric Meteor Radar. In Proceedings of the Workshop on the Applications of Radio Science, Hobart, TAS, Australia, 18–20 February 2004. [Google Scholar]
- McCant, M. Median RCS Values. 2017. Available online: https://www.prismnet.com/~mmccants/catalogs/index.html (accessed on 21 May 2021).
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. Coherent integration with range migration using keystone formatting. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 863–868. [Google Scholar]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather. 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric effects on GPS. In Chapter 12 of Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1996; Volume 1, p. 30. [Google Scholar]
- Seemala, G.K. Estimation of ionospheric total electron content (TEC) from GNSS observations. In Atmospheric Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2023; pp. 63–84. [Google Scholar]
- Wilkinson, P.J. Predictability of ionospheric variations for quiet and disturbed conditions. J. Atmos. Terr. Phys. 1995, 57, 1469–1481. [Google Scholar] [CrossRef]
- Heading, E.; Nguyen, S.T.; Holdsworth, D.; Field, D.; Reid, I. Analysis of RF Signatures for Space Domain Awareness using VHF radar. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York City, NY, USA, 21–25 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Heading, E.; Nguyen, S.T.; Holdsworth, D.; Field, D.; Reid, I. Micro-Doppler Signature Analysis for Space Domain Awareness using VHF radar. Remote Sens. 2024, in press. [Google Scholar]
- Jonker, J.R.; Cervera, M.A.; Holdsworth, D.A.; Harris, T.J.; MacKinnon, A.D.; Neudegg, D.; Reid, I.M. Impact of Ionospheric Doppler Perturbations on Space Domain Awareness Observations. In Proceedings of the International Conference on Radar, Sydney, NSW, Australia, 6–10 November 2023. [Google Scholar]
- Jonker, J.R.; Cervera, M.A.; Harris, T.J.; Holdsworth, D.A.; MacKinnon, A.D.; Neudegg, D.; Reid, I.M. Observational evidence of EMIC waves propagating in the mid-latitude ionospheric waveguide using ground-based HF and VHF radar. Adv. Space Res. 2024. [Google Scholar]
- Harris, T.J.; Quinn, A.D.; Pederick, L.H. The DST group ionospheric sounder replacement for JORN. Radio Sci. 2016, 51, 563–572. [Google Scholar] [CrossRef]
- Barnes, R.I.; Gardiner-Garden, R.S.; Harris, T.J. Real time ionospheric models for the Australian Defence Force. In Proceedings of the Workshop for Applications of Radio Science (WARS), Leura, NSW, Australia, 20–22 February 2002. [Google Scholar]
- Reinisch, B.; Galkin, I.; Huang, X.; Vesnin, A.; Bilitza, D. The Ionosphere Real-Time Assimilative Model, IRTAM-A Status Report. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; Volume 16. [Google Scholar]
- Edwards, D.J.; Chambers, T.E.; Cervera, M.A. CLIMF2: A Climatological Model of the Ionospheric F2 Layer. Part 2: Validation and Comparison with IRI. Adv. Space Res. 2023. [Google Scholar] [CrossRef]
- Sato, T.; Kimura, I.; Kayama, H.; Furusawa, A. MU radar measurements of orbital debris. J. Spacecr. Rocket. 1991, 28, 677–682. [Google Scholar] [CrossRef]
- Renkwitz, T.; Stober, G.; Latteck, R.; Singer, W.; Rapp, M. New experiments to validate the radiation pattern of the Middle Atmosphere Alomar Radar System (MAARSY). Adv. Radio Sci. 2013, 11, 283–289. [Google Scholar] [CrossRef][Green Version]

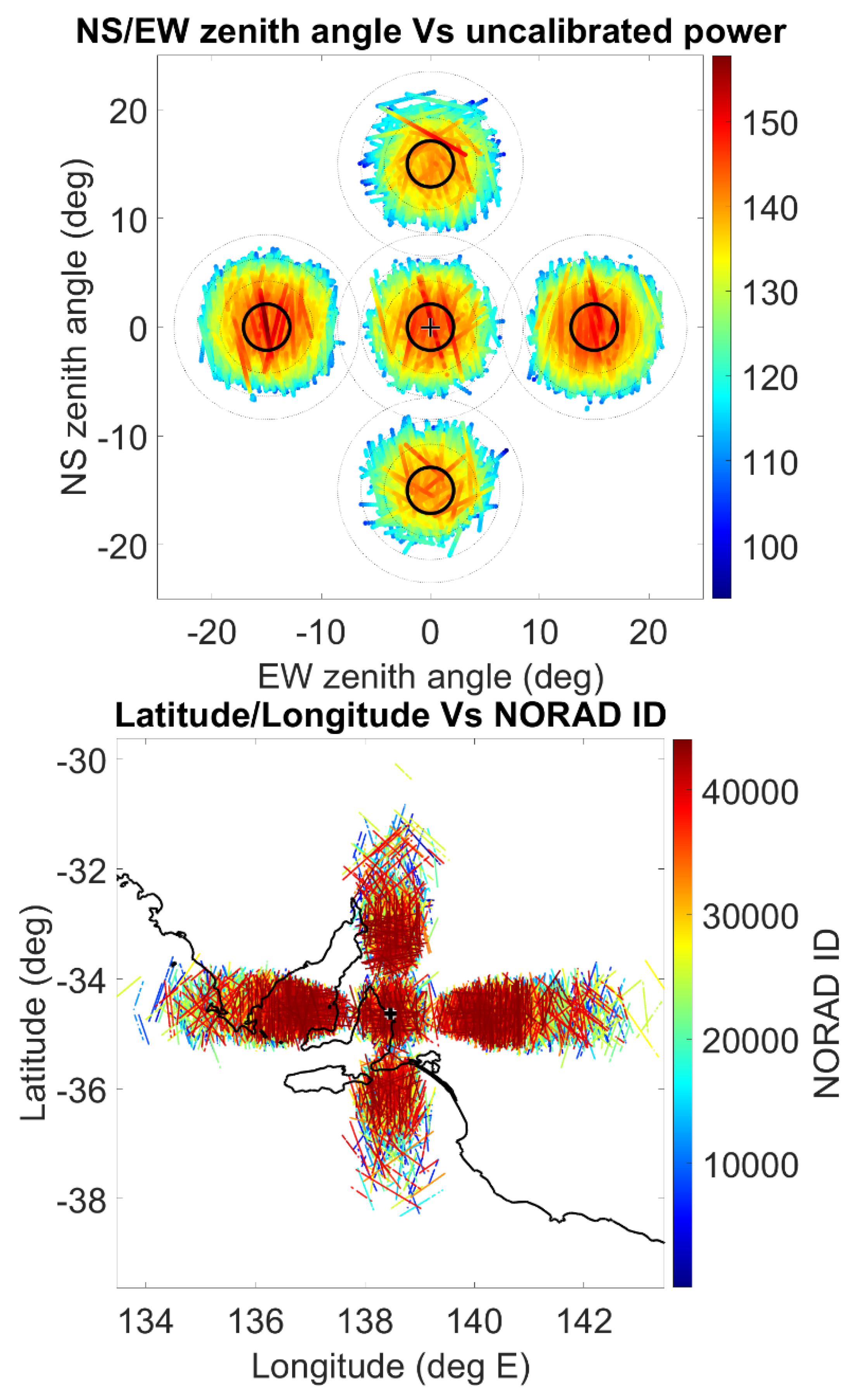

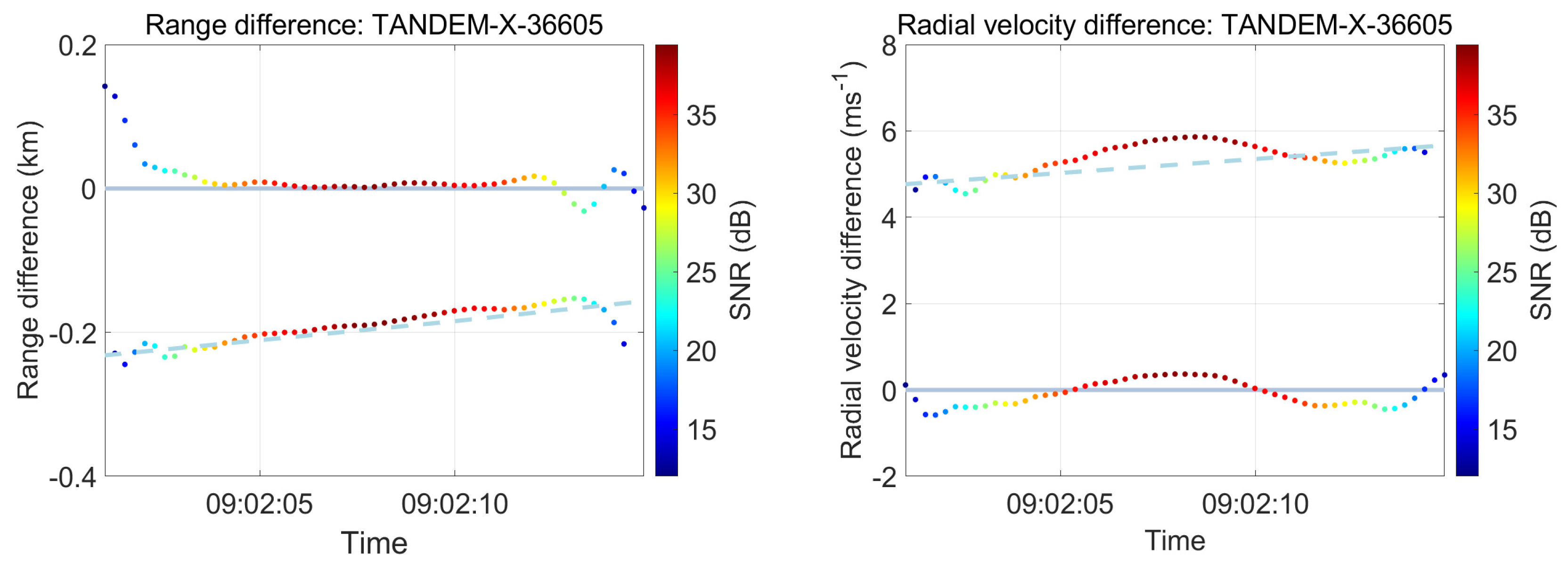


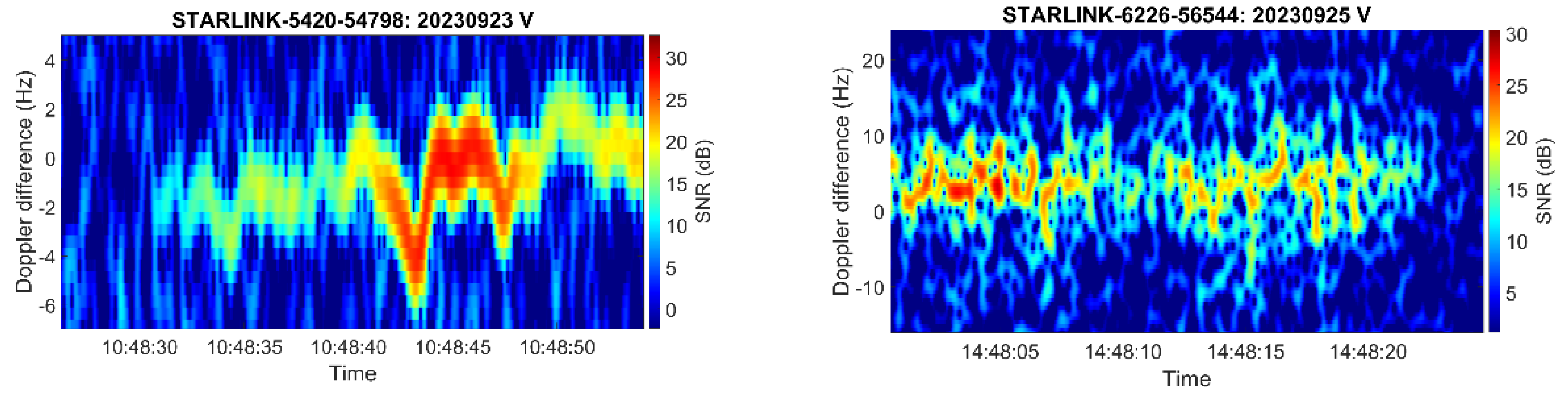
| Parameter | Value(s) |
|---|---|
| Frequency, f (MHz) | 55 |
| Maximum Transmit Power (kW) | 40 (12 4 kW modules, i.e., 48 kW at the transmitter) |
| Maximum Duty Cycle (%) | 10 |
| Pulse Types | Monopulse, Barker, and Complementary Codes |
| Receiver Filter Widths (kHz) | 4, 8, 16, 32 |
| Pulse-to-pulse Frequency Extent | ±50 kHz |
| Maximum Pulse Repetition Frequency (kHz) | 20 |
| Number of Transmit Antennae | 144 |
| Number of Receive Antennae | 144 (Main array), 5 (Meteor array) |
| Combined Tx/Rx Main Array Beam Width (°) | 7 |
| Pulse Widths (m) | 100–4000 |
| Pulse Widths (μs) | 0.67–26.67 |
| Number of Receivers | 6 (1–5: Meteor array, 6: Main array) |
| Range Sampling Resolution, Δr (km) | 0.05–2 |
| Beam Directions (Azimuth, Zenith) (degrees) | (0, 0) “Vertical”, (0, 15) “North”, (90, 15) “East” (180, 15) “South”, (270, 15) “West” |
| Detection Mode |
| Loop over overlap processing intervals |
| Data selection |
| Acceleration processing |
| Doppler processing |
| Peak detection and interpolation |
| Whitening |
| Peak selection |
| Loop over concurrent propagation state vectors |
| Associate peaks to propagation state vectors |
| Declare RSO detected if sufficient associated peaks |
| Catalogue Maintenance Mode |
| Loop over concurrent propagation state vectors |
| Data selection |
| Loop over overlap processing intervals |
| Acceleration processing |
| Doppler processing |
| Peak detection and interpolation |
| Whitening |
| Peak selection |
| Associate peaks to propagation state vectors |
| Declare RSO detected if sufficient associated peaks |
| Parameter | Standard Mode | High Resolution |
|---|---|---|
| Pulse repetition frequency (Hz) | 1953, 2000 | 9950, 10,000 |
| Number of coherent averages | 2 | 6 |
| Dwell length (s) | 56 | 56 |
| Range ambiguity (km) | 76.8, 75 | 15.08, 15 |
| Radial velocity resolution 1 (ms−1) | 1.36 | 1.36 |
| Pulse type | 13-bit Barker | 13-bit Barker |
| Pulse width (km) | 0.5 | 0.1 |
| Pulse width (μs) | 3.33 | 0.67 |
| Receiver filter width (kHz) | 128 | 640 |
| Minimum range (km) | 7.5 | 2.5 |
| Maximum range (km) | 69 | 12.5 |
| Range sampling resolution (km) | 0.25 | 0.1 |
| Loop over Concurrent Propagation State Vectors |
| Apply Keystone-Like Processing |
| Loop over Overlap Processing Intervals |
| Data selection |
| Acceleration processing |
| Doppler processing |
| Peak detection and interpolation |
| Whitening |
| Peak selection |
| Associate peaks to zero range and Doppler difference |
| Declare RSO detected if sufficient associated peaks |
| Loop over Concurrent Propagation State Vectors |
| Apply Keystone-Like Processing |
| Loop over Overlap Processing Interval Start Times |
| Loop over Overlap Processing Interval End Times |
| Data selection |
| Acceleration processing |
| Doppler processing |
| Peak detection and interpolation |
| Whitening |
| Peak selection |
| Associate peaks to zero range and Doppler difference |
| Declare RSO detected if sufficient associated peaks |
| If RSO detected, select start and end times with yielding maximum SNR |
| RSO | QCMM SNR (dB) | MDQCMM SNR (dB) | QCMM Duration (s) | MDQCMM Duration (s) |
|---|---|---|---|---|
| THEOS | 23.32 | 29.90 | 12.84 | 16.77 |
| CZ 2C R-B | 26.19 | 30.96 | 16.90 | 10.24 |
| Processing Type | DM | CMM | QCMM | MDQCMM |
|---|---|---|---|---|
| Processing time (s) | 1204.8 | 39.9 | 5.7 | 77.6 |
| Date | DM | QCMM | QCMM/IC | MDQCMM | MDQCMM/IC |
|---|---|---|---|---|---|
| 22 March 2019 | 372 | 460 | 457 | 580 | 589 |
| 23 March 2019 | 302 | 406 | 399 | 493 | 520 |
| 24 March 2019 | 372 | 473 | 472 | 604 | 624 |
| 25 March 2019 | 383 | 484 | 484 | 615 | 636 |
| 26 March 2019 | 389 | 490 | 496 | 612 | 632 |
| 27 March 2019 | 358 | 447 | 441 | 583 | 595 |
| 28 March 2019 | 290 | 365 | 366 | 483 | 495 |
| 29 March 2019 | 316 | 397 | 395 | 497 | 501 |
| 1 April 2019 | 416 | 507 | 504 | 634 | 646 |
| 2 April 2019 | 400 | 481 | 579 | 627 | 636 |
| Total | 3598 | 4510 | 4593 | 5728 | 5874 |
| Propagation Type | Mean Doppler Difference | Standard Deviation of Doppler Difference |
|---|---|---|
| TLE/SGP4 | −5.41 | 3.96 |
| SP | −0.01 | 1.13 |
| SP with ionospheric correction | −0.02 | 0.86 |
| ILRS | −0.19 | 0.37 |
| ILRS with ionospheric correction | −0.05 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holdsworth, D.A.; Spargo, A.J.; Reid, I.M.; Adami, C.L. Space Domain Awareness Observations Using the Buckland Park VHF Radar. Remote Sens. 2024, 16, 1252. https://doi.org/10.3390/rs16071252
Holdsworth DA, Spargo AJ, Reid IM, Adami CL. Space Domain Awareness Observations Using the Buckland Park VHF Radar. Remote Sensing. 2024; 16(7):1252. https://doi.org/10.3390/rs16071252
Chicago/Turabian StyleHoldsworth, David A., Andrew J. Spargo, Iain M. Reid, and Christian L. Adami. 2024. "Space Domain Awareness Observations Using the Buckland Park VHF Radar" Remote Sensing 16, no. 7: 1252. https://doi.org/10.3390/rs16071252
APA StyleHoldsworth, D. A., Spargo, A. J., Reid, I. M., & Adami, C. L. (2024). Space Domain Awareness Observations Using the Buckland Park VHF Radar. Remote Sensing, 16(7), 1252. https://doi.org/10.3390/rs16071252






