A Reliable Observation Point Selection Method for GB-SAR in Low-Coherence Areas
Abstract
1. Introduction
2. Phase Information Estimation and Filtering
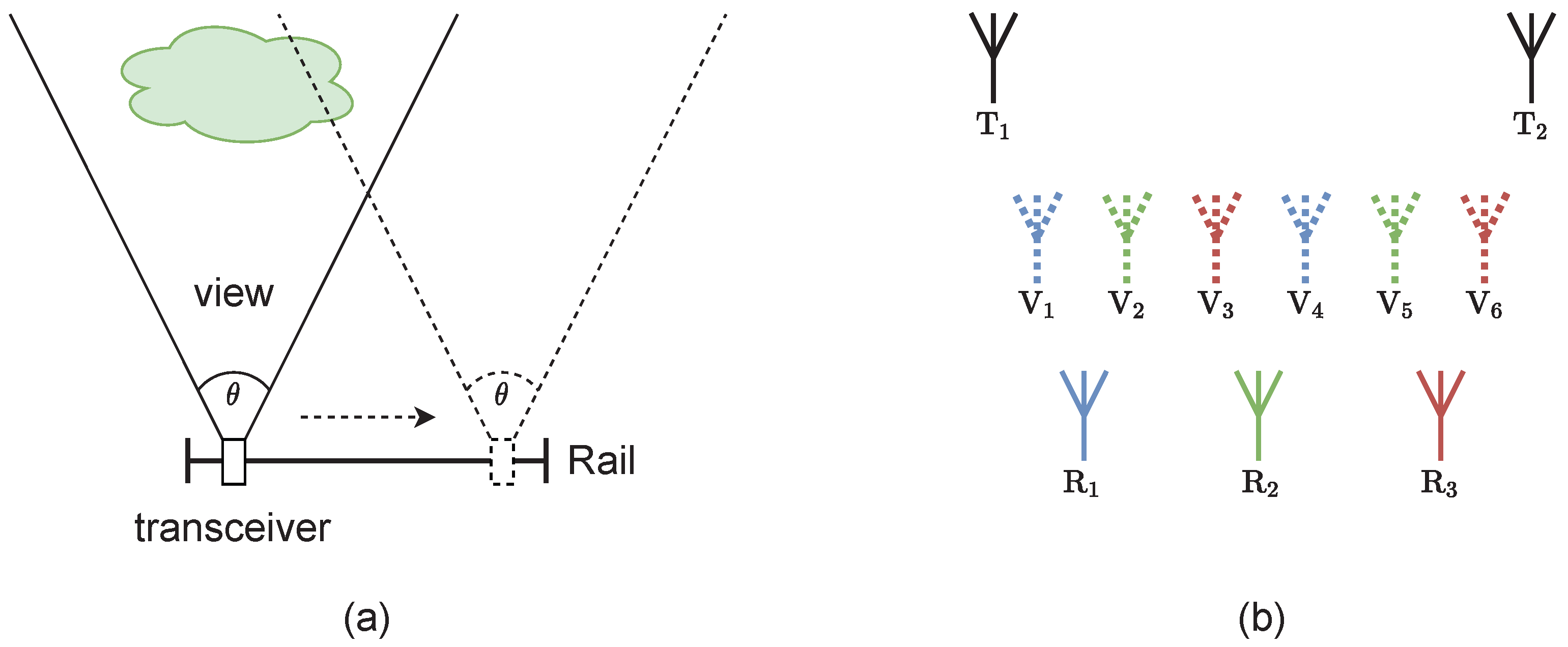
2.1. MIMO GB-SAR and Phase Analysis
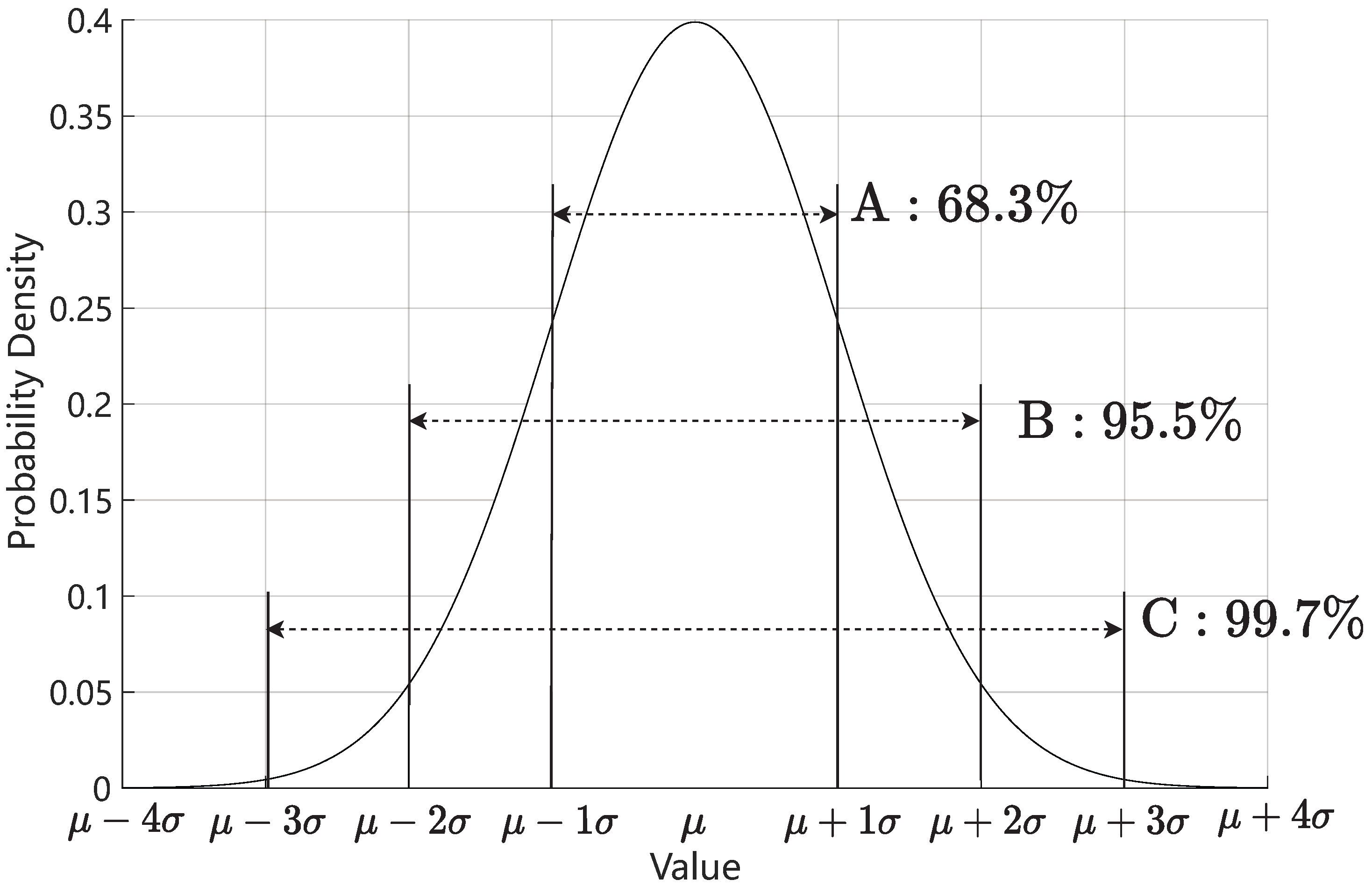
2.2. Phase Distribution Maximum Likelihood Estimation
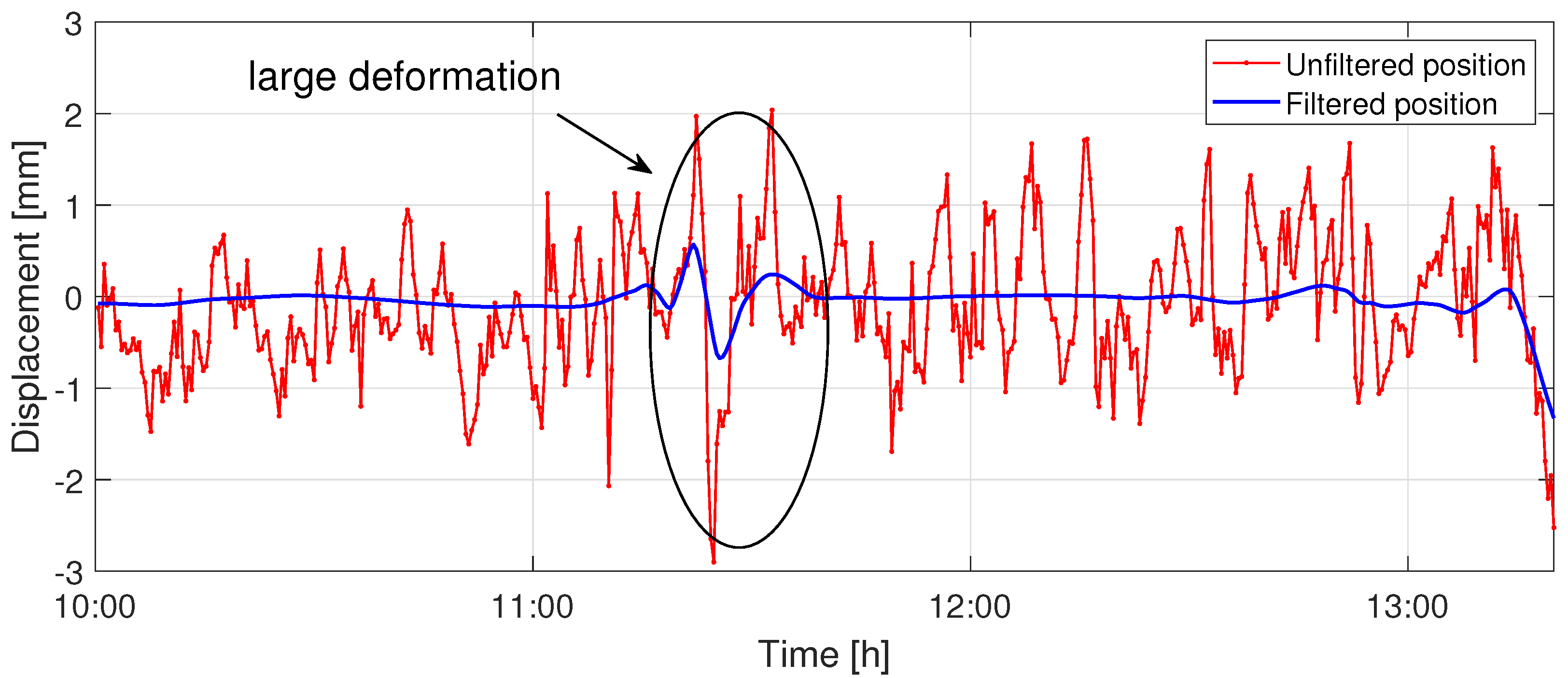
2.3. Wavelet Filter
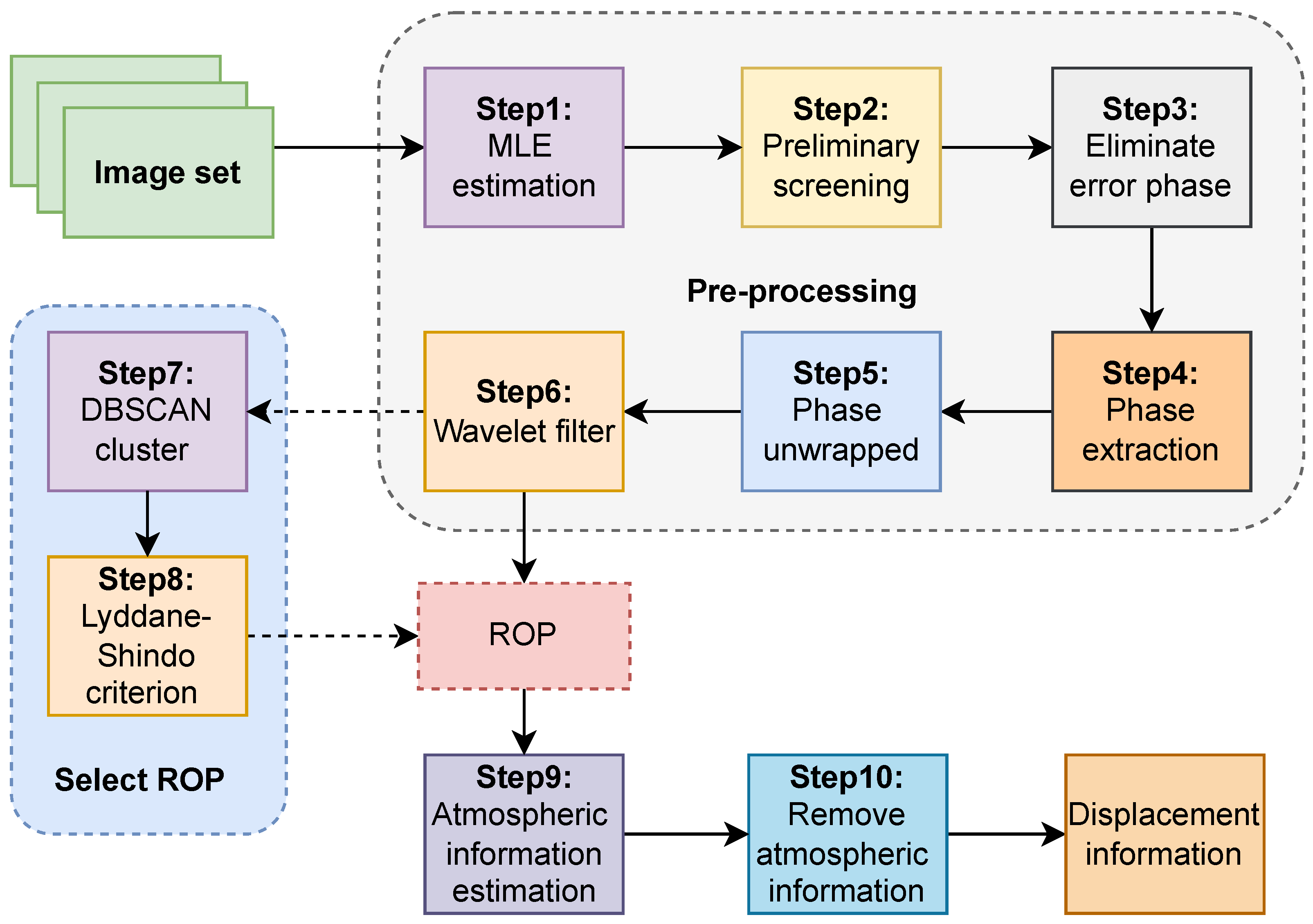
3. Reliable Observation Point Selecting Process
3.1. Data Acquisition and Pre-Processing
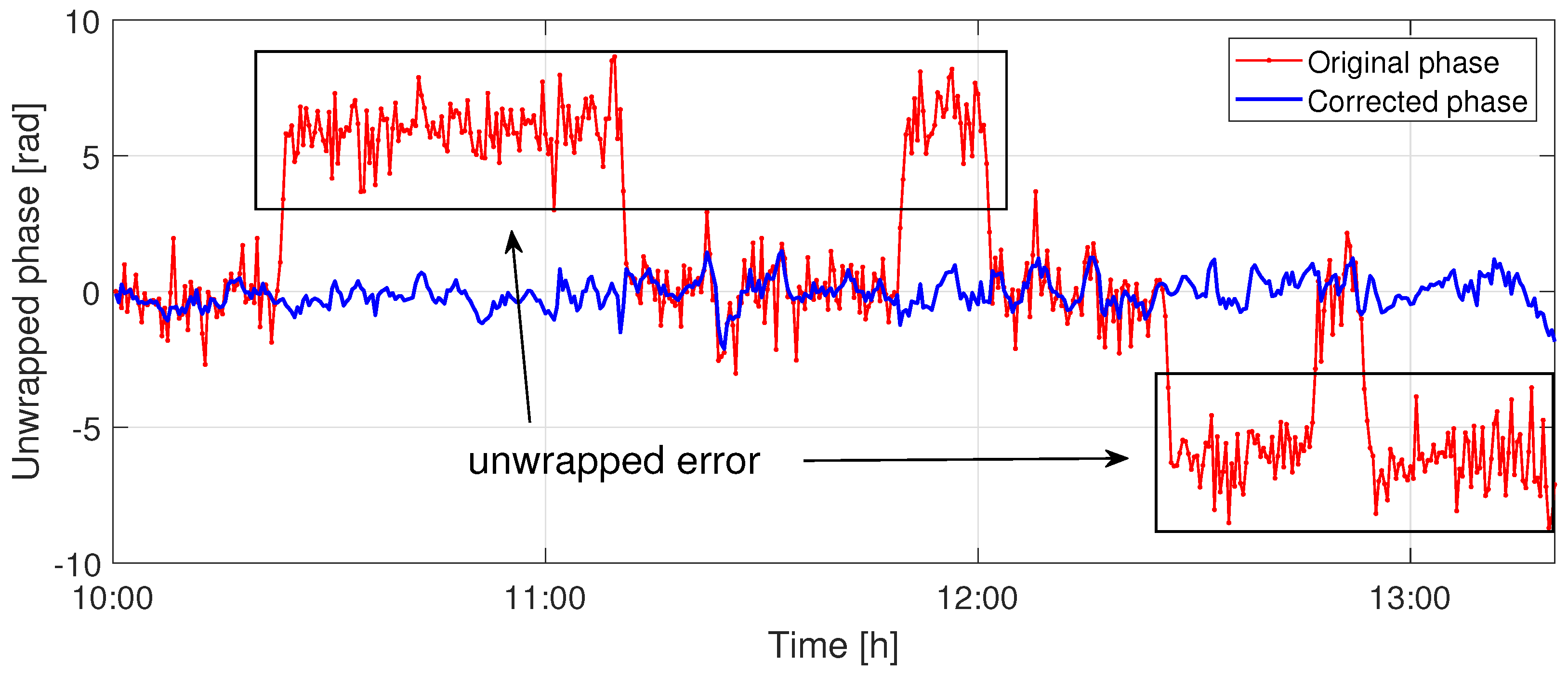
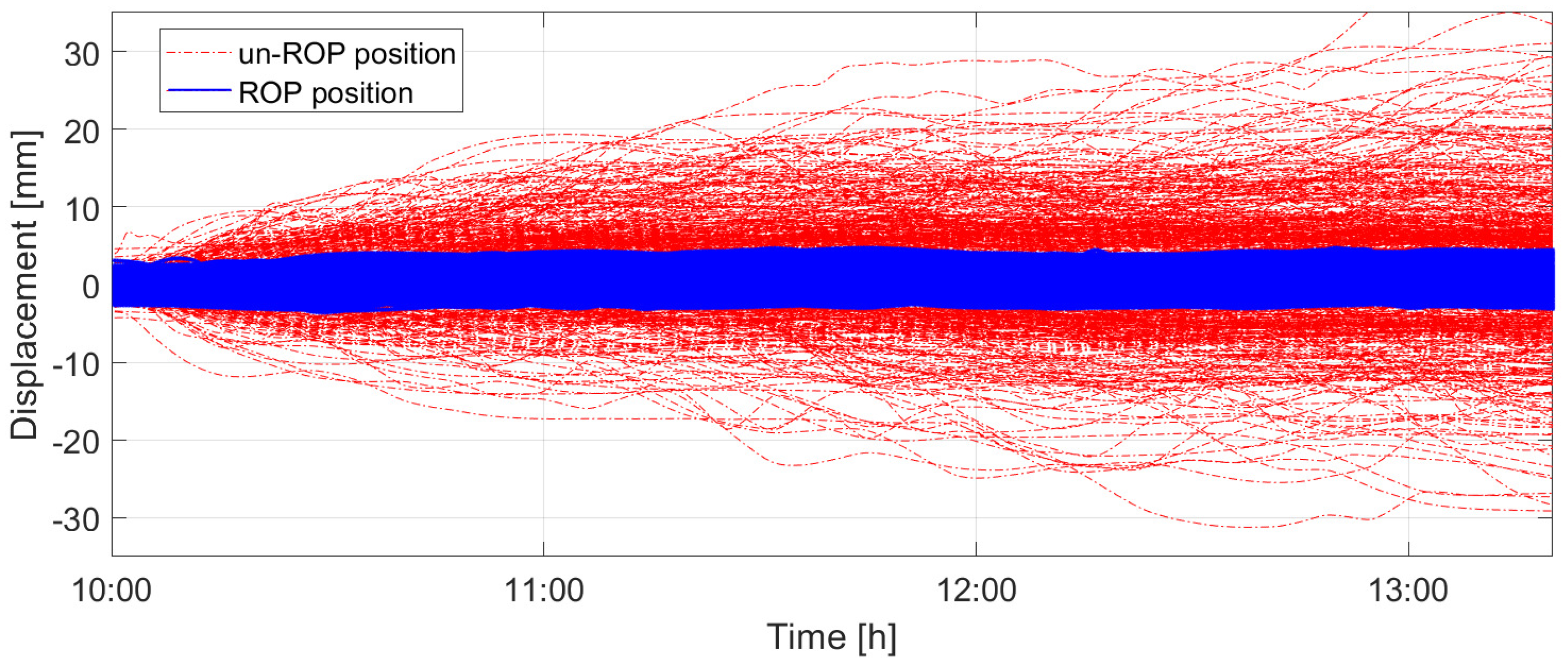
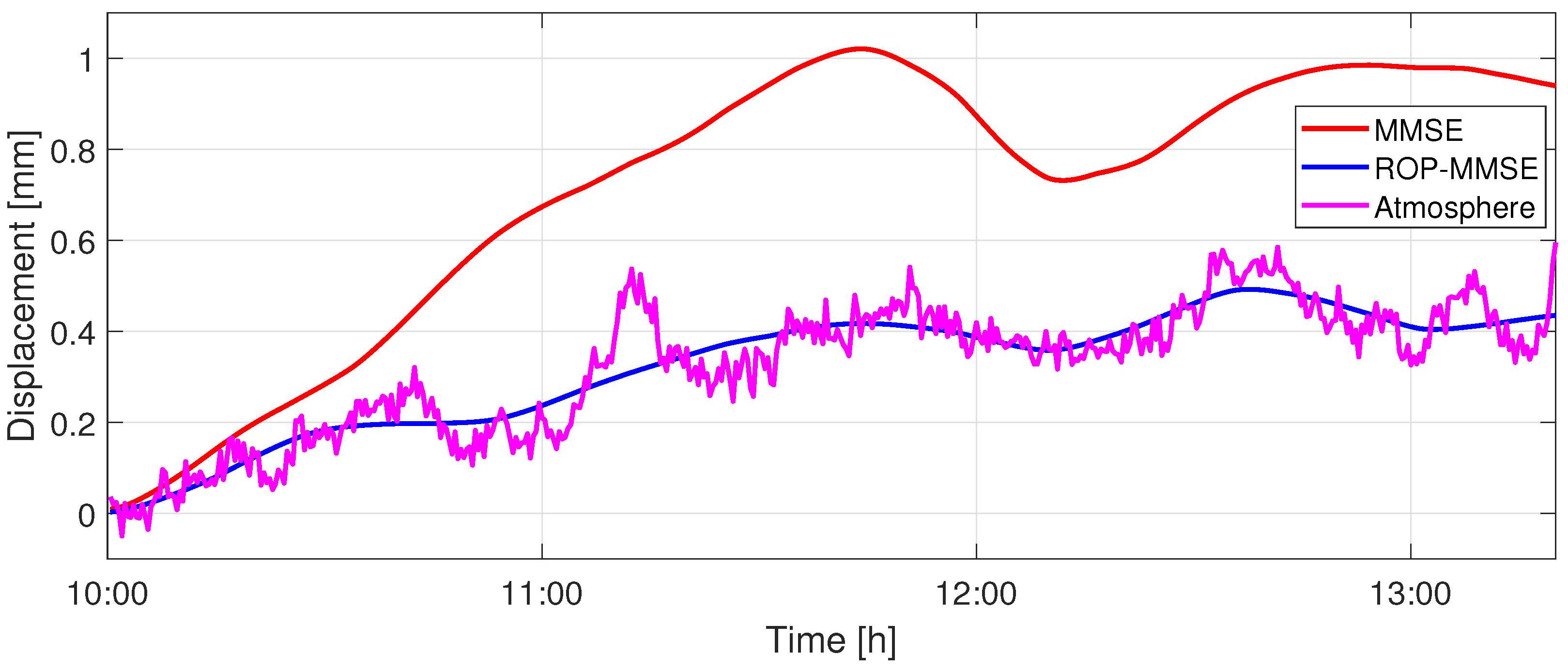
3.2. Reliable Observation Point Screening and Atmospheric Phase Processing
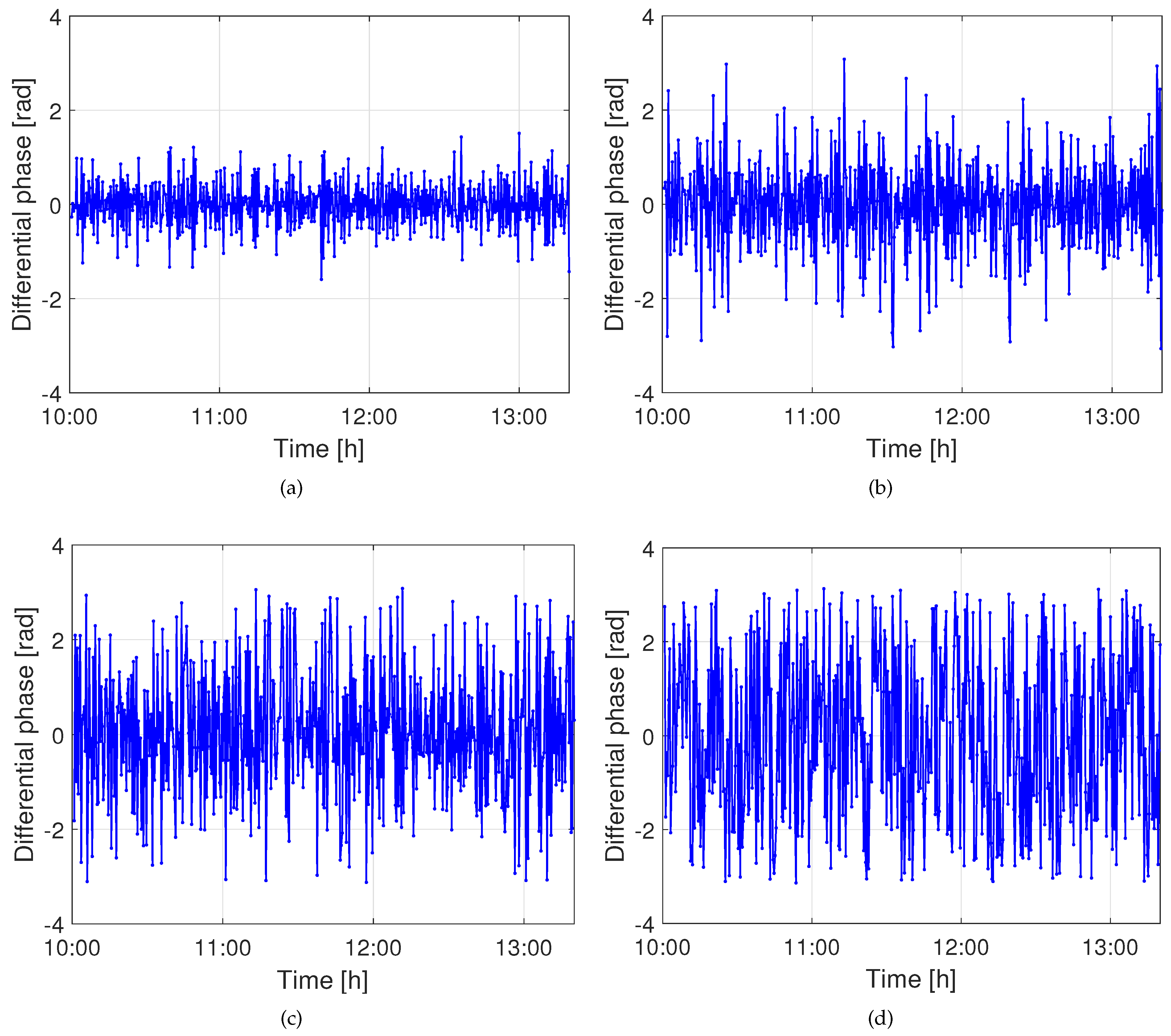
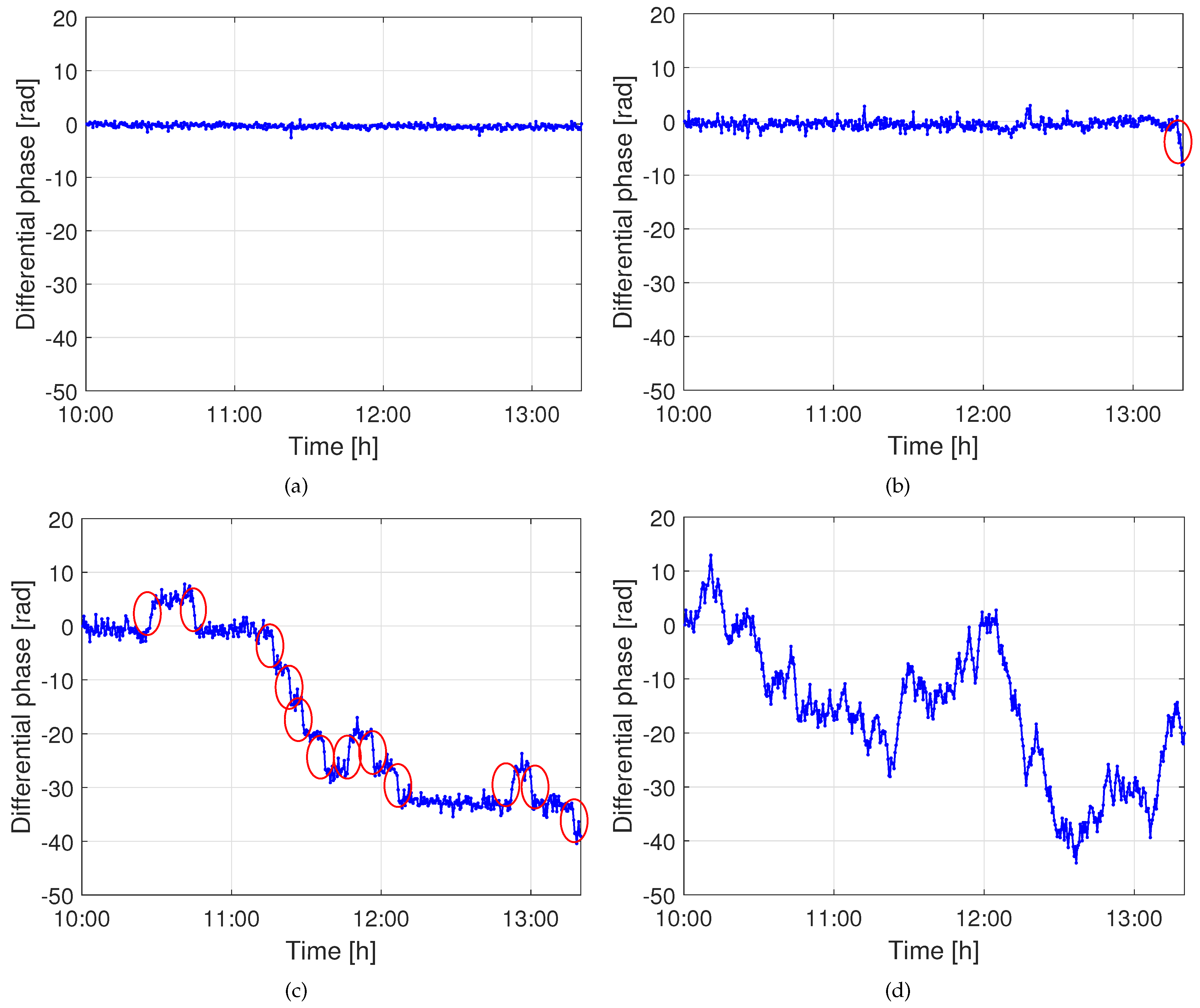
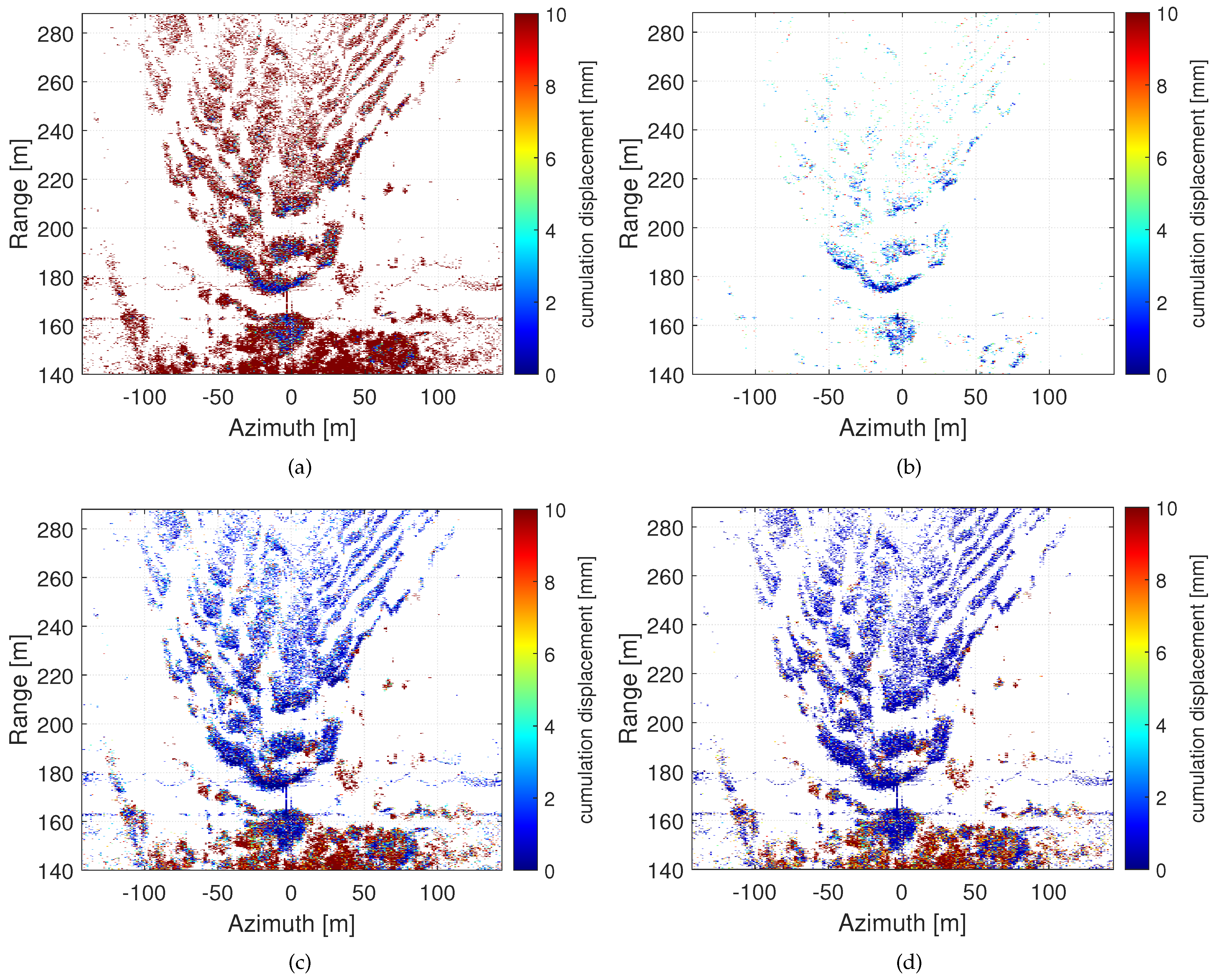
4. Experimental Results and Analysis
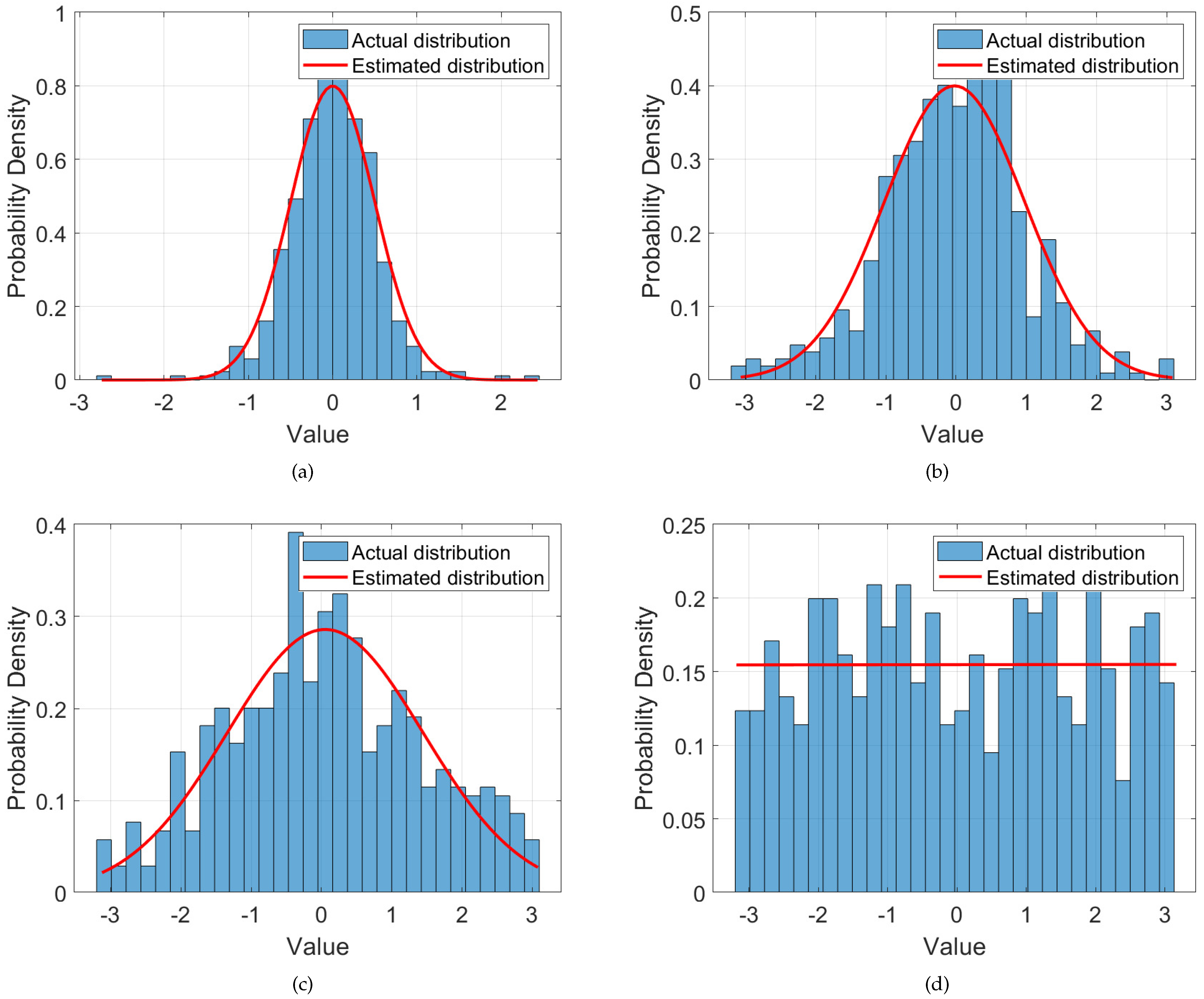
4.1. Data Pre-Processing
4.2. Clustering–Screening and Atmospheric Phase Estimation
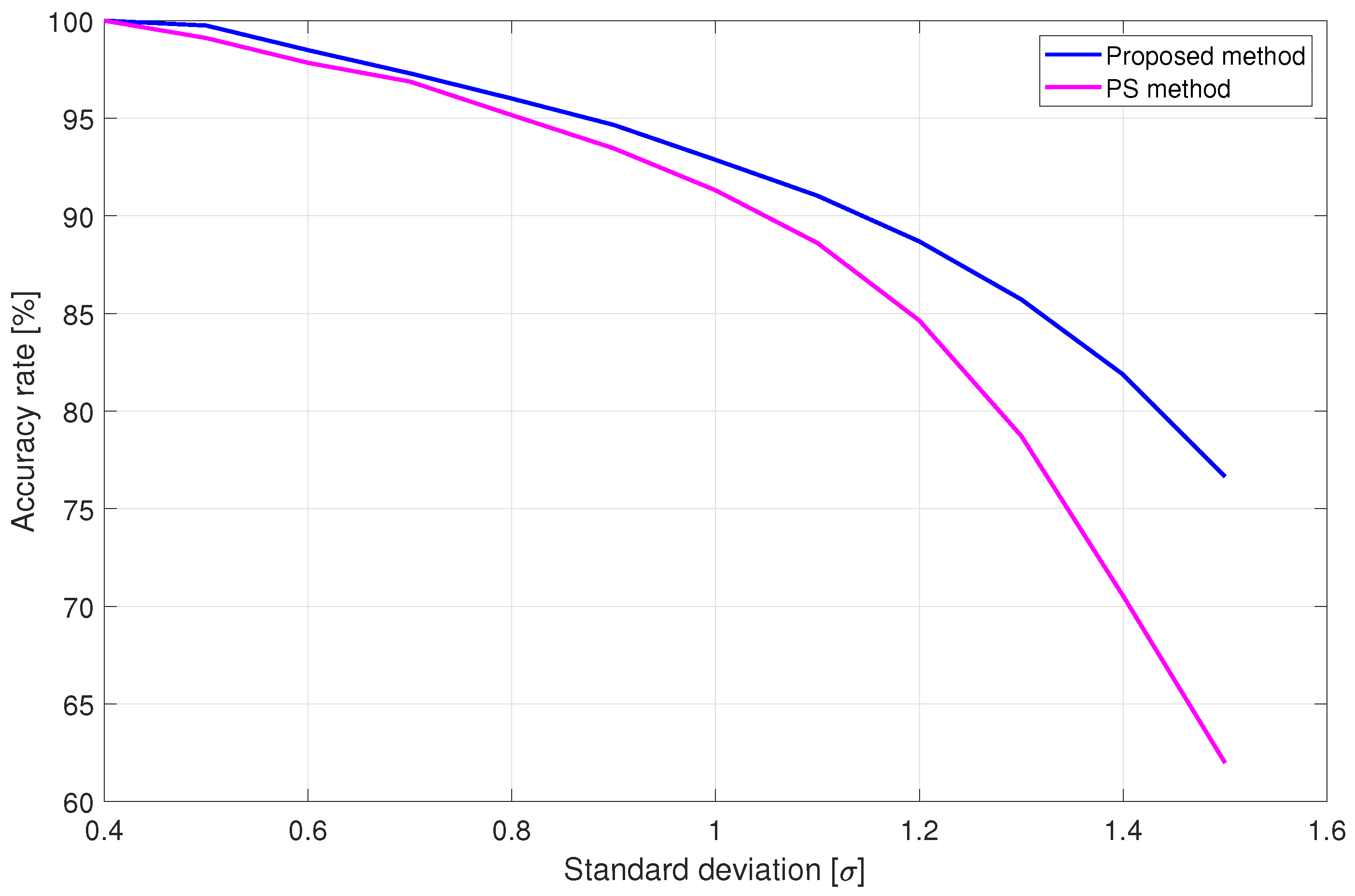
4.3. Comparison with Amplitude Deviation PS Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog-to-Digital Converter |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| FMCW | Frequency Modulated Continuous Wave |
| GB-SAR | Ground-Based Synthetic Aperture Radar |
| MIMO | Multiple Input Multiple Output |
| MLE | Maximum Likelihood Estimation |
| MMSE | Minimum Mean Square Error |
| MSE | Mean Square Error |
| PS | Permanent Scatterer |
| ROP | Reliable Observation Point |
| SAR | Synthetic Aperture Radar |
References
- Wang, Q.; Huang, H.; Yu, A.; Dong, Z. An Efficient and Adaptive Approach for Noise Filtering of SAR Interferometric Phase Images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1140–1144. [Google Scholar] [CrossRef]
- Chang, L.; Dollevoet, R.P.B.J.; Hanssen, R.F. Nationwide Railway Monitoring Using Satellite SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 596–604. [Google Scholar] [CrossRef]
- Tian, F.; Suo, Z.; Wang, Y.; Lu, Z.; Wang, Z.; Li, Z. A Unified Algorithm for the Sliding Spotlight and TOPS Modes Data Processing in Bistatic Configuration of the Geostationary Transmitter with LEO Receivers. Remote Sens. 2022, 14, 2006. [Google Scholar] [CrossRef]
- Noferini, L.; Takayama, T.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Analysis of Ground-Based SAR Data with Diverse Temporal Baselines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1614–1623. [Google Scholar] [CrossRef]
- Luzi, G.; Noferini, L.; Mecatti, D.; Macaluso, G.; Pieraccini, M.; Atzeni, C.; Schaffhauser, A.; Fromm, R.; Nagler, T. Using a Ground-Based SAR Interferometer and a Terrestrial Laser Scanner to Monitor a Snow-Covered Slope: Results From an Experimental Data Collection in Tyrol (Austria). IEEE Trans. Geosci. Remote Sens. 2009, 47, 382–393. [Google Scholar] [CrossRef]
- Zeng, T.; Mao, C.; Hu, C.; Tian, W. Ground-Based SAR Wide View Angle Full-Field Imaging Algorithm Based on Keystone Formatting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2160–2170. [Google Scholar] [CrossRef]
- Monti Guarnieri, A.; Scirpoli, S. Efficient Wavenumber Domain Focusing for Ground-Based SAR. IEEE Geosci. Remote Sens. Lett. 2010, 7, 161–165. [Google Scholar] [CrossRef]
- Takahashi, K.; Matsumoto, M.; Sato, M. Continuous Observation of Natural-Disaster-Affected Areas Using Ground-Based SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1286–1294. [Google Scholar] [CrossRef]
- Zhang, Z.; Suo, Z.; Tian, F.; Qi, L.; Tao, H.; Li, Z. A Novel GB-SAR System Based on TD-MIMO for High-Precision Bridge Vibration Monitoring. Remote Sens. 2022, 14, 6383. [Google Scholar] [CrossRef]
- Hosseiny, B.; Amini, J.; Safavi-Naeini, S. Simulation and Evaluation of an mm-Wave MIMO Ground-Based SAR Imaging System for Displacement Monitoring. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 8213–8216. [Google Scholar] [CrossRef]
- Qiu, Z.; Jiao, M.; Jiang, T.; Zhou, L. Dam Structure Deformation Monitoring by GB-InSAR Approach. IEEE Access 2020, 8, 123287–123296. [Google Scholar] [CrossRef]
- Hu, J.; Guo, J.; Xu, Y.; Zhou, L.; Zhang, S.; Fan, K. Differential Ground-Based Radar Interferometry for Slope and Civil Structures Monitoring: Two Case Studies of Landslide and Bridge. Remote Sens. 2019, 11, 2887. [Google Scholar] [CrossRef]
- Kuras, P.; Ortyl, Ł.; Owerko, T.; Salamak, M.; Łaziński, P. GB-SAR in the Diagnosis of Critical City Infrastructure—A Case Study of a Load Test on the Long Tram Extradosed Bridge. Remote Sens. 2020, 12, 3361. [Google Scholar] [CrossRef]
- Diaferio, M.; Fraddosio, A.; Daniele Piccioni, M.; Castellano, A.; Mangialardi, L.; Soria, L. Some issues in the structural health monitoring of a railway viaduct by ground based radar interferometry. In Proceedings of the 2017 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS), Milan, Italy, 24–25 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Baumann-Ouyang, A.; Butt, J.A.; Salido-Monzú, D.; Wieser, A. MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations. Remote Sens. 2021, 13, 4290. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Tamburini, A.; Atzeni, C. Monitoring of an Alpine Glacier by Means of Ground-Based SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 495–499. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Luzi, G.; Cuevas-González, M.; Devanthéry, N. A Noninterferometric Procedure for Deformation Measurement Using GB-SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 34–38. [Google Scholar] [CrossRef]
- Liu, B.; Ge, D.; Li, M.; Zhang, L.; Wang, Y.; Zhang, X. Using GB-SAR technique to monitor displacement of open pit slope. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5986–5989. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Dai, H.; Wang, C.; Tang, W.; Zou, L.; Tang, Y. Landslide Identification and Gradation Method Based on Statistical Analysis and Spatial Cluster Analysis. Remote Sens. 2022, 14, 4504. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 8 June–2 July 1999; Volume 3, pp. 1528–1530. [Google Scholar] [CrossRef]
- Duan, H.; Li, Y.; Li, B.; Li, H. Fast InSAR Time-Series Analysis Method in a Full-Resolution SAR Coordinate System: A Case Study of the Yellow River Delta. Sustainability 2022, 14, 10597. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Pauciullo, A.; Reale, D.; Franzé, W.; Fornaro, G. Multi-Look in GLRT-Based Detection of Single and Double Persistent Scatterers. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5125–5137. [Google Scholar] [CrossRef]
- Pauciullo, A.; De Maio, A.; Perna, S.; Reale, D.; Fornaro, G. Detection of Partially Coherent Scatterers in Multidimensional SAR Tomography: A Theoretical Study. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7534–7548. [Google Scholar] [CrossRef]
- Iglesias, R.; Mallorqui, J.J.; López-Dekker, P. DInSAR Pixel Selection Based on Sublook Spectral Correlation Along Time. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3788–3799. [Google Scholar] [CrossRef]
- Navneet, S.; Kim, J.W.; Lu, Z. A New InSAR Persistent Scatterer Selection Technique Using Top Eigenvalue of Coherence Matrix. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1969–1978. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Matsuoka, T.; Tamura, M. Persistent Scatterer Selection Incorporating Polarimetric SAR Interferograms Based on Maximum Likelihood Theory. IEEE Trans. Geosci. Remote Sens. 2017, 55, 38–50. [Google Scholar] [CrossRef]
- Pipia, L.; Fabregas, X.; Aguasca, A.; Lopez-Martinez, C. Polarimetric Temporal Analysis of Urban Environments with a Ground-Based SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2343–2360. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter Accuracy of InSAR Time Series: Experimental Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Lu, Z. Modeling PSInSAR Time Series without Phase Unwrapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 547–556. [Google Scholar] [CrossRef]
- De Maio, A.; Fornaro, G.; Pauciullo, A. Detection of Single Scatterers in Multidimensional SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2284–2297. [Google Scholar] [CrossRef]
- Mora, O.; Lanari, R.; Mallorqui, J.; Berardino, P.; Sansosti, E. A new algorithm for monitoring localized deformation phenomena based on small baseline differential SAR interferograms. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; Volume 2, pp. 1237–1239. [Google Scholar] [CrossRef]
- Su, Y.; Yang, H.; Peng, J.; Liu, Y.; Zhao, B.; Shi, M. A Novel Near-Real-Time GB-InSAR Slope Deformation Monitoring Method. Remote Sens. 2022, 14, 5585. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- Kulshrestha, A.; Chang, L.; Stein, A. Use of LSTM for Sinkhole-Related Anomaly Detection and Classification of InSAR Deformation Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4559–4570. [Google Scholar] [CrossRef]
- Beni, A.; Miccinesi, L.; Pieraccini, M. Kalman Filter Application to GBSAR Interferometry for Slope Monitoring. IEEE Access 2022, 10, 102148–102156. [Google Scholar] [CrossRef]
- Hu, F.; van Leijen, F.J.; Chang, L.; Wu, J.; Hanssen, R.F. Combined Detection of Surface Changes and Deformation Anomalies Using Amplitude-Augmented Recursive InSAR Time Series. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.A.; Corominas, J. Atmospheric Phase Screen Compensation in Ground-Based SAR With a Multiple-Regression Model Over Mountainous Regions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2436–2449. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, G.; Li, T.; Huang, L.; Yu, B.; Chen, Q.; Li, Z. An Integrated Model for Extracting Surface Deformation Components by PSI Time Series. IEEE Geosci. Remote Sens. Lett. 2014, 11, 544–548. [Google Scholar] [CrossRef]
- Union, I.T. The Radio Refractive Index: Its Formula and Refractivity Data; Radiocommunication Sector of ITU: Geneva, Switzerland, 2019; p. 453. [Google Scholar]
- Lu, J.Y.; Lin, H.; Ye, D.; Zhang, Y.S. A New Wavelet Threshold Function and Denoising Application. Math. Probl. Eng. 2016, 2016, 8. [Google Scholar] [CrossRef]
- Hanssen, R. Radar Interferometry: Data Interpretation and Error Analysis; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]



| Items | Value |
|---|---|
| Center frequency | 30 GHz |
| Frequency band | 1000 MHz |
| ADC sampling rate | 400 MSPS |
| Single ramp time T | ≥20 μs |
| Time for a single full scan | ≥4.96 ms |
| Detection distance | 20–2000 m |
| Standard Deviation | Total ROP Number | Amplitude PS Method Accuracy Rate [%] | Proposed Method Accuracy Rate [%] | Amplitude Dispersion Index |
|---|---|---|---|---|
| 1222 | 100.0 | 100.0 | 0.278 | |
| 2024 | 99.75 | 99.11 | 0.319 | |
| 2912 | 98.49 | 97.84 | 0.350 | |
| 4005 | 97.30 | 96.88 | 0.378 | |
| 5309 | 96.01 | 95.16 | 0.402 | |
| 6869 | 94.66 | 93.46 | 0.423 | |
| 8864 | 92.87 | 91.31 | 0.441 | |
| 11,155 | 91.03 | 88.61 | 0.456 | |
| 14,022 | 88.69 | 84.64 | 0.469 | |
| 17,526 | 85.72 | 78.73 | 0.478 | |
| 22,098 | 81.87 | 70.53 | 0.485 | |
| 27,707 | 76.64 | 61.98 | 0.491 | |
| 45,718 | 55.07 | 44.73 | 0.501 | |
| 78,070 | 36.10 | 30.90 | 0.510 | |
| 162,860 | 17.91 | 19.25 | 0.531 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, Z.; Suo, Z.; Qi, L.; Tang, F.; Guo, H.; Tao, H. A Reliable Observation Point Selection Method for GB-SAR in Low-Coherence Areas. Remote Sens. 2024, 16, 1251. https://doi.org/10.3390/rs16071251
Zhang Z, Li Z, Suo Z, Qi L, Tang F, Guo H, Tao H. A Reliable Observation Point Selection Method for GB-SAR in Low-Coherence Areas. Remote Sensing. 2024; 16(7):1251. https://doi.org/10.3390/rs16071251
Chicago/Turabian StyleZhang, Zexi, Zhenfang Li, Zhiyong Suo, Lin Qi, Fanyi Tang, Huancheng Guo, and Haihong Tao. 2024. "A Reliable Observation Point Selection Method for GB-SAR in Low-Coherence Areas" Remote Sensing 16, no. 7: 1251. https://doi.org/10.3390/rs16071251
APA StyleZhang, Z., Li, Z., Suo, Z., Qi, L., Tang, F., Guo, H., & Tao, H. (2024). A Reliable Observation Point Selection Method for GB-SAR in Low-Coherence Areas. Remote Sensing, 16(7), 1251. https://doi.org/10.3390/rs16071251





