Abstract
The large quantity of resident space objects orbiting Earth poses a threat to safety and efficient operations in space. Radar sensors are well suited to detecting objects in space including decommissioned satellites and debris, whereas the more commonly used optical sensors are limited by daylight and weather conditions. Observations of three non-operational satellites using a VHF radar system are presented in this paper in the form of micro Doppler signatures associated with rotational motion. Micro Doppler signatures are particularly useful for characterising resident space objects at VHF given the limited bandwidth resulting in poor range resolution. Electromagnetic simulations of the micro Doppler signatures of the defunct satellites are also presented using simple computer-aided design (CAD) models to assist with interpretation of the radar observations. The simulated micro Doppler results are verified using the VHF radar data and provide insight into the attitude and spin axis of the three resident space objects. As future work, this approach will be extended to a larger number of resident space objects which requires a automated processing.
1. Introduction
Space domain awareness (SDA) has been a topic of global concern due to the large number of resident space objects orbiting Earth [1,2,3,4,5,6,7]. Resident space objects refer to both active and inactive satellites, spacecraft, debris or any human-made object in space. The number of satellites being launched into orbit is rapidly increasing due to mega constellations developed by companies including SpaceX, OneWeb, Amazon, Telesat and GW [8]. Space debris in particular poses a significant risk to the operation of global positioning systems, telecommunications and weather forecasting because the debris can deorbit, explode or cause collisions creating even more debris [9].
Space operations requiring SDA are supported with networks of space surveillance sensors including ground-based radar and optical sensors in addition to space-based optical sensors [1]. In Australia, there are various radar systems that perform SDA functions. The C band Space Surveillance Radar located in Exmouth, Western Australia, is capable of tracking several hundreds of space objects per day and forms a node in the US global Space Surveillance Network [5]. Two S band radar systems, known as the Western Australia Space Radar (WASR) located in Bunbury, Western Australia, have been operational since 2023 and form part of the the LeoLabs global network of phased array radars. Existing radar systems have been considered to contribute to the SDA effort in Australia including an experimental HF line-of-sight system [6,7], the Murchison Widefield Array used in a passive radar configuration [3,4] and the Australian Telescope Compact Array used in a bistatic configuration [10]. In South Australia, a VHF radar system at Buckland Park typically performs lower atmosphere wind profiling measurements, and further research dedicated to SDA has resulted in reliable detections of up to 1000 space objects per day [1,11].
Rotational motion of resident space objects has been observed using photometric light curves from optical sensors and basic polyhedron shapes have been determined when using multiple sites [12,13,14]. The rotational motion can provide information about the stability of the resident space object in orbit. In [13], the attitude and spin axis of a non-operational satellite TOPEX/Poseidon (NORAD ID: 22076) indicated a great possibility of overturn at precession angles greater than 55 degrees. In comparison to optical sensors, radar sensors have the advantage of operating in poor visibility and can also provide wide-area surveillance for the detection and tracking of resident space objects by utilising broad transmit beamwidths, and multiple receive beams from antenna arrays. The Buckland Park VHF radar in South Australia demonstrated that the defunct satellite Telkom 3 (NORAD ID: 38744) increased in rotation rate prior to decaying to Earth, indicating the importance of monitoring these features [11]. Earlier work with the S band Chibolton radar also observed a periodic radar cross section (RCS) from the defunct GEO-IK-2 satellite (NORAD ID: 37362) at a rate of Hz from the object’s rotational motion [15]. Further investigations were conducted into the effect of the attitude of the satellite RCS which introduced a second-order “stability index” [16]. More recently, a long baseline bistatic radar system has observed the tumbling motion of the Delta 4 rocket body (NORAD ID: 40535) using a network of radio telescopes operating at L band [17]. The variation in RCS from the tumbling motion of the rocket body was used to estimate the rotation period and tomographic images were formed to estimate the approximate size and shape of the resident space object.
Historically, radar imaging has been used to identify object features in two dimensions and Inverse Synthetic Aperture Radar (ISAR) imaging has been explored based on the rotational motion of resident space objects [2]. However, ISAR imaging is not applicable for radar systems operating at low frequencies with limited bandwidth. Direct analysis of time-frequency transforms has been found to be suitable for feature extraction of rotating resident space objects [11,18] and is well suited to observations at VHF. Computational electromagnetic simulations offer the flexibility of easily generating data for different attitude and spin axes in order to characterise a given resident space object. Large amounts of simulated data can also be produced and used as training data in supervised learning algorithms to automatically classify different shaped objects [19,20]. However, a deep understanding of the features in the data and the scattering effects in the surrounding environment is needed for reliable and meaningful solutions.
This paper presents the analysis of micro Doppler signatures induced by the rotational motion of three non-operational satellites, which were chosen to be representative of typical observations provided by the Buckland Park VHF Radar in South Australia. The Buckland Park VHF radar is described in further detail in Section 2 followed by the translational motion compensation processing in Section 3. Section 4 illustrates the CAD models for the three resident space objects and describes the electromagnetic simulations. Further analysis of the simulated and measured micro Doppler signatures is presented in Section 5 to gain insights into the attitude, spin axis and object features. The limitations and approximations used in the simulations are discussed in further detail in Section 6, and the complexity of extending this approach to a larger number of resident space objects is discussed as future work.
2. Buckland Park VHF Radar
The Buckland Park Stratosphere–Troposphere (BPST) VHF radar shown in Figure 1 (−, ) is located 35 km north of Adelaide in South Australia. The radar is a pulsed monostatic system operating in the VHF band at a frequency of 55 MHz ( m), with a peak transmit power of 40 kW and maximum duty cycle of . The BPST radar was designed and manufactured by ATRAD and is operated by the University of Adelaide and ATRAD. The radar is designed primarily for the measurement of tropospheric and stratospheric winds (–20 km) [21]. The transmit array (hereafter “main array”) consists of a 12 × 12 array of gamma-matched linearly-polarised Yagi antennas. The inter-antenna spacing is , giving an aperture size of m by m. The array allows 5-beam directions to be used: vertical and off zenith in cardinal directions (north, east, south, west). For the observations described in this paper, reception is performed using a single receiver connected to the main array. The combined transmit/receive main array beam width is (half-power beamwidth). The use of the BPST radar for resident space objects (RSO) observations is described in [1], revealing detection rates of 200 RSO’s per day. Subsequent signal processing and scheduling improvements now allow detection rates up to 1000 RSO’s per day. The typical parameters used for the majority of observations presented in this paper are shown in Table 1, which illustrates the limited range resolution and the need for Doppler processing to obtain high resolution radar signatures. Coherent averaging was performed for data compression as outlined in [1].

Figure 1.
The location of the Buckland Park Stratosphere–Troposphere VHF radar in South Australia shown approximately 35 km north of Adelaide (left) and the 12 × 12 antenna array [22] (right).

Table 1.
Typical radar parameters used for the Buckland Park Radar for satellite observations.
The analysis employed in this paper is a variation on the “catalogue maintenance mode” (CMM) described in [1], referred to as the “quick catalogue maintenance mode” (QCMM). This uses “Keystone-like” processing using the predicted RSO state-vectors (generated through the Simplified General Perturbations Model (SGP4) forward propagated two-line elements (TLEs) or using Special Perturbations (SP) data) to transform the range–time data into range difference and Doppler difference data. The TLE and SP data are made available from the US Space Surveillance Network. This processing is computationally less intensive than CMM as the second step in the Keystone-like processing also removes the effects of radial acceleration. This obviates the need to incorporate a bank of acceleration hypotheses into the processing, thereby reducing the analysis dimension from 3-dim (range, time, acceleration) to 2-dim (range difference, Doppler difference). However, like CMM, the QCMM processing assumes that the RSO state-vectors are accurately predicted, and it is not applicable to non-catalogued RSOs for which state-vector predictions are unavailable. In the following section, a detailed description of the analysis is discussed.
3. Automatic Translational Motion Compensation
Generally, the translational motion is dominant compared to the rotational motion of the resident space object. For example, the translational velocity of a satellite in low earth orbit is approximately 7–8 km/s, while the spin rate of RHESSI (NORAD ID: 27370) has been reported to have a nominal spin rate of 15 rpm. In order to observe the micro Doppler signature due to the potential spinning motion of the space object of interest, the effects of translational motion will first need to be compensated in the radar data. It is desirable to automate the process of obtaining the translational motion compensated signal when there are large datasets.
The method used to automate the translational motion compensation is based on the Keystone transform. The Keystone-like processing is applied to the range–time radar returns in two steps. The range and phase is corrected using the propagated range , i.e., the range from the radar to the object over time obtained from the propagated state vector, as demonstrated in Figure 2:
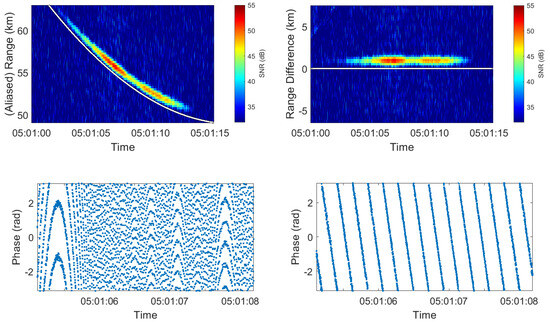
Figure 2.
Example of the application of “Keystone-like” processing. Top left: range–time signal representing the transit of the International Space Station (ISS) where the white line indicates the satellite propagated range. Top right: Associated range-corrected time plot . Bottom left: phase difference obtained at the corrected range where signal power is maximised after applying the first step of the Keystone-like processing. Bottom right: phase difference variation after applying the final step of the Keystone–like processing.
- Range migration correction: The propagated range is used to convert the range–time data into “range-corrected” time data . This is achieved by interpolating in the range dimension similar to the technique used in the Keystone transform [23]. Alternatively, a circular shift can be performed on the data in the range dimension by samples, where represents the rounding up operator and is the range resolution. The latter option is feasible for the data presented in this paper as is oversampled by at least a factor of two.
- Phase correction: The “range-corrected” time data are then multiplied by a phase term based on the propagated range in (1) to compensate for phase differences introduced in step one.
The satellite data collected using the BPST data are subject to the effects of ionospheric group retardation which is evident by the measured range exceeding the predicted range shown in the top left plot in Figure 2. The top right plot in Figure 2 shows that the corrected range exceeds zero, which typically varies from km (night) to km (day). Following the Keystone-like processing in which translational motion has been accounted for, a spectrogram is produced using data at the appropriate range difference cell containing the target of interest. If the propagated state vectors are sufficiently accurate, the resulting phase difference will be zero and the corresponding spectrogram will be centred at zero Doppler. In typical circumstances where no rotational/spin motion exists, the spectrogram features a single peak centred around zero Hz, as shown for the ALOS-2 satellite (NORAD ID 39766) at the top of Figure 3. The backscattered power is relatively constant during the observation time. However, in some circumstances, this is not the case, as is illustrated for RHESSI (NORAD ID 27370) in the middle plot of Figure 3. This spectrogram shows significant Doppler broadening compared to ALOS-2, and a one-second periodicity. This periodicity occurs because RHESSI is designed to spin at 15 revolutions per minute [24] and has four perpendicular banks of solar panels, such that reflections from the solar panels occur every second. The bottom of Figure 3 shows the Telkom 3 satellite (NORAD ID 38744) with identifying features of the solar panels as the satellite rotates in time.
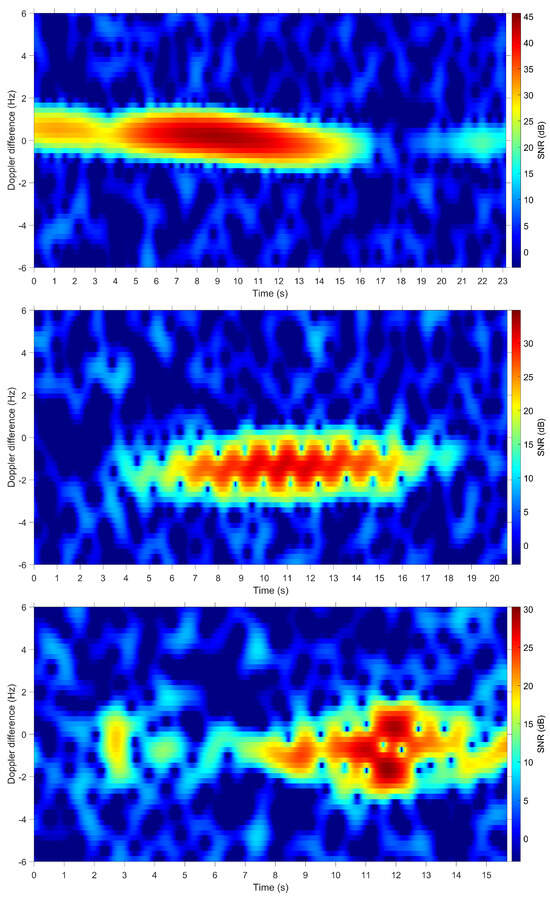
Figure 3.
After Keystone-like processing. Top: spectrogram of ALOS-2 showing a single peak; middle: spectrogram of RHESSI showing Doppler broadening and periodic RCS pattern; bottom: spectrogram of Telkom 3 showing micro Doppler features.
4. Simulations
Simulated data provide a means of understanding the scattering characteristics of resident space objects of interest. For ease of interpretation, purely rotational motion was considered in isolation from noise and ionospheric effects. A simple computer-aided design (CAD) model provided the basis for electromagnetic simulation, where fine details were excluded and the material properties of the CAD model were assumed to be perfectly electrically conducting due to the relatively large wavelength at VHF. Three space objects of different electrical sizes are described in the following sections with the associated CAD model used in the electromagnetic simulations in the CST Microwave Studio. The system scenario for the simulations is described in Figure 4 defining the plane of rotation, spin axis and elevation angle relative to the BPST VHF radar.
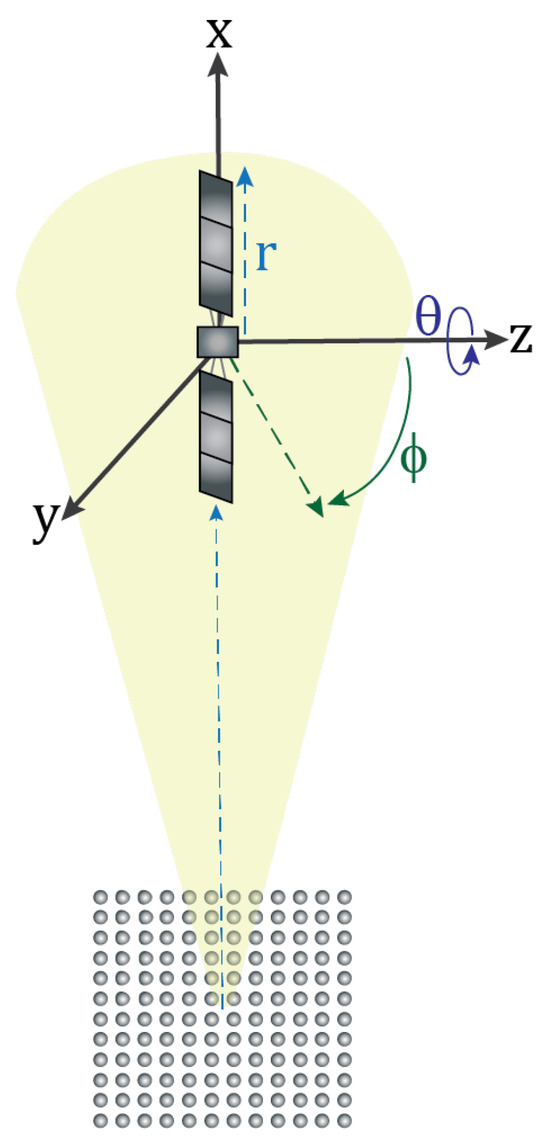
Figure 4.
Radar system scenario with the object’s azimuth angle defined as a rotation about the z axis (spin axis) and elevation angle defined as angle from the spin axis to the x–y plane (plane of rotation), which defines the object’s attitude.
4.1. Satellite Information
The NASA Ramaty High Energy Solar Spectroscopic Imager (RHESSI) was launched into low earth orbit in 2002 to perform high resolution imaging of solar flares. During operations, the satellite was reported to rotate on an axis at a rate of 15 rpm with the imager directed at the sun [25]. RHESSI was deactivated in 2018 and remained in low earth orbit until April 2023 [26]. An image of RHESSI is depicted in Figure 5 with the CAD model designed in CST Microwave Studio. RHESSI is m by m in size which is comparable to the BPST VHF radar wavelength of m [27].

Figure 5.
Image of RHESSI (left) and simplified CAD model designed in CST Studio Suite (right).
The TOPEX/Poseidon satellite was a joint development between the United States and French space agencies to measure the ocean topography of the Earth from space. The satellite was launched in 1992 and decommissioned in 2006 after a stabilisation system malfunction resulting in the satellite being unable to reside in its intended orbital orientation. Photometric observations of TOPEX/Poseidon have shown that that the satellite is undergoing spinning motion at a rotation rate of about s [13]. An image of TOPEX/Poseidon is shown in Figure 6 with the corresponding CAD design in CST Studio Suite. The main bus structure is m which is comparable to the radar wavelength with a single solar panel of dimensions m by m [28]. The electrical size is approximately twice the wavelength of the BPST VHF radar.

Figure 6.
Image of TOPEX/Poseidon (left) and simplified CAD model designed in CST Studio Suite (right).
Telkom 3 was an Indonesian telecommunications satellite built by ISS Reshetnev and was launched in February in 2012. An image of Telkom 3 is shown in Figure 7 with the associated CAD model designed in CST Studio Suite. The satellite was intended for geostationary orbit but was stranded in an unusable orbit due to an upper stage failure of the Proton-M/Breeze-M launch vehicle [29]. The satellite decayed to Earth in February 2021. There is limited information publicly available on the physical dimensions of the satellite; however, the main bus structure was based on the Ekspress 1000N platform produced by Reshetnev. An estimation of the bus size for Telkom 3 from [30] was approximately 3 m × 2 m × m. The solar panels were assumed to be the same dimensions as the sides of the bus structure, with a length multiplied by three when extended from the stowed position. The maximum dimension of the satellite is 23 m, providing an electrical size of approximately four wavelengths of the BPST VHF radar which is expected to be a good candidate for representing micro Doppler features.
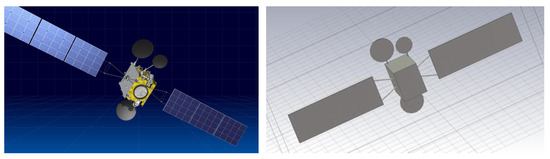
Figure 7.
Image of Telkom 3 (left) and simplified CAD model designed in CST Studio Suite (right) [31].
4.2. Simulated Results
CST Studio Suite was used to simulate the electric field scattered from the satellite CAD models. Due to the electrical size being comparable to the radar wavelength, a full wave solver was required to capture the appropriate scattering characteristics. The electric field was calculated spanning around the CAD model with a step size in the plane of rotation at a defined elevation angle. This effectively provides the scattered signal as though the object was rotating uniformly in a plane.
Typically, the radar cross section is extracted from electromagnetic simulations; however, Doppler information can be provided if a common phase centre is defined across the angular samples for the electric field calculations. Doppler information can be retrieved from angular samples equivalently to time samples [32], which effectively creates an angular sampling rate conversion of in samples/radian [33]. In practice, the angular sampling rate is defined as the total number of angular samples, divided by the maximum angular extent. The angular Doppler frequency changing in time due to the effective object rotation can be observed using a short–time Fourier transform (STFT) by means of a spectrogram. This kind of signal representation is collectively known as a micro Doppler signature. The extent of the micro Doppler frequency is given by (2) where is the maximum radial distance of the object from the origin of rotation and is the rotation rate. From inspection of a spectrogram, the micro Doppler frequency can be converted back to a measurement of distance or size with the simple multiplication factor of .
The resolution of the spectrogram is constrained by three factors based on the Doppler ambiguity condition, the linear approximation of the Fourier transform and the Doppler migration condition [33]. The Doppler migration condition is inversely proportional to the electrical size () of the resident space object and determines the angular bin size used in the spectrogram. The results provided in Section 5 use a Doppler migration constraint of to generate sufficient resolution to observe features in the spectrogram, which may include some non-linear effects.
5. Micro-Doppler Signature Analysis
The micro-Doppler signature is presented for three defunct satellites using both measured data from the BPST VHF radar owned and operated by The University of Adelaide and ATRAD in South Australia and the simulated electric field from CST Studio Suite manufactured by Dassault Systemes in France.
5.1. RHESSI
A typical observation of RHESSI from the BPST VHF radar is presented in Figure 8, highlighting the Doppler broadening as the satellite rotates with a periodic signature across time. The Doppler spread is indicative of the rotational motion of the solar panels. From inspection of the data, the time between the solar panels is approximately s resulting in a rotation period of s and rotation rate of radians per second. The TLE information used for the translational motion compensation provides a good estimate of the radial velocity and range over time resulting in the centring of the signal around zero Doppler.
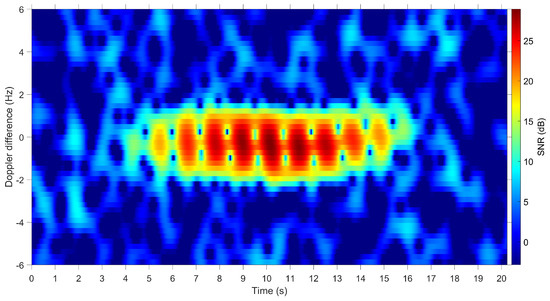
Figure 8.
Spectrogram obtained using observations of the RHESSI satellite from the BPST VHF radar.
The corresponding spectrogram using simulated data from the RHESSI CAD model shown in Figure 5 is presented in Figure 9 for a single rotation. The RHESSI satellite is known to spin on its axis with the solar panels rotating around the axis of the imager. The scenario for maximum Doppler return occurs when the satellite is rotating in the same plane as the radar beam with the solar panels oriented in the same plane. The features of the solar panels are most prominent with vertical polarisation and similarly present a spread in Doppler frequency with a repeated pattern as shown previously with the measured data in Figure 8.
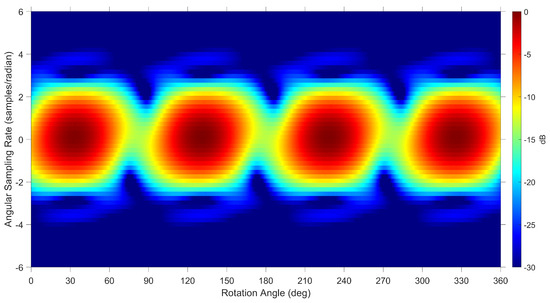
Figure 9.
Spectrogram using simulated data using the RHESSI CAD model at an elevation of with vertical polarisation at a frequency of 55 MHz.
5.2. TOPEX/Poseidon
The measured spectrogram for Topex/Poseidon from the BPST VHF radar is provided in Figure 10, indicating a general sinusoidal pattern with Doppler spread indicative of a solar panel. From inspection of the data, the time between the solar panels is approximately s resulting in a rotation period of 11 s and rotation rate of radians per second.
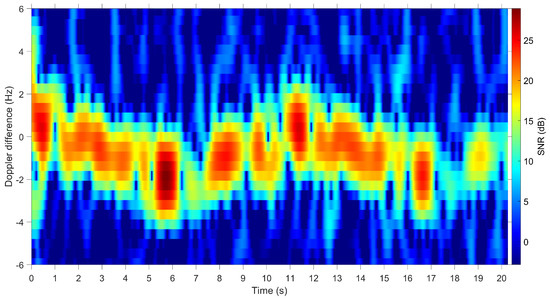
Figure 10.
Spectrogram obtained using observations of TOPEX/Poseidon satellite from the BPST VHF radar.
Using the CAD model of TOPEX/Poseidon in Figure 6, the simulated result is provided in Figure 11. The scenario for the maximum Doppler frequency occurs when the solar panel is rotating in the same plane as the radar line of sight. A sinusoidal pattern is shown with intense specular flashes at and similar to the measured data in Figure 10. The main bus structure of TOPEX/Poseidon is oriented asymmetrically from the location of the solar panel which causes the asymmetrical Doppler signature in Figure 11.
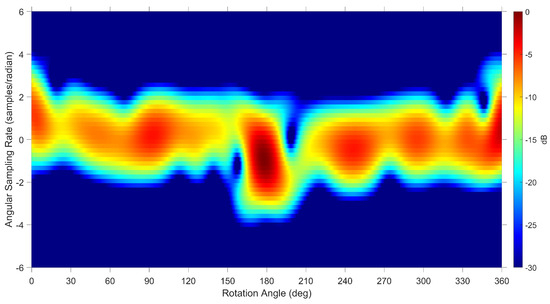
Figure 11.
Spectrogram using simulated data with TOPEX/Poseidon CAD model at an elevation of with vertical polarisation at a frequency of 55 MHz.
5.3. Telkom 3
The spectrogram from the BPST VHF radar for Telkom 3 is presented in Figure 12. The measured data shows specular reflections corresponding to the two solar panels and adjacent returns close to zero Doppler from the antennas. From inspection of the data, the time between the solar panels is approximately s resulting in a rotation period of s and rotation rate of radians per second.
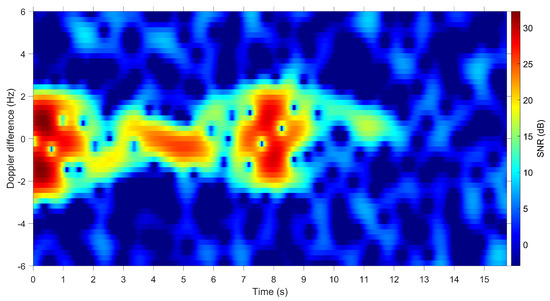
Figure 12.
Spectrogram obtained using observations of Telkom 3 satellite from the BPST VHF radar.
The resulting spectrogram using the Telkom 3 CAD model from Figure 7 simulated at 55 MHz with linear vertical polarisation is presented in Figure 13 for elevation angle. The specular reflections from the solar panels are present across positive and negative Doppler centred at a rotation angle of with adjacent reflections close to zero Doppler corresponding to the antenna dishes.
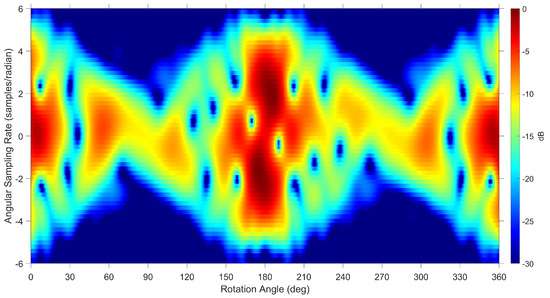
Figure 13.
Spectrogram using simulated data with Telkom 3 CAD model at an elevation of with vertical polarisation at a frequency of 55 MHz.
The corresponding spectrogram at an elevation angle of is shown in Figure 14, illustrating a different micro Doppler signature than is shown in Figure 13, highlighting the dependency of the received radar returns on the satellite orientation.
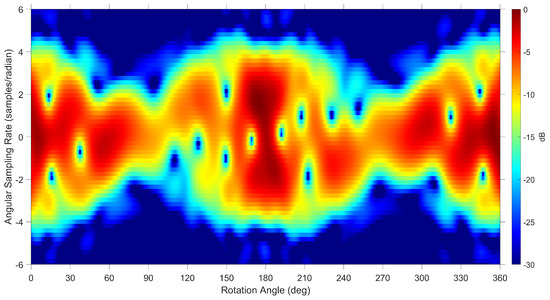
Figure 14.
Spectrogram using simulated data with Telkom 3 CAD model at an elevation of with vertical polarisation at a frequency of 55 MHz.
Finer details are not present in the spectrogram when using a lower number of samples in the Doppler or angular sampling rate dimension to process the micro Doppler information. For example, the same data were used to generate the results in Figure 15 as used in Figure 13 but with half the number of samples. The bottom plot in Figure 3 shows the measured data with a similar micro Doppler pattern as Figure 15 illustrating that care needs to be taken in choosing an appropriate number of samples as outlined in Section 4.2.
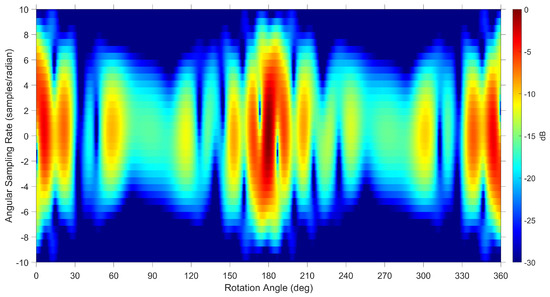
Figure 15.
Spectrogram using the Telkom 3 CAD model at an elevation of with the angular sampling rate downsampled by a factor of 2 with vertical polarisation at a frequency of 55 MHz.
If the rotation rate is known or estimated, then the angular sampling rate can be converted to the traditional time-based sampling rate . Measured radar observations can be used to estimate using the time taken between the solar panel specular reflections in a rotation; however, each observation of the satellite may present variations in the rotation rate.
As an example, the simulated RCS pattern of Telkom 3 is provided in Figure 16 which indicates maximum peaks occurring every corresponding to the broadside orientation of the satellite. The RCS pattern could be used in a similar way to monitor the spinning motion as observed by the Chibolton radar in [15].
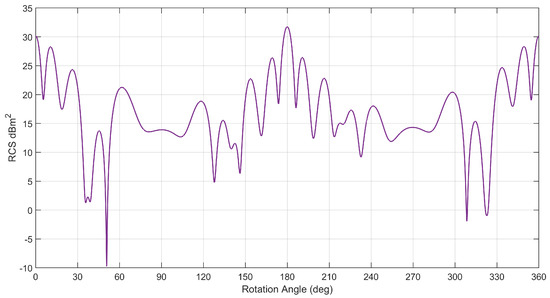
Figure 16.
Simulated RCS of Telkom 3 at an elevation of with vertical polarisation at a frequency of 55 MHz.
6. Discussion
The observed micro-Doppler signatures for all three defunct satellites using the BPST VHF radar in Section 5 indicate that there are features changing in time, indicative of rotational motion. The simulated data assisted with interpreting the resident space object’s spin axis as well as identifying returns from the antennas and solar panels. It was observed that the largest micro-Doppler extent corresponded to the length and number of solar panels. The symmetry of the micro-Doppler pattern enables the number of solar panels to be extracted from the data. In Figure 11, the asymmetrical returns around zero Doppler indicate an odd number of solar panels only occurring at and indicative of a single panel for TOPEX/Poseidon. The simulated micro-Doppler features for RHESSI are symmetrical in Figure 9 indicating an even number of solar panels, where the returns occur every 90 degrees indicating that there are four panels, whereas the results for Telkom 3 in Figure 13 show symmetrical returns from the panels that occur every indicative of two panels. When the simulated data are compared to the measured data, the number of solar panels can be verified and assessed as to whether a solar panel is damaged or missing.
A range of spin axes were examined in the simulated data in order to find the best agreement with the measured data. Figure 17 shows the resulting attitude for each resident space object including RHESSI with the spin axis along the x direction, TOPEX/Poseidon with spin axis in the y direction and Telkom 3 with the spin axis in the z direction assuming the radar is looking in the negative y direction. Different elevation angles were also investigated when comparing the simulated and measured data, where the elevation angle is defined as the angle from the spin axis to the rotation plane. The results in Figure 9 show that the elevation angle of degrees has the best agreement with the measurements of RHESSI and TOPEX/Poseidon. However, the zero degree elevation angle in Figure 13 showed the best agreement for Telkom 3.
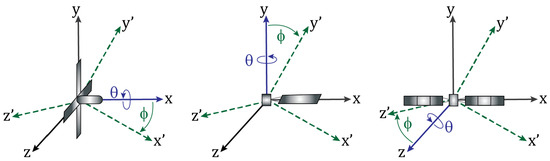
Figure 17.
The rotation axis identified for RHESSI (left), TOPEX/Poseidon (middle) and Telkom3 (right).
A summary of the insights gained from the analysis of the simulated micro-Doppler signatures is provided in Table 2. The spin axis, elevation angle and polarisation estimations were able to be determined from the comparison of the micro-Doppler pattern from the simulated data and the BPST VHF radar observations.

Table 2.
Summary of object features extracted from the simulated micro-Doppler results.
The simulated micro-Doppler pattern for a single rotation assisted with interpretation of the measured results. Once the number of solar panels were known from comparing the simulated and measured results, the estimated Doppler extent, rotation period, rotation rate and total object length were extracted from inspection of the measured BPST VHF radar data. The summary of the features extracted from the measured data is presented in Table 3.

Table 3.
Summary of object features extracted from the measured micro-Doppler results.
Several assumptions were made in order to conduct the computational electromagnetic simulations to synthesise the BPST VHF radar setup and environmental effects. Although the BPST VHF radar transmitted a linear vertically polarised signal, the received signal may be subjected to Faraday polarisation rotation caused by the interaction of the signal with the ionosphere [34]. As a result, the polarisation of the received signal could be rotated by an unknown amount in the polarisation plane. This study was confined to simulating the horizontal (aligned wit the z axis) and vertical (aligned with the x axis) polarisation to reduce the complexity of the problem. The results give an indication of whether the received signal was closer to horizontal or vertical polarisation rather than determining the exact rotation angle in the polarisation plane. This assumption means that the simulated micro-Doppler features will highlight the dominantly horizontal or vertical components of the structure rather than match the exact polarisation of the measured radar data.
There were also constraints placed on the simulated motion of the resident space object including a fixed elevation angle and constant rotation rate, whereas in reality, this may not be the case. Large variations in the motion of the resident space object could impact the micro-Doppler signature, but it is expected that the variations are minimal for non-operational satellites within the small observation times shown in this paper. All material properties of the CAD model used in the simulations were assumed to be perfectly electrically conducting which may slightly overestimate the intensity of the micro-Doppler signature. The CAD models were also rotated to examine different spin axes to find the best fit with the simulated and measured results. Consequently, the simulated micro-Doppler signatures are an approximate indication of polarisation, spin axis and elevation angle. However, the simulated data show good agreement with the measured BPST VHF radar data and validate the CAD models to show that the object structure is largely intact, and micro Doppler features were found to be consistent with the solar panels and antennas.
This study focuses on characterising a representative set of different resident space objects that are typical of what the BPST VHF radar may observe to gain insight into the scattering characteristics and extract object features. However, there are a vast number of resident space objects the BPST VHF radar is capable of observing which would require an automated process and management of a large simulated dataset incorporating a range of spin axes, elevation angles and polarisation rotation angles. This problem is well suited to machine learning to automatically extract target features and classify objects for situational awareness and monitoring of abnormal behaviour of resident space objects. The ease of producing simulated data is beneficial for generating training data for supervised learning algorithms. The results in Section 5 have shown that low–medium fidelity CAD models simulated with the full-wave solver agree with the measured BPST radar data to a good approximation. The automated process of extracting information from a larger number of resident space objects is a logical next step to progress this research in future work.
7. Conclusions
The micro Doppler signatures for three defunct satellites were studied using measured radar observations from the BPST VHF radar in South Australia. Computational electromagnetic simulations assisted with interpreting the measured radar data in order to characterise the three resident space objects. Several insights were gained from the comparison of the simulated and measured micro-Doppler signatures including an estimation of the spin axis, attitude, number of solar panels, rotation rate and approximate size. In future work, this initial research will be extended to a larger number of resident space objects requiring automated processing with particular consideration of the complexities involved in generating the simulated data.
Author Contributions
Conceptualisation, D.H., S.T.N. and E.H.; methodology, D.H., S.T.N. and E.H.; software, D.H., S.T.N. and E.H.; validation, D.H. and E.H.; formal analysis, D.H., E.H. and S.T.N.; investigation, D.H. and E.H.; resources, D.H. and I.M.R.; data curation, D.H. and I.M.R.; writing E.H. and D.H.; visualisation, D.H., S.T.N. and E.H.; supervision, I.M.R.; project administration, D.H. and E.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data used in this research are not publicly available.
Acknowledgments
The authors would like to thank the University of Adelaide and ATRAD for use of the BPST VHF radar to perform the measurements and Defence Science and Technology Group for supporting this research. We would also like to thank Bobby Yau and Stephen McClanachan for sharing their expertise on computational electromagnetic simulations, and we acknowledge discussions with Brendan Hennessy, Kruger White, An Phan and Hai-Tan Tran from Defence Science and Technology Group.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Holdsworth, D.; Spargo, A.; Reid, I.; Adami, C. Low Earth Orbit object observations using the Buckland Park VHF radar. Radio Sci. 2020, 55, e2019RS006873. [Google Scholar] [CrossRef]
- Anger, S.; Anglberger, H.; Jirousek, M.; Dill, S.; Peichl, M. ISAR Imaging of Satellites in Space–Simulations and Measurements. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hennessy, B.; Tingay, S.; Hancock, P.; Young, R.; Tremblay, S.; Wayth, R.B.; Morgan, J.; McSweeney, S.; Crosse, B.; Johnston-Hollitt, M.; et al. Improved Techniques for the Surveillance of the Near Earth Space Environment with the Murchison Widefield Array. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Palmer, J.E.; Hennessy, B.; Rutten, M.; Merrett, D.; Tingay, S.; Kaplan, D.; Ord, S.T.S.M.; Morgan, J.; Wayth, R.B. Surveillance of Space using passive radar and the Murchison Widefield Array. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017. [Google Scholar]
- Smith, C.H.; Greene, B.; Bold, M.; Drury, R. Development of a new SSA facility at Learmonth Australia. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 11–14 September 2018. [Google Scholar]
- Frazer, G.J.; Meehan, D.H.; Warne, G.M. Decametric measurements of the ISS using an experimental HF line-of-sight radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, Australia, 9–12 September 2013. [Google Scholar]
- Frazer, G.J.; Rutten, M.; Cheung, B.; Cervera, M.A. Orbit determination using a decametric line-of-site radar. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 9–12 September 2014. [Google Scholar]
- Boley, A.; Byers, M. Satellite mega-constellations create risks in Low Earth Orbit, the atmosphere and on Earth. Sci. Rep. 2021, 11, 10642. [Google Scholar] [CrossRef] [PubMed]
- NASA Office of Inspector General Office of Audits. NASA’s Efforts to Mitigate the Risks Exposed by Orbital Debris; Technical Report IG-21-011; NASA: Washington, DA, USA, 2021. [Google Scholar]
- Nosrati, H.; Smith, S.; Hayman, D.; Horiuchi, S.; Hellicar, A. Bi-static Radar Interferometric Localization of MEO and GEO Space Debris using Australia Telescope Compact Array. In Proceedings of the Advanced Maui Optical and Space Technologies Conference, Maui, HI, USA, 27–30 September 2022. [Google Scholar]
- Heading, E.; Nguyen, S.; Holdsworth, D.; Field, D.; Reid, I. Analysis of RF Signatures for Space Domain Awareness using VHF radar. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Benson, C.; Scheeres, D.; Moskovitz, N. Light-curves of Retired Geosynchronous Satellites. In Proceedings of the 76th European Conference on Space Debris, Darmstadt, Germany, 17–21 April 2017; Volume 7. [Google Scholar]
- Kudak, V.I.; Epishev, C.P.; Perig, V.M. Determining the orientation and spin period of TOPEX/Poseidon satellite by a photometric method. Astrophys. Bull. 2017, 72, 340–348. [Google Scholar] [CrossRef]
- Fulcoly, D.O.; Kalamaroff, K.I.; Chun, F.K. Determining Basic Satellite Shape from Photometric Light Curves. J. Spacecr. Rocket. 2012, 49, 76–82. [Google Scholar] [CrossRef]
- Eastment, J.D.; Ladd, D.N.; Walden, C.J.; Trethewey, M.L. Satellite observations using the Chibolton radar during the initial ESA ’CO-Vi’ tracking campaign. In Proceedings of the European Space Surveillance Conference, Madrid, Spain, 7–9 June 2011. [Google Scholar]
- Stevenson, M.; Nicolls, M.; Rosner, C. Space Object Attitude Stability Determined from Radar Cross-Section Statistics. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 17–20 September 2019. [Google Scholar]
- Uysal, F.; van Dorp, P.; Serrano, A.; Kobsa, A.; Ghio, S.; Kintz, A.; Bassa, C.; Garrington, S.; Caro Cuenca, M.; Otten, M.; et al. Large Baseline Bistatic Radar Imaging for Space Domain Awareness. In Proceedings of the Radar 2023, Berlin, Germany, 20–22 September 2023. [Google Scholar]
- Ghio, S.; Martorella, M. Estimation of rotating RSO parameters using radar data and joint time-frequency transforms. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017. [Google Scholar]
- Jung, K.; Lee, J.I.; Kim, N.; Oh, S.; Seo, D.W. Classification of Space Objects by using Deep Learning with Micro Doppler Signature Images. Sensors 2021, 21, 4365. [Google Scholar] [CrossRef] [PubMed]
- Cammenga, Z.A.; Baker, C.J.; Smith, G.E.; Ewing, R. Micro-Doppler target scattering. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 9–23 May 2014; pp. 1451–1455. [Google Scholar] [CrossRef]
- Dolman, B.; Reid, I.; Tingwell, C. Stratospheric tropospheric wind profiling radars in the Australian network. Earth Planets Space 2018, 70, 170. [Google Scholar] [CrossRef]
- Adelaide, T.U. Buckland Park VHF ST Radar. 2024. Available online: http://www.physics.adelaide.edu.au/atmospheric/vhf.html (accessed on 1 February 2024).
- Richards, M. The keystone transformation for correcting range migration in range-doppler processing. Pulse 2014, 1000, 13–14. [Google Scholar]
- Lin, R.P.; Dennis, B.R.; Hurford, G.J.; Smith, D.M.; Zehnder, A.; Harvey, P.R.; Conway, A. The Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI); Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Krebs, G.D. RHESSI (RHESSI, Reuven Ramaty, SMEX 6, Explorer 81). 2023. Available online: https://space.skyrocket.de/doc_sdat/explorer_hessi.htm (accessed on 1 February 2024).
- Hill, D. NASA Retired Solar Energy Imager Spacecraft Reenters Atmosphere. 2023. Available online: https://www.nasa.gov/feature/nasa-retired-solar-energy-imager-spacecraft-reenters-atmosphere (accessed on 1 February 2024).
- Dennis, B. RHESSI MISSION FACTS. 2023. Available online: https://hesperia.gsfc.nasa.gov/rhessi2/mission/mission-facts/index.html (accessed on 1 February 2024).
- NASA. TOPEX/Poseidon. 2021. Available online: https://sealevel.jpl.nasa.gov/system/documents/files/1674_tp-fact-sheet.pdf (accessed on 1 February 2024).
- Page, G.S. Telkom 3. 2021. Available online: https://space.skyrocket.de/doc$_$sdat/telkom-3.htm (accessed on 1 February 2024).
- Technology, A. Telkom-3 Communications Satellite, Indonesia. 2021. Available online: https://www.aerospace-technology.com/projects/telkom3-communication-satellite-indonesia (accessed on 1 February 2024).
- Reshetnev, J.A.M. Information Satellite Systems. 2021. Available online: http://www.iss-reshetnev.com/spacecraft/spacecraft-communications/telkom-3 (accessed on 1 February 2022).
- Munson, D.; O’Brien, J.; Jenkins, W. A tomographic formulation of spotlight mode synthetic aperture radar. Proc. IEEE 1983, 71, 917–925. [Google Scholar] [CrossRef]
- Tran, H.T.; Heading, E.; Ng, B.H. On the Slow-Time k-Space and its Augmentation in Doppler Radar Tomography. Sensors 2020, 20, 513. [Google Scholar] [CrossRef] [PubMed]
- Klobuchar, J. Ionospheric Effects on Earth-Space Propagation; Technical Report AFGL-TR-84-0004; Ionospheric Physics Division: Air Force Geophysics Laboratory: Bedford, MA, USA, 1983. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).