Abstract
International terrestrial reference frame (ITRF) input data, generated by Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), Very Long Baseline Interferometry (VLBI), and Doppler Orbitography and Radiopositioning integrated by satellite (DORIS) combination centers (CCs), are considered to be relatively high-quality and accurate solutions. Every few years, these input data are submitted to the three ITRS combination centers, namely Institut Géographique National (IGN), Deutsches Geodätisches Forschungsinstitut at the Technische Universität München (DGFI-TUM), and Jet Propulsion Laboratory (JPL), to establish a multi-technique combined terrestrial reference frame (TRF). Generally, these solutions have undergone three rounds of outlier removal: the first at the technique analysis centers during solution generations and the second during the technique-specific combination by the CCs; ITRS CCs then perform a third round of outlier removal and preprocessing during the multi-technique combination of TRFs. However, since the primary objective of CCs is to release the final TRF product, they do not emphasize the publication of analytical preprocessing results, such as the outlier rejection rate. In this paper, our specific focus is on assessing the precision improvement of ITRF input data from 2014 to 2020, which includes evaluating the accuracy of coordinates, the datum accuracy, and the precision of the polar motions, for all four techniques. To achieve the above-mentioned objectives, we independently propose a TRF stacking approach to establish single technical reference frameworks, using software developed by us that is different from the ITRF generation. As a result, roughly 0.5% or less of the SLR observations are identified as outliers, while the ratio of DORIS, GNSS, and VLBI observations are below 1%, around 2%, and ranging from 1% to 1.2%, respectively. It is shown that the consistency between the SLR scale and ITRF has improved, increasing from around −5 mm in ITRF2014 datasets to approximately −1 mm in ITRF2020 datasets. The scale velocity derived from fitting the VLBI scale parameter series with all epochs in ITRF2020 datasets differs by approximately 0.21 mm/year from the velocity obtained by fitting the data up to 2013.75 because of the scale drift of VLBI around 2013. The decreasing standard deviations of the polar motion parameter (XPO, YPO) offsets between Stacking TRFs and 14C04 (20C04) indicate an improvement in the precision of polar motion observations for all four techniques. From the perspective of the weighted root mean square (WRMS) in station coordinates, since the inception of the technique, the station coordinate WRMS of DORIS decreased from 30 mm to 5 mm for X and Y components, and 25 mm to 5 mm for the Z component; SLR WRMS decreased from 20 mm to better than 10 mm (X, Y and Z); GNSS WRMS decreased from 4 mm to 1.5 mm (X and Y) and 5 mm to 2 mm (Z); while VLBI showed no significant change.
1. Introduction
A unique standard terrestrial reference frame (TRF) is fundamental to ensure inter-operability and consistency of geodetic products and to adequately exploit various measurements collected by ground-based sensors, or via artificial satellites for Earth science and geodesy applications [1,2,3], including plate tectonics [4,5], co-seismic and post-seismic deformations [6,7], global geophysical fluid dynamics [8,9], ice melting [10], accurately determining point positions, and the rate of sea level rise [11,12], etc.
Generally, the most widely utilized reference framework is the International Terrestrial Reference Frame (ITRF) series [13], which has a history spanning four decades. Since its inception in 1988, the ITRF has undergone 14 versions, namely ITRF 88, 89, 90, 91, 92, 93, 94, 96, 97, 00, 05, 08, 14, and 20. Additionally, starting from 2003 and 2008, two other International Terrestrial Reference System (ITRS) analysis centers, namely the Deutsches Geodätisches Forschungsinstitut at the Technische Universität München (DGFI-TUM) and the Jet Propulsion Laboratory (JPL), began to use the normal equation and the Kalman filter method to combine TRFs, respectively [14,15]. Furthermore, in the establishment process of the latest 2014 and 2020 versions of ITRS, they have both released their own versions, namely DTRF2014, DTRF2020 and JTRF2014, JTRF2020 (https://dtrf.dgfi.tum.de/en/, accessed on 19 March 2024; https://www.jpl.nasa.gov/site/jsgt/jtrf/, accessed on 19 March 2024).
The current ITRF2020 encompasses the positions, velocities, and annual and semi-annual signals of globally distributed reference stations, integrating the strengths of the four Space Geodesy techniques: Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), Very Long Baseline Interferometry (VLBI), and Doppler Orbitography and Radiopositioning integrated by satellite (DORIS) [2]. The post-seismic deformation (PSD) signal was fitted during preprocessing and then removed from the original observations. Typically, analysis centers (ACs) for GNSS, SLR, VLBI, and DORIS reprocess historical observations employing the latest optimal computation strategies and models. Then, the solutions from these centers are combined by the combination centers (CCs) for the four techniques, namely the International GNSS Service (IGS), International VLBI Service (IVS), International Laser Ranging Service (ILRS), and International DORIS Service (IDS). These combined outcomes are considered to be relatively high-quality and accurate solutions because of the latest processing strategies and models, and the correction of system errors of different ACs, and are submitted as the input data for establishing and updating ITRF.
Generally, these solutions have undergone three rounds of outlier removal: the first at the technique ACs during solution generations and the second during the technique-specific combination by the CCs; CCs then perform a third round of outlier removal and preprocessing during the combination of TRFs. However, as the primary goal of the CCs is to release the final TRF product, they do not prioritize the publication of analytical preprocessing results. Yet, some unpublished or under-researched aspects remain meaningful, such as the outlier rejection rate.
Unlike ACs and CCs, in this paper, our specific focus is on assessing the precision improvement of ITRF input data from 2014 to 2020, which includes evaluating the accuracy of coordinates, the datum precision, and the accuracy of polar motions, for all four techniques.
Basically, SLR employs a loosely constrained solution, VLBI utilizes a normal equation, and DORIS derives a technical solution from internal constraints. Consequently, the solutions of these three techniques are not aligned to a fixed frame, and traditional time series analysis methods prove insufficient in assessing the quality of these solutions. Additionally, traditional time series analysis methods cannot assess the datum information for all four techniques. Therefore, we independently propose a TRF stacking approach following Altamimi et al. [16] to achieve the previously mentioned objectives: investigating the improvement in observation precision of GNSS, SLR, VLBI, and DORIS inputs from ITRF2014 to ITRF2020. TRF stacking accumulates epoch solutions to long-term TRF expressed by coordinates and velocities in a specific epoch, enabling us to evaluate observational qualities and the datum precision. Furthermore, to establish 2014 and 2020 ITRF, solutions of each Space Geodesy technique incorporated new strategies and models, and we can investigate the impact of these strategies at the stacking TRF level.
In general, the solutions for each technique in 2020 exhibit significant improvements compared to the previous versions. For GNSS, the new International Earth Rotation Service (IERS) secular pole model was adopted in Repro3, replacing the previous mean pole model used in Repro2 from the original IERS 2010 Conventions. Consequently, Repro3 and IGS14 exhibit systematic biases, making alignment impractical. Therefore, a special reference frame, IGSR3, was utilized, aligning with the new IERS secular pole model, the igsR3.atx satellite phase center offsets (PCOs), and the igsR3.atx ground antenna calibrations [17]. More basic information about IGS Repro2 and IGS Repro3 can be found at the following URLs: http://acc.igs.org/reprocess2.html (accessed on 19 March 2024), http://acc.igs.org/repro3/repro3.html (accessed on 19 March 2024).
For SLR, a series of improvement measures were implemented to address its systematic biases [18], like enhancements to the satellite center of mass model corrections [19]. A comprehensive investigation into the site-specific systematic errors in the data collected since 1983 was conducted [20]. Regardless of reported issues or configuration changes at the sites, both the coordinates and systematic biases were simultaneously estimated for all of the 7 ACs and CCs (ASI, BKG, DGFI, ESA, GFZ, JCET, NSGF [21].
For VLBI, some new and improved models for the IVS analysis have been applied, including a constant drift of 5.8 µas/year on Galactic aberration. Additionally, mid-session-epoch solutions are calculated to present the best performance of VLBI, but they are transformed to 12 h to ensure the consistency with the epochs of other techniques which are submitted for establishing the ITRF [22,23].
When combining results from various ACs, IDS avoids introducing external reference frames and employs internal constraints during technical within-group combinations [24]. Consequently, the geocenter and scale results from DORIS observations directly reflect its precision in determining geocenter and scale. Compared to 2014, DORIS 2020 solution has undergone some new improvements: the application of new phase center variations for Alcatel DORIS ground antennas and the gradual replacement of Alcatel with Starec antennas over time, better modeling the surface forces on the satellites [24,25].
2. Methods
2.1. Stacking Model
A significant application of space geodetic observations is the continuous determination of ground station coordinates [26]. Using four techniques, i.e., GNSS, SLR, VLBI, and DORIS, coordinates sets and their internally consistent Earth Orientation Parameters (EOPs) can be estimated based on observations collected at each measurement interval, daily and weekly [27]. Due to the complex surface deformation characteristics of the Earth, the coordinates of individual epochs not only include Earth’s crustal movements, terrain variations, and surface loads as geophysical signals but also involve various random errors. Consequently, in order to mitigate the influence of random factors and better apply physical signals, it is common to stack observations from individual epochs over a certain time span to coordinates, velocities, and other modelable parameters (such as periodic signals) at a specific reference epoch. This process yields a reference framework through the stacking of observations, which we call the TRF Stacking method.
The transformation relationship between TRFs is typically represented using the Helmert similarity transformation model. For a station of technique s, located in a specific epoch , the coordinates in the epoch reference frame are related to the stacking reference frame coordinates at the reference epoch , as well as the EOPs in the two reference frames, according to the following transformation:
where 1.002737909350795, represents the three translation parameters, denotes scale parameters, signifies rotation parameters, and . If there is a need to model additional signals such as periodic terms for the stations, further model optimization can be performed in Equation (1). Corresponding adjustments should be made in the subsequent datum definition part [2]. As for the information we currently wish to investigate, namely characteristics of datum, polar motions, etc., it is still feasible to consider only velocity terms and can be compared with the results of ITRF2020, which take into account both velocity and periodic terms. It is crucial to emphasize that the nonlinear characteristics of TRFs are indeed important, but we believe that these nonlinear features require dedicated and thorough research. Additionally, solutions for SLR, DORIS, and VLBI do not have defined a datum, and we think fitting periodic terms to these results requires separate study as well. Therefore, this contribution only includes linear terms. We aim to investigate nonlinear features such as periodic terms, noise, and earth surface loadings in future research, specifically and comprehensively.
It is necessary to provide a supplementary explanation for Equation (1). In addition to the velocity terms modeled in Equation (1) and the periodic terms modeled, like ITRF2020 as mentioned above, the observations may also include post-seismic deformation and discontinuities. Post-seismic deformation is typically addressed by modeling with a combination of exponential and logarithmic functions, and by removing the post-seismic deformation signal during preprocessing. For discontinuities, the common approach is piecewise linear fitting. If there are no velocity discontinuities, constraints enforcing equal velocities between segments need to be added, typically with a constraint precision of 0.05 mm/yr.
2.2. Datum Definition
According to Equation (1), the introduction of transformation parameter time series and the estimation of station coordinate velocities result in a rank deficiency in the normal equations, with a rank deficiency of 14 [28]. It can also be considered that the datum for the stacking TRF, and , is undefined. The rank deficiency can be addressed by datum defining.
According to the definition by the International Earth Rotation and Reference Systems Service (IERS), the datum for ITRS includes the origin, scale, orientation, and their variations over time [29].
Due to the distinct characteristics of various space geodetic techniques, such as SLR, GNSS, and DORIS, which are sensitive to the Earth’s center of mass, the TRF origin can be defined [30,31].
The scale, by definition, should be the scale of a local TRF in the sense of general relativity. The other three techniques, apart from GNSS, are sensitive to the scale, and in practical applications, physical parameters (such as Earth’s gravitational constant GM and the speed of light c) and a certain relativistic correction model are employed to determine it. If different techniques use distinct physical parameter values and models, their scales may differ. However, adopting recommended values from the IERS specifications in data processing tends to minimize scale differences determined by various techniques. For GNSS, the igsR3.atx file used in Repro3 was generated with respect to externally calibrated Galileo phase center variation (PCV)/PCO values rather than ITRF. This enables GNSS solutions, for the first time, to observe the scale independent of ITRF [17].
The orientation of the current ITRS has evolved from the orientation defined by BIH1984.0, and new versions of ITRS maintain consistency with the previous version’s orientation by conforming to the no-net-rotation (NNR) condition, which ensures horizontal motion relative to the Earth’s surface [32].
In mathematics, the definition of a datum is typically realized through the imposition of constraints. Generally, two constraint methods are employed: when defining the datum using a set of external reference coordinates and their velocities, denoted as and , the minimum constraint approach is utilized; when preserving the intrinsic physical parameter information associated with , the minimum constraint is applied.
Minimum constraint means the minimization of Helmert transformation parameters between external reference frames, , , and the Stacking TRF, , [33]. The relationship of , and , can be defined as:
encompasses the seven transformation parameters and their rates, the matrix A includes the partial derivatives of the transformation parameters, and the design matrix A is defined as:
Expressing Equation (3) as , where is the least squares solution and given by:
and letting , considering as the observed quantity with a weight , and treating as the parameter, the minimization condition leads to the normal equation for Equation (5):
where represents the correction to the parameters .
Internal constraint signifies that for all transformation parameters within the span, they are set to zero at the reference epoch , including both the values and velocities.
Following the derivation, we obtain:
where refers to all of the observation epochs involved in the calculation.
2.3. Outliers and Variance Component Estimation
Based on the posterior residuals , the posterior variance factor can be computed by:
where is the weight matrix of the observations (obtained by taking the inverse of the covariance matrix), and is:
This variance component estimation approach is also described by Davies and Blewitt [34]. It can serve as a residual-based posterior weighting method until approaches unity. Observations with normalized residuals (residual divided by their standard deviation) exceeding 4 are considered outliers and are subsequently removed during this rescale process.
The weighted root mean square (WRMS) is computed as:
3. Data Introduction and Preprocessing
The selected data for this study are presented in Table 1. To ensure a stable estimation of velocities and prevent situations where only one observation exists in a segment, making velocity unsolvable, stations with an observation count greater than 50 were chosen (i.e., 50 days for daily solutions and 50 weeks for weekly solution). For VLBI, we opted to use data from a minimum of three stations per session, starting from the 600th GPS week (19910707) onwards. For 2014, 2887 sessions were chosen, with 20 sessions excluded due to abnormal transformation parameters. In 2020, 4433 sessions were selected, and 11 sessions with abnormal transformation parameters were excluded. Mid-session epoch solutions were used rather than 12 h epoch solutions. Regarding SLR, the 2014 solutions had fixed weekly solutions from the 678th GPS week (19930103) onwards, so both the 2020 and 2014 SLR datasets were selected from weeks beyond the 678th GPS week (19930103). For GNSS, weekly solutions rather than daily solutions were utilized here. All weekly solutions of IDS-09 for 2014 and IDS-16 for 2020 were selected for DORIS. Core stations were selected and referred to ITRF2014 and ITRF2020 core-networks, and for DORIS 2014, we selected more core stations, because there are only two DORIS stations in ITRF2014 core-network.

Table 1.
Space Geodesy inputs utilized in this work. TN in the first column identifies the technique type. Then TS designates the time span. SOL specifies the kind of Solution Independent Exchange Format (SINEX) format released by the four corresponding technique centers: VC stands for variance–covariance, NE for normal equations. TR and CONs relate to the temporal resolution and the constraint type, respectively. At last, SN in the sixth column is the solution number, namely SINEX file numbers for each technique selected here.
When conducting datum definition or orientation, the external reference frame coordinates of a set of core stations from each technique are employed; station and core station distributions are illustrated in Figure 1. Generally, the utilized station numbers of GNSS, SLR, VLBI, DORIS are 911, 56, 56, 146 (1656, 33, 30, 57) for 2014 and 1181, 63, 63, 175 (2773, 34, 25, 80) for 2020, where the numbers in parentheses indicate the count of segments due to discontinuities. We can observe that there is an abundance of GNSS stations, mainly concentrated in terrestrial regions. VLBI and SLR have a relatively limited number of stations, and the north–south distribution is uneven for all three techniques. DORIS stations, on the other hand, exhibit a more uniform north–south distribution, and multiple stations often exist within one site.
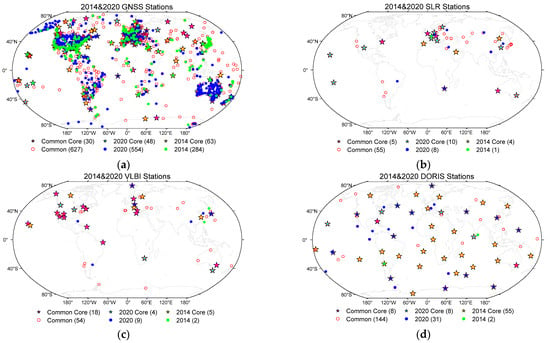
Figure 1.
Station and core station distributions of Space Geodesy input data. “Common” and “Common Core” refers to stations and core stations used in both 2014 and 2020. “2020”, “2014”, “2020 Core” and “2014 Core” means stations and core stations used only in 2014 or 2020. The numbers of stations are given in parentheses. Subfigures (a), (b), (c) and (d) are station distribution maps of GNSS, SLR, VLBI and DORIS respectively.
SLR inputs consist of solutions with loose constraints, and the substantial formal errors documented in the SINEX files result from the relaxed positional constraints implemented during laser range data reductions. These errors are indicative of rotational noise associated with the reference frame. To mitigate this effect, the covariance matrices of the solutions are adjusted by imposing the no-net-rotation (NNR) condition. No no-net-scale (NNS) condition or no-net-translation (NNT) is applied to preserve the intrinsic SLR origin and scale [35,36,37].
The Normal Equations (NEQs) for each VLBI session are inverted by incorporating NNT and NNR conditions into the a priori station position coordinates provided in the input SINEX files. To maintain the inherent scale of VLBI, no NNS condition is applied during the inversion of the NEQs.
The post-seismic deformations for all four techniques are initially subtracted based on the analysis results from the ITRF. The segmentation of the time series also refers to the results obtained from the ITRF. Corresponding file download links can be accessed at the following address: https://itrf.ign.fr/ (accessed on 20 March 2024).
4. Results and Analysis
4.1. Stacking Results
We performed outlier removal of the coordinate observations and posterior scaling of the covariance matrix through iterative Space Geodesy TRF (single technique) stacking. Observations with normalized residuals exceeding 4 are considered outliers and are subsequently removed. This iterative process continues until no outliers can be detected and the variance scale factor approaches 1. The iteration results are tabulated in Table 2.

Table 2.
Outlier ratios (OR), covariance scale factor () and number of iterations (Num). Covariance scale factors of ITRF () and JTRF () are also listed in the table for comparison.
From Table 2, it can be observed that the covariance scale factor of 5.29 [1], as reported by ITRF2014 and based on daily GNSS solutions, is smaller than both JTRF2014 (32.49) [38] and the value of 25.07 presented in this paper, which relies on weekly GNSS solutions. The covariance scale factor for SLR suggests that our findings are in close agreement with ITRF2014, ITRF2020 and JTRF2014. Notably, the VLBI covariance scale factor in ITRF2020 exhibits an exceptionally large value [2]. However, it is essential to highlight that ITRF2020 adopts 12 h epoch solutions for VLBI data, whereas our analysis employs mid-session epoch solutions. Additionally, we utilized VLBI data collected after 1991. As for DORIS, our analytical results demonstrate consistency. Theoretically, since this paper does not introduce periodic terms, the covariance scale factor should exceed that of the ITRF analysis. Nevertheless, the result of 7.78 in this paper is slightly lower than the ITRF analysis result of 8.53 in DORIS 2020. This discrepancy could stem from the selection of stations with more than 50 observation epochs in this study, or it may warrant an investigation into the details of the implementation of periodic terms. Hence, this paper initially concentrates solely on velocity and intends to explore periodic terms in further detail separately at a later stage.
Two datum definition strategies are utilized for TRF stacking. Initially, to understand the characteristics of the origin and scale determination for GNSS, SLR, and DORIS techniques, we applied internal constraints to their translation and scale parameters to retain their internally determined origin and scale information. Since the results from GNSS are already fixed to ITRF2014 and IGSR3 for Repro2 and Repro3, the origin and scale derived from GNSS observations represent the origin and scale discrepancy with respect to their corresponding reference frame. Additionally, to study the frame characteristics of each technique relative to ITRF, we defined the translation and scale parameters through the ITRF core stations using minimum constraints. Both orientation schemes align with either ITRF2014 or ITRF2020. As VLBI is not sensitive to the origin, when solving with an internal constraint scheme, only scale parameters are constrained, and other reference datum information is still defined by ITRF.
Table 3 illustrates the 14 transformation parameters between the Stacking Space Geodesy TRFs of single technique and the ITRF2014 (ITRF2020). The transformation parameters are computed based on the core station networks. When the origin and scale are aligned with the ITRF, the 14 transformation parameters between the Stacking Space Geodesy TRF and ITRF generally approach zero. However, when the origin and scale of the Space Geodesy TRFs are defined using internal constraints, the transformation parameters then reflect the differences between the techniques and the ITRF.

Table 3.
The 14 transformation parameters between Stacking Space Geodesy TRFs and ITRF2104 (ITRF2020) and their standard deviations.
4.2. Analysis of Translation and Scale Time Series
Figure 2 presents the series of translation and scale parameters between the observations and the Stacking Space Geodesy TRFs under two types of constraints: internal constraints and minimum constraints.
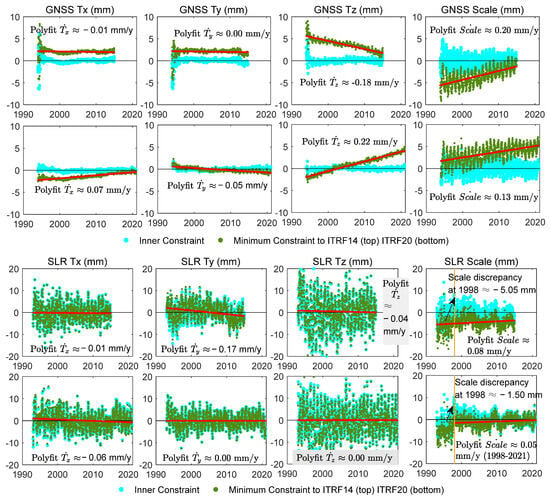
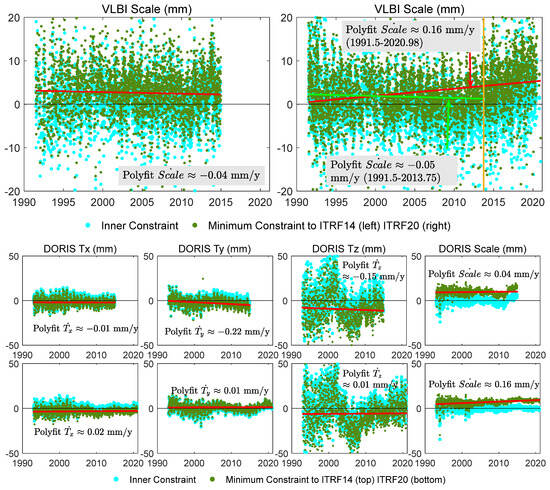
Figure 2.
Translation and scale parameter series between the observations and the Stacking Space Geodesy TRFs under two types of constraints: internal (inner) constraints and minimum constraints. The linear fit lines along with their slopes for the results of minimum constraints are also illustrated.
When internal constraints are applied, the translation and scale parameters of GNSS characterize the observational datum precision of GNSS in its aligned reference framework, specifically ITRF2008 and IGSR3. In the GNSS 2014 Stacking TRF, under the minimum constraint definition, the translation parameter Tx and Ty are approximately 2 mm, with their velocities essentially close to zero. The 2014 GNSS input data reference frame is fixed to ITRF2008, and after stacking and defining the reference frame to ITRF2014, the calculated Tx and Ty values reflect the differences between ITRF2008 and ITRF2014. The drift of the translation parameter in the Z direction and the scale parameter is primarily influenced by the technical characteristics of GNSS [39,40]. In 2020, GNSS adopted a secular polar motion model during the data processing, resulting in non-zero translation velocities for both Tx and Ty where and (by linear fit). In general, although GNSS provides numerous stations and high precision in positioning, its datum observation lacks stability, especially in the Z component and scale [41]. The GNSS coordinate calculations exhibit a significant dependence on the reference framework. Consequently, notable differences exist between the outcomes obtained under the two types of datum definitions.
From Figure 2, it is evident that the translational parameter series of SLR exhibit excellent consistency between internal and minimum constraints. This is attributed to the stability in determining the origin by the SLR. The translation velocity of in SLR 2014 is due to the drift at around 2010, which can be also found in ITRF2014 results. From the scale parameter time series, it is noticeable that there is a drift in the SLR scale around 1998. Therefore, for defining the scale in ITRF2020, only SLR data from after 1997.75 are chosen [2]. The consistency of scale between SLR and ITRF has improved, increasing from around −5 mm in 2014 to approximately −1 mm in 2020.
The determination of scale parameters in VLBI exhibits a significant level of noise, with a consistency of 3 mm with ITRF2014 and 2 mm with ITRF2020. A noticeable drift in VLBI scale occurred around 2013, prompting ITRF2020 to only incorporate data before 2013.75 when defining the scale using VLBI. Consequently, the scale velocity derived from fitting the VLBI scale parameter series with all epochs in 2020 differs by approximately 0.21 mm/year from the velocity obtained by fitting the data up to 2013.75.
The origin determinations in the X and Y directions from DORIS demonstrate accuracy comparable to SLR. However, there is notable variability in the Z direction. The translation velocity of in DORIS 2014 may be caused by the selected core station network. The consistency in scale between DORIS and ITRF is approximately within the range of 5–10 mm, and not stable enough compared to SLR and VLBI.
4.3. Analysis of Coordinate Residuals
Figure 3 illustrates the WRMS of the station coordinate residuals for each technique across their time span. Since the WRMS of the 2014 datasets are similar to those for the 2020 datasets during the same period, only 2020 WRMS are presented. It is evident that the accuracy of DORIS, SLR, and GNSS techniques gradually improves over time. The WRMS for the DORIS in the X and Y directions decreased from 30 mm to 5 mm, while the Z direction WRMS decreased from 25 mm to 5 mm. For SLR, the WRMS in the X, Y, and Z directions decreased from 20 mm to better than 10 mm. In the case of GNSS, the WRMS in the X and Y directions decreased from 4 mm to 1.5 mm, while the Z direction WRMS decreased from 5 mm to 2 mm. The station coordinates’ precision of DORIS surpasses SLR slightly after 2015, with GNSS exhibiting the highest coordinate precision. The variation in DORIS station coordinate precision is closely linked to changes in the DORIS satellite constellation [24,25]. VLBI shows significant variability in position precision within individual sessions and exhibits no significant change over time.
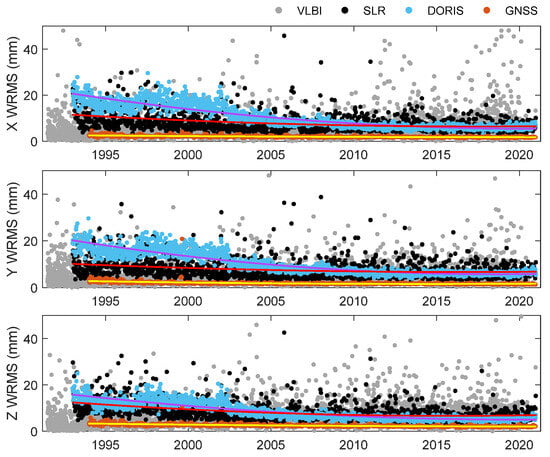
Figure 3.
WRMS of posterior station coordinate residuals between observations and stacked Space Geodesy TRFs. To better identify variations in station accuracy, quadratic polynomial fits were applied to the WRMS series for GNSS (yellow line), SLR (red line), and DORIS (purple line).
Furthermore, Table 4 displays the average WRMS for each technique calculated separately for each station. The precision of stations for GNSS, SLR, and DORIS in the 2020 version is improved compared to that in 2014.

Table 4.
The average WRMS for the four techniques, calculated by taking the mean of the WRMS values from each station.
4.4. XPO and YPO Residuals Compared to 14C04 and 20C04
As depicted in Figure 4, a comparison is made between the stacking polar motion parameters (XPO, YPO) with the corresponding IERSC04 series and ITRF EOP series, namely IERS14C04, IERS20C04, and EOP of ITRF2014 and ITRF2020. Mean residuals and standard deviations were calculated to characterize the observational precision of polar motion parameters for each technique. The results indicate that GNSS has the highest precision in polar motion measurement, with a difference standard deviation of approximately 0.05mas compared to C04. However, it is important to emphasize that IERSC04 is largely dominated by IGS (i.e., GNSS) EOP, therefore, the (XPO, YPO) standard deviation of GNSS is very small. VLBI exhibits relatively large noise in polar motion observations. The polar motion observations of SLR show differences with C04 within 0.3mas. The precision of DORIS polar motion observations gradually improves, with differences from C04 within 0.2 mas after the year 2015. The residuals of SLR, VLBI, and DORIS with respect to C04 and ITRF EOP in terms of (XPO, YPO) are essentially similar. However, the residuals of GNSS with respect to ITRF EOP display clear periodic terms and have a smaller standard deviation than IERSC04. This further indicates that the precision of ITRF (XPO, YPO) is primarily determined by GNSS.
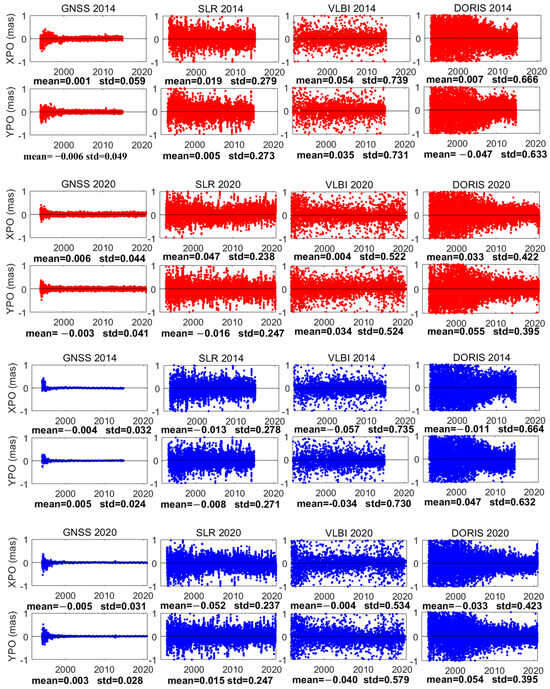
Figure 4.
Residuals of XPO and YPO from Stacking Space Geodesy TRFs compared to IERS14C04, IERS20C04 (red) and ITRF2014 EOP, ITRF2020 EOP (blue). The mean and standard deviation (std) statistics for the residual sequences are presented below the respective graphs.
5. Conclusions
In this study, we employed the TRF stacking method to assess the improvement in observation precision of GNSS, SLR, VLBI, and DORIS inputs from ITRF2014 to ITRF2020. The evaluation encompassed outlier removal, post-rescaling of covariance matrices, datum analysis, coordinate precision analysis, and polar motion precision analysis.
Roughly 0.5% or less of the SLR observations are identified as outliers, while the ratio of DORIS, GNSS, and VLBI observations are below 1%, around 2%, and ranging from 1% to 1.2%, respectively. In 2014, the post-rescaling covariance scale factors are 25.07, 27.25, 18.84, and 6.98 for GNSS, SLR, VLBI, and DORIS, respectively. The results for JTRF2014 were 32.49, 27.04, 34.81, and 7.29 [38], respectively, while ITRF2014 yielded 5.29, 25.20, 23.04, and 6.86 [1], respectively. In 2020, the post-rescaling covariance scale factors are 8.95, 14.9, 16.8, and 7.78, respectively, with ITRF2020 results being 6.76, 15.44, 133.63, and 8.53 [2], respectively. It is important to note that ITRF uses daily solutions for GNSS data instead of weekly solutions, and the epoch spans for VLBI and SLR selected by us differ from those in JTRF and ITRF. Furthermore, ITRF2020 uses 12-h epoch solutions for VLBI data, whereas our analysis utilizes mid-session epoch solutions. These are the primary reasons for the differences in covariance matrix rescale factors.
Based on the datum analysis results, it is shown that the data processing strategy for SLR has improved the consistency of SLR scale with ITRF from −5 mm in ITRF2014 datasets to −1 mm in ITRF2020 datasets. VLBI exhibits a drift in scale around 2013, resulting in an approximate scale difference of 0.21 mm/year. Therefore, when using VLBI for scale definition, this drift needs to be taken into consideration. The stability of DORIS origin observations has been enhanced, with the scale consistency with ITRF falling within the range of 5–10 mm. The datum accuracy of DORIS significantly improves with the progression of time. The rates of X and Y translation components between GNSS 2020 input data and ITRF2020 indicate and .
The decreasing standard deviations of the polar motion parameter (XPO, YPO) discrepancies between Stacking TRFs and 14C04 (20C04) indicate an improvement in the precision of polar motion observations for all four techniques. The standard deviations of (XPO, YPO) offsets from 2014 to 2020 are: (0.059, 0.049) to (0.044, 0.041) for GNSS, (0.279, 0.273) to (0.238, 0.247) for SLR, (0.739, 0.731) to (0.522, 0.524) for VLBI, and (0.666, 0.633) to (0.422, 0.395) for DORIS in milliarcseconds.
From the perspective of the WRMS in station coordinates, since the inception of the technique, the station coordinate WRMS of DORIS decreased from 30 mm to 5 mm for X and Y components, and 25 mm to 5 mm for Z component; SLR WRMS decreased from 20 mm to better than 10 mm (X, Y, and Z); GNSS WRMS decreased from 4 mm to 1.5 mm (X and Y) and 5 mm to 2 mm (Z); and VLBI showed no significant change.
Author Contributions
J.Z. did conceptualization, methodology, software, writing original draft. C.H. and L.L. designed this research, did review and editing. S.Z. and all the other authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grants 12233010, 11903065).
Data Availability Statement
Space Geodesy solutions can be found at: ftp://gdc.cddis.eosdis.nasa.gov (accessed on 19 March 2024).
Acknowledgments
We appreciate the IGS, ILRS, IVS, and IDS for providing the Space Geodesy solutions. We also thank ITRF for the post-seismic deformation results and discontinuity detection results.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Analysis Center |
| CC | Combination Center |
| CM | Center of Mass |
| DORIS | Doppler Orbitography and Radiopositioning Integrated by Satellite |
| EOP | Earth Orientation Parameter |
| GNSS | Global Navigation Satellite System |
| ITRF | International Terrestrial Reference Frame |
| NNR | No-net-rotation |
| NNT | No-net-translation |
| NNS | No-net-scale |
| PCO | Antenna Phase Center Offset |
| SLR | Satellite Laser Ranging |
| TRF | Terrestrial Reference Frame |
| VLBI | Very Long Baseline Interferometry |
References
- Altamimi, Z.; Rebischung, P.; Metivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Lian, L.-Z.; Wang, J.-X.; Huang, C.-L.; Xu, M.-H. Weekly inter-technique combination of SLR, VLBI, GPS and DORIS at the solution level. Res. Astron. Astrophys. 2018, 18, 119. [Google Scholar] [CrossRef]
- Altamimi, Z.; Métivier, L.; Rebischung, P.; Collilieux, X.; Chanard, K.; Barnéoud, J. ITRF2020 Plate Motion Model. Geophys. Res. Lett. 2023, 50, e2023GL106373. [Google Scholar] [CrossRef]
- Argus, D.F.; Heflin, M.B. Plate motion and crustal deformation estimated with geodetic data from the Global Positioning System. Geophys. Res. Lett. 2012, 22, 1973–1976. [Google Scholar] [CrossRef]
- Gomez, D.D.; Pinon, D.A.; Smalley, R.; Bevis, M.; Cimbaro, S.R.; Lenzano, L.E.; Baron, J. Reference frame access under the effects of great earthquakes: A least squares collocation approach for non-secular post-seismic evolution. J. Geod. 2016, 90, 263–273. [Google Scholar] [CrossRef]
- Xu, C.Y.; Chao, B.F. Seismological versus geodetic reference frames for seismic dislocation: Consistency under momentum conservations. Geophys. J. Int. 2015, 200, 998–1002. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Borsa, A.A.; Agnew, D.C.; Cayan, D.R. Remote Hydrology. Ongoing drought-induced uplift in the western United States. Science 2014, 345, 1587–1590. [Google Scholar] [CrossRef]
- Argus, D.F.; Peltier, W.R.; Watkins, M.M. Glacial isostatic adjustment observed using very long baseline interferometry and satellite laser ranging geodesy. J. Geophys. Res. Solid Earth 1999, 104, 29077–29093. [Google Scholar] [CrossRef]
- Collilieux, X.; Wöppelmann, G. Global sea-level rise and its relation to the terrestrial reference frame. J. Geod. 2010, 85, 9–22. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Liu, P.; Tan, W.; Dong, D.; Qu, W. Comparison and Assessment of Three ITRS Realizations. Remote Sens. 2021, 13, 2304. [Google Scholar] [CrossRef]
- Wu, X.; Abbondanza, C.; Altamimi, Z.; Chin, T.M.; Collilieux, X.; Gross, R.S.; Heflin, M.B.; Jiang, Y.; Parker, J.W. KALREFA Kalman filter and time series approach to the International Terrestrial Reference Frame realization. J. Geophys. Res. Solid Earth 2015, 120, 3775–3802. [Google Scholar] [CrossRef]
- Angermann, D.; Drewes, H.; Seitz, M.; Meisel, B.; Gerstl, M.; Kelm, R.; Müller, H.; Seemüller, W.; Tesmer, V. ITRS Combination Center at DGFI: A Terrestrial Reference Frame Realization 2003; Reihe B: Angewandte Geodäsie, Heft Nr. 313; Deutsche Geodätische Kommission bei der Bayerischen Akademie der Wissenschaften: München, Germany, 2004; pp. 1–141. ISBN 3-7696-8593-8. ISSN 0065-5317.
- Altamimi, Z.; Collilieux, X.; Legrand, J.; Garayt, B.; Boucher, C. ITRF2005: A new release of the International Terrestrial Reference Frame based on time series of station positions and earth orientation parameters. J. Geophys. Res. Solid Earth 2007, 112, 19. [Google Scholar] [CrossRef]
- Villiger, A.; Dach, R. International GNSS Service Technical Report 2019 (IGS Annual Report); IGS Central Bureau and University of Bern: Bern, Switzerland; Bern Open Publishing: Bern, Switzerland, 2020. [Google Scholar]
- Luceri, V.; Pirri, M.; Rodríguez, J.; Appleby, G.; Pavlis, E.C.; Müller, H. Systematic errors in SLR data and their impact on the ILRS products. J. Geod. 2019, 93, 2357–2366. [Google Scholar] [CrossRef]
- Rodríguez, J.; Appleby, G.; Otsubo, T. Upgraded modelling for the determination of centre of mass corrections of geodetic SLR satellites: Impact on key parameters of the terrestrial reference frame. J. Geod. 2019, 93, 2553–2568. [Google Scholar] [CrossRef]
- Appleby, G.; Rodriguez, J.; Altamimi, Z. Assessment of the accuracy of global geodetic satellite laser ranging observations and estimated impact on ITRF scale: Estimation of systematic errors in LAGEOS observations 1993–2014. J. Geod. 2016, 90, 1371–1388. [Google Scholar] [CrossRef]
- Pavlis, E.; Luceri, V.; Basoni, A.; Sarrocco, D.; Kuzmicz-Cieslak, M.; Evans, K.; Bianco, G. ITRF2020: The ILRS Contribution and Operational Implementation. Authorea 2023. [Google Scholar] [CrossRef]
- Hellmers, H.; Modiri, S.; Bachmann, S.; Thaller, D.; Bloßfeld, M.; Seitz, M.; Gipson, J. Combined IVS Contribution to the ITRF2020. In Geodesy for a Sustainable Earth, Proceedings of the 2021 Scientific Assembly of the International Association of Geodesy, Beijing, China, 28 June–2 July 2021; Freymueller, J.T., Sánchez, L., Eds.; Springer: Cham, Switzerland, 2023; pp. 3–13. [Google Scholar]
- Bachmann, S.; Thaller, D.; Roggenbuck, O.; Lösler, M.; Messerschmitt, L. IVS contribution to ITRF2014. J. Geod. 2016, 90, 631–654. [Google Scholar] [CrossRef]
- Moreaux, G.; Lemoine, F.G.; Capdeville, H.; Otten, M.; Štěpánek, P.; Saunier, J.; Ferrage, P. The international DORIS service contribution to ITRF2020. Adv. Space Res. 2023, 72, 65–91. [Google Scholar] [CrossRef]
- Moreaux, G.; Lemoine, F.G.; Capdeville, H.; Kuzin, S.; Otten, M.; Stepanek, P.; Willis, P.; Ferrage, P. The International DORIS Service contribution to the 2014 realization of the International Terrestrial Reference Frame. Adv. Space Res. 2016, 58, 2479–2504. [Google Scholar] [CrossRef]
- Metivier, L.; Altamimi, Z.; Rouby, H. Past and present ITRF solutions from geophysical perspectives. Adv. Space Res. 2020, 65, 2711–2722. [Google Scholar] [CrossRef]
- Belda, S.; Heinkelmann, R.; Ferrandiz, J.M.; Nilsson, T.; Schuh, H. On the consistency of the current conventional EOP series and the celestial and terrestrial reference frames. J. Geod. 2017, 91, 135–149. [Google Scholar] [CrossRef]
- Blewitt, G.; Heflin, M.B.; Webb, F.H.; Lindqwister, U.J.; Malla, R.P. Global coordinates with centimeter accuracy in the International Terrestrial Reference Frame using GPS. Geophys. Res. Lett. 1992, 19, 853–856. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS conventions (2010). Tech. Rep. DTIC Doc. 2010, 36, 180. [Google Scholar]
- Dong, D.; Yunck, T.; Heflin, M. Origin of the International Terrestrial Reference Frame. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Huang, C.; Jin, W.; Xu, H. The terrestrial and lunar reference frame in lunar laser ranging. J. Geod. 1999, 73, 125–129. [Google Scholar] [CrossRef]
- Kwak, Y.; Blossfeld, M.; Schmid, R.; Angermann, D.; Gerstl, M.; Seitz, M. Consistent realization of Celestial and Terrestrial Reference Frames. J. Geod. 2018, 92, 1047–1061. [Google Scholar] [CrossRef]
- Kotsakis, C. Reference frame stability and nonlinear distortion in minimum-constrained network adjustment. J. Geod. 2012, 86, 755–774. [Google Scholar] [CrossRef]
- Davies, P.; Blewitt, G. Methodology for global geodetic time series estimation: A new tool for geodynamics. J. Geophys. Res. Solid Earth 2000, 105, 11083–11100. [Google Scholar] [CrossRef]
- Altamimi, Z.; Sillard, P.; Boucher, C. ITRF2000: A new release of the International Terrestrial Reference frame for earth science applications. J. Geophys. Res. Solid Earth 2002, 107, 19. [Google Scholar] [CrossRef]
- Sillard, P.; Boucher, C. A review of algebraic constraints in terrestrial reference frame datum definition. J. Geod. 2001, 75, 63–73. [Google Scholar] [CrossRef]
- Song, S.Z.; Zhang, Z.K.; Wang, G.L. Toward an Optimal Selection of Constraints for Terrestrial Reference Frame (TRF). Remote Sens. 2022, 14, 1173. [Google Scholar] [CrossRef]
- Abbondanza, C.; Chin, T.M.; Gross, R.S.; Heflin, M.B.; Parker, J.W.; Soja, B.S.; van Dam, T.; Wu, X. JTRF2014, the JPL Kalman filter and smoother realization of the International Terrestrial Reference System. J. Geophys. Res. Solid Earth 2017, 122, 8474–8510. [Google Scholar] [CrossRef]
- Altamimi, Z.; Collilieux, X. IGS contribution to the ITRF. J. Geod. 2009, 83, 375–383. [Google Scholar] [CrossRef]
- Collilieux, X.; Metivier, L.; Altamimi, Z.; van Dam, T.; Ray, J. Quality assessment of GPS reprocessed terrestrial reference frame. Gps Solut. 2011, 15, 219–231. [Google Scholar] [CrossRef]
- Haines, B.J.; Bar-Sever, Y.E.; Bertiger, W.I.; Desai, S.D.; Harvey, N.; Sibois, A.E.; Weiss, J.P. Realizing a terrestrial reference frame using the Global Positioning System. J. Geophys. Res. Solid Earth 2015, 120, 5911–5939. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).