Evaluation and Selection of Multi-Spectral Indices to Classify Vegetation Using Multivariate Functional Principal Component Analysis
Abstract
1. Introduction
- Do supervised hybrid classification approaches based on FDA produce a higher accuracy compared to machine learning methods directly applied to raw multi-temporal data in both test sites?
- Among the examined hybrid approaches, is there one that consistently achieves the highest accuracy in both test sites?
- Among the explored formulas, is there one that consistently produces the highest accuracy in both test sites?
- Can an appropriate set of indices be identified for each study site?
2. Materials and Methods
2.1. Study Area
2.2. Target Classes and Reference Data
2.3. Remote Sensing Data Collection and Generation of Vegetation Indices
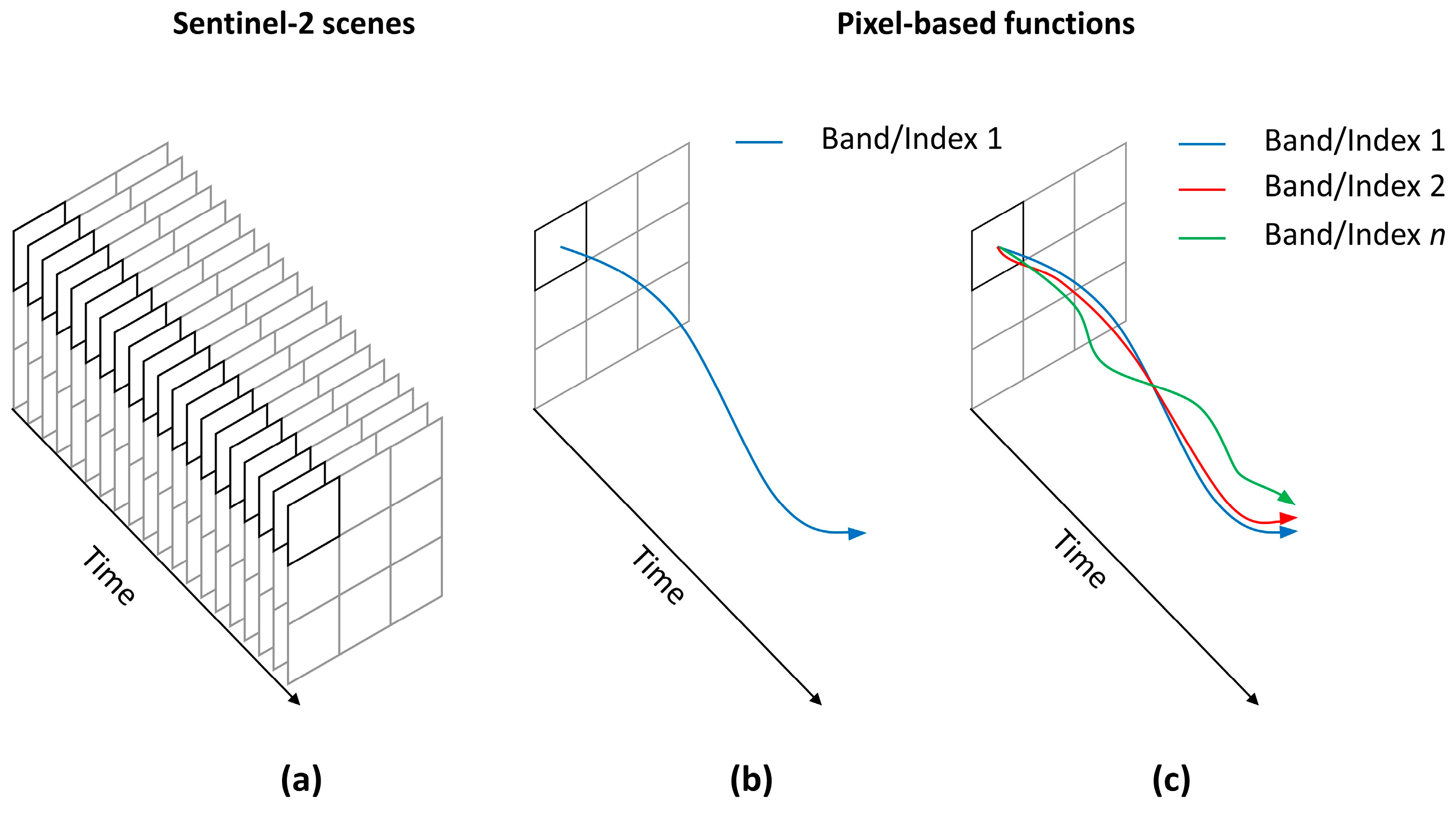
2.4. Time Series as Functional Data
2.5. Analysis of Functional Data Using FPCA and MFPCA
2.6. Random Forest Classifier
2.7. Supervised Classification Approaches
2.7.1. Pure Machine Learning Approach
2.7.2. Hybrid Statistical–Functional–Machine Learning Approach
2.8. Accuracy Evaluation and Models Comparison
3. Results
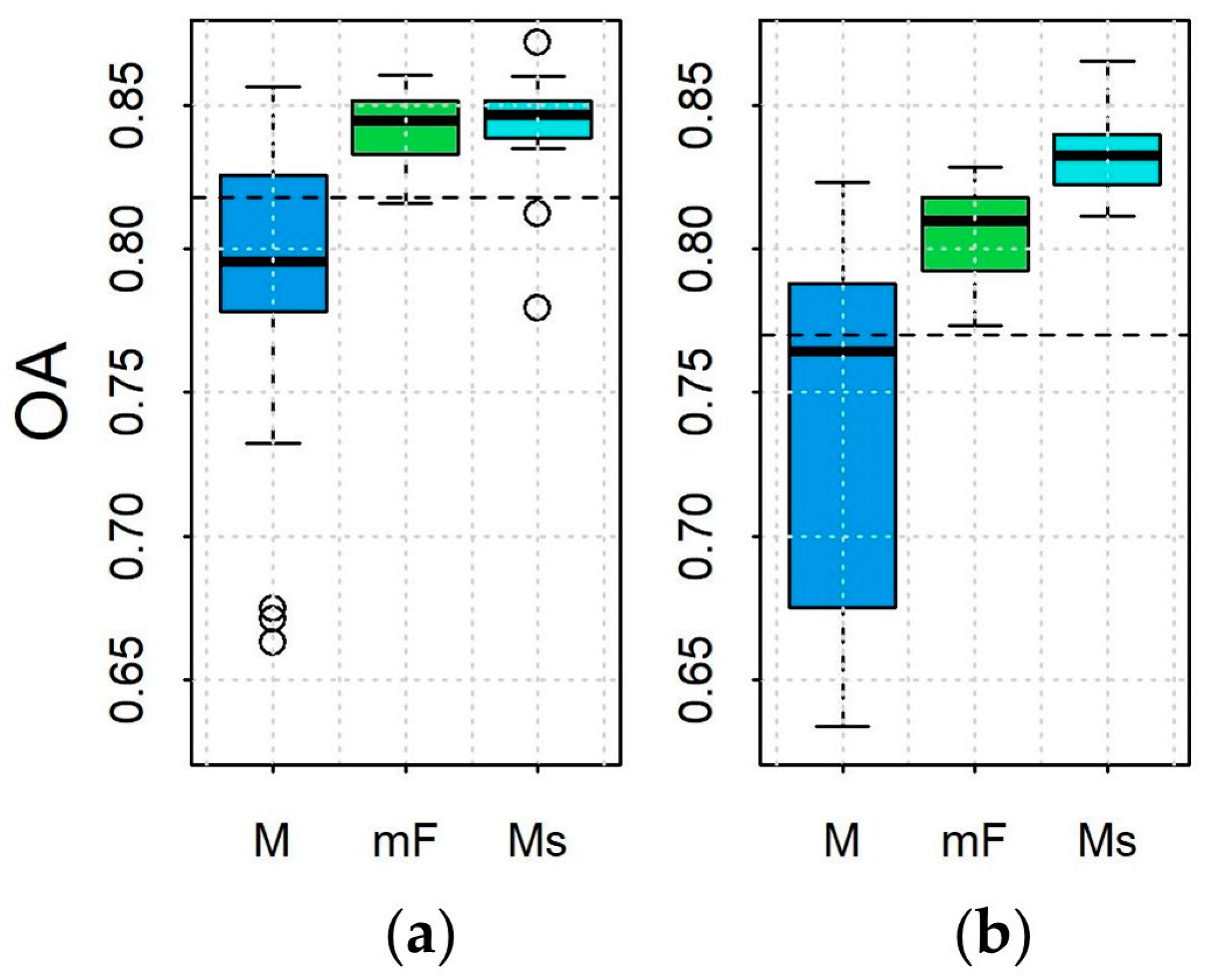
3.1. Models Performance and Comparison
3.2. Best Models
3.2.1. Mount Conero Area
3.2.2. Frasassi Gorge Area
4. Discussion
4.1. Main Results
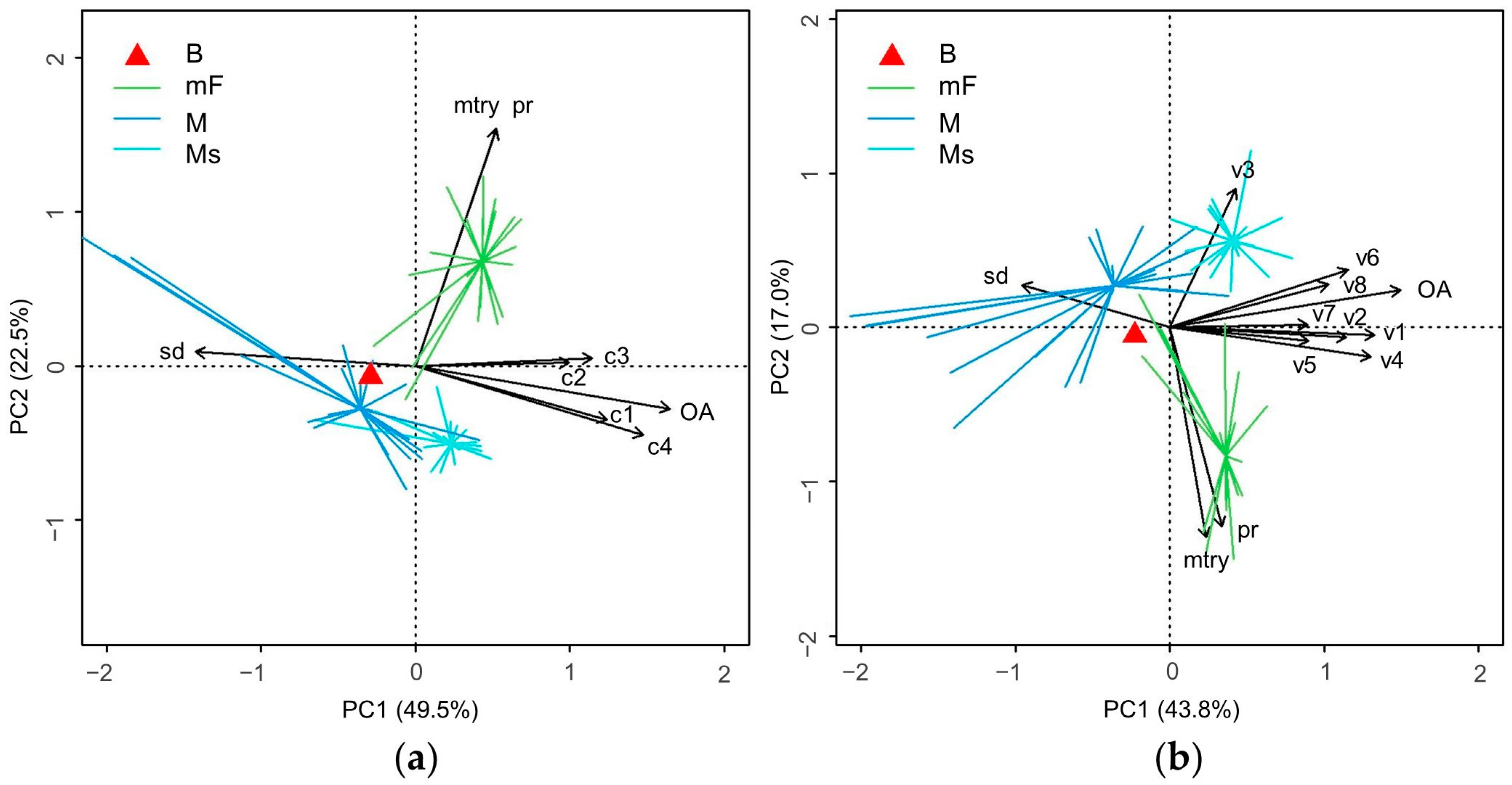
4.2. Models Comparison
4.2.1. Pure Machine Learning Approach: B Models
4.2.2. Hybrid Statistical–Functional–Machine Learning Approach
4.3. Formula Comparison
4.4. Limits and Future Works
5. Conclusions
- The Hybrid supervised classification approaches based on FDA produce higher accuracy than common machine learning methods applied directly to raw multi-temporal data in both test areas.
- Among the hybrid approaches examined, the Ms models achieve the highest accuracy in both test sites. These models effectively combine FDA, by exploiting MFPCA that compresses multiple time series based on different vegetation indices, with the use of RF. Using a forward selection strategy, we identified a limited set of indices that meaningfully represent crucial multispectral seasonal variations obtaining really good results. Ms models are remarkably efficient, producing high accuracies with a low number of input data.
- Among the formulas explored for calculating vegetation indices, the formula id #15 proved to be the best performing one in both study areas. However, other formulas have achieved good results (e.g., formula ids #17, #1), suggesting that further studies could be conducted in different study areas and with more reference data. In general, the use of indices rather than individual bands achieves better results.
- This study demonstrated that Ms models can effectively identify a specific set of indices for each study area, adapting to the ecological characteristics and vegetation of the respective areas.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Num | Date | Doy | Week | Month | Num | Date | Doy | Week | Month |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 April 2017 | 111 | 16 | 4 | 48 | 13 October 2018 | 286 | 41 | 10 |
| 2 | 1 May 2017 | 121 | 18 | 5 | 49 | 12 November 2018 | 316 | 46 | 11 |
| 3 | 31 May 2017 | 151 | 22 | 5 | 50 | 7 December 2018 | 341 | 49 | 12 |
| 4 | 20 June 2017 | 171 | 25 | 6 | 51 | 12 December 2018 | 346 | 50 | 12 |
| 5 | 10 July 2017 | 191 | 28 | 7 | 52 | 27 December 2018 | 361 | 52 | 12 |
| 6 | 20 July 2017 | 201 | 29 | 7 | 53 | 31 January 2019 | 31 | 5 | 1 |
| 7 | 30 July 2017 | 211 | 31 | 7 | 54 | 26 January 2019 | 26 | 4 | 1 |
| 8 | 9 August 2017 | 221 | 32 | 8 | 55 | 5 February 2019 | 36 | 6 | 2 |
| 9 | 19 August 2017 | 231 | 33 | 8 | 56 | 15 February 2019 ** | 46 | 7 | 2 |
| 10 | 29 August 2017 | 241 | 35 | 8 | 57 | 20 February 2019 * | 51 | 8 | 2 |
| 11 | 18 September 2017 | 261 | 38 | 9 | 58 | 25 February 2019 | 56 | 8 | 2 |
| 12 | 8 October 2017 | 281 | 41 | 10 | 59 | 2 March 2019 ** | 61 | 9 | 3 |
| 13 | 18 October 2017 | 291 | 42 | 10 | 60 | 12 March 2019 | 71 | 11 | 3 |
| 14 | 28 October 2017 | 301 | 43 | 10 | 61 | 17 March 2019 | 76 | 11 | 3 |
| 15 | 27 November 2017 | 331 | 48 | 11 | 62 | 22 March 2019 *,** | 81 | 12 | 3 |
| 16 | 7 December 2017 | 341 | 49 | 12 | 63 | 1 April 2019 ** | 91 | 13 | 4 |
| 17 | 22 December 2017 | 356 | 51 | 12 | 64 | 16 April 2019 * | 106 | 16 | 4 |
| 18 | 6 January 2018 | 6 | 1 | 1 | 65 | 31 May 2019 | 151 | 22 | 5 |
| 19 | 15 February 2018 | 46 | 7 | 2 | 66 | 5 June 2019 *,** | 156 | 23 | 6 |
| 20 | 6 April 2018 | 96 | 14 | 4 | 67 | 15 June 2019 | 166 | 24 | 6 |
| 21 | 16 April 2018 | 106 | 16 | 4 | 68 | 25 June 2019 | 176 | 26 | 6 |
| 22 | 21 April 2018 | 111 | 16 | 4 | 69 | 30 June 2019 * | 181 | 26 | 6 |
| 23 | 26 April 2018 | 116 | 17 | 4 | 70 | 5 July 2019 | 186 | 27 | 7 |
| 24 | 11 May 2018 | 131 | 19 | 5 | 71 | 20 July 2019 * | 201 | 29 | 7 |
| 25 | 16 May 2018 | 136 | 20 | 5 | 72 | 25 July 2019 ** | 206 | 30 | 7 |
| 26 | 21 May 2018 | 141 | 21 | 5 | 73 | 30 July 2019 | 211 | 31 | 7 |
| 27 | 31 May 2018 | 151 | 22 | 5 | 74 | 4 August 2019 * | 216 | 31 | 8 |
| 28 | 10 June 2018 | 161 | 23 | 6 | 75 | 9 August 2019 | 221 | 32 | 8 |
| 29 | 15 June 2018 | 166 | 24 | 6 | 76 | 14 August 2019 | 226 | 33 | 8 |
| 30 | 20 June 2018 | 171 | 25 | 6 | 77 | 19 August 2019 ** | 231 | 33 | 8 |
| 31 | 30 June 2018 | 181 | 26 | 6 | 78 | 24 August 2019 | 236 | 34 | 8 |
| 32 | 10 July 2018 | 191 | 28 | 7 | 79 | 29 August 2019 * | 241 | 35 | 8 |
| 33 | 15 July 2018 | 196 | 28 | 7 | 80 | 8 September 2019 | 251 | 36 | 9 |
| 34 | 20 July 2018 | 201 | 29 | 7 | 81 | 13 September 2019 | 256 | 37 | 9 |
| 35 | 25 July 2018 | 206 | 30 | 7 | 82 | 18 September 2019 ** | 261 | 38 | 9 |
| 36 | 30 July 2018 | 211 | 31 | 7 | 83 | 8 October 2019 * | 281 | 41 | 10 |
| 37 | 4 August 2018 | 216 | 31 | 8 | 84 | 23 October 2019 ** | 296 | 43 | 10 |
| 38 | 9 August 2018 | 221 | 32 | 8 | 85 | 7 November 2019 | 311 | 45 | 11 |
| 39 | 19 August 2018 | 231 | 33 | 8 | 86 | 1 January 2020 | 1 | 1 | 1 |
| 40 | 24 August 2018 | 236 | 34 | 8 | 87 | 6 January 2020 | 6 | 1 | 1 |
| 41 | 29 August 2018 | 241 | 35 | 8 | 88 | 5 February 2020 | 36 | 6 | 2 |
| 42 | 3 September 2018 | 246 | 36 | 9 | 89 | 15 February 2020 | 46 | 7 | 2 |
| 43 | 8 September 2018 | 251 | 36 | 9 | 90 | 20 February 2020 | 51 | 8 | 2 |
| 44 | 18 September 2018 | 261 | 38 | 9 | 91 | 11 March 2020 | 71 | 11 | 3 |
| 45 | 23 September 2018 | 266 | 38 | 9 | 92 | 16 March 2020 | 76 | 11 | 3 |
| 46 | 28 September 2018 | 271 | 39 | 9 | 93 | 21 March 2020 | 81 | 12 | 3 |
| 47 | 3 October 2018 | 276 | 40 | 10 |
| Model | Formula | pr | mtry | OA | sd | c1 | c2 | c3 | c4 |
|---|---|---|---|---|---|---|---|---|---|
| B | 0 | 38 | 4 | 0.818 | 0.095 | 0.768 | 0.893 | 0.477 | 0.837 |
| M | 0 | 6 | 1 | 0.812 | 0.076 | 0.692 | 0.901 | 0.538 | 0.844 |
| M | 1 | 2 | 1 | 0.838 | 0.085 | 0.730 | 0.887 | 0.754 | 0.867 |
| M | 2 | 18 | 1 | 0.768 | 0.082 | 0.757 | 0.887 | 0.015 | 0.800 |
| M | 3 | 6 | 1 | 0.825 | 0.076 | 0.654 | 0.941 | 0.462 | 0.878 |
| M | 4 | 34 | 1 | 0.790 | 0.081 | 0.714 | 0.930 | 0.031 | 0.841 |
| M | 5 | 36 | 2 | 0.793 | 0.075 | 0.768 | 0.899 | 0.015 | 0.859 |
| M | 6 | 30 | 5 | 0.675 | 0.092 | 0.400 | 0.893 | 0.138 | 0.704 |
| M | 7 | 26 | 5 | 0.802 | 0.082 | 0.703 | 0.927 | 0.385 | 0.807 |
| M | 8 | 34 | 5 | 0.663 | 0.120 | 0.454 | 0.930 | 0.185 | 0.567 |
| M | 9 | 36 | 3 | 0.797 | 0.091 | 0.703 | 0.935 | 0.262 | 0.807 |
| M | 10 | 14 | 1 | 0.778 | 0.087 | 0.768 | 0.918 | 0.000 | 0.789 |
| M | 11 | 10 | 2 | 0.790 | 0.088 | 0.686 | 0.868 | 0.508 | 0.830 |
| M | 12 | 22 | 3 | 0.732 | 0.088 | 0.708 | 0.882 | 0.000 | 0.730 |
| M | 13 | 10 | 1 | 0.827 | 0.074 | 0.719 | 0.955 | 0.354 | 0.844 |
| M | 14 | 34 | 4 | 0.671 | 0.098 | 0.562 | 0.859 | 0.385 | 0.570 |
| M | 15 | 10 | 3 | 0.856 | 0.072 | 0.762 | 0.938 | 0.615 | 0.870 |
| M | 16 | 6 | 2 | 0.814 | 0.076 | 0.659 | 0.904 | 0.615 | 0.848 |
| M | 17 | 6 | 2 | 0.838 | 0.081 | 0.730 | 0.899 | 0.585 | 0.893 |
| M | 18 | 10 | 2 | 0.829 | 0.081 | 0.714 | 0.913 | 0.492 | 0.878 |
| M | 19 | 18 | 4 | 0.794 | 0.081 | 0.735 | 0.904 | 0.354 | 0.796 |
| M | 20 | 36 | 6 | 0.793 | 0.090 | 0.703 | 0.921 | 0.215 | 0.826 |
| mF | 0 | 46 | 2 | 0.826 | 0.084 | 0.751 | 0.910 | 0.477 | 0.852 |
| mF | 1 | 258 | 11 | 0.816 | 0.082 | 0.714 | 0.893 | 0.492 | 0.863 |
| mF | 2 | 274 | 13 | 0.844 | 0.079 | 0.773 | 0.921 | 0.554 | 0.859 |
| mF | 3 | 290 | 7 | 0.849 | 0.074 | 0.719 | 0.944 | 0.615 | 0.870 |
| mF | 4 | 290 | 7 | 0.857 | 0.070 | 0.746 | 0.938 | 0.631 | 0.881 |
| mF | 5 | 630 | 15 | 0.857 | 0.070 | 0.751 | 0.955 | 0.585 | 0.867 |
| mF | 6 | 674 | 21 | 0.841 | 0.074 | 0.741 | 0.930 | 0.585 | 0.856 |
| mF | 7 | 294 | 15 | 0.854 | 0.066 | 0.724 | 0.924 | 0.738 | 0.878 |
| mF | 8 | 954 | 22 | 0.831 | 0.084 | 0.757 | 0.930 | 0.508 | 0.830 |
| mF | 9 | 818 | 19 | 0.856 | 0.071 | 0.730 | 0.972 | 0.523 | 0.870 |
| mF | 10 | 518 | 21 | 0.835 | 0.077 | 0.757 | 0.907 | 0.554 | 0.863 |
| mF | 11 | 658 | 20 | 0.860 | 0.072 | 0.751 | 0.963 | 0.631 | 0.856 |
| mF | 12 | 910 | 28 | 0.842 | 0.078 | 0.746 | 0.941 | 0.477 | 0.867 |
| mF | 13 | 118 | 2 | 0.828 | 0.084 | 0.703 | 0.907 | 0.631 | 0.859 |
| mF | 14 | 710 | 20 | 0.845 | 0.071 | 0.762 | 0.938 | 0.615 | 0.833 |
| mF | 15 | 634 | 24 | 0.845 | 0.072 | 0.730 | 0.927 | 0.662 | 0.863 |
| mF | 16 | 674 | 11 | 0.833 | 0.088 | 0.724 | 0.907 | 0.600 | 0.867 |
| mF | 17 | 610 | 7 | 0.847 | 0.070 | 0.730 | 0.932 | 0.646 | 0.863 |
| mF | 18 | 610 | 3 | 0.850 | 0.066 | 0.730 | 0.949 | 0.631 | 0.856 |
| mF | 19 | 250 | 6 | 0.852 | 0.077 | 0.735 | 0.944 | 0.600 | 0.870 |
| mF | 20 | 122 | 3 | 0.818 | 0.094 | 0.708 | 0.882 | 0.692 | 0.841 |
| Ms | 0 | 14 | 3 | 0.812 | 0.086 | 0.730 | 0.913 | 0.354 | 0.848 |
| Ms | 1 | 6 | 1 | 0.835 | 0.075 | 0.719 | 0.938 | 0.431 | 0.878 |
| Ms | 2 | 19 | 3 | 0.839 | 0.073 | 0.762 | 0.944 | 0.369 | 0.867 |
| Ms | 3 | 10 | 2 | 0.849 | 0.082 | 0.746 | 0.932 | 0.615 | 0.867 |
| Ms | 4 | 8 | 3 | 0.779 | 0.086 | 0.719 | 0.834 | 0.338 | 0.856 |
| Ms | 5 | 10 | 2 | 0.859 | 0.072 | 0.751 | 0.941 | 0.677 | 0.870 |
| Ms | 6 | 14 | 2 | 0.842 | 0.071 | 0.697 | 0.961 | 0.585 | 0.848 |
| Ms | 7 | 6 | 1 | 0.860 | 0.082 | 0.697 | 0.958 | 0.769 | 0.863 |
| Ms | 8 | 10 | 2 | 0.838 | 0.082 | 0.778 | 0.927 | 0.431 | 0.859 |
| Ms | 9 | 10 | 3 | 0.848 | 0.072 | 0.708 | 0.966 | 0.523 | 0.870 |
| Ms | 10 | 24 | 4 | 0.840 | 0.081 | 0.751 | 0.944 | 0.631 | 0.815 |
| Ms | 11 | 14 | 2 | 0.860 | 0.074 | 0.757 | 0.938 | 0.646 | 0.881 |
| Ms | 12 | 10 | 1 | 0.851 | 0.074 | 0.686 | 0.972 | 0.662 | 0.852 |
| Ms | 13 | 10 | 3 | 0.844 | 0.084 | 0.751 | 0.932 | 0.523 | 0.870 |
| Ms | 14 | 10 | 2 | 0.838 | 0.077 | 0.762 | 0.913 | 0.554 | 0.859 |
| Ms | 15 | 10 | 2 | 0.872 | 0.078 | 0.800 | 0.966 | 0.585 | 0.867 |
| Ms | 16 | 10 | 3 | 0.844 | 0.079 | 0.795 | 0.938 | 0.446 | 0.848 |
| Ms | 17 | 6 | 1 | 0.847 | 0.079 | 0.757 | 0.938 | 0.554 | 0.856 |
| Ms | 18 | 10 | 3 | 0.857 | 0.073 | 0.773 | 0.921 | 0.677 | 0.874 |
| Ms | 19 | 10 | 2 | 0.850 | 0.075 | 0.741 | 0.930 | 0.646 | 0.867 |
| Ms | 20 | 6 | 2 | 0.851 | 0.075 | 0.697 | 0.941 | 0.754 | 0.863 |
| Model | Formula | pr | mtry | OA | sd | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0 | 62 | 3 | 0.770 | 0.071 | 0.829 | 0.507 | 0.804 | 0.910 | 0.313 | 0.707 | 0.813 | 0.922 |
| M | 0 | 26 | 4 | 0.785 | 0.070 | 0.771 | 0.571 | 0.857 | 0.813 | 0.350 | 0.707 | 0.850 | 0.974 |
| M | 1 | 26 | 5 | 0.778 | 0.076 | 0.882 | 0.436 | 0.864 | 0.871 | 0.287 | 0.653 | 0.825 | 0.935 |
| M | 2 | 30 | 5 | 0.675 | 0.083 | 0.676 | 0.371 | 0.696 | 0.794 | 0.550 | 0.600 | 0.775 | 0.791 |
| M | 3 | 30 | 5 | 0.817 | 0.063 | 0.853 | 0.600 | 0.839 | 0.877 | 0.400 | 0.827 | 0.875 | 0.974 |
| M | 4 | 34 | 5 | 0.733 | 0.080 | 0.682 | 0.421 | 0.718 | 0.903 | 0.550 | 0.653 | 0.813 | 0.930 |
| M | 5 | 34 | 5 | 0.731 | 0.079 | 0.700 | 0.529 | 0.721 | 0.826 | 0.525 | 0.707 | 0.800 | 0.883 |
| M | 6 | 34 | 5 | 0.646 | 0.078 | 0.682 | 0.314 | 0.857 | 0.587 | 0.137 | 0.293 | 0.675 | 0.887 |
| M | 7 | 34 | 5 | 0.823 | 0.080 | 0.924 | 0.500 | 0.879 | 0.865 | 0.413 | 0.893 | 0.800 | 0.978 |
| M | 8 | 36 | 6 | 0.644 | 0.081 | 0.618 | 0.300 | 0.893 | 0.613 | 0.187 | 0.093 | 0.588 | 0.948 |
| M | 9 | 22 | 2 | 0.754 | 0.077 | 0.747 | 0.386 | 0.843 | 0.761 | 0.425 | 0.747 | 0.850 | 0.957 |
| M | 10 | 36 | 4 | 0.667 | 0.081 | 0.506 | 0.393 | 0.718 | 0.710 | 0.512 | 0.640 | 0.750 | 0.900 |
| M | 11 | 36 | 6 | 0.708 | 0.075 | 0.712 | 0.164 | 0.768 | 0.839 | 0.463 | 0.680 | 0.775 | 0.952 |
| M | 12 | 36 | 4 | 0.668 | 0.090 | 0.588 | 0.407 | 0.743 | 0.626 | 0.375 | 0.613 | 0.763 | 0.913 |
| M | 13 | 30 | 3 | 0.764 | 0.074 | 0.835 | 0.307 | 0.896 | 0.787 | 0.300 | 0.747 | 0.775 | 0.974 |
| M | 14 | 34 | 3 | 0.634 | 0.072 | 0.659 | 0.179 | 0.882 | 0.690 | 0.050 | 0.053 | 0.838 | 0.870 |
| M | 15 | 30 | 4 | 0.798 | 0.069 | 0.841 | 0.543 | 0.829 | 0.897 | 0.375 | 0.773 | 0.788 | 0.978 |
| M | 16 | 18 | 3 | 0.788 | 0.071 | 0.771 | 0.536 | 0.904 | 0.787 | 0.400 | 0.693 | 0.875 | 0.948 |
| M | 17 | 18 | 2 | 0.810 | 0.071 | 0.812 | 0.521 | 0.843 | 0.839 | 0.562 | 0.893 | 0.825 | 0.978 |
| M | 18 | 18 | 4 | 0.813 | 0.078 | 0.924 | 0.586 | 0.807 | 0.852 | 0.463 | 0.787 | 0.813 | 0.978 |
| M | 19 | 30 | 4 | 0.764 | 0.071 | 0.841 | 0.486 | 0.825 | 0.761 | 0.338 | 0.773 | 0.813 | 0.935 |
| M | 20 | 34 | 4 | 0.786 | 0.070 | 0.771 | 0.493 | 0.861 | 0.890 | 0.325 | 0.760 | 0.800 | 0.978 |
| mF | 0 | 58 | 2 | 0.773 | 0.073 | 0.735 | 0.614 | 0.839 | 0.839 | 0.312 | 0.493 | 0.938 | 0.970 |
| mF | 1 | 250 | 3 | 0.773 | 0.066 | 0.806 | 0.550 | 0.850 | 0.819 | 0.350 | 0.640 | 0.863 | 0.922 |
| mF | 2 | 275 | 16 | 0.816 | 0.067 | 0.924 | 0.571 | 0.814 | 0.903 | 0.613 | 0.680 | 0.813 | 0.948 |
| mF | 3 | 202 | 7 | 0.829 | 0.062 | 0.912 | 0.579 | 0.807 | 0.942 | 0.588 | 0.707 | 0.875 | 0.978 |
| mF | 4 | 550 | 22 | 0.811 | 0.065 | 0.924 | 0.550 | 0.821 | 0.890 | 0.488 | 0.733 | 0.813 | 0.961 |
| mF | 5 | 550 | 9 | 0.819 | 0.073 | 0.935 | 0.600 | 0.821 | 0.890 | 0.525 | 0.720 | 0.813 | 0.952 |
| mF | 6 | 202 | 12 | 0.808 | 0.072 | 0.947 | 0.564 | 0.768 | 0.903 | 0.450 | 0.760 | 0.913 | 0.943 |
| mF | 7 | 606 | 15 | 0.818 | 0.066 | 0.953 | 0.579 | 0.789 | 0.897 | 0.563 | 0.693 | 0.813 | 0.978 |
| mF | 8 | 530 | 2 | 0.816 | 0.065 | 0.894 | 0.500 | 0.893 | 0.884 | 0.350 | 0.707 | 0.938 | 0.970 |
| mF | 9 | 998 | 17 | 0.816 | 0.062 | 0.853 | 0.529 | 0.900 | 0.871 | 0.475 | 0.720 | 0.813 | 0.978 |
| mF | 10 | 470 | 21 | 0.792 | 0.065 | 0.894 | 0.536 | 0.782 | 0.865 | 0.550 | 0.707 | 0.850 | 0.935 |
| mF | 11 | 606 | 12 | 0.825 | 0.065 | 0.912 | 0.536 | 0.882 | 0.890 | 0.500 | 0.707 | 0.813 | 0.978 |
| mF | 12 | 886 | 20 | 0.825 | 0.065 | 0.935 | 0.529 | 0.879 | 0.923 | 0.550 | 0.707 | 0.813 | 0.935 |
| mF | 13 | 498 | 1 | 0.785 | 0.064 | 0.853 | 0.493 | 0.879 | 0.832 | 0.375 | 0.627 | 0.863 | 0.935 |
| mF | 14 | 782 | 26 | 0.798 | 0.071 | 0.947 | 0.571 | 0.786 | 0.871 | 0.350 | 0.720 | 0.875 | 0.948 |
| mF | 15 | 646 | 25 | 0.806 | 0.067 | 0.935 | 0.557 | 0.761 | 0.910 | 0.475 | 0.707 | 0.850 | 0.978 |
| mF | 16 | 470 | 1 | 0.784 | 0.068 | 0.835 | 0.464 | 0.868 | 0.839 | 0.413 | 0.653 | 0.863 | 0.943 |
| mF | 17 | 510 | 10 | 0.813 | 0.066 | 0.906 | 0.600 | 0.786 | 0.903 | 0.500 | 0.693 | 0.875 | 0.978 |
| mF | 18 | 438 | 12 | 0.805 | 0.066 | 0.912 | 0.571 | 0.779 | 0.871 | 0.488 | 0.707 | 0.875 | 0.978 |
| mF | 19 | 202 | 4 | 0.820 | 0.063 | 0.906 | 0.607 | 0.814 | 0.890 | 0.575 | 0.693 | 0.813 | 0.978 |
| mF | 20 | 474 | 6 | 0.789 | 0.067 | 0.788 | 0.557 | 0.846 | 0.858 | 0.338 | 0.707 | 0.925 | 0.952 |
| Ms | 0 | 22 | 3 | 0.812 | 0.076 | 0.865 | 0.586 | 0.821 | 0.839 | 0.625 | 0.733 | 0.813 | 0.970 |
| Ms | 1 | 22 | 4 | 0.845 | 0.065 | 0.929 | 0.550 | 0.839 | 0.923 | 0.663 | 0.827 | 0.825 | 0.987 |
| Ms | 2 | 26 | 1 | 0.824 | 0.073 | 0.924 | 0.471 | 0.893 | 0.884 | 0.475 | 0.840 | 0.925 | 0.922 |
| Ms | 3 | 18 | 2 | 0.829 | 0.075 | 0.953 | 0.543 | 0.839 | 0.942 | 0.713 | 0.693 | 0.762 | 0.930 |
| Ms | 4 | 22 | 1 | 0.832 | 0.081 | 0.912 | 0.579 | 0.871 | 0.910 | 0.425 | 0.800 | 0.863 | 0.970 |
| Ms | 5 | 14 | 2 | 0.842 | 0.070 | 0.924 | 0.714 | 0.846 | 0.813 | 0.587 | 0.773 | 0.863 | 0.978 |
| Ms | 6 | 22 | 4 | 0.815 | 0.065 | 0.941 | 0.464 | 0.814 | 0.903 | 0.437 | 0.813 | 0.925 | 0.970 |
| Ms | 7 | 18 | 3 | 0.836 | 0.065 | 0.971 | 0.514 | 0.868 | 0.890 | 0.525 | 0.867 | 0.775 | 0.974 |
| Ms | 8 | 34 | 3 | 0.840 | 0.075 | 0.900 | 0.679 | 0.879 | 0.897 | 0.437 | 0.733 | 0.925 | 0.952 |
| Ms | 9 | 18 | 1 | 0.840 | 0.060 | 0.906 | 0.486 | 0.936 | 0.806 | 0.437 | 0.973 | 0.875 | 1.000 |
| Ms | 10 | 18 | 2 | 0.811 | 0.071 | 0.959 | 0.579 | 0.846 | 0.852 | 0.400 | 0.747 | 0.825 | 0.930 |
| Ms | 11 | 22 | 2 | 0.828 | 0.075 | 0.853 | 0.450 | 0.893 | 0.935 | 0.625 | 0.787 | 0.813 | 0.978 |
| Ms | 12 | 18 | 2 | 0.814 | 0.087 | 0.900 | 0.529 | 0.843 | 0.890 | 0.437 | 0.907 | 0.813 | 0.939 |
| Ms | 13 | 22 | 4 | 0.833 | 0.074 | 0.924 | 0.600 | 0.864 | 0.865 | 0.538 | 0.787 | 0.813 | 0.970 |
| Ms | 14 | 22 | 3 | 0.840 | 0.074 | 0.865 | 0.664 | 0.868 | 0.897 | 0.525 | 0.840 | 0.888 | 0.948 |
| Ms | 15 | 22 | 3 | 0.865 | 0.070 | 0.953 | 0.586 | 0.921 | 0.935 | 0.575 | 0.773 | 0.888 | 0.978 |
| Ms | 16 | 22 | 4 | 0.828 | 0.064 | 0.906 | 0.493 | 0.896 | 0.845 | 0.425 | 0.880 | 0.900 | 0.974 |
| Ms | 17 | 22 | 4 | 0.856 | 0.055 | 1.000 | 0.550 | 0.893 | 0.910 | 0.550 | 0.827 | 0.838 | 0.978 |
| Ms | 18 | 22 | 2 | 0.835 | 0.055 | 0.953 | 0.457 | 0.889 | 0.910 | 0.613 | 0.827 | 0.838 | 0.943 |
| Ms | 19 | 26 | 4 | 0.811 | 0.063 | 0.894 | 0.493 | 0.864 | 0.890 | 0.425 | 0.773 | 0.863 | 0.957 |
| Ms | 20 | 22 | 2 | 0.822 | 0.064 | 0.747 | 0.621 | 0.929 | 0.865 | 0.550 | 0.707 | 0.763 | 1.000 |
References
- The Habitats Directive. Council Directive 92/43/EEC of 21 May 1992 on the Conservation of Natural Habitats and of Wild Fauna and Flora. Off. J. L 1992, 206, 7–50. [Google Scholar]
- Evans, D. The Habitats of the European Union Habitats Directive. Biol. Environ. Proc. R. Irish Acad. 2006, 106B, 167–173. [Google Scholar] [CrossRef]
- Corbane, C.; Lang, S.; Pipkins, K.; Alleaume, S.; Deshayes, M.; García Millán, V.E.; Strasser, T.; Vanden Borre, J.; Toon, S.; Michael, F. Remote Sensing for Mapping Natural Habitats and Their Conservation Status—New Opportunities and Challenges. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 7–16. [Google Scholar] [CrossRef]
- Vanden Borre, J.; Paelinckx, D.; Mücher, C.A.; Kooistra, L.; Haest, B.; De Blust, G.; Schmidt, A.M. Integrating Remote Sensing in Natura 2000 Habitat Monitoring: Prospects on the Way Forward. J. Nat. Conserv. 2011, 19, 116–125. [Google Scholar] [CrossRef]
- Schmidt, T.; Schuster, C.; Kleinschmit, B.; Förster, M. Evaluating an Intra-Annual Time Series for Grassland Classification—How Many Acquisitions and What Seasonal Origin Are Optimal? IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3428–3439. [Google Scholar] [CrossRef]
- Rapinel, S.; Rozo, C.; Delbosc, P.; Bioret, F.; Bouzillé, J.B.; Hubert-Moy, L. Contribution of Free Satellite Time-Series Images to Mapping Plant Communities in the Mediterranean Natura 2000 Site: The Example of Biguglia Pond in Corse (France). Mediterr. Bot. 2020, 41, 181–191. [Google Scholar] [CrossRef]
- Marzialetti, F.; Giulio, S.; Malavasi, M.; Sperandii, M.G.; Acosta, A.T.R.; Carranza, M.L. Capturing Coastal Dune Natural Vegetation Types Using a Phenology-Based Mapping Approach: The Potential of Sentinel-2. Remote Sens. 2019, 11, 1506. [Google Scholar] [CrossRef]
- Bajocco, S.; Ferrara, C.; Alivernini, A.; Bascietto, M.; Ricotta, C. Remotely-Sensed Phenology of Italian Forests: Going beyond the Species. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 314–321. [Google Scholar] [CrossRef]
- Grignetti, A.; Salvatori, R.; Casacchia, R.; Manes, F. Mediterranean Vegetation Analysis by Multi-Temporal Satellite Sensor Data. Int. J. Remote Sens. 1997, 18, 1307–1318. [Google Scholar] [CrossRef]
- Marzialetti, F.; Di Febbraro, M.; Malavasi, M.; Giulio, S.; Acosta, A.T.R.; Carranza, M.L. Mapping Coastal Dune Landscape through Spectral Rao’s Q Temporal Diversity. Remote Sens. 2020, 12, 2315. [Google Scholar] [CrossRef]
- Sittaro, F.; Hutengs, C.; Semella, S.; Vohland, M. A Machine Learning Framework for the Classification of Natura 2000 Habitat Types at Large Spatial Scales Using MODIS Surface Reflectance Data. Remote Sens. 2022, 14, 823. [Google Scholar] [CrossRef]
- Mahmud, S.; Redowan, M.; Ahmed, R.; Khan, A.A.; Rahman, M.M. Phenology-Based Classification of Sentinel-2 Data to Detect Coastal Mangroves. Geocarto Int. 2022, 37, 14335–14354. [Google Scholar] [CrossRef]
- Raab, C.; Stroh, H.G.; Tonn, B.; Meißner, M.; Rohwer, N.; Balkenhol, N.; Isselstein, J. Mapping Semi-Natural Grassland Communities Using Multi-Temporal RapidEye Remote Sensing Data. Int. J. Remote Sens. 2018, 39, 5638–5659. [Google Scholar] [CrossRef]
- Hubert-Moy, L.; Fabre, E.; Rapinel, S. Contribution of SPOT-7 Multi-Temporal Imagery for Mapping Wetland Vegetation. Eur. J. Remote Sens. 2020, 53, 201–210. [Google Scholar] [CrossRef]
- Jarocińska, A.; Kopeć, D.; Niedzielko, J.; Wylazłowska, J.; Halladin-Dąbrowska, A.; Charyton, J.; Piernik, A.; Kamiński, D. The Utility of Airborne Hyperspectral and Satellite Multispectral Images in Identifying Natura 2000 Non-Forest Habitats for Conservation Purposes. Sci. Rep. 2023, 13, 4549. [Google Scholar] [CrossRef] [PubMed]
- Tarantino, C.; Forte, L.; Blonda, P.; Vicario, S.; Tomaselli, V.; Beierkuhnlein, C.; Adamo, M. Intra-Annual Sentinel-2 Time-Series Supporting Grassland Habitat Discrimination. Remote Sens. 2021, 13, 277. [Google Scholar] [CrossRef]
- Buck, O.; Millán, V.E.G.; Klink, A.; Pakzad, K. Using Information Layers for Mapping Grassland Habitat Distribution at Local to Regional Scales. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 83–89. [Google Scholar] [CrossRef]
- Rapinel, S.; Mony, C.; Lecoq, L.; Clément, B.; Thomas, A.; Hubert-Moy, L. Evaluation of Sentinel-2 Time-Series for Mapping Floodplain Grassland Plant Communities. Remote Sens. Environ. 2019, 223, 115–129. [Google Scholar] [CrossRef]
- Durell, L.; Scott, J.T.; Hering, A.S. Hybrid Forecasting for Functional Time Series of Dissolved Oxygen Profiles. Data Sci. Sci. 2023, 2, 2152401. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A Commentary Review on the Use of Normalized Difference Vegetation Index (NDVI) in the Era of Popular Remote Sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Vanden Borre, J.; Spanhove, T.; Haest, B. Towards a Mature Age of Remote Sensing for Natura 2000 Habitat Conservation: Poor Method Transferability as a Prime Obstacle. In The Roles of Remote Sensing in Nature Conservation; Springer International Publishing: Cham, Switzerland, 2017; pp. 11–37. [Google Scholar]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Fatima, N.; Javed, A. Assessment of Land Use Land Cover Change Detection Using Geospatial Techniques in Southeast Rajasthan. J. Geosci. Environ. Prot. 2021, 9, 299–319. [Google Scholar] [CrossRef]
- Barrett, B.; Raab, C.; Cawkwell, F.; Green, S. Upland Vegetation Mapping Using Random Forests with Optical and Radar Satellite Data. Remote Sens. Ecol. Conserv. 2016, 2, 212–231. [Google Scholar] [CrossRef] [PubMed]
- Nagendra, H.; Lucas, R.; Honrado, J.P.; Jongman, R.H.G.; Tarantino, C.; Adamo, M.; Mairota, P. Remote Sensing for Conservation Monitoring: Assessing Protected Areas, Habitat Extent, Habitat Condition, Species Diversity, and Threats. Ecol. Indic. 2013, 33, 45–59. [Google Scholar] [CrossRef]
- Pasquarella, V.J.; Holden, C.E.; Kaufman, L.; Woodcock, C.E. From Imagery to Ecology: Leveraging Time Series of All Available Landsat Observations to Map and Monitor Ecosystem State and Dynamics. Remote Sens. Ecol. Conserv. 2016, 2, 152–170. [Google Scholar] [CrossRef]
- Gillanders, S.N.; Coops, N.C.; Wulder, M.A.; Gergel, S.E.; Nelson, T. Multitemporal Remote Sensing of Landscape Dynamics and Pattern Change: Describing Natural and Anthropogenic Trends. Prog. Phys. Geogr. Earth Environ. 2008, 32, 503–528. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis; Ramsay, R., Silverman, B., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 2005; ISBN 978-0-387-40080-8. [Google Scholar]
- Pesaresi, S.; Mancini, A.; Quattrini, G.; Casavecchia, S. Functional Analysis for Habitat Mapping in a Special Area of Conservation Using Sentinel-2 Time-Series Data. Remote Sens. 2022, 14, 1179. [Google Scholar] [CrossRef]
- Pesaresi, S.; Mancini, A.; Quattrini, G.; Casavecchia, S. Mapping Mediterranean Forest Plant Associations and Habitats with Functional Principal Component Analysis Using Landsat 8 NDVI Time Series. Remote Sens. 2020, 12, 1132. [Google Scholar] [CrossRef]
- Coviello, L.; Martini, F.M.; Cesaretti, L.; Pesaresi, S.; Solfanelli, F.; Mancini, A. Clustering of Remotely Sensed Time Series Using Functional Principal Component Analysis to Monitor Crops. In Proceedings of the 2022 IEEE Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Perugia, Italy, 3–5 November 2022; pp. 141–145. [Google Scholar]
- Hurley, M.A.; Hebblewhite, M.; Gaillard, J.; Dray, S.; Taylor, K.A.; Smith, W.K.; Zager, P.; Bonenfant, C. Functional Analysis of Normalized Difference Vegetation Index Curves Reveals Overwinter Mule Deer Survival Is Driven by Both Spring and Autumn Phenology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130196. [Google Scholar] [CrossRef]
- Pesaresi, S.; Mancini, A.; Casavecchia, S. Recognition and Characterization of Forest Plant Communities through Remote-Sensing NDVI Time Series. Diversity 2020, 12, 313. [Google Scholar] [CrossRef]
- Ramsay, J.O. When the Data Are Functions. Psychometrika 1982, 47, 379–396. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Andréfouët, S.; Cohen, W.B.; Gómez, C.; Griffiths, P.; Hais, M.; Healey, S.P.; Helmer, E.H.; Hostert, P.; Lyons, M.B.; et al. Bringing an Ecological View of Change to Landsat-Based Remote Sensing. Front. Ecol. Environ. 2014, 12, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Levitin, D.J.; Nuzzo, R.L.; Vines, B.; Ramsay, J.O. Introduction to Functional Data Analysis. Can. Psychol. 2007, 48, 135–155. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Dalzell, C.J. Some Tools for Functional Data Analysis. J. R. Stat. Soc. Ser. B 1991, 53, 539–572. [Google Scholar] [CrossRef]
- Happ, C.; Greven, S. Multivariate Functional Principal Component Analysis for Data Observed on Different (Dimensional) Domains. J. Am. Stat. Assoc. 2018, 113, 649–659. [Google Scholar] [CrossRef]
- Wang, J.-L.; Chiou, J.-M.; Müller, H.-G. Functional Data Analysis. Annu. Rev. Stat. Its Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef]
- Geobotanic Group at Università Politecnica delle Marche. Dataset and R Code Related to the Habitat Mapping with Functional Hybrid Machine Learning. Available online: https://github.com/geobotany (accessed on 15 January 2024).
- Rivas-Martínez, S.; Sáenz, S.R.; Penas, A. Worldwide Bioclimatic Classification System. Glob. Geobot. 2011, 1, 1–634. [Google Scholar]
- Pesaresi, S.; Biondi, E.; Casavecchia, S. Bioclimates of Italy. J. Maps 2017, 13, 955–960. [Google Scholar] [CrossRef]
- Biondi, E.; Casavecchia, S.; Gigante, D. Contribution to the Syntaxonomic Knowledge of the Quercus Ilex L. Woods of the Central European Mediterranean Basin. Fitosociologia 2003, 40, 129–156. [Google Scholar]
- Biondi, E.; Gubellini, L.; Pinzi, M.; Casavecchia, S. The Vascular Flora of Conero Regional Nature Park (Marche, Central Italy). Flora Mediterr. 2012, 22, 67–167. [Google Scholar] [CrossRef]
- Biondi, E. L’ostrya Carpinifolia Scop. Sul Litorale Delle Marche (Italia Centrale). Stud. Geobot. 1982, 2, 141–147. [Google Scholar]
- Baiocco, M.; Casavecchia, S.; Biondi, E.; Pietracapina, A. Indagini Geobotaniche per Il Recupero Del Rimboschimento Del Monte Conero (Italia Centrale). Doc. Phytosociol. 1996, 16, 387–425. [Google Scholar]
- Blasi, C.; Di Pietro, R.; Filesi, L. Syntaxonomical Revision of Quercetalia Pubescenti-Petraeae in the Italian Peninsula. Fitosociologia 2004, 41, 87–164. [Google Scholar]
- Blasi, C.; Feoli, E.; Avena, G.C. Due Nuove Associazioni Dei Quercetalia Pubescentis Dell’Appennino Centrale. Stud. Geobot. 1982, 2, 155–167. [Google Scholar]
- Pedrotti, F.; Ballelli, S.; Biondi, E.; Cortini Pedrotti, C.; Orsomando, E. Resoconto Dell’escursione Della Società Italiana Di Fitosociologia Nelle Marche Ed in Umbria (11–14 Giugno 1979). Not. Fitosociologico 1980, 16, 73–75. [Google Scholar]
- Allegrezza, M.; Pesaresi, S.; Ballelli, S.; Tesei, G.; Ottaviani, C. Influences of Mature Pinus Nigra Plantations on the Floristic-Vegetational Composition along an Altitudinal Gradient in the Central Apennines, Italy. iForest 2020, 13, 279–285. [Google Scholar] [CrossRef]
- Biondi, E.; Casavecchia, S. Inquadramento Fitosociologico Della Vegetazione Arbustiva Di Un Settore Dell’Appennino Settentrionale. Fitosociologia 2002, 39, 65–73. [Google Scholar]
- Biondi, E.; Allegrezza, M.; Zuccarello, V. Syntaxonomic Revision of the Apennine Grasslands Belonging to Brometalia Erecti, and an Analysis of Their Relationships with the Xerophilous Vegetation of Rosmarinetea Officinalis (Italy). Phytocoenologia 2005, 35, 129–164. [Google Scholar] [CrossRef]
- Allegrezza, M.; Biondi, E.; Ballelli, S.; Formica, E. La Vegetazione Dei Settori Rupestri Calcarei Dell’Italia Centrale. Fitosociologia 1997, 32, 91–120. [Google Scholar]
- Ranghetti, L.; Boschetti, M.; Nutini, F.; Busetto, L. “Sen2r”: An R Toolbox for Automatically Downloading and Preprocessing Sentinel-2 Satellite Data. Comput. Geosci. 2020, 139, 104473. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical Vegetation Indices for Monitoring Terrestrial Ecosystems Globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- ESA. Sentinel-2 User Handbook. Available online: https://sentinel.esa.int/documents/247904/685211/sentinel-2_user_handbook (accessed on 15 January 2024).
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green Leaf Phenology at Landsat Resolution: Scaling from the Field to the Satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
- Schuster, C.; Schmidt, T.; Conrad, C.; Kleinschmit, B.; Förster, M. Grassland habitat mapping by intra-annual time series analysis—Comparison of RapidEye and TerraSAR-X satellite data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 25–34. [Google Scholar] [CrossRef]
- Lambert, J.; Drenou, C.; Denux, J.; Balent, G.; Cheret, V. Monitoring Forest Decline through Remote Sensing Time Series Analysis. GISci. Remote Sens. 2013, 50, 437–457. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting Functions for Time Series and Linear Models. R Package Version 8.6. Available online: https://cran.r-project.org/package=forecast (accessed on 3 August 2020).
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The Forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC: New York, NY, USA, 2017; ISBN 9781315370279. [Google Scholar]
- Younes, N.; Joyce, K.E.; Maier, S.W. All Models of Satellite-Derived Phenology Are Wrong, but Some Are Useful: A Case Study from Northern Australia. Int. J. Appl. Earth Obs. Geoinf. 2021, 97, 102285. [Google Scholar] [CrossRef]
- Di Salvo, F.; Ruggieri, M.; Plaia, A. Functional Principal Component Analysis for Multivariate Multidimensional Environmental Data. Environ. Ecol. Stat. 2015, 22, 739–757. [Google Scholar] [CrossRef]
- Dai, X.; Hadjipantelis, P.Z.; Han, K.; Ji, H. Fdapace: Functional Data Analysis and Empirical Dynamics. R Package Version 0.5.5. Available online: https://cran.r-project.org/package=fdapace (accessed on 3 August 2020).
- Happ-Kurz, C. MFPCA: Multivariate Functional Principal Component Analysis for Data Observed on Different Dimensional Domains. R Package Version 1.3-6. Available online: https://cran.r-project.org/web/packages/MFPCA/index.html (accessed on 22 March 2022).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Evans, J.S.; Cushman, S.A. Gradient Modeling of Conifer Species Using Random Forests. Landsc. Ecol. 2009, 24, 673–683. [Google Scholar] [CrossRef]
- Le Dez, M.; Robin, M.; Launeau, P. Contribution of Sentinel-2 Satellite Images for Habitat Mapping of the Natura 2000 Site ‘Estuaire de La Loire’ (France). Remote Sens. Appl. Soc. Environ. 2021, 24, 100637. [Google Scholar] [CrossRef]
- Marcinkowska-Ochtyra, A.; Ochtyra, A.; Raczko, E.; Kopeć, D. Natura 2000 Grassland Habitats Mapping Based on Spectro-Temporal Dimension of Sentinel-2 Images with Machine Learning. Remote Sens. 2023, 15, 1388. [Google Scholar] [CrossRef]
- Wakulińska, M.; Marcinkowska-Ochtyra, A. Multi-Temporal Sentinel-2 Data in Classification of Mountain Vegetation. Remote Sens. 2020, 12, 2696. [Google Scholar] [CrossRef]
- Congalton, R.G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Pham-Duc, B.; Nguyen, H.; Phan, H.; Tran-Anh, Q. Trends and Applications of Google Earth Engine in Remote Sensing and Earth Science Research: A Bibliometric Analysis Using Scopus Database. Earth Sci. Inform. 2023, 16, 2355–2371. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the Satellite-Derived NDVI to Assess Ecological Responses to Environmental Change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest Stand Species Mapping Using the Sentinel-2 Time Series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation Phenology from Sentinel-2 and Field Cameras for a Dutch Barrier Island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]
- Pasquarella, V.J.; Holden, C.E.; Woodcock, C.E. Improved Mapping of Forest Type Using Spectral-Temporal Landsat Features. Remote Sens. Environ. 2018, 210, 193–207. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Sirjacobs, D.; Barth, A.; Beckers, J.-M. Outlier Detection in Satellite Data Using Spatial Coherence. Remote Sens. Environ. 2012, 119, 84–91. [Google Scholar] [CrossRef]
- Balestra, M.; Pierdicca, R.; Cesaretti, L.; Quattrini, G.; Mancini, A.; Galli, A.; Malinverni, E.S.; Casavecchia, S.; Pesaresi, S. A comparison of pre-processing approaches for remotely sensed time series classification based on functional analysis. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023. [Google Scholar] [CrossRef]
- Liu, C.; Ray, S.; Hooker, G.; Friedl, M. Functional Factor Analysis for Periodic Remote Sensing Data. Ann. Appl. Stat. 2012, 6, 601–624. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Forster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of Feature Reduction Algorithms for Classifying Tree Species with Hyperspectral Data on Three Central European Test Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Saini, R.; Ghosh, S.K. Analyzing the Impact of Red-Edge Band on Land Use Land Cover Classification Using Multispectral RapidEye Imagery and Machine Learning Techniques. J. Appl. Remote Sens. 2019, 13, 044511. [Google Scholar] [CrossRef]
- Schuster, C.; Förster, M.; Kleinschmit, B. Testing the Red Edge Channel for Improving Land-Use Classifications Based on High-Resolution Multi-Spectral Satellite Data. Int. J. Remote Sens. 2012, 33, 5583–5599. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Meyer, G.E.; Neto, J.C. Verification of Color Vegetation Indices for Automated Crop Imaging Applications. Comput. Electron. Agric. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Alcaraz-Segura, D.; Cabello, J.; Paruelo, J. Baseline Characterization of Major Iberian Vegetation Types Based on the NDVI Dynamics. Plant Ecol. 2009, 202, 13–29. [Google Scholar] [CrossRef]
- Saini, R. Integrating Vegetation Indices and Spectral Features for Vegetation Mapping from Multispectral Satellite Imagery Using AdaBoost and Random Forest Machine Learning Classifiers. Geomat. Environ. Eng. 2022, 17, 57–74. [Google Scholar] [CrossRef]
- Illarionova, S.; Shadrin, D.; Trekin, A.; Ignatiev, V.; Oseledets, I. Generation of the NIR Spectral Band for Satellite Images with Convolutional Neural Networks. Sensors 2021, 21, 5646. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Jo, P. A Simple Method for Reconstructing a High-Quality NDVI Time-Series Data Set Based on the Savitzky–Golay Filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.; Jing, Y.; Yin, H.; Li, X.; Guan, X. High-Quality Vegetation Index Product Generation: A Review of NDVI Time Series Reconstruction Techniques. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102640. [Google Scholar] [CrossRef]
- Marcinkowska-Ochtyra, A.; Gryguc, K.; Ochtyra, A.; Kopeć, D.; Jarocińska, A.; Sławik, Ł. Multitemporal Hyperspectral Data Fusion with Topographic Indices—Improving Classification of Natura 2000 Grassland Habitats. Remote Sens. 2019, 11, 2264. [Google Scholar] [CrossRef]
- Tuia, D.; Persello, C.; Bruzzone, L. Domain Adaptation for the Classification of Remote Sensing Data: An Overview of Recent Advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Piel, A.K.; Crunchant, A.; Knot, I.E.; Chalmers, C.; Fergus, P.; Mulero-Pázmány, M.; Wich, S.A. Noninvasive Technologies for Primate Conservation in the 21st Century. Int. J. Primatol. 2022, 43, 133–167. [Google Scholar] [CrossRef]
- Suir, G.; Saltus, C.; Sasser, C.; Harris, J.; Reif, M.; Diaz, R.; Giffin, G. Evaluating Drone Truthing as an Alternative to Ground Truthing: An Example with Wetland Plant Identification; Engineer Research and Development Center (U.S.): Vicksburg, MS, USA, 2021. [Google Scholar]
- Szantoi, Z.; Smith, S.E.; Strona, G.; Koh, L.P.; Wich, S.A.; Szantoi, Z.; Smith, S.E.; Strona, G.; Koh, L.P.; Serge, A. Mapping Orangutan Habitat and Agricultural Areas Using Landsat OLI Imagery Augmented with Unmanned Aircraft System Aerial Photography. Int. J. Remote Sens. 2017, 38, 2231–2245. [Google Scholar] [CrossRef]
- Wich, S.A.; Koh, L.P. Conservation Drones: Mapping and Monitoring Biodiversity; Oxford University Press: Oxford, UK, 2018; pp. 51–54. [Google Scholar]
- Onishi, M.; Ise, T. Explainable Identification and Mapping of Trees Using UAV RGB Image and Deep Learning. Sci. Rep. 2021, 11, 903. [Google Scholar] [CrossRef]
- Gigante, D.; Attorre, F.; Venanzoni, R.; Acosta, A.T.R.; Agrillo, E.; Aleffi, M.; Alessi, N.; Allegrezza, M.; Angelini, P.; Angiolini, C.; et al. A Methodological Protocol for Annex I Habitats Monitoring: The Contribution of Vegetation Science. Plant Sociol. 2016, 53, 77–87. [Google Scholar] [CrossRef]
- Correll, M.D.; Hantson, W.; Hodgman, T.P.; Cline, B.B.; Elphick, C.S.; Gregory Shriver, W.; Tymkiw, E.L.; Olsen, B.J. Fine-Scale Mapping of Coastal Plant Communities in the Northeastern USA. Wetlands 2019, 39, 17–28. [Google Scholar] [CrossRef]
- Epifanio, I.; Ventura-Campos, N. Hippocampal Shape Analysis in Alzheimer’s Disease Using Functional Data Analysis. Stat. Med. 2014, 33, 867–880. [Google Scholar] [CrossRef] [PubMed]
- Ramsay, J.O.; Silverman, B.W. Applied Functional Data Analysis: Methods and Case Studies; Ramsay, J.O., Silverman, B.W., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 2002; Volume 45, ISBN 978-0-387-95414-1. [Google Scholar]



| Class | Plant Association (Syntaxa) | Habitat Code | Plots |
|---|---|---|---|
| Mount Conero area | 172 | ||
| Woods | |||
| c1 | Quercus ilex evergreen forest with a high occurrence of Mediterranean species Cyclamino hederifolii-Quercetum ilicis [43]. | 9340 | 34 |
| c2 | Quercus ilex with deciduous trees mixed forest Cephalanthero longifoliae-Quercetum ilicis subass. ruscetosum hypoglossy [43]. | 9340 | 71 |
| c3 | Ostrya carpinifolia coastal deciduous forest Asparago acutifolii–Ostryetum carpinifoliae [44,45]. | - | 13 |
| c4 | Evergreen conifer forest plantations mostly dominated by Pinus halepensis and P. pinea [46]. | - | 54 |
| Frasassi Gorge area | 241 | ||
| Woods | |||
| v1 | Quercus ilex (with deciduous trees) appenninic forest Cephalanthero longifoliae-Quercetum ilicis subass. lathyretosum veneti [43]. | 9340 | 34 |
| v2 | Quercus pubescens deciduous forest—Cytiso sessilifolii-Quercetum pubescentis [47,48]. | 91AA * | 28 |
| v3 | Ostrya carpinifolia deciduous appenninic forest—Scutellario columnae-Ostryetum carpinifoliae [49]. | - | 56 |
| v4 | Evergreen conifer forest plantations mostly dominated Pinus nigra ssp. nigra and P. halepensis Mill. [50]. | - | 31 |
| Shrublands | |||
| v5 | Spartium junceum Shrub—Spartio juncei-Cytisetum sessilifolii Spartium junceum variant (Edoardo Biondi & Casavecchia, 2002). | - | 16 |
| v6 | Junyperus oxycedrus shrub—Spartio juncei-Cytisetum sessilifolii Juniperus oxycedrus variant [51]. | - | 15 |
| Grasslands | |||
| v7 | Bromus erectus grassland—Asperulo purpureae-Brometum erecti [52]. | 6210 * | 16 |
| Mosaic of garrigues and vegetation of rock and scree | |||
| v8 | Satureja montana Garrigues Cephalario leucanthae-Saturejetum montanae (could include 6110 and 6220 habitats); Potentilla caulescens and Moehringia papulosa chasmophytic vegetation of shady and wet rocky gorge’s wall—Moehringio papulosae-Potentilletum caulescentis (habitat 8210 “Calcareous rocky slopes with chasmophytic vegetation”) [52,53]. | 6110, 6220, 8210 | 46 |
| Formula #id | Formula | # of Operands | Constraint #1 | Constraint #2 | # of Combinations |
|---|---|---|---|---|---|
| 0 | 1 | - | - | 9 | |
| 1 | 2 | - | 36 | ||
| 2 | 2 | - | 36 | ||
| 3 | 2 | - | 36 | ||
| 4 | 3 | 84 | |||
| 5 | 3 | 84 | |||
| 6 | 3 | 84 | |||
| 7 | 3 | 84 | |||
| 8 | 4 | 126 | |||
| 9 | 4 | 126 | |||
| 10 | 3 | - | 84 | ||
| 11 | 3 | - | 84 | ||
| 12 | 4 | - | - | 126 | |
| 13 | 3 | - | 84 | ||
| 14 | 4 | 126 | |||
| 15 | 3 | 84 | |||
| 16 | 3 | 84 | |||
| 17 | 3 | 84 | |||
| 18 | 3 | 84 | |||
| 19 | 2 | - | - | 36 | |
| 20 | 3 | - | 84 |
| Mount Conero | Frasassi Gorge | |||||||
|---|---|---|---|---|---|---|---|---|
| Formula #id | B | mF | M | Ms | B | mF | M | Ms |
| 0 | 0.818 | 0.826 | 0.812 | 0.812 | 0.769 | 0.773 | 0.785 | 0.812 |
| 1 | 0.816 | 0.838 | 0.835 | 0.773 | 0.778 | 0.845 | ||
| 2 | 0.844 | 0.768 | 0.839 | 0.816 | 0.675 | 0.824 | ||
| 3 | 0.849 | 0.825 | 0.849 | 0.829 | 0.817 | 0.829 | ||
| 4 | 0.857 | 0.790 | 0.779 | 0.811 | 0.733 | 0.832 | ||
| 5 | 0.857 | 0.793 | 0.859 | 0.819 | 0.731 | 0.842 | ||
| 6 | 0.841 | 0.675 | 0.842 | 0.808 | 0.646 | 0.815 | ||
| 7 | 0.854 | 0.802 | 0.860 | 0.818 | 0.823 | 0.836 | ||
| 8 | 0.831 | 0.663 | 0.838 | 0.816 | 0.644 | 0.840 | ||
| 9 | 0.856 | 0.797 | 0.848 | 0.816 | 0.754 | 0.840 | ||
| 10 | 0.835 | 0.778 | 0.840 | 0.792 | 0.667 | 0.811 | ||
| 11 | 0.860 | 0.790 | 0.860 | 0.825 | 0.708 | 0.828 | ||
| 12 | 0.842 | 0.732 | 0.851 | 0.825 | 0.668 | 0.814 | ||
| 13 | 0.828 | 0.826 | 0.844 | 0.784 | 0.764 | 0.832 | ||
| 14 | 0.844 | 0.819 | 0.838 | 0.802 | 0.778 | 0.840 | ||
| 15 | 0.847 | 0.838 | 0.872 | 0.813 | 0.810 | 0.865 | ||
| 16 | 0.832 | 0.814 | 0.843 | 0.783 | 0.787 | 0.828 | ||
| 17 | 0.845 | 0.671 | 0.847 | 0.798 | 0.634 | 0.856 | ||
| 18 | 0.845 | 0.856 | 0.857 | 0.806 | 0.798 | 0.835 | ||
| 19 | 0.850 | 0.829 | 0.850 | 0.805 | 0.813 | 0.811 | ||
| 20 | 0.852 | 0.794 | 0.851 | 0.820 | 0.764 | 0.822 | ||
| mean | 0.818 | 0.843 | 0.786 | 0.844 | 0.8 | 0.806 | 0.742 | 0.831 |
| B | Ms-Formula id #15 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | Reference | ||||||||||||
| c1 | c2 | c3 | c4 | UA | c1 | c2 | c3 | c4 | UA | ||||
| Pred | c1 | 16.2 | 3.2 | 0.0 | 2.1 | 75.5 | Pred | c1 | 39.2 | 3.7 | 3.1 | 3.4 | 79.4 |
| c2 | 4.0 | 36.2 | 3.9 | 3.0 | 76.9 | c2 | 1.3 | 16.9 | 0.0 | 0.7 | 89.7 | ||
| c3 | 0.0 | 0.3 | 3.5 | 0.0 | 91.2 | c3 | 0.0 | 0.0 | 4.3 | 0.0 | 100.0 | ||
| c4 | 0.9 | 0.8 | 0.0 | 25.8 | 93.8 | c4 | 0.1 | 0.6 | 0.0 | 26.7 | 97.5 | ||
| PA | 76.8 | 89.3 | 47.7 | 83.7 | PA | 96.6 | 80.0 | 58.5 | 86.7 | ||||
| OA | 81.79 (±9.50) | OA | 87.18 (±7.82) | ||||||||||
| K | 0.72 (±0.14) | K | 0.80 (±0.11) | ||||||||||
| B | ||||||||||
| reference | ||||||||||
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | |||
| pred | v1 | 11.7 | 0 | 1.32 | 0.74 | 0 | 0 | 0 | 0 | 84.9 |
| v2 | 0 | 5.87 | 1.49 | 0 | 1.07 | 0 | 0.17 | 0 | 68.3 | |
| v3 | 0.58 | 4.96 | 18.6 | 0.41 | 1.16 | 0 | 0 | 0 | 72.3 | |
| v4 | 1.4 | 0 | 0.33 | 11.7 | 0 | 0.83 | 0 | 0 | 82.0 | |
| v5 | 0.17 | 0.74 | 0.17 | 0 | 2.07 | 0 | 0.25 | 0.41 | 54.3 | |
| v6 | 0 | 0 | 0 | 0 | 0.66 | 4.38 | 0 | 0.83 | 74.6 | |
| v7 | 0 | 0 | 0.41 | 0 | 0.33 | 0 | 5.37 | 0.25 | 84.4 | |
| v8 | 0.25 | 0 | 0.83 | 0 | 1.32 | 0.99 | 0.83 | 17.5 | 80.6 | |
| PA | 82.9 | 50.7 | 80.4 | 91.0 | 31.3 | 70.7 | 81.3 | 92.2 | ||
| OA | 76.99 (±7.07) | |||||||||
| K | 0.72 (±0.08) | |||||||||
| Ms-Formula id #15 | ||||||||||
| reference | ||||||||||
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | UA | ||
| pred | v1 | 13.4 | 0.0 | 0.6 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 95.3 |
| v2 | 0.0 | 6.8 | 0.9 | 0.3 | 0.6 | 0.0 | 0.0 | 0.0 | 78.8 | |
| v3 | 0.4 | 4.3 | 21.3 | 0.4 | 0.2 | 0.4 | 0.0 | 0.0 | 78.9 | |
| v4 | 0.2 | 0.0 | 0.3 | 12.0 | 0.0 | 0.0 | 0.0 | 0.0 | 95.4 | |
| v5 | 0.0 | 0.2 | 0.0 | 0.0 | 3.8 | 0.0 | 0.4 | 0.0 | 85.2 | |
| v6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 4.8 | 0.0 | 0.0 | 95.1 | |
| v7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.4 | 5.9 | 0.4 | 86.6 | |
| v8 | 0.0 | 0.2 | 0.0 | 0.0 | 1.7 | 0.6 | 0.3 | 18.6 | 86.5 | |
| PA | 95.3 | 58.6 | 92.1 | 93.5 | 57.5 | 77.3 | 88.8 | 97.8 | ||
| OA | 86.51 (±6.99) | |||||||||
| K | 0.83 (±0.08) | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesaresi, S.; Mancini, A.; Quattrini, G.; Casavecchia, S. Evaluation and Selection of Multi-Spectral Indices to Classify Vegetation Using Multivariate Functional Principal Component Analysis. Remote Sens. 2024, 16, 1224. https://doi.org/10.3390/rs16071224
Pesaresi S, Mancini A, Quattrini G, Casavecchia S. Evaluation and Selection of Multi-Spectral Indices to Classify Vegetation Using Multivariate Functional Principal Component Analysis. Remote Sensing. 2024; 16(7):1224. https://doi.org/10.3390/rs16071224
Chicago/Turabian StylePesaresi, Simone, Adriano Mancini, Giacomo Quattrini, and Simona Casavecchia. 2024. "Evaluation and Selection of Multi-Spectral Indices to Classify Vegetation Using Multivariate Functional Principal Component Analysis" Remote Sensing 16, no. 7: 1224. https://doi.org/10.3390/rs16071224
APA StylePesaresi, S., Mancini, A., Quattrini, G., & Casavecchia, S. (2024). Evaluation and Selection of Multi-Spectral Indices to Classify Vegetation Using Multivariate Functional Principal Component Analysis. Remote Sensing, 16(7), 1224. https://doi.org/10.3390/rs16071224






