An Updated Estimate of Geocenter Variation from Analysis of SLR Data
Abstract
1. Introduction
2. Theory
2.1. Definition of Geocenter Motion
2.2. Surface Loading and GPS Global Inversion
3. Determination of the Geocenter Variations Obtained Using SLR
3.1. Method
3.2. SLR Range Bias, Atmospheric Troposphere Delay, and Gradients
3.2.1. Seasonal Variations in SLR Range Bias
3.2.2. Tropospheric Zenith Delay and Gradients
3.2.3. High-Degree Surface-Loading-Induced Station Displacement
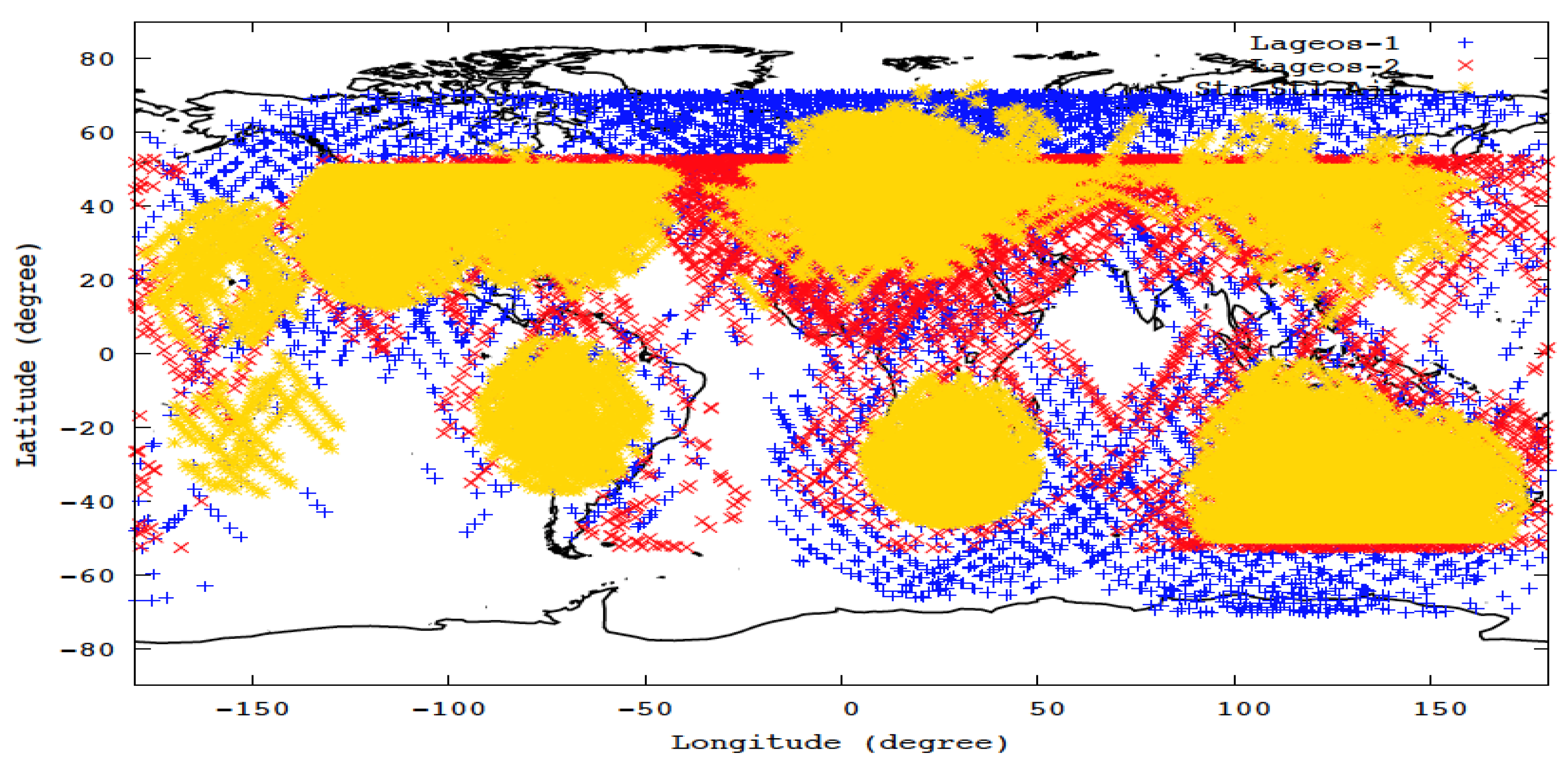
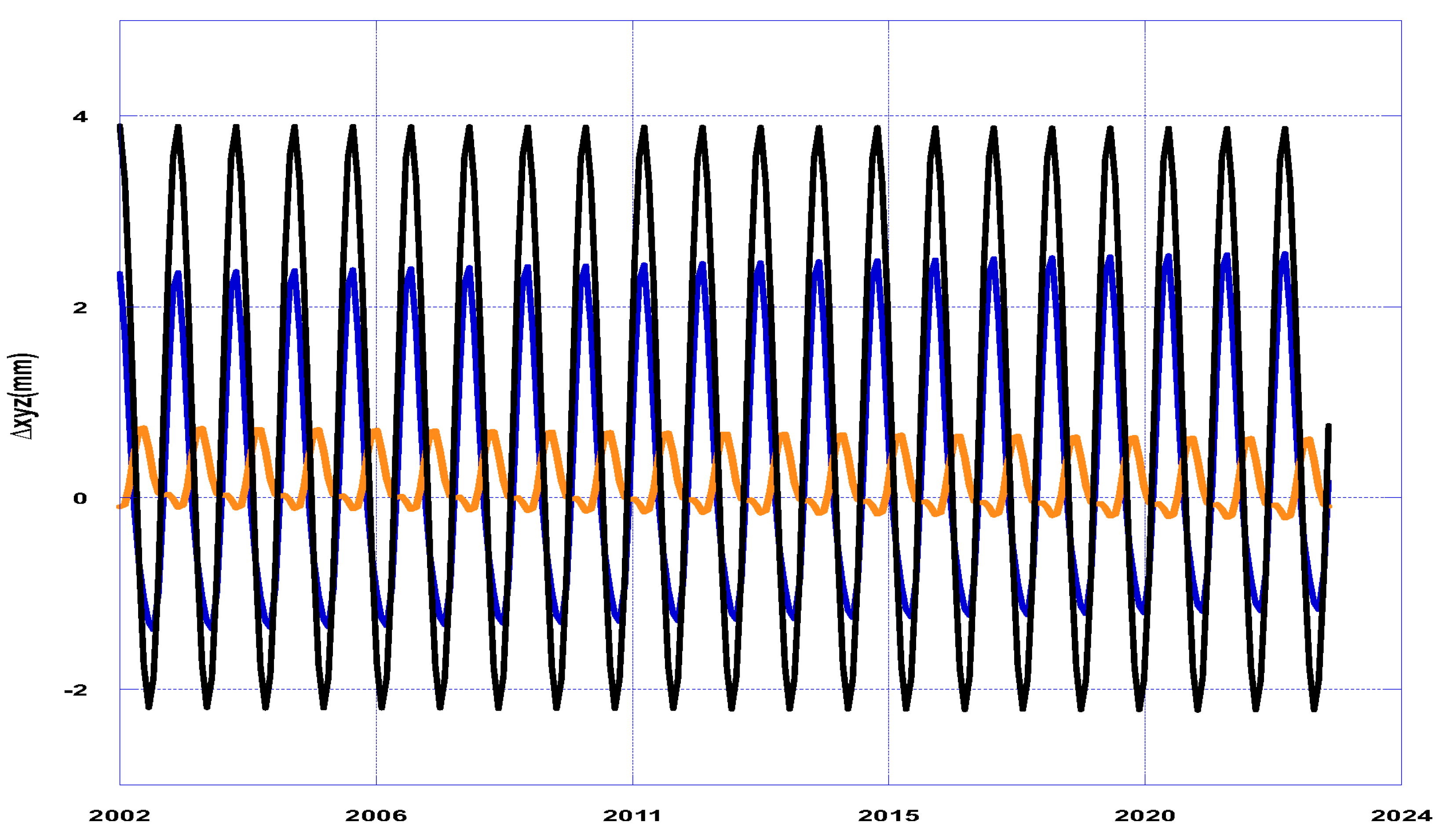
3.3. Satellite Ground Track
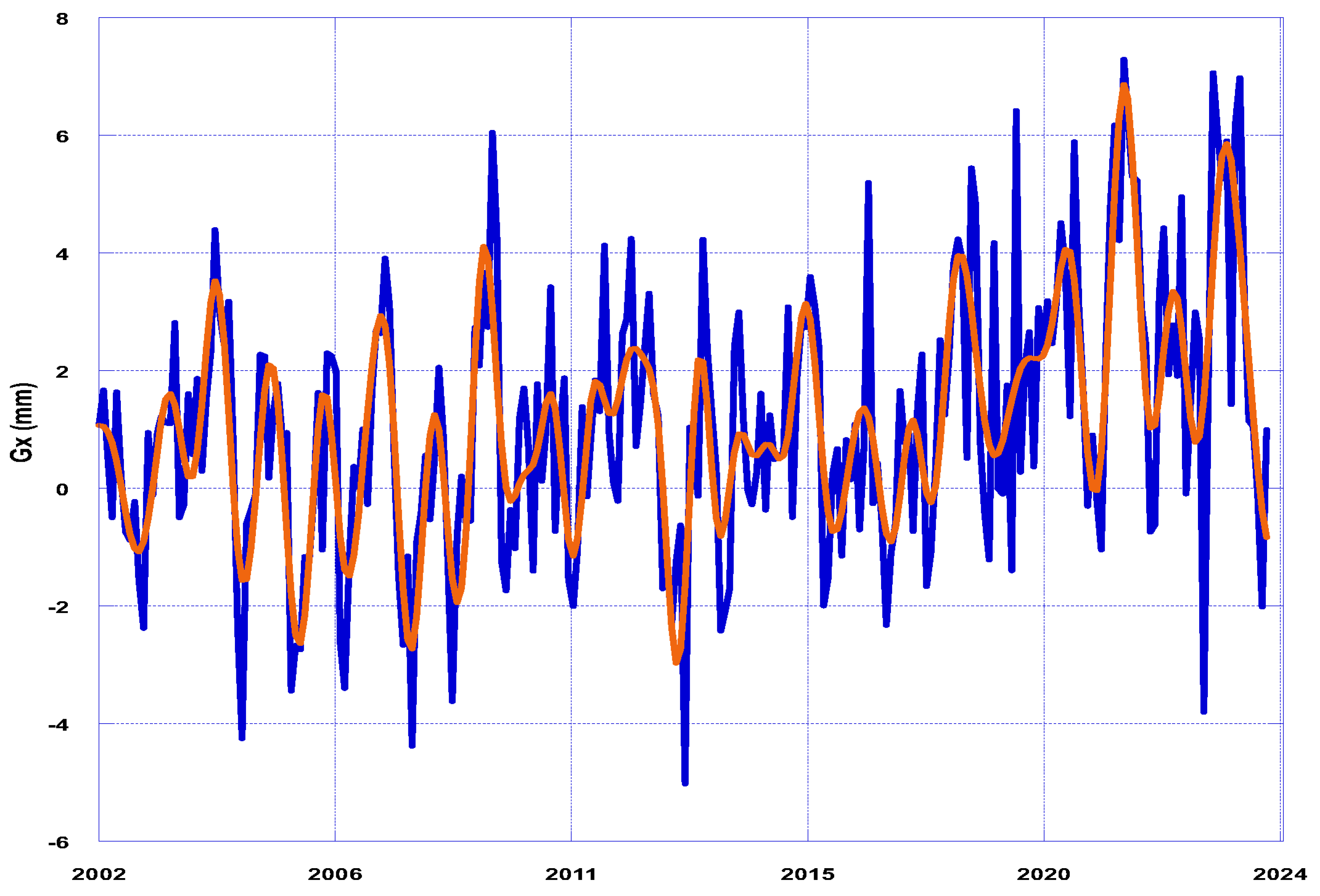
3.4. Solution to Geocenter Variation from SLR
4. Comparison and Discussion
4.1. Annual Geocenter Variation
4.2. Drift of the Geocenter
4.3. Uncertainty Estimate
5. Conclusions
- The signal in the station range bias is a part of the surface-loading-induced variations (including a higher degree of loading) and the mismodeling of the thermosphere zenith delay, which can be separated from each other.
- Measurements of the gravitational signal, including the geocenter variations from the SLR data, depend on the distribution of the suborbital points or ground tracking of satellites, instead of the geographic distribution of the tracking stations.
- A new monthly time series of geocenter variation was determined by simultaneously adjusting the station range bias and the thermosphere delay parameters from SLR data. This improved solution is comparable to the solution obtained from global conversions based on GPS displacements.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trupin, A.S.; Meier, M.F.; Wahr, J. Effects of melting glaciers on the Earth’s rotation and gravitational field: 1965–1984. Geophys. J. Int. 1992, 108, 1–15. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Wu, X.; Ray, J.; van Dam, T. Geocenter motion and its geodetic and geophysical implications. J. Geodyn. 2012, 58, 44–61. [Google Scholar] [CrossRef]
- Wu, X.; Kusche, J.; Landerer, F.W. A new unified approach to determine geocenter motion using space geodetic and GRACE gravity data. Geophys. J. Int. 2017, 209, 1398–1402. [Google Scholar] [CrossRef]
- Rietbroek, R.; Brunnabend, S.E.; Dahle, C.; Kusche, J.; Flechtner, F.; Schröter, J.; Timmermann, R. Changes in total ocean mass derived from GRACE, GPS, and ocean modeling with weekly resolution. J. Geophys. Res. Oceans 2009, 114, C11004. [Google Scholar] [CrossRef]
- Watkins, M.M.; Eanes, R.J. Observations of tidally coherent diurnal and semi-diurnal variations in the geocenter. Geophys. Res. Lett. 1997, 24, 2231–2234. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebisschung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Cheng, M.K.; Ries, J.C.; Tapley, B.D. Geocenter Variations from Analysis of SLR data. In Reference Frames for Applications in Geosciences; IAG (International Association of Geodesy); Altamimi, Z., Collilieux, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 138, pp. 19–25. [Google Scholar]
- Sosnica, K.; Jaggi, A.; Thaller, D.; Beutler, G.; Dach, R. Contribution of Starlette, Stella, and AJISAI to the SLR-derived global reference frame. J. Geod. 2014, 88, 789–804. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.; Chen, J.; Ries, J.; Bettadpur, S. Geocenter variations derived from GPS tracking of the GRACE satellites. J. Geod. 2009, 83, 895–901. [Google Scholar] [CrossRef]
- van Helleputte, T.; Visser, P. GPS based orbit determination using accelerometer data. Aerosp. Sci. Technol. 2008, 12, 478–484. [Google Scholar] [CrossRef]
- Kuang, D.A.; Bertiger, W.; Desai, S.; Haines, B.J.; Yuan, D.-N. Observed geocenter motion from precise orbit determination of GRACE satellites using GPS tracking and accelerometer data. J. Geod. 2019, 93, 1835–1844. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Landerer, F. Jet Propulsion Laboratory (JPL), GRACE Technical Note 13. Contact: Grace@jpl.nasa.gov. Available online: https://podaac.jpl.nasa.gov/gravity/grace-documentation (accessed on 15 March 2024).
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; K¨onig, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef]
- van den Dool, H.; Huang, J.; Fan, Y. Performance and analysis of the constructed analogue method applied to US soil moisture applied over 1981–2001. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Co.: San Francisco, CA, USA; London, UK, 1967. [Google Scholar]
- Lambeck, K. Geophysical Geodesy; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Blewitt, G. Self-consistency in reference frames, geocenter definition, and surface loading of the solid Earth. J. Geophys. Res. Solid Earth 2003, 108, 2103. [Google Scholar] [CrossRef]
- Wahr, J.; Molenar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loading. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E.J.O. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. Solid Earth 2005, 110, B09409. [Google Scholar] [CrossRef]
- Melachroinosa, S.A.; Lemoine, F.G.; Zelensky, N.P.; Rowlands, D.D.; Luthcke, S.B.; Bordyugov, O. The effect of geocenter motion on Jason-2 orbits and the mean sea level. Adv. Space Res. 2013, 51, 1323–1334. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); IERS Technical Note No. 36; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 2010. [Google Scholar]
- Choi, E.-J.; Bang, S.-C.; Sung, K.-P.; Lim, H.-C.; Jung, C.-G.; Kim, I.-Y.; Choi, J.-S. Design and Development of High-Repetition-Rate Satellite Laser Ranging System. J. Astron. Space Sci. 2015, 32, 209–219. [Google Scholar] [CrossRef][Green Version]
- Luceri, V.; Pirri, M.; Rodríguez, J.; Appleby, G.; Pavlis, E.C.; Müller, H. Systematic errors in SLR data and their impact on the ILRS products. J. Geod. 2019, 93, 2357–2366. [Google Scholar] [CrossRef]
- Drozdzewski, M.; Sosnica, K. Tropospheric and range biases in Satellite Laser Ranging. J. Geod. 2021, 95, 100. [Google Scholar] [CrossRef]
- Mendes, V.B. Modeling the Neutral-Atmosphere Propagation Delay in Radiometric Space Techniques. Ph.D. Thesis, University of New Brunswick, Fredericton, NB, Canada, 1999. [Google Scholar]
- Saastamoinen, J. Contributions to the theory of atmospheric refrac- tion, part II, Refraction corrections in satellite geodesy. Bull. Géodésique 1973, 107, 13–24. [Google Scholar] [CrossRef]
- Marini, J.W.; Murray, C.W. Correction of Laser Range Tracking Data for Atmospheric Refraction at Elevations above 10 Degrees. International Patent Application NASA-TM-X-70555; Patent Application No. X-591-73-351, 1 November 1973. [Google Scholar]
- Mendes, V.B.; Prates, G.; Pavlis, E.C.; Pavlis, D.E.; Langley, R.B. Improved mapping functions for atmospheric refraction correction in SLR. Geophys. Res. Lett. 2002, 29, 53-1–53-4. [Google Scholar] [CrossRef]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, L14602. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Böhm, J.; Hobiger, T.; Ichikawa, R.; Kondo, T.; Koyama, Y.; Pany, A.; Schuh, H.; Teke, K. Asymmetric tropospheric delays from numerical weather models for UT1 determination from VLBI Intensive sessions on the baseline Wettzell-Tsukuba. J. Geod. 2010, 84, 319–325. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Drozdzewski, M.; Sosnica, K.; Zus, F.; Balidakis, K. Troposphere delay modeling with horizontal gradients for satellite laser ranging. J. Geod. 2019, 93, 1853–1866. [Google Scholar] [CrossRef]
- Dong, D.; Dickey, J.O.; Chao, Y.; Cheng, M.K. Geocenter variations caused by atmosphere, ocean and surface ground water. Geophys. Res. Lett. 1997, 24, 1867–1870. [Google Scholar] [CrossRef]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the International Terrestrial Reference Frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Greff-Lefftz, M. Secular variation of the geocenter. J. Geophys. Res. Solid Earth 2000, 105, 25685–25692. [Google Scholar] [CrossRef]
- Métivier, L.; Grefftz-Lefftz, M.; Atamimi, Z. On secular geocenter motion: The impact of climate changes. Earth Planet. Sci. Lett. 2010, 296, 360–366. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Noll, C.E.; Pavlis, E.C.; Lemoine, F.G.; Combrink, L.; Degnan, J.L.; Kirchner, G.; Schreiber, U. The ILRS: Approaching 20 years and planning for the future. J. Geod. 2019, 93, 2161–2180. [Google Scholar] [CrossRef]



| Case | Solution | Rb (A/Ψ) | ∆z (A/Ψ) | GN (A/Ψ) | GE (A/Ψ) |
|---|---|---|---|---|---|
| 1 | Rb only | 4.41/152 | |||
| 2 | Rb + ∆z + hg | 8.11/151 | 2.13/330 | 0.05/12 | 0.16/25 |
| 3 | Rb + hg | 4.43/151 | 0.12/147 | 0.30/10 | |
| 4 | Rb + ∆z | 9.29/154 | 2.41/332 | ||
| 5 | ∆z + hg | 1.22/139 | 0.14/166 | 0.39/07 | |
| 6 | Up + ∆z + hg | 7.47/331 * | 2.24/337 | 0.04/41 | 0.18/15 |
| Solution | E (mm/deg) | N (mm/deg) | Up (mm/deg) |
|---|---|---|---|
| GRACE | 0.228/322 | 0.165/299 | 1.77/327 |
| ITRF2020 | 0.851(±0.24)/64(±46) | 2.369(±0.44)/269(±46) | 3.65(±0.31)/317(±45) |
| SLR (1) | 3.90(±0.09)/322(±5) | ||
| SLR (10) | 7.98(±0.09)/335(±5) | ||
| SLR (10*) | 6.52(±0.09)/354±5) |
| Case | Solution Case | X (A/Ψ) | Y (A/Ψ) | Z (A/Ψ) |
|---|---|---|---|---|
| 1 | Rb | 1.82/35 | 2.87/301 | 2.11/24 |
| 2 | Rb + ∆z + hg | 1.82/47 | 2.90/302 | 2.44/20 |
| 3 | Rb + ∆z | 1.23/63 | 3.27/304 | 1.57/31 |
| 4 | Rb + hg | 2.81/27 | 2.47/295 | 3.28/16 |
| 5 | ∆z + hg | 4.02/17 | 1.88/284 | 4.35/10 |
| 6 | Up (1 mm) | 3.33/20 | 2.91/299 | 4.31/13 |
| 7 | Up (10 mm) | 1.22/65 | 3.35/307 | 1.83/28 |
| 8 | Up + ∆z | 1.25/63 | 3.31/304 | 1.44/37 |
| 9 | Up + ∆z + hg | 1.78/50 | 3.13/304 | 2.35/22 |
| Solutions | X (Amp/Phase) | Y (Amp/Phase) | Z (Amp/Phase) |
|---|---|---|---|
| ITRF2014 | 2.6 ± 0.1/46 ± 3 | 3.1 ± 0.1/320 ± 2 | 5.7 ± 0.2/28 ± 2 |
| ITRF2020 | 1.2 ± 0.2/57 ± 7 | 3.5 ± 0.2/332 ± 3 | 2.8 ± 0.3/41 ± 7 |
| SLR (gbse) | 3.2 ± 0.2/17 ± 5 | 2.5 ± 0.4/301 ± 6 | 4.7 ± 0.4/10 ± 5 |
| SLR (mbse) | 1.5 ± 0.3/63 ± 5 | 3.3 ± 0.2/306 ± 4 | 2.6 ± 0.3/31 ± 6 |
| Global Inv1 | 1.8 ± 0.2/49 ± 4 | 2.7 ± 0.2/325 ± 2 | 4.2 ± 0.2/31 ± 3 |
| Global Inv-2 | 1.3 ± 0.1/46 ± 4 | 3.0 ± 0.2/330 ± 2 | 3.3 ± 0.2/26 ± 3 |
| TN13 (JPL) | 1.5/53 | 2.6/326 | 3.3/46 |
| GRACE GPS | 1.1/54 | 2.8/332 | 3.6/45 |
| AOD | 1.2/148 | 1.4/171 | 1.8/157 |
| CPC | 0.7/131 | 0.6/247 | 1.1/73 |
| AOD + CPC | 1.9/141 | 1.6/192 | 2.2/128 |
| Solution | X | Y | Z |
|---|---|---|---|
| ITRF2020 | −0.00 ± 0.2 | −0.1 ± 0.1 | −0.2 ± 0.1 |
| SLR-gbse | −0.01 ± 0.01 | 0.00 ± 0.01 | 0.25 ± 0.01 |
| SLR-mbse | 0.07 ± 0.02 | 0.01 ± 0.01 | 0.31 ± 0.01 |
| TN13 (JPL) | −0.11 | 0.07 | −0.54 |
| Model | ~0.2 | ~0.2 | 0.3–0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M. An Updated Estimate of Geocenter Variation from Analysis of SLR Data. Remote Sens. 2024, 16, 1189. https://doi.org/10.3390/rs16071189
Cheng M. An Updated Estimate of Geocenter Variation from Analysis of SLR Data. Remote Sensing. 2024; 16(7):1189. https://doi.org/10.3390/rs16071189
Chicago/Turabian StyleCheng, Minkang. 2024. "An Updated Estimate of Geocenter Variation from Analysis of SLR Data" Remote Sensing 16, no. 7: 1189. https://doi.org/10.3390/rs16071189
APA StyleCheng, M. (2024). An Updated Estimate of Geocenter Variation from Analysis of SLR Data. Remote Sensing, 16(7), 1189. https://doi.org/10.3390/rs16071189







