Improved Approaches for 3D Gravity and Gradient Imaging Based on Potential Field Separation: Application to the Magma Chamber in Wudalianchi Volcanic Field, Northeastern China
Abstract
1. Introduction
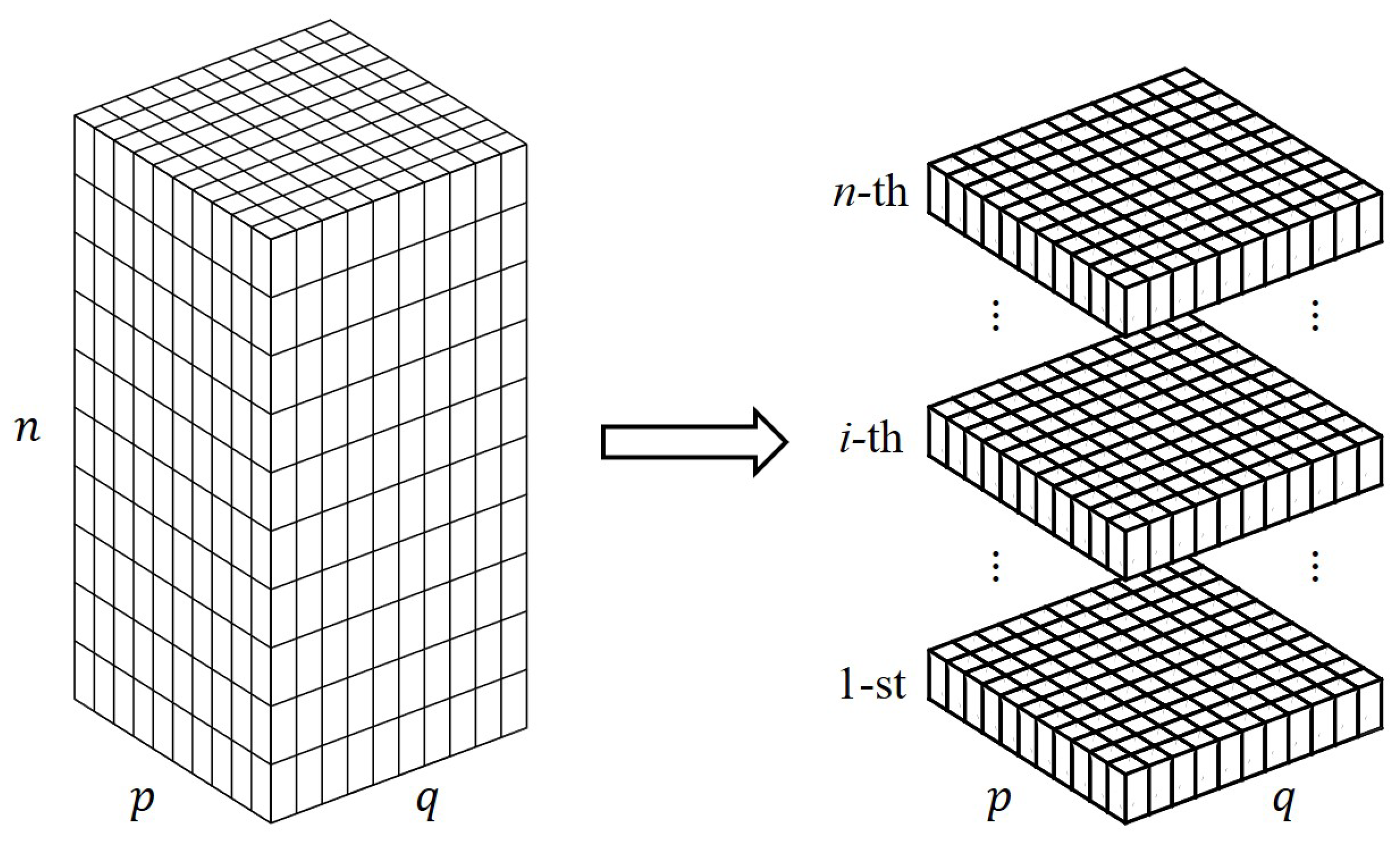
2. Methodology
2.1. Preferential Continuation Filter
2.2. Wave-Number-Domain Density Imaging
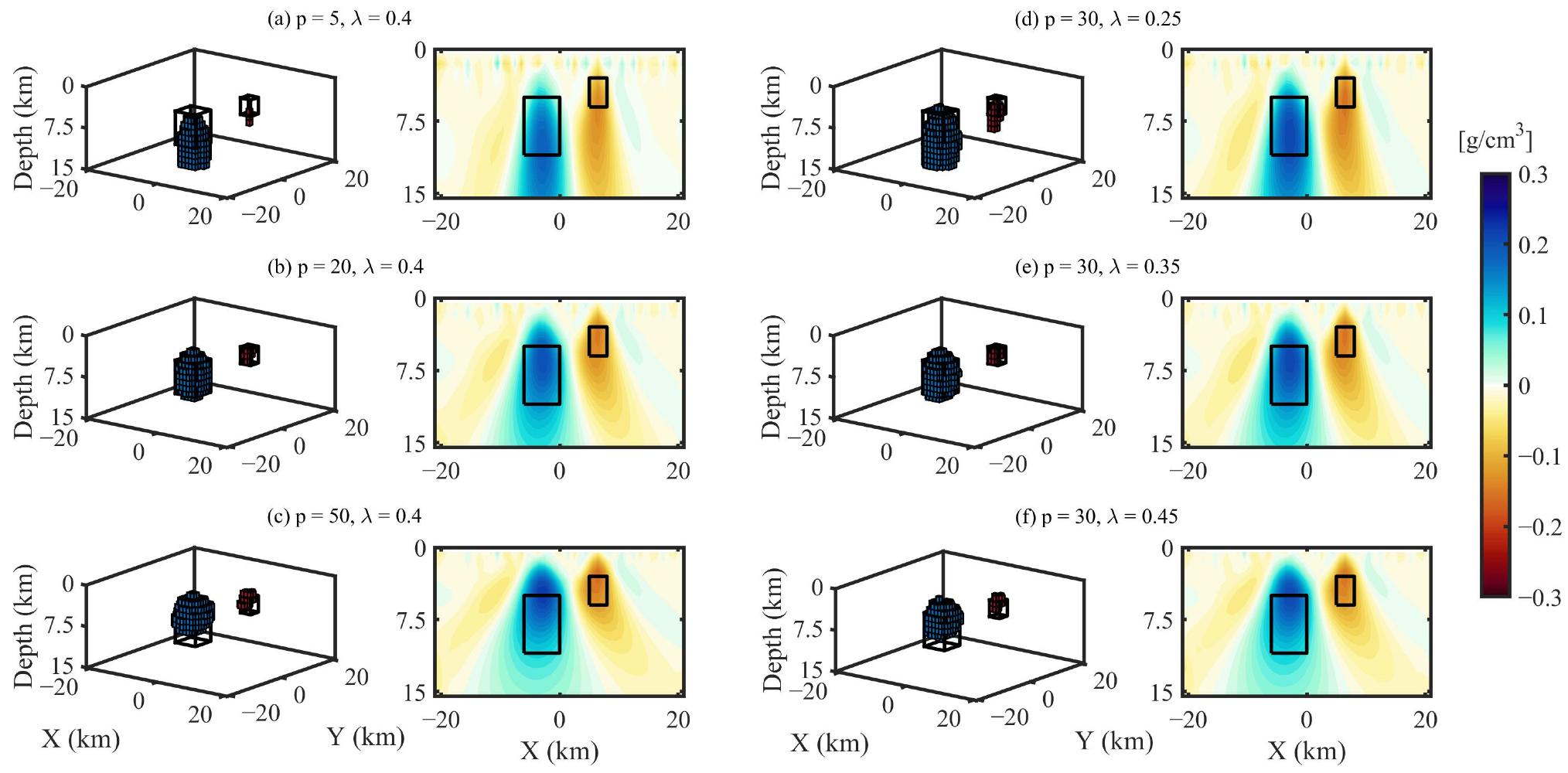
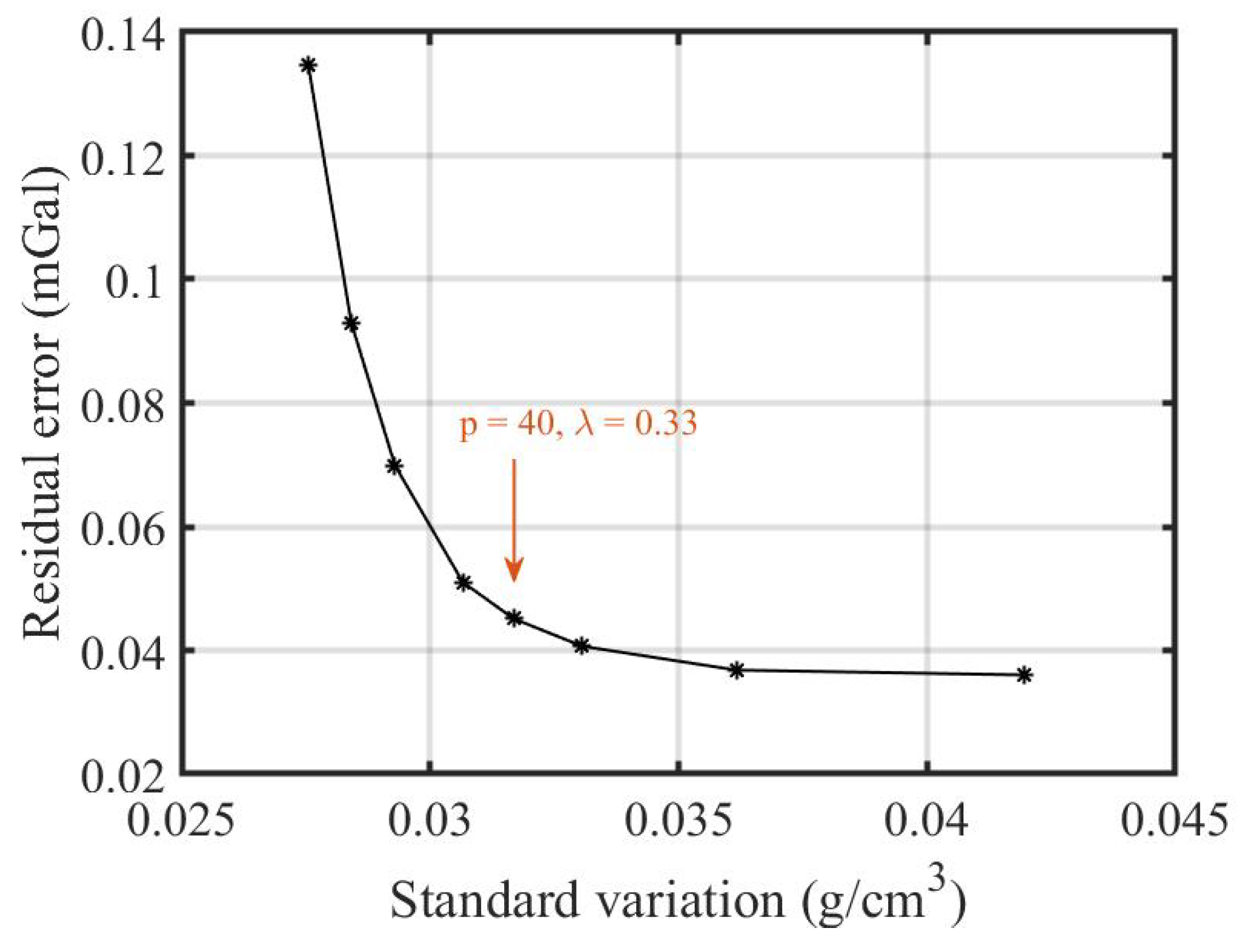
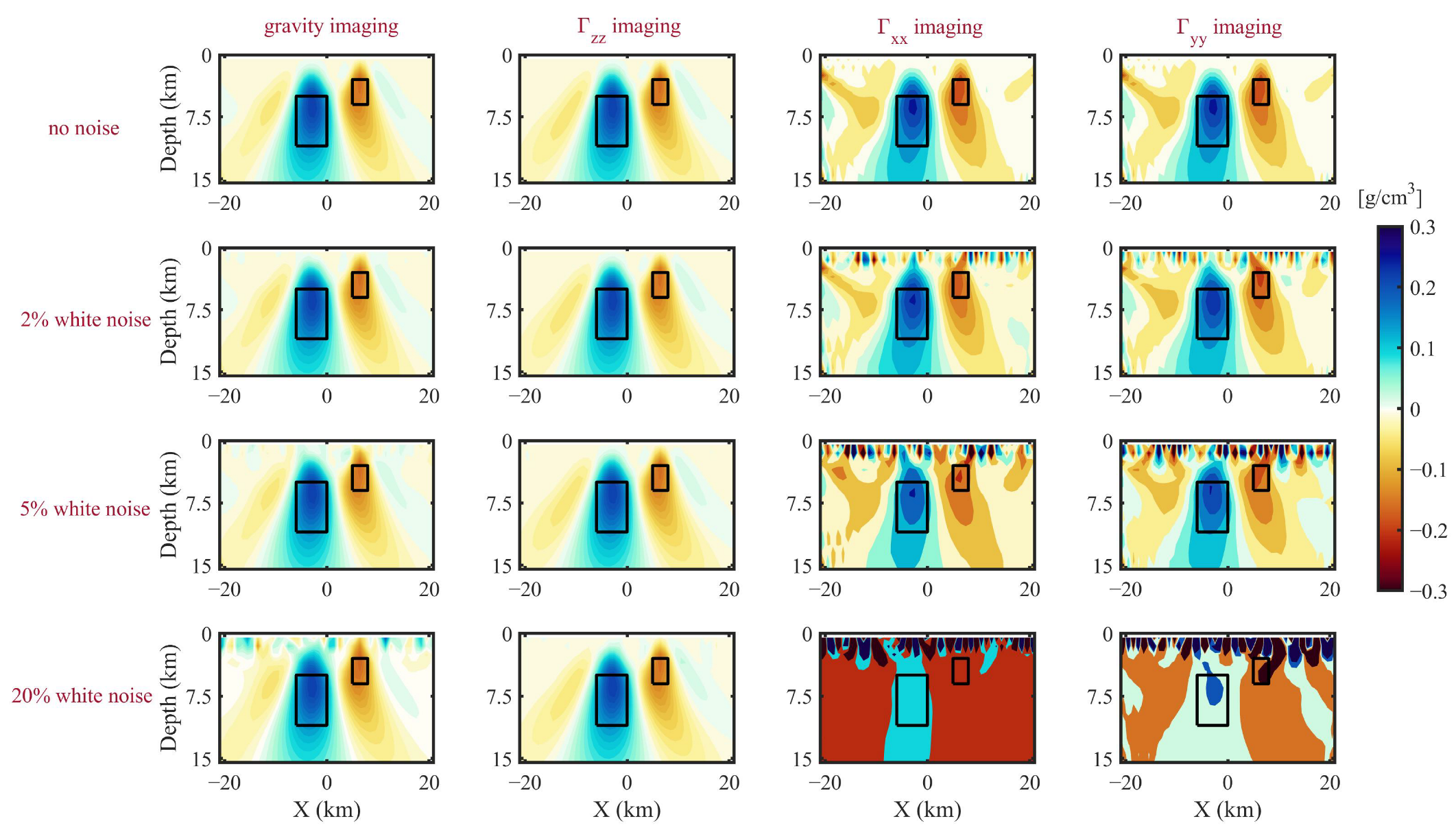
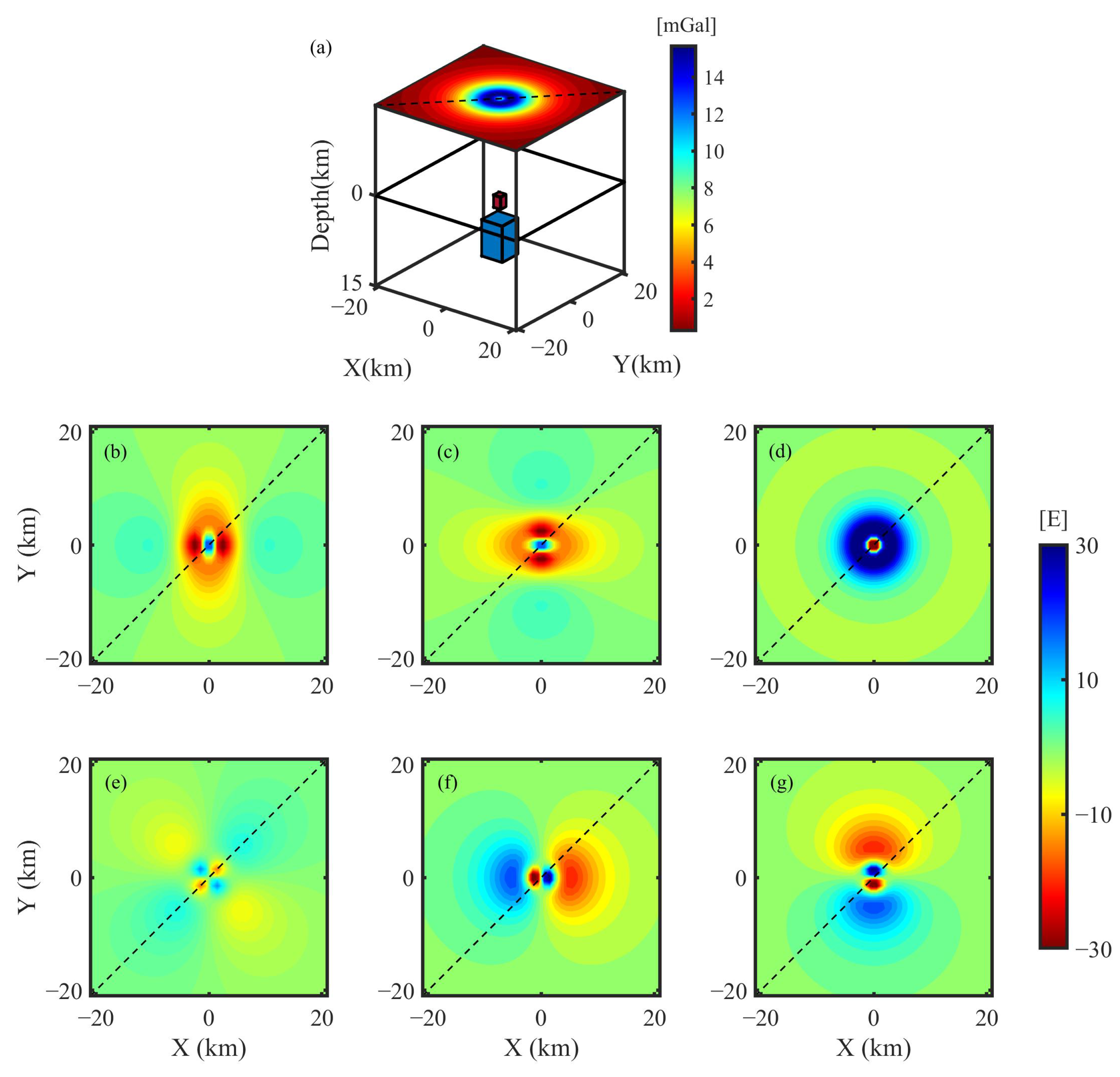
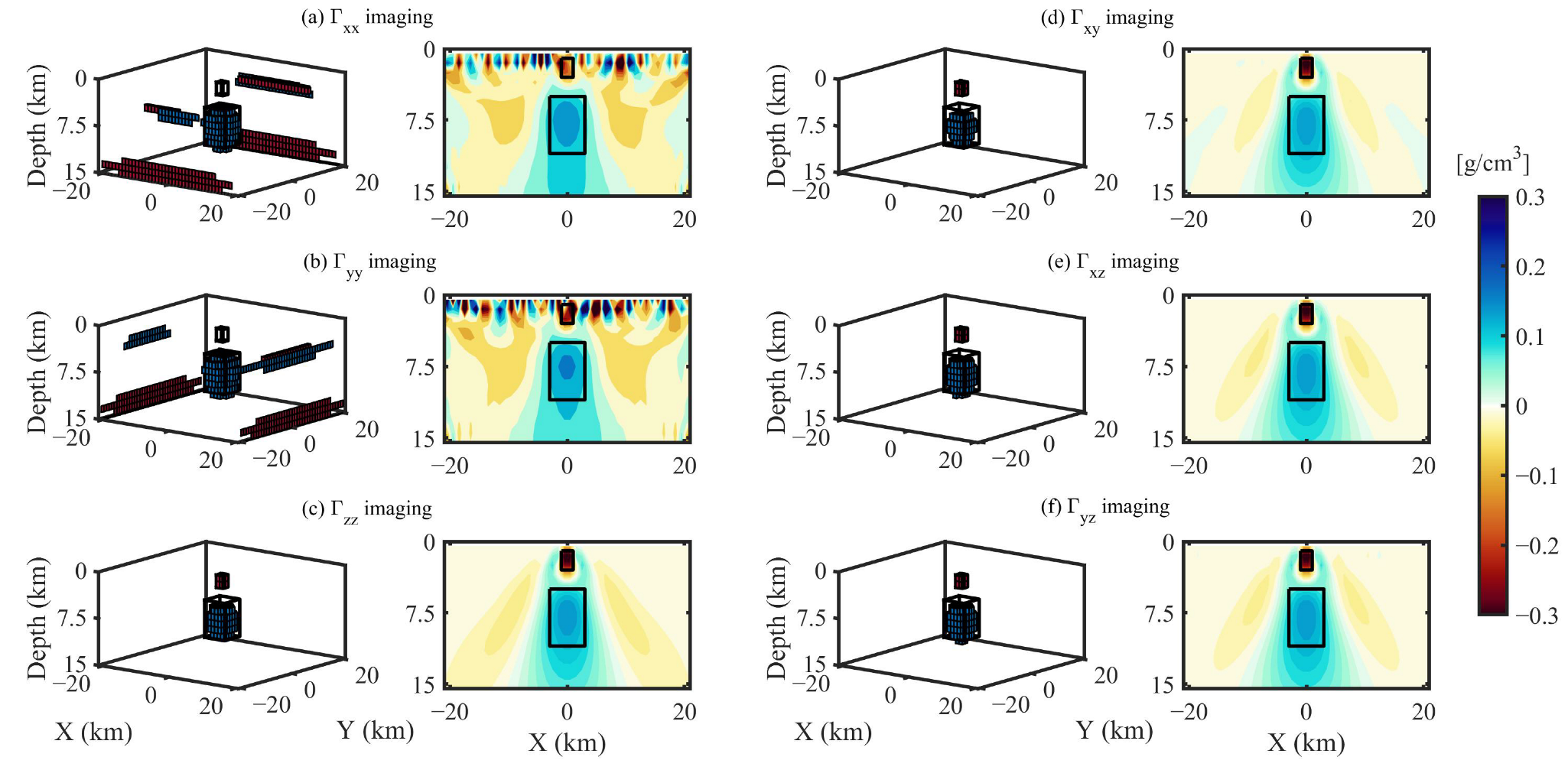
3. Synthetic Tests
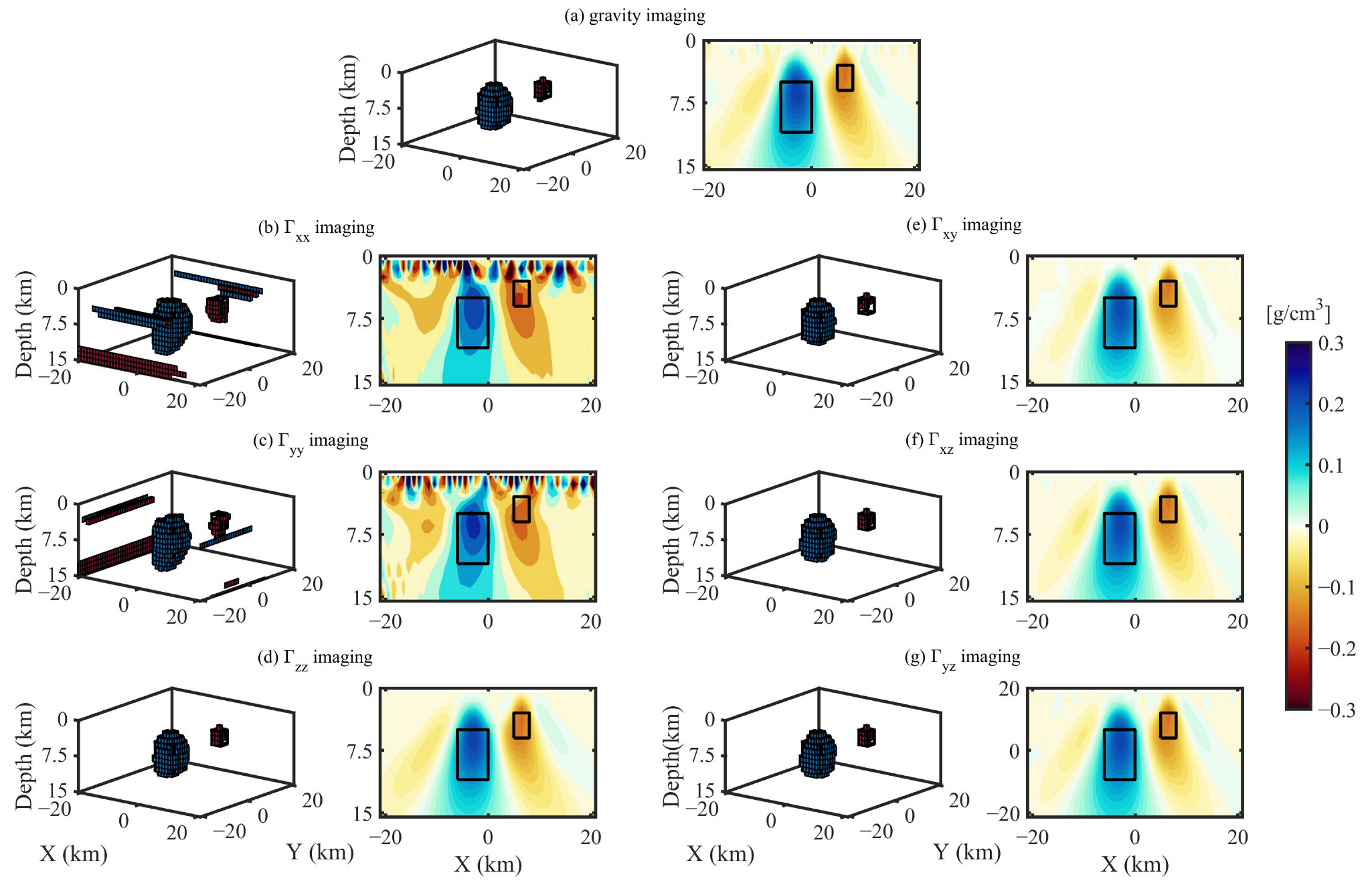
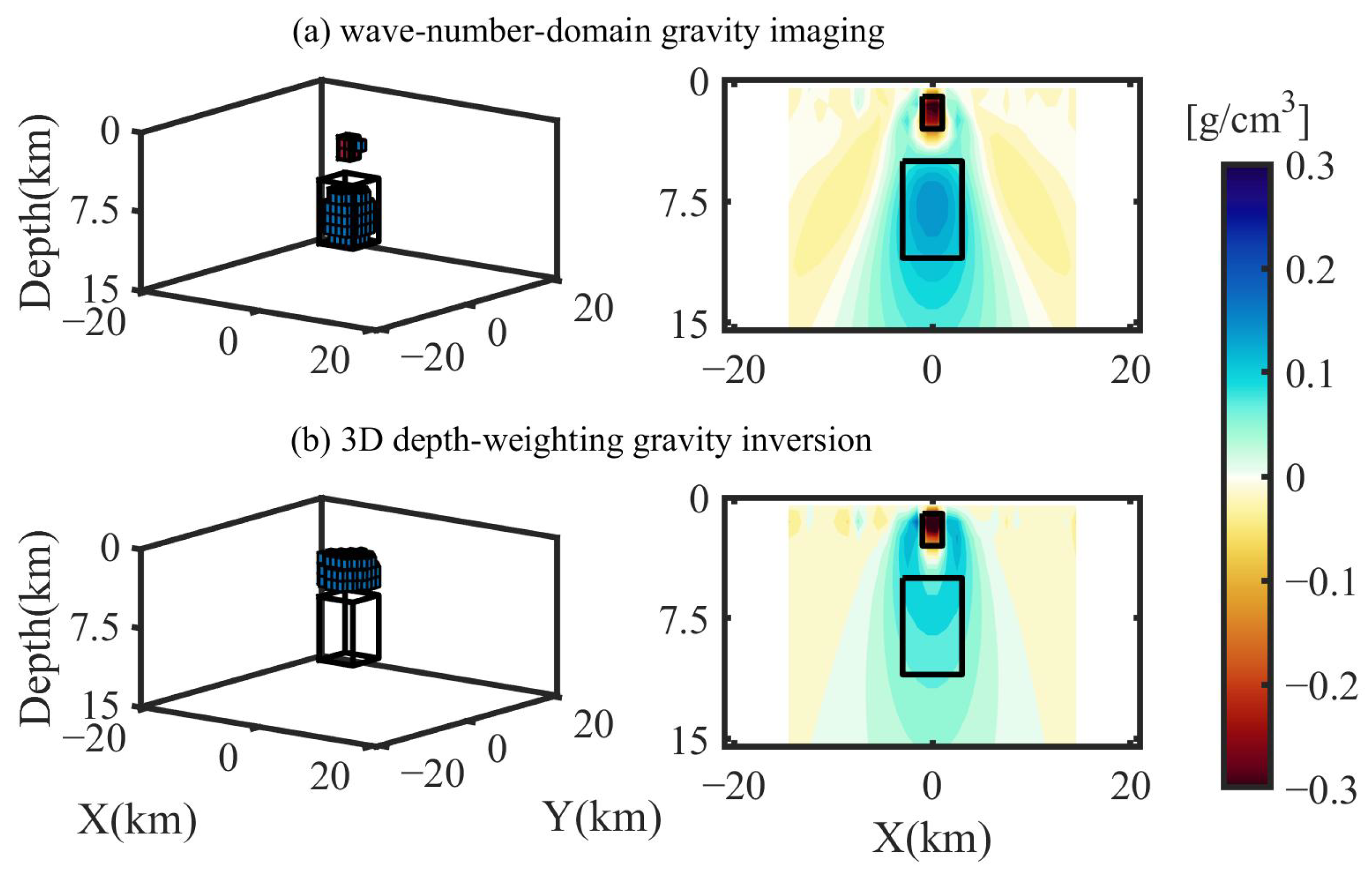
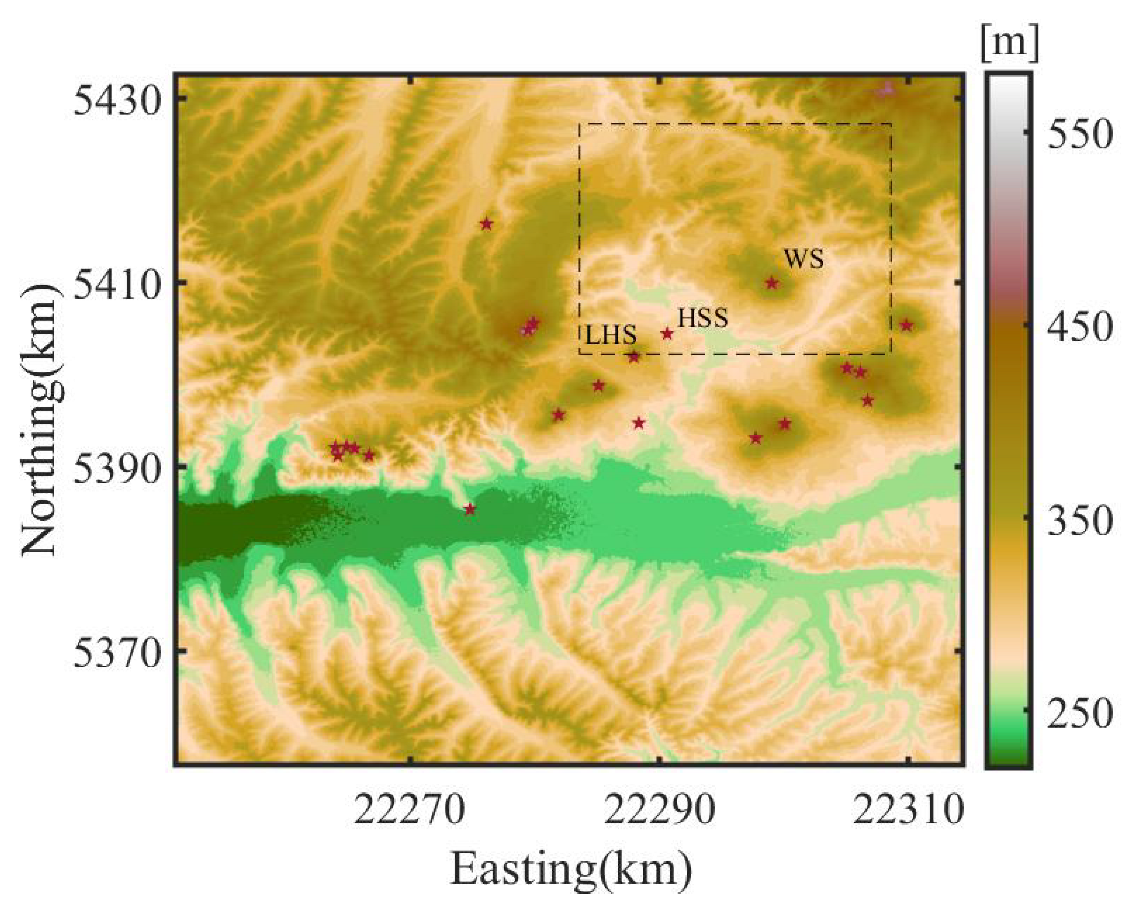
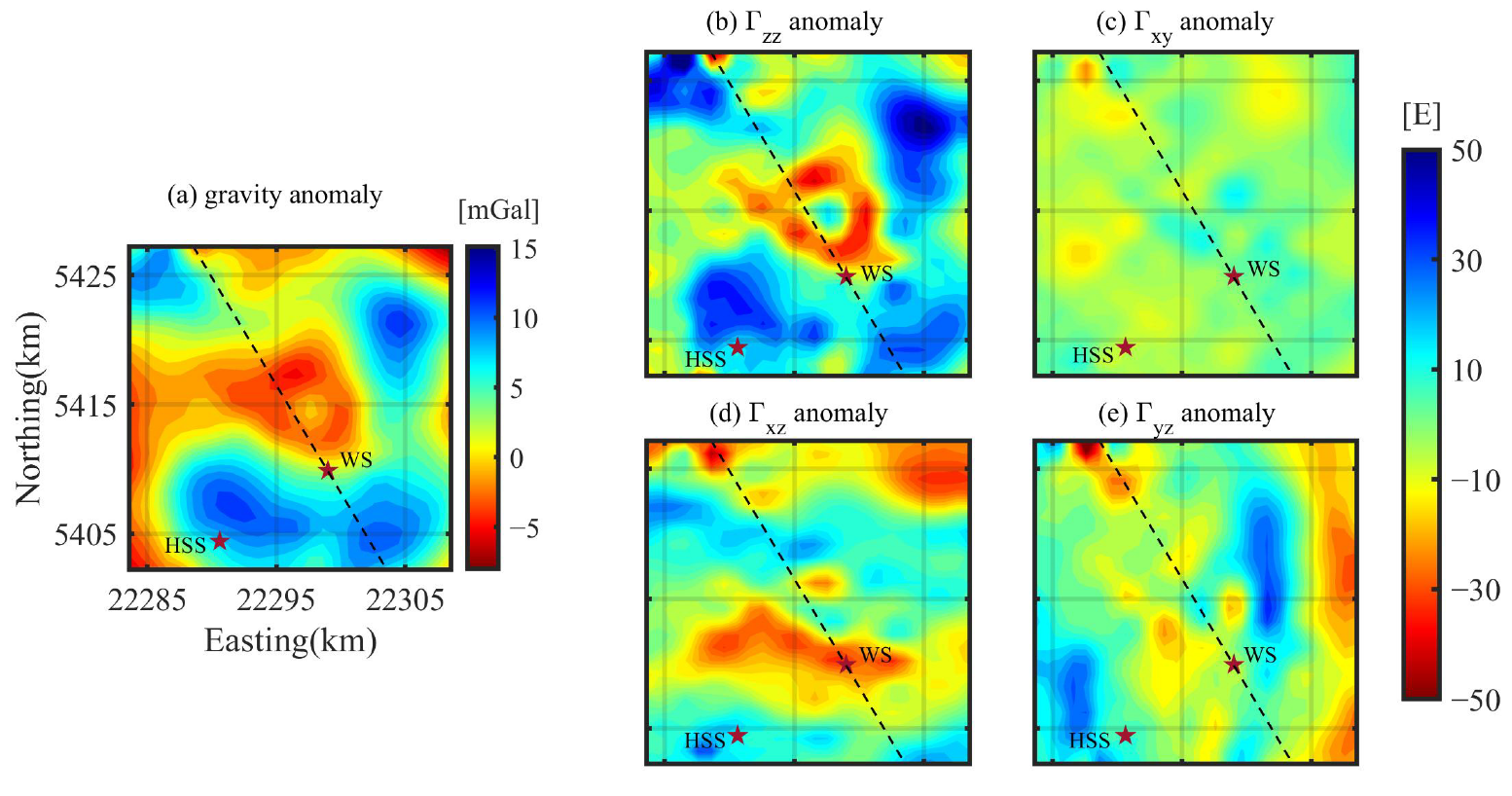
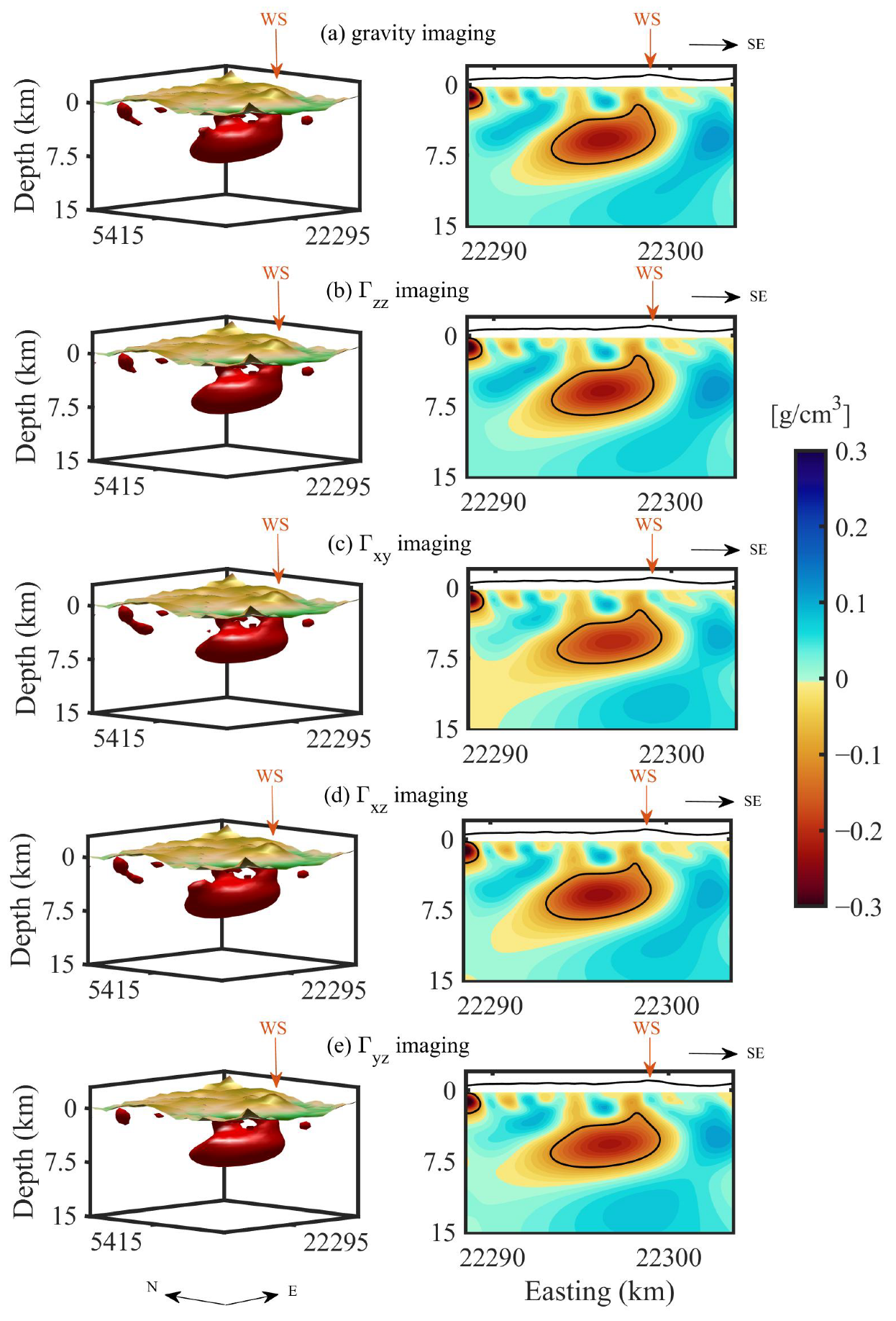
4. Applications
5. Conclusions and Outlooks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hofmann-Wellenhof, B.; Morisz, H. Physical Geodesy; Springer: Wien, Austria, 2005. [Google Scholar]
- Braitenberg, C.; Zadro, M.; Fang, J.; Wang, Y.; Hsu, H. The gravity and isostatic Moho undulations in Qinghai–Tibet plateau. J. Geodyn. 2000, 30, 489–505. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y. Gravity data inversion for the lithospheric density structure beneath North China Craton from EGM 2008 model. Phys. Earth Planet. Inter. 2011, 189, 9–26. [Google Scholar] [CrossRef]
- Motavalli-Anbaran, S.H.; Zeyen, H.; Ebrahimzadeh Ardestani, V. 3D joint inversion modeling of the lithospheric density structure based on gravity, geoid and topography data—Application to the Alborz Mountains (Iran) and South Caspian Basin region. Tectonophysics 2013, 586, 192–205. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Z.; Hou, Z.; Yu, C. Three Dimensional Crustal Density Structure of Central Asia and its Geological Implications. Acta Geophys. 2016, 64, 1257–1274. [Google Scholar] [CrossRef]
- Tian, Y.; Li, H.; Wang, Y.; Ye, Q.; Guo, A. Gravity Gradient Inversion of Gravity Field and Steady-State Ocean Circulation Explorer Satellite Data for the Lithospheric Density Structure in the Qinghai-Tibet Plateau Region and the Surrounding Regions. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021291. [Google Scholar] [CrossRef]
- Haas, P.; Ebbing, J.; Szwillus, W. Cratonic crust illuminated by global gravity gradient inversion. Gondwana Res. 2023, 121, 276–292. [Google Scholar] [CrossRef]
- Bear, G.W.; Al-Shukri, H.J.; Rudman, A.J. Linear inversion of gravity data for 3-D density distributions. Geophysics 1995, 60, 1354–1364. [Google Scholar] [CrossRef]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Pilkington, M. Analysis of gravity gradiometer inverse problems using optimal design measures. Geophysics 2012, 77, G25–G31. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Li, Y. 3-D inversion of gravity gradiometer data. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: San Antonio, TX, USA, 2001; pp. 1470–1473. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 659–992. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 877–1103. [Google Scholar] [CrossRef]
- Ma, G.; Wang, T.; Meng, Q.; Li, Z.; Wang, T.; Li, L. 3-D inversion of gravity anomalies by combining power-spectrum derived adaptive weighting and cross-gradient regulation: Application to Molybdenum–Copper deposit. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Meng, Z. 3D inversion of full gravity gradient tensor data using SL0 sparse recovery. J. Appl. Geophys. 2016, 127, 112–128. [Google Scholar] [CrossRef]
- Li, Z.; Yao, C.; Zheng, Y. 3D inversion of gravity data using Lp-norm sparse optimization. Chin. J. Geophys. 2019, 62, 3699–3709. [Google Scholar] [CrossRef]
- Calvetti, D.; Somersalo, E. Inverse problems: From regularization to Bayesian inference. WIREs Comput. Stat. 2018, 10, e1427. [Google Scholar] [CrossRef]
- Qin, P.; Huang, D.; Yuan, Y.; Geng, M.; Liu, J. Integrated gravity and gravity gradient 3D inversion using the non-linear conjugate gradient. J. Appl. Geophys. 2016, 126, 52–73. [Google Scholar] [CrossRef]
- Camacho, A.G.; Montesinos, F.G.; Vieira, R. Gravity inversion by means of growing bodies. Geophysics 2000, 65, 95–101. [Google Scholar] [CrossRef]
- Nagihara, S.; Hall, S.A. Three-dimensional gravity inversion using simulated annealing: Constraints on the diapiric roots of allochthonous salt structures. Geophysics 2001, 66, 1438–1449. [Google Scholar] [CrossRef]
- Montesinos, F.G.; Arnoso, J.; Vieira, R. Using a genetic algorithm for 3-D inversion of gravity data in Fuerteventura (Canary Islands). Int. J. Earth Sci. 2005, 94, 301–316. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, G.; Liu, Y.; Fan, Z. Deep Learning for 3-D Inversion of Gravity Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef]
- Davis, K.; Li, Y. Fast solution of geophysical inversion using adaptive mesh, space-filling curves and wavelet compression. Geophys. J. Int. 2011, 185, 157–166. [Google Scholar] [CrossRef]
- Sun, S.Y.; Yin, C.C.; Gao, X.H.; Liu, Y.H.; Ren, X.Y. Gravity compression forward modeling and multiscale inversion based on wavelet transform. Appl. Geophys. 2018, 15, 342–352. [Google Scholar] [CrossRef]
- Mauriello, P.; Patella, D. Gravity probability tomography: A new tool for buried mass distribution imaging. Geophys. Prospect. 2001, 49, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Wong, Y.S. BTTB-based numerical schemes for three-dimensional gravity field inversion. Geophys. J. Int. 2015, 203, 243–256. [Google Scholar] [CrossRef]
- Renaut, R.A.; Hogue, J.D.; Vatankhah, S.; Liu, S. A fast methodology for large-scale focusing inversion of gravity and magnetic data using the structured model matrix and the 2-D fast Fourier transform. Geophys. J. Int. 2020, 223, 1378–1397. [Google Scholar] [CrossRef]
- Xu, S.; Yu, H.; Li, H.; Tian, G.; Yang, J. The inversion of apparent density based on the separation and continuation of potential field. Chin. J. Geophys. 2009, 52, 1592–1598. (In Chinese) [Google Scholar] [CrossRef]
- Cui, Y.; Guo, L. A wavenumber-domain iterative approach for rapid 3-D imaging of gravity anomalies and gradients. IEEE Access 2019, 7, 34179–34188. [Google Scholar] [CrossRef]
- Qiang, J.; Xu, J.; Lu, K.; Guo, Z. A Fast Forward and Inversion Strategy for Three-Dimensional Gravity Field. Mathematics 2023, 11, 962. [Google Scholar] [CrossRef]
- Pawlowski, R.S. Preferential continuation for potential-field anomaly enhancement. Geophysics 1995, 60, 390–398. [Google Scholar] [CrossRef]
- Meng, X.; Guo, L.; Chen, Z.; Li, S.; Shi, L. A method for gravity anomaly separation based on preferential continuation and its application. Appl. Geophys. 2009, 6, 217–225. [Google Scholar] [CrossRef]
- Guo, L.; Meng, X.; Chen, Z.; Li, S.; Zheng, Y. Preferential filtering for gravity anomaly separation. Comput. Geosci. 2013, 51, 247–254. [Google Scholar] [CrossRef]
- Christensen, A.N. Results from FALCON Airborne Gravity Gradiometer surveys over the Kauring AGG Test site. In Proceedings of the 23rd ASEG-PESA International Geophysical Conference and Exhibition, ASEG Extended Abstracts, Melbourne, Australia, 11–14 August 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, M.; Li, W.K.; Feng, W.; Pail, R.; Wu, Y.G.; Zhong, M. Integration of Residual Terrain Modelling and the Equivalent Source Layer Method in Gravity Field Synthesis for Airborne Gravity Gradiometer Test Site Determination. Remote Sens. 2023, 15, 5190. [Google Scholar] [CrossRef]
- Blakely, R. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Fedi, M.; Florio, G. A stable downward continuation by using the ISVD method. Geophys. J. Int. 2002, 151, 146–156. [Google Scholar] [CrossRef]
- Florio, G.; Fedi, M.; Pasteka, R. On the application of Euler deconvolution to the analytic signal. Geophysics 2006, 71, L87–L93. [Google Scholar] [CrossRef]
- Ma, G.; Liu, C.; Huang, D.; Li, L. A stable iterative downward continuation of potential field data. J. Appl. Geophys. 2013, 98, 205–211. [Google Scholar] [CrossRef]
- Xu, S.; Yang, J.; Yang, C.; Xiao, P.; Chen, S.; Guo, Z. The iteration method for downward continuation of a potential field from a horizontal plane. Geophys. Prospect. 2007, 55, 883–889. [Google Scholar] [CrossRef]
- Pawlowski, R.S. Green’s equivalent-layer concept in gravity band-pass filter design. Geophysics 1994, 59, 69–76. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Parker, R. The rapid calculation of potential anomalies. Geophys. J. Res. Astron. Soc. 1972, 31, 447–455. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of Incorrectly Formulated Problems and the Regularization Method. Sov. Math. Dokl. 1963, 4, 1035–1038. [Google Scholar]
- Ghari, H.; Varfinezhad, R.; Parnow, S. 3D joint interpretation of potential field, geology, and well data to evaluate a salt dome in the Qarah-Aghaje area, Zanjan, NW Iran. Near Surf. Geophys. 2023, 21, 233–246. [Google Scholar] [CrossRef]
- Deng, F.; Connor, C.B.; Malservisi, R.; Connor, L.J.; White, J.T.; Germa, A.; Wetmore, P.H. A Geophysical Model for the Origin of Volcano Vent Clusters in a Colorado Plateau Volcanic Field. J. Geophys. Res. Solid Earth 2017, 122, 8910–8924. [Google Scholar] [CrossRef]
- Miller, C.A.; Williams-Jones, G.; Fournier, D.; Witter, J. 3D gravity inversion and thermodynamic modelling reveal properties of shallow silicic magma reservoir beneath Laguna del Maule, Chile. Earth Planet. Sci. Lett. 2017, 459, 14–27. [Google Scholar] [CrossRef]
- Zhang, M.; Qiao, J.; Zhao, G.; Lan, X. Regional gravity survey and application in oil and gas exploration in China. China Geol. 2019, 2, 382–390. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W. The evolving rift belt-Wudalianchi volcanic rock belt. Earth Sci. Front. 2008, 15, 241–250. (In Chinese) [Google Scholar]
- Zhao, Y.W.; Li, N.; Fan, Q.C.; Zou, H.; Xu, Y.G. Two episodes of volcanism in the Wudalianchi volcanic belt, NE China: Evidence for tectonic controls on volcanic activities. J. Volcanol. Geotherm. Res. 2014, 285, 170–179. [Google Scholar] [CrossRef]
- Rasskazov, S.V.; Chuvashova, I.S.; Sun, Y.m.; Yang, C.; Xie, Z.; Yasnygina, T.A.; Saranina, E.V.; Fang, Z. Sources of Quaternary Potassic Volcanic Rocks from Wudalianchi, China: Control by Transtension at the Lithosphere–Asthenosphere Boundary Layer. Geodyn. Tectonophys. 2016, 7, 555–592. [Google Scholar] [CrossRef]
- Li, Z.; Ni, S.; Zhang, B.; Bao, F.; Zhang, S.; Deng, Y.; Yuen, D.A. Shallow magma chamber under the Wudalianchi Volcanic Field unveiled by seismic imaging with dense array. Geophys. Res. Lett. 2016, 43, 4954–4961. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, X.; Zhang, Y.; Li, S.; Li, Z.; Tian, P.; Ming, Y.; Zhang, C. Volcanic magma chamber survey and geothermal geological condition analysis for hot dry rock at the Weishan Volcano in Wudalianchi Region, Heilongjinag Province. Acta Geol. Sin. 2017, 91, 1–16. (In Chinese) [Google Scholar]
- Gao, J.; Zhang, H.; Zhang, S.; Xin, H.; Li, Z.; Tian, W.; Bao, F.; Cheng, Z.; Jia, X.; Fu, L. Magma recharging beneath the Weishan volcano of the intraplate Wudalianchi volcanic field, northeast China, implied from 3-D magnetotelluric imaging. Geology 2020, 48, 913–918. [Google Scholar] [CrossRef]
- Sun, X.; Zhan, Y.; Zhao, L.; Xu, J.; Zhao, Y.; Zhao, B.; Yang, W. Does a Shallow Magma Reservoir Exist in the Wudalianchi Volcanic Field? Constraints From Magnetotelluric Imaging. Geophys. Res. Lett. 2023, 50, e2023GL104318. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Yang, M.; Feng, W.; Zhong, M. Improved Approaches for 3D Gravity and Gradient Imaging Based on Potential Field Separation: Application to the Magma Chamber in Wudalianchi Volcanic Field, Northeastern China. Remote Sens. 2024, 16, 1187. https://doi.org/10.3390/rs16071187
Li W, Yang M, Feng W, Zhong M. Improved Approaches for 3D Gravity and Gradient Imaging Based on Potential Field Separation: Application to the Magma Chamber in Wudalianchi Volcanic Field, Northeastern China. Remote Sensing. 2024; 16(7):1187. https://doi.org/10.3390/rs16071187
Chicago/Turabian StyleLi, Weikai, Meng Yang, Wei Feng, and Min Zhong. 2024. "Improved Approaches for 3D Gravity and Gradient Imaging Based on Potential Field Separation: Application to the Magma Chamber in Wudalianchi Volcanic Field, Northeastern China" Remote Sensing 16, no. 7: 1187. https://doi.org/10.3390/rs16071187
APA StyleLi, W., Yang, M., Feng, W., & Zhong, M. (2024). Improved Approaches for 3D Gravity and Gradient Imaging Based on Potential Field Separation: Application to the Magma Chamber in Wudalianchi Volcanic Field, Northeastern China. Remote Sensing, 16(7), 1187. https://doi.org/10.3390/rs16071187





