Abstract
In this study, a new vegetation observable derived from spaceborne Global Navigation Satellite System-Reflectometry (GNSS-R) was developed. Firstly, a linear relationship between the Cyclone Global Navigation Satellite System (CYGNSS) reflectivity and soil moisture was derived based on the tau-omega () model. The intercept and slope of this linear function were associated with the vegetation properties. Moreover, the intercept is not affected by soil moisture and depends only on vegetation properties. Secondly, to validate the new observable, the intercept demonstrated a significant correlation with vegetation water content (VWC), with the highest correlation coefficient of 0.742. Based on the intercept and slope, a linear model and an artificial neural network (ANN) model were established to retrieve VWC by combining geographical location and land cover information. The correlation coefficient and root-mean-square error (RMSE) of VWC retrieval based on the linear model were 0.795 and 2.155 kg/m2, respectively. The correlation coefficient and RMSE for the ANN model were 0.940 and 1.392 kg/m2, respectively. Compared with the linear model, the ANN model greatly improves the global VWC retrieval in accuracy, especially in areas with poor linear model retrieval results. Therefore, compared with conventional remote sensing techniques, the spaceborne GNSS-R can provide a new and effective approach to global VWC monitoring.
1. Introduction
Vegetation is a crucial component of terrestrial ecosystems, playing a significant role in carbon sequestration and oxygen release. As a key variable of vegetation properties, vegetation water content (VWC) can be used to evaluate forest fire disasters and crop drought. High-precision and long-term monitoring of VWC can contribute to our understanding of vegetation and better forest fire disaster and crop drought assessment.
Recently, Global Navigation Satellite System (GNSS) has been developed in various fields [1,2]. With using the Earth’s surface reflected GNSS signals, GNSS-Reflectometry (GNSS-R) has been developed as a new remote sensing technique for earth surface physical parameters retrieval. Because the L-band signals utilized by GNSS-R can effectively penetrate atmosphere and rain, GNSS-R can easily sense vegetation properties under clouds and rain. Moreover, the GNSS-R receiver eliminates the need for an extra transmitter, thereby enhancing the sustained high spatial and temporal coverage of GNSS-R observables. This design also promotes the development of compact, cost-effective, and energy-efficient GNSS-R receivers with reduced volume.
The remote sensing observation of earth surface physical parameters using GNSS-reflected signals can be traced back to the early 1990s. In 1993, Martin-Neira (1993) suggested the use of GNSS-reflected signals to retrieve sea surface height [3]. Subsequently, GNSS-R-based ground-based platforms and space-based platforms have shown the capacity for surface geophysical parameter retrievals, such as snow depth [4,5], sea surface height [6,7,8], and soil moisture [9,10,11]. With the efforts of scholars and experts, the platform of GNSS-R has expanded from ground-based to spaceborne. With the unique advantage of rapidly obtaining a large range of surface physical parameter information, spaceborne GNSS-R has broader application prospects. Earlier applications of spaceborne GNSS-R were focused on cryosphere/polar applications and ocean parameters, such as sea ice remote sensing [12,13,14], sea surface wind field [15,16,17,18], significant wave height [19,20] etc. The applications of spaceborne GNSS-R on land surfaces are later than those on ocean surfaces owing to the more complex scene of the land surface. The received reflected signal power from the land surface is not only affected by soil moisture but also by surface vegetation and surface roughness [21]. Therefore, information on soil moisture, vegetation parameters, roughness, and other land surface physical parameters can be retrieved by obtaining the relevant information of the reflected signals. GNSS-R has been shown to have the capacity for monitoring land surface geophysical parameters, such as soil moisture [22,23,24], wetlands [25,26], flood inundation [27,28], roughness [29], freeze/thaw [30] etc.
Recently, spaceborne GNSS-R has shown great potential in remote sensing observations of vegetation. Carreno-Luengo et al. (2017) first used spaceborne GNSS-R data to retrieve the soil moisture and above ground biomass (AGB) in a rainforest [31]. Carreno-Luengo et al. (2020) proposed a new observable named “length of the trailing edge” (TE) for AGB retrieval, and the results showed that TE increased with AGB [32]. However, the spaceborne GNSS-R reflectivity is affected by the combination of soil moisture and vegetation effects. Considering the effect of soil moisture, Chen et al. (2021) proposed an AGB retrieval method considering the influence of soil moisture [33]. Although the results had shown some improvements, it cannot entirely eliminate the effects of soil moisture or roughness. Furthermore, the above research showed that dry mass of vegetation (i.e., AGB) is highly correlated with signal attenuation. However, as description in [21], VWC also affects signal attenuation. Motivated by this, we aimed to develop an observable based solely on vegetation and investigate its correlation with AGB and VWC. In the derivation, the tau-omega model is used, which has been previously considered in GNSS-R [34,35]. In addition, the semiempirical model established by Yueh et al. [21] is also used. Through a comparison of the two model derivations, we obtained a new GNSS-R observable that exhibits a stronger correlation with vegetation. Based on these findings, we proposed a VWC retrieval method utilizing spaceborne GNSS-R.
2. Data
The data used in this study were derived from CYGNSS, Soil Moisture Active Passive (SMAP) and Moderate-resolution Imaging Spectroradiometer (MODIS). Note that the data derived from CYGNSS and the soil moisture data derived from SMAP were initially matched in terms of time and space. Since soil moisture exhibits minimal daily variation, the CYGNSS data and soil moisture data were collocated daily in EASE 2.0 36 km grid. Then, for convenient comparison, the new vegetation observables and VWC were collocated monthly and half-year (January to June and July to December) in EASE 2.0 36 km grid. Since there is a single map of land cover dataset, the land cover dataset was collocated once in EASE 2.0 36 km grid.
2.1. CYGNSS
The primary purpose of the NASA CYGNSS mission was to monitor hurricanes using a revised Space GNSS Receiver Remote Sensing Instrument (SGR-ReSI). Using eight microsatellites, CYGNSS cover the regions within latitudes of approximately 38° N and 38° S and reduces the revisit time by several hours. Most recently, in addition to ocean applications, CYGNSS has shown the potential to retrieve the Earth’s geophysical parameters. The CYGNSS has the advantages of great spatial coverage and high temporal resolution for VWC monitoring.
The CYGNSS provides data with four different processing levels. Since the temporal resolution of CYGNSS data was improved by twice (=2 Hz) after July 2019, the Level 1 data in NetCDF format, from Jan 2019 to December 2019, were used for further analysis in this study. Data collected from July 2019 to December 2019 were used to retrieve VWC. These data are available at https://podaac.jpl.nasa.gov, accessed on 1 August 2022. The observables derived from Level 1 data are DDM bin analog power, Specular point latitude and longitude, GPS effective isotropic radiated power, antenna gain, ranges from specular point to satellite and receiver, and incidence angle.
2.2. VWC
The VWC dataset used in this study was provided by SMAP, which is based on the land cover and normalized difference vegetation index (NDVI) derived from MODIS and can be available at https://nsidc.org/data/smap/smap-data.html, accessed on 1 August 2022 [36]. The VWC algorithm of SMAP is given by [36]
where the stem factor is the peak amount of water residing in the stems. This algorithm has been shown the capacity for global VWC reasonable estimations [36,37]. Figure 1a shows the monthly VWC in kg/m2 for each land cover in 2019. Figure 2 shows average VWC from July to December 2019. Figure 2 illustrates that VWC varies relatively small in each land cover category. It should be noted that due to the limited amount of data for Barren or Sparsely Vegetated, there were significant fluctuations in VWC as shown in Figure 1b. In other words, the limited amount of data may be derived from high or low VWC areas, which may lead to gross error.
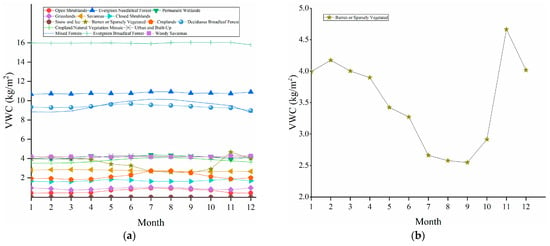
Figure 1.
(a) Monthly VWC in kg/m2 for each land cover in 2019. (b) Monthly VWC in kg/m2 VWC for land cover of Barren or Sparsely Vegetated in 2019.
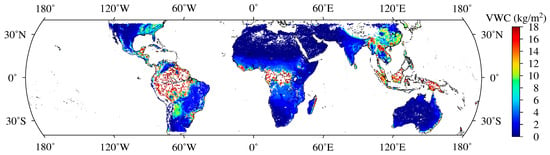
Figure 2.
Average VWC provided by the Soil Moisture Active Passive mission from July to December 2019.
2.3. Soil Moisture
The SMAP mission was launched by NASA in January 2015, and it provides global soil moisture data for land within 45°N–45°S, every 2–3 days, with high accuracy and spatial resolution. This data can be downloaded at https://nsidc.org/data/smap/smap-data.html, accessed on 1 August 2022. The SMAP L3 radiometer global daily 36 km EASE-Grid soil moisture product, from January 2019 to December 2019, was used in this study. As example, Figure 3 shows the average soil moisture obtained from the SMAP from January to June 2019.
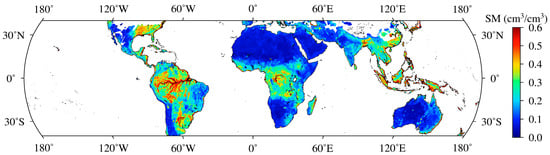
Figure 3.
Average soil moisture (SM) obtained from SMAP from January to June 2019.
2.4. Land Cover
The other auxiliary data was land cover. This dataset was extracted from the Terra data using different classification schemes based on land cover characteristics every year. It was re-projected to geographic coordinates in GeoTIFF format with a spatial resolution of 0.5°, covering a longitude range of 180°W–180°E and a latitude range of 64°S–84°N. The land cover classification is defined by the International Geosphere–Biosphere Programme (IGBP), which consists of 11 categories of natural vegetation, 3 categories of land use and land mosaics, and 3 categories of non-vegetative land, as shown in Figure 4.
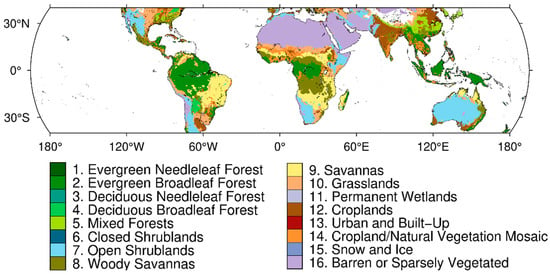
Figure 4.
Distribution of land cover types defined by the IGBP.
3. Derivation of the Vegetation Observables and the Correlation Analysis
3.1. Derivation of the Vegetation Observables from CYGNSS
When vegetation grows on the soil surface, the reflected signals from the soil are attenuated. For low vegetation, the effect of vegetation on the reflected signals for the microwave band can be modeled using the tau-omega model [38] as follows.
where E is the surface emissivity; represents the reflectivity of the bare soil surface, which depends on soil surface properties (such as moisture, texture, roughness, and salinity); w represents the single scattering albedo, mainly related to the vegetation canopy; L is the vegetation attenuation. L and E can be expressed as
where is the optical depth; is the incidence angle. is given by [39]
where is Fresnel reflection coefficient; denotes scattering loss due to the surface roughness; k is the electromagnetic wavenumber, and h is the root-mean-square (rms) surface height. As described in [21,39], can be expressed as a function of soil moisture. Therefore, is assumed to be a function of soil moisture, which can be represented as
where is a function of soil properties (including texture, roughness, and salinity) and the incident angle; SM is soil moisture. Therefore, by combining Equations (2), (4) and (6)
According to the relationship between the surface emissivity and the reflectivity [38], for GNSS-R, E is given as
where represents the normalized reflected power, which can be derived from DDM (Delay Doppler Map); Note that, E does not depend on the reflectivity of GNSS-R but on soil’s properties (moisture, texture, roughness et al.). Equation (8) means that the variation of the surface emissivity (E) can be indirectly reflected through the reflectivity of GNSS-R. The GNSS-R reflectivity () is given as [15]
where and are the transmitter-to-surface and surface-to-receiver ranges, respectively; represents the GNSS effective isotropic radiated power (EIRP); is the peak power of DDM; is the receiver gain. The relationship between and is given as
where represents the maximum value in array , while represents the minimum value in array . Because the maximum and minimum values are determined for each set of numbers, and are constants. Thus, Equation (7) can be further derived as
Here, assuming that
Equation (11) can be written as
where coefficient A depends mainly on soil properties (including texture, roughness, and salinity) and the incident angle. Note that, as description in [38], the single scattering albedo (w) can be considered a constant. Therefore, intercept feature B depends on L, which is directly related to vegetation properties. From Equation (3), L depends on , which is commonly assumed to be linearly proportional to VWC [40]
Thus, intercept feature B is related to VWC. Therefore, intercept feature B was used for VWC retrieval. In addition, although coefficient A is mainly related to soil properties and the incident angle, it is also related to vegetation properties. Thus, coefficient A was further used to retrieve VWC. Note that VWC is depends on AGB and relative water content (RWC) [41]
Therefore, the analysis of the relationship between intercept feature B and AGB was further conducted. Due to intercept feature B was directly related to VWC, the focus of this paper was on VWC retrieval.
The mentioned above showed the linear relationship between the spaceborne GNSS-R reflectivity and soil moisture based on the tau-omega model. In this regression relationship, the coefficient A depends mainly on soil properties while the intercept feature B is a quantity directly related to vegetation properties. Here, to extract coefficient A and intercept feature B, we utilize matched data of CYGNSS and soil moisture from each month and half-year (January to June and July to December) to establish a linear relationship between spaceborne GNSS-R reflectivity and soil moisture.
3.2. Correlation Analysis Correlation Analysis between the GNSS-R Observables and Vegetation Parameters (VWC, AGB)
As previously mentioned, intercept feature B is more suitable for characterizing vegetation properties in theory compared to coefficient A. Additionally, the intercept feature B is directly related to VWC and indirectly related to AGB. To verify this relationship, an analysis of the correlation between the new observables and VWC, AGB was conducted. The AGB data was obtained from LUCID (Land use, Carbon & Emission Data, http://lucid.wur.nl/datasets, accessed on 1 August 2022). Note that, the coefficients and intercepts derived from Equation (14) may change over time due to errors in soil moisture provided by SMAP and changes in VWC. Therefore, to assess its stability, a correlation analysis was conducted between the new observables and VWC as well as AGB in different periods. Specifically, monthly and semi-annual analyses were carried out. Furthermore, to evaluate the performance of the new observables, a correlation analysis between the traditional observable () and VWC as well as AGB.
Figure 5 and Figure 6 display the global distribution of coefficient A and intercept feature B from January to June 2019, respectively. The correlation coefficients are presented in Table 1. Figure 2 and Figure 6 reveal that the global distribution of coefficient A differed significantly from the VWC distribution. Conversely, intercept feature B display consistency with the reference VWC distribution presented in Figure 2.
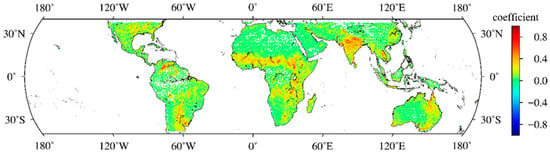
Figure 5.
Global distribution of coefficient A.
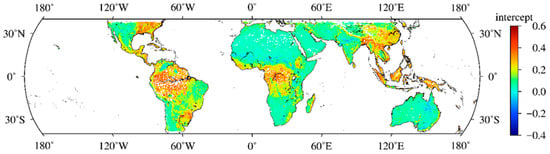
Figure 6.
Global distribution of intercept feature B.

Table 1.
Correlation coefficients between the GNSS-R observables and vegetation parameters (VWC, AGB) in 2019.
Table 1 shows that the correlation coefficients between A and VWC as well as A and AGB were small, with the values less than 0.25. Meanwhile, the absolute correlation coefficients between and VWC as well as and AGB are less than 0.33. However, the correlation coefficients between B and VWC as well as B and AGB are large, with the values greater than 0.6. Furthermore, the correlation coefficients between B and VWC are higher than the correlation coefficients between B and AGB. These results confirm that, compared with the coefficient A and , intercept feature B are more sensitive to VWC and AGB. Additionally, in most subsets, the correlation coefficients between January and June are smaller than those between July and December. This was because the temporal resolution of CYGNSS data was improved by twice (=2 Hz) after July 2019, resulting in an increase in the amount of matched data in each pixel and a more stable regression effect. Therefore, to improve regression stability, the data from July to December 2019 were used to extract coefficient A and intercept feature B.
4. VWC Retrieval Models
As previously mentioned, we utilized the coefficient A and intercept feature B derived from the tau-omega model to retrieve VWC. Because of the different VWC values under different land cover and geographical location (i.e., latitude and longitude), land cover and geographical location information are also used to retrieve VWC. Based on these input features, namely coefficient A, intercept feature B, land cover, and geographical location, we proposed five linear models and five ANN models in this study. Furthermore, to reduce the impact of random errors, we performed regression using half-year data.
4.1. Linear Model
To verify the contribution of coefficient A, intercept feature B, land cover, and geographical location to VWC retrieval, five VWC retrieval linear models were adopted in this study as follows.
where A is coefficient A; B is intercept feature B; Landcover is land cover; lat is latitude; lon is longitude; the last term in all the formulas is the constant to be fitted. Note that because there is no specific numerical value for land cover, different land cover values were assigned in this study, as shown in Figure 4. To obtain a more stable model, the data was divided into training set, verification set and test set. The training set comprises 25% of the total data, while the validation set and the test set each account for 10% and 65%, respectively.
4.2. ANN Model
In theory, the relationship between the input features and vegetation properties is complex. Since ANNs can learn the complex relationship between input features and vegetation properties, an BP neural network was applied here. Similar to linear models, five different ANN models were established to retrieve VWC using the input features of coefficient A, intercept feature B, land cover, and geographical location. The input features of different ANN models were shown in Table 2.

Table 2.
Input features of different artificial neural network models.
As shown in Figure 7, structurally, the BP neural network typically consists of three layers: the input layer, the hidden layer, and the output layer. Each layer contains nodes, and the nodes in adjacent layers are interconnected through weights. However, the nodes within each layer operate independently. The principle of forward propagation in a BP neural network can be succinctly described mathematically as follows.
where W and b are training parameters; σ is the nonlinear function, such as the sigmoid function, hyperbolic tangent function, and rectified linear units (RELUs). These functions are given as
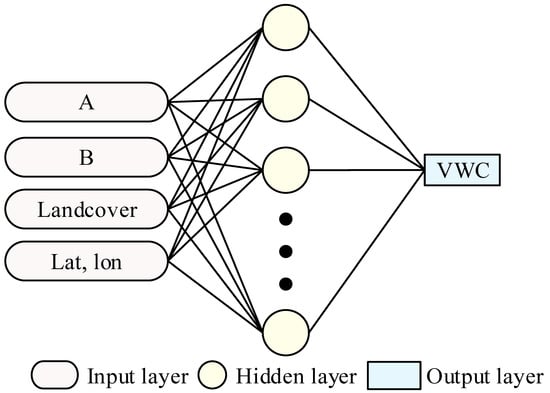
Figure 7.
The architecture and input features of the ANN models.
In this study, hyperbolic tangent function was used. After testing, when the number of hidden layers was one and the number of neurons in the hidden layer was 15, the training results of each model were relatively better. Additionally, the training set comprises 25% of the total data, while the validation set and the test set account for 10% and 65%, respectively.
5. VWC Retrievals
We evaluated the performance of the linear models and ANN models using mean absolute error (MAE), mean relative absolute error (MRAE), root mean square error (RMSE), and correlation coefficient. The MAE and MRAE are given by
where is the reference VWCs; n is the number of samples; is the VWC retrievals; is the mean reference VWC.
Table 3 summarized the MAE, MRAE, RMSE, correlation coefficient and samples of each linear and ANN model. Table 3 demonstrated that when using intercept feature B alone of Linear model 1 achieved an MAE of 1.759, MRAE of 0.644, RMSE of 2.751 kg/m2, and correlation coefficient of 0.741 for VWC retrieval. Similarly, with intercept feature B alone, ANN Model 1 achieved an MAE of 1.623, MRAE of 0.593, RMSE of 2.506 kg/m2, and correlation coefficient of 0.773 for VWC retrieval. After adding other features, the MAE, MRAE, and RMSE of the VWC retrieval were reduced, and the correlation coefficient was increased. According to the accuracy improvement in Table 3, it can be inferred that intercept feature B contributed the most to the VWC retrieval, followed by land cover, geographical location, and finally coefficient A. Compared with using intercept feature B alone, the performance of Linear model 5 was further improved after adding coefficient A, land cover, and geographical location, with RMSE reduced by 21.66% and the correlation coefficient increased by 7.28%. Meanwhile, the RMSE and correlation coefficient of ANN model 5 were reduced by 44.45% and increased by 21.60%, respectively, after adding land cover, geographical location, and coefficient A. Moreover, compared with the Linear model, the ANN model had better performance.

Table 3.
VWC retrieval performance of different Models.
To further analyze the performance of the proposed models, for avoiding repetition, only the specific retrievals of Linear model 5 and ANN model 5 were given, as shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Figure 8 and Figure 9 displayed the global distribution of VWC values retrieved by Linear Model 5 and ANN Model 5. Figure 10 depicted a scatter plot of the VWC reference values provided by SMAP and the VWC retrievals of Linear Model 5 and ANN Model 5. Figure 11, Figure 12, Figure 13 and Figure 14 showed the absolute bias and MRAE of the VWC retrievals derived from Linear Model 5 and ANN Model 5, respectively. It should be noted that, due to the elimination of pixels with more than 10% water body during data processing, the resolution was poor in some regions, such as the Amazon region.
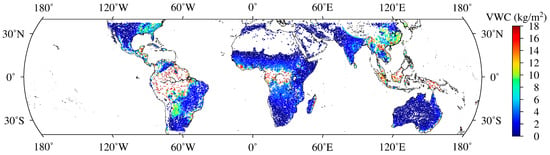
Figure 8.
Global distribution of VWC retrievals based on Linear Model 5.
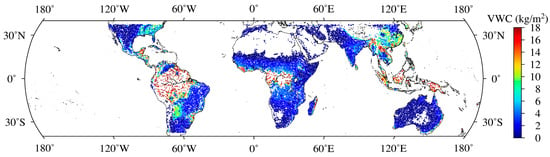
Figure 9.
Global distribution of VWC retrievals based on ANN Model 5.
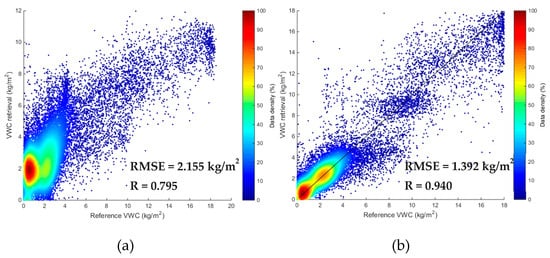
Figure 10.
(a) VWC retrievals from CYGNSS based on linear Model 5 and reference VWCs. (b) VWC retrievals from CYGNSS based on ANN Model 5 and reference VWCs. The black line represents a 1:1 line between VWC retrievals and the reference VWCs.
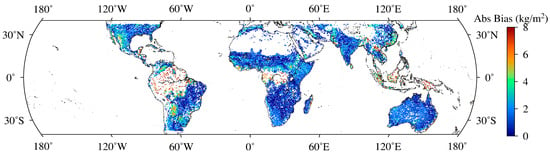
Figure 11.
Global distribution of absolute bias in VWC retrievals based on Linear Model 5.
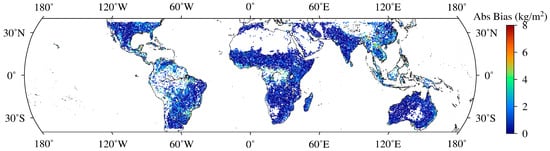
Figure 12.
Global distribution of absolute bias in VWC retrievals based on ANN Model 5.
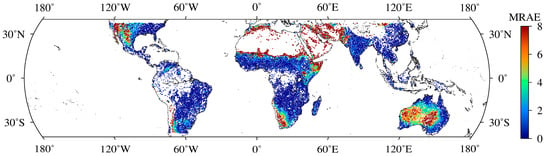
Figure 13.
Global distribution of MRAE in VWC retrievals based on Linear Model 5.
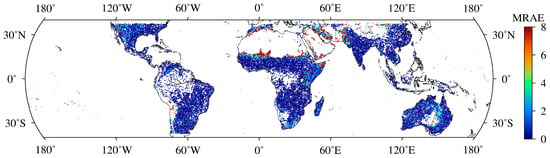
Figure 14.
Global distribution of MRAE in VWC retrievals based on ANN Model 5.
Figure 8 and Figure 9 showed that the CYGNSS VWC retrievals based on Linear Model 5 and ANN Model 5 were in good agreement with the global distribution of the reference VWC. Figure 10a,b demonstrated that the CYGNSS VWC retrievals based on Linear Model 5 and ANN Model 5 and reference VWC values were scattered around the 1:1 line. However, there was an obvious angle between 2 kg/m2 and 4 kg/m2 in the scatter distribution of the Linear Model 5 retrievals. Compared to the Linear Model 5, the angle of the scatter distribution in ANN Model 5 disappeared. The reason could be that the ANN model is more adept at learning intricate nonlinear relationships among the input features. The aforementioned analysis revealed that Linear Model 5 and ANN Model 5 exhibited good performance on a global scale. Moreover, the performance of ANN Model 5 was better than Linear Model 5.
For local areas, more details must be explored. For example, from Figure 11, the absolute bias values in the VWC retrievals of Linear Model 5 were greater than 4 in northern Argentina, southern Bolivia, western Paraguay, northern Brazil, northern Laos, northern Vietnam, northern Burma, and Malay Archipelago. Compared to the Linear Model 5, although Figure 12 showed that the absolute bias values of ANN Model 5 decreased significantly in these areas, the absolute bias values of these areas were still large. It can be found that these areas were mostly located in high vegetation with high VWC. This is not surprising since a small error in these areas can lead to a large absolute bias. In addition, GNSS-R signals mostly depend on vegetation volume scattering in these areas, which weakens the regression between the GNSS-R observables and soil moisture. Therefore, MRAE was more suitable for evaluating the accuracy of the models in these areas.
As shown in Figure 13, the MRAEs in the VWC retrievals of Linear Model 5 were greater than 5 in local areas, including southern Sahara Desert, central Australia, Iraq, southern Iran, Pakistan, Afghanistan. This is possibly because the linear model cannot accurately reflect the relationship between the observables and VWC. Furthermore, Figure 10a illustrated that, there was an obvious angle between 2 kg/m2 and 4 kg/m2 in the scatter distribution of the retrievals. Thus, it can be inferred that the relationship between the observable and VWC is nonlinear. Compared to the Linear Model 5, although ANN Model 5 showed better performance overall, there were some low VWC areas showing poor performance with an MRAE greater than 5 (e.g., southern Sahara Desert, parts of the Middle East) as shown in Figure 14. This is because most of these areas are desert areas with low VWC values. Compared with high VWC areas, small changes in VWC in these areas can lead to larger MRAE values compared to areas with high VWC.
All the above analyses and results demonstrated that not only new significant vegetation information can be provided by intercept feature B, but also a high VWC retrieval performance can be obtained using the ANN model based on intercept feature B. However, the VWC retrieval resolution in this study was 36 km, which is lower than that of the traditional remote sensing method. Therefore, improving the spatial resolution of spaceborne GNSS-R VWC retrieval is a problem that needs to be solved in the future.
6. Conclusions
In this study, we developed a linear relationship between the CYGNSS reflectivity observable and soil moisture based on the tau-omega model. We discovered that the slope (coefficient A) and intercept (intercept feature B) of this linear function were associated with vegetation properties. Moreover, intercept feature B was solely dependent on vegetation properties and unaffected by soil moisture. Additionally, intercept feature B was highly correlated with VWC measurements derived from SMAP, with the highest correlation coefficient of 0.742. Hence, intercept feature B can provide crucial vegetation information.
To demonstrate the capability of the spaceborne GNSS-R for VWC retrieval, based on coefficient A and intercept feature B, a linear model and an ANN model were established to retrieve VWC by combining the latitude, longitude, and land cover information. The results show that the CYGNSS VWC retrievals were in good agreement with reference VWCs. Moreover, the performance of the ANN model was better than that of the linear model with a correlation coefficient of 0.940 and RMSE of 1.392 kg/m2. Additionally, compared with conventional remote sensing techniques, these results show that spaceborne GNSS-R can not only compensate for the limitations of traditional optical remote sensing in meteorological effects but also provide a new effective approach to global VWC monitoring.
Author Contributions
Conceptualization, F.C. and F.G.; methodology, F.C.; software, F.C.; validation, F.C., F.G., L.L. and L.H.; formal analysis, F.C.; investigation, F.C.; resources, F.C.; data curation, F.C.; writing—original draft preparation, F.C.; writing—review and editing, F.C., F.G., L.L. and L.H.; visualization, L.L., F.G.; supervision, F.G.; project administration, F.C.; funding acquisition, F.C. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the Science and Technology Planning Foundation of Guangxi (guikeAD23026257) and the National Natural Science Foundation of China (41825009, 42074029, and 42064002).
Data Availability Statement
The CYGNSS data is available at https://podaac.jpl.nasa.gov, accessed on 1 August 2022. The VWC, soil moisture and land cover data are available at https://nsidc.org/data/smap/smap-data.html, accessed on 1 August 2022. The AGB data can be downloaded at http://lucid.wur.nl/datasets, accessed on 1 August 2022.
Acknowledgments
The authors would like to thank NASA for providing CYGNSS, SMAP mission data as well as LUCID for providing AGB data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kaplan, E.; Hegarty, C. Understanding GPS Principles and Applications, 2nd ed.; British Library Cataloguing in Publication Data; Artech House: Boston, MA, USA, 2006; pp. 1–723. [Google Scholar]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. PPP-RTK functional models formulated with undifferenced and uncombined GNSS observations. Satell. Navig. 2022, 3, 3. [Google Scholar] [CrossRef]
- Martin-Neira, M. A Pasive Reflectometry and Interferometry System (PARIS) Application to Ocean Altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Yu, K.; Li, Y.; Chang, X. Snow Depth Estimation Based on Combination of Pseudorange and Carrier Phase of GNSS Dual-Frequency Signals. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 1817–1828. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X. Triple-frequency Multi-GNSS reflectometry Snow Depth Retrieval by Using Clustering and Normalization Algorithm to Compensate Terrain variation. GPS Solut. 2020, 24, 52. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Xiao, R.; Song, M.; Jia, D. Millimeter to Centimeter Scale Precision Water-level Monitoring Using GNSS Reflectometry: Application to the South-to-North Water Diversion Project, China. Remote Sens. Environ. 2021, 265, 112645. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhang, Q. Evaluation and Combination of Quad-constellation Multi-GNSS Multipath Reflectometry Applied to Sea Level Retrieval. Remote Sens. Environ. 2019, 231, 111229. [Google Scholar] [CrossRef]
- Tabibia, S.; Geremia-Nievinskib, F.; Francisa, O.; van Dam, T. Tidal Analysis of GNSS Reflectometry Applied for Coastal Sea Level Sensing in Antarctica and Greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS Receivers as A Soil Moisture Network for Water Cycle Studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Wang, L.; Zhang, J.; Peng, J.; Liu, Q. Evaluation of GNSS-IR for Retrieving Soil Moisture and Vegetation Growth Characteristics in Wheat Farmland. J. Surv. Eng. 2021, 147, 4021009. [Google Scholar] [CrossRef]
- Li, Y.; Yu, K.; Li, J.; Jin, T.; Chang, X.; Zhang, Q.; Yang, S. Measuring Soil Moisture with Refracted GPS Signals. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 2504205. [Google Scholar] [CrossRef]
- Alonsoarroyo, A.; Zavorotny, V.U.; Camps, A. Sea Ice Detection Using GNSS-R Data from UK TDS-1. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Li, W.; Estel, C.; Fran, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First Spaceborne Phase Altimetry Over Sea Ice Using TechDemoSat-1 GNSS-R Signals. Geophys. Res. Lett. 2017, 16, 8369–8376. [Google Scholar] [CrossRef]
- Cartwright, J.C.; Banks, J.; Srokosz, M. Sea Ice Detection Using GNSS-R Data from TechDemoSat-1. J. Geophys. Res. Ocean. 2019, 124, 5801–5810. [Google Scholar] [CrossRef]
- Zavorotnyand, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Clariziaand, M.P.; Ruf, C.S. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission. IEEE T. Geosci. Remote 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Zhelavskaya, I.; Foti, G.; Reich, S.; Wickert, J. A GNSS-R Geophysical Model Function: Machine Learning for Wind Speed Retrievals. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1333–1337. [Google Scholar] [CrossRef]
- Addabbo, P.; Di Bisceglie, M.; Galdi, C.; Giangregorio, G. An Algorithm for Wind Speed Retrieval from CYGNSS Space Observatories. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Alonso-Arroyo, A.; Camps, A.; Park, H.; Pascual, D.; Onrubia, R.; Martín, F. Retrieval of Significant Wave Height and Mean Sea Surface Level Using the GNSS-R Interference Pattern Technique: Results from a Three-Month Field Campaign. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3198–3209. [Google Scholar] [CrossRef]
- Wang, F.; Yang, D.K.; Li, W.Q.; Zhang, Y.Z. A New Retrieval Method of Significant Wave Height Based on Statistics of Scattered BeiDou GEO Signals. In Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (Ion Gnss+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Yueh, S.H.; Shah, R.; Chaubell, M.J. A Semiempirical Modeling of Soil Moisture, Vegetation, and Surface Roughness Impact on CYGNSS Reflectometry Data. IEEE Trans. Geosci. Remote Sens. 2020, 60, 5800117. [Google Scholar] [CrossRef]
- Tyagi, S.; Pandey, D.K.; Putrevu, D. Sensitivity Analysis of CYGNSS Derived Radar Reflectivity for Soil Moisture Retrieval over India: Initial results. In Proceedings of the 2019 IEEE 16th India Council International Conference (INDICON), Rajkot, India, 13–15 December 2019. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating Soil Moisture Remote Sensing with Observations from the UK TechDemoSat-1 Satellite Mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical Soil Moisture Mapping Based on A Three-layer Model from CYGNSS GNSS-R Data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Morris, M.; Chew, C.; Reager, J.T.; Shah, R.; Zuffada, C. A Novel Approach to Monitoring Wetland Dynamics Using CYGNSS: Everglades Case Study. Remote Sens. Environ. 2019, 233, 111417. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Zuffada, C.; Shah, R.; Chew, C.; Lowe, S.T.; Mannucci, A.J.; Cardellach, E.; Brakenridge, G.R.; Geller, G.; Rosenqvist, A. Wetland Monitoring with Global Navigation Satellite System Reflectometry. Earth Space Sci. 2017, 4, 16–39. [Google Scholar] [CrossRef] [PubMed]
- Unnithan, S.L.K.; Biswal, B.; Rudiger, C. Flood Inundation Mapping by Combining GNSS-R Signals with Topographical Information. Remote Sens. 2020, 12, 3026. [Google Scholar] [CrossRef]
- Loria, E.; O’Brien, A.; Zavorotny, V.; Downs, B.; Zuffada, C. Analysis of Scattering Characteristics from Inland Bodies of Water Observed by CYGNSS. Remote Sens. Environ. 2020, 245, 111825. [Google Scholar] [CrossRef]
- Stilla, D.; Zribi, M.; Pierdicca, N.; Baghdadi, N.; Huc, M. Desert Roughness Retrieval Using CYGNSS GNSS-R Data. Remote Sens. 2020, 12, 743. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Ruf, C.S. Retrieving Freeze/thaw Surface State from CYGNSS Measurements. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4302313. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Lowe, S.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP Mission: First Assessment of Polarimetric Scatterometry over Land and Cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CYGNSS. Remote Sens. 2020, 12, 1368. [Google Scholar] [CrossRef]
- Chen, F.; Guo, F.; Liu, L.; Nan, Y. An Improved Method for Pan-Tropical Above-Ground Biomass and Canopy Height Retrieval Using CYGNSS. Remote Sens. 2021, 13, 2491. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.-W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J.-STARS 2016, 9, 4730–4742. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Sensitivity of CYGNSS Bistatic Reflectivity and SMAP Microwave Radiometry Brightness Temperature to Geophysical Parameters over Land Surfaces. IEEE J.-STARS 2018, 12, 107–122. [Google Scholar] [CrossRef]
- Chan, S.; Bindlish, R.; Hunt, R.; Jackson, T.; Kimball, J. Ancillary Data Report: Vegetation Water Content. SMAP Proj. Doc., JPL D-53061. SMAP Data Documents. 2013. Available online: https://smap.jpl.nasa.gov/system/internal_resources/details/original/289_047_veg_water.pdf (accessed on 1 August 2022).
- Zheng, X.; Ding, Y.; Zhao, X.; Yu, B.; Xiaofeng, L.; Kai, Z.; Tao, J. Uncertainty Evaluation at Three Spatial Scales for the NDVI-based VWC Estimation Method Used in the SMAP Algorithm. Remote Sens. Lett. 2019, 10, 563–572. [Google Scholar]
- Camps, A.; Park, H.; Bandeiras, J.; Barbosa, J.; Sousa, A.; d’Addio, S.; Martin-Neira, M. Microwave Imaging Radiometers by Aperture Synthesis—Performance Simulator (Part 1): Radiative Transfer Module. J. Imaging 2016, 2, 17. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Konings, A.G.; Piles, M.; Rötzer, K.; McColl, K.A.; Chan, S.K.; Entekhabi, D. Vegetation Optical Depth and Scattering Albedo Retrieval Using Time Series of Dual-polarized L-band Radiometer Observations. Remote Sens. Environ. 2016, 172, 178–189. [Google Scholar] [CrossRef]
- Konings, A.G.; Saatchi, S.S.; Frankenberg, C.; Keller, M.; Leshyk, V.; Anderegg, W.R.; Humphrey, V.; Matheny, A.M.; Trugman, A.; Sack, L.; et al. Detecting Forest Response to Droughts with Global Observations of Vegetation Water Content. Glob. Chang. Biol. 2021, 27, 6005–6024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).