Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios
Abstract
1. Introduction
2. Materials and Methods
2.1. Method Framework Design
2.2. Task Preprocessing Method
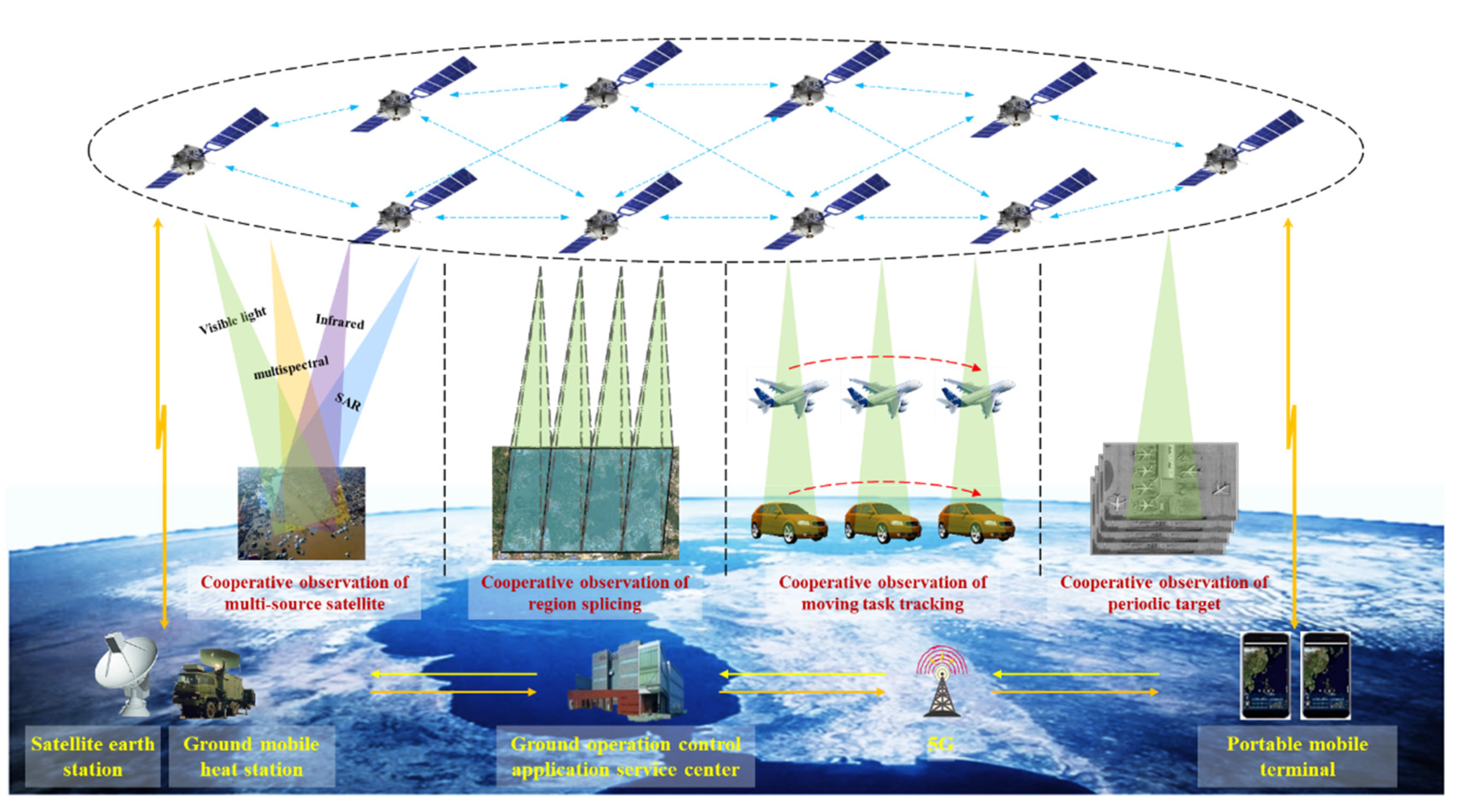
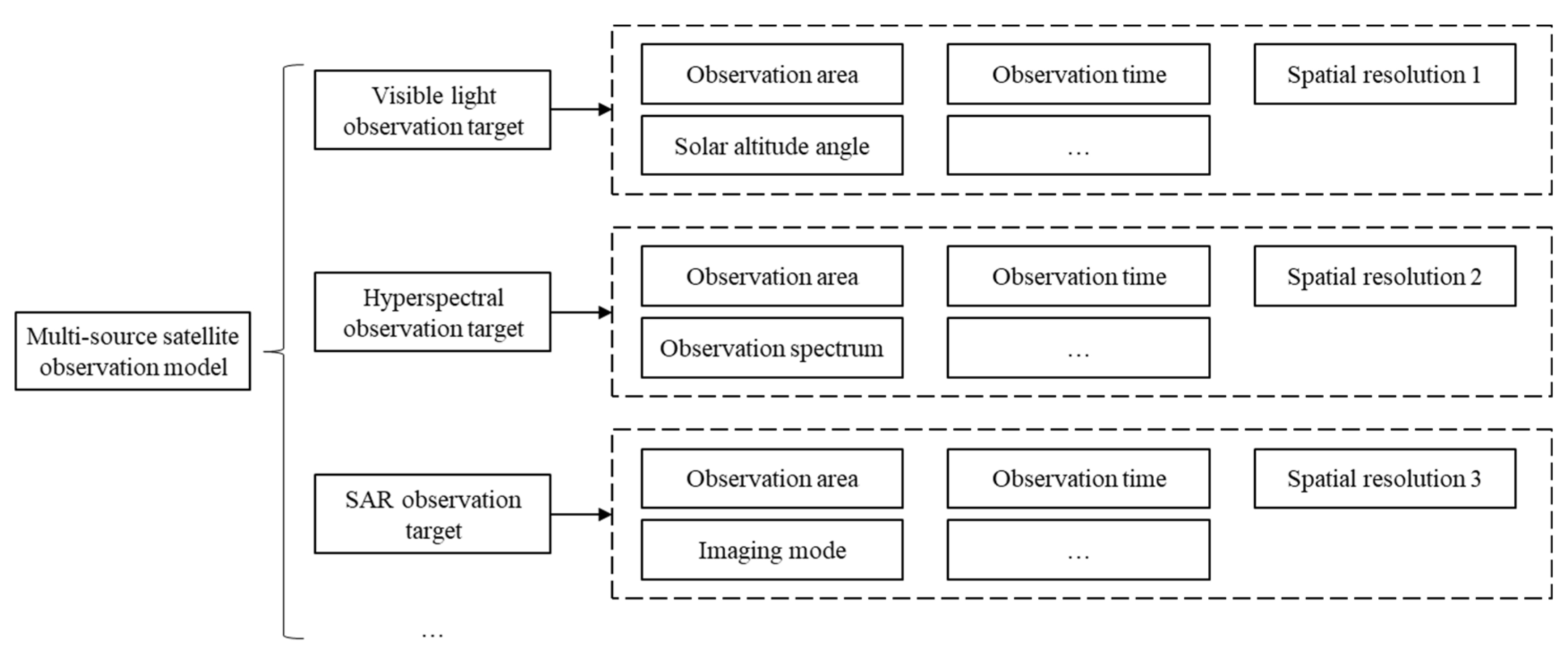
- Multi-source satellite cooperative observation mode
- Regional stitching cooperative observation mode
- Moving target tracking cooperative observation mode
- Periodic target cooperative observation mode
- (1)
- Task decomposition for the multi-source remote sensing satellite cooperative observation mode
- (2)
- Task decomposition for the regional stitching cooperative observation mode
- (3)
- Task decomposition for the moving target tracking cooperative observation mode
- (4)
- Task decomposition for periodic target cooperative observation mode
2.3. Resource Allocation Method
2.3.1. Generalized Multi-Satellite Cooperative Observation Task Planning Method
- (1)
- Time window constraint
- (2)
- Observation time constraint
- (3)
- Satellite resource uniqueness constraint
- (4)
- Observation target uniqueness constraint
- (5)
- Cloud cover constraint
2.3.2. Method for Dynamic Adjustment of New Task Planning Schemes
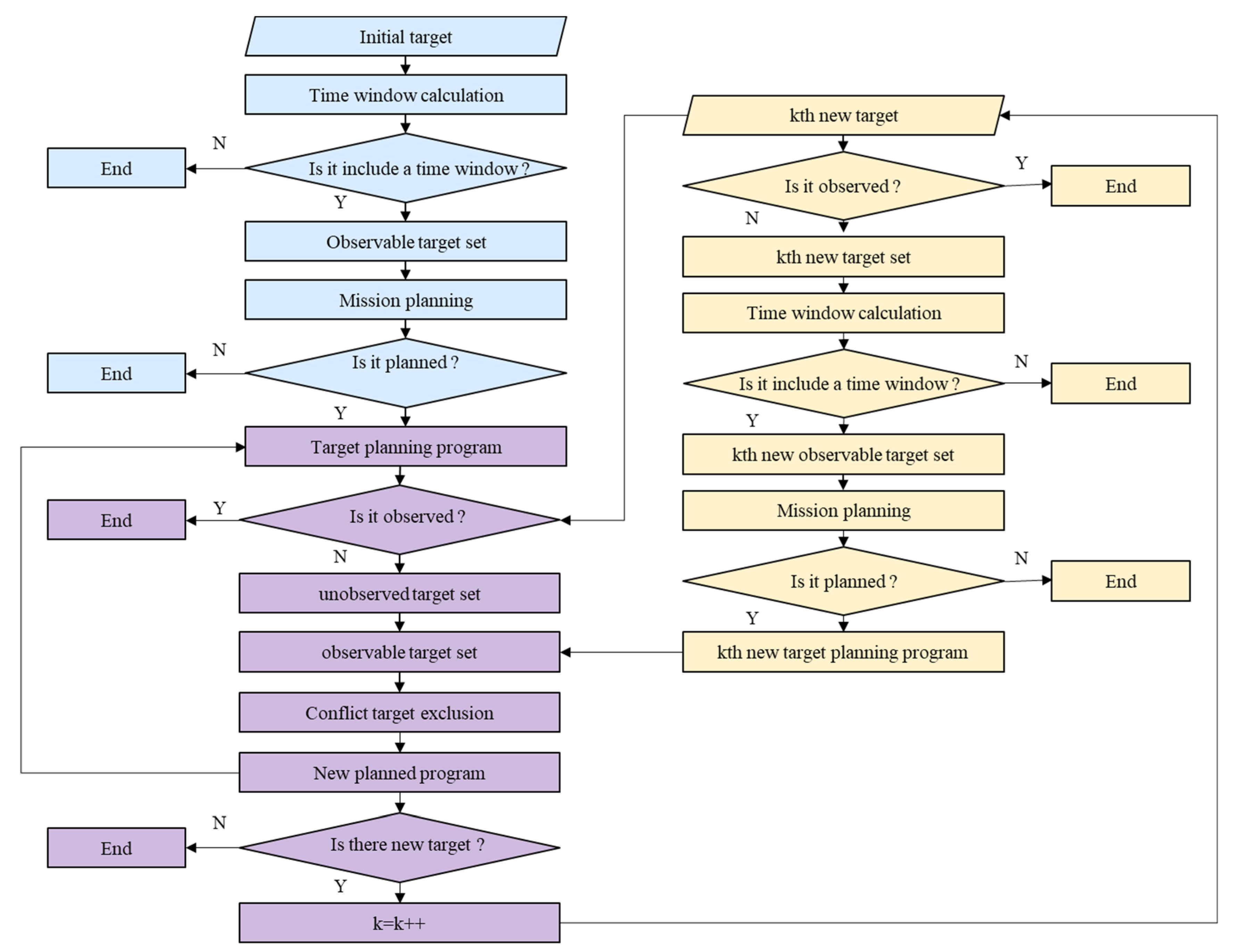
2.3.3. Dynamic Task Planning Solution Algorithm for Multi-Satellite Cooperative Observation
- Initially, task planning is conducted for the initial targets, calculating their time windows and classifying those with effective time windows into an observable target collection. Subsequently, task planning is performed for the targets within this collection, forming a task planning scheme.
- When the k-th new task arises, it is first determined whether the new target duplicates tasks in the existing planning scheme. Otherwise, the target is classified into the k-th new target collection. Then, time windows for targets within this collection are calculated, and those with effective time windows are classified into the k-th new observable target collection. Task planning is conducted for targets within this collection, forming the k-th new target task planning scheme.
- Subsequently, whether targets in the existing planning scheme have been observed or are currently being observed is assessed. Otherwise, the unobserved target schemes are categorized into the unobserved target collection and merged with the targets to be observed in the k-th new target task planning scheme. This step forms the k-th collection of targets to be observed, followed by the application of dynamic scheme adjustment methods to eliminate targets with time conflicts, thus forming a new planning scheme.
- When new task requirements emerge again, steps 1–3 are repeated to adjust the planning scheme anew.
3. Design of Experiments
3.1. Experimental Environment and Data
3.2. Evaluation Indices
- (1)
- Total number of planned targets
- (2)
- Total computational time
- (3)
- Sum of task priorities
- (4)
- Total satellite resource value
- (5)
- Comprehensive benefit value
3.3. Experiment and Results
3.3.1. Introduction to Different Methods
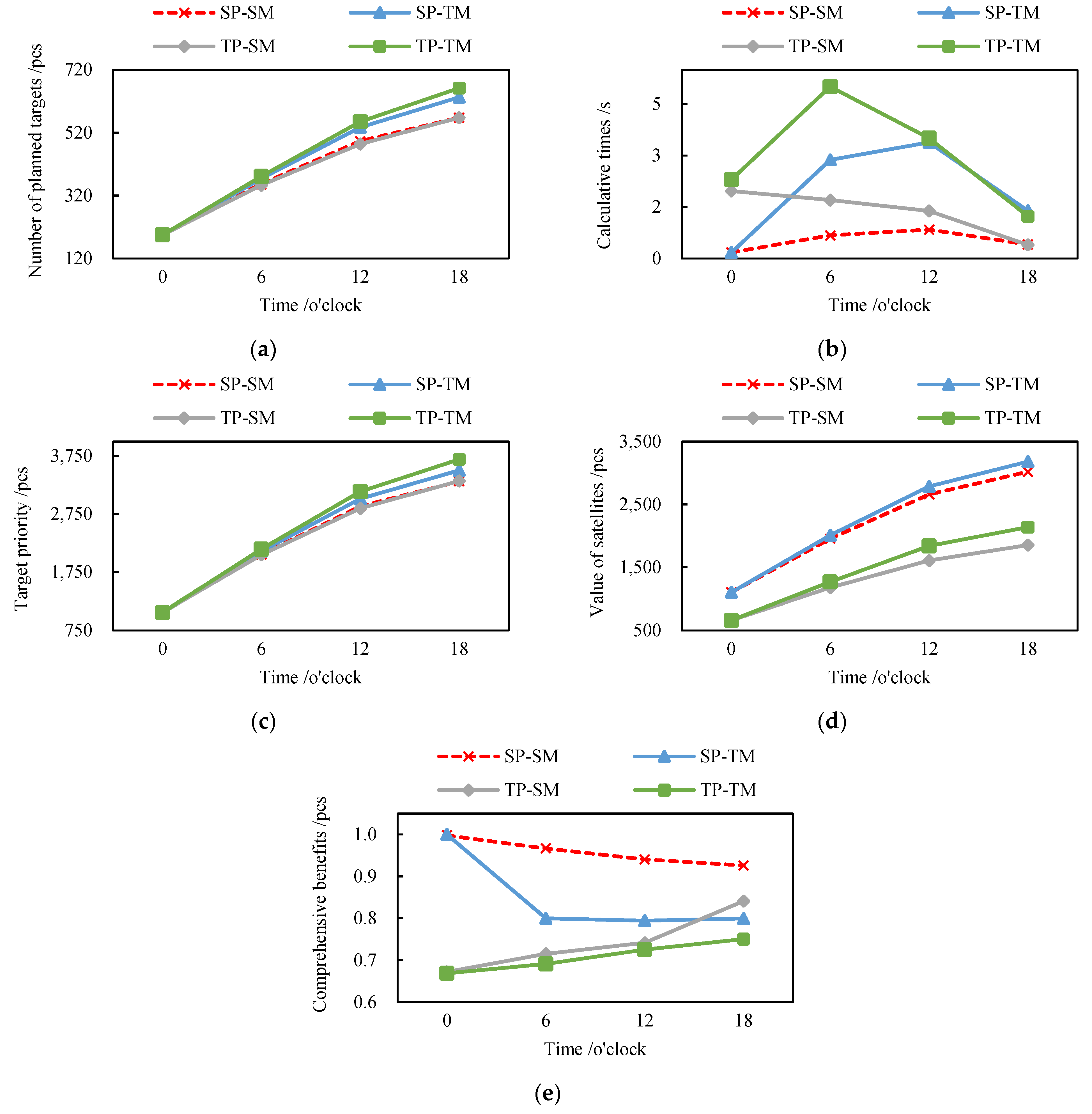
3.3.2. Experimental Results
4. Discussion
4.1. Comparison of Experimental Results
4.2. Analysis of the Experimental Results
- (1)
- Analysis of task planning results at different observation times
- (2)
- Analysis of task planning results for different numbers of targets
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, F.; Liu, S.Y.; Zhao, J.; Zheng, Q.B. Technology Prospective of Intelligent Remote Sensing Satellite. Spacecr. Eng. 2017, 26, 74–81. [Google Scholar]
- Wang, M.; Yang, F. Intelligent remote sensing satellite and remote sensing image realtime intelligent service. Acta Geod. Cart. Sin. 2019, 48, 1586–1594. [Google Scholar]
- Marinelli, F.; Nocella, S.; Rossi, F.; Smriglio, S. A Lagrangian heuristic for satellite range scheduling with resource constraints. Comput. Oper. Res. 2011, 38, 1572–1583. [Google Scholar] [CrossRef]
- Barkaoui, M.; Berger, J. A new hybrid genetic algorithm for the collection scheduling problem for a satellite constellation. J. Oper. Res. Soc. 2020, 71, 1390–1410. [Google Scholar] [CrossRef]
- Wang, H.J.; Yang, Z.; Zhou, W.G.; Li, D.L. Online scheduling of image satellites based on neural networks and deep reinforcement learning. Chin. J. Aeronaut. 2019, 32, 1011–1019. [Google Scholar] [CrossRef]
- Beaumet, G.; Verfaillie, G.; Charmeau, M.C. Feasibility of autonomous decision making on board an agile earth-observing satellite. Comput. Intell. 2011, 27, 123–139. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, D.X.; Chen, Z.H.; Chen, J.L.; Shao, X.W. Multi-type multi-objective imaging scheduling method based on improved NSGA-III for satellite formation system. Adv. Space Res. 2019, 63, 2551–2565. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, Y.; Xia, L.; Zhu, Z.; Wang, J. A method of network satellite on-orbit distributed collaborative mission scheduling. Harbin Gongcheng Daxue Xuebao J. Harbin Eng. Univ. 2019, 40, 393–399. [Google Scholar]
- Zhu, W.M.; Hu, X.X.; Xia, W.; Sun, H.Q. A three-phase solution method for the scheduling problem of using earth observation satellites to observe polygon requests. Comput. Ind. Eng. 2019, 130, 97–107. [Google Scholar] [CrossRef]
- Zhu, W.M.; Hu, X.X.; Xia, W.; Jin, P. A two-phase genetic annealing method for integrated Earth observation satellite scheduling problems. Soft Comput. 2019, 23, 181–196. [Google Scholar]
- Cho, D.H.; Kim, J.H.; Choi, H.L.; Ahn, J. Optimization-Based Scheduling Method for Agile Earth-Observing Satellite Constellation. J. Aerosp. Inf. Syst. 2018, 15, 611–626. [Google Scholar] [CrossRef]
- Huang, W.Q.; Wang, H.; Yi, D.B.; Wang, S.; Zhang, B.; Cui, J.W. A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions. Remote Sens. 2023, 15, 5317. [Google Scholar] [CrossRef]
- Zhao, Z.G.; Hu, C.; Wang, K.; Zhang, Y.X.; Xu, Z.Y.; Ding, X. An Earth Observation Task Representation Model Supporting Dynamic Demand for Flood Disaster Monitoring and Management. Remote Sens. 2023, 15, 2193. [Google Scholar] [CrossRef]
- Chen, Y.X.; Shen, X.; Zhang, G.; Lu, Z.Z. Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping. Remote Sens. 2023, 15, 4178. [Google Scholar] [CrossRef]
- Wu, G.; Ma, M.; Wang, H.; Qiu, D. Multi-satellite observation scheduling based on task clustering. Acta Aeronaut. Astronaut. Sin. 2011, 32, 1275–1282. [Google Scholar]








| Number | Name | Spatial Resolution | Resolution Level | Orbital Altitude (km) | Revisit Period (Day) | Width (km) | Satellite Resource Value |
|---|---|---|---|---|---|---|---|
| 1 | GAOFEN 2 | 1/4 | meter scale | 631 | 5 | 45 | 1 |
| 2 | ZY 1-02C | 5/10 | meter scale | 780 | 3 | 60 | 3 |
| 3 | ZY 3 | 6 | meter scale | 506 | 5 | 51 | 5 |
| 4 | ZY 3-2 | 5.8 | meter scale | 505 | 3 | 51 | 4 |
| 5 | SJ-9A | 2.5/10 | meter scale | 645 | 4 | 30 | 2 |
| 6 | GAOFEN 1 | 16 | Ten-meter scale | 645 | 2 | 800 | 6 |
| 7 | HJ-1A | 30 | Ten-meter scale | 649 | 4 | 360 | 8 |
| 8 | HJ-1B | 30 | Ten-meter scale | 649 | 4 | 360 | 9 |
| 9 | GAOFEN 6 | 16 | Ten-meter scale | 644.5 | 2 | 800 | 7 |
| 10 | CBERS 4 | 73 | Ten-meter scale | 778 | 3 | 866 | 10 |
| Experimental Target Number Benchmarks | Number of New Targets at 0 O’clock | Number of New Targets at 6 O’clock | Number of New Targets at 12 O’clock | Number of New Targets at 18 O’clock |
|---|---|---|---|---|
| 50 | 50 | 50 | 50 | 50 |
| 100 | 100 | 100 | 100 | 100 |
| 150 | 150 | 150 | 150 | 150 |
| 200 | 200 | 200 | 200 | 200 |
| Method | Abbreviation | Description |
|---|---|---|
| Satellite Priority-Scheme Merging | SP-SM | On the premise of maximizing the acquisition of high-resolution data, this approach involves the amalgamation of planning schemes for newly added objectives with those unobserved targets in the original planning scheme, thereby formulating a novel planning scheme. |
| Satellite Priority-Tasks Merging | SP-TM | Based on the premise of maximizing the acquisition of high-resolution data, this method entails the amalgamation of newly added objectives with unobserved targets from the original planning scheme. This integrated approach facilitates the collective planning of tasks, culminating in the formulation of a revised planning scheme. |
| Task-Priority-Scheme Merging | TP-SM | Focused on the objective of observing as many targets as possible, this method involves the integration of planning schemes for newly added targets with those of unobserved targets in the original plan. This process results in the formation of a new, comprehensive planning scheme. |
| Task-Priority-Tasks Merging | TP-TM | Based on the objective of maximizing the number of observed targets, this approach involves the amalgamation of newly added targets with those unobserved in the original planning scheme. By collectively planning these tasks, a new and comprehensive planning scheme is developed. |
| Method | Target Number | Planning Quantity at 0 | Calculated Elapsed time at 0/s | Number of Targets Observed at 6 | Planning Quantity at 6 | Calculated Elapsed Time at 6/s | Number of Targets Observed at 12 | Planning Quantity at 12 | Calculated Elapsed time at 12/s | Number of Targets Observed at 18 | Planning Quantity at 18 | Calculated Elapsed time at 18/s | Total Number of Targets Observed | Total Time of Calculate | Total Task Priority | Total Satellite Resource Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SP-SM | 50 | 49 | 0.0186 | 14 | 82 | 0.0652 | 29 | 96 | 0.0795 | 51 | 76 | 0.0584 | 170 | 0.2218 | 979 | 864 |
| 100 | 97 | 0.0534 | 18 | 170 | 0.2234 | 61 | 186 | 0.2474 | 100 | 136 | 0.1472 | 315 | 0.6713 | 1715 | 1618 | |
| 150 | 148 | 0.1072 | 53 | 220 | 0.3554 | 79 | 258 | 0.4785 | 141 | 167 | 0.2222 | 440 | 1.1633 | 2429 | 2255 | |
| 200 | 195 | 0.1743 | 55 | 302 | 0.6705 | 105 | 333 | 0.8434 | 180 | 228 | 0.4064 | 568 | 2.0945 | 3314 | 3020 | |
| SP-TM | 50 | 49 | 0.0185 | 14 | 83 | 0.1631 | 29 | 98 | 0.1569 | 52 | 77 | 0.0944 | 172 | 0.4328 | 985 | 872 |
| 100 | 97 | 0.0523 | 18 | 176 | 0.9918 | 65 | 196 | 0.7729 | 104 | 143 | 0.2610 | 330 | 2.0780 | 1777 | 1665 | |
| 150 | 148 | 0.1055 | 53 | 230 | 1.3756 | 80 | 282 | 1.7792 | 155 | 191 | 0.7685 | 479 | 4.0287 | 2567 | 2374 | |
| 200 | 195 | 0.1727 | 55 | 319 | 2.8737 | 111 | 371 | 3.3854 | 196 | 271 | 1.3883 | 633 | 7.8201 | 3504 | 3182 | |
| TP-SM | 50 | 49 | 0.1247 | 30 | 67 | 0.1180 | 46 | 65 | 0.0959 | 43 | 52 | 0.0659 | 171 | 0.4045 | 988 | 557 |
| 100 | 97 | 0.4181 | 38 | 140 | 0.4648 | 95 | 126 | 0.2803 | 86 | 89 | 0.1246 | 308 | 1.2876 | 1699 | 1038 | |
| 150 | 148 | 1.0722 | 87 | 183 | 1.0532 | 113 | 197 | 0.7218 | 143 | 112 | 0.2225 | 455 | 3.0697 | 2502 | 1520 | |
| 200 | 195 | 1.9660 | 107 | 246 | 1.7009 | 155 | 222 | 1.3846 | 155 | 151 | 0.3961 | 568 | 5.4476 | 3320 | 1853 | |
| TP-TM | 50 | 49 | 0.1220 | 30 | 68 | 0.2176 | 46 | 67 | 0.1545 | 45 | 56 | 0.1084 | 177 | 0.6025 | 1014 | 567 |
| 100 | 97 | 0.3832 | 38 | 156 | 1.6669 | 109 | 134 | 0.6276 | 93 | 97 | 0.2535 | 337 | 2.9311 | 1814 | 1129 | |
| 150 | 148 | 1.1897 | 87 | 199 | 2.0059 | 126 | 213 | 1.7851 | 156 | 133 | 0.6626 | 502 | 5.6433 | 2699 | 1658 | |
| 200 | 195 | 2.2973 | 107 | 274 | 5.0093 | 174 | 274 | 3.5068 | 197 | 184 | 1.2316 | 662 | 12.045 | 3694 | 2139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Pan, J.; Wang, M. Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios. Remote Sens. 2024, 16, 657. https://doi.org/10.3390/rs16040657
Wu Q, Pan J, Wang M. Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios. Remote Sensing. 2024; 16(4):657. https://doi.org/10.3390/rs16040657
Chicago/Turabian StyleWu, Qianyu, Jun Pan, and Mi Wang. 2024. "Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios" Remote Sensing 16, no. 4: 657. https://doi.org/10.3390/rs16040657
APA StyleWu, Q., Pan, J., & Wang, M. (2024). Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios. Remote Sensing, 16(4), 657. https://doi.org/10.3390/rs16040657











