Abstract
To obtain new information about surface waves, it is proposed to use an underwater acoustic wave gauge, and an assessment of its effectiveness can be performed using a numerical simulation and field experiment. A new device, an underwater acoustic wave gauge named “Kalmar”, was developed by the Institute of Applied Physics of the Russian Academy of Sciences for long-term, all-weather monitoring of wind waves. The instrument uses ultrasound to probe the water surface from underwater and can be used to verify remote sensing data. In this work, the capabilities of the device are tested and compared with ADCP data. Two independent methods for processing underwater acoustic wave gauge data are discussed and compared. One of them is completely new for acoustic measurements and is based on the analysis of the shape of the reflected acoustic pulse averaged over space and time. The other allows processing individual reflected pulses and calculating the time implementation of the distance to the water surface. It is shown that two independent methods of significant wave height retrieval from the acoustic wave gauge measurements are highly correlated. The “Kalmar” acoustic wave gauge and the RDI WH-600 acoustic Doppler current profiler operated simultaneously at the test site in Gelendzhik from 1 February to 10 February 2020. The significant wave heights measured by the two instruments are in good agreement.
1. Introduction
Operational and global monitoring of the state of the surface of the world ocean receives great attention due to its significant impact on the Earth’s climate. The launching of measuring equipment into space and improved data-processing methods can provide a solution to this problem and will make it possible to monitor the processes of interaction between the atmosphere and the ocean [1,2].
For radar remote sensing, processing algorithms that retrieve thematic information, i.e., the speed and direction of surface wind, significant wave heights, and the variance of sea surface slopes, are extremely important. To validate and verify algorithms for radar data processing, as well as assess their accuracy, contact measurement data are used.
The main source of reliable information is sea buoys, which measure the speed and direction of surface wind, the spectrum of long waves (>5 m), and the significant wave height [3]. Unlike string [4,5] or laser [6,7] wave gauges, sea buoys do not require installation on an offshore platform and can be placed almost anywhere in the world ocean.
ADCPs (acoustic Doppler current profilers) are autonomous devices, but their disadvantage is their low spatial resolution, which is about 5–6 m depending on the diving depth [8,9,10,11,12]. As a result, information about the short-wave part of the wave spectrum (from approximately a few meters to several centimeters), which is most sensitive to surface wind speed [13], is not measured.
Since microwaves are usually used for radar remote sensing of the Earth, the short-wave part of the wave spectrum has the greatest influence on the power of the reflected signal. Therefore, expanding the range of surface wavelengths measured from underwater from 5 m to several centimeters is an important fundamental and applied problem.
The underwater pulsed acoustic wave gauge being developed at the Institute of Applied Physics will be able to solve this problem. To assess its potential, this work proposes the following approach. First, we consider a theoretical model for describing the impulse reflected by the water surface and compare it with the traditionally used Brown model [14]. We tested the model of the reflected pulse within the framework of the numerical simulation of the experiment and, based on the results obtained, we proposed an algorithm for retrieving wave parameters (retracking algorithm). Then, we tested the retracking algorithm as part of a long-term experiment at the test site of the southern branch of the Institute of Oceanology of the Russian Academy of Sciences with an underwater pulsed acoustic wave gauge.
2. Materials and Methods
2.1. Acoustic Pulse Model Considering Slope Variance
Consider the monostatic case of sea surface remote sensing according to the measurement scheme in Figure 1.
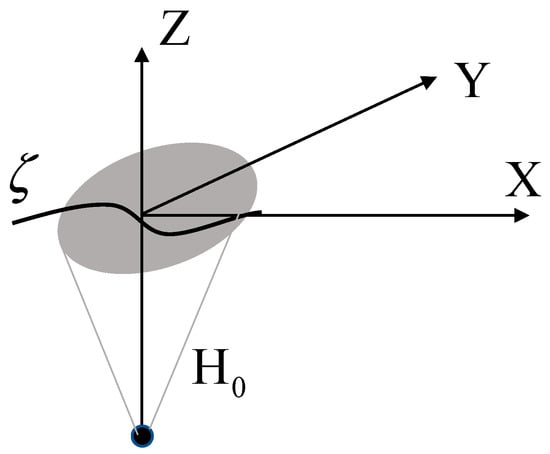
Figure 1.
Problem statement.
An acoustical transceiver antenna is located at a depth in one place under the water and is directed vertically upward. The main lobe of the transceiver antenna beam pattern (AP) is assumed to be symmetrical and Gaussian and has a width at half-power. Function —ordinates of the water surface. The illumination area corresponding to the intersection of the antenna radiation pattern with the z = 0 plane coinciding with the unperturbed water surface is highlighted in gray.
The actual sea surface has a wide range of scales of irregularities from capillary components of the spectrum to the long gravity waves, so to calculate the scattered field characteristics, the concept of a two-scale model of the sea surface is often used. Under this model, the sea surface is represented as a large-scale surface (compared with a wavelength) covered by small ripples and satisfying a number of conditions [15,16]. The field scattered by a large-scale component of surface waves can be calculated by the tangent plane approximation (Kirchhoff approximation) [15,16,17,18,19], and the impact of the small-scale surface on the scattered field is taken into account via perturbation theory, and in the quasispecular region of scattering, it appears in an effective reflection coefficient.
In the tangent plane approximation (Kirchhoff approximation), the final formula for the reflected pulse is expressed as follows [20]:
where —current time, and functions , , and are the sum of the “x” and “y” components; for example, , where:
where , —radiating pulse duration, —sound speed in media (for acoustic waves in water equal to 1490 m/s), —wave height variance, , —slope variance along the i-axes, i stands for “x” and “y” components, and Φ is the Gauss error function (erf function). —the effective reflection coefficient for the average field corresponding to a stationary point, which corresponds to the mirror beam directed at the receiving point. In addition to the physical parameters of the media at the boundary, the effective reflection coefficient depends on the intensity of small-scale surface waves . In Formulas (1) and (2), the effective reflection coefficient is introduced instead of the Fresnel reflection coefficient to take into account the weakening of quasispecular components due to scattering (Bragg scattering) on a small ripple, located on a large wave. It should be noted that in the case of using a symmetric antenna oriented exactly vertically, it is possible to use an equivalent slope variance equal to half the total slope variance: . Henceforth in this work, we will call Formula (1) Karaev’s formula since he first obtained it in [20].
Let us consider the shapes of the reflected pulse according to this model depending on the significant wave heights and the total variance of slopes of large-scale waves in comparison with the Brown model in Figure 2. The immersion depth is 30 m, = 60 µs, and the antenna radiation pattern is 15 degrees; for Figure 2a, the total variance of slopes is 0.022; and for Figure 2b, the significant wave height is 0.56 m.
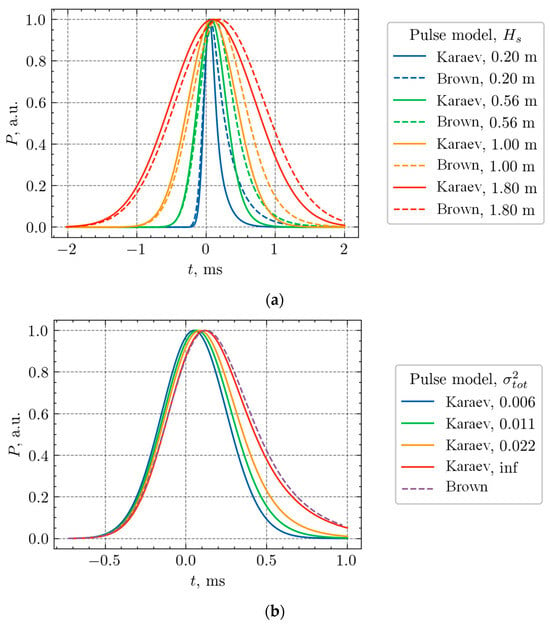
Figure 2.
Comparison of reflected pulse models for different significant wave heights (a) and large-scale wave slope variance (b).
The figure shows that the leading edge of the reflected pulse of both models changes equally when the significant wave heights change, which makes it possible to use general algorithms for retrieving the significant wave heights. Changing the variance of large-scale wave slopes will not affect the shape of the reflected pulse for the Brown model. It should be noted that in the limiting case of a very large slope variance, the Karaev model passes into the Brown model.
Thus, by measuring the shape of the reflected pulse with an antenna with a wide pattern (at least 14 degrees), it is possible to measure the variance of large-scale wave slopes. Moreover, in the case of a multi-frequency acoustic system, the variance of large-scale wave slopes will be different for each sonar wavelength. The difference in slope variances of large-scale waves measured by sonars at different frequencies contains information about the intensity of waves in the interval determined by the boundary wavenumbers, which depend on the sonar wavelength and wave parameters.
2.2. Numerical Simulation of Reflected Acoustic Pulse and Retracking
Numerical simulation is a necessary stage in the development of new remote sensing instruments, for example, low-flying radar [21,22], the SWIM space wave scatterometer [23], and the fan beam antenna scatterometer [24] during the CFOSAT satellite concept preparation phase. In these works, within the framework of a “numerical” experiment, a reflecting water surface is modeled for a given wave spectrum; then, the reflected signal is calculated from the geometry of the measurement scheme and radar parameters. The signal “measured” in the “numerical” experiment is compared with the analytical model. Next, this “measured” signal is used as an input parameter in algorithms for solving the inverse problem (retracking algorithms). This work implemented this approach.
For the selected measurement scheme of the underwater acoustic wave gauge in Figure 1, the sea surface was modeled, located above the wave gauge and forming the reflected signal. When modeling waves, the speed of the surface wind at a height of 10 m and the length of the wind fetch were specified. The modeled surface had a Gaussian probability density function of heights and slopes. The most well-known way to model the sea surface from a wave spectrum is to sum harmonics with deterministic amplitudes and random phases.
Reflected power is calculated as an incoherent (without taking into account the phase) sum from all reflective points of the surface:
where the summation is performed over all reflecting points, is the distance from the emitter to the reflecting point, α is a certain constant coefficient, including the effective reflection coefficient, is the speed of sound in water, and is the radiation pattern of the antenna in the direction of a point with radius vector :
—the coordinates of the center of illumination of the average level of the water surface by the antenna radiation pattern, —the width of the antenna pattern at the half-power level, and —the shape of the emitted pulse. In this work, the pulse is assumed to be rectangular:
When summing, a modeled surface area is considered a “mirror” if the normal to the area is parallel to the radius vector from the sonar to a given point. We assume that specular reflection occurs from an area of the surface if the angle between the normal and the radius vector does not exceed 1°. To match the amplitude of the model pulse to Karaev’s Formula (1), it is necessary to perform the following normalization:
where —maximum of the model pulse in amplitude, and —backscattering cross-section of a reflecting surface for the corresponding antenna.
Within the framework of theoretical models [14,20], the maximum of the reflected pulse is associated with the backscattering cross-section. The backscattering cross-section is calculated as follows:
When performing the “numerical” experiment with a sonar in this work, the implementation of a 58 m × 58 m sea surface with a step of 50 cm was calculated for a radiation wavelength of 8 mm. The wavelength of the sonar affects the surface parameters that contribute to the characteristics of the reflected radiation [15,19,25]. Wave statistics for surface modeling are calculated using a wave spectrum model [26]. In all cases, wind waves were considered fully developed and propagating along the X axis. The wind speed was set at a height of 10 m. The pulse repetition rate of the simulated sonar determines the time step for the simulated surface and, in this case, was equal to 0.25 Hz, and the accumulation time was 800 s. The width of the antenna pattern was 30 degrees. The installation depth of the sonar was assumed to be 100 m. For modeling, we assumed the speed of sound in water to be 1500 m/s. The length of the emitted pulse was 60 μs. Based on the resulting averaged reflected impulse, the retracking algorithm used the Karaev formula to calculate the statistical parameters of the surface: the distance from the sonar to the level of the undisturbed surface, the significant wave heights = , as well as the total variance of the slopes of large-scale waves. Retrieving the distance to the level of the undisturbed water surface is not discussed in this work.
Let us compare the results of the numerical simulation of the reflected pulse with the calculation using Karaev’s formula for wind speeds of 3 m/s and 8 m/s in Figure 3.
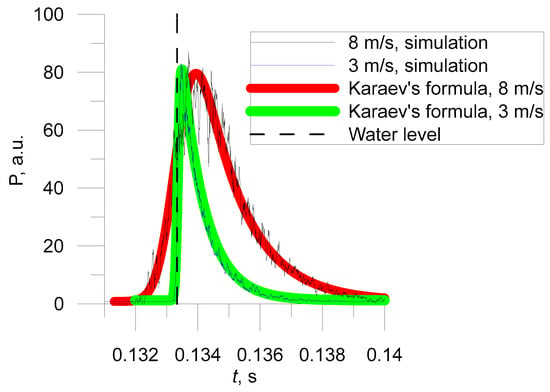
Figure 3.
Comparison of reflected impulses obtained in numerical simulation and according to Karaev’s formula for wind speeds of 3 m/s and 8 m/s.
It can be seen from the figure that when the wind speed changes, both the leading and trailing edges of the reflected pulse change greatly, since when the wind speed changes, the height of the waves and the variance of the slopes of large-scale waves change. Figure 3 also shows the coincidence of the shape of the pulses obtained by two independent methods.
Let us consider the operation of the method for retrieving wave parameters from the shape of the reflected pulse. The method is based on the selection (retracking) of model parameters for the pulse shape. When approximating the simulated average reflected pulse with Karaev’s formula, the least squares method is used [27]. As a result, the distance from the sonar to the undisturbed water surface, the variance of surface ordinates, and the total variance of large-scale wave slopes are retrieved.
A comparison of the retracking results with the wave parameters observed during the simulation for 800 s is presented in Figure 4.
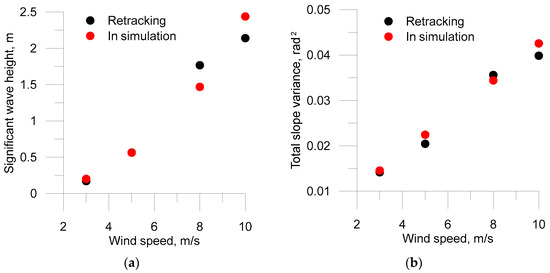
Figure 4.
A comparison of the retracking results with the wave parameters observed during the simulation for 800 s for different near surface wind speed: (a) significant wave height; (b) total slope variance.
It can be seen from the figure that with increasing wind speed, a difference appears between the significant wave heights and the variances of slopes, retrieved using the retracking algorithm and specified during the simulation. The result in this case was influenced by the fact that, in 800 s, a statistically reliable estimate of wave parameters for wind speeds of 8 m/s and 10 m/s did not have time to accumulate. In addition, more averaging time (more pulses) was also required to form a stable-shaped reflected pulse. The unstable, “ragged” shape of the reflected pulse led to a decrease in the accuracy of the retracking algorithm. To refine the operation of the retracking algorithm, it is necessary to either increase the illumination area by increasing the depth or increase the averaging time.
2.3. Test Site and Instruments
The ADCP RDI WHS-600 with a wave measurement function and the underwater acoustic wave gauge are parts of the multifunctional system for the online monitoring of aquatic environment parameters installed at the Gelendzhik test site at a distance of 1 km from the coast (the red triangle BS1 closer to the coast in Figure 5a).
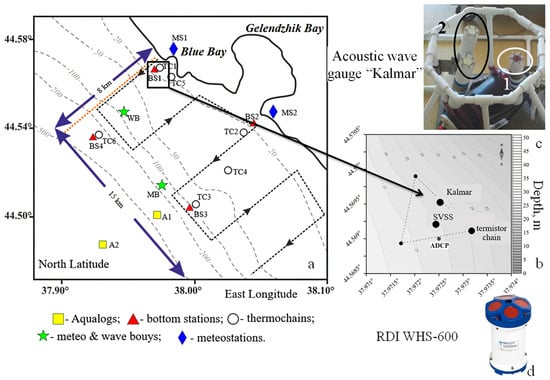
Figure 5.
Gelendzhik test site view as of 2020 and the appearance of the devices: (a) general layout; (b) multifunctional system for online monitoring of aquatic environment parameters; (c) acoustic wave gauge “Kalmar”; (d) ADCP RDI WH-600.
The multifunctional system also includes a stationary vertical profiling station [28] (SVSS in Figure 5b) and a thermochain [29]. Data are transmitted from the instruments to the data acquisition system unit and then via fiber-optic cable to the coastal computer, from where it can be downloaded via the Internet. Figure 5a shows the general layout of the test site.
The acoustic wave gauge “Kalmar” has two channels: (1) a pulse altimeter that emits and receives acoustic pulses, and (2) a Doppler sonar that emits a continuous harmonic signal and allows measuring the Doppler spectrum of the reflected acoustic signal. Measurements in different channels are performed sequentially. Paper [30] presented the first results of field measurements carried out in the Black Sea at the Gelendzhik test site. The device can also be used in freezing water bodies, where it can determine the thickness of the freshwater ice cover.
The underwater acoustic wave gauge “Kalmar” is installed at the test site, and the appearance of the device is shown in Figure 5c. The device is equipped with sonars that provide operation in pulsed (red transducer is marked “1”) and continuous mode (two white transducers are marked “2”).
The “Kalmar” underwater acoustic wave gauge and RDI WHS-600 were installed at the bottom station at a depth of 28 m; the distance between the instruments is 60 m (see Figure 5b). RDI WHS-600 is shown in Figure 5d (red circles—hydroacoustic emitters). The operational frequency of the ADCP is 600 kHz, and the antenna pattern is less than 2 degrees. The velocities of water movement were determined every 30 s with a vertical resolution of 0.5 m. Wave measurements were carried out for 40 min. RDI WHS-600 measures the wave spectrum using three different approaches: by measuring the reflection from the water surface in the side beams (Echo), using the conversion of the velocity spectrum to the elevation spectrum (Velocity), and using the pressure sensor (Pressure). All three methods are described in the documentation for the ADCP data-processing program [31]. For comparison with the data from the “Kalmar” acoustic wave gauge, we used data on the wave spectrum obtained in the “Echo” mode.
The recording time of the instruments is different: for the acoustic wave gauge “Kalmar”, it is 15 min (this is enough for the statistical validity of the measurements obtained), and for the ADCP, it is 40 min; the instruments are 60 m apart.
In the diagram in Figure 5a, the following designations are used: triangles—bottom stations equipped with an ADCP and thermochains; squares—profiler stations “Aqualog” [28]; stars denote sea meteorological stations; rhombuses—ground meteorological stations; and dashed broken line—vessel tacks for measuring the spatial structure of currents with a towed ADCP.
The “pyramid” with a fixed acoustic wave gauge was installed on the bottom so that the transceiver antenna of the pulse sonar was oriented toward the zenith on the sea surface. The sonar (the generator frequency is 200 kHz) emits pulses with a duration of 5, 10, 20, or 40 μs, and the pulse repetition rate is 2 Hz. The width of the symmetrical radiation pattern of the transmitting and receiving antenna is 15 degrees. Thus, the diameter of the circle on the water surface determined by the antenna pattern is about 7.4 m. The antenna unit of the continuous channel is oriented at an angle of 5 degrees from the vertical. In continuous mode, the wave gauge emits a harmonic signal with a frequency of 200 kHz and measures the Doppler spectrum of the signal reflected by the water surface. The acoustic wave gauge worked with short breaks from August 2018 to September 2020.
In this paper, only measurements in pulse mode are discussed. In this mode, we used 2 approaches to analyze the reflected radiation. The first is standard for acoustic measurements (let us call it the “Spectrum” method), for example, for some ADCPs that are equipped with a vertical transceiver. Within the framework of this method, for each reflected pulse, the time to the maximum of the reflected pulse is recorded, which can be recalculated into the realization of the distance from time, with a time frequency of pulse repetition rates. Using this implementation, using the Fourier transform, it is possible to obtain an omnidirectional wave spectrum and then, from the spectrum, calculate different wave parameters (for example, the significant wave heights). An important disadvantage of this approach is sensitivity to the antenna pattern and immersion depth.
The second approach is new for acoustic measurements of wave parameters (let us call it the “Pulse” method). An important difference between the device proposed in this work and the traditional one is the use of a wide antenna pattern for the transceiver antenna. A wide antenna pattern allows, when analyzing the average shape of the reflected pulse (described in Section 2.1 and Section 2.2), the retrieval of the variance of the slopes of large-scale waves in comparison with the radiation wavelength. Moreover, in the case of the acoustic wave gauge “Kalmar” with a radiation wavelength of 8 mm, large-scale waves already begin with sea wavelengths of the order of 2 cm (depending on the waves). Moreover, for the average reflected pulse, the traditional approach for satellite altimeters will work for determining the significant wave heights from the leading edge of the reflected pulse.
3. Results
A comparison of the pulse measured on 3 February 2020 at 7:24 am and averaged over 15 min with the pulse obtained by a theoretical formula using retracking wave parameters is shown in Figure 6.
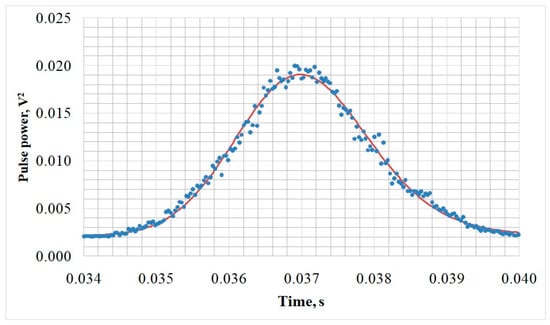
Figure 6.
Measured average pulse (blue dots) and Karaev’s model retracking (red curve).
Due to time averaging, it is possible to minimize noise, and the pulse shape becomes quite stable (smooth). The measured pulses are shown in blue in the figure.
The SWH was calculated as an integral from the spectrum (the “Spectrum” method) and it was retrieved using Karaev’s model retracking of the average pulse (the “Pulse” method). The two methods were compared (see Figure 7). For 1–10 February 2020, 56 measurements were analyzed. It can be seen that during the measurements, the SWH varied from 0.3 m to 3 m.
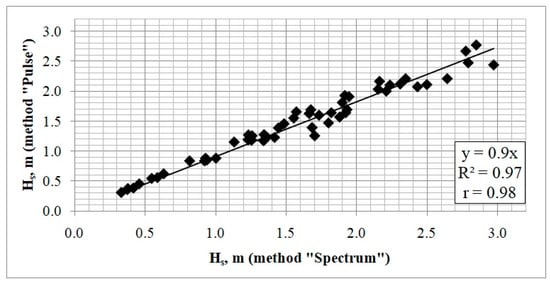
Figure 7.
SWH as an integral from the spectrum (“Spectrum” method) versus SWH calculated from the shape of the reflected pulse (“Pulse” method). Black boxes show measured values, straight line is linear regression.
It is necessary to emphasize that the accuracy of the method does not depend on the depth of the instrument installation. From Figure 7, it can be seen that both methods are in good agreement with each other. The acoustic wave gauge allows for retrieving SWH using two independent methods.
Let us consider the comparison of the acoustic wave gauge and ADCP data-processing results for 1–10 February 2020 in Figure 8. The figure shows comparisons of the significant wave heights according to the acoustic wave gauge (“Pulse” method) and the Echo ADCP spectrum.
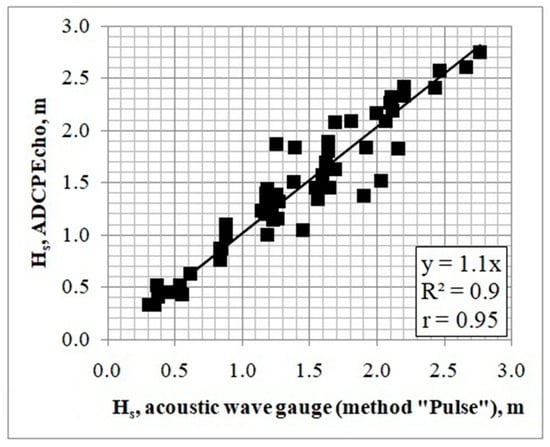
Figure 8.
Comparison of the significant wave heights according to the acoustic wave gauge and the Echo ADCP spectrum. Black boxes show measured values, straight line is linear regression.
Thus, the significant wave heights calculated from the averaged pulse retracking algorithm and from the spectra measured by the ADCP are close.
The equivalent slope variance and significant wave height retrieved by Karaev’s model retracking of the reflected pulse are shown in Figure 9. Data were observed from 16 August to 10 September 2018. Measurements were performed once a day. Each pulse was averaged over 5 min.
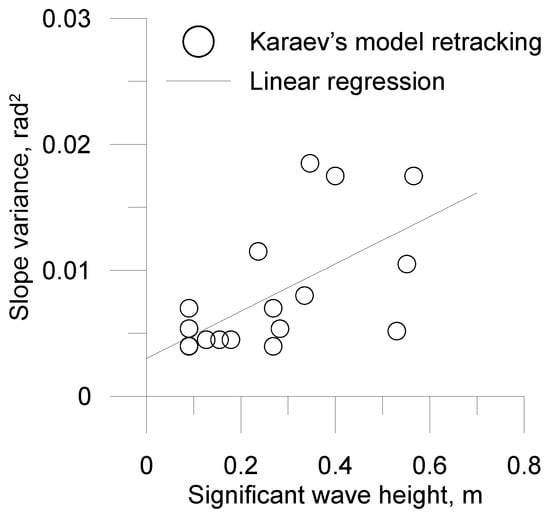
Figure 9.
The equivalent slope variance and significant wave height retrieved by the Karaev’s model retracking of the reflected pulse.
Figure 9 shows some connection between the slope variance and the intensity of waves, but it is rather weak. The slope variance is not directly related to the significant wave height but is determined by wind fetch, wind speed, and the arrival of swell waves (mixed waves). For example, at the measurement site, the arrival of swell waves is often observed, which do not affect the slope variance, but have a strong effect on the wave height. A strong wind can also blow from the shore, due to which the height of the wave practically does not change, while the slope variance can greatly increase.
Currently, an underwater acoustic wave gauge with a wide antenna pattern is the only “quasi-contact” device that can measure the variance of large-scale wave slopes compared to the radiation wavelength. A comparison can be made with radar measurements from an airplane or satellite, but this is a separate, complex task that requires the location of the underwater device at a much greater distance from the shore. However, this comparison is the goal of further work.
4. Discussion
Within the framework of the two-scale model of the scattering surface and the Kirchhoff method for describing the shape of the reflected pulse, two models were compared: the Brown model and the Karaev model. The comparison showed a significant difference between the models for the case of a wide antenna pattern. Both models described the leading edge of the reflected pulse in the same way; however, for a wide antenna pattern, significant differences in the behavior of the trailing edge were observed. This is because the Brown model does not consider the variance of the slopes of large-scale waves, which affects the power of the reflected pulse at an oblique incidence of the probing radiation. As a result, the trailing edge of the reflected pulse turns out to be more “drawn out” compared to Karaev’s model, all other things being equal.
The results of comparing the theoretical formula and the results of numerical simulations simultaneously confirmed the effectiveness of the numerical experiment and the reliability of Karaev’s theoretical model for the shape of the reflected pulse. Therefore, in the future, to solve the inverse problem, it is necessary to use Karaev’s formula.
For the first time, a processing method (retracking) was tested to retrieve wave parameters based on Karaev’s model. For the first time, simulated pulses were used in a new processing method, and the significant wave heights and the variance of slopes of large-scale waves were retrieved.
An important advantage of the proposed slope variance measurement approach is the ability to perform measurements at multiple frequencies. The variance of the slopes of large-scale waves, compared to the sonar wavelength [32,33,34], affecting the reflected signal, depends on the radiation frequency, and it is assumed that the main information parameter will be the difference in the variances of the slopes of large-scale waves. The variance of the slopes of large-scale waves, which can be measured by a sonar, is determined by the integral of the spectrum of surface slopes, taken in the range from 0 to the cutoff wavenumber, which depends on the intensity of the waves and the wavelength of the radiation. The difference in slope variances measured by sonars operating at different wavelengths will be determined by the integral over the slope spectrum within the boundary wavenumbers of the sonars used. The difference slope variances calculated in this way will contain information about waves for the selected wavelength range. A feature of calculating the slope difference is the subtraction of large-scale waves, which includes the long-wave part of the wave spectrum, capable of propagating over long distances and not associated with local wind. The difference in the variances of large-scale wave slopes measured in different frequency ranges can become a new integral parameter for characterizing surface waves. This parameter will allow us to study the influence of various conditions for the formation of waves (wind speed, the length of wind fetch, swell waves) in the short-wave part of the wave spectrum (the range of surface wave lengths from 50 cm to several centimeters).
As part of a long-term field experiment, we obtained high accuracy in the algorithm for retrieving the significant wave heights when retracking the shape of the averaged pulse when compared with both the traditional processing method for range implementation and the ADCP, which are considered standard for such measurements. An important advantage of the retracking algorithm compared to the traditional one is the insensitivity of the result to the sonar installation depth and the antenna pattern. On the contrary, the deeper the possible installation depth of the sonar and the larger the illumination area, the faster the accumulation of reflected pulses for retracking.
The experiment shows the possibility of retrieving the variance of large-scale wave slopes because of retracking (according to Karaev’s model) the shape of the average reflected pulse. Moreover, this is precisely the variance of slopes that affects the reflected radar signal in the Ka band, for example, when sensing from space. The standard Brown model does not consider the variance of wave slopes at all.
5. Conclusions
As part of this work, we considered a theoretical description of the shape of a reflected pulse for antennas with a wide radiation pattern, considering the variance of large-scale wave slopes. The numerical “experiment” showed good agreement for the reflected pulse with the theoretical formula and demonstrated the possibility of retrieving significant wave heights and the variance of slopes of large-scale waves in retracking. As a result of a long-term experiment with an underwater acoustic wave gauge, “Kalmar”, the performance of the proposed retracking algorithm was demonstrated and the significant wave heights and the variance of slopes of large-scale waves were retrieved. The high accuracy of the new approach to significant wave height retrieval was confirmed, which was controlled by comparison with an ADCP located near the measurement site. It is important to note that the measured variance of large-scale wave slopes is the same as that which affects the reflection of electromagnetic waves of the same wavelength. This opens opportunities for the ground-based calibration of satellite slope variance retrieval algorithms, for example, using TRMM [34], GPM [35], and CFOSAT data [36].
Author Contributions
Conceptualization, Y.T.; methodology, G.J.; software, K.P.; validation, M.R.; formal analysis, Y.H.; investigation, V.K.; writing—original draft preparation, Y.T.; writing—review and editing, Y.T. and Y.H.; visualization and data processing, V.B. and V.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the CAS International Talent Program for 2023 International Visiting Scholar No. 2023VMB0006 and National Science Foundation of China No. U2106211. Data processing and visualization were carried out by Vladimir Baranov and Vladimir Ocherednik within the framework of the state assignment of IO RAS FMWE-2024-0027. The work of Kirill Ponur and Maria Ryabkova was supported by the state assignment FFUF-2024-0033.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Barale, V.; Gower, J.F.; Alberotanza, L. Oceanography from Space: Revisited; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Halpern, D. Satellites, Oceanography and Society; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- NDBC. Handbook of Automated Data Quality Control Checks and Procedures; Technical Document 09-02; National Data Buoy Center: Hancock County, MI, USA, 2009.
- Dulov, V.A.; Korinenko, A.E.; Kudryavtsev, V.N.; Malinovsky, V.V. Modulation of Wind-Wave Breaking by Long Surface Waves. Remote Sens. 2021, 13, 2825. [Google Scholar] [CrossRef]
- Bondur, V.G.; Dulov, V.A.; Murynin, A.B.; Yurovsky, Y.Y. A study of sea-wave spectra in a wide wavelength range from satellite and in-situ data. Izv. Atmos. Ocean. Phys. 2016, 52, 888–903. [Google Scholar] [CrossRef]
- Hwang, P.A. Microstructure of Ocean Surface Roughness: A Study of Spatial Measurement and Laboratory Investigation of Modulation Analysis. J. Atmos. Ocean. Technol. 1999, 16, 1619–1629. [Google Scholar] [CrossRef]
- Sterlyadkin, V.V.; Kulikovsky, K.V.; Kuzmin, A.V.; Sharkov, E.A.; Likhacheva, M.V. Scanning Laser Wave Recorder with Registration of “Instantaneous” Sea Surface Profiles. J. Atmos. Ocean. Technol. 2021, 38, 1415–1424. [Google Scholar] [CrossRef]
- Dally, W.R.; Osiecki, D.A. Comparison of Deep-water ADCP and NDBC Buoy Measurements to Hindcast Parameters. In Proceedings of the 8th International Workshop on Wave Hindcasting and Forecasting, Honolulu, HI, USA, 14–19 November 2004. [Google Scholar]
- Strong, B.; Brumley, B.; Terray, E.; Stone, G. The performance of ADCP-derived directional wave spectra and comparison with other independent measurements. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; pp. 1195–1203. [Google Scholar]
- Birch, R.; Fissel, D.B.; Borg, K.; Lee, V.; English, D. The capabilities of Doppler current profilers for directional wave measurements in coastal and nearshore waters. In Proceedings of the Oceans ‘04 MTS/IEEE Techno-Ocean ‘04 (IEEE Cat. No.04CH37600), Kobe, Japan, 9–12 November 2004; Volume 1413, pp. 1418–1427. [Google Scholar]
- Churchill, J.H.; Plueddemann, A.J.; Faluotico, S.M. Extracting Wind Sea and Swell from Directional Wave Spectra Derived from a Bottom-Mounted ADCP; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 2003; p. 41. [Google Scholar]
- Ryabkova, M.; Titchenko, Y.; Karaev, V.; Meshkov, E.; Belyaev, R.; Panfilova, M.; Baranov, V.; Ocherednik, V. Experimental Measurements of the Statistical Charachteristics of the Sea Waves Using Underwater Acoustic Wavegauge and Comparison with ADCP Measurements. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7545–7548. [Google Scholar]
- Troitskaya, Y.I.; Rybushkina, G.V. Quasi-linear model of interaction of surface waves with strong and hurricane winds. Izv. Atmos. Ocean. Phys. 2008, 44, 621–645. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Bass, F.G.; Fuks, I.M. Scattering of Waves by Statistically Rough Surfaces; Pergamon Press: Oxford, UK, 1979. [Google Scholar]
- Elfouhaily, T.; Guérin, C. A critical survey of approximate scattering wave theories from random rough surfaces. Waves Random Media 2004, 14, R1–R40. [Google Scholar] [CrossRef]
- Barrick, D. Rough Surface Scattering Based on the Specular Point Theory. IEEE Trans. Antennas Propag. 1968, 16, 449–454. [Google Scholar] [CrossRef]
- Voronovic, A.G.; Zavorotny, V.U. Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves. Waves Random Media 2001, 11, 247–269. [Google Scholar] [CrossRef]
- Valenzuela, G. Theories for interaction of electromagnetic and oceanic waves: A review. Bound. Layer Meteorol. 1978, 13, 61–86. [Google Scholar] [CrossRef]
- Karaev, V.Y.; Meshkov, M.E.; Titchenko, Y.A. Underwater Acoustic Altimeter. Radiophys. Quantum Electron. 2014, 57, 488–497. [Google Scholar] [CrossRef]
- Baskakov, A.I.; Komarov, A.A.; Mikhailov, M.S. Methodical Errors of a High-Precision Airborne Radio Altimeter Operating at Low Altitudes Above the Sea Surface. Radiophys. Quantum Electron. 2017, 60, 467–474. [Google Scholar] [CrossRef]
- Baskakov, A.I.; Komarov, A.A.; Ruban, A.V.; Ka, M.-H. Limiting Accuracy of Height Measurement for a Precision Radar Altimeter in a Low Altitude Flying Vehicle above the Sea Surface. Remote Sens. 2021, 13, 2660. [Google Scholar] [CrossRef]
- Hauser, D.; Soussi, E.; Thouvenot, E.; Rey, L. SWIMSAT: A Real-Aperture Radar to Measure Directional Spectra of Ocean Waves from Space—Main Characteristics and Performance Simulation. J. Atmos. Ocean. Technol. 2001, 18, 421–437. [Google Scholar] [CrossRef]
- Lin, W.; Dong, X.; Portabella, M.; Lang, S.; He, Y.; Yun, R.; Wang, Z.; Xu, X.; Zhu, D.; Liu, J. A Perspective on the Performance of the CFOSAT Rotating Fan-Beam Scatterometer. IEEE Trans. Geosci. Remote Sens. 2019, 57, 627–639. [Google Scholar] [CrossRef]
- Nouguier, F.; Mouche, A.; Rascle, N.; Chapron, B.; Vandemark, D. Analysis of Dual-Frequency Ocean Backscatter Measurements at Ku- and Ka-Bands Using Near-Nadir Incidence GPM Radar Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1310–1314. [Google Scholar] [CrossRef]
- Ryabkova, M.; Karaev, V.; Guo, J.; Titchenko, Y. A Review of Wave Spectrum Models as Applied to the Problem of Radar Probing of the Sea Surface. J. Geophys. Res. Ocean. 2019, 124, 7104–7134. [Google Scholar] [CrossRef]
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.-L.; Callahan, P.S. Chapter 1 Satellite Altimetry. In International Geophysics; Fu, L.-L., Cazenave, A., Eds.; Academic Press: Cambridge, MA, USA, 2001; Volume 69, pp. 1–133. [Google Scholar]
- Ostrovskii, A.G.; Zatsepin, A.G.; Soloviev, V.A.; Tsibulsky, A.L.; Shvoev, D.A. Autonomous system for vertical profiling of the marine environment at a moored station. Oceanology 2013, 53, 233–242. [Google Scholar] [CrossRef]
- Ocherednik, V.V.; Baranov, V.I.; Zatsepin, A.G.; Kyklev, S.B. Thermochains of the Southern Branch, Shirshov Institute of Oceanology, Russian Academy of Sciences: Design, Methods, and Results of Metrological Investigations of Sensors. Oceanology 2018, 58, 661–671. [Google Scholar] [CrossRef]
- Titchenko, Y.; Karaev, V.; Ryabkova, M.; Kuznetsova, A.; Meshkov, E. Peculiarities of the Acoustic Pulse Formation Reflected by the Water Surface: A Numerical Experiments and the Results of Long-term Measurements Using the “Kalmar” Sonar. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019; pp. 1–7. [Google Scholar]
- Waves User’s Guide; P/N 957-6148-00; RD Instruments: San Diego, CA, USA, 2011; p. 74.
- Zapevalov, A.; Pokazeev, K.; Chaplina, T. The Distribution of the Variance of the Sea Surface Slopes on the Spatial Scales Creating Their Waves. In Simulation of the Sea Surface for Remote Sensing; Springer International Publishing: Cham, Switzerland, 2021; pp. 157–172. [Google Scholar]
- Danilytchev, M.V.; Kutuza, B.G.; Nikolaev, A.G. The Application of Sea Wave Slope Distribution Empirical Dependences in Estimation of Interaction Between Microwave Radiation and Rough Sea Surface. IEEE Trans. Geosci. Remote Sens. 2009, 47, 652–661. [Google Scholar] [CrossRef]
- Freilich, M.H.; Vanhoff, B.A. The Relationship between Winds, Surface Roughness, and Radar Backscatter at Low Incidence Angles from TRMM Precipitation Radar Measurements. J. Atmos. Ocean. Technol. 2003, 20, 549–562. [Google Scholar] [CrossRef]
- Chen, P.; Zheng, G.; Hauser, D.; Xu, F. Quasi-Gaussian probability density function of sea wave slopes from near nadir Ku-band radar observations. Remote Sens. Environ. 2018, 217, 86–100. [Google Scholar] [CrossRef]
- Hauser, D.; Tison, C.; Amiot, T.; Delaye, L.; Corcoral, N.; Castillan, P. SWIM: The First Spaceborne Wave Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3000–3014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).