Abstract
To overcome the problems of the high sidelobe levels and low computational efficiency of traditional Capon-based beamformers in optimizing the two-dimensional (elevation–azimuth) beampatterns of conformal arrays, in this paper, we propose a robust Capon beamforming method with sparse group constraints that is solved using the alternating-direction method of multipliers (ADMM). A robustness constraint based on worst-case performance optimization (WCPO) is imposed on the standard Capon beamformer (SCB) and then the sparse group constraints are applied to reduce the sidelobe level. The constraints are two sparsity constraints: the group one and the individual one. The former was developed to exploit the sparsity between groups based on the fact that the sidelobe can be divided into several different groups according to spatial regions in two-dimensional beampatterns, rather than different individual points in one-dimensional (azimuth-only) beampatterns. The latter is considered to emphasize the sparsity within groups. To solve the optimization problem, we introduce the ADMM to obtain the closed-form solution iteratively, which requires less computational complexity than the existing methods, such as second-order cone programming (SOCP). Numerical examples show that the proposed method can achieve flexible sidelobe-level control, and it is still effective in the case of steering vector mismatch.
1. Introduction
In the past decades, conformal arrays have been widely used in sonars [1,2,3] and radars [4,5] because they improve the dynamic characters of vehicles and offer three-dimensional observation. The core function of conformal arrays is beamforming, which performs weighted summation on the received data of arrays to suppress noise and interference [6], improving the postprocessing performance in applications such as detection [7]. The beampattern can evaluate the performance of the spatial filtering of the beamforming, which is worthy of proper design. Unlike the azimuth-only beampatterns of linear and circular arrays, the beamformers of conformal arrays can be steered at an arbitrary spatial angle without the direction ambiguity found in elevation–azimuth beampatterns, which has attracted much attention in relevant fields.However, the implementation of the beamforming of conformal arrays is more difficult than for other arrays due to the complexity of their array geometry and computation. Up to now, beamforming algorithms have been mainly applied to linear and circular arrays, so the study of the beamforming of conformal arrays is urgently needed.
Among the many beamfomers, theoretically, the Capon beamformer [8] can adaptively suppress interference and minimize the output noise power while maintaining the distortionless response of the desired signal. However, a Capon beamformer often suffers from severe performance degradation in practical applications, which is mainly caused by various types of steering vector (SV) mismatch. This SV mismatch not only causes signal self-cancellation in the mainlobe, but it also leads to an intolerable increase in the sidelobe level (SLL). Several approaches have been developed to improve robustness against SV mismatch. The diagonal loading technique (DL) [9] is adopted to alleviate the imperfect information in the covariance matrix of training data. To determine the diagonal loading factor reasonably, a series of algorithms based on uncertainty sets of SVs have been proposed, such as worst-case performance optimization (WCPO) [10,11] and robust Capon beamforming (RCB) [12]. On this basis, several approaches to synthesizing beampatterns with robust sidelobe control [13,14] have been developed.
Even if the problem of SV mismatch has been resolved, the inherent SLL of the beampatterns of conformal arrays is still too high to meet practical requirements, being restricted by geometry [15], aperture [16], and other factors [17]. It is necessary to artificially impose constraints to further optimize the SLL of the beampattern. Sidelobe control algorithms based on adaptive array theory [18,19] can be applied to arbitrary geometry arrays by adding virtual interference in the sidelobe region to reduce the SLL of the beampattern. The drawbacks of these algorithms are that the convergence is highly reliant on the iteration gain and that there is no clear criterion to determine the mainlobe region in each iteration.To reduce the computational complexity and improve flexibility, accurate array response control algorithms [20,21,22] have been developed; these are able to control multipoint responses simultaneously using closed-form solutions. For the design of two-dimensional (2D) beampatterns of conformal arrays, increased constraints in the sidelobe region reduce the degree of freedom of the beamformer, and a higher amount of computation is consumed. Consequently, finding a principle to reduce the SLL with as few constraints as possible has become an important issue. One method is to use the concept of the sparsity constraint [23], which refers to the requirement that the vector being sought or optimized must have as few non-zero entries as possible. Recently, this has been used for sidelobe suppression [24,25,26], and it was shown to be flexible and effective for the adjustment of the SLL and increased robustness. The sidelobes in azimuth-only beampatterns can be discretized into different single directions, and regularization [27] is usually employed to achieve individual sparsity. The sidelobes in 2D beampatterns can be further divided into block-regions composed of local directions, which suggests that group sparsity [28] with regularization is more appropriate for describing the features of the sidelobes in 2D beampatterns than individual sparsity. Up until now, group sparsity has not been utilized in beampattern optimization.
Besides the above problems, computational complexity is another important issue in the study of 2D beampattern optimization with conformal arrays. The number of spatial angles scanned using the elevation–azimuth beampattern of conformal arrays increases exponentially compared with that scanned using the azimuth-only beampattern of linear or circular arrays; hence, the design of 2D beampatterns entails a high computational cost. The algorithms in Refs. [10,12,13,24,25,26] can be easily transformed into the form of either second-order cone programming (SOCP) or semidefinite programming (SDP), followed by the use of software packages such as CVX [29]. The interior-point method used in CVX suffers from a high computational burden, so it is not applicable in the scenario of 2D beampattern optimization. To alleviate the complexity arising from additional computation, recently, the alternating-direction method of multipliers (ADMM) [30] has attracted much attention and has been applied to RCB [31] and beampattern synthesis [32,33,34,35,36], as well as other areas of signal processing [37,38]. The ADMM decouples the global problem into several more local subproblems that are easier to solve, and it obtains the solution of the global problem by coordinating the solutions to the subproblems. Benefiting from fast processing and good convergence, it is suitable for solving large-scale beamforming optimization problems. However, ADMM has not been exploited to solve the optimization problem of a 2D beampattern with sparsity constraints.
This paper is dedicated to the 2D beampattern optimization problem of a Capon beamformer with conformal arrays. We developed a robust Capon beamformer utilizing sparse group constraints that can reduce the SLL flexibly and achieve a robustness of interference suppression in the case of the SV mismatch. We first explore the properties of the 2D beampattern, introducing the group sparsity constraints [39] into the optimization problem, which forms the sparse group constraints together with the individual sparsity constraint. Based on the RCB, the sparse group-constrained robust Capon beamformer (SG-RCB) is then proposed. In order to reduce the computational complexity of the SG-RCB, the ADMM is employed to determine its weight vector. The optimization problem of the SG-RCB is divided into two independent subproblems with the help of a generalized sidelobe canceler (GSC) [40]; one is the WCPO, used to obtain the SV of the desired signal, and the other is the sparse group least absolute shrinkage and selection operator (SGLASSO) [41], used to solve adaptive weight in the GSC. Combining the solutions of the two subproblems, the weight vector is derived in closed form. We show that the proposed beamformer can dramatically reduce the SLL of the 2D beampattern without requiring heavy computational cost, which is significant in practical applications.
The rest of the paper is organized as follows. In Section 2, we review the signal model and concepts on the Capon beamforming and beampatterns. In Section 3, the RCB with sparse group constraints is proposed. In Section 4, the ADMM is introduced to solve the optimization problem of the SG-RCB. In Section 5, we demonstrate the improvement of the proposed method on the 2D beampattern of a conformal array. In Section 6, conclusions are drawn.
Notation 1.
Let us denote matrices and vectors as bold upper-case and lower-case letters, respectively. In particular, denotes an array of all ones and stands for the identity matrix. . and denote the sets of real and complex numbers, respectively. and are the real part and imaginary part of the argument, respectively. The superscripts and denote the transpose operator and the conjugate-transpose operator, respectively. denotes the norm of the input vector . is the principle component of the input matrix.
2. Problem Formulation
2.1. Signal Model
Consider an array with an arbitrary configuration composed of identical M omnidirectional hydrophones. The m hydrophone’s position in the three-dimensional Cartesian coordinate system is represented as
where
: the length of the mth hydrophone’s radius vector.
: the elevation and azimuth angles of the m hydrophone, respectively.
Suppose that a source in the farfield is in the direction of where and . The SV of the plane wave of this source is defined as
where represents the wave number of the plane wave, where f is the frequency and c is the speed of sound.
As shown in Figure 1, suppose there are D far-field narrowband uncorrelated signals (plane waves) impinging on the array, one of which is the desired signal while the other are interferences. The signals received by the array can be written as [6]
where
t: the arbitrary sampling time.
: the received data sampled by the array.
: the actual SV of the desired signal.
: the SV of the dth interference.
: the wavefront of the desired signal.
: the wavefront of the dth interference.
: the zero-mean Gaussian white noise, representing additive noise in the environment received by the array.
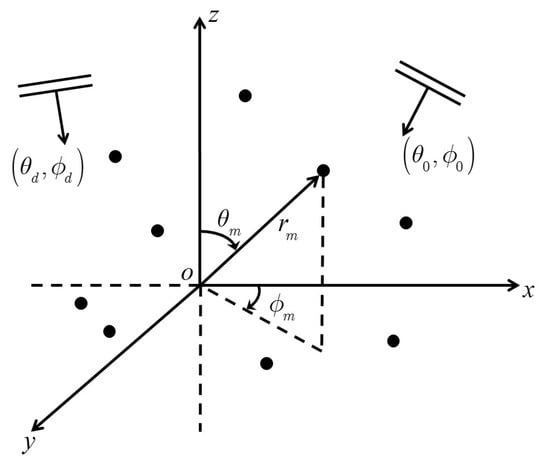

Figure 1.
Illustration of the array with arbitrary geometry, in which is the incidence angle of the desired signal and is the incidence angle of the dth interference.
Assuming that the desired signal, interferences, and noise are uncorrelated with each other, the noise on each hydrophone is also uncorrelated. The covariance matrix of is given as
where
: the statistical expectation.
: the covariance matrix of the desired signal.
: the covariance interference-plus-noise matrix.
: the covariance matrix of the Gaussian white noise.
: the power of the desired signal.
: the power of the dth interference.
: the power of noise.
The signal-to-noise ratio (SNR) and interference-to-noise ratio (INR) of the dth interference are defined as [6], respectively, and . In practice, the covariance matrix of is estimated with a finite number of samples. The sample covariance matrix of is written as
where L denotes the sample size.
2.2. The Two-Dimensional Beampattern
Beamforming is a technique of weighted summation of the received signals to obtain the beam output of the array [6]. The output of the beamformer is
where denotes the weight vector of the beamformer.
The beampattern is an important measurement to evaluate the performance of the beamformer, which describes the response of the beamformer to a signal impinging on the array in the direction of . The response is defined as
For symmetric configuration arrays such as uniform linear arrays (ULA), the beamformer can be only steered in the azimuth. The resulting beampattern is mathematically represented as a one-dimensional vector , where is the number of scanning points in the azimuth (as shown in Figure 2a).
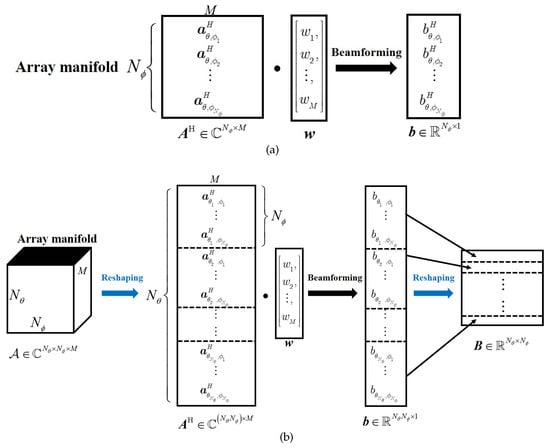
Figure 2.
Implementation of (a) one-dimensional (azimuth-only) beampatterns; (b) 2D beampatterns. The arrows in blue represent the reshaping operation and the arrows in black represent the beamforming operation.
As a result, it can not be employed in applications where full beam steering in three-dimensional space is needed. Arrays similar to that shown in Figure 1 offer three-dimensional steering of the beamformer, which is defined as the elevation–azimuth steering in the coordinate system. The resulting beampattern is mathematically represented as a two-dimensional matrix (as shown in Figure 2b).
where is the number of scanning points in the elevation. It can be seen from Figure 2 that a beampattern is derived by solving a weight vector .
2.3. Capon-Based Beamforming
The standard Capon beamformer (SCB) minimizes the output power of the interference-plus-noise under the distortionless constraint of the desired signal. Then, the of the SCB is obtained by solving the following optimization problem:
In practice, the is often unavailable and replaced with the sample covariance matrix . Substituting into (9), the solution to (9) is given by
The SCB should achieve the optimal performance if the covariance matrix and steering vector are accurately known. In practical scenarios, the estimated matrix carries imprecise knowledge of the real one, leading to an increase in the SLL of the beampattern and affecting its suppression ability. There exists a mismatch between the presumed steering vector and the actual one; the beampattern of the SCB rejects the desired signal as interference and suffers robustness degradation.
When there is a mismatch between the presumed SV and the actual one (denoted as ), an improved Capon beamformer against the SV mismatch can be designed by
where specifies the uncertainty level of the norm of difference between the actual SV and the presumed one. The optimization problem (11) is well known as WCPO [10], which has been proven to be a diagonal loading method [9]. The weight vector of the WCPO improves the robustness of the SCB to a certain extent, but the 2D beampattern’s SLL of the WCPO is still high.
It can be seen from Figure 2 that the implementation of the 2D beampattern is more complex and computationally intensive than that of the one-dimensional beampattern in the past. Based on (11), the objective of beamforming in this paper is to find a weight vector through a computational efficient algorithm, such that it can reduce the SLL of the 2D beampattern on the basis of maintaining robustness.
3. The Proposed Robust Capon Beamformer with Sparse Group Constraints
3.1. Individual Sparsity Constraint
The sidelobe control is an important task of beampattern optimization. For the desired beampattern, we hope that the SLL is as low as possible to suppress noise and interference. Now, we consider the fact that the mainlobe region is much smaller than the sidelobe region in the spatial domain, and the average beam response of the mainlobe is much higher than that of the sidelobe. Therefore, the beam response of the 2D beampattern has the property of sparsity distribution, that is, the values of the responses in the mainlobe are far greater than zero, and the rest is equal or approximate to zero. The sparsity constraint is introduced to reduce the SLL based on (11), and the optimization problem (11) is rewritten as
where
: the individual sparse parameter that is usually determined empirically.
: the array manifold matrix of the sidelobe region.
Mathematically, norm regularization is adopted to describe the sparsity constraint. The smaller the norm of the beam response in the sidelobe region, the lower the SLL of the 2D beampattern. The objective function in (12) is a remarkable model called the least absolute shrinkage and selection operator (LASSO) [42], and (12) is called the robust Capon beamforming with a sparse constraint (S-RCB). The constraint in (12) assumes that the elements in the constrained vector are independent of each other. Such constraint emphasizes controlling each beam response individually in sidelobe region, which meets the condition of the design of the one-dimensional (or azimuth-only) beampattern. This sparsity can be further subdivided into individual sparsity.
3.2. Group Sparsity Constraint
Compared with one-dimensional beampatterns, the property of the sidelobe region of 2D beampatterns is changed. Figure 3 shows the sketch of a 2D beampattern, and we will interpret this property in combination with it.
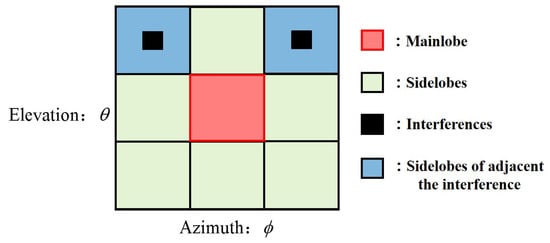
Figure 3.
Sketch of the top view of a 2D beampattern.
In Figure 3, we assume that the ordinate is the elevation and the abscissa is the azimuth, both of which are discretized into several scanning points (the number of scanning points is and , respectively). Any set of coordinates on the two-dimensional grid determines one direction of the spatial angles. A complete 2D beampattern is composed of the beam responses in all scanned directions.
Interference can be properly suppressed without errors according to the nature of Capon beamforming. If the errors are considered, the directions of the interference estimated from the sample covariance matrix are disturbed, which are too “small” to identify on the whole grid plane. In order to improve the tolerance of interference suppression, the interference directions are expanded into small areas centered on the presumed interference directions (black regions in Figure 3). The sidelobe region can be further divided into normal sidelobe regions (green regions in Figure 3) and regions adjacent to the interferences (blue regions in Figure 3) due to the presence of interference.
The sidelobe regions of a 2D beampattern can be briefly divided into the three types mentioned above. The beam responses within each region have approximately the same design requirements, while regions are independent due to their different locations. We hope that the beam responses in the interference regions are lowest in the beampattern. At the same time, the beam responses of the regions adjacent to the interferences should be lower than the normal regions to improve the robustness of interference suppression and the display effect of the beampattern.
Combining the above with the introduction of Figure 3, it can be concluded that the sidelobe of the 2D beampattern is expected to have “regional sparsity” in addition to individual sparsity, and the object subject to sparsity constraints is expanded from a single azimuth to a region composed of multiple spatial angles. Mathematically, this “regional sparsity” is defined as group sparsity [28], which acts like the individual sparsity at the group level. Replacing the individual sparsity in (12) with the group sparsity, the optimization problem (12) is rewritten as
where
: the parameter of group sparsity that is usually determined empirically.
: the qth array manifold matrix of , i.e., , where Q is the number of sidelobe regions.
: the regional sparsity parameter of the qth sidelobe region, and we define .
The norm is introduced in (13), which is a rotational invariant of the norm [43] and defined as
where . The norm in (13) represents the norm of beam responses of the Q sidelobe regions. Therefore, the sparse constraint in (13) is applied to sidelobe regions rather than directions of spatial angles. The objective function in (13) is called the group LASSO (G-LASSO) model [44], based on the LASSO. When and , (13) is equivalent to (12). Equation (13) is called the robust Capon beamforming with a sparse group constraint (G-RCB).
3.3. Robust Capon Beamforming with Sparse Group Constraints (SG-RCB)
Combining (12) and (13), the optimization problem of the 2D beampattern with both sparsity constraints in this paper is finally given by
The objective function in (15) is called the sparse group LASSO (SG-LASSO) model [41], which takes advantage of the sparsity at both the group and individual level within groups in the 2D beampattern. Now, we finally refer to the method of 2D beampattern optimization as the robust Capon beamforming with the sparse group constraints (SG-RCB), which can be seen as a generalization of the S-RCB() and G-RCB(). Optimization problems like (12), (13), and (15) are usually solved by convex optimization toolboxes utilizing the interior-point method (IPM). In this paper, the ADMM framework is adopted to obtain iterative solutions with lower computational complexity that are suitable for large-element array processing.
4. The Solution of the SG-RCB via ADMM
4.1. The Generalized Sidelobe Canceler
To simplify the process of solving the optimization problem (15), first we introduce the GSC. The weight vector to be solved in (15) is written as
where represents the actual steering vector and is also the unadaptive weight in the GSC; is called the adaptive weight of the GSC; represents the block matrix, which is a semi-unitary matrix orthogonal to , i.e., and . Here, is selected as the principal component of : , where . The structure of the GSC is shown in Figure 4.
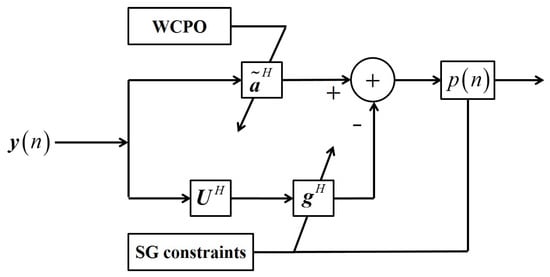
Figure 4.
Structure of the SG-RCB based on GSC.
Substituting (16) into (15), (15) is rewritten as
Combining (16) and (17) with Figure 4, the following corollaries can be drawn:
Corollary 1.
The value of essentially depends on the source, propagation environment, and physical feature of the array. Assuming that they remain unchanged in the problem, once is determined, it remains unchanged in the whole optimization problem, and so does . Therefore, the solving process of is independent to that of and the sparsity constraints, and can be solved by transforming WCPO into RCB [12].
Corollary 2.
The GSC appropriately adjusts according to the received data and constraints to meet the design requirements. Combined with Figure 4 and Corollary 1, it can be seen that the sparsity constraint can only affect the value of .
Corollary 3.
The bottom branch of the GSC is to suppress noise and interference in the received data according to the nature of the Capon beamformer. Combining Corollary 1, Corollary 2, and Figure 4, it can be seen that the influence of the robustness constraint on the value of is fixed once the values of and are known; that is to say, the robustness constraint only affects the value of through the quadratic term of the objective function in (15) or (17).
Corollary 4.
Based on Corollary 1–Corollary 3, the unadaptive weight and the adaptive weight are orthogonal and can be solved independently because .
4.2. Subproblem One: Solve Using the ADMM-RCB
Ignoring the sparse constraints, (17) is simplified to the WCPO of (11). The WCPO is equivalently written as
Let us define the steering vector and the sample covariance matrix in real domain:
where and .
Let . Constructing the auxiliary variable and substituting (19)–(21) into (18), (18) is rewritten as
The augmented Lagrangian function (ALM) corresponding to (22) is
where
: Lagrangian multiplier.
: penalty factor.
The ADMM fixes the remaining variables to remain unchanged when updating a variable in one iteration, iterating the unknown variables in the objective function alternately until all variables converge. One iteration is as follows:
Step 1: Updating .
Step 2: Updating .
Step 3: Updating .
where k denotes iterations. The specific process of each step is described below.
Step 1: Updating .
In iteration , let the partial derivative of with respect to equal to zero. Then, in iteration is obtained:
Step 2: Updating .
In the th iteration, we ignore the terms unrelated to and write the ALM corresponding to (25):
Let The updated in iteration is then derived by
where is the ith element of .
If , the inequality constraint in (25) is not activated, and the obtained is a solution that satisfies (25). On the contrary, the value of is obtained on the boundary of the inequality constraint, i.e., , and substituting it into (28) to obtain , the updated in in the th iteration can be represented by
Step 3: Updating .
Let . The updated in the th iteration is then derived as
In the ADMM of subproblem one, steps 1–3 are alternately cycled until the following two termination conditions are met simultaneously:
where and are the tolerances of the feasibility conditions, respectively, and ”primary” and ”dual” refer to the primal feasibility and the dual feasibility, respectively. Their values are determined jointly by the absolute tolerance and the relative tolerance [30]. The complex solution of subproblem one is finally obtained according to the relationship shown in (19) and (20):
is also determined with derived. The algorithm of solving subproblem one is called the robust Capon beamforming based on the alternating-direction method of multipliers, abbreviated as the ADMM-RCB and summarized in Algorithm 1.
| Algorithm 1: ADMM-RCB |
|
4.3. Subproblem Two: Solve Using the ADMM-SGLASSO
When and have been solved, (17) can be simplified as the standard SGLASSO:
We now define the following real variables:
where , , and . By substituting (20), (21), and (35)–(37) into (34), it can be rewritten as
where is derived by substituting into (21), represents the auxiliary variable, and is the qth group of auxiliary variables, which corresponds to the beam responses of each spatial angle in the qth sidelobe region. The ALM corresponding to (38) is written as follows:
where is the Lagrange multiplier. One iteration of the subproblem two is as follows:
Step 1: Updating .
Step 2: Updating .
Step 3: Updating .
The specific process of each step is described below:
Step 1: Updating .
Constructing the auxiliary variable , in the th iteration, (40) can be equivalently expressed as
which can also be iteratively solved by the ADMM. The ALM corresponding to (43) is
where is the Lagrange multiplier. For step 1, and are regarded as constants, and , and are the variables that need to be iteratively solved. This is similar to subproblem two; step 1 in subproblem two can be solved by the ADMM as follows:
Substep 1.1: Updating .
Substep 1.2: Updating .
Substep 1.3: Updating .
where denotes the iterations in step 1. The following describes the specific process:
Substep 1.1: Updating .
In the th iteration, by taking the partial derivative of the ALM in (45) with respect to and then making it zero, the expression of is derived as
where
where is in the real form of .
Substep 1.2: Updating .
In the th iteration, ignoring terms unrelated to , (46) is written as
Let . The last row of (51) is the proximal mapping of . For a given , the elements in can be expressed by soft thresholding as
where represents the soft thresholding operator, the diagram of which is shown in Figure 5a. It can be seen from Figure 5a that the operator performs a “zero” on some elements of the argument, thereby satisfying the sparsity constraint.
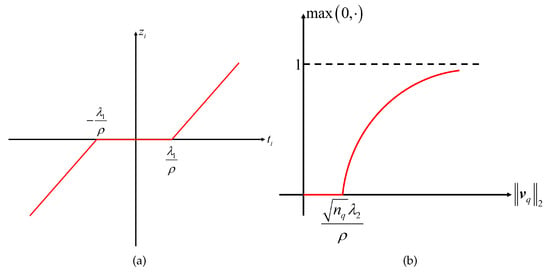
Figure 5.
Diagrams of two soft thresholding operators: (a) the soft thresholding operator ; (b) the block soft thresholding operator .
Substep 1.3: Updating .
Let the partial derivative of the ALM regarding in (47) be zero. Then, in the ()th iteration is derived as
Substeps 1.1 to 1.3 are alternately cycled until both of the following iteration termination conditions are met:
where and are the tolerances of the feasibility conditions, respectively. is yielded as the output of the th iteration in subproblem two.
Step 2: Updating .
According to (38), the auxiliary variable is divided into Q groups for the group sparsity, and each has its own regional sparsity parameter, so it needs to be calculated separately. Ignoring the terms unrelated to , in the th iteration, the optimization problem on in (41) can be expressed as
where represents the part of corresponding to . Similar to (51), let . Then, the elements in can be expressed by block soft thresholding as
where is the block soft thresholding operator. is the function that indicates the maximum value after the input and zero are compared. The diagram of is shown in Figure 5b. Here, it can be seen that the value less than in the augment is set to zero, and the remaining value is reduced. is obtained by performing the operator in (56) on each corresponding to the qth region and combining them together.
Step 3: Updating .
Let the partial derivative of the ALM with respect to in (42) be zero. Then, is expressed as
In subproblem two, steps 1–3 are performed alternately until the following two iteration termination conditions are met simultaneously:
where and are the tolerances of feasibility conditions, respectively. The solution of subproblem two is finally obtained according to the vector relationship shown in (35):
The complete method for solving subproblem two is called the sparse group LASSO based on the alternating-direction method of multipliers, abbreviated as the ADMM-SGLASSO and summarized in Algorithm 2. Substituting (33) and (59) into (16) yields the weight vector of the SG-RCB beamformer. The flowchart of the SG-RCB is shown in Figure 6.
| Algorithm 2: ADMM-SGLASSO |
|
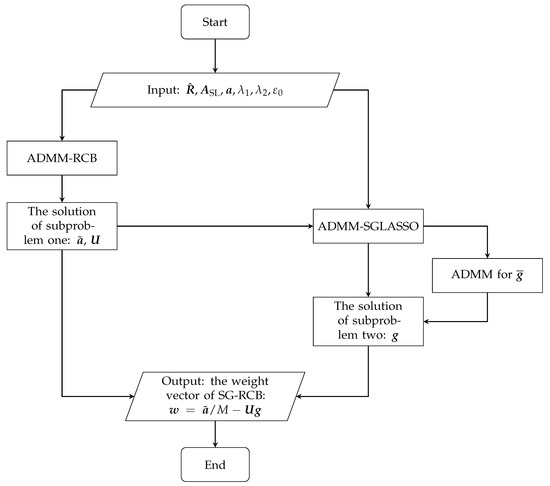
Figure 6.
Flowchart of the SG-RCB.
4.4. Computational Complexity Analysis
We describe the computational complexity of the proposed SG-RCB as measured by the number of multiplication operations. The SG-RCB consists of two algorithms, the ADMM-RCB and the ADMM-SGLASSO. As Algorithms 1 and 2 show, each algorithm is divided into two stages: preprocessing and iteration. For simplicity, the complexity of one iteration is discussed.
In the preprocessing stage of the ADMM-RCB, and are calculated in advance, resulting in costs of and , respectively. In one complete iteration, the computational costs of steps 4–6 in the ADMM-RCB are , , and , respectively.
In the preprocessing stage of the ADMM-SGLASSO, , , , and are calculated and fixed in irritations, which cost multiplications in total. At the iteration stage, the computational costs of steps 7–10 in the ADMM-SGLASSO are , , , and , respectively.
The computational costs of steps 13 and 14 in the ADMM-SGLASSO are and , respectively. Therefore, the dominant order of the per-iteration computational complexity of the proposed SG-RCB is . The computation in the preprocessing only needs to be calculated once, which has little impact on the overall complexity of the SG-RCB, although its complexity increases rapidly with the increase in the dimension of variables.
Now, let us compare the SG-RCB with other ADMM-based beamforming methods, for instance, the methods proposed in Refs. [35,36]. In the preprocessing stage, the dominant order of the computational costs of the method in Ref. [35] is , while the computational complexity in this stage is not discussed in [36]. In practice, the number of hydrophones is lower than the number of scanning directions in the sidelobes; thus, the computational complexity of the SG-RCB in the preprocessing stage is lower than that of the method in Ref. [35]. In the iteration stage, both methods proposed in Refs. [35,36] have same dominant cost of in per iteration, which is also equal to that of the SG-RCB.
Next, we discuss the complexity of the SOCP for comparison. In the preprocessing stage, the computational cost of the SOCP is of the same order as that of the SG-RCB, i.e., . In the iteration stage, however, the SOCP adopts the IPM, which costs at each iteration. The overall computational complexity of the SG-RCB is lower than that of the SOCP solved by the IPM with the variable dimension becoming larger; thus, the proposed SG-RCB has a significant advantage in computational complexity in the case of large-element conformal arrays.
5. Simulation Results
5.1. Parameter Setting
A half-cylindrical conformal array consisting of 40 hydrophones is analyzed in this section. The geometry and parameters of the conformal array are shown in Figure 7. Table 1 presents the relevant parameters shown in Figure 7d.
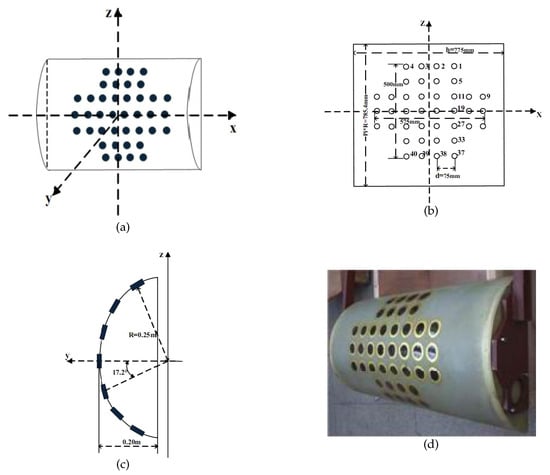
Figure 7.
Diagram of the half-cylindrical conformal array (HCCA) configuration: (a) three-dimensional diagram (solid black dots represent hydrophones); (b) front view (the top left circle represents hydrophone number 1, the bottom right circle represents hydrophone number 40, and the labels of hydrophones increase from top left corner to bottom right corner); (c) side view; (d) the real object.

Table 1.
The physical parameters of the HCCA in Figure 7.
We consider the simulation being implemented in an underwater free field where the sound velocity is constant at 1500 m/s. The point sources are single-frequency with a frequency of 10 kHz. The receiving array is located in the far field relative to the source, and the transmission loss is not considered.
Assuming that the look direction is , the signal-to-noise ratio (SNR) of the desired signal is 10 dB. There are two interferences in the direction of and , and their interference-to-noise ratios (INRs) are 35 dB. The grouping of the sidelobe is shown in Figure 8, in which the number of regions of sidelobes and interferences are indicated, respectively. The scanning intervals of elevation and azimuth are , respectively, and the interval of the interference regions in the elevation and azimuth are both . Our codes were written in MATLAB R2023a. All our numerical experiments were conducted on a laptop computer with an AMD CPU (3.20 GHz) and 32 GB RAM running Windows 11.
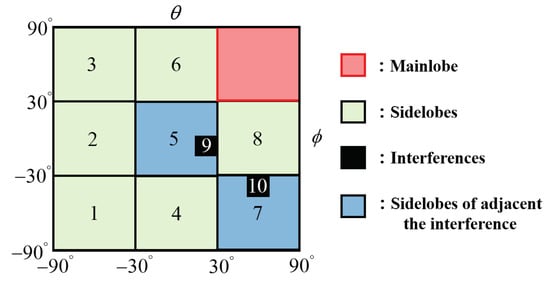
Figure 8.
Grouping of sidelobe regions. The numbers indicate the sequence numbers of the different sidelobe regions.
5.2. Cpu Times
Some existing methods were selected to compare the ADMM to in order to show its advantage in terms of computational efficiency. Here, the ADMM-RCB in subproblem one is compared with the RCB with the SOCP solved by CVX [29], which is abbreviated as the SOCP-RCB, and the in (18) is set to 1. For the SG-RCB, the SOCP is selected for comparison, which is abbreviated as the SOCP-SG-RCB. The and in (12), (13), and (15) are set to 0.01 and 0.1 [41,45], respectively. In the ADMM-based methods, the values of the absolute tolerance and the relative tolerance are unified and set to and , respectively [30].
Figure 9 shows the computing time (CPU time) of the different studied methods. We compare the ADMM-RCB with the SOCP-RCB in Figure 9a. It is easily observed that the CPU time of the ADMM is much shorter than that of the SOCP. The average time of the SOCP-RCB is 0.3293 s, while that of the ADMM-RCB is 0.009 s.
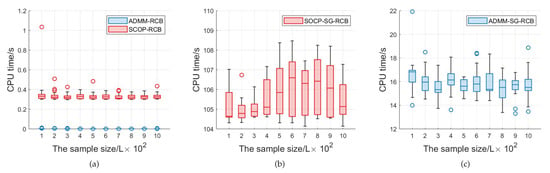
Figure 9.
Boxcharts of the computing times of different methods: (a) ADMM–RCB and SOCP–RCB; (b) SOCP–SG–RCB; (c) ADMM–SG–RCB.
Next, we compare the computing time of different methods to solve the SG-RCB. Figure 9b,c show the CPU time of the SOCP, as well as of the ADMM for solving the SG-RCB. The SOCP-SG-RCB involves a long running time, and its average time is 105.6675 s. The SOCP belongs to interior-point method; it is not applicable to the 2D beampatterns because of its high computational complexity. Comparing Figure 9c with Figure 9b, it can be found that the CPU time of the ADMM-SG-RCB is much less than that of the SOCP-SG-RCB (15.8016 s).
5.3. Beampatterns of Different Methods
In this subsection, we further explore the 2D beampatterns of different beamformers. All used parameters are the same as those in Section 5.2. First, we present the beampatterns of some fundamental beamformers in Figure 10, in which the beam responses of two interferences are labeled. It is observed that the CBF beampattern can not suppress two interferences, while the SCB beampatterns distort and their SLL is even higher than the response in the actual signal direction. In accordance with Figure 9a, the ADMM-RCB beampattern is superior to that of the SOCP-RCB, even though their beampatterns are close.
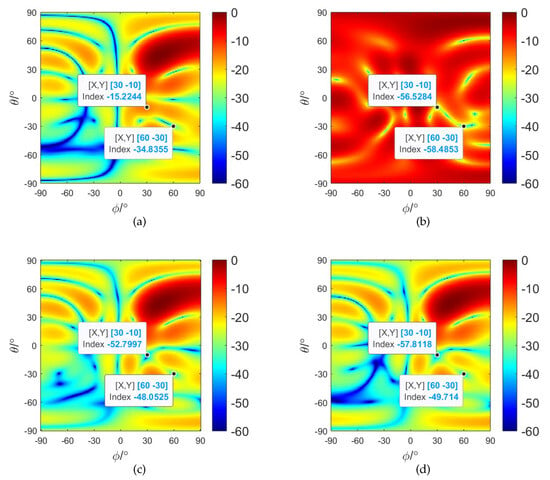
Figure 10.
Beampatterns of some fundamental beamformers: (a) CBF; (b) SCB; (c) SOCP–RCB; (d) ADMM–RCB.
Then, the beampattern of the SG-RCB is analyzed, while the S-RCB and G-RCB are run for comparison. Figure 11 shows the beampatterns of the three beamformers, in which the first row is the three-dimensional view and the second is the top view. It can be seen from Figure 11d that the S-RCB makes the beam responses of sidelobe regions as low as possible at the cost of increasing the mainlobe width. In Figure 11e, the mainlobe width of the G-RCB is narrower than that of the S-RCB, but its SLL is higher. The constraint of the G-RCB is imposed on regions of the sidelobe and interferences separately, and the beam responses of the interferences of the G-RCB are lower than those of the sidelobes. The SG-RCB’s beampattern in Figure 11c,f can be seen as a combination of the above two beamformers, which ensures a low SLL and a narrow mainlobe width while keeping the beamformer from losing its interference suppression capability.
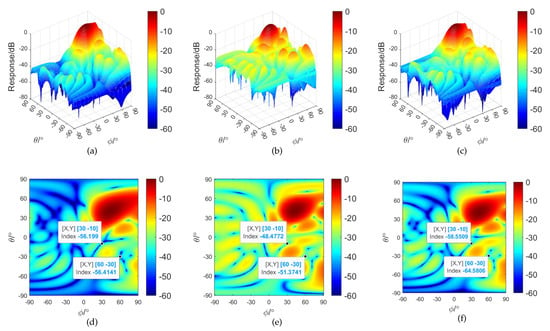
Figure 11.
Beampatterns among the S–RCB, G–RCB and SG–RCB: (a) 2D beampattern of the S–RCB ( and ); (b) 2D beampattern of the G–RCB ( and ); (c) 2D beampattern of the SG–RCB ( and ); (d) top view of the S–RCB result; (e) top view of the G–RCB result; (f) top view of the SG–RCB result.
In Table 2, we compare the specific performance of the beampattern obtained by different beamformers in terms of the width of the mainlobe (taking a dB beam width as an example ()), the SLL, and the beam responses of the interferences. It is shown that the beampattern optimized by the G-RCB has the narrowest mainlobe width instead of that of the CBF among the beamformers in Table 2 with respect to the conformal array. The similarity of the three sparsity-constrained beamformers is that the SLL is significantly reduced, in which the SLL of the S-RCB is more than 4 dB lower than that of the conventional beamforming (CBF). The SG-RCB combines the advantages of the S-RCB and G-RCB, which can achieve the optimal interference suppression while maintaining the mainlobe width almost unchanged. It is also implied that the SG-RCB can make a flexible tradeoff between the mainlobe width and the SLL by adjusting the values of and according to the actual situation.

Table 2.
Performance comparison of beampatterns of different beamformers. The red indicates the optimal value in this column.
5.4. SINRout versus SNR and the Sample Size
Now, we compare of the SG-RCB with other methods, which is calculated by
Particularly, the optimal is calculated by the SCB with the theoretical covariance matrix for performance evaluation. It is observed from Figure 12a that the SCB suffers a poor performance. The of other methods is similar, with a low (≤10 dB). With the increase in the , an inaccurate estimation of the sample covariance matrix is amplified so that the of these methods slightly decreases. The of the S-RCB, G-RCB, and SG-RCB is higher than that of the RCB; furthermore, the of the SG-RCB increases by approximately 3 dB compared to the RCB. Figure 12b shows that three sparsity-class methods do not only quickly converge to their corresponding optimal values, but their is also higher than that of the RCB in the case of a low number of samples. Figure 12 indicates that the RCB with sparsity constraints is basically effective in optimizing 2D beampatterns, although a certain is lost when is high.
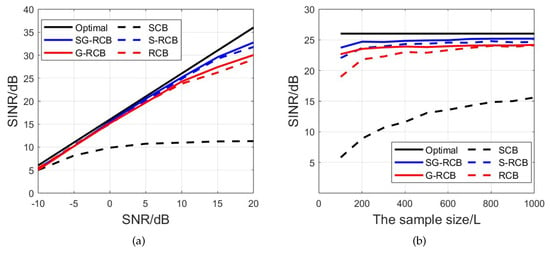
Figure 12.
Performance comparison of different methods: (a) versus , L = 800; (b) versus the sample size. = 10 dB.
5.5. Beampatterns with Different Regional Sparsity Parameters
In Section 5.2, Section 5.3 and Section 5.4, we uniformly set the regional sparsity parameters to , i.e., . In this subsection, the influence of the regional sparsity parameters on the beampattern is verified.
According to the grouping in Figure 8, one value of in this subsection is set as follows:
where the two number 10s represent the parameters of the interference regions (black regions) in Figure 8. Substituting (61) into (15), the beampattern of the SG-RCB based on (61) is shown in Figure 13, in which the regions of the sidelobes adjacent to interferences and the interferences are marked out by the red dashed line and the red solid line, respectively. It can been seen from Figure 13b that the nulls in the interference regions are widened so that the interferences can be correctly suppressed.
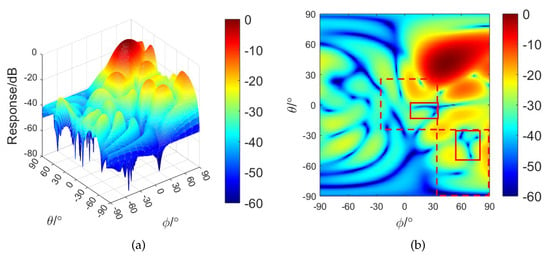
Figure 13.
Influence of on the beampattern of the SG–RCB: (a) two–dimensional view; (b) top view.
The other value of is set blow.
where the two number 5s represent the parameters of the sidelobes adjacent to the interferences (blue regions in Figure 8). The beampatterns of the SG-RCB using are shown in Figure 14. It is observed that the beam responses in the fifth and seventh sidelobe regions marked by the red dashed line decrease further, but the cost is that the mainlobe is obviously widened. As a summary, the beam responses in the sidelobe regions can be adjusted by the regional sparsity parameters. The greater the parameters, the lower the responses, but their values need to balance the relationship between the mainlobe width and the SLL.
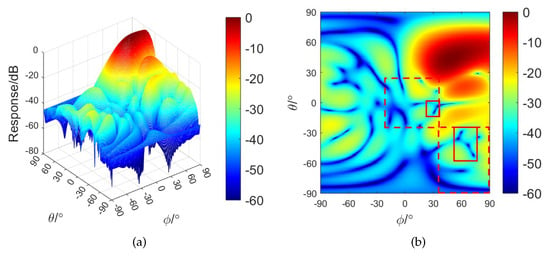
Figure 14.
Influence of on the beampattern of the SG–RCB: (a) two–dimensional view; (b) top view.
5.6. Interference Suppression in the Presence of the SV Mismatch
The array manifold of the conformal array is susceptible to distortion caused by various factors, especially the scattering of baffles. The robustness of the SG-RCB is tested in this subsection. The SVs of the desired signal and interferences in this subsection are obtained by the finite-element software COMSOL [46] to guarantee the model in practice [47], which converts the physical model into the finite-element mesh model and then carries out the numerical calculation.
First, we consider . Substituting such SVs into the optimization problem of the SG-RCB, the resulting beampatterns are shown in Figure 15. The mainlobes of the beampatterns are not distorted under the robustness constraint, but each beamformer has poor performance in interference suppression due to the SV mismatch.
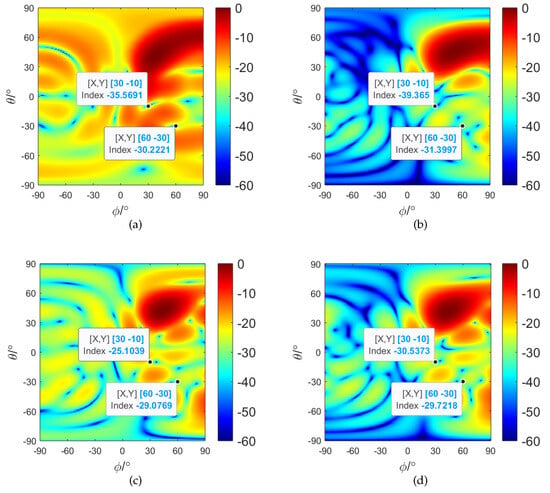
Figure 15.
Beampatterns in the case of the SV mismatch: (a) ADMM–RCB; (b) S–RCB; (c) G–RCB; (d) SG–RCB.
Then, we investigate the effect of and on interference suppression. The beampattern using is shown in Figure 16. It is observed that the beam responses of the two interferences are reduced by about 10 dB compared with the results of Figure 15d.
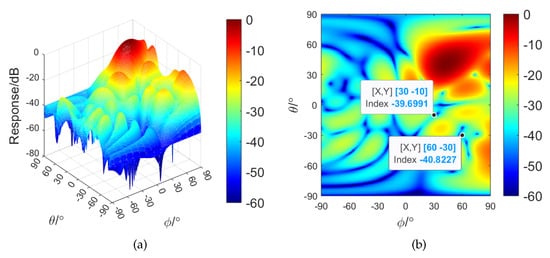
Figure 16.
Performance of interference suppression of the SG–RCB using : (a) two–dimensional view; (b) top view.
Furthermore, by replacing with in the SG-RCB, the resulting beampattern is obtained, as shown in Figure 17. It can be seen that the beam responses of the interferences and the sidelobes decrease further at the cost of the mainlobe widening. It can be seen from Figure 16 and Figure 17 that setting the regional sparsity parameters properly can improve the interference suppression without changing the overall performance of the 2D beampattern when the SV mismatch exists.
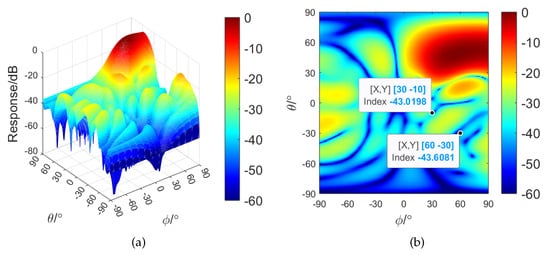
Figure 17.
Performance of interference suppression of the SG–RCB using : (a) two–dimensional view; (b) top view.
6. Conclusions
In this paper, we developed the SG-RCB, which utilizes sparse group constraints based on the RCB to reduce the SLL of the 2D beampattern for conformal arrays. By introducing the GSC framework, the original optimization problem was divided into two subproblems. The first is the RCB problem and the second is the SGLASSO problem. To handle these problems, the ADMM was employed to solve them in closed form.
The main advantages of the proposed method for 2D beampattern optimization are as follows: The SLL of the 2D beampattern is greatly reduced by the sparse group constraints. The ADMM is applied to solve the optimization problem, which greatly improves the computational efficiency compared with other existing methods. The interference suppression of the proposed method in the presence of the SV mismatch can be recovered by adjusting the regional sparsity parameters.
The SG-RCB has broad application prospects in various underwater scenarios. For example, the SG-RCB can be applied to the arrays of autonomous underwater vehicles (AUV) or unmanned underwater vehicles (UUV) to realize the detection and direction of arrival (D.O.A) estimation of the target. In addition, the SG-RCB has potential applications in the real-time processing of received signals due to its significant computational efficiency.
Author Contributions
Conceptualization, Y.D.; methodology, Y.D. and C.S.; validation, Y.D.; formal analysis, Y.D.; investigation, Y.D.; resources, C.S.; data curation, Y.D.; writing—original draft preparation, Y.D.; writing—review and editing, C.S. and X.L.; supervision, C.S.; project administration, C.S.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (U2341203, 12274346).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Frank, T.H.; Kesner, J.W.; Gruen, H.M. Conformal array beam patterns and directivity indices. J. Acoust. Soc. Am. Mar. 1978, 63, 841–847. [Google Scholar] [CrossRef]
- Traweek, C.M. Optimal Spatial Filtering for Design of a Conformal Velocity Sonar Array. Ph.D. Thesis, Pennsylvania State University, University Park, PA, USA, 2003. [Google Scholar]
- Yang, Y.; Wang, Y.; Ma, Y.; Sun, C. Experimental Study on Robust Supergain Beamforming for Conformal Vector Arrays; OCEANS: San Diego, CA, USA, 2013; pp. 1–5. [Google Scholar]
- Josefsson, L.; Persson, P. Conformal Array Antenna Theory and Design; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zhang, H.; Guo, D.; Cao, X. An Airborne Conformal Array Beampattern Optimization Algorithm Based on Convex Optimization. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons Ltd.: New York, NY, USA, 2002. [Google Scholar]
- Zhu, J.; Song, Y.; Jiang, N.; Xie, Z.; Fan, C.; Huang, X. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Carlson, B.D. Covariance matrix estimation errors and diagonal loading in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 397–401. [Google Scholar] [CrossRef]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.-Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Huang, Y.; Fu, H.; Vorobyov, S.A.; Luo, Z.Q. Robust Adaptive Beamforming via Worst-Case SINR Maximization With Nonconvex Uncertainty Sets. IEEE Trans. Signal Process. 2023, 71, 218–232. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Zhang, X.; He, Z.; Zhang, X.; Xie, J. Robust Sidelobe Control via Complex-Coefficient Weight Vector Orthogonal Decomposition. IEEE Trans. Antennas Propag. 2019, 67, 5411–5425. [Google Scholar] [CrossRef]
- Li, H.; Ran, L.; He, C.; Ding, Z.; Chen, S. Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array. Remote Sens. 2023, 15, 4929. [Google Scholar] [CrossRef]
- Wu, R.; Bao, Z.; Ma, Y. Control of peak sidelobe level in adaptive arrays. IEEE Trans. Antennas Propag. 1996, 44, 1341–1347. [Google Scholar]
- Yan, S.F. Optimal Array Signal Processing: Beamforming Design Theory and Methods; Science Press: Beijing, China, 2018. [Google Scholar]
- Liu, L.; Liang, X.; Li, Y.; Liu, Y.; Bu, X.; Wang, M. A Spatial-Temporal Joint Radar-Communication Waveform Design Method with Low Sidelobe Level of Beampattern. Remote Sens. 2023, 15, 1167. [Google Scholar] [CrossRef]
- Olen, C.A.; Compton, R.T. A numerical pattern synthesis algorithm for arrays. IEEE Trans. Antennas Propag. 1990, 38, 1666–1676. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.; Gong, J.; Tan, M.; Chen, G. Robust Suppression of Deceptive Jamming with VHF-FDA-MIMO Radar under Multipath Effects. Remote Sens. 2022, 14, 942. [Google Scholar] [CrossRef]
- Zhang, X.; He, Z.; Liao, B.; Zhang, X.; Peng, W. Pattern Synthesis With Multipoint Accurate Array Response Control. IEEE Trans. Antennas Propag. 2017, 65, 4075–4088. [Google Scholar] [CrossRef]
- Zhang, X.; He, Z.; Xia, X.-G.; Liao, B.; Zhang, X.; Yang, Y. OPARC: Optimal and Precise Array Response Control Algorithm—Part II: Multi-Points and Applications. IEEE Trans. Signal Process. 2019, 67, 668–683. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, X.; He, Z.; Xie, J.; Han, C. Beampattern synthesis for large-scale antenna array via accurate array response control. Digit. Signal Process. 2021, 117, 103152. [Google Scholar] [CrossRef]
- Rao, B.D. Signal processing with the sparseness constraint. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98, Seattle, WA, USA, 12–15 May 1998; Volume 3, pp. 1861–1864. [Google Scholar]
- Zhang, Y.; Zhao, H.; Ng, B.P.; Lie, J.P.; Wan, Q. Robust Beamforming Technique with Sidelobe Suppression Using Sparse Constraint on Beampattern. ACES J. 2010, 25, 947–955. [Google Scholar]
- Liu, Y.; Wan, Q. A Robust Beamformer Based on Weighted Sparse Constraint. Prog. Electromagn. Res. Lett. 2010, 16, 53–60. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Zhu, S.; Lan, L.; Li, X.; Liu, Z.; Wu, Z. Range-Ambiguous Clutter Suppression via FDA MIMO Planar Array Radar with Compressed Sensing. Remote Sens. 2022, 14, 1926. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted l1 Minimization. J. Fourier Anal Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Bakin, S. Adaptive Regression and Model Selection in Data Mining Problems. Ph.D. Thesis, School of Mathematical Sciences, Australian National University, Canberra, Australia, 1999. [Google Scholar]
- Grant, M.C.; Boyd, S.P. The CVX Users’ Guide, Release 2.2; CVX Research, Inc.: Austin, TX, USA, 2020; Available online: http://cvxr.com/cvx (accessed on 14 January 2024).
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Now Found. Trends Mach. Learn. 2011, 3, 1122. [Google Scholar]
- Fan, W.; Liang, J.; Yu, G.; So, H.C.; Li, J. Robust Capon Beamforming via ADMM. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4345–4349. [Google Scholar]
- Liang, J.; Fan, X.; Fan, W.; Zhou, D.; Li, J. Phase-Only Pattern Synthesis for Linear Antenna Arrays. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3232–3235. [Google Scholar] [CrossRef]
- Yang, J.; Lin, J.; Shi, Q.; Li, Q. An ADMM-Based Approach to Robust Array Pattern Synthesis. IEEE Signal Process. Lett. 2019, 26, 898–902. [Google Scholar] [CrossRef]
- Tian, X.; Chen, H.; He, M.M.; Wang, W.Q. Fast Beampattern Synthesis Algorithm for Flexible Conformal Array. IEEE Signal Process. Lett. 2022, 29, 2417–2421. [Google Scholar] [CrossRef]
- Wang, W.; Yan, S.; Mao, L.; Guo, X. Robust Minimum Variance Beamforming With Sidelobe-Level Control Using the Alternating Direction Method of Multipliers. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3506–3519. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, J.; Wu, X.; Pan, Y. A distributed approach to robust minimum variance distortionless response beamforming in large-scale arrays. IET Commun. 2023, 17, 950–959. [Google Scholar] [CrossRef]
- Chen, C.; Liu, T.; Liu, Y.; Yang, B.; Su, Y. Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging. Remote Sens. 2022, 14, 682. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Tian, H.; Ling, B.W.-K.; Zhang, Z. DeepRED Based Sparse SAR Imaging. Remote Sens. 2024, 16, 212. [Google Scholar] [CrossRef]
- Wu, T.T.; Lange, K.L. Coordinate descent algorithms for lasso penalized regression. Ann. Appl. Stat. 2008, 2, 224244. [Google Scholar] [CrossRef]
- Griffiths, L.; Jim, C. An alternative approach to linearly constrained adaptive beamforming. IEEE Trans. Antennas Propag. 1982, 30, 27–34. [Google Scholar] [CrossRef]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. A Sparse-Group Lasso. J. Comput. Graph. Stat. 2013, 22, 231–245. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Ding, C.; Zhou, D.; He, X.; Zha, H. R1-PCA: Rotational invariant L1-norm principal component analysis for robust subspace factorization. In Proceedings of the 23rd international conference on Machine learning (ICML’06), Pittsburgh, PA, USA, 21–26 June 2006; Association for Computing Machinery: New York, NY, USA, 2006; pp. 281–288. [Google Scholar]
- Yuan, M.; Lin, Y. Model Selection and Estimation in Regression with Grouped Variables. J. R. Stat. Soc. Ser. Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Liu, J.; Ji, S.; Ye, J. SLEP: Sparse Learning with Efficient Projections. Arizona State University. 2009. Available online: http://yelabs.net/software/SLEP (accessed on 14 January 2024).
- COMSOL Multiphysics® v.5.2. Acoustics Module Users’ Guide. COMSOL AB, Stockholm, Sweden. 2021. Available online: https://cn.comsol.com/models/acoustics-module (accessed on 14 January 2024).
- Yang, B.; Sun, C.; Chen, Y.L. Conformal Array Beampattern Optimization Method and Experimental Research Based on Sound Field Forecast. Torpedo Technol. 2006, 14, 18–20. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).