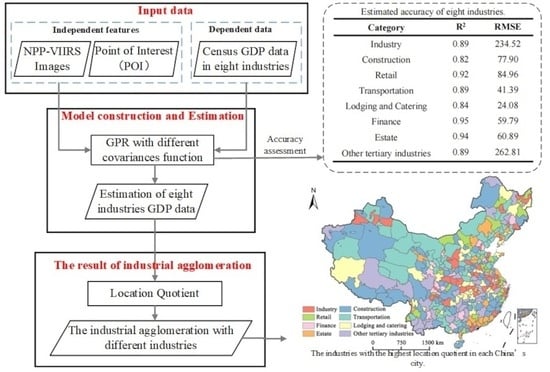
The Assessment of Industrial Agglomeration in China Based on NPP-VIIRS Nighttime Light Imagery and POI Data
Abstract
1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. Materials
2.2.1. Nighttime Light Data
2.2.2. POI Data
2.2.3. Auxiliary Data
2.2.4. Statistical GDP Data
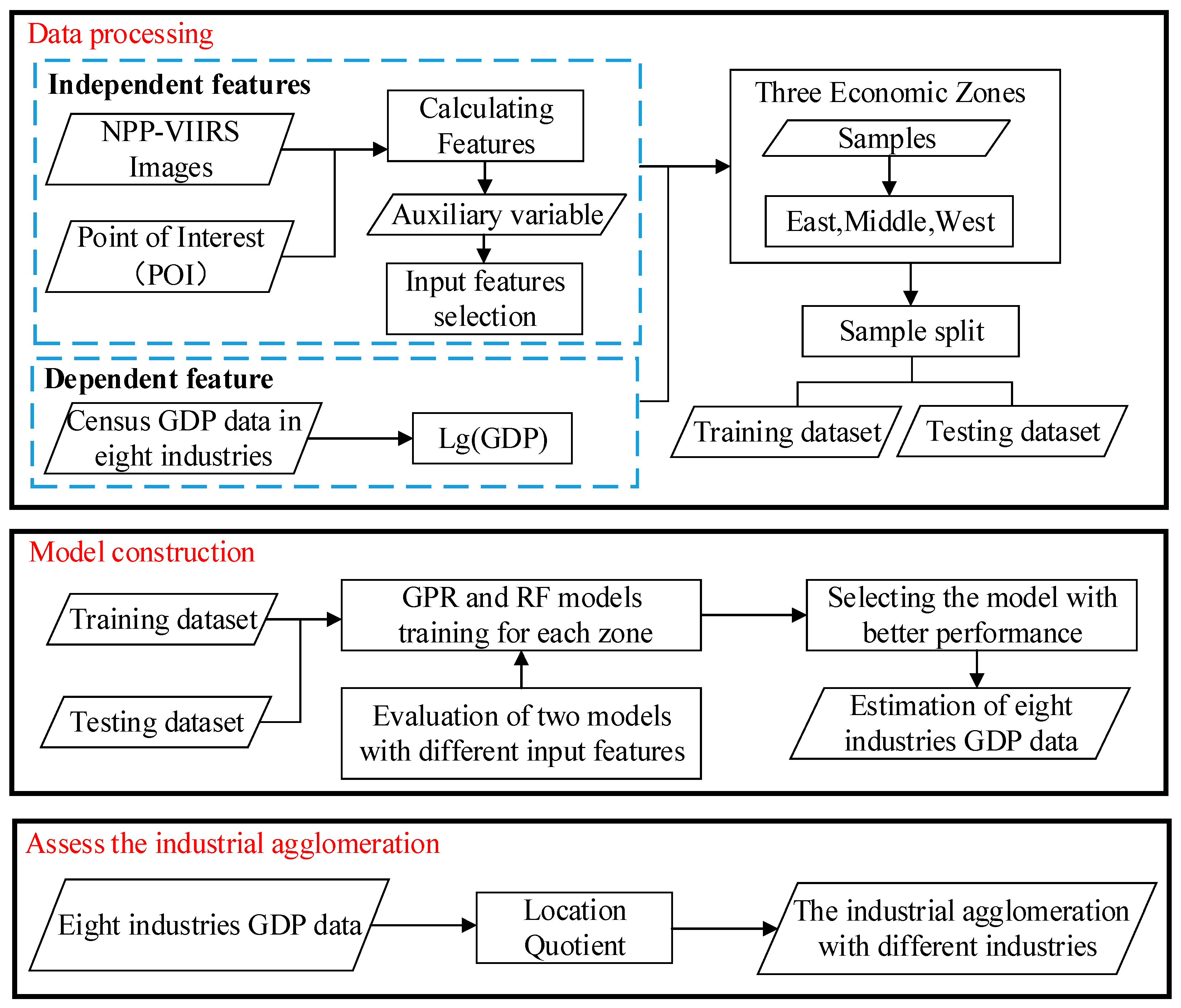
3. Methods
3.1. The Location Quotient
3.2. GDP Estimation
3.2.1. Selection of NTL and POI Features
3.2.2. Gaussian Process Regression
3.2.3. The Random Forest
3.3. Model Construction and Evaluation
4. Results
4.1. Selection Input Features and Model Comparison
4.2. Estimated GDP of Eight Industries
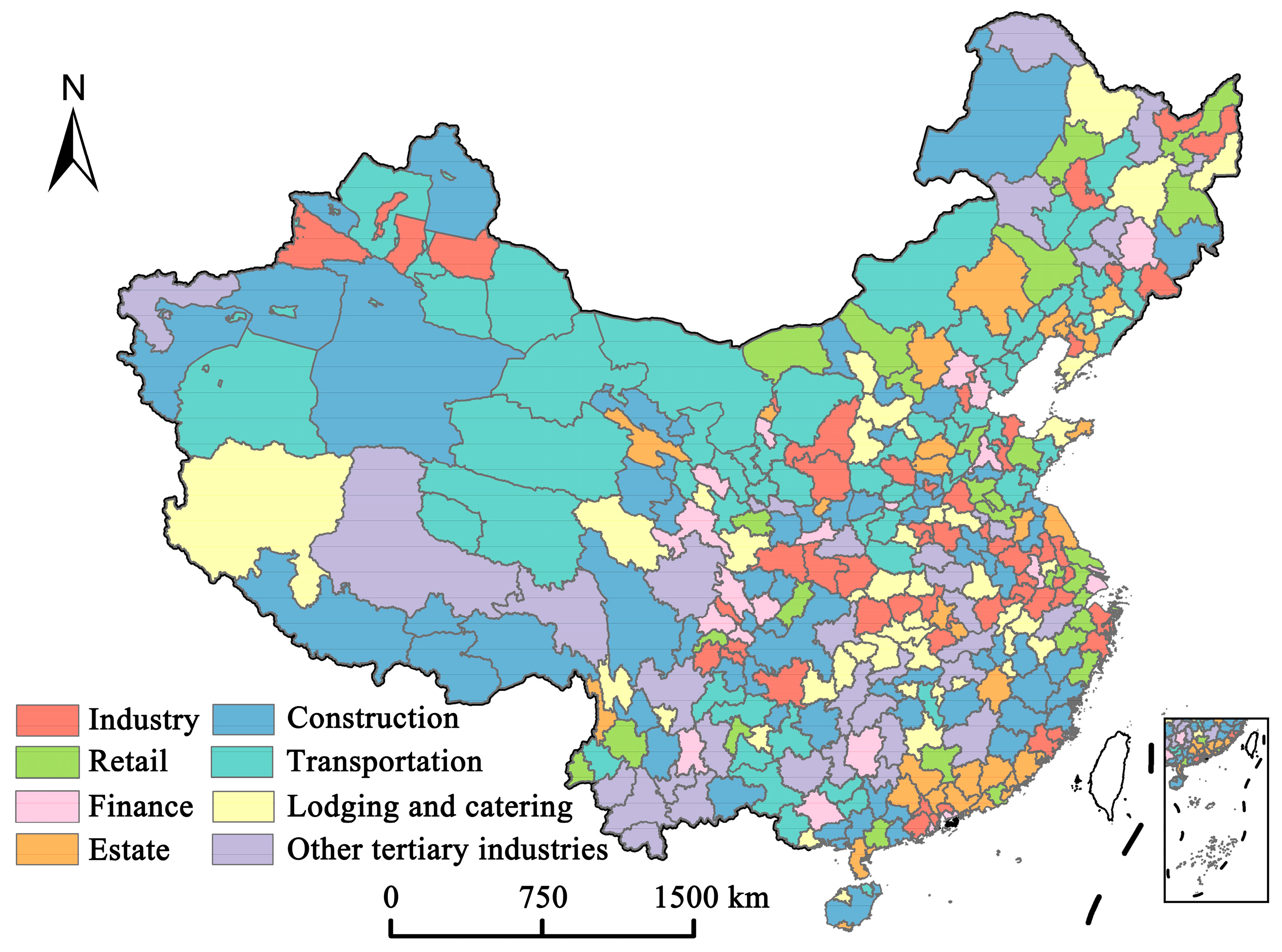
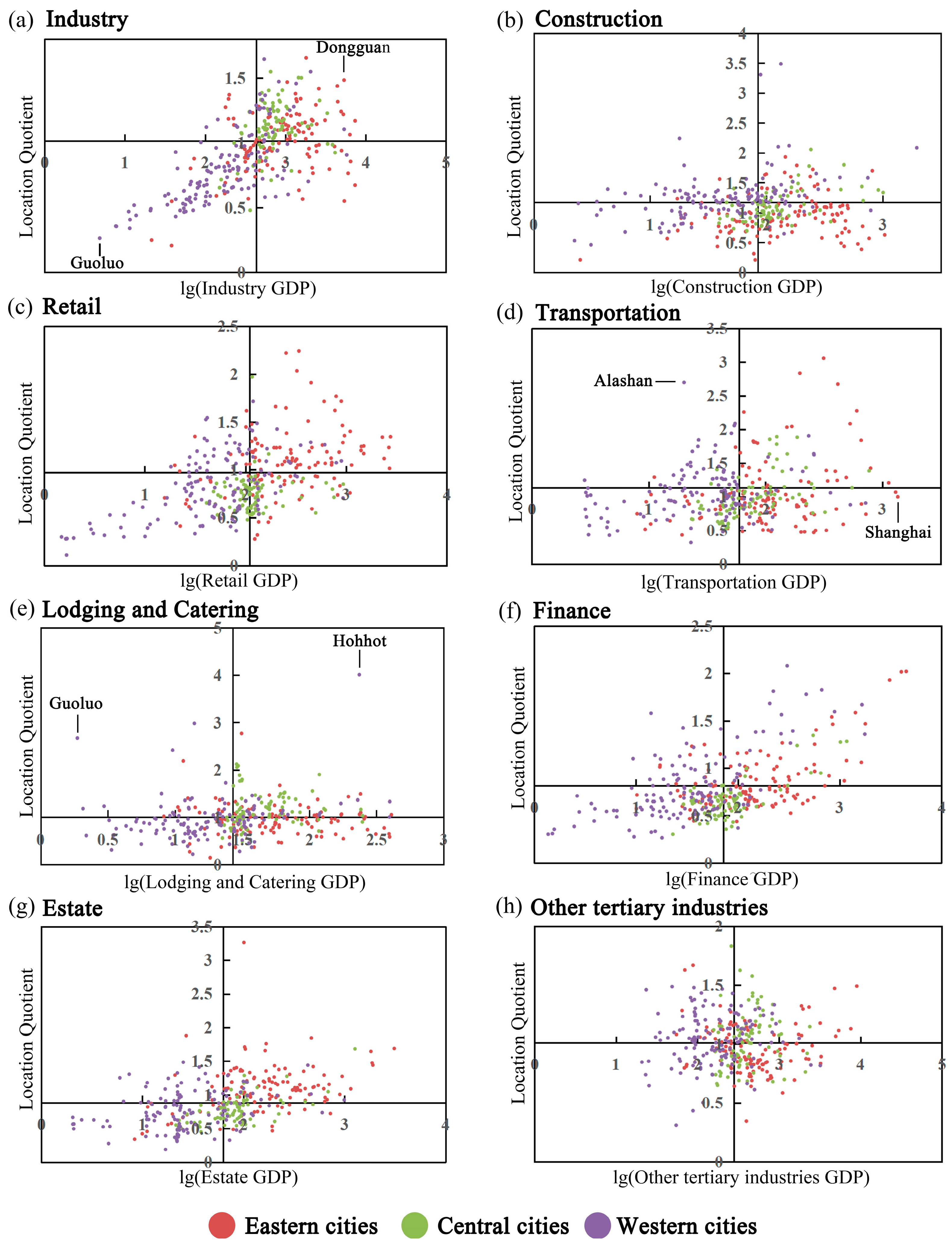
4.3. Industrial Agglomeration Measurement of Different Industries
5. Discussion
5.1. Accuracy Assessment and Residual Analysis
5.2. Analysis of the Relationship between GDP and Industrial Agglomeration
5.3. Policy Implications
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Zhang, X. Industrial agglomeration, technological innovation and carbon productivity: Evidence from China. Resour. Conserv. Recycl. 2021, 166, 105330. [Google Scholar] [CrossRef]
- Guo, S.; Ma, H. Does industrial agglomeration promote high-quality development of the Yellow River Basin in China? Empirical test from the moderating effect of environmental regulation. Growth Chang. 2021, 52, 2040–2070. [Google Scholar] [CrossRef]
- Wu, J.; Tu, Y.; Chen, Z.; Yu, B. Analyzing the Spatially Heterogeneous Relationships between Nighttime Light Intensity and Human Activities across Chongqing, China. Remote Sens. 2022, 14, 5695. [Google Scholar] [CrossRef]
- Wang, L.; Fan, H.; Wang, Y. Improving population mapping using Luojia 1-01 nighttime light image and location-based social media data. Sci. Total Environ. 2020, 730, 139148. [Google Scholar] [CrossRef]
- Song, Y.; Li, X.; Tao, G.; Liu, J. Exploring the Characteristics and Drivers of Expansion in the Shandong Peninsula Urban Agglomeration Based on Nighttime Light Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8535–8549. [Google Scholar] [CrossRef]
- Shi, K.; Chang, Z.; Chen, Z.; Wu, J.; Yu, B. Identifying and evaluating poverty using multisource remote sensing and point of interest (POI) data: A case study of Chongqing, China. J. Clean. Prod. 2020, 255, 120245. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef] [PubMed]
- Dai, Z.; Hu, Y.; Zhao, G. The Suitability of Different Nighttime Light Data for GDP Estimation at Different Spatial Scales and Regional Levels. Sustainability 2017, 9, 305. [Google Scholar] [CrossRef]
- Doll, C.N.H.; Muller, J.-P.; Morley, J.G. Mapping regional economic activity from night-time light satellite imagery. Ecol. Econ. 2006, 57, 75–92. [Google Scholar] [CrossRef]
- Forbes, D.J. Multi-scale analysis of the relationship between economic statistics and DMSP-OLS night light images. GIScience Remote Sens. 2013, 50, 483–499. [Google Scholar] [CrossRef]
- Chen, Q. Improved GDP spatialization approach by combining land-use data and night-time light data: A case study in China’s continental coastal area. Int. J. Remote Sens. 2016, 37, 4610–4622. [Google Scholar] [CrossRef]
- Chen, Q.; Ye, T.; Zhao, N.; Ding, M.; Ouyang, Z.; Jia, P.; Yue, W.; Yang, X. Mapping China’s regional economic activity by integrating points-of-interest and remote sensing data with random forest. Environ. Plan. B Urban Anal. City Sci. 2020, 48, 1876–1894. [Google Scholar] [CrossRef]
- Shi, K.; Wu, Y.; Li, D.; Li, X. Population, GDP, and Carbon Emissions as Revealed by SNPP-VIIRS Nighttime Light Data in China With Different Scales. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liang, H.; Guo, Z.; Wu, J.; Chen, Z. GDP spatialization in Ningbo City based on NPP/VIIRS night-time light and auxiliary data using random forest regression. Adv. Space Res. 2020, 65, 481–493. [Google Scholar] [CrossRef]
- Sun, J.; Di, L.; Sun, Z.; Wang, J.; Wu, Y. Estimation of GDP Using Deep Learning With NPP-VIIRS Imagery and Land Cover Data at the County Level in CONUS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1400–1415. [Google Scholar] [CrossRef]
- Shi, K. Evaluating the Ability of NPP-VIIRS Nighttime Light Data to Estimate the Gross Domestic Product and the Electric Power Consumption of China at Multiple Scales: A Comparison with DMSP-OLS Data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Zhao, M. GDP Spatialization and Economic Differences in South China Based on NPP-VIIRS Nighttime Light Imagery. Remote Sens. 2017, 9, 673. [Google Scholar] [CrossRef]
- Gašpar, A.; Seljan, S.; Kučiš, V. Measuring Terminology Consistency in Translated Corpora: Implementation of the Herfindahl-Hirshman Index. Information 2022, 13, 43. [Google Scholar] [CrossRef]
- Xu, C.; Chen, G.; Huang, Q.; Su, M.; Rong, Q.; Yue, W.; Haase, D. Can improving the spatial equity of urban green space mitigate the effect of urban heat islands? An empirical study. Sci. Total Environ. 2022, 841, 156687. [Google Scholar] [CrossRef]
- Arruda, V.C.L.; Marques, A.S.; Moreira, J.L.B.; Lago, T.G.S. Location and specialization indicators of animal bioenergetic potential in Paraiba (Brazil). Energy Sustain. Dev. 2023, 76, 101304. [Google Scholar] [CrossRef]
- Dong, F.; Wang, Y.; Zheng, L.; Li, J.; Xie, S. Can industrial agglomeration promote pollution agglomeration? Evidence from China. J. Clean. Prod. 2020, 246, 118960. [Google Scholar] [CrossRef]
- Billings, S.B.; Johnson, E.B. The location quotient as an estimator of industrial concentration. Reg. Sci. Urban Econ. 2012, 42, 642–647. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social Sensing: A New Approach to Understanding Our Socioeconomic Environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, D.; Yu, C.; Di, Y.; Wang, S.; Liu, M. Appraising regional anthropogenic heat flux using high spatial resolution NTL and POI data: A case study in the Beijing-Tianjin-Hebei region, China. Environ. Pollut. 2022, 292, 118359. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.; Alves, A.; Bento, C. POI Mining for Land Use Classification: A Case Study. ISPRS Int. J. Geo-Inf. 2020, 9, 493. [Google Scholar] [CrossRef]
- Cui, Y.; Shi, K.; Jiang, L.; Qiu, L.; Wu, S. Identifying and Evaluating the Nighttime Economy in China Using Multisource Data. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1906–1910. [Google Scholar] [CrossRef]
- Long, Y.; Shen, Y.; Jin, X. Mapping Block-Level Urban Areas for All Chinese Cities. Ann. Am. Assoc. Geogr. 2015, 106, 96–113. [Google Scholar] [CrossRef]
- McKenzie, G.; Janowicz, K.; Gao, S.; Yang, J.-A.; Hu, Y. POI Pulse: A Multi-granular, Semantic Signature–Based Information Observatory for the Interactive Visualization of Big Geosocial Data. Cartogr. Int. J. Geogr. Inf. Geovis. 2015, 50, 71–85. [Google Scholar] [CrossRef]
- Wu, R.; Wang, J.; Zhang, D.; Wang, S. Identifying different types of urban land use dynamics using Point-of-interest (POI) and Random Forest algorithm: The case of Huizhou, China. Cities 2021, 114, 103202. [Google Scholar] [CrossRef]
- Zhao, N.; Ghosh, T.; Samson, E.L. Mapping spatio-temporal changes of Chinese electric power consumption using night-time imagery. Int. J. Remote Sens. 2012, 33, 6304–6320. [Google Scholar] [CrossRef]
- Ye, T. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model. Sci. Total Environ. 2019, 658, 936–946. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Nghiem, T.; Morari, M.; Mangharam, R. Learning and Control Using Gaussian Processes. In Proceedings of the 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018; pp. 140–149. [Google Scholar]
- GB/T 4754—2017; Industrial Classification for National Economic Activities. Standards Press of China: Beijing, China, 2017.
- de Marsily, G.; Delay, F.; Gonçalvès, J.; Renard, P.; Teles, V.; Violette, S. Dealing with spatial heterogeneity. Hydrogeol. J. 2005, 13, 161–183. [Google Scholar] [CrossRef]
- Liu, H.; Huang, B.; Gao, S.; Wang, J.; Yang, C.; Li, R. Impacts of the evolving urban development on intra-urban surface thermal environment: Evidence from 323 Chinese cities. Sci. Total Environ. 2021, 771, 144810. [Google Scholar] [CrossRef] [PubMed]
- Dijk, M.P.v. A Different Development Model in China’s Western and Eastern Provinces? Mod. Econ. 2011, 02, 757–768. [Google Scholar] [CrossRef]
- Bennett, M.M.; Smith, L.C. Advances in using multitemporal night-time lights satellite imagery to detect, estimate, and monitor socioeconomic dynamics. Remote Sens. Environ. 2017, 192, 176–197. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, S.; Liu, Y.; Tian, L. Identifying the urban-rural fringe using wavelet transform and kernel density estimation: A case study in Beijing City, China. Environ. Model. Softw. 2016, 83, 286–302. [Google Scholar] [CrossRef]
- Wang, N.; Du, Y.; Liang, F.; Wang, H.; Yi, J. The spatiotemporal response of China’s vegetation greenness to human socio-economic activities. J. Environ. Manag. 2022, 305, 114304. [Google Scholar] [CrossRef]
- Yin, G.; Lin, Z.; Jiang, X.; Qiu, M.; Sun, J. How do the industrial land use intensity and dominant industries guide the urban land use? Evidences from 19 industrial land categories in ten cities of China. Sustain. Cities Soc. 2020, 53, 101978. [Google Scholar] [CrossRef]
- Alebele, Y.; Zhang, X.; Wang, W.; Yang, G.; Yao, X.; Zheng, H.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of Canopy Biomass Components in Paddy Rice from Combined Optical and SAR Data Using Multi-Target Gaussian Regressor Stacking. Remote Sens. 2020, 12, 2564. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dhibi, K.; Fezai, R.; Mansouri, M.; Trabelsi, M.; Kouadri, A.; Bouzara, K.; Nounou, H.; Nounou, M. Reduced Kernel Random Forest Technique for Fault Detection and Classification in Grid-Tied PV Systems. IEEE J. Photovolt. 2020, 10, 1864–1871. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Yang, Y.; Li, X.; He, C. Development of Different Energy Storage Systems in the Xinjiang Uygur Autonomous Region: Problems and Solutions. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 305–310. [Google Scholar]
- Wang, B. Social Infrastructure Development Aid for Xinjiang and Lessons for CPEC: A Case Study of Shanghai-Kashgar Paired Assistance Program. In The Political Economy of the China-Pakistan Economic Corridor; Springer Nature: Singapore, 2023; pp. 219–251. [Google Scholar]
- Zhang, J.; Zheng, H.; He, W.; Huang, W. West-east gas pipeline project. Front. Eng. Manag. 2020, 7, 163–167. [Google Scholar] [CrossRef]
- Xu, J.; Guo, J.; Sun, Y.; Tang, Q.; Zhang, J. Why China must build Sichuan-Tibet railway: From the perspective of regional comprehensive transportation network optimization. J. Intell. Fuzzy Syst. 2021, 40, 9741–9763. [Google Scholar] [CrossRef]
- Lan, F.; Jiao, C.; Deng, G.; Da, H. Urban agglomeration, housing price, and space–time spillover effect—Empirical evidences based on data from hundreds of cities in China. Manag. Decis. Econ. 2021, 42, 898–919. [Google Scholar] [CrossRef]
- Zhao, J.; Rong, W.; Liu, D. Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China. Sustainability 2023, 15, 6450. [Google Scholar] [CrossRef]
- Wang, X. The changing geographies of financial centres in China: The case of commercial banking. Growth Chang. 2018, 50, 164–183. [Google Scholar] [CrossRef]
- Cerutti, E.; Dagher, J.; Dell’Ariccia, G. Housing finance and real-estate booms: A cross-country perspective. J. Hous. Econ. 2017, 38, 1–13. [Google Scholar] [CrossRef]
- Kang, J.; Yang, C.; Ning, Y. Analysis of Regional Division of Labor in Value Chain Patterns and Driving Factors in the Yangtze River Delta Region Using the Electronic Information Manufacturing Industry as an Example. Sustainability 2023, 15, 4393. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, H.; Yang, D.; Liu, H. Effects of urbanization on freight transport carbon emissions in China: Common characteristics and regional disparity. J. Clean. Prod. 2019, 211, 481–489. [Google Scholar] [CrossRef]
- Li, J.; Yan, X.; Li, Y.; Dong, X. Optimizing the Agricultural Supply Chain through E-Commerce: A Case Study of Tudouec in Inner Mongolia, China. Int. J. Environ. Res. Public. Health 2023, 20, 3775. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. The Research on the Efficiency of Financial Support for the Development of Real Economy-A Case Study Based on the Data of the Silk Road Belt. CONVERTER 2021, 2021, 258–272. [Google Scholar]
- Orazgaliyev, S. The Overland Silk Road: China’s Energy Cooperation with Central Asia in the Context of Industry Competition. China Int. J. 2019, 17, 62–75. [Google Scholar] [CrossRef]
- Xu, X.E.; Chen, T. The effect of monetary policy on real estate price growth in China. Pac.—Basin Financ. J. 2012, 20, 62–77. [Google Scholar] [CrossRef]
- Hou, G.; Zou, Z.; Zhang, T.; Meng, Y. Analysis of the Effect of Industrial Transformation of Resource-Based Cities in Northeast China. Economies 2019, 7, 40. [Google Scholar] [CrossRef]
- Fan, J.; Ma, T.; Zhou, C.; Zhou, Y.; Xu, T. Comparative Estimation of Urban Development in China’s Cities Using Socioeconomic and DMSP/OLS Night Light Data. Remote Sens. 2014, 6, 7840–7856. [Google Scholar] [CrossRef]
- Fang, Y.; Ying, B. Spatial distribution of mountainous regions and classifications of economic development in China. J. Mt. Sci. 2016, 13, 1120–1138. [Google Scholar] [CrossRef]
- Li, X.; Hui, E.C.-m.; Lang, W.; Zheng, S.; Qin, X. Transition from factor-driven to innovation-driven urbanization in China: A study of manufacturing industry automation in Dongguan City. China Econ. Rev. 2020, 59, 101382. [Google Scholar] [CrossRef]
- Wu, H.; Fan, W.; Lu, J. Researching on the Sustainability of Transportation Industry Based on a Coupled Emergy and System Dynamics Model: A Case Study of Qinghai. Sustainability 2021, 13, 6804. [Google Scholar] [CrossRef]
- Chen, D.; Song, D.; Yang, Z. A review of the literature on the belt and road initiative with factors influencing the transport and logistics. Marit. Policy Manag. 2022, 49, 540–557. [Google Scholar] [CrossRef]
- Andersson, M.; Hall, O.; Archila, M.F. How Data-Poor Countries Remain Data Poor: Underestimation of Human Settlements in Burkina Faso as Observed from Nighttime Light Data. ISPRS Int. J. Geo-Inf. 2019, 8, 498. [Google Scholar] [CrossRef]
- Kinzey, B.R.; Perrin, T.E.; Miller, N.J.; Kocifaj, M.; Aube, M.; Lamphar, H.A. An Investigation of LED Street Lighting’s Impact on Sky Glow; Pacific Northwest National Lab (PNNL): Richland, WA, USA, 2017.

| Category | Content |
|---|---|
| Industry | Mineral processing, mini company, factory, etc. |
| Construction | Decoration company, construction company, etc. |
| Retail | Supermarket, emporium, shopping center, convenience store, etc. |
| Transportation | Transit station, expressway service area, filling station, park, physical distribution, postal service, etc. |
| Lodging and catering | Hotel, restaurant, etc. |
| Finance | Bank, securities company, insurance company, etc. |
| Estate | Areola, real estate intermediary, estate company, etc. |
| Other tertiary industries | Educational institution, hospital, media, gymnasium, photography services, etc. |
| Category | NTL Features without Auxiliary Variables | POI Features without Auxiliary Variables | ||||||
|---|---|---|---|---|---|---|---|---|
| NTL-Area | NTL-Mean | NTL- Std | NTL- Sum | POI- Area | POI- Mean | POI- Std | POI- Num | |
| Industry | 0.17 | 0.20 | 0.25 | 0.76 ** | 0.55 | 0.28 | 0.11 * | 0.75 ** |
| Construction | 0.40 | 0.23 | 0.33 | 0.64 ** | 0.44 | 0.19 | 0.08 * | 0.64 ** |
| Retail | 0.17 | 0.21 * | 0.36 | 0.67 ** | 0.56 | 0.24 ** | 0.09 ** | 0.70 ** |
| Transportation | 0.12 | 0.21 | 0.36 * | 0.70 ** | 0.53 | 0.18 | 0.09 | 0.73 ** |
| Lodging and Catering | 0.18 | 0.23 * | 0.37 | 0.59 ** | 0.46 | 0.24 ** | 0.08 ** | 0.62 ** |
| Finance | 0.21 | 0.30 | 0.52 ** | 0.86 ** | 0.58 | 0.31 | 0.13 ** | 0.88 * |
| Estate | 0.47 | 0.38 | 0.45 | 0.75 ** | 0.52 | 0.21 ** | 0.04 ** | 0.81 ** |
| Other tertiary industries | 0.09 | 0.30 | 0.50 | 0.76 ** | 0.54 | 0.28 | 0.11 * | 0.76 ** |
| Category | NTL Features with Auxiliary Variables | POI Features with Auxiliary Variables | ||||||
|---|---|---|---|---|---|---|---|---|
| NTL-Area | NTL-Mean | NTL- Std | NTL- Sum | POI- Area | POI- Mean | POI- Std | POI- Num | |
| Industry | 0.81 ** | 0.78 ** | 0.77 | 0.87 ** | 0.77 | 0.80 ** | 0.81 ** | 0.83 ** |
| Construction | 0.62 ** | 0.62 ** | 0.62 ** | 0.63 ** | 0.62 ** | 0.65 ** | 0.68 ** | 0.62 * |
| Retail | 0.82 ** | 0.79 | 0.79 | 0.89 ** | 0.79 | 0.79 | 0.79 | 0.81 ** |
| Transportation | 0.80 ** | 0.75 | 0.76 | 0.82 ** | 0.76 | 0.76 | 0.78 ** | 0.85 ** |
| Lodging and Catering | 0.70 ** | 0.69 ** | 0.68 ** | 0.76 ** | 0.67 | 0.68 ** | 0.72 ** | 0.77 ** |
| Finance | 0.73 ** | 0.72 * | 0.72 | 0.79 ** | 0.72 | 0.73 ** | 0.75 ** | 0.82 ** |
| Estate | 0.82 ** | 0.82 ** | 0.81 | 0.86 ** | 0.82 ** | 0.85 ** | 0.84 ** | 0.89 ** |
| Other tertiary industries | 0.75 ** | 0.74 | 0.74 | 0.74 | 0.76 ** | 0.74 | 0.78 ** | 0.74 * |
| Category | Exponential | Squared Exponential | Matern 3/2 | Matern 5/2 | Rational Quadratic | Random Forest | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Industry | 0.88 | 257.59 | 0.84 | 268.36 | 0.85 | 262.07 | 0.83 | 283.18 | 0.86 | 260.10 | 0.80 | 565.97 |
| Construction | 0.81 | 79.52 | 0.80 | 80.02 | 0.82 | 77.90 | 0.78 | 88.37 | 0.77 | 83.11 | 0.73 | 118.68 |
| Retail | 0.82 | 107.14 | 0.85 | 104.03 | 0.82 | 111.24 | 0.83 | 112.04 | 0.86 | 98.06 | 0.83 | 146.61 |
| Transportation | 0.82 | 58.23 | 0.85 | 48.65 | 0.81 | 60.05 | 0.82 | 57.02 | 0.83 | 49.03 | 0.84 | 65.05 |
| Lodging and Catering | 0.73 | 39.67 | 0.80 | 30.04 | 0.72 | 39.92 | 0.75 | 35.18 | 0.72 | 36.62 | 0.81 | 30.22 |
| Finance | 0.95 | 59.79 | 0.92 | 74.39 | 0.90 | 78.14 | 0.92 | 70.84 | 0.89 | 79.38 | 0.85 | 219.71 |
| Estate | 0.84 | 84.26 | 0.89 | 76.96 | 0.89 | 69.89 | 0.91 | 67.85 | 0.90 | 70.17 | 0.84 | 128.41 |
| Other tertiary industries | 0.89 | 266.34 | 0.82 | 317.10 | 0.88 | 283.69 | 0.83 | 305.96 | 0.82 | 309.02 | 0.77 | 520.89 |
| Category | Exponential | Squared Exponential | Matern 3/2 | Matern 5/2 | Rational Quadratic | Random Forest | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Industry | 0.85 | 272.68 | 0.84 | 274.64 | 0.88 | 241.86 | 0.89 | 234.52 | 0.89 | 237.31 | 0.84 | 358.87 |
| Construction | 0.80 | 82.03 | 0.77 | 84.26 | 0.80 | 81.55 | 0.76 | 85.69 | 0.76 | 86.14 | 0.77 | 105.68 |
| Retail | 0.83 | 118.18 | 0.87 | 92.44 | 0.81 | 119.22 | 0.92 | 84.96 | 0.80 | 120.79 | 0.90 | 96.32 |
| Transportation | 0.89 | 41.39 | 0.79 | 62.41 | 0.78 | 63.97 | 0.80 | 58.80 | 0.87 | 45.61 | 0.86 | 50.89 |
| Lodging and Catering | 0.84 | 24.08 | 0.66 | 50.40 | 0.78 | 31.57 | 0.72 | 40.19 | 0.80 | 29.89 | 0.82 | 28.71 |
| Finance | 0.86 | 99.68 | 0.83 | 108.31 | 0.82 | 112.49 | 0.80 | 124.62 | 0.82 | 111.73 | 0.79 | 128.65 |
| Estate | 0.88 | 77.50 | 0.80 | 119.44 | 0.94 | 60.89 | 0.84 | 83.31 | 0.92 | 68.79 | 0.89 | 75.23 |
| Other tertiary industries | 0.89 | 262.81 | 0.83 | 310.76 | 0.86 | 283.77 | 0.83 | 309.82 | 0.85 | 287.04 | 0.80 | 358.32 |
| Category | Percentage of Percent Error (%) | ||
|---|---|---|---|
| Inaccuracy (>50%) | Moderate Accuracy (30–50%) | High Accuracy (0–30%) | |
| Industry | 9.58 | 22.08 | 68.34 |
| Construction | 16.66 | 22.50 | 60.84 |
| Retail | 9.17 | 16.67 | 74.16 |
| Transportation | 8.33 | 22.50 | 69.17 |
| Lodging and Catering | 12.08 | 26.67 | 61.25 |
| Finance | 8.33 | 11.67 | 80.00 |
| Estate | 7.50 | 12.08 | 80.42 |
| Other tertiary industries | 8.75 | 15.83 | 75.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, W.; Zhao, Z. The Assessment of Industrial Agglomeration in China Based on NPP-VIIRS Nighttime Light Imagery and POI Data. Remote Sens. 2024, 16, 417. https://doi.org/10.3390/rs16020417
Chen Z, Xu W, Zhao Z. The Assessment of Industrial Agglomeration in China Based on NPP-VIIRS Nighttime Light Imagery and POI Data. Remote Sensing. 2024; 16(2):417. https://doi.org/10.3390/rs16020417
Chicago/Turabian StyleChen, Zuoqi, Wenxiang Xu, and Zhiyuan Zhao. 2024. "The Assessment of Industrial Agglomeration in China Based on NPP-VIIRS Nighttime Light Imagery and POI Data" Remote Sensing 16, no. 2: 417. https://doi.org/10.3390/rs16020417
APA StyleChen, Z., Xu, W., & Zhao, Z. (2024). The Assessment of Industrial Agglomeration in China Based on NPP-VIIRS Nighttime Light Imagery and POI Data. Remote Sensing, 16(2), 417. https://doi.org/10.3390/rs16020417