The Impact of the Expansion and Contraction of China Cities on Carbon Emissions, 2002–2021, Evidence from Integrated Nighttime Light Data and City Attributes
Abstract
1. Introduction
2. Materials and Methods
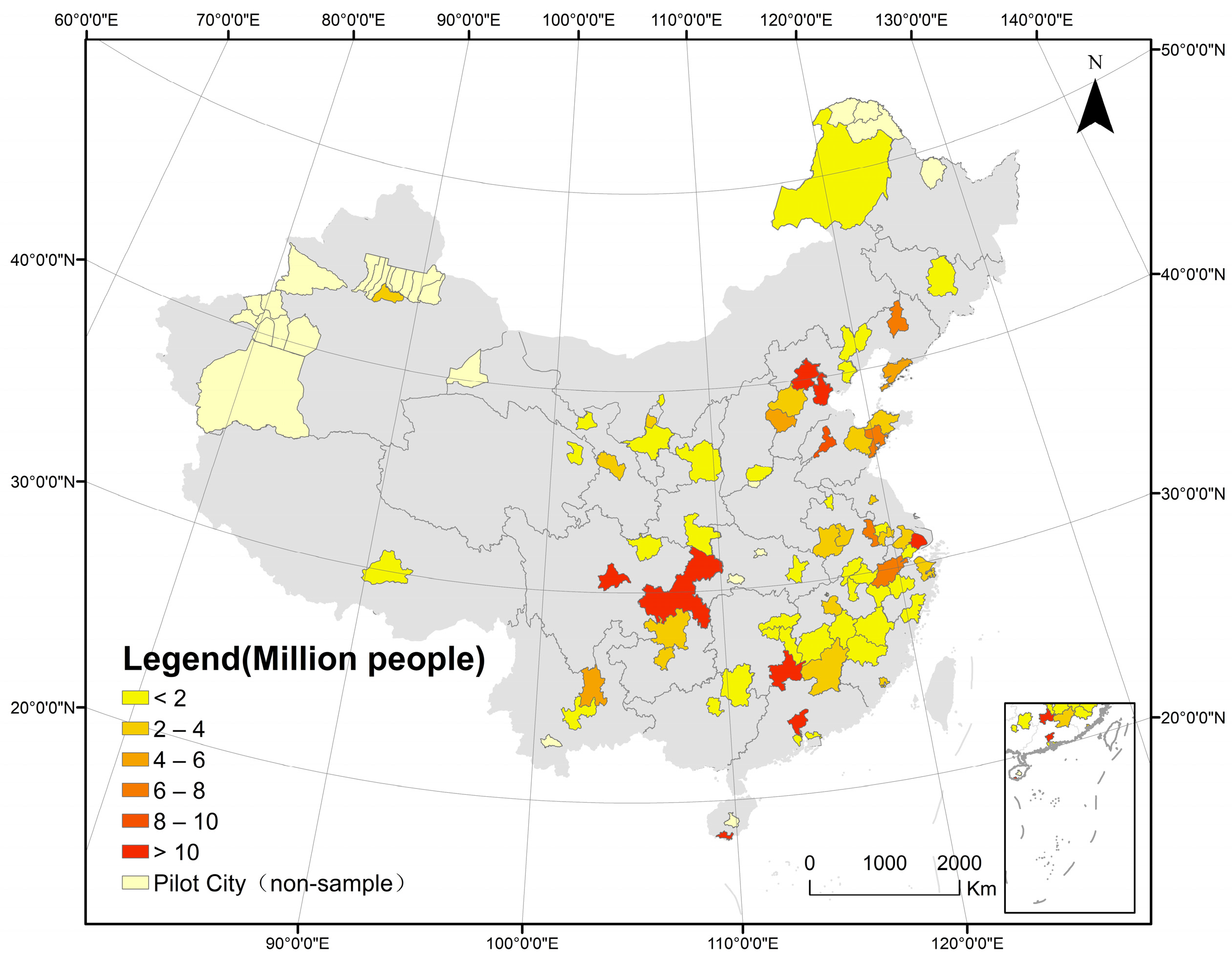
2.1. Study Area
2.2. Data Sources
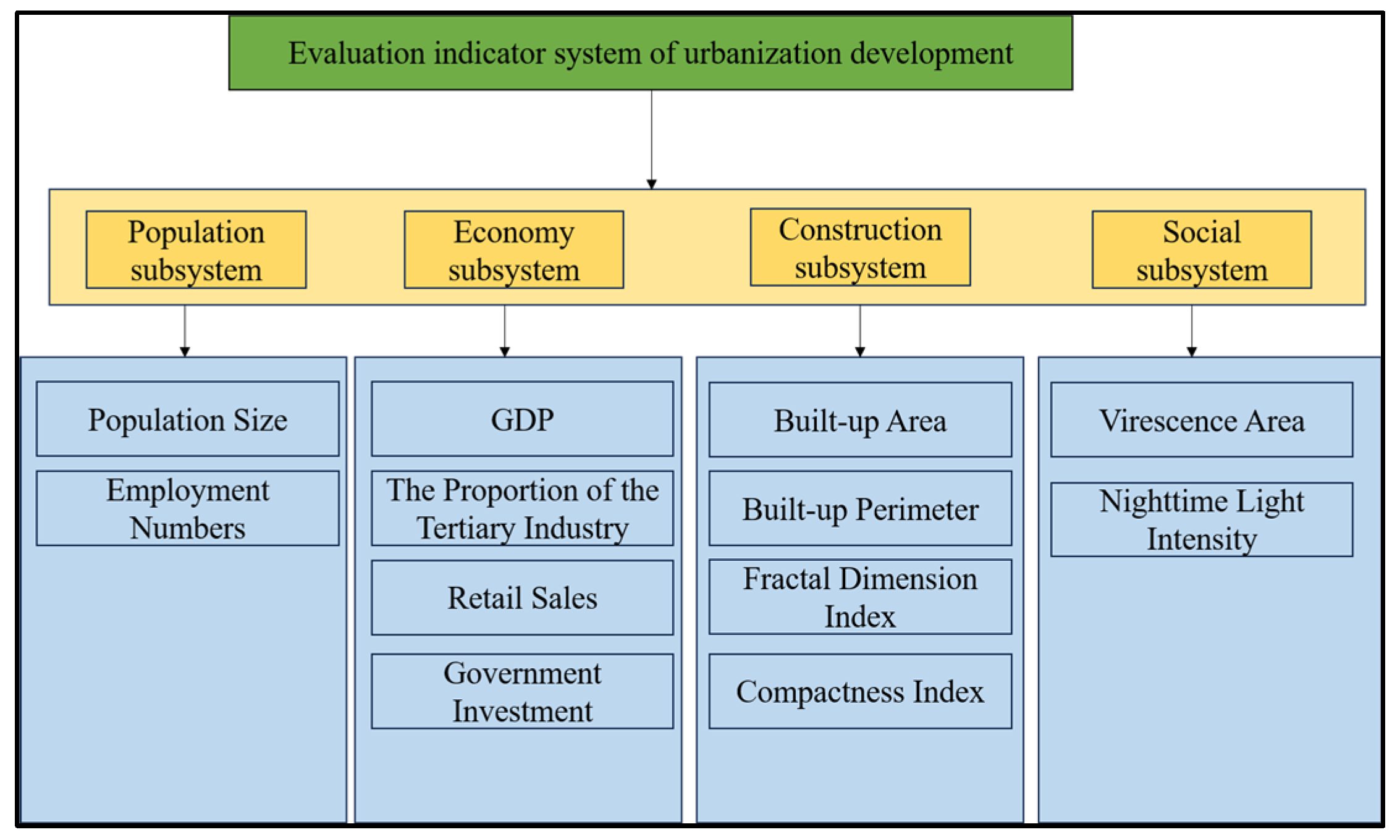
2.3. Urban Development Evaluation System
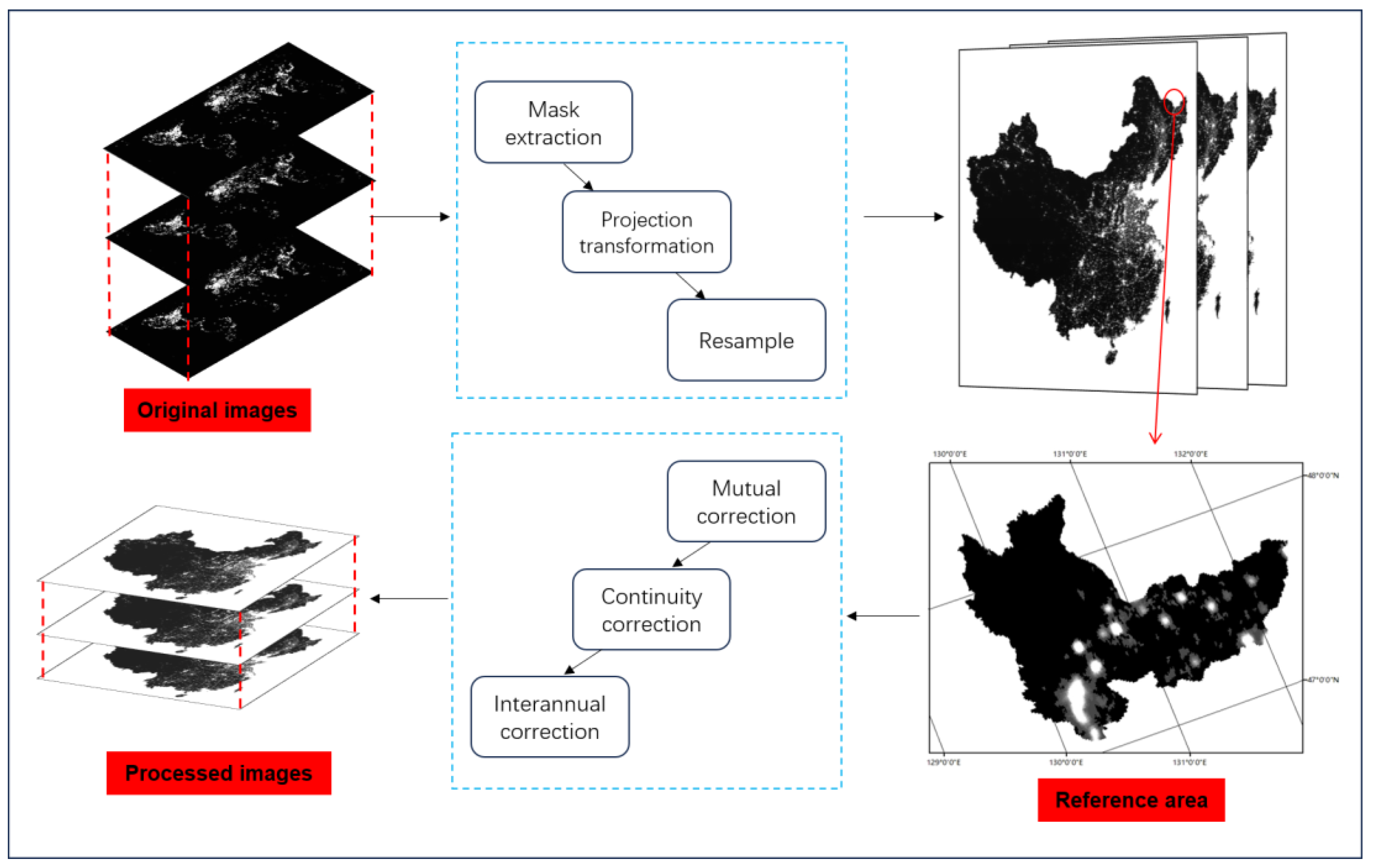
2.4. Using Nighttime Light Images to Extract Built-Up Areas
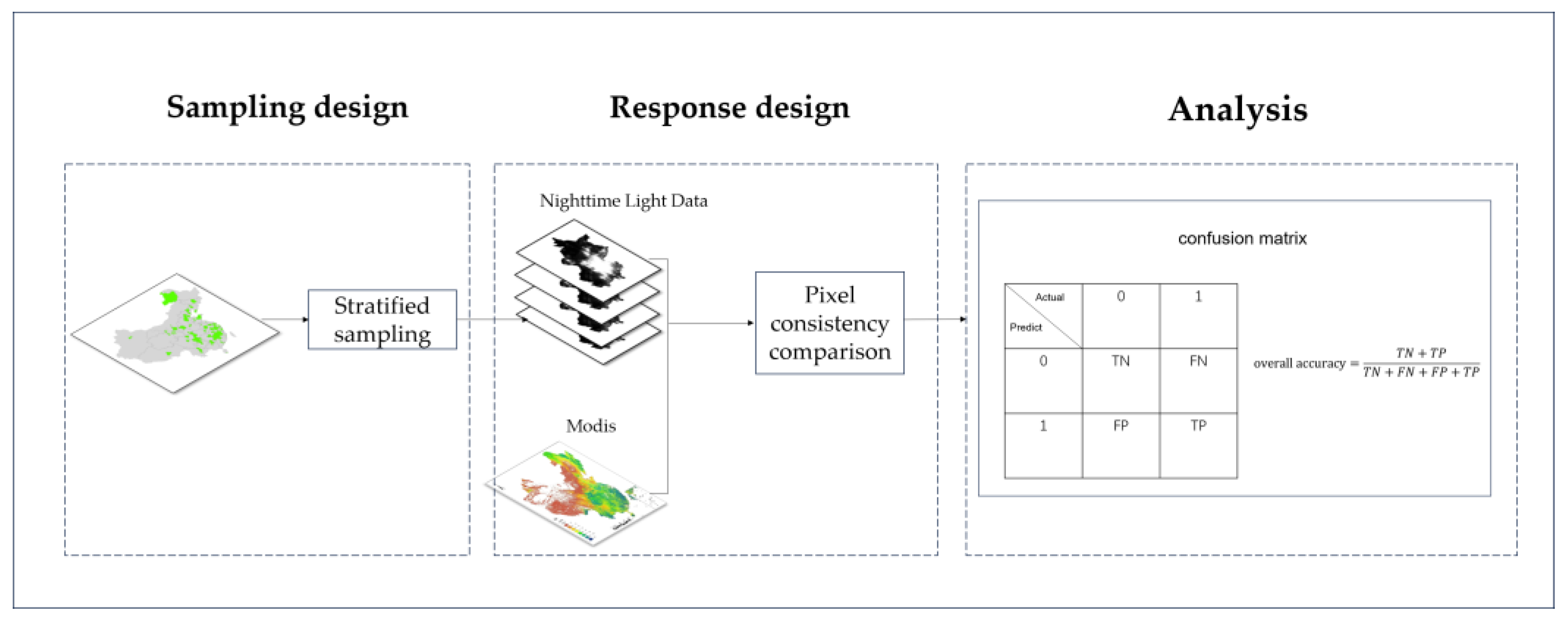
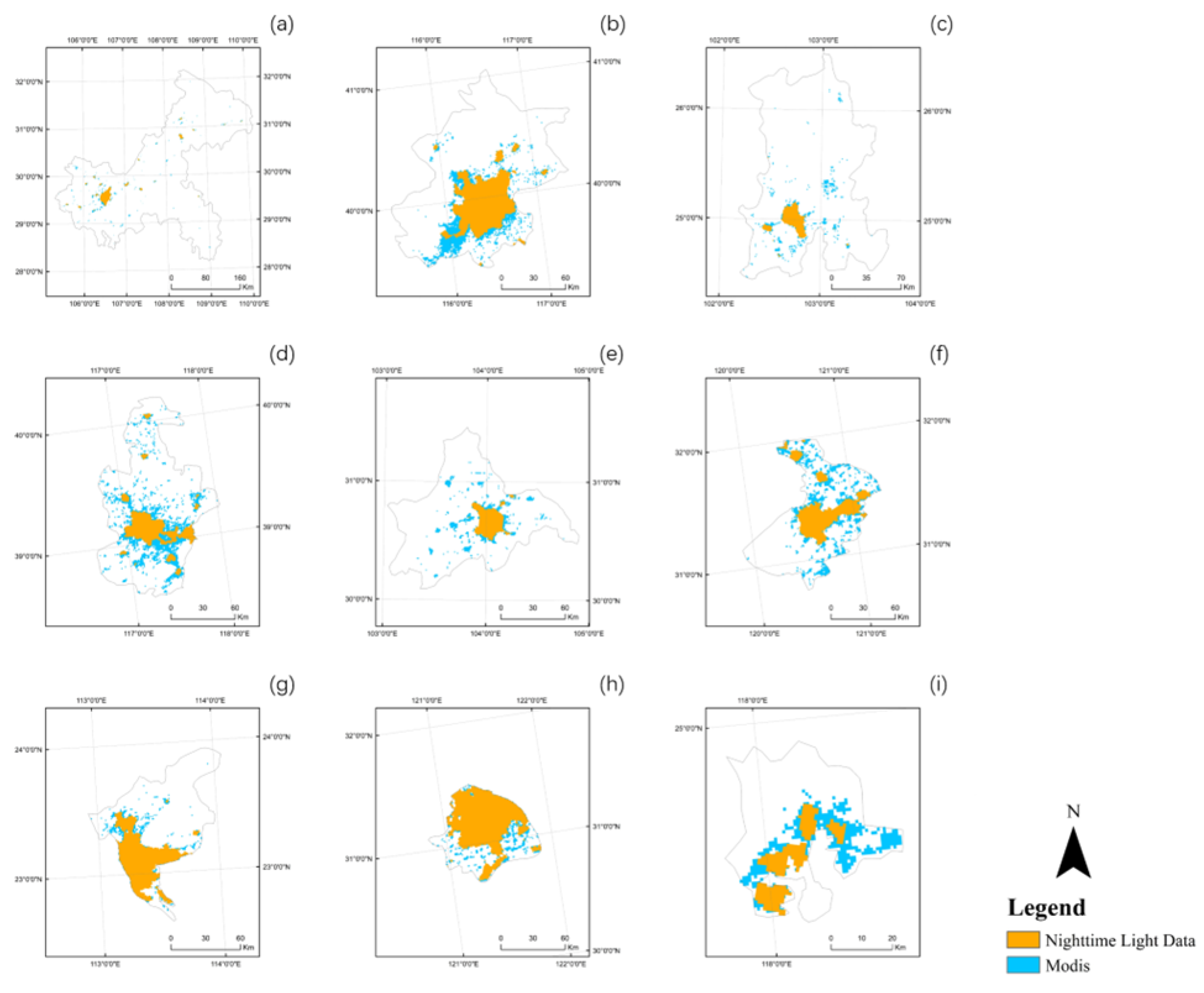
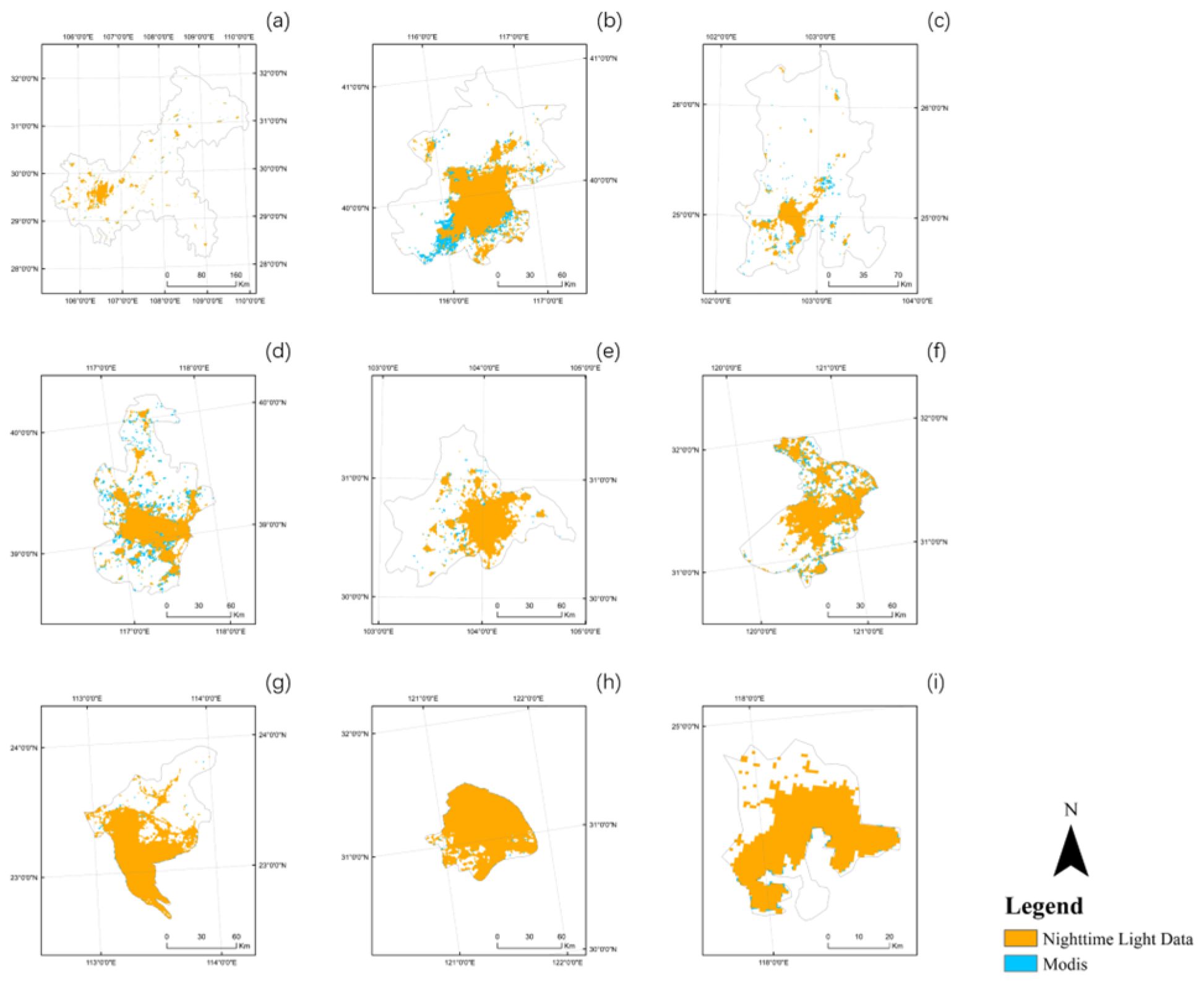
2.5. Validation for Urban Built-Up Area Extraction Results
2.6. Methods for Factors Influencing Carbon Emissions
2.6.1. Lasso
2.6.2. Hierarchical Regression Model
3. Results
3.1. Extraction of Built-Up Areas
3.2. Result of Establishment of Urban Development Evaluation System
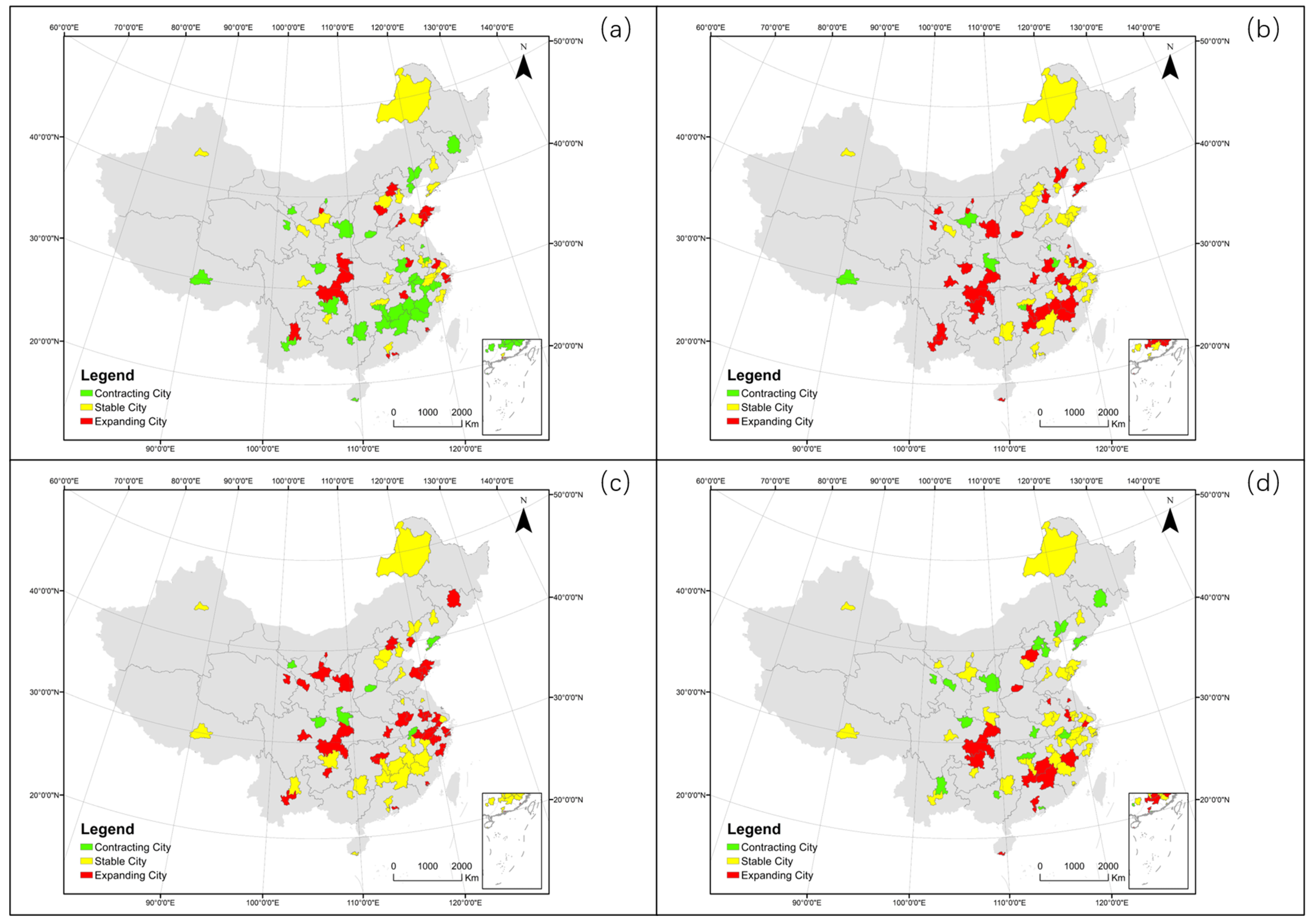
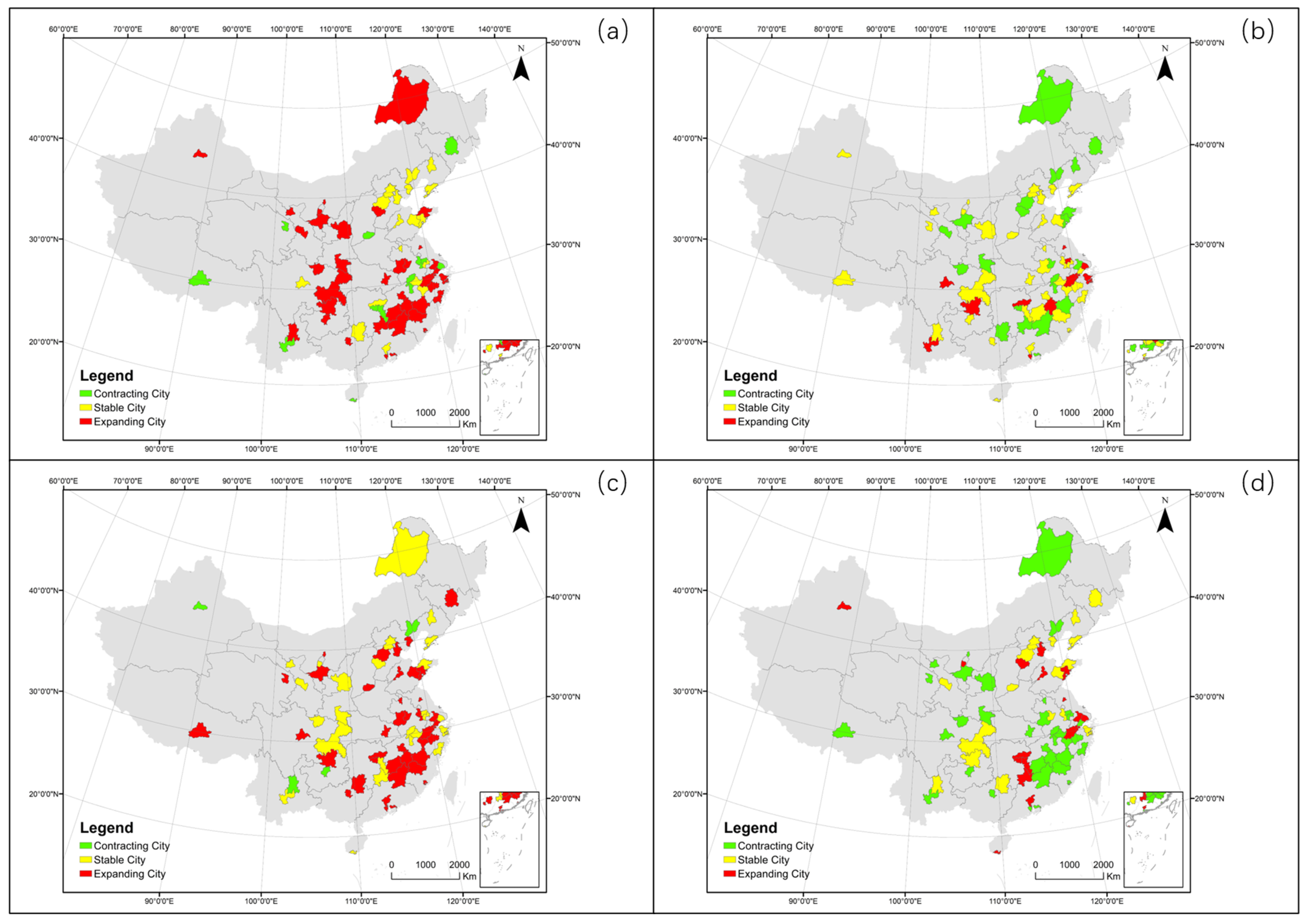
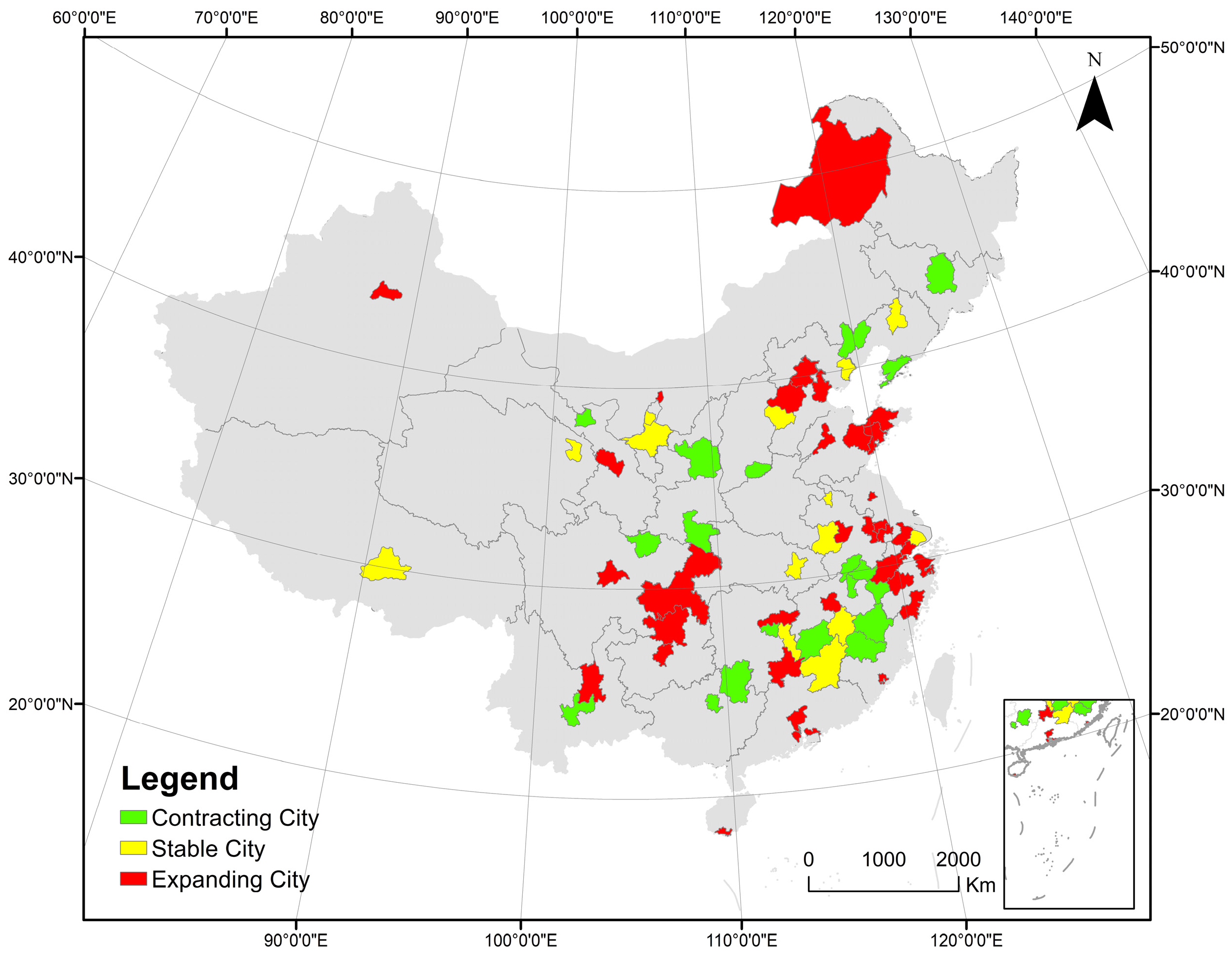
3.2.1. Overall Development of the 68 Cities
3.2.2. The Development of the Population Subsystem
3.2.3. The Development of the Economy Subsystem
3.2.4. The Development of the Construction Subsystem
3.2.5. The Development of the Society Subsystems
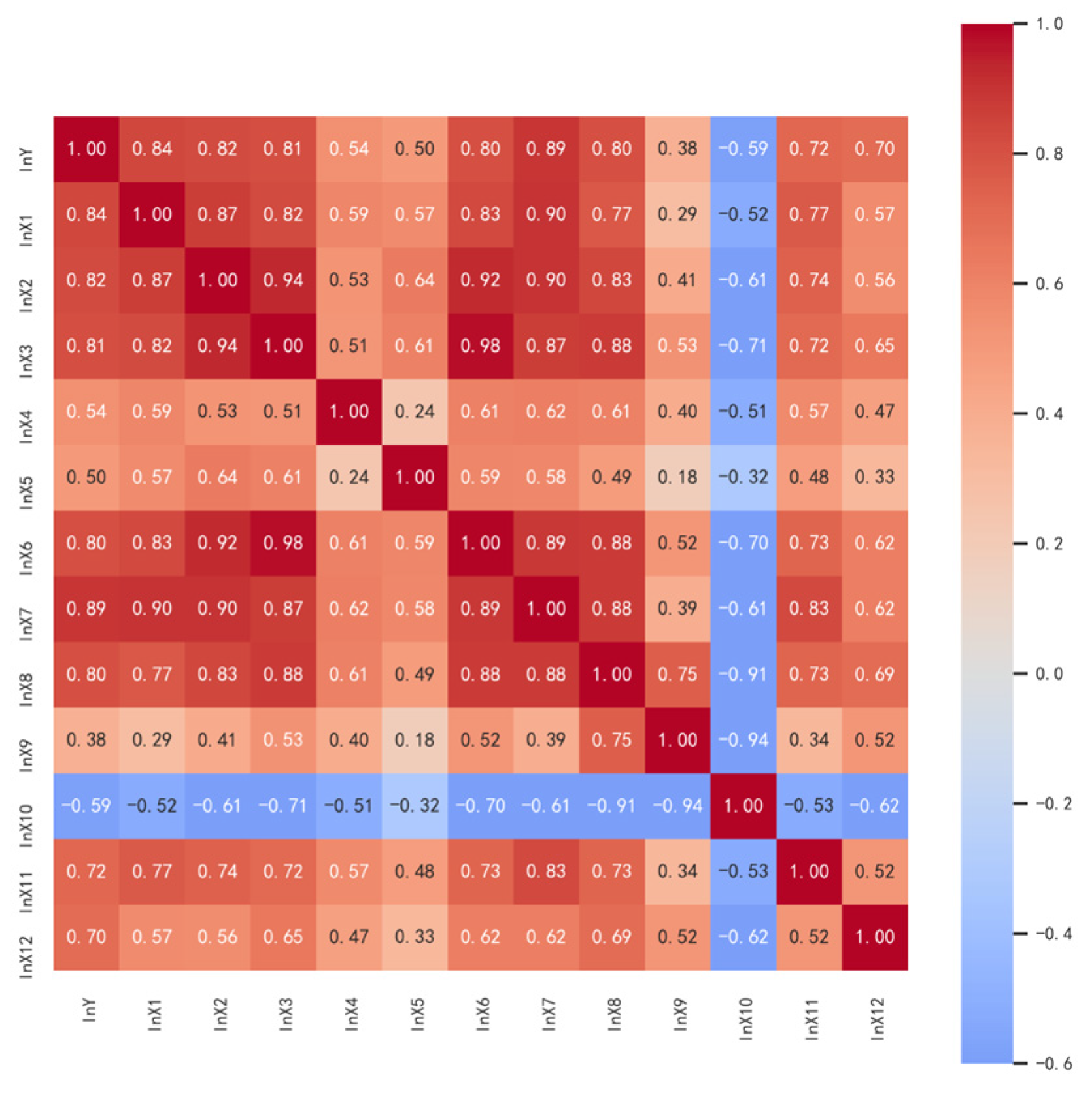
3.3. Influence Factor of CO2
4. Discussion
4.1. Urbanization Development
4.2. Urbanization and Carbon Emissions
4.3. Limitations
4.4. The Socio-Ecological Implications of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Number | City | Number | City | Number | City |
|---|---|---|---|---|---|
| 1 | Huai’an | 24 | Chengdu | 47 | Qinhuangdao |
| 2 | Hulun Buir | 25 | Beijing | 48 | Qingdao |
| 3 | Fuzhou | 26 | Changzhou | 49 | Ningbo |
| 4 | Chizhou | 27 | Baoding | 50 | Nanping |
| 5 | Chongqing | 28 | Ankang | 51 | Lu’an |
| 6 | Changsha | 29 | Zunyi | 52 | Liuzhou |
| 7 | Yinchuan | 30 | Zhuzhou | 53 | Lhasa |
| 8 | Xining | 31 | Zhongshan | 54 | Jingdezhen |
| 9 | Wuhan | 32 | Zhenjiang | 55 | Jinhua |
| 10 | Urumqi | 33 | Yuxi | 56 | Jinchang |
| 11 | Tianjin | 34 | Yantai | 57 | Jilin |
| 12 | Shijiazhuang | 35 | Yan’an | 58 | Jiaxing |
| 13 | Shenyang | 36 | Xiangtan | 59 | Ji’an |
| 14 | Shanghai | 37 | Xiamen | 60 | Huangshan |
| 15 | Nanjing | 38 | Wuzhong | 61 | Huaibei |
| 16 | Nanchang | 39 | Wuhai | 62 | Guilin |
| 17 | Lanzhou | 40 | Wenzhou | 63 | Guangyuan |
| 18 | Kunming | 41 | Weifang | 64 | Ganzhou |
| 19 | Jinan | 42 | Suzhou | 65 | Dalian |
| 20 | Hefei | 43 | Shenzhen | 66 | Chenzhou |
| 21 | Hangzhou | 44 | Sanya | 67 | Chaoyang |
| 22 | Guiyang | 45 | Sanming | 68 | Jincheng |
| 23 | Guangzhou | 46 | Quzhou |
References
- Morikawa, H. Urbanization and Urban System; Damingtang Press: Hangzhou, China, 1989. [Google Scholar]
- Liu, R.; Wang, M.; Chen, W. The influence of urbanization on organic carbon sequestration and cycling in soils of Beijing. Landsc. Urban Plan. 2018, 169, 241–249. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, B.; Luo, D. Effects of land use and transportation on carbon sources and carbon sinks: A case study in Shenzhen, China. Landsc. Urban Plan. 2014, 122, 175–185. [Google Scholar] [CrossRef]
- Anderson, W. Urban form, energy and the environment: A review of issues, evidence and policy. Urban Stud. 1996, 33, 7–36. [Google Scholar] [CrossRef]
- Shahbaz, M.; Sbia, R.; Hamdi, H.; Ozturk, I. Economic growth, electricity consumption, urbanization and environmental degradation relationship in United Arab Emirates. Ecol. Indic. 2014, 45, 622–631. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, Z.-Y.; Liao, H.; Wei, Y.-M.; Wang, S. Is CO2 emission a side effect of financial development? An empirical analysis for China. Environ. Sci. Pollut. Res. 2016, 23, 21041–21057. [Google Scholar] [CrossRef]
- Sadorsky, P. The effect of urbanization on CO2 emissions in emerging economies. Energy Econ. 2014, 41, 147–153. [Google Scholar] [CrossRef]
- Wang, S.; Fang, C.; Guan, X.; Pang, B.; Ma, H. Urbanisation, energy consumption, and carbon dioxide emissions in China: A panel data analysis of China’s provinces. Appl. Energy 2014, 136, 738–749. [Google Scholar] [CrossRef]
- Parikh, J.; Shukla, V. Urbanization, energy use and greenhouse effects in economic development. Glob. Environ. Chang. 1995, 5, 87–103. [Google Scholar] [CrossRef]
- Gam, I.; Ben Rejeb, J. Electricity demand in Tunisia. Energy Policy 2012, 45, 714–720. [Google Scholar] [CrossRef]
- Mishra, V.; Sharma, S.; Smyth, R. Are fluctuations in energy consumption per capita transitory? Evidence from a panel of Pacific Island countries. Energy Policy 2009, 37, 2318–2326. [Google Scholar] [CrossRef]
- Martínez-Zarzoso, I.; Maruotti, A. The impact of urbanization on CO2 emissions: Evidence from developing countries. Ecol. Econ. 2011, 70, 1344–1353. [Google Scholar] [CrossRef]
- Shafiei, S.; Salim, R.A. Non-renewable and renewable energy consumption and CO2 emissions in OECD countries: A comparative analysis. Energy Policy 2014, 66, 547–556. [Google Scholar] [CrossRef]
- Xu, L.; Qu, J.; Li, H.; Zeng, J.; Zhang, H. Analysis and forecasting of carbon emissions from residential energy consumption in China. Ecol. Econ. 2019, 35, 19–23, 29. [Google Scholar]
- Xue, B.; Li, C.; Liu, Z.; Geng, Y.; Xi, F. Analysis of the relationship between global carbon emissions and urbanization from 1970 to 2007. Adv. Clim. Chang. Res. 2011, 7, 423–427. [Google Scholar]
- Cai, B.; Guo, H.; Cao, L.; Guan, D.; Bai, H. Local strategies for China’s carbon mitigation: An investigation of chinese city-level CO2 emissions. J. Clean. Prod. 2018, 178, 890–902. [Google Scholar] [CrossRef]
- Li, H.; Qi, Y. Comparative scenarios of carbon emissions in China by 2050. Adv. Clim. Chang. Res. 2011, 7, 271–280. [Google Scholar]
- Yang, M.; Guo, X.; Wu, L. Combined Land-Use and Transportation Demand Modeling Based on Equitableness. In Proceedings of the 2008 Workshop on Power Electronics and Intelligent Transportation System, Guangzhou, China, 2–3 August 2008; pp. 505–510. [Google Scholar] [CrossRef]
- Dhakal, S. Urban energy use and carbon emissions from cities in China and policy implications. Energy Policy 2009, 37, 4208–4219. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Cheng, X.-M. Energy consumption, carbon emissions, and economic growth in China. Ecol. Econ. 2009, 68, 2706–2712. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, X.; Chen, W.; Zhao, M.; Wang, B. Exploring the spatial effect of urbanization on multi-sectoral CO2 emissions in China. Atmos. Pollut. Res. 2019, 10, 1610–1620. [Google Scholar] [CrossRef]
- Pan, W. What type of mixed-use and open? A critical environmental analysis of three neighborhood types in China and insights for sustainable urban planning. Landsc. Urban Plan. 2021, 216, 104221. [Google Scholar] [CrossRef]
- Li, H.; Peng, J.; Yanxu, L.; Yi’na, H. Urbanization impact on landscape patterns in Beijing City, China: A spatial heterogeneity perspective. Ecol. Indic. 2017, 82, 50–60. [Google Scholar] [CrossRef]
- Liddle, B.; Lung, S. Age-structure, urbanization, and climate change in developed countries: Revisiting STIRPAT for disaggregated population and consumption-related environmental impacts. Popul. Environ. 2010, 31, 317–343. [Google Scholar] [CrossRef]
- Qi, X.; Han, Y.; Kou, P. Population urbanization, trade openness and carbon emissions: An empirical analysis based on China. Air Qual. Atmos. Health 2020, 13, 519–528. [Google Scholar] [CrossRef]
- Gurney, K.R.; Romero-Lankao, P.; Seto, K.C.; Hutyra, L.R.; Duren, R.; Kennedy, C.; Grimm, N.B.; Ehleringer, J.R.; Marcotullio, P.; Hughes, S.; et al. Climate change: Track urban emissions on a human scale. Nature 2015, 525, 179–181. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-H.; Chen, N.; Chan, S.-L. A gravity model integrating high-speed rail and seismic-hazard mitigation through land-use planning: Application to California development. Habitat Int. 2017, 62, 51–61. [Google Scholar] [CrossRef]
- Aunan, K.; Wang, S. Internal migration and urbanization in China: Impacts on population exposure to household air pollution (2000–2010). Sci. Total Environ. 2014, 481, 186–195. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, C.; Liu, X. The Exploration of China New Urbanization Theory. Urban Stud. 2017, 24, 26–34. [Google Scholar]
- Zhou, C.; Wang, S.; Wang, J. Examining the influences of urbanization on carbon dioxide emissions in the Yangtze River Delta, China: Kuznets curve relationship. Sci. Total Environ. 2019, 675, 472–482. [Google Scholar] [CrossRef]
- Wu, W.; Tan, W.; Wang, R.; Chen, W.Y. From quantity to quality: Effects of urban greenness on life satisfaction and social inequality. Landsc. Urban Plan. 2023, 238, 104843. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Zhang, X.; Zhang, H. Influencing mechanism of energy-related carbon emissions in Xinjiang based on the input-output and structural decomposition analysis. J. Geogr. Sci. 2017, 27, 365–384. [Google Scholar] [CrossRef]
- Baiocchi, G.; Minx, J.; Hubacek, K. The Impact of Social Factors and Consumer Behavior on Carbon Dioxide Emissions in the United Kingdom: A Regression Based on Input−Output and Geodemographic Consumer Segmentation Data. J. Ind. Ecol. 2010, 14, 50–72. [Google Scholar] [CrossRef]
- Xu, Q.; Dong, Y.; Yang, R. Urbanization impact on carbon emissions in the Pearl River Delta region: Kuznets curve relationships. J. Clean. Prod. 2018, 180, 514–523. [Google Scholar] [CrossRef]
- Elvidge, C.; Ziskin, D.; Baugh, K.; Tuttle, B.; Ghosh, T.; Pack, D.; Erwin, E.; Zhizhin, M. A Fifteen Year Record of Global Natural Gas Flaring Derived from Satellite Data. Energies 2009, 2, 595–622. [Google Scholar] [CrossRef]
- Stewart, B.; Addison, D. Nighttime Lights Revisited: The Use of Nighttime Lights Data as a Proxy for Economic Variables; The World Bank Group: Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Yin, Z.; Li, X.; Tong, F.; Li, Z.; Jendryke, M. Mapping urban expansion using night-time light images from Luojia1-01 and International Space Station. Int. J. Remote Sens. 2020, 41, 2603–2623. [Google Scholar] [CrossRef]
- Wang, L.; Jia, Y.; Li, X.; Gong, P. Analysing the Driving Forces and Environmental Effects of Urban Expansion by Mapping the Speed and Acceleration of Built-Up Areas in China between 1978 and 2017. Remote Sens. 2020, 12, 3929. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Song, W.; Liu, H.; Wu, Q.; Shi, K.; Wu, J. A New Approach for Detecting Urban Centers and Their Spatial Structure With Nighttime Light Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6305–6319. [Google Scholar] [CrossRef]
- Ye, Y.; Yun, G.; He, Y.; Lin, R.; He, T.; Qian, Z. Spatiotemporal Characteristics of Urbanization in the Taiwan Strait Based on Nighttime Light Data from 1992 to 2020. Remote Sens. 2023, 15, 3226. [Google Scholar] [CrossRef]
- Lu, C.; Li, L.; Lei, Y.; Ren, C.; Su, Y.; Huang, Y.; Chen, Y.; Lei, S.; Fu, W. Coupling Coordination Relationship between Urban Sprawl and Urbanization Quality in the West Taiwan Strait Urban Agglomeration, China: Observation and Analysis from DMSP/OLS Nighttime Light Imagery and Panel Data. Remote Sens. 2020, 12, 3217. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Liu, J.; Mi, Z.; Liu, Z.; Liu, J.; Schroeder, H.; Cai, B.; Chen, Y.; Shao, S.; et al. Methodology and applications of city level CO2 emission accounts in China. J. Clean. Prod. 2017, 161, 1215–1225. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, Y.; Hang, Y.; Zheng, H.; Li, Y.; Guan, D.; Li, J.; Zhou, Y.; Li, L.; Hubacek, K. City-level emission peak and drivers in China. Sci. Bull. 2022, 67, 1910–1920. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, J.; Liu, Z.; Shao, S.; Guan, D. An emissions-socioeconomic inventory of Chinese cities. Sci. Data 2019, 6, 190027. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Tian, L.; Liu, Y.; Zhao, M.; Hu, Y.; Wu, J. Ecosystem services response to urbanization in metropolitan areas: Thresholds identification. Sci. Total Environ. 2017, 607–608, 706–714. [Google Scholar] [CrossRef] [PubMed]
- Friedmann, J. Four Theses in the Study of China’s Urbanization. Int. J. Urban Reg. Res. 2006, 30, 440–451. [Google Scholar] [CrossRef]
- Tian, Y.; Tsendbazar, N.-E.; van Leeuwen, E.; Fensholt, R.; Herold, M. A global analysis of multifaceted urbanization patterns using Earth Observation data from 1975 to 2015. Landsc. Urban Plan. 2022, 219, 104316. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Shi, Y. Spatial expansion of urban built-up areas in Zhengzhou based on GIS and its influencing factors. Henan Sci. 2017, 35, 1883–1888. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Wang, R.; Liu, S. Evaluation of sustainable urbanization status in the Yangtze River Economic Belt. Resour. Dev. Mark. 2023, 39, 188–198. [Google Scholar]
- Yu, M.; Guo, S.; Guan, Y.; Cai, D.; Zhang, C.; Fraedrich, K.; Liao, Z.; Zhang, X.; Tian, Z. Spatiotemporal heterogeneity analysis of yangtze river delta urban agglomeration: Evidence from nighttime light data (2001–2019). Remote Sens. 2021, 13, 1235. [Google Scholar] [CrossRef]
- Zhao, M.; Zhou, Y.; Li, X.; Zhou, C.; Cheng, W.; Li, M.; Huang, K. Building a Series of Consistent Night-Time Light Data (1992–2018) in Southeast Asia by Integrating DMSP-OLS and NPP-VIIRS. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1843–1856. [Google Scholar] [CrossRef]
- Li, X.; Xu, H.; Chen, X.; Li, C. Potential of NPP-VIIRS Nighttime Light Imagery for Modeling the Regional Economy of China. Remote Sens. 2013, 5, 3057–3081. [Google Scholar] [CrossRef]
- Imhoff, M. Using nighttime DMSP/OLS images of city lights to estimate the impact of urban land use on soil resources in the United States. Remote Sens. Environ. 1997, 59, 105–117. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Woodcock, S.V.S.C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. Interdiscip. J. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Stehman, S.V.; Selkowitz, D.J. A spatially stratified, multi-stage cluster sampling design for assessing accuracy of the alaska (USA) national land cover database (NLCD). Int. J. Remote Sens. 2010, 31, 1877–1896. [Google Scholar] [CrossRef]
- Cakir, H.I.; Khorram, S.; Sac, N. Correspondence analysis for detecting land cover change. Remote Sens. Environ. Interdiscip. J. 2006, 102, 306–317. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Wang, P.; Hou, G. Research on the carbon peak path of Henan Province based on the Lasso-BP neural network model. Environ. Eng. 2022, 40, 151–156. [Google Scholar]
- Chikán, A.; Czakó, E.; Kiss-Dobronyi, B.; Losonci, D. Firm competitiveness: A general model and a manufacturing application. Int. J. Prod. Econ. 2022, 243, 108316. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, X.; Wang, H. Regional logistics efficiency and performance in China along the Belt and Road Initiative: The analysis of integrated DEA and hierarchical regression with carbon constraint. J. Clean. Prod. 2020, 276, 123649. [Google Scholar] [CrossRef]
- Joseph, S.; Jonathan, L. Greening the rust belt: A green infrastructure model for right sizing america’s shrinking cities. J. Am. Plan. Assoc. 2008, 74, 451–466. [Google Scholar]
- Turok, I.; Mykhnenko, V. The trajectories of european cities, 1960–2005. Cities 2007, 24, 165–182. [Google Scholar] [CrossRef]
- Wiechmann, T.; Pallagst, K.M. Urban shrinkage in Germany and the USA: A comparison of transformation patterns and local strategies. Int. J. Urban Reg. Res. 2012, 36, 261–280. [Google Scholar] [CrossRef]
- Hollander, J.B.; Németh, J. The bounds of smart decline: A foundational theory for planning shrinking cities. Hous. Policy Debate 2011, 21, 349–367. [Google Scholar] [CrossRef]
- Haase, A.; Rink, D.; Grossmann, K.; Bernt, M.; Mykhnenko, V. Conceptualizing urban shrinkage. Environ. Plan. A 2014, 46, 1519–1534. [Google Scholar] [CrossRef]
- Martinez-Fernandez, C.; Audirac, I.; Sylvie, F.; Emmanuèle Cunningham-Sabot. Shrinking Cities: Urban Challenges of Globalization. Int. J. Urban Reg. Res. 2012, 36, 213–225. [Google Scholar] [CrossRef]
- Du, Z.W.; Li, X. New phenomena of growth and contraction in the rapid urbanization of the Pearl River Delta. Acta Geogr. Sin. 2017, 72, 1800–1811. [Google Scholar]
- Zhang, S.; Wang, C.; Wang, J.; Yao, S.; Zhang, F.; Yin, G.; Xu, X. Comprehensive measurement of urban shrinkage in China and its temporal and spatial heterogeneity. Chin. J. Popul. Resour. Environ. 2020, 30, 72–82. [Google Scholar]
- Anser, M.K.; Alharthi, M.; Aziz, B.; Wasim, S. Impact of urbanization, economic growth, and population size on residential carbon emissions in the saarc countries. Clean Technol. Environ. Policy 2020, 22, 923–936. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, C.; Gao, C.; Ding, L. Analysis of the spatiotemporal distribution characteristics and influencing factors of carbon emissions in the Zhejiang Bay Area Economic Belt based on urbanization. J. Nat. Resour. 2020, 35, 329–342. [Google Scholar]
- Xue, J.; Zhang, X. Research on the Evolution and Influencing Factors of Urban Carbon Emissions under the “Dual Carbon” Goal: A Case Study of the Yellow River “Several Bend” Urban Agglomeration. Frontier 2023, 125–136. [Google Scholar]
- Liddle, B. Demographic dynamics and per capita environmental impact: Using panel regressions and household decompositions to examine population and transport. MPIDR Work. Pap. 2003, 26, 23–39. [Google Scholar] [CrossRef]
- Chen, H.; Jia, B.; Lau, S. Sustainable urban form for Chinese compact cities: Challenges of a rapid urbanized economy. Habitat Int. 2008, 32, 28–40. [Google Scholar] [CrossRef]
- Di Vittorio, A.V.; Simmonds, M.B.; Nico, P. Quantifying the effects of multiple land management practices, land cover change, and wildfire on the California landscape carbon budget with an empirical model. PLoS ONE 2021, 16, e0251346. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Zhang, L.; Qiu, B.; Zhao, Y.; Wei, C. Spatiotemporal Analysis of Land Use Patterns on Carbon Emissions in China. Land 2021, 10, 141. [Google Scholar] [CrossRef]
- Tao, Y.; Li, F.; Wang, R.; Zhao, D. Effects of land use and cover change on terrestrial carbon stocks in urbanized areas: A study from Changzhou, China. J. Clean. Prod. 2015, 103, 651–657. [Google Scholar] [CrossRef]
- Wang, J.; He, A. Psychological Attribution and Policy Intervention Paths of Consumers’ Low-Carbon Consumption Behavior: An Exploratory Study Based on Grounded Theory. Nankai Bus. Rev. 2011, 14, 80–89, 99. [Google Scholar]
- Ma, Q.; Men, Y. The Impact of Consumption Values and Social Consumption Culture on Public Low-Carbon Consumption Behavior under a Low-Carbon Background. Commer. Econ. Res. 2022, 69–73. [Google Scholar]
- Gim, T.H.T. Analyzing the city-level effects of land use on travel time and co 2 emissions: A global mediation study of travel time. Int. J. Sustain. Transp. 2021, 16, 496–513. [Google Scholar] [CrossRef]
- Lu, J.; Li, B.; Li, H.; Al-Barakani, A. Expansion of city scale, traffic modes, traffic congestion, and air pollution. Cities 2020, 108, 102974. [Google Scholar] [CrossRef]
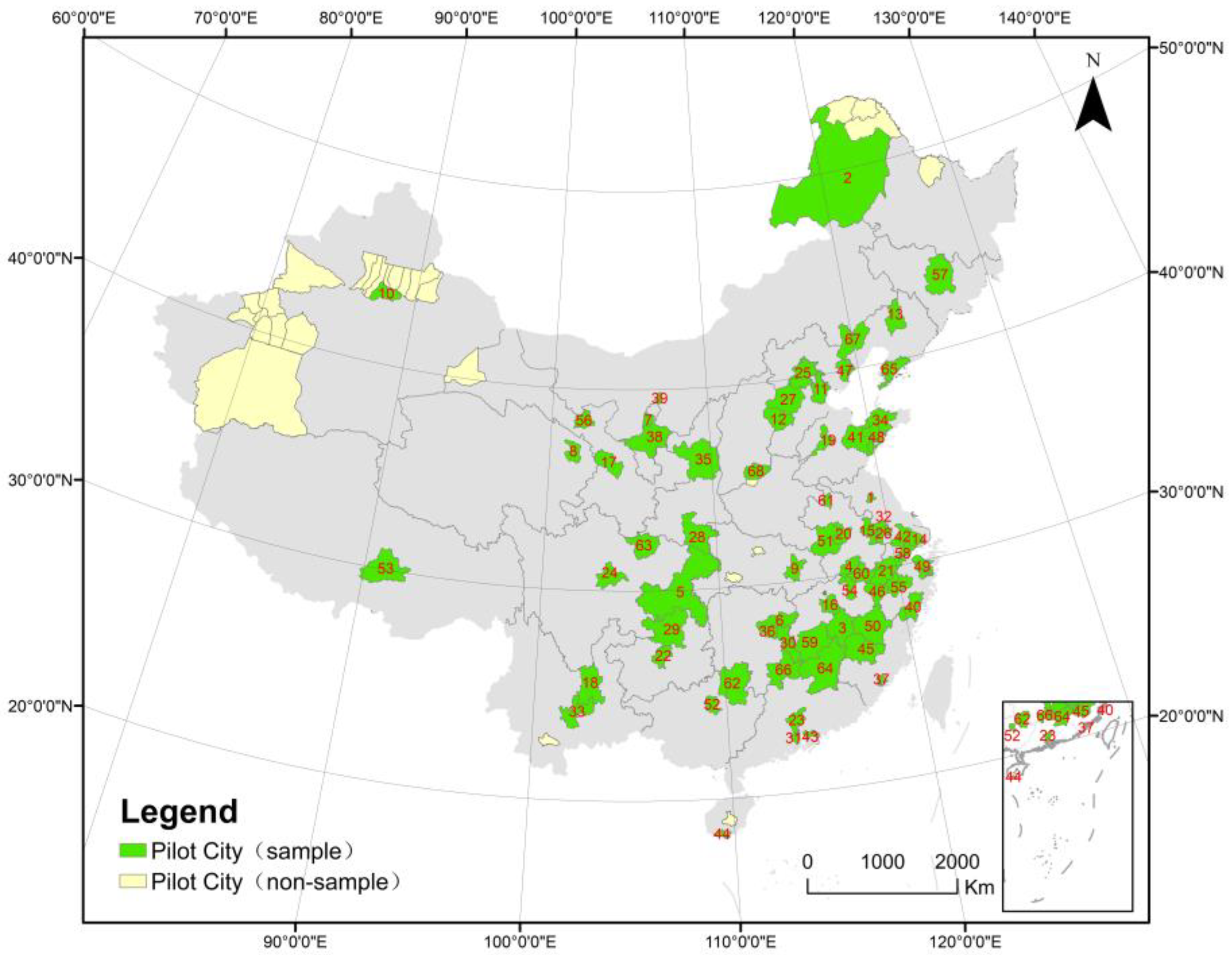
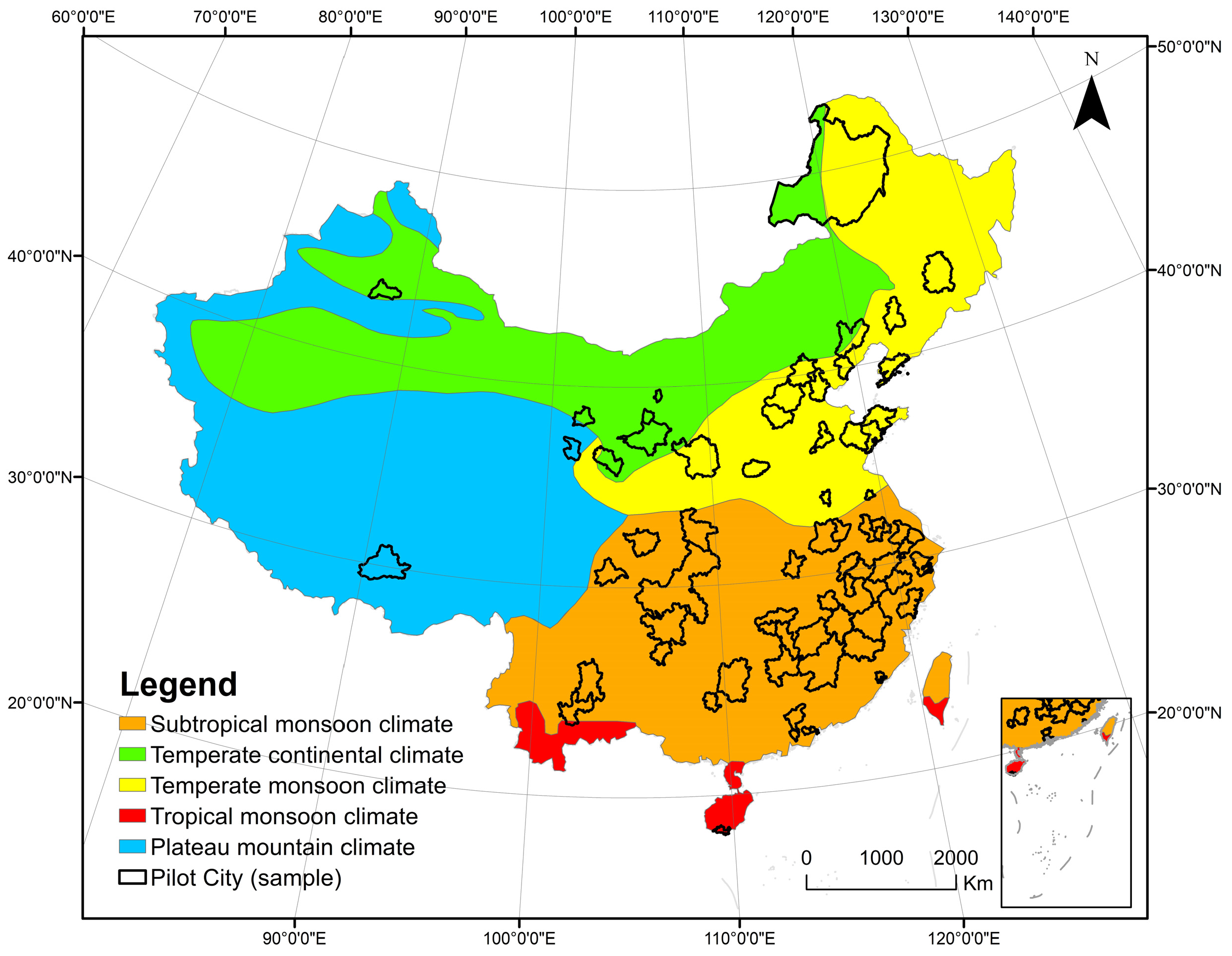
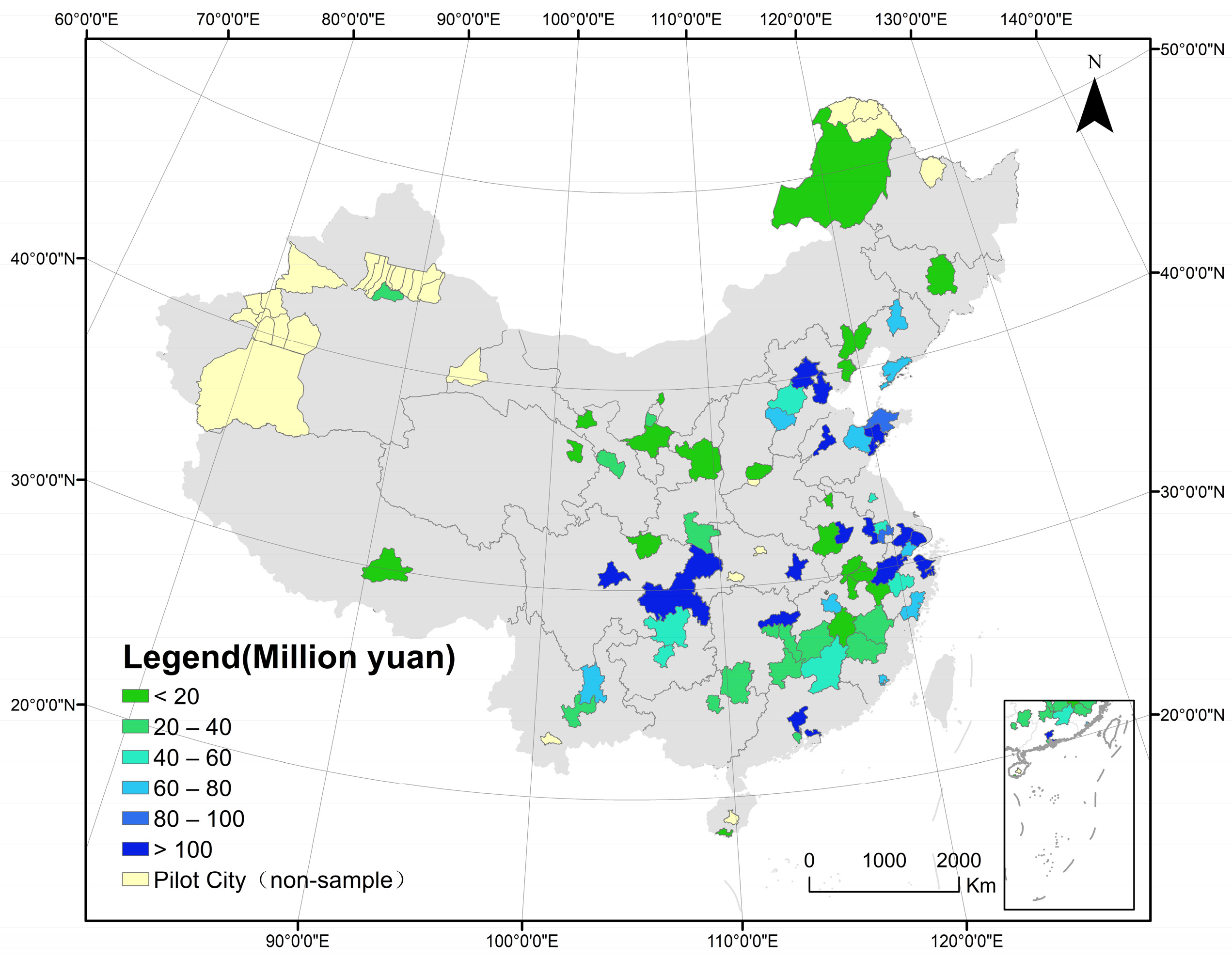
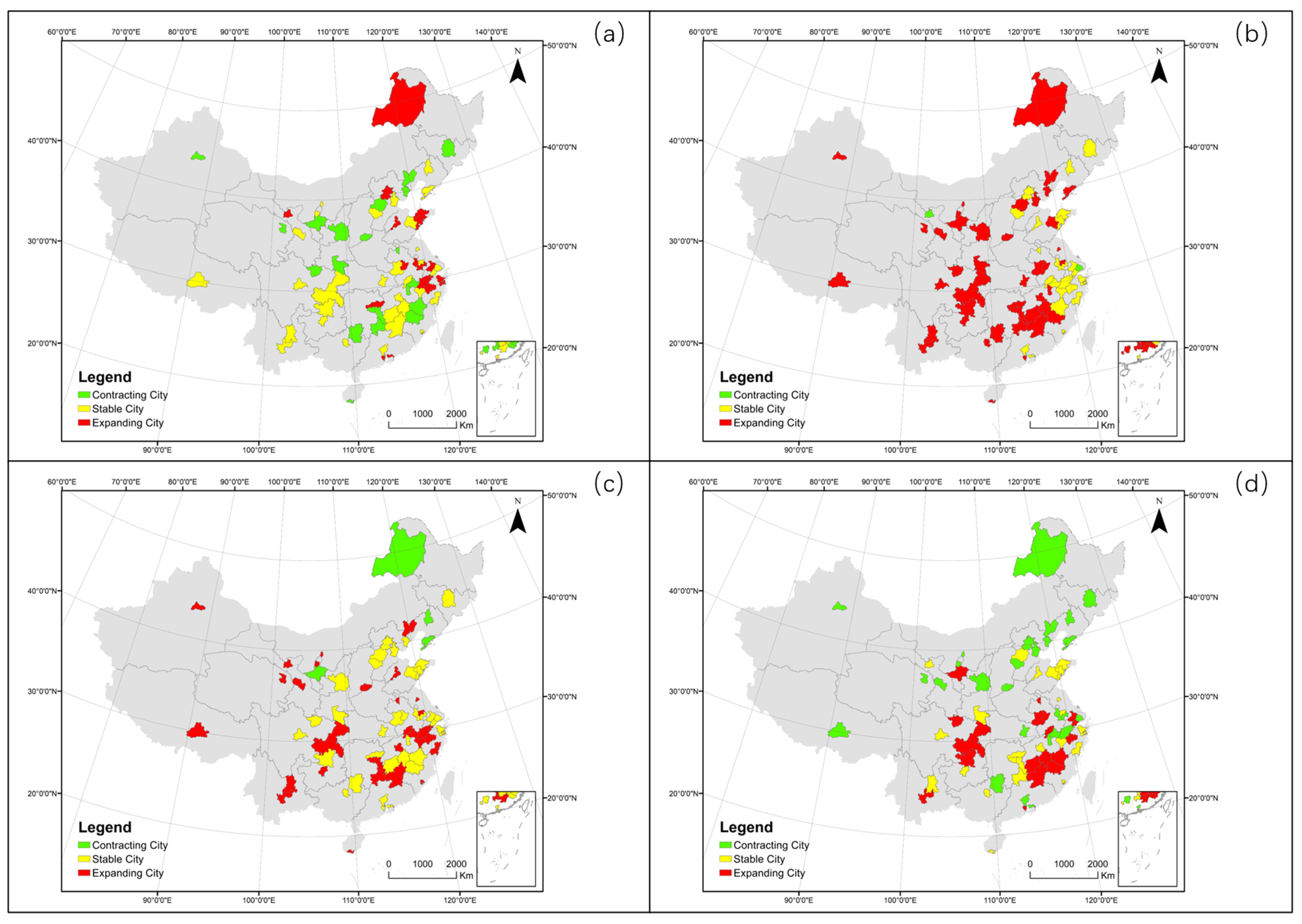
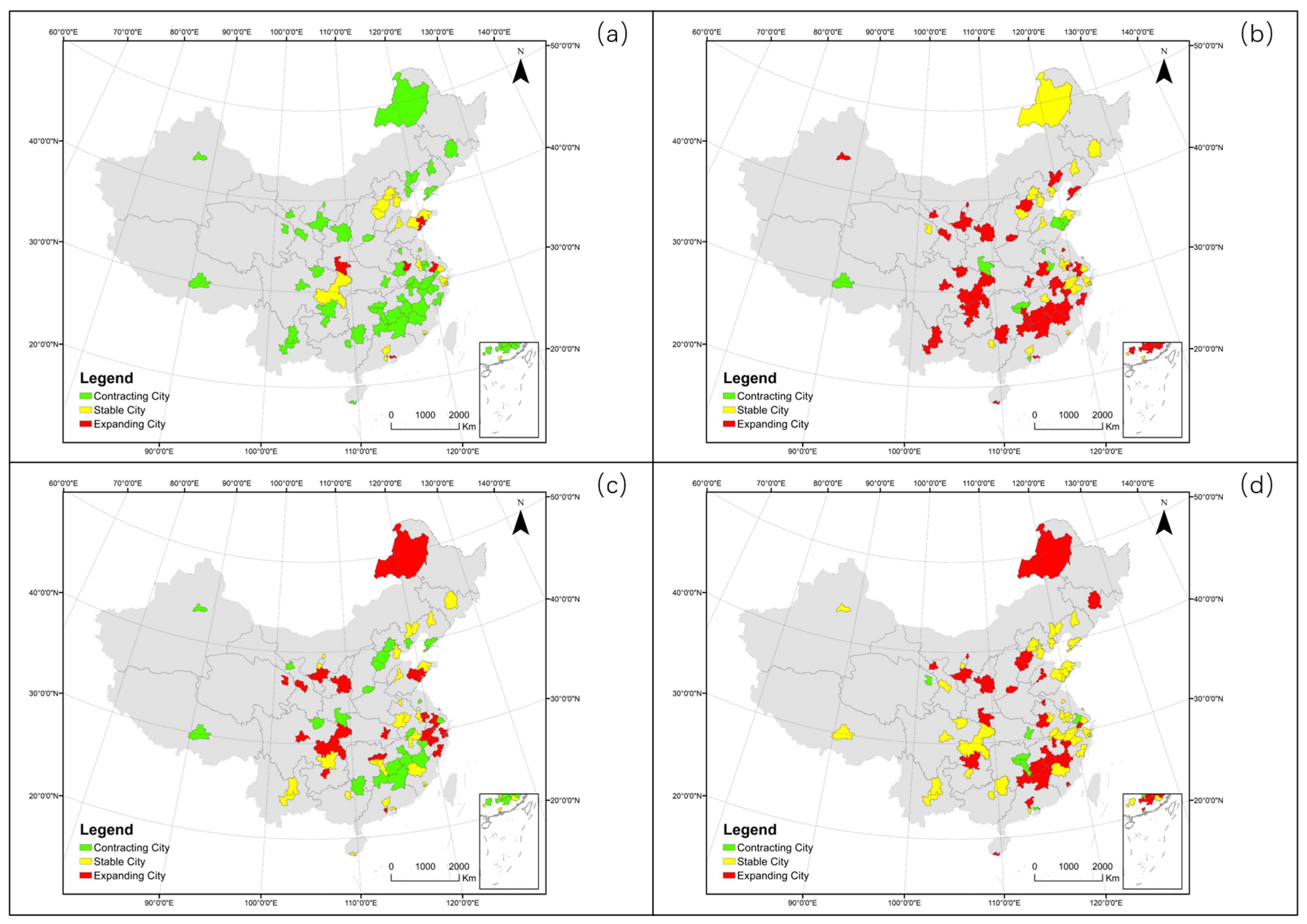
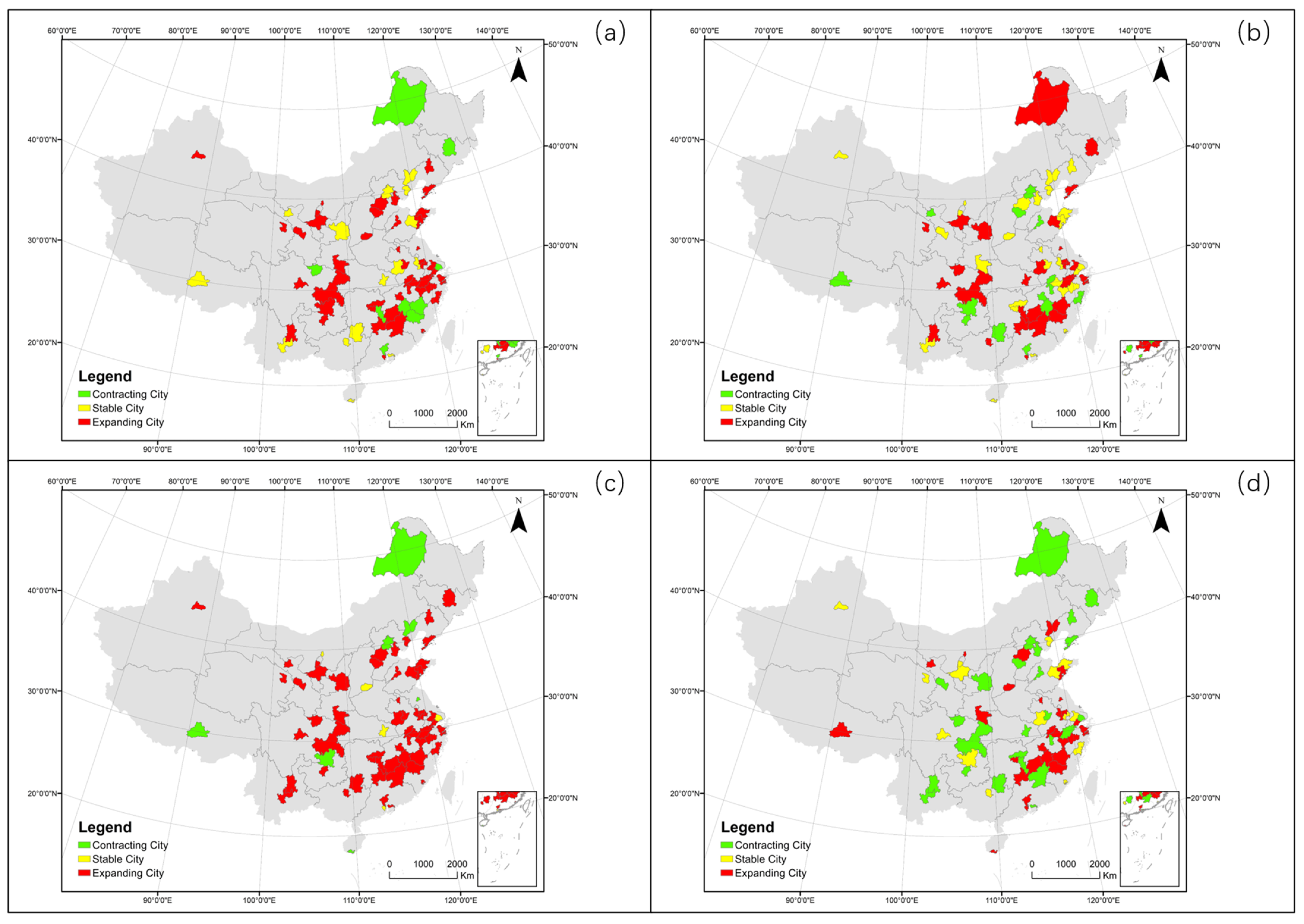
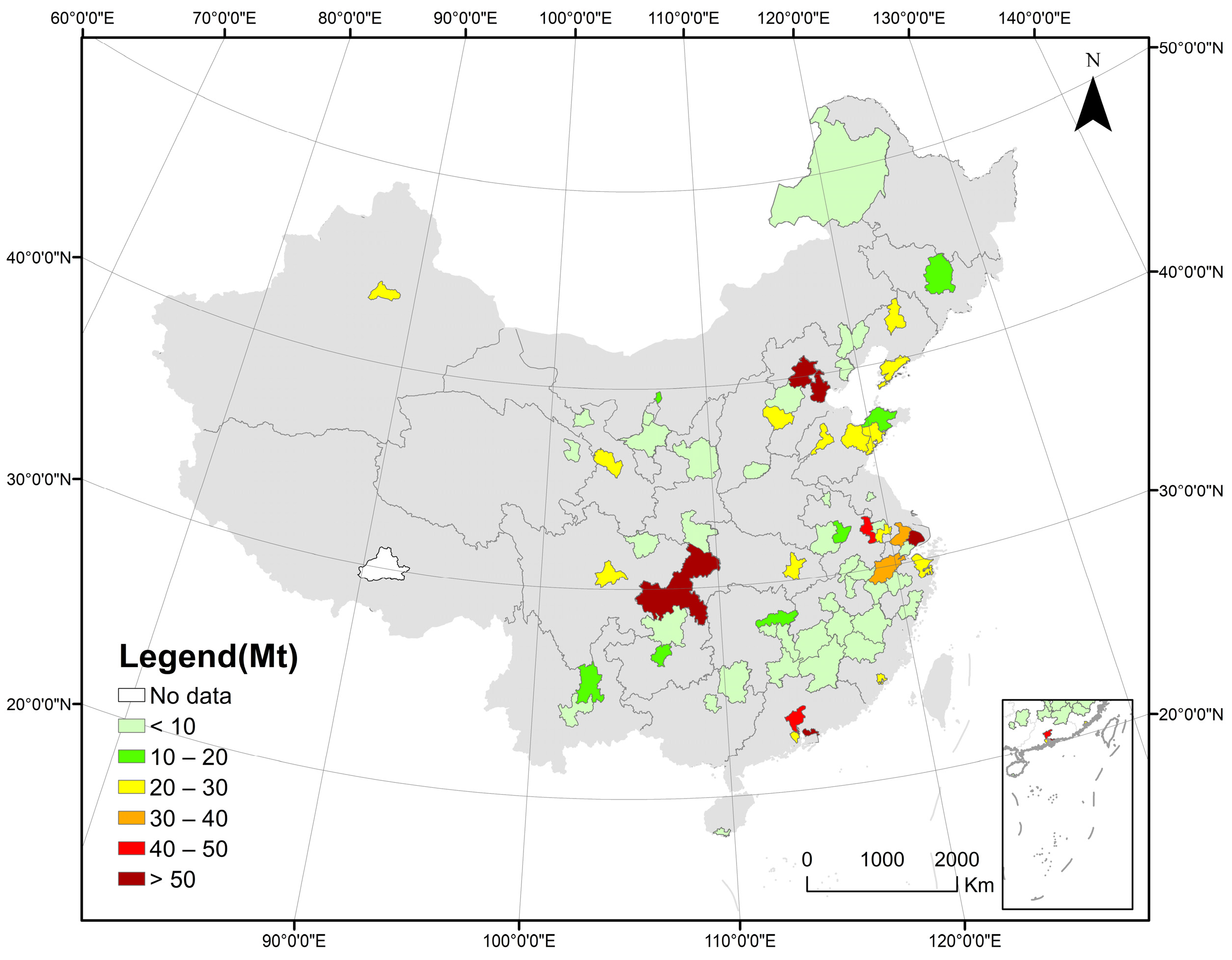

| Dataset | Data | Source |
|---|---|---|
| DMSP/OLS nighttime light data | 2002–2013 | https://eogdata.mines.edu/products/vnl/ (accessed on 1 September 2023) |
| NPP-VIIRS nighttime light data | 2012–2021 | |
| The MODIS land cover type product MCD12Q1 | 2010, 2020 | https://ladsweb.modaps.eosdis.nasa.gov |
| The China Emission Accounts and Datasets (CEADs) | 2006–2019 | https://www.ceads.net.cn/ |
| The urban statistical data and energy data | 2002–2021 | http://www.stats.gov.cn/ |
| Method | Step | Formula | Meaning |
|---|---|---|---|
| Min–Max Normalization | . is the minimum and maximum values in the data of 68 cities in year t. | ||
| Information Entropy Method | to all cities | . . is the number of sample cities. . | |
| Urban development change rate | . |
| Step | Formula | Meaning |
|---|---|---|
| Mutual correction | a, b, c are the parameters obtained from quadratic regression. | |
| Continuity correction | . . | |
| Interannual correction | years. |
| Fit Method | Formula | Meaning | R-Squared (R2) |
|---|---|---|---|
| Exponential function | x is the corresponding DN value of NPP/VIIRS images | 0.8200 | |
| Linear function | 0.9830 | ||
| Logarithmic function | 0.7510 | ||
| Power function | 0.9836 |
| ID | Meaning | Abbreviations |
|---|---|---|
| Y | Carbon emission | CE |
| X1 | Population size | PS |
| X2 | Employment numbers | EN |
| X3 | GDP | GDP |
| X4 | The proportion of tertiary industry | PTI |
| X5 | Retail sales | RS |
| X6 | Government investment | GI |
| X7 | Built-up area | BA |
| X8 | Built-up perimeter | BP |
| X9 | Fractal dimension | FDI |
| X10 | Compactness index | CI |
| X11 | Virescence area | VA |
| X12 | Nighttime light intensity | NLI |
| Number | City | Time | Overall Accuracy |
|---|---|---|---|
| (a) | Chongqing | 2010 | 90.22% |
| 2020 | 88.76% | ||
| (b) | Beijing | 2010 | 98.87% |
| 2020 | 97.27% | ||
| (c) | Kunming | 2010 | 97.27% |
| 2020 | 95.05% | ||
| (d) | Tianjin | 2010 | 85.53% |
| 2020 | 85.82% | ||
| (e) | Chengdu | 2010 | 94.49% |
| 2020 | 86.18% | ||
| (f) | Suzhou | 2010 | 82.73% |
| 2020 | 80.73% | ||
| (g) | Guangzhou | 2010 | 89.12% |
| 2020 | 71.49% | ||
| (h) | Shanghai | 2010 | 82.08% |
| 2020 | 71.49% | ||
| (i) | Xiamen | 2010 | 79.33% |
| 2020 | 70.90% |
| 2002–2006 | 2007–2011 | 2012–2016 | 2017–2021 | |
|---|---|---|---|---|
| Contracting City | 31 | 6 | 6 | 15 |
| Stable City | 21 | 30 | 29 | 38 |
| Expanding City | 16 | 32 | 33 | 15 |
| 2002–2006 | 2007–2011 | 2012–2016 | 2017–2021 | ||
|---|---|---|---|---|---|
| Population subsystem | Contracting City | 13 | 22 | 4 | 35 |
| Stable City | 18 | 35 | 25 | 17 | |
| Expanding City | 37 | 11 | 39 | 16 | |
| Economy subsystem | Contracting City | 21 | 2 | 4 | 27 |
| Stable City | 31 | 23 | 34 | 23 | |
| Expanding City | 16 | 43 | 30 | 18 | |
| Construction subsystem | Contracting City | 49 | 9 | 21 | 7 |
| Stable City | 14 | 20 | 25 | 35 | |
| Expanding City | 4 | 39 | 22 | 26 | |
| Society subsystem | Contracting City | 9 | 14 | 7 | 25 |
| Stable City | 15 | 27 | 5 | 15 | |
| Expanding City | 44 | 27 | 56 | 28 |
| Variable | VIF |
|---|---|
| X8 | 83.1233 |
| X10 | 58.7077 |
| X3 | 54.2692 |
| X6 | 45.3954 |
| X7 | 34.1285 |
| X9 | 19.7756 |
| X2 | 13.1348 |
| X1 | 6.6273 |
| X11 | 3.3523 |
| X4 | 3.0207 |
| X12 | 2.3542 |
| X5 | 1.7763 |
| Df | %Dev | Lambda | |
|---|---|---|---|
| 1 | 0 | 0 | 1.062 |
| 2 | 1 | 13.49 | 0.9673 |
| 3 | 1 | 24.7 | 0.8814 |
| … | … | … | … |
| 53 | 9 | 83.63 | 0.01112 |
| 54 | 9 | 83.67 | 0.01013 |
| 55 | 9 | 83.69 | 0.00923 |
| 56 | 10 | 83.87 | 0.00636 |
| 57 | 10 | 83.91 | 0.0058 |
| 58 | 10 | 83.94 | 0.00528 |
| 59 | 11 | 83.97 | 0.00481 |
| 60 | 11 | 84.04 | 0.00439 |
| 61 | 11 | 84.09 | 0.004 |
| 62 | 12 | 84.2 | 0.00364 |
| 63 | 12 | 84.48 | 0.00276 |
| Variable | Coefficient | Result |
|---|---|---|
| X1 | 0.2060 | Reserve |
| X2 | 0.0444 | Reserve |
| X3 | 0.0064 | Reserve |
| X4 | −0.1708 | Reserve |
| X5 | −0.0209 | Reserve |
| X6 | 0.0000 | Discard |
| X7 | 0.6569 | Reserve |
| X8 | 0.0000 | Discard |
| X9 | 0.3582 | Reserve |
| X10 | −0.0681 | Reserve |
| X11 | −0.0181 | Reserve |
| X12 | 0.3143 | Reserve |
| (1) lnY | (2) lnY | (3) lnY | (4) lnY | (5) lnY | |
|---|---|---|---|---|---|
| lnX7 | 0.939 *** | 0.848 *** | 0.472 *** | 0.696 *** | 0.736 *** |
| (33.677) | (32.079) | (8.034) | (7.387) | (7.804) | |
| lnX12 | 0.300 *** | 0.275 *** | 0.290 *** | 0.296 *** | |
| (10.015) | (8.848) | (9.413) | (9.688) | ||
| lnX1 | 0.429 *** | 0.432 *** | 0.459 *** | ||
| (7.378) | (7.563) | (8.009) | |||
| lnX10 | −0.777 *** | −0.777 ** | |||
| (−4.871) | (−4.781) | ||||
| lnX4 | −0.351 ** | ||||
| (−2.912) | |||||
| Constant | 2.063 *** | 1.791 *** | 1.711 *** | 3.163 *** | 3.613 *** |
| (13.438) | (12.866) | (12.406) | (7.646) | (7.646) | |
| Observations | 377 | 377 | 377 | 377 | 377 |
| R-squared | 0.752 | 0.803 | 0.826 | 0.828 | 0.837 |
| F | 240.592 | 136.907 | 97.007 | 77.144 | 63.469 |
| (1) lnY | (2) lnY | (3) lnY | (4) lnY | (5) lnY | |
|---|---|---|---|---|---|
| lnX7 | 0.949 *** | 0.848 *** | 0.627 *** | 0.734 *** | 0.543 *** |
| (15.511) | (32.079) | (7.326) | (7.375) | (4.304) | |
| lnX12 | 0.378 *** | 0.414 *** | 0.412 *** | 0.519 *** | |
| (3.958) | (4.006) | (4.021) | (4.897) | ||
| lnX2 | 0.278 | 0.268 *** | 0.373 *** | ||
| (2.866) | (2.787) | (3.674) | |||
| lnX11 | −0.104 ** | −0.124 ** | |||
| (−0.258) | (−2.473) | ||||
| lnX10 | −1.733 *** | ||||
| (−3.006) | |||||
| Constant | 1.845 *** | 2.048 *** | 1.832 *** | 1.595 *** | 2.672 *** |
| (7.353) | (8.270) | (7.305) | (5.821) | (6.393) | |
| Observations | 203 | 203 | 203 | 203 | 203 |
| R-squared | 0.738 | 0.760 | 0.783 | 0.788 | 0.801 |
| F | 240.592 | 136.907 | 78.558 | 64.720 | 50.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Guan, Y.; Yang, T.; Ruan, A.; Yao, W.; Deng, R.; Wei, Z.; Zhang, C.; Guo, S. The Impact of the Expansion and Contraction of China Cities on Carbon Emissions, 2002–2021, Evidence from Integrated Nighttime Light Data and City Attributes. Remote Sens. 2024, 16, 3274. https://doi.org/10.3390/rs16173274
Qian J, Guan Y, Yang T, Ruan A, Yao W, Deng R, Wei Z, Zhang C, Guo S. The Impact of the Expansion and Contraction of China Cities on Carbon Emissions, 2002–2021, Evidence from Integrated Nighttime Light Data and City Attributes. Remote Sensing. 2024; 16(17):3274. https://doi.org/10.3390/rs16173274
Chicago/Turabian StyleQian, Jiaqi, Yanning Guan, Tao Yang, Aoming Ruan, Wutao Yao, Rui Deng, Zhishou Wei, Chunyan Zhang, and Shan Guo. 2024. "The Impact of the Expansion and Contraction of China Cities on Carbon Emissions, 2002–2021, Evidence from Integrated Nighttime Light Data and City Attributes" Remote Sensing 16, no. 17: 3274. https://doi.org/10.3390/rs16173274
APA StyleQian, J., Guan, Y., Yang, T., Ruan, A., Yao, W., Deng, R., Wei, Z., Zhang, C., & Guo, S. (2024). The Impact of the Expansion and Contraction of China Cities on Carbon Emissions, 2002–2021, Evidence from Integrated Nighttime Light Data and City Attributes. Remote Sensing, 16(17), 3274. https://doi.org/10.3390/rs16173274





