Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and eXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen
Abstract
1. Introduction
2. Materials and Methods
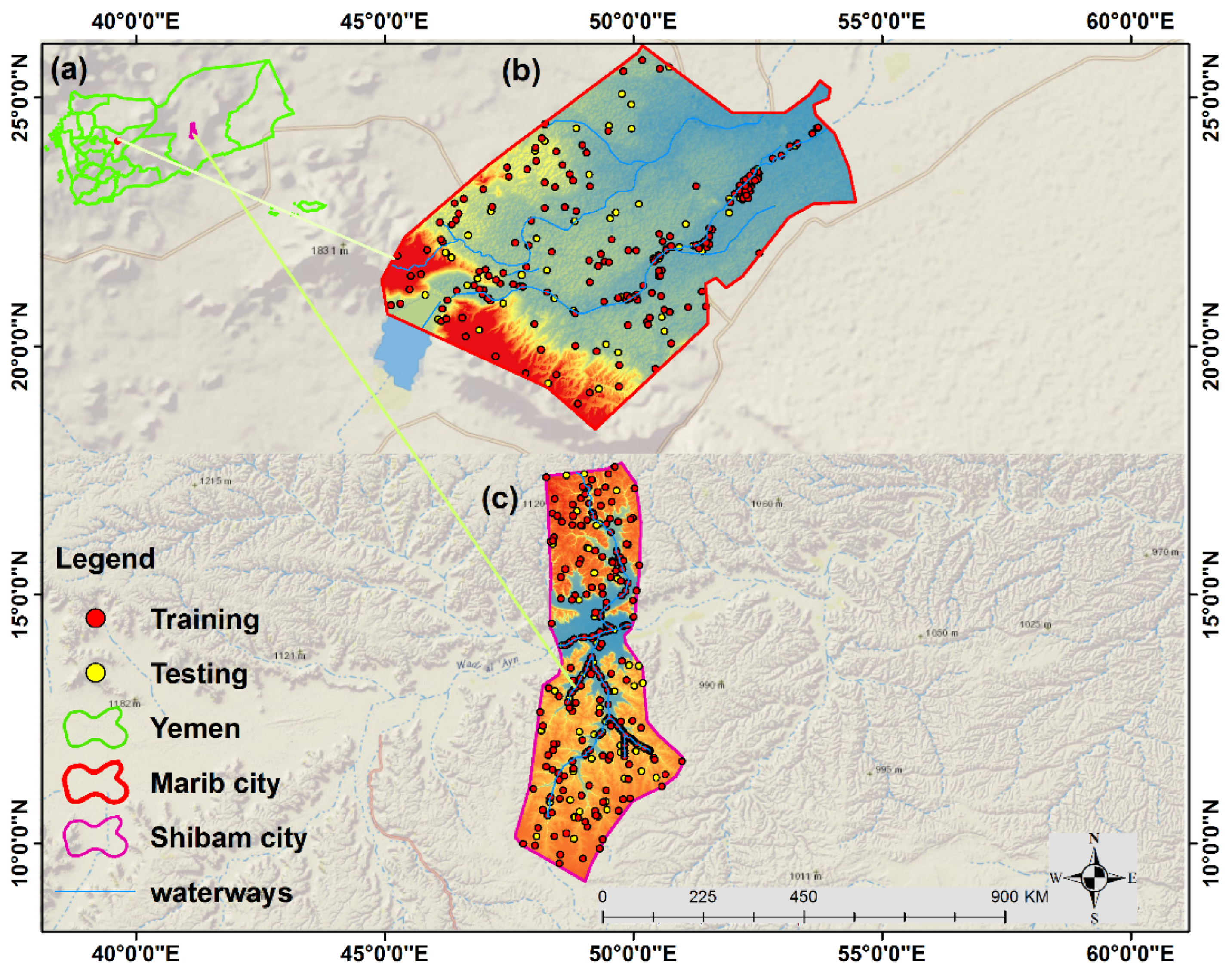
2.1. The Case Studies
2.1.1. Marib City
2.1.2. Shibam City
2.2. Data Sources
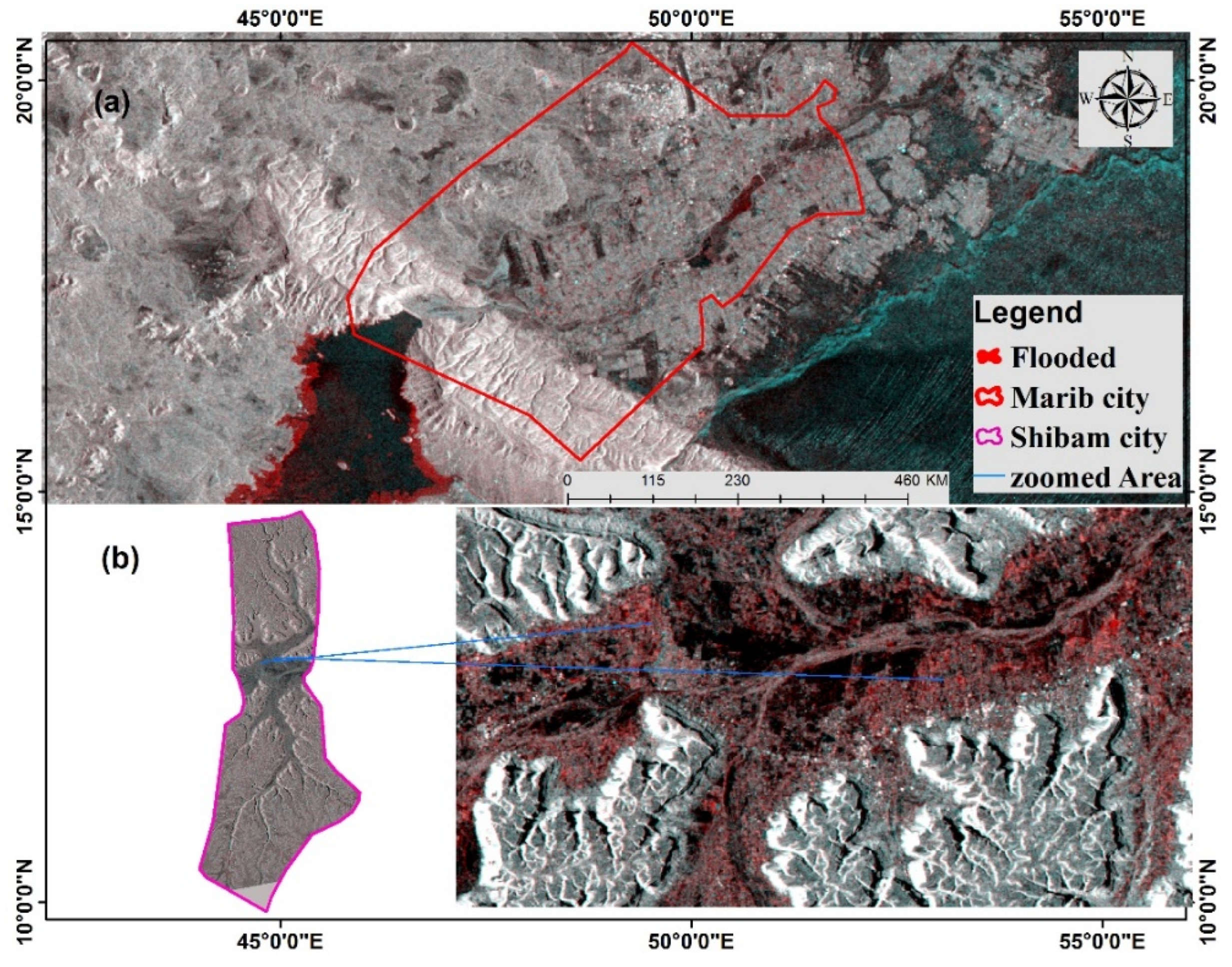
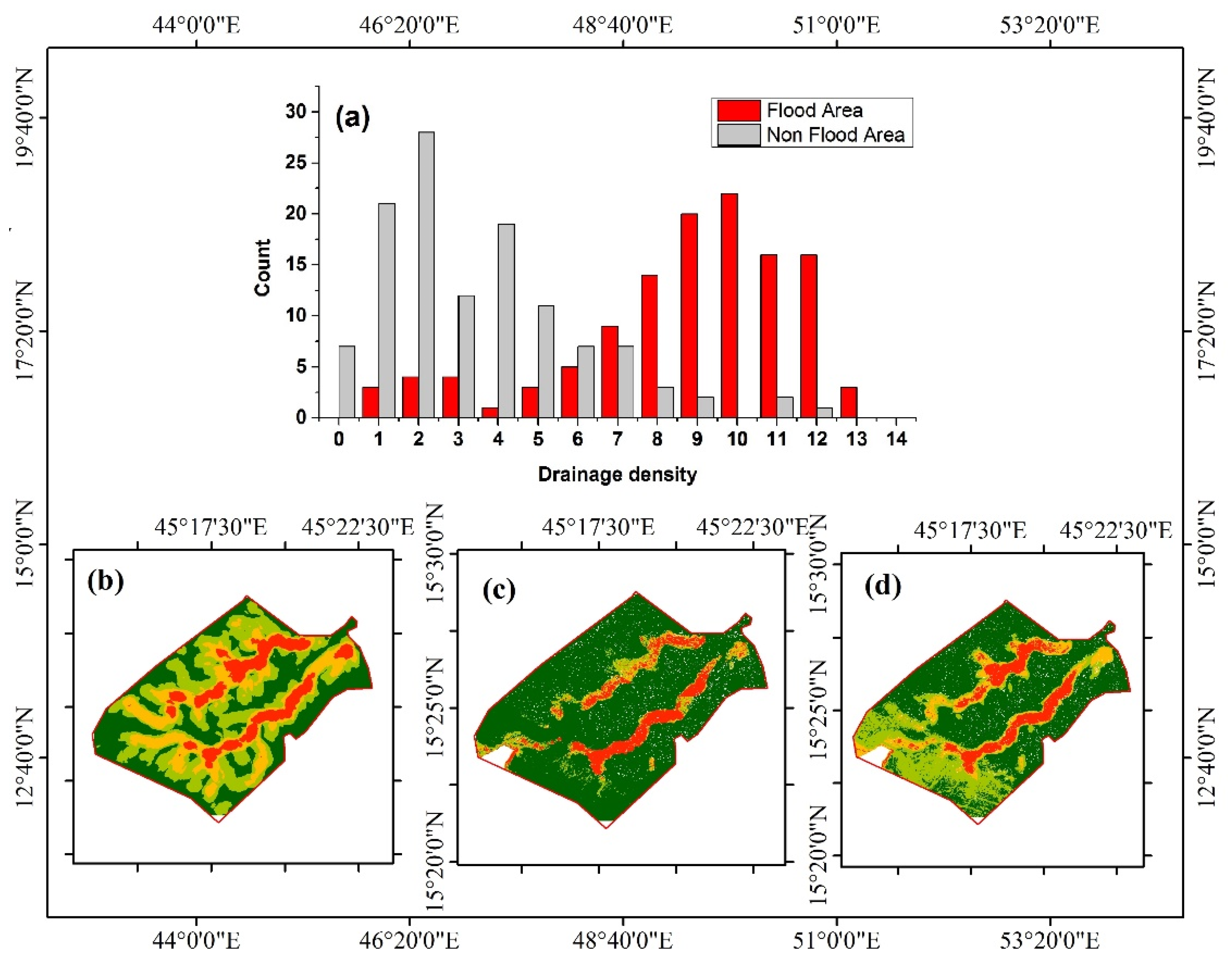
2.2.1. Flood Inventory Map
2.2.2. Flood Conditioning Factors
2.3. Method
2.3.1. RF Model
2.3.2. XGB Model
2.3.3. Hyper-Parameter Optimization
2.3.4. Model Assessment
2.4. Development of Flood Probability Maps
3. Results
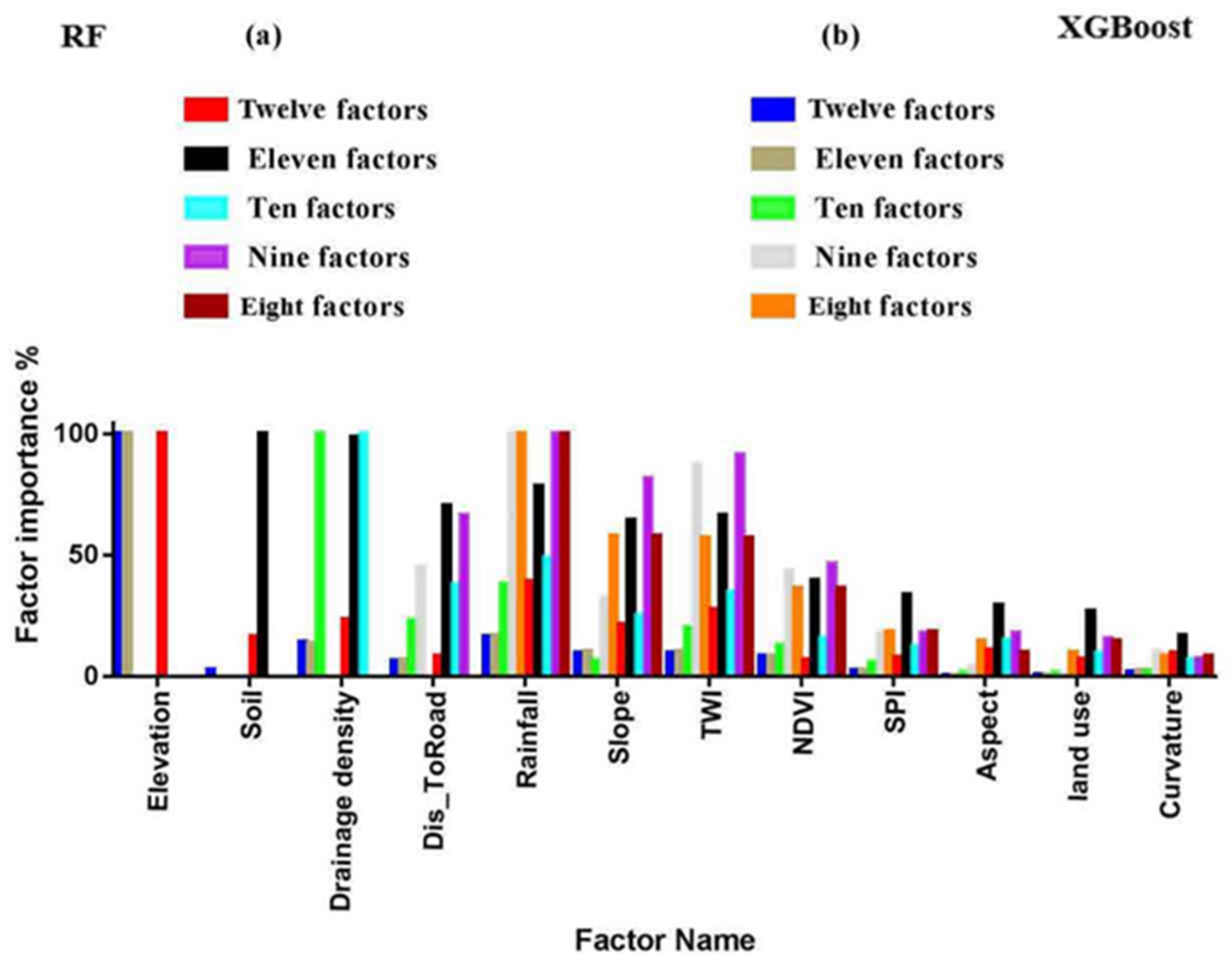
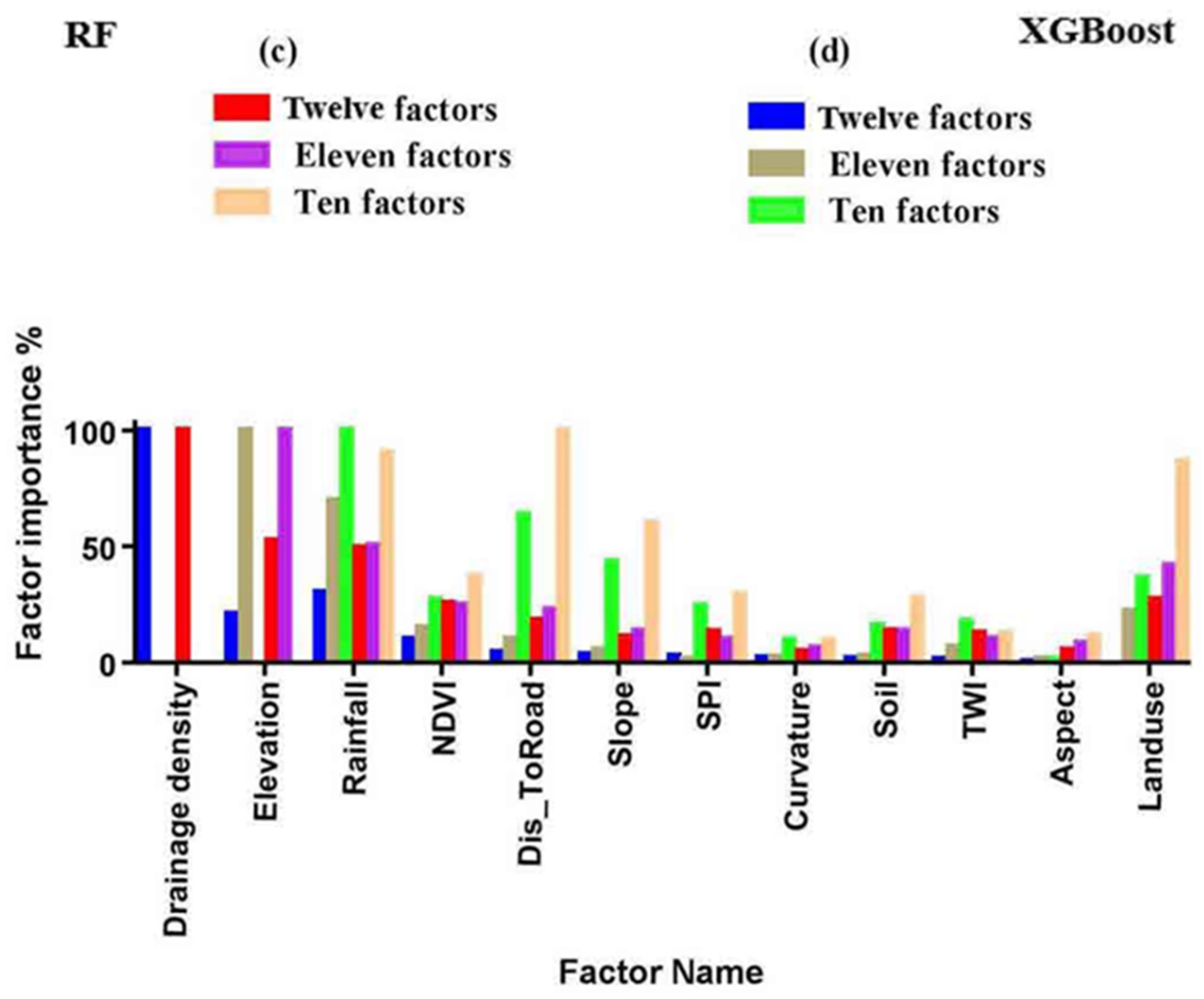
3.1. Visualization of Prediction Variables
3.2. Modeling Using Default Settings
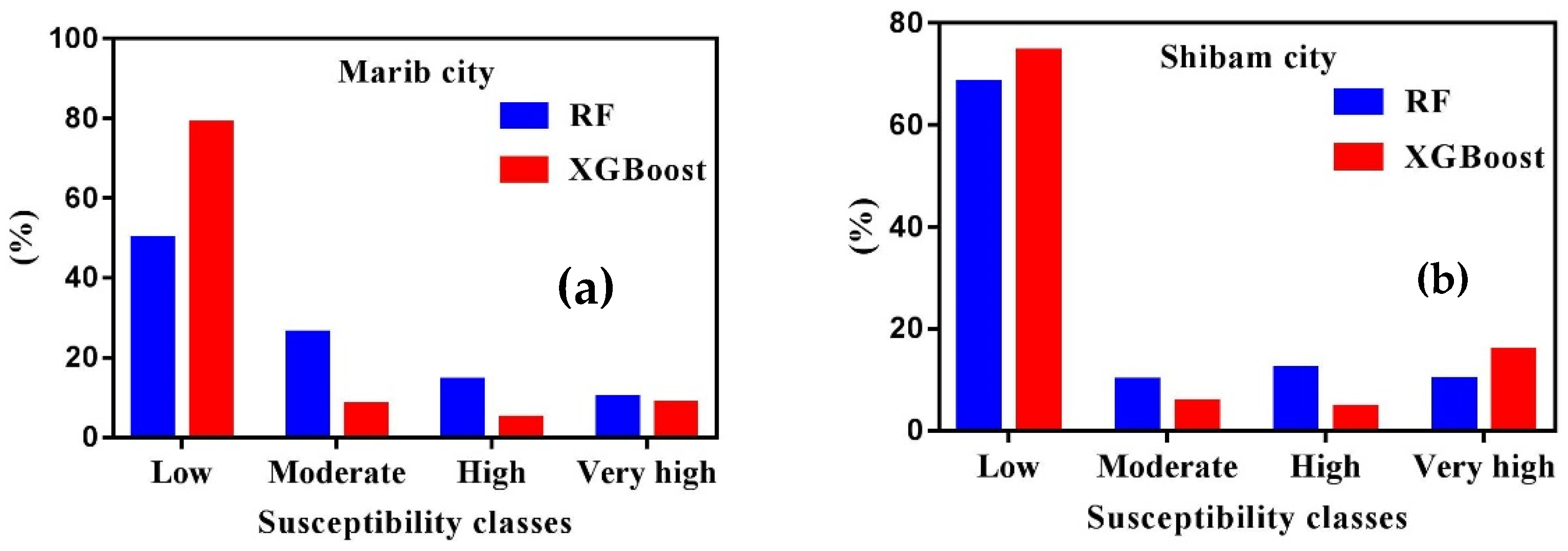
3.3. Selecting the Most Optimized Model for Susceptibility Mapping
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rehman, S.; Sahana, M.; Hong, H.; Sajjad, H.; Ahmed, B. Bin A systematic review on approaches and methods used for flood vulnerability assessment: Framework for future research. Nat. Hazards 2019, 96, 975–998. [Google Scholar] [CrossRef]
- Shaw, R.; Surjan, A.; Parvin, G.A. Urban disasters and approaches to resilience. In Urban Disasters and Resilience in Asia; Elsevier: Amsterdam, The Netherlands, 2016; pp. 1–19. [Google Scholar]
- Pangali Sharma, T.P.; Zhang, J.; Khanal, N.R.; Nepal, P.; Pangali Sharma, B.P.; Nanzad, L.; Gautam, Y. Household Vulnerability to Flood Disasters among Tharu Community, Western Nepal. Sustainability 2022, 14, 12386. [Google Scholar] [CrossRef]
- Wiebelt, M.; Breisinger, C.; Ecker, O.; Al-Riffai, P.; Robertson, R.; Thiele, R. Climate Change and Floods in Yemen: Impacts on Food Security and Options for Adaptation; IFPRI Discussion Paper. 2011. Available online: https://www.preventionweb.net/publication/climate-change-and-floods-yemen-impacts-food-security-and-options-adaptation (accessed on 29 June 2021).
- Zaid, H.A.H.; Jamaluddin, T.A.; Arifin, M.H. Overview of slope stability, earthquakes, flash floods and expansive soil hazards in the Republic of Yemen. Bull. Geol. Soc. Malays. 2021, 71, 71–78. [Google Scholar] [CrossRef]
- Breisinger, C.; Ecker, O.; Thiele, R.; Wiebelt, M. The Impact of the 2008 Hadramout Flash Flood in Yemen on Economic Performance and Nutrition: A Simulation Analysis; Kiel Working Paper 1758; Kiel Institute for the World Economy: Kiel, Germany, 2012; pp. 1–28. [Google Scholar]
- Lackner, H. Global Warming, the Environmental Crisis and Social Justice in Yemen. Asian Aff. 2020, 51, 859–874. [Google Scholar] [CrossRef]
- Edouard, S.; Vincendon, B.; Ducrocq, V. Ensemble-based flash-flood modelling: Taking into account hydrodynamic parameters and initial soil moisture uncertainties. J. Hydrol. 2018, 560, 480–494. [Google Scholar] [CrossRef]
- Lin, L.; Wu, Z.; Liang, Q. Urban flood susceptibility analysis using a GIS-based multi-criteria analysis framework. Nat. Hazards 2019, 97, 455–475. [Google Scholar] [CrossRef]
- Rahman, M.; Ningsheng, C.; Islam, M.M.; Dewan, A.; Iqbal, J.; Washakh, R.M.A.; Shufeng, T. Flood susceptibility assessment in Bangladesh using machine learning and multi-criteria decision analysis. Earth Syst. Environ. 2019, 3, 585–601. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Karatzas, G.P. Flood management and a GIS modelling method to assess flood-hazard areas—A case study. Hydrol. Sci. J. –J. Des Sci. Hydrol. 2011, 56, 212–225. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Norallahi, M.; Kaboli, H.S. Urban flood hazard mapping using machine learning models: GARP, RF, MaxEnt and NB. Nat. Hazards 2021, 106, 119–137. [Google Scholar] [CrossRef]
- Eini, M.; Kaboli, H.S.; Rashidian, M.; Hedayat, H. Hazard and vulnerability in urban flood risk mapping: Machine learning techniques and considering the role of urban districts. Int. J. Disaster Risk Reduct. 2020, 50, 101687. [Google Scholar] [CrossRef]
- Guo, E.; Zhang, J.; Ren, X.; Zhang, Q.; Sun, Z. Integrated risk assessment of flood disaster based on improved set pair analysis and the variable fuzzy set theory in central Liaoning Province, China. Nat. Hazards 2014, 74, 947–965. [Google Scholar] [CrossRef]
- Joy, S.; Lu, X.X. Application of Remote Sensing in Flood Management with Special Reference to Monsoon Asia: A Review. Nat. Hazards 2004, 33, 283–301. [Google Scholar]
- Burgan, H.I.; Icaga, Y. Flood analysis using adaptive hydraulics (AdH) model in Akarcay Basin. Tek. Dergi 2019, 30, 9029–9051. [Google Scholar] [CrossRef]
- Hussain, M.; Tayyab, M.; Zhang, J.; Shah, A.A.; Ullah, K.; Mehmood, U.; Al-Shaibah, B. GIS-Based Multi-Criteria Approach for Flood Vulnerability Assessment and Mapping in District Shangla: Khyber Pakhtunkhwa, Pakistan. Sustainability 2021, 13, 3126. [Google Scholar] [CrossRef]
- Ullah, K.; Zhang, J. GIS-based flood hazard mapping using relative frequency ratio method: A case study of panjkora river basin, eastern Hindu Kush, Pakistan. PLoS ONE 2020, 15, e0229153. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Chen, N.; Elbeltagi, A.; Islam, M.M.; Alam, M.; Pourghasemi, H.R.; Tao, W.; Zhang, J.; Shufeng, T.; Faiz, H.; et al. Application of stacking hybrid machine learning algorithms in delineating multi-type flooding in Bangladesh. J. Environ. Manag. 2021, 295, 113086. [Google Scholar] [CrossRef] [PubMed]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Ullah, K.; Wang, Y.; Fang, Z.; Wang, L.; Rahman, M. Multi-hazard susceptibility mapping based on Convolutional Neural Networks. Geosci. Front. 2022, 13, 101425. [Google Scholar] [CrossRef]
- Khosla, E.; Ramesh, D.; Sharma, R.P.; Nyakotey, S. RNNs-RT: Flood based prediction of human and animal deaths in Bihar using recurrent neural networks and regression techniques. Procedia Comput. Sci. 2018, 132, 486–497. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Shapiro, J.L. Does overfitting affect performance in estimation of distribution algorithms. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 433–434. [Google Scholar] [CrossRef]
- Abedi, R.; Costache, R.; Shafizadeh-Moghadam, H.; Pham, Q.B. Flash-flood susceptibility mapping based on XGBoost, random forest and boosted regression trees. Geocarto Int. 2021, 37, 5479–5496. [Google Scholar] [CrossRef]
- Aydin, H.E.; Iban, M.C. Predicting and analyzing flood susceptibility using boosting-based ensemble machine learning algorithms with SHapley Additive exPlanations. Nat. Hazards 2023, 116, 2957–2991. [Google Scholar] [CrossRef]
- Roelofs, R.; Shankar, V.; Recht, B.; Fridovich-Keil, S.; Hardt, M.; Miller, J.; Schmidt, L. A meta-analysis of overfitting in machine learning. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://dl.acm.org/doi/pdf/10.5555/3454287.3455110 (accessed on 29 June 2021).
- Ying, X. An overview of overfitting and its solutions. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1168, p. 22022. [Google Scholar]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early stopping and non-parametric regression: An optimal data-dependent stopping rule. J. Mach. Learn. Res. 2014, 15, 335–366. [Google Scholar]
- Zanotti, C.; Rotiroti, M.; Sterlacchini, S.; Cappellini, G.; Fumagalli, L.; Stefania, G.A.; Nannucci, M.S.; Leoni, B.; Bonomi, T. Choosing between linear and nonlinear models and avoiding overfitting for short and long term groundwater level forecasting in a linear system. J. Hydrol. 2019, 578, 124015. [Google Scholar] [CrossRef]
- Besler, E.; Wang, Y.C.; Chan, T.C.; Sahakian, A.V. Real-time monitoring radiofrequency ablation using tree-based ensemble learning models. Int. J. Hyperth. 2019, 36, 427–436. [Google Scholar] [CrossRef]
- Mutasa, S.; Sun, S.; Ha, R. Understanding artificial intelligence based radiology studies: What is overfitting? Clin. Imaging 2020, 65, 96–99. [Google Scholar] [CrossRef]
- AlThuwaynee, O.F.; Kim, S.-W.; Najemaden, M.A.; Aydda, A.; Balogun, A.-L.; Fayyadh, M.M.; Park, H.-J. Demystifying uncertainty in PM10 susceptibility mapping using variable drop-off in extreme-gradient boosting (XGB) and random forest (RF) algorithms. Environ. Sci. Pollut. Res. 2021, 28, 43544–43566. [Google Scholar] [CrossRef]
- Wilby, R.L.; Yu, D. Mapping Climate Change Impacts on Smallholder Agriculture in Yemen Using GIS Modeling Approaches; Final Technical Report on behalf of the International Fund for Agricultural Development; IFAD: Rome, Italy, 2013. [Google Scholar]
- Kruck, W.; Schäffer, U.; Thiele, J. Explanatory Notes on the Geological Map of the Republic of Yemen-Western Part-(Former Yemen Arab Republic). 1996. Available online: https://www.schweizerbart.de/publications/detail/isbn/9783510962594/Geologisches_Jahrbuch_Reihe_B_Heft (accessed on 27 June 2021).
- Weiss, C.; O′Neill, D.A.; Koch, R.; Gerlach, I. Petrological characterisation of ‘alabaster’from the Marib province in Yemen and its use as an ornamental stone in Sabaean culture. Arab. Archaeol. Epigr. 2009, 20, 54–63. [Google Scholar] [CrossRef]
- Bruggeman, H.Y. Agro-Climatic Resources of Yemen. Part 1. Agro-Climatic Inventory; FAO Project GCP/YEM/021/ NET, Field Document 11; AREA: Dhamar, Yemen, 1997. [Google Scholar]
- Al-Akad, S.; Akensous, Y.; Hakdaoui, M.; Al-Nahmi, F.; Mahyoub, S.; Khanbari, K.; Swadi, H. Mapping of Land-Cover Change Analysis in Ma’rib at Yemen Using Remote Sensing and GIS Techniques. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4212, 1–10. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction. Satellite Detected Waters in Marib Governorate of Yemen. 2020. Available online: https://www.preventionweb.net/publication/satellite-detected-waters-marib-governorate-yemen-15-august-2020 (accessed on 27 July 2021).
- Soliman, M.M.; El Tahan, A.H.M.H.; Taher, A.H.; Khadr, W.M.H. Hydrological analysis and flood mitigation at Wadi Hadramawt, Yemen. Arab. J. Geosci. 2015, 8, 10169–10180. [Google Scholar] [CrossRef]
- Al-Masawa, M.I.; Manab, N.A.; Omran, A. The effects of climate change risks on the mud architecture in Wadi Hadhramaut, Yemen. In The Impact of Climate Change on Our Life; Springer: Singapore, 2018; pp. 57–77. [Google Scholar] [CrossRef]
- El Tahan, A.H.M.H.; Elhanafy, H.E.M. Statistical analysis of morphometric and hydrologic parameters in arid regions, case study of Wadi Hadramaut. Arab. J. Geosci. 2016, 9, 88. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Kumar, L. The application of a Dempster–Shafer-based evidential belief function in flood susceptibility mapping and comparison with frequency ratio and logistic regression methods. Environ. Earth Sci. 2018, 77, 490. [Google Scholar] [CrossRef]
- Al-Aizari, A.R.; Al-Masnay, Y.A.; Aydda, A.; Zhang, J.; Ullah, K.; Islam, A.R.M.T.; Habib, T.; Kaku, D.U.; Nizeyimana, J.C.; Al-Shaibah, B.; et al. Assessment Analysis of Flood Susceptibility in Tropical Desert Area: A Case Study of Yemen. Remote Sens. 2022, 14, 4050. [Google Scholar] [CrossRef]
- Pradhan, B.; Tehrany, M.S.; Jebur, M.N. A new semiautomated detection mapping of flood extent from TerraSAR-X satellite image using rule-based classification and taguchi optimization techniques. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4331–4342. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Jones, S.; Shabani, F. Identifying the essential flood conditioning factors for flood prone area mapping using machine learning techniques. CATENA 2019, 175, 174–192. [Google Scholar] [CrossRef]
- Mudashiru, R.B.; Sabtu, N.; Abustan, I. Quantitative and semi-quantitative methods in flood hazard/susceptibility mapping: A review. Arab. J. Geosci. 2021, 14, 941. [Google Scholar] [CrossRef]
- Mohammadi, A.; Kamran, K.V.; Karimzadeh, S.; Shahabi, H.; Al-Ansari, N. Flood detection and susceptibility mapping using sentinel-1 time series, alternating decision trees, and bag-adtree models. Complexity 2020, 2020, 4271376. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Arora, A.; Arabameri, A.; Pandey, M.; Siddiqui, M.A.; Shukla, U.K.; Bui, D.T.; Mishra, V.N.; Bhardwaj, A. Optimization of state-of-the-art fuzzy-metaheuristic ANFIS-based machine learning models for flood susceptibility prediction mapping in the Middle Ganga Plain, India. Sci. Total Environ. 2021, 750, 141565. [Google Scholar] [CrossRef] [PubMed]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood detection and susceptibility mapping using Sentinel-1 remote sensing data and a machine learning approach: Hybrid intelligence of bagging ensemble based on K-Nearest Neighbor classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R. Identification of critical flood prone areas in data-scarce and ungauged regions: A comparison of three data mining models. Water Resour. Manag. 2017, 31, 1473–1487. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Pal, S.C.; Janizadeh, S.; Santosh, M.; Roy, P.; Chowdhuri, I.; Saha, A. Impact of Climate Change on Future Flood Susceptibility: An Evaluation Based on Deep Learning Algorithms and GCM Model. Water Resour. Manag. 2021, 35, 4251–4274. [Google Scholar] [CrossRef]
- Roy, P.; Pal, S.C.; Chakrabortty, R.; Chowdhuri, I.; Malik, S.; Das, B. Threats of climate and land use change on future flood susceptibility. J. Clean. Prod. 2020, 272, 122757. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Chen, W.; Roy, J.; Pradhan, B.; Bui, D.T. Flash flood susceptibility modelling using functional tree and hybrid ensemble techniques. J. Hydrol. 2020, 587, 125007. [Google Scholar] [CrossRef]
- Almeshreki, D.; Mohamed, H.A. Renewable Natural Resources Research Center (RNRRC) in the Agricultural Research & Extension Authority (AREA), Dhamar, Yemen. Geocarto Int. 2006. [Google Scholar]
- Rahmati, O.; Pourghasemi, H.R.; Zeinivand, H. Flood susceptibility mapping using frequency ratio and weights-of-evidence models in the Golastan Province, Iran. Geocarto Int. 2016, 31, 42–70. [Google Scholar] [CrossRef]
- Ha, H.; Luu, C.; Bui, Q.D.; Pham, D.-H.; Hoang, T.; Nguyen, V.-P.; Vu, M.T.; Pham, B.T. Flash flood susceptibility prediction mapping for a road network using hybrid machine learning models. Nat. Hazards 2021, 109, 1247–1270. [Google Scholar] [CrossRef]
- Pham, B.T.; Phong, T.V.; Nguyen, H.D.; Qi, C.; Al-Ansari, N.; Amini, A.; Ho, L.S.; Tuyen, T.T.; Yen, H.P.H.; Ly, H.-B. A comparative study of kernel logistic regression, radial basis function classifier, multinomial naïve bayes, and logistic model tree for flash flood susceptibility mapping. Water 2020, 12, 239. [Google Scholar] [CrossRef]
- Tsagkrasoulis, D.; Montana, G. Random forest regression for manifold-valued responses. Pattern Recognit. Lett. 2018, 101, 6–13. [Google Scholar] [CrossRef]
- Breiman, L.; Last, M.; Rice, J. Random forests: Finding quasars. In Statistical Challenges in Astronomy; Springer: New York, NY, USA, 2003; pp. 243–254. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. Mapping flood susceptibility in an arid region of southern Iraq using ensemble machine learning classifiers: A comparative study. Arab. J. Geosci. 2018, 11, 218. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.-T. Rainfall-induced shallow landslide susceptibility mapping at two adjacent catchments using advanced machine learning algorithms. ISPRS Int. J. Geo-Inf. 2020, 9, 569. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H. Xgboost: Extreme gradient boosting. R Packag. Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Hariri-Ardebili, M.A.; Barak, S. A series of forecasting models for seismic evaluation of dams based on ground motion meta-features. Eng. Struct. 2020, 203, 109657. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the spatial prediction of soil organic carbon content in two contrasting climatic regions by stacking machine learning models and rescanning covariate space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. Hands-on Machine Learning with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; ISBN 0367816377. [Google Scholar]
- Torlay, L.; Perrone-Bertolotti, M.; Thomas, E.; Baciu, M. Machine learning–XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017, 4, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Probst, P.; Boulesteix, A.-L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Mangukiya, N.K.; Sharma, A. Flood risk mapping for the lower Narmada basin in India: A machine learning and IoT-based framework. Nat. Hazards 2022, 113, 1285–1304. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef] [PubMed]
- Remondo, J.; González, A.; De Terán, J.R.D.; Cendrero, A.; Fabbri, A.; Chung, C.-J.F. Validation of landslide susceptibility maps; examples and applications from a case study in Northern Spain. Nat. Hazards 2003, 30, 437–449. [Google Scholar] [CrossRef]
- Avand, M.; Kuriqi, A.; Khazaei, M.; Ghorbanzadeh, O. DEM resolution effects on machine learning performance for flood probability mapping. J. Hydro-Environ. Res. 2022, 40, 1–16. [Google Scholar] [CrossRef]
- Yariyan, P.; Janizadeh, S.; Van Phong, T.; Nguyen, H.D.; Costache, R.; Van Le, H.; Pham, B.T.; Pradhan, B.; Tiefenbacher, J.P. Improvement of Best First Decision Trees Using Bagging and Dagging Ensembles for Flood Probability Mapping. Water Resour. Manag. 2020, 34, 3037–3053. [Google Scholar] [CrossRef]
- Baig, M.A.; Xiong, D.; Rahman, M.; Islam, M.M.; Elbeltagi, A.; Yigez, B.; Rai, D.K.; Tayab, M.; Dewan, A. How do multiple kernel functions in machine learning algorithms improve precision in flood probability mapping? Nat. Hazards 2022, 113, 1543–1562. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility analysis and its verification using a novel ensemble support vector machine and frequency ratio method. Stoch. Environ. Res. Risk Assess. 2015, 29, 1149–1165. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P.; Rubin, V.; Verbeek, H.M.W.; van Dongen, B.F.; Kindler, E.; Günther, C.W. Process mining: A two-step approach to balance between underfitting and overfitting. Softw. Syst. Model. 2010, 9, 87–111. [Google Scholar] [CrossRef]
- Erzin, Y.; Cetin, T. The prediction of the critical factor of safety of homogeneous finite slopes using neural networks and multiple regressions. Comput. Geosci. 2013, 51, 305–313. [Google Scholar] [CrossRef]
- Hasanuzzaman, M.; Islam, A.; Bera, B.; Shit, P.K. A comparison of performance measures of three machine learning algorithms for flood susceptibility mapping of river Silabati (tropical river, India). Phys. Chem. Earth Parts A/B/C 2022, 127, 103198. [Google Scholar] [CrossRef]
- Antzoulatos, G.; Kouloglou, I.-O.; Bakratsas, M.; Moumtzidou, A.; Gialampoukidis, I.; Karakostas, A.; Lombardo, F.; Fiorin, R.; Norbiato, D.; Ferri, M. Flood Hazard and Risk Mapping by Applying an Explainable Machine Learning Framework Using Satellite Imagery and GIS Data. Sustainability 2022, 14, 3251. [Google Scholar] [CrossRef]
- Arabameri, A.; Seyed Danesh, A.; Santosh, M.; Cerda, A.; Chandra Pal, S.; Ghorbanzadeh, O.; Roy, P.; Chowdhuri, I. Flood susceptibility mapping using meta-heuristic algorithms. Geomat. Nat. Hazards Risk 2022, 13, 949–974. [Google Scholar] [CrossRef]
- Sachdeva, S.; Kumar, B. Flood susceptibility mapping using extremely randomized trees for Assam 2020 floods. Ecol. Inform. 2022, 67, 101498. [Google Scholar] [CrossRef]
- Saqalli, M.; Hamrita, A.; Maestripieri, N.; Boussetta, A.; Rejeb, H.; Mata Olmo, R.; Kassouk, Z.; Belem, M.; Saenz, M.; Mouri, H. “Not seen, not considered”: Mapping local perception of environmental risks in the Plain of Mornag and Jebel Ressass (Tunisia). Euro-Mediterr. J. Environ. Integr. 2020, 5, 30. [Google Scholar] [CrossRef]
- Ghosh, S.; Saha, S.; Bera, B. Flood susceptibility zonation using advanced ensemble machine learning models within Himalayan foreland basin. Nat. Hazards Res. 2022, 2, 363–374. [Google Scholar] [CrossRef]



| No | Data Type | Source | Period | Mapping Output | Justification |
|---|---|---|---|---|---|
| 1 | ALOSPALSAR (DEM/12.5 m) | Alaska satellite facility (ASF) https://search.asf.alaska.edu (accessed on 1 April 2021) | 2021 | Elevation, Slope, Aspect, Curvature, SPI, Drainage Density, and TWI | Tehrany et al. [49] demonstrate the importance of topographic data in flood susceptibility, supporting the inclusion of these features in our study. |
| 2 | Sentinel 2 (10 m) | https://scihub.copernicus.eu (accessed on 6 April 2021) | 2021 | NDVI map | The significance of NDVI in flood susceptibility, as high-lighted by Lin and Wu [9], validates its use in our analysis. |
| 3 | Landuse/Landcover (10 m) | https://livingatlas.arcgis.com/landcover (accessed on 26 June 2021) | 2021 | LU/LC map | Rahman et al. [10] emphasize the importance of land use/cover in assessing flood susceptibility, justifying its inclusion in our methodology. |
| 4 | Rainfall data | https://power.larc.nasa.gov/data-access-viewer (accessed on 23 June 2021) | 2010–2019 | Rainfall map | We incorporated rainfall data as Pham et al. [63] underline its role in flash flood susceptibility modeling. |
| 5 | Soil type Data | (RNRRC.) in (AREA), Dhamar, Yemen (accessed on 19 August 2021) | 2006 | Soil type | Almeshreki et al. [60] discuss the impact of soil types on environmental conditions, which supports the inclusion of this factor in our flood study. |
| 6 | Distance to road | https://www.diva-gis.org/ (accessed on 25 June 2021) | 2021 | The data were obtained from the road networks inside the district and transformed into a raster format with a cell size of 12.5 m × 12.5 m. These data represent the distance to the nearest road. | The relevance of road networks in flood dynamics, as discussed in Norallahi and Kaboli [13] backs the inclusion of this factor in our model. |
| RF | XGB | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mtry | ntree | repeats | search | eta | max depth | gamma | colsample bytree | min child weight | subsample | nrounds |
| 7 | 500 | 3 | Grid | 0.3 | 6 | 0.01 | 0.75 | 0 | 1 | 200 |
| XGB | ||||||||
|---|---|---|---|---|---|---|---|---|
| Study Area | Training Dataset | Testing Dataset | ||||||
| R2 | RMSE | MAE | MSE | R2 | RMSE | MAE | MSE | |
| Shibam | 1.00 | 0.06154 | 0.00433 | 0.00379 | 1.00 | 0.06874 | 0.00655 | 0.00473 |
| Marib | 1.00 | 0.07167 | 0.00782 | 0.00514 | 1.00 | 0.08010 | 0.00641 | 0.00641 |
| RF | ||||||||
| Shibam | 1.00 | 0.00760 | 0.00054 | 0.00006 | 1.00 | 0.02212 | 0.00211 | 0.00049 |
| Marib | 1.00 | 0.00829 | 0.00091 | 0.00007 | 1.00 | 0.07846 | 0.00628 | 0.00616 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Aizari, A.R.; Alzahrani, H.; AlThuwaynee, O.F.; Al-Masnay, Y.A.; Ullah, K.; Park, H.-J.; Al-Areeq, N.M.; Rahman, M.; Hazaea, B.Y.; Liu, X. Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and eXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen. Remote Sens. 2024, 16, 336. https://doi.org/10.3390/rs16020336
Al-Aizari AR, Alzahrani H, AlThuwaynee OF, Al-Masnay YA, Ullah K, Park H-J, Al-Areeq NM, Rahman M, Hazaea BY, Liu X. Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and eXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen. Remote Sensing. 2024; 16(2):336. https://doi.org/10.3390/rs16020336
Chicago/Turabian StyleAl-Aizari, Ali R., Hassan Alzahrani, Omar F. AlThuwaynee, Yousef A. Al-Masnay, Kashif Ullah, Hyuck-Jin Park, Nabil M. Al-Areeq, Mahfuzur Rahman, Bashar Y. Hazaea, and Xingpeng Liu. 2024. "Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and eXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen" Remote Sensing 16, no. 2: 336. https://doi.org/10.3390/rs16020336
APA StyleAl-Aizari, A. R., Alzahrani, H., AlThuwaynee, O. F., Al-Masnay, Y. A., Ullah, K., Park, H.-J., Al-Areeq, N. M., Rahman, M., Hazaea, B. Y., & Liu, X. (2024). Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and eXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen. Remote Sensing, 16(2), 336. https://doi.org/10.3390/rs16020336