Joint Analysis and Morphological Characterization of HFSWR Echo Properties during Severe Typhoon Muifa
Abstract
1. Introduction
- This manuscript delineates the identification of joint gravity wave signatures observed in the HFSWR ocean and ionosphere echoes. It also compares the variations in these signatures before and after the typhoon enters the detection range of HFSWR, using time–frequency analysis and 2D localized methods.
- Furthermore, the evolution of the gravity wave signatures of the HFSWR echoes is quantitatively characterized by reconstructing the chaotic attractor.
- Then, this study proposes a chaotic characterization scheme for HFSWR joint gravity wave signatures based on the largest Lyapunov exponents.
- The experimental results corroborate the validity and application extension of the novel proposed gravity wave pattern characterization scheme.
2. Introduction to Typhoon Periods and Information
3. Experimental Analysis
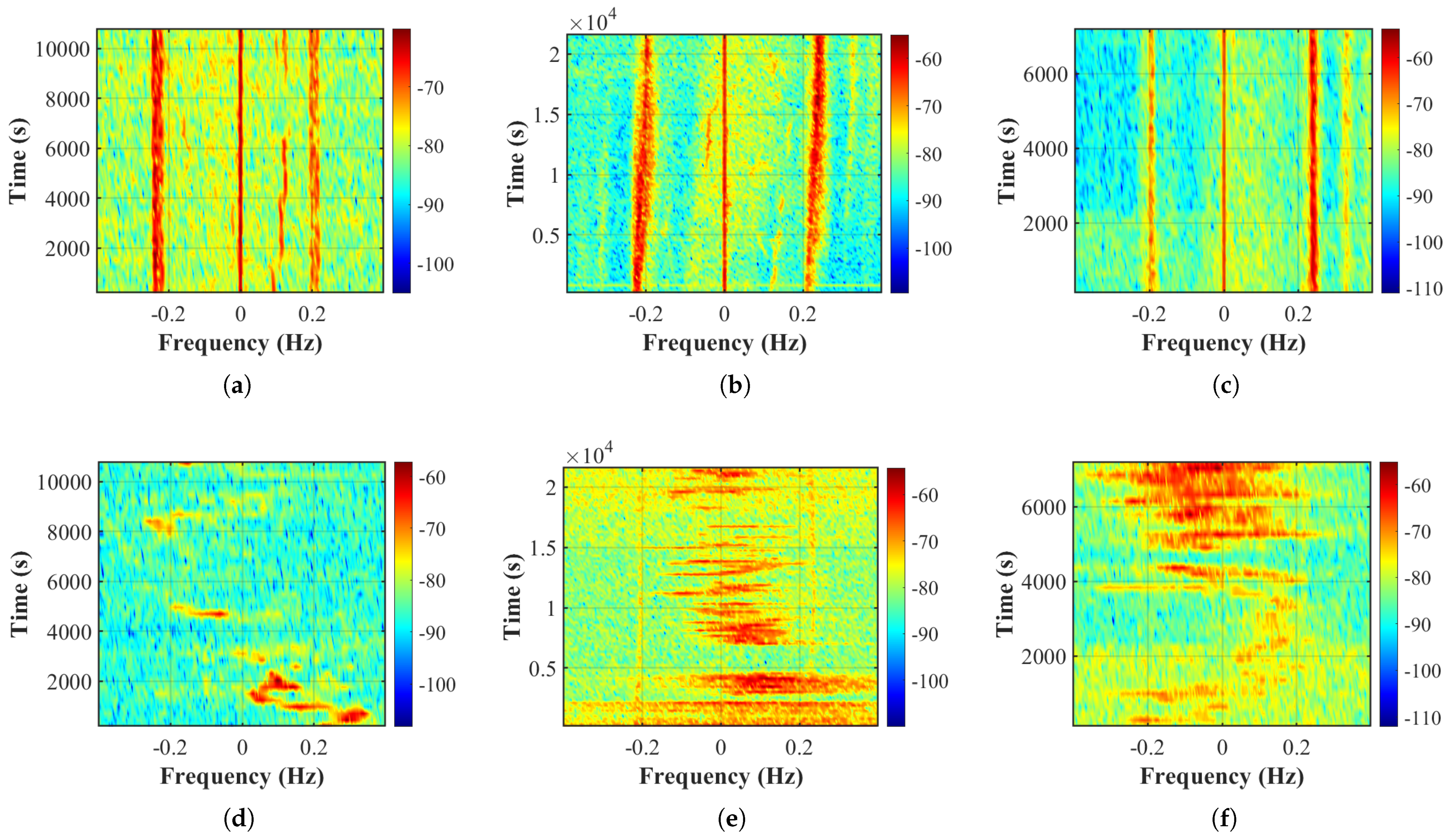
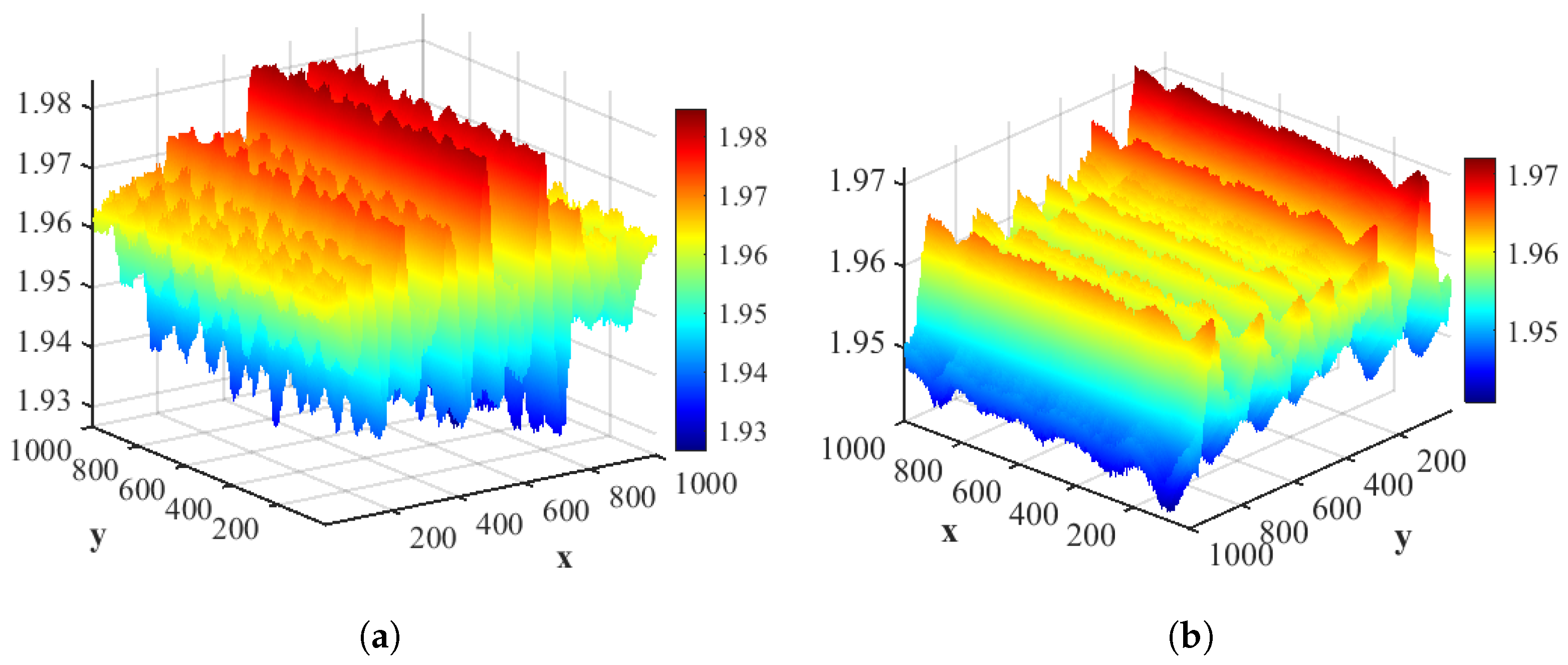
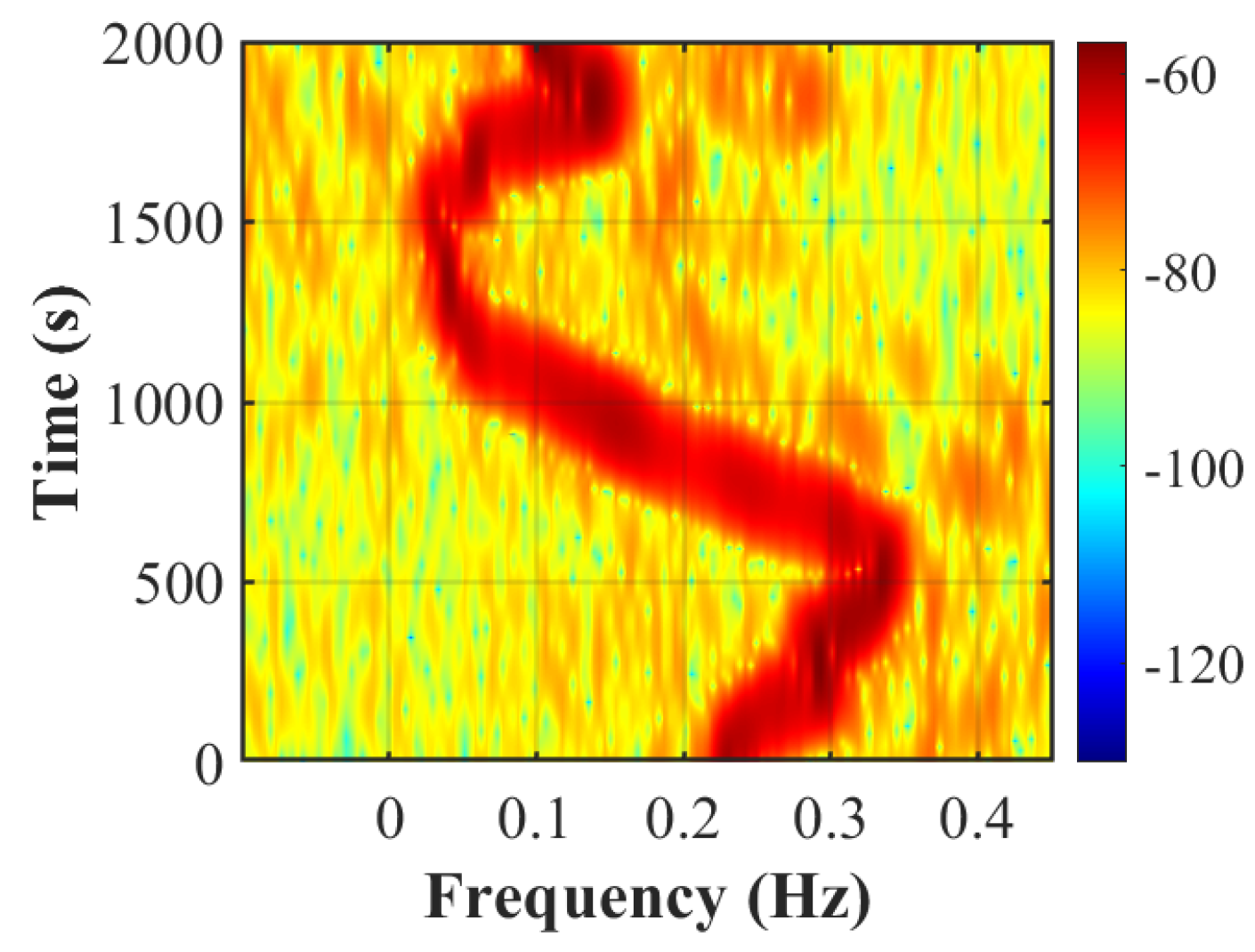
3.1. Analysis of HFSWR Ocean and Ionosphere Echoes
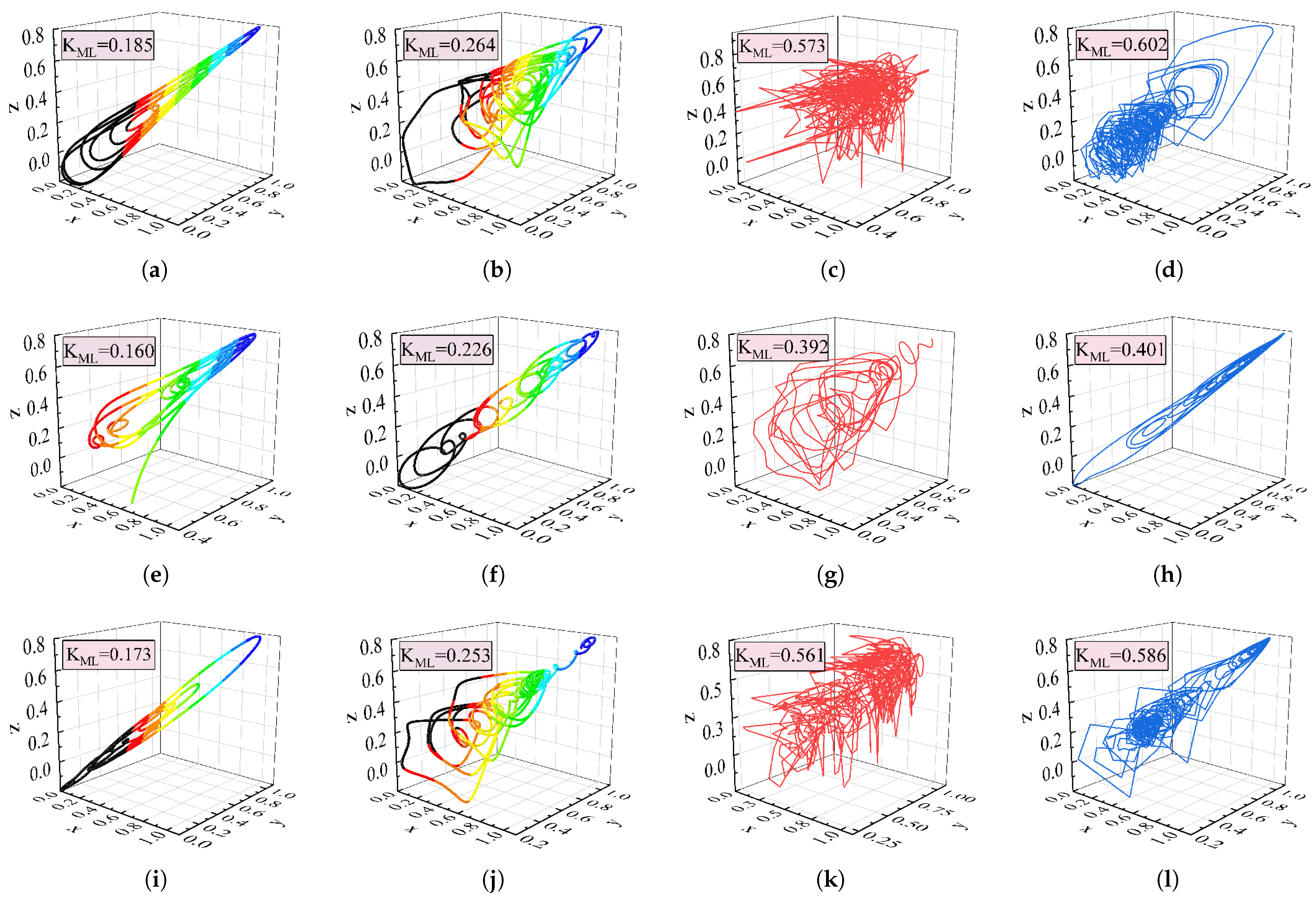
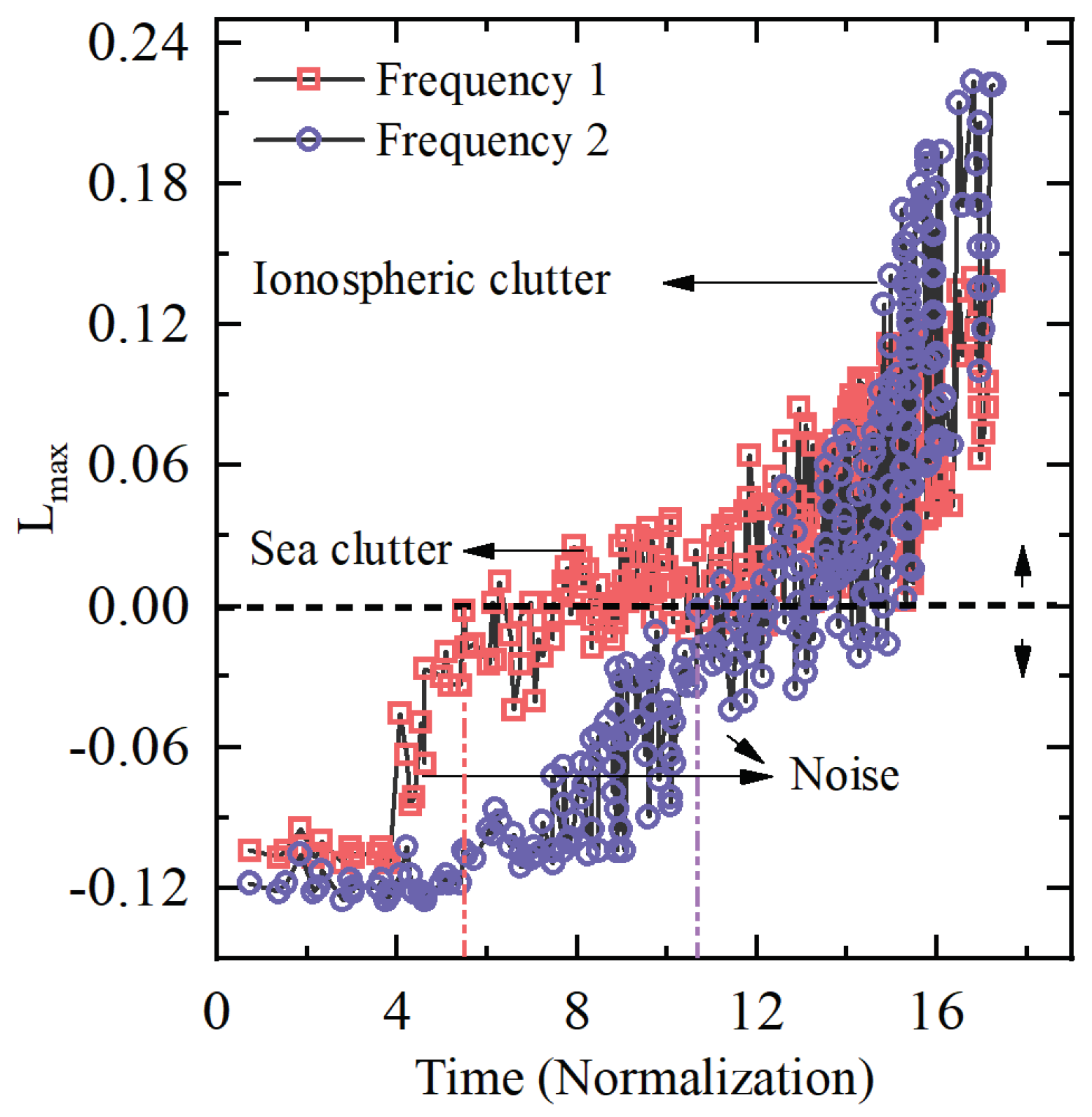
3.2. Chaotic Characterization of HFSWR Ocean and Ionosphere Echoes
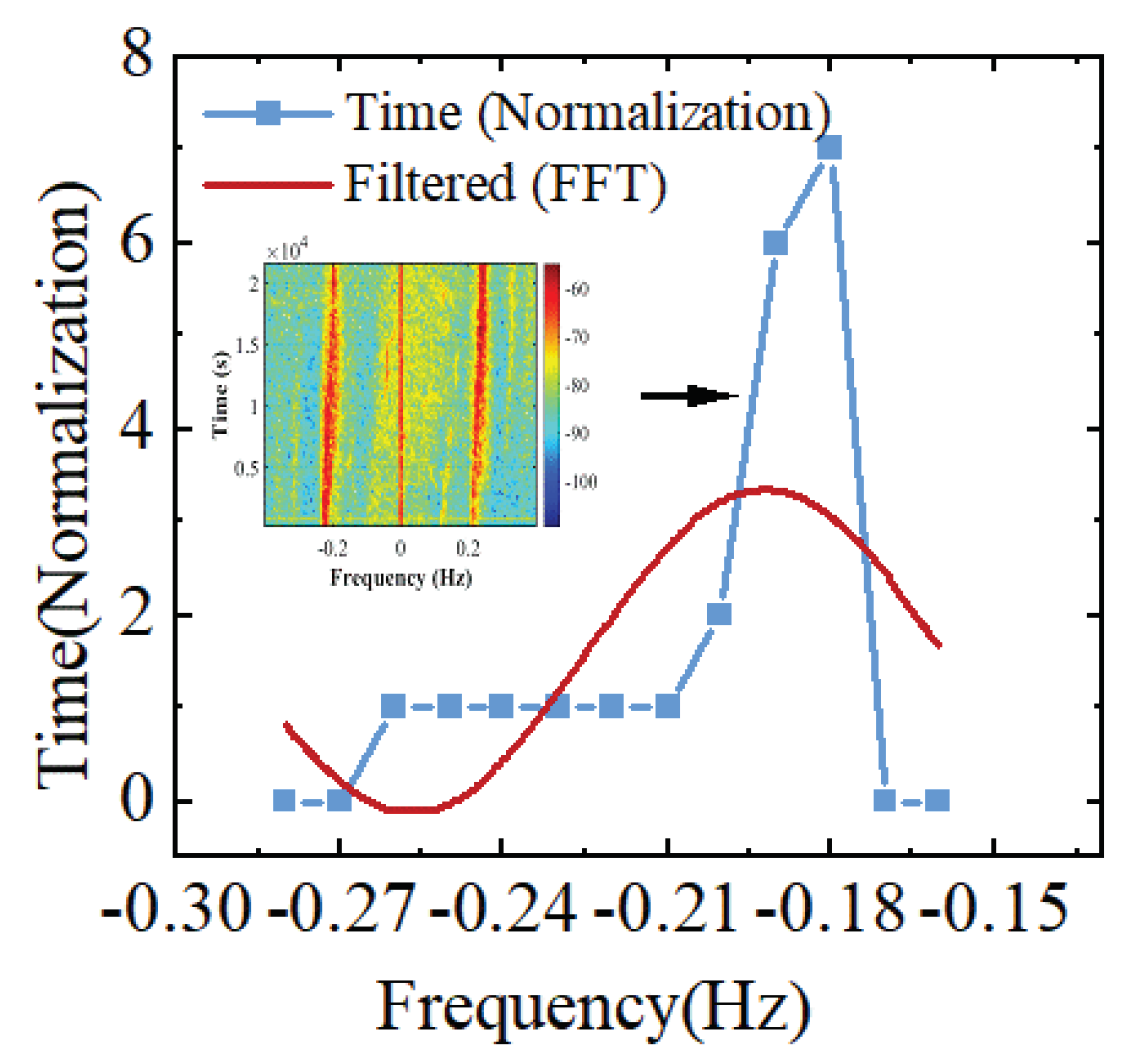
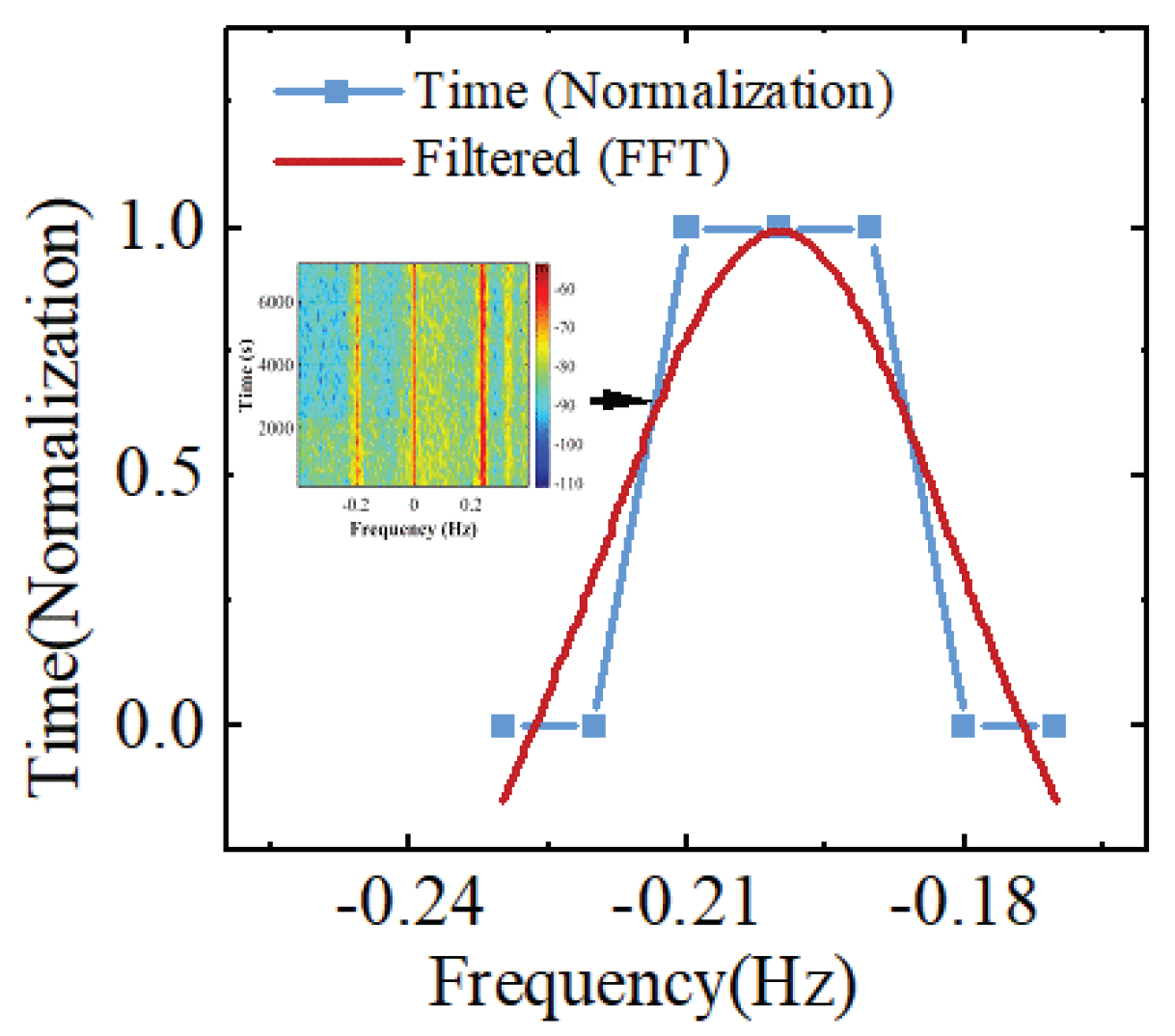
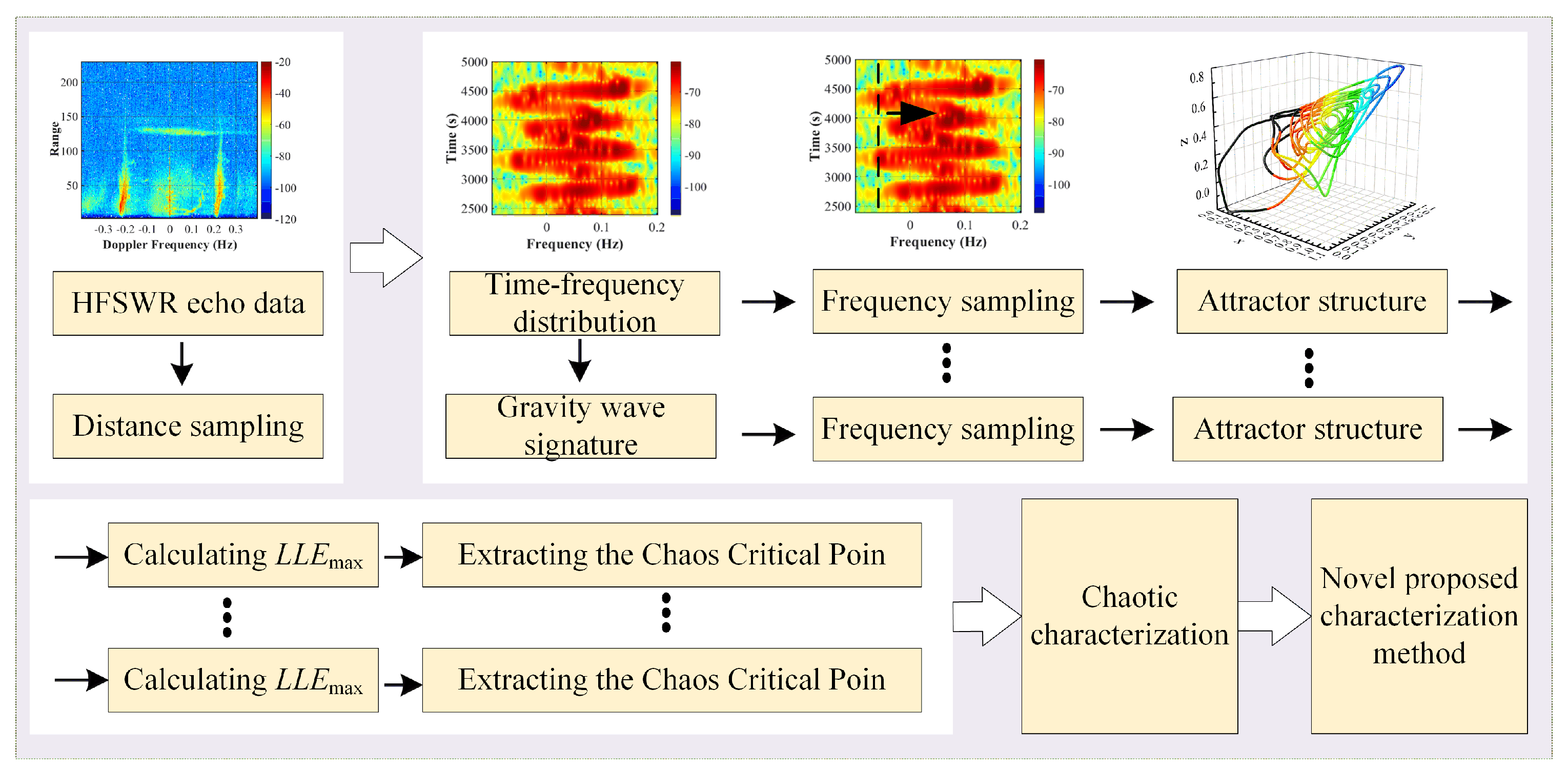
- Extraction of long-term domain signals: Perform time–frequency preprocessing to obtain the time–frequency distribution of ocean and ionospheric echoes, and then perform frequency sampling to obtain the long-term domain signals of ocean and ionospheric echoes at different frequencies.
- Analysis of chaotic dynamic behavior: Extract continuous short-time domain signals from the long-term domain signals and calculate their maximum Lyapunov exponent. Obtain the time series of the maximum Lyapunov exponent in the long-term domain signals at different sampling frequencies for the analysis of the chaotic dynamic behavior of ocean and ionospheric echoes.
- Characterization of chaotic dynamics: Furthermore, based on the time series of the maximum Lyapunov exponent in the long-term domain signals, extract the chaotic critical points of HFSWR ocean and ionospheric echoes, i.e., the frequencies and sampling moments of HFSWR echoes when chaos occurs, and obtain the two-dimensional chaotic characterization of chaotic critical points at different frequencies.
3.2.1. Analysis of Chaotic Dynamic Behavior
3.2.2. Characterization of Chaotic Dynamics
3.3. Novel Proposed Characterization Method of HFSWR Ocean and Ionosphere Echoes with Gravity Wave Features during Severe Typhoon Muifa
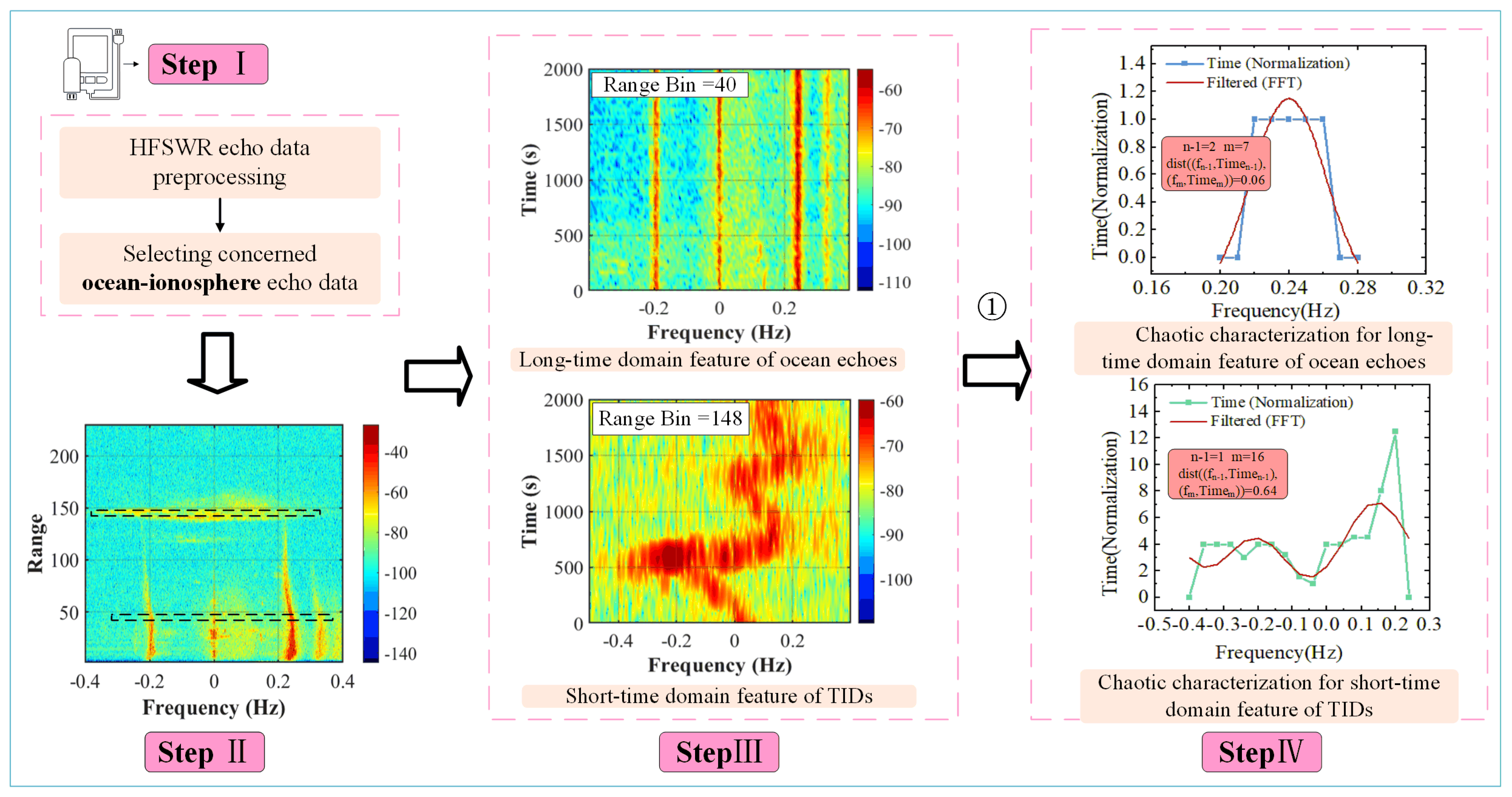
- 1.
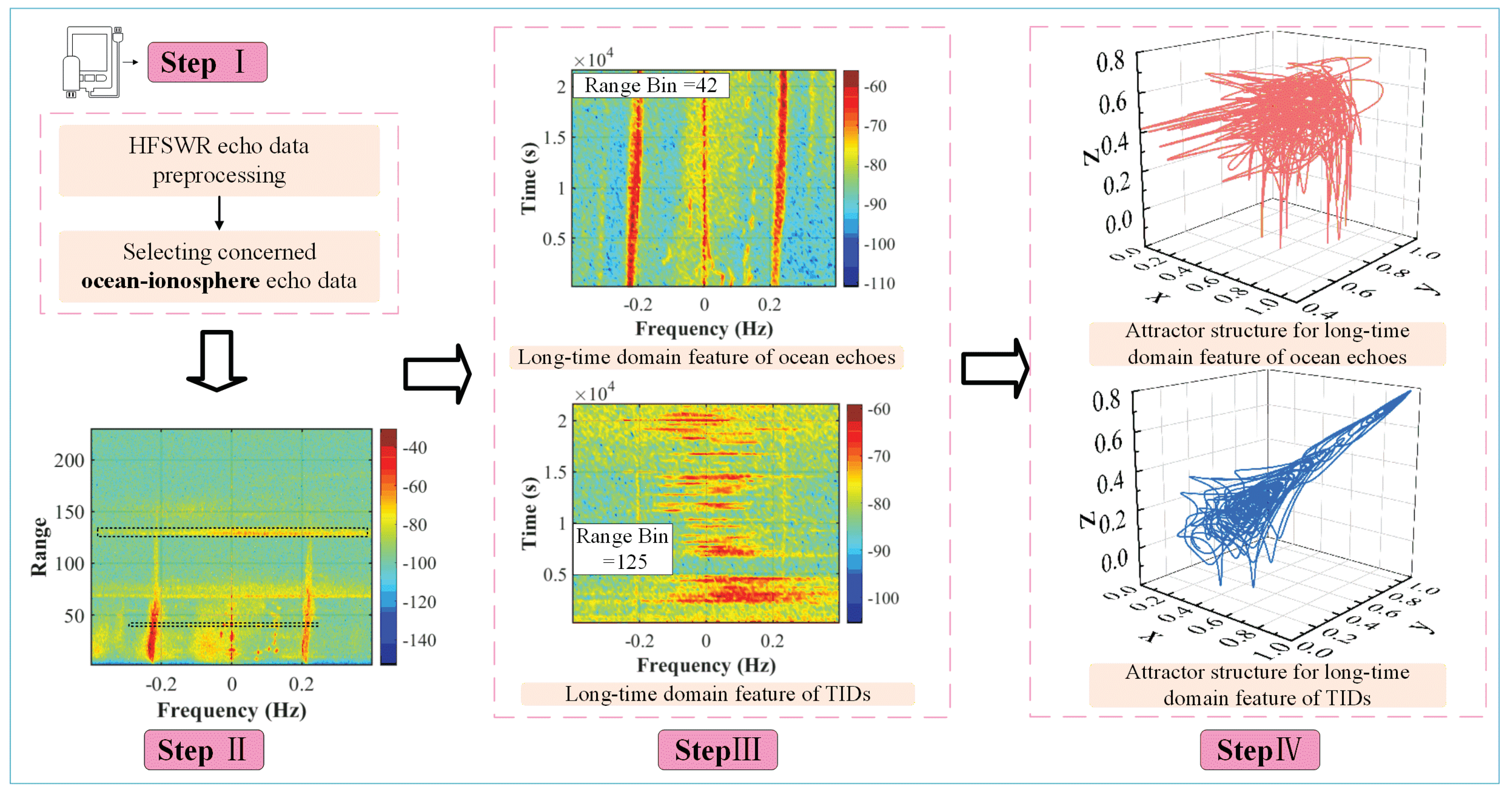
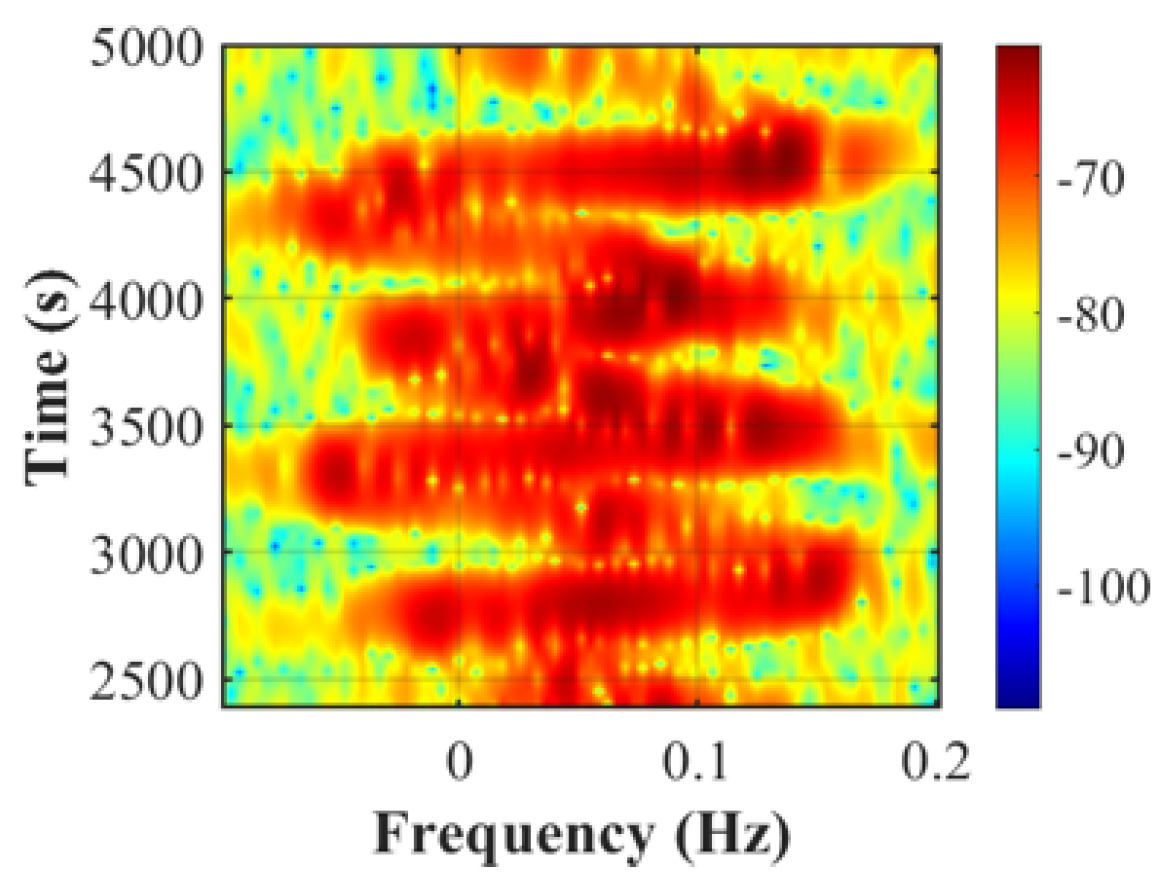
- The long-time domain feature of ocean echoes (a clear, slightly S-shaped shift in frequency, termed an HFSWR ocean–ionospheric echo with gravity wave signature). Sampling points at the given frequencies need to be significantly Doppler-shifted to match the features of this class. This type of feature occurs when the typhoon is in the detection range of the HFSWR, as shown in Figure 16.
- 2.
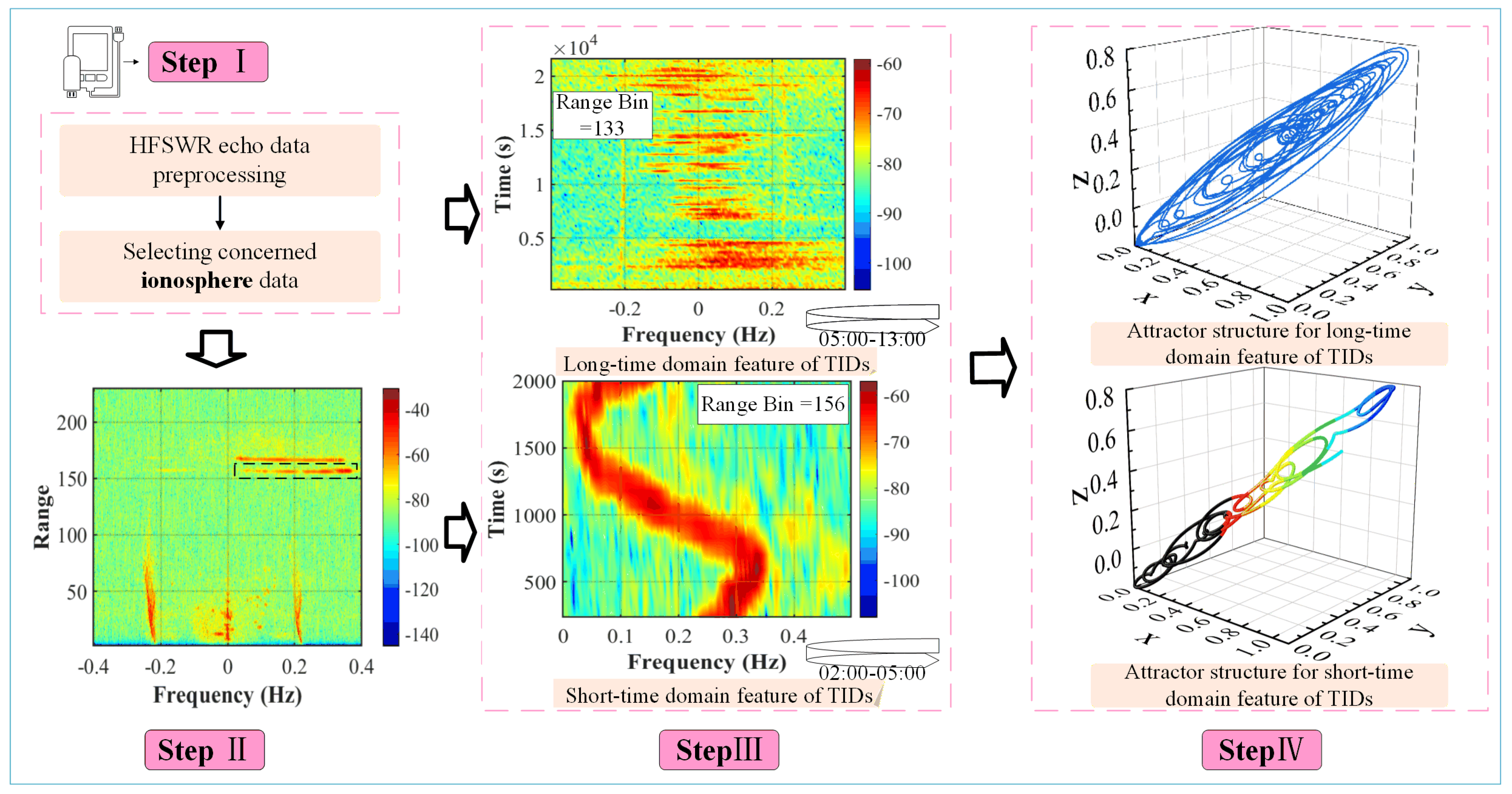
- Short-time domain feature of TIDs. The short-time domain of TIDs is characterized by a quasi-periodic sinusoidal “S” shape, as shown in Figure 12. The short-time domain feature of TIDs appears before the typhoon enters the detection range of HFSWR, the related research on the short-time domain feature of TIDs may have a positive impact on HFSWR typhoon detection and early warning.
- 3.
- Long-time domain feature of TIDs. The long-time domain features of TIDs are in the form of multilevel continuous TIDs, consisting of multiple short-time domain features of TIDs, which appear when the typhoon is within the detection range of the HFSWR. The specific pattern is shown in Figure 17.
- 1.
- If there exists dist d1, then it is the long-time domain feature of the TIDs at that range bin.
- 2.
- If there exists dist d2, then it is the short-time domain feature of the TIDs at that range bin.
- 3.
- If there exists dist , then it is the long-time domain feature of the sea echoes at that range bin.
4. Conclusions
- 1.
- Further refining the characterization methods for HFSWR oceanic and ionospheric echoes during typhoon events.
- 2.
- Developing a two-dimensional model for HFSWR oceanic and ionospheric echoes based on the chaotic characteristics observed during typhoon events.
- 3.
- Additionally, establishing a joint cancellation model for HFSWR oceanic and ionospheric echoes using control methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HFSWR | High-frequency surface wave radar |
| STFT | Short-time Fourier transform |
| TIDs | Traveling ionospheric disturbances |
| Largest Lyapunov exponents | |
| RD | Range-Doppler |
References
- Nemchinov, I.V.; Zetzer, Y.I.; Kovalev, A.T.; Shuvalov, V.V. Perturbations in the ionosphere and magnetosphere during the fall of cosmic bodies onto land or ocean. Dokl. Earth Sci. 2006, 409, 736–738. [Google Scholar] [CrossRef]
- Lee, S.M. A Far Field Solution of the Slowly Varying Drift Force on an Offshore Structure in Bichromatic Waves—Two Dimensional Problems. J. Ocean. Eng. Technol. 2008, 2, 7–12. [Google Scholar]
- Isaev, N.V.; Chmyrev, V.M.; Serebryakova, O.N.; Yushchenko, A.K. Disturbance of the Electric Field in the Ionosphere by Sea Storms and Typhoons. Cosm. Res. 2002, 40, 547–553. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Isaev, N.V.; Yaschenko, A.K.; Chmyrev, V.M.; Hayakawa, M. Strong DC electric field formation in the low latitude ionosphere over typhoons. J. Atmos. Sol.-Terr. Phys. 2002, 67, 1269–1279. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1424–1427. [Google Scholar] [CrossRef]
- Xiao, G.; Hao, Y.; Zhang, D.; Xiao, Z. A case study on whole response processes of the ionosphere to typhoons. Chin. J. Geophys. 2006, 49, 623–628. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, D.; Xiao, Z. Study on the detectability of typhoon-generated acoustic-gravity waves. Chin. J. Space Sci. 2007, 27, 35–40. [Google Scholar] [CrossRef]
- Yang, X.G. Research on Ionospheric Echo Mechanism and Application of High-Frequency Surface Wave Radar. Doctoral Dissertation, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Collinson, G.; Fadden, J.M.; Mitchell, D.; Grebowsky, J.; Benna, M.; Espley, J.; Jakosky, B. Traveling Ionospheric Disturbances at Mars. Geophys. Res. Lett. 2019, 46, 4554–4563. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, H.; Tian, Y.; Huang, W.; Shen, W. Improving Ship Detection in Clutter-Edge and Multi-Target Scenarios for High-Frequency Radar. Remote Sens. 2021, 13, 4305. [Google Scholar] [CrossRef]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P.; Hao, X. A Vessel Azimuth and Course Joint Re-Estimation Method for Compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1041–1051. [Google Scholar] [CrossRef]
- Sun, W.; Li, X.; Pang, Z.; Ji, Y.; Dai, Y.; Huang, W. Track-to-Track Association Based on Maximum Likelihood Estimation for T/R-R Composite Compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Zhao, C.; Deng, M.; Chen, Z.; Ding, F.; Huang, W. Ocean Wave Parameters and Nondirectional Spectrum Measurements Using Multifrequency HF Radar. IEEE Trans. Geosci. Remote Sens. 2022, 13, 1–13. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Zhao, C.; Li, J.; Huang, W.; Gill, E.W. Observation and Intercomparison of Wave Motion and Wave Measurement Using Shore-Based Coherent Microwave Radar and HF Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7594–7605. [Google Scholar] [CrossRef]
- Huang, W.; Gill, E.; Wu, X.; Li, L. Measurement of Sea Surface Wind Direction Using Bistatic High-Frequency Radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4117–4122. [Google Scholar] [CrossRef]
- Huang, W.; Carrasco, R.; Shen, C.; Gill, E.W.; Horstmann, J. Surface Current Measurements Using X-Band Marine Radar with Vertical Polarization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2988–2997. [Google Scholar] [CrossRef]
- Walsh, J.; Chen, S.; Gill, E.; Huang, W. High frequency radar clutter power for mixed ionosphere-ocean propagation. In Proceedings of the 2014 16th International Symposium on Antenna Technology and Applied Electromagnetics, Victoria, BC, Canada, 13–16 July 2014. [Google Scholar]
- Walsh, J.; Gill, E.W.; Huang, W.; Chen, S. On the Development of a High-Frequency Radar Cross Section Model for Mixed Path Ionosphere-Ocean Propagation. IEEE Trans. Antennas Propag. 2015, 63, 2655–2664. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Gill, E.W. First-order bistatic high-frequenc y radar power for mixed-path ionosphere-ocean propagation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1940–1944. [Google Scholar] [CrossRef]
- Walsh, J.; Huang, W.; Gill, E. The second-order high frequency radar ocean surface cross section for an antenna on a floating platform. IEEE Trans. Antennas Propag. 2012, 60, 4804–4813. [Google Scholar] [CrossRef]
- Chen, S.; Gill, E.W.; Huang, W. A High-Frequency Surface Wave Radar Ionospheric Clutter Model for Mixed-Path Propagation With the Second-Order Sea Scattering. IEEE Trans. Antennas Propag. 2016, 64, 5373–5381. [Google Scholar] [CrossRef]
- Li, Z.; Jia, C.; Huang, D. Research on characteristics of ionospheric echo based on ocean. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xian, China, 3–5 October 2016. [Google Scholar]
- Chung, Y.J.; Chen, H.C.; Chen, Y.R.; Chiao Tsai, S.; Yang, Y.J.; Chuang, L.Z.H. Clutter Analysis of the Range-Doppler Spectra under the Influence of Typhoon. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019. [Google Scholar]
- Zhou, H.; Wen, B.; Wu, S. Ionosphere Probing with a high frequency surface wave radar. Prog. Electromagn. Res. C 2011, 20, 203–214. [Google Scholar] [CrossRef]
- Typhoon Naming List. Available online: https://baike.baidu.com/reference/61965809/249aq-yVKPZIddilmkCD3P$_$fWj8GAY6FZUFdKrkJkmLsHuDDalxhHM7t8UIte5wFNCjIruwTEXknt7tMrOzq1W179oH6tJ$\protect\discretionary{\char\hyphenchar\font}{}{}$eNm16tamB4hw9n2$_$fXHo (accessed on 27 December 2023).
- Typhoon Ocean. Available online: https://baike.baidu.com/reference/61965809/19f7yHPMec-gZ2x0OXjnzUwNVNIL5cbK3h0PX7aKXRAg3lMd7qK9v5H-ub$_$bkRHYnctec28gJXMNvOWPrHzHe$_$b-R5pBHvTPzmt5N209Q (accessed on 27 December 2023).
- Samden! Typhoon “Muifa” Has Made Landfall in Qingdao as the Latest Typhoon in Shandong. Available online: https://baike.baidu.com/reference/61965809/5ac9STppICJsUy-27jC8xFNSuSx1NtHumm408RlZaA0YPU-igb6vKxQnaKU8b0yT785cOZlAUXPaNzup$_$COvxcwqwIwSXgkaBholUMduNWqOjgvTux5NMGSDqY-PNL9oUtm (accessed on 27 December 2023).
- Pilipovic, S.; Prangoski, B. On the Characterizations of Wave Front Sets in Terms of the Short-Time Fourier Transform. Math. Notes 1019, 105, 153–157. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Farmer, J.D.; Packard, N.H.; Shaw, R.S. Chaos. Sci. Am. 1986, 254, 46–57. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Am. Phys. Soc. 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Schouten, J.C.; Takens, F.; Bleek, C. Maximum-likelihood estimation of the entropy of an attractor. Phys. Rev. E 1994, 49, 126–129. [Google Scholar] [CrossRef]
- Urzagasti, D.; Laroze, D.; Pleiner, H. Two-dimensional localized chaotic patterns in parametrically driven systems. Phys. Rev. E 2017, 95, 052216. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpian, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A Math. Gen. 1996, 30, 1–26. [Google Scholar] [CrossRef]
- Cao, S.; Li, H.; Zhang, K.; Yang, C.; Sun, F.; Wang, Z. An improved chaotic recognition method for weak signal frequency and its application to fault diagnosis of planetary gearboxes. Meas. Sci. Technol. 2016, 33, 105113. [Google Scholar] [CrossRef]

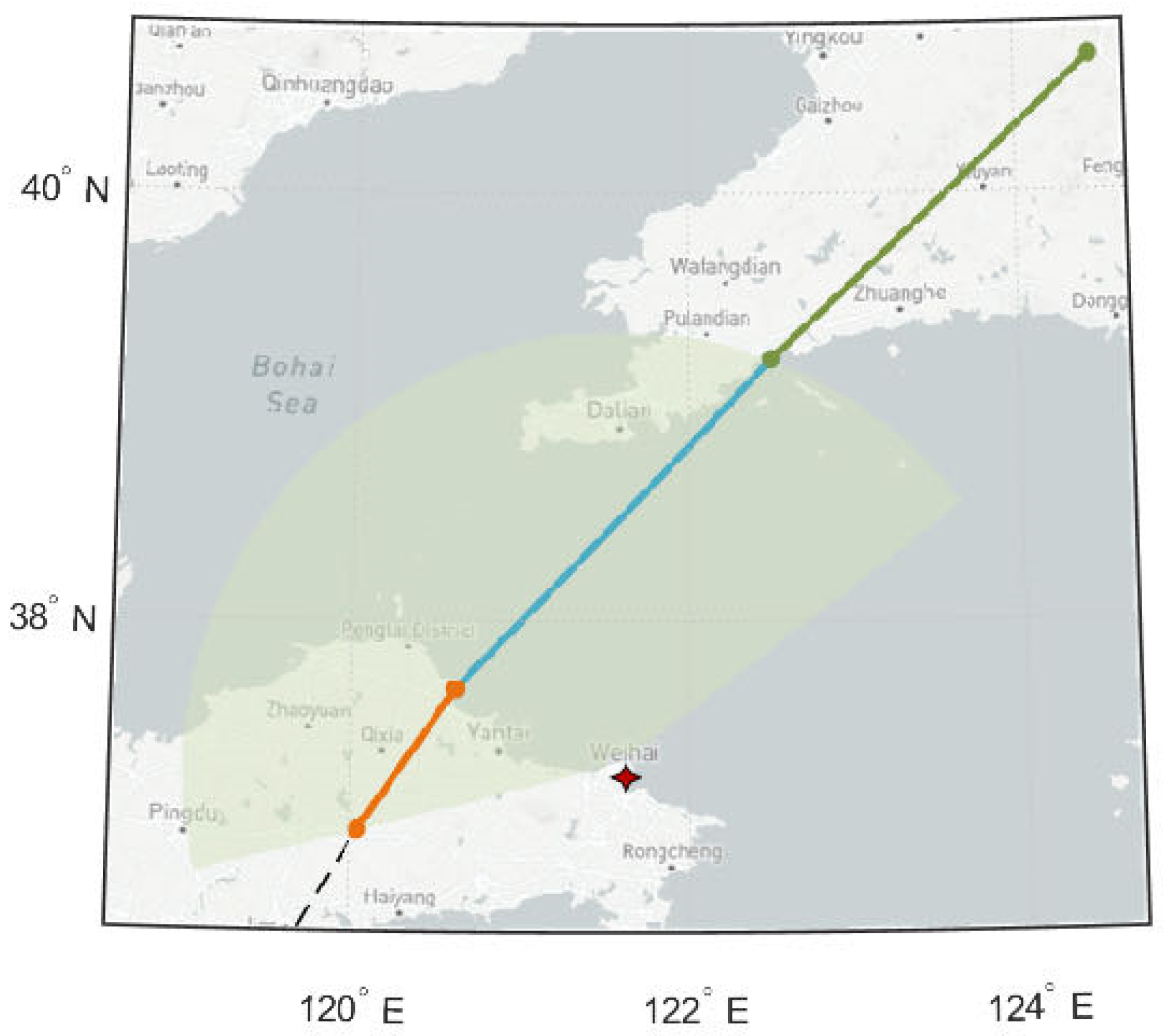

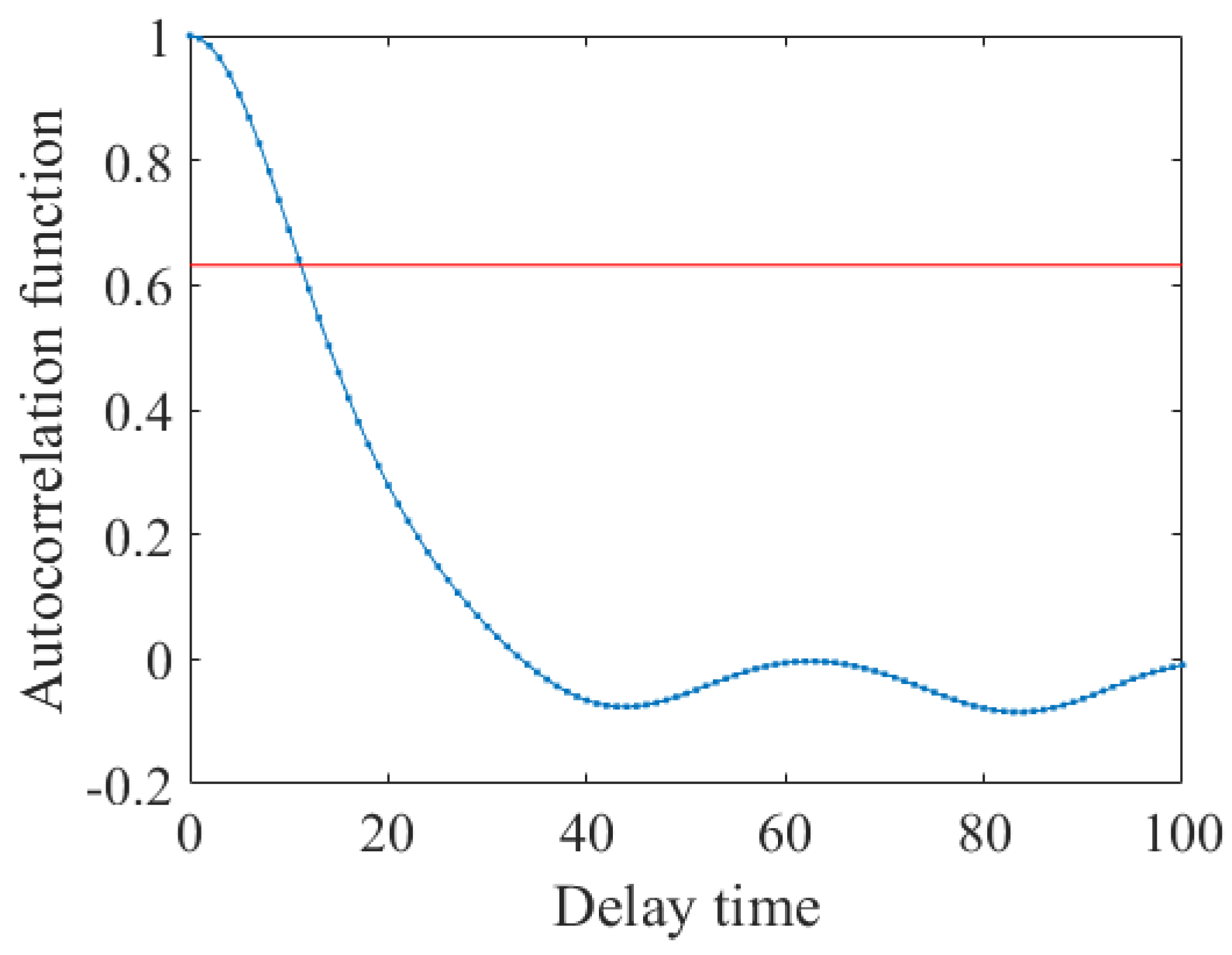
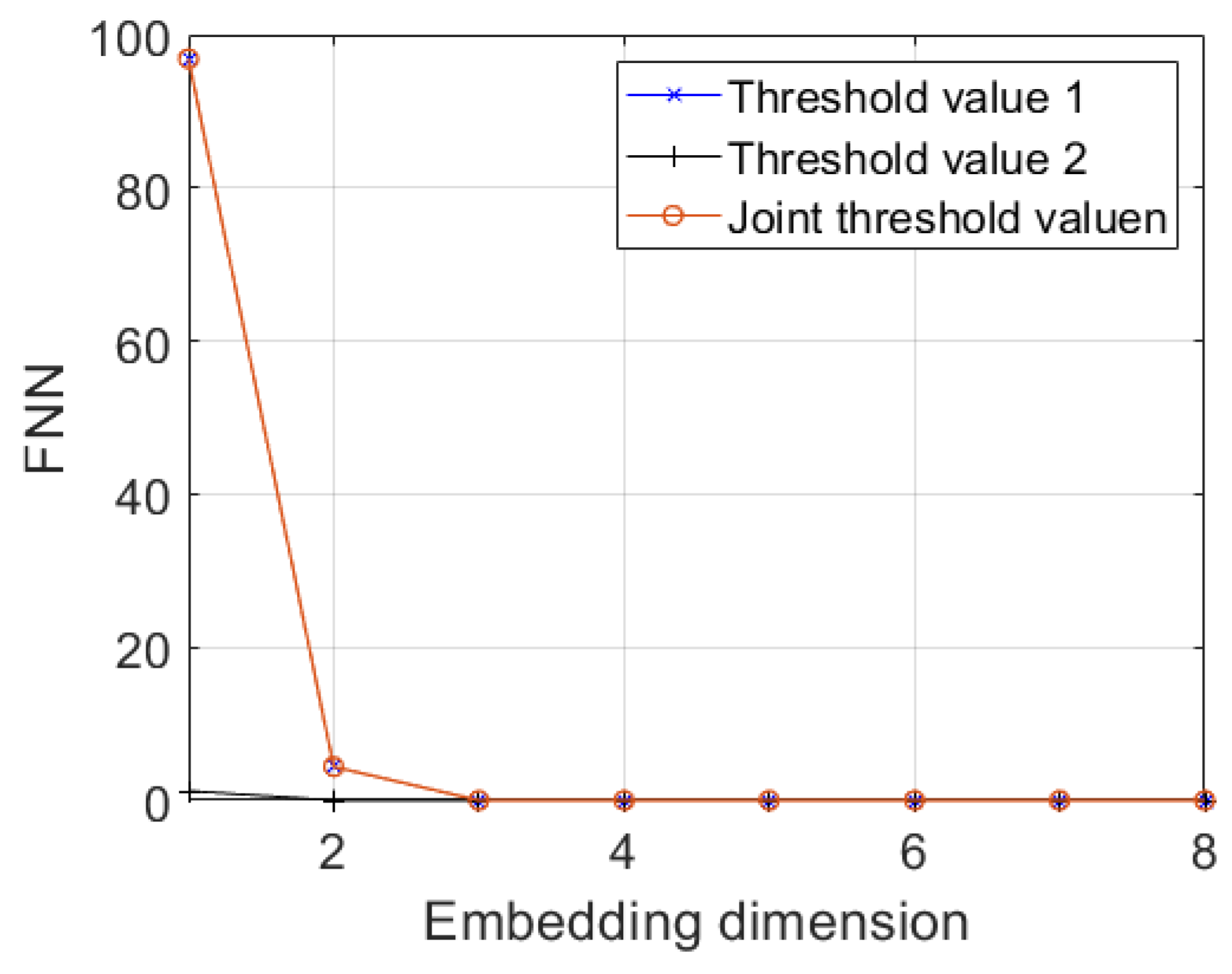


| Parameter | Value |
|---|---|
| Location | 37.37N, 122E |
| Operating frequency | 4.90 MHz |
| Pulse recurrence interval | 3.63 ms |
| Distance accuracy | 3.7 km |
| Sampling frequency | 400 kHz |
| Sampling time | 16 September 2022 02:00–15:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Lyu, Z.; Yu, C.; Liu, A.; Quan, T. Joint Analysis and Morphological Characterization of HFSWR Echo Properties during Severe Typhoon Muifa. Remote Sens. 2024, 16, 267. https://doi.org/10.3390/rs16020267
Wang R, Lyu Z, Yu C, Liu A, Quan T. Joint Analysis and Morphological Characterization of HFSWR Echo Properties during Severe Typhoon Muifa. Remote Sensing. 2024; 16(2):267. https://doi.org/10.3390/rs16020267
Chicago/Turabian StyleWang, Rong, Zhe Lyu, Changjun Yu, Aijun Liu, and Taifan Quan. 2024. "Joint Analysis and Morphological Characterization of HFSWR Echo Properties during Severe Typhoon Muifa" Remote Sensing 16, no. 2: 267. https://doi.org/10.3390/rs16020267
APA StyleWang, R., Lyu, Z., Yu, C., Liu, A., & Quan, T. (2024). Joint Analysis and Morphological Characterization of HFSWR Echo Properties during Severe Typhoon Muifa. Remote Sensing, 16(2), 267. https://doi.org/10.3390/rs16020267





