Abstract
Regarding the terrestrial water storage anomaly (TWSA) gap between the Gravity Recovery and Climate Experiment (GRACE) and GRACE Follow-on (-FO) gravity satellite missions, a BEAST (Bayesian estimator of abrupt change, seasonal change and trend)+GMDH (group method of data handling) gap-filling scheme driven by hydrological and meteorological data is proposed. Considering these driving data usually cannot fully capture the trend changes of the TWSA time series, we propose first to use the BEAST algorithm to perform piecewise linear detrending for the TWSA series and then fill the gap of the detrended series using the GMDH algorithm. The complete gap-filling TWSAs can be readily obtained after adding back the previously removed piecewise trend. By comparing the simulated gap filled by BEAST + GMDH using Multiple Linear Regression and Singular Spectrum Analysis with reference values, the results show that the BEAST + GMDH scheme is superior to the latter two in terms of the correlation coefficient, Nash-efficiency coefficient, and root-mean-square error. The real GRACE/GFO gap filled by BEAST + GMDH is consistent with those from hydrological models, Swarm TWSAs, and other literature regarding spatial distribution patterns. The correlation coefficients there between are, respectively, above 0.90, 0.80, and 0.90 in most of the global river basins.
1. Introduction
Since April 2002, the Gravity Recovery and Climate Experiment (GRACE) and its successor mission GRACE Follow-on (-FO) have been observing changes of the global gravity field with unprecedented accuracy and spatiotemporal resolution. The terrestrial water storage anomalies (TWSAs) inferred from these missions have always played a crucial role in global and regional water cycles and climate change studies, including issues closely related to human destiny, such as groundwater depletion, ice sheet melting, sea-level rise, extreme droughts, flood disasters, and catastrophic earthquakes [1,2,3,4,5,6]. However, an 11-month gap between GRACE and GRACE-FO hinders continuous monitoring of global climate change and Earth system variations. This gap may introduce biases and uncertainties in subsequent geoscientific applications, leading to misconceptions of actual geophysical phenomena and ultimately misguiding decision-making [7,8,9,10]. Therefore, filling the missing TWSA values during the GRACE/GRACE-FO gap is vital for its geoscientific applications.
In recent years, various methods have been proposed to fill the missing values during the GRACE/GRACE-FO gap, which can be primarily categorized into three types.
(i) The first type involves using the orbit data from the magnetic field satellite, i.e., Swarm, to invert the time-variable gravity field and subsequently generate the TWSAs to fill the gap. Currently, the internationally released monthly solutions of Swarm time-variable gravity fields can typically be expanded to spherical harmonics of 40 to 60 degrees. Still, the maximum effective degree is much lower than this [11]. Therefore, the spatial resolution of the Swarm time-variable gravity field is significantly lower than that of GRACE/GRACE-FO, particularly in small basins and high-latitude regions where there is considerable uncertainty. The value of Swarm satellites in filling the gap is thus limited.
(ii) The second type employs statistical methods such as Singular Spectrum Analysis (SSA) [12], Multi-channel SSA (MSSA) [13], Principal Component Analysis (PCA) [14] and a two-step linear model [15] for gap filling. These methods essentially fill the gaps based on the inherent temporal correlations of the time series without introducing any new or real information. As a result, the filled results cannot capture any climatic anomaly events.
(iii) The third type of gap-filling method is based on hydrological and meteorological data-driven approaches, utilizing statistical methods or machine learning algorithms. Examples include Multiple Linear Regression (MLR) [16], Autoregressive Exogenous (ARX) models [17], Bayesian Convolutional Neural Networks (BCNNs) [18], the Deep Belief Network (DBN) [19], and the Deep Convolutional Auto-Encoder (DCAE) [20]. Considering that hydrological and meteorological driving data may not adequately capture the trend changes in TWSAs, the traditional approaches pre-process the TWSA time series by removing a long-term trend component. Subsequently, the driving data are used to fill the de-trended TWSA series, and the long-term trend is then added back to obtain the final filled results. However, the question remains whether simply removing a long-term trend from the TWSA series is sufficient, and whether the driving data can adequately capture the residual short-term trend of TWSAs after the long-term trend is removed. This may lead to significant uncertainty in the short-term trends before and after the gap period in the filled results, and related issues warrant further investigation.
Drawing on the hydrological and meteorological data-driven approaches, this paper proposes using the group method of data handling (GMDH) [21] to fill the monthly TWSAs during the GRACE/GRACE-FO gap. GMDH, also known as a polynomial neural network, can determine the optimal complexity of the model structure based on external criteria by gradually increasing the number of model components, thereby achieving simultaneous optimization of the model structure and parameters. To address the issue that the driving data do not fully reflect the trend of the TWSA series, a Bayesian estimator of abrupt change, seasonal change, and trend (BEAST) [22] is employed to pre-process the TWSA series by removing piecewise trends. The filling is then performed only on the piecewise de-trended TWSA series, and the subtracted piecewise trends are re-added to obtain the final filled TWSAs during the GRACE/GRACE-FO gap.
The rest of the paper is organized as follows: Section 2 introduces research data involving JPL mascon solutions to be filled, hydrological data, meteorological data and the Swarm time-variable gravity field. The principal methodology is presented in Section 3, where the piecewise detrending algorithm, i.e., BEAST, and the gap-filling algorithm, i.e., GMDH, are introduced. In Section 4, both the simulated gap and real GRACE/GRACE-FO gap are filled and analyzed to check the performance of the proposed BEAST + GMDH method. The paper is concluded in Section 5.
2. Research Data
The GRACE/GRACE-FO JPL mascon solutions are the dataset with a gap to be filled. The driving datasets employed include hydrological data and meteorological grid data, denoted as temperature T and precipitation P. The TWSAs inferred from the Swarm time-variable gravity field serve as a rough validation dataset for the gap-filling results.
2.1. JPL Mascon Solutions
The global TWSA series with the gap to be filled is the JPL RL06 mascon v2.0 solutions from April 2002 to September 2021 [23]. The dataset is sampled at 0.5°×0.5°, with an actual spatial resolution of 3° × 3°, and has been adjusted to remove the mean values over the period 2004.000–2009.999 before release. The 11-month period from July 2017 to May 2018 corresponds to the gap of the GRACE/GRACE-FO missions. During the GRACE mission, the missing mascon solutions were filled by spline interpolation from adjacent months. As a result, the interpolated GRACE mascon monthly solutions span a total of 183 months from April 2002 to June 2017. The GRACE-FO mascon solutions cover a total of 40 months from June 2018 to September 2021. Excluding the Antarctic and global ocean regions, we only consider the TWSAs over land north of 60° south latitude.
2.2. Hydrological Data
Hydrological data are provided by the Global Land Data Assimilation System (GLDAS), which aims to generate the optimal state and flux fields of the land surface through advanced land surface modeling and data assimilation techniques, combined with satellite and ground-based observation data. Currently, GLDAS incorporates four land surface models: Noah, CLSM, CLM, and VIC. We use the Level-4 GLDAS Noah v2.1 monthly land surface model dataset [24], with a resolution 0.25° × 0.25°. The following state variables are extracted or synthesized and then resampled to 0.5° × 0.5°:
(1) Global Evapotranspiration (ET)
(2) Surface Water Storage Anomaly (SWSA)
where ΔSM represents the soil moisture change, ΔSWE denotes the change in snow water equivalent, and ΔPCSW is the change in vegetation canopy water, all of which can be readily extracted from the monthly GLDAS Noah v2.1 model.
(3) Cumulative Water Storage Change (CWSC)
where P denotes precipitation, SF represents snowfall, Qs is surface storm runoff, and Qb indicates baseflow, all extracted from the GLDAS Noah v2.1 model. CWSC represents the difference between the inputs (precipitation and snowfall) and outputs (evapotranspiration and runoff) within the basin.
2.3. Meteorological Data
The global temperature grid dataset is generated from a combination of observation datasets from two large-scale networks: the Global Historical Climatology Network (GHCN) and the Climate Anomaly Monitoring System (CAMS). The dataset is sampled at 0.5° × 0.5° and employs some unique interpolation methods, such as the interpolation method with spatiotemporally varying temperature lapse rates, to detect the most common spatiotemporal characteristics in climatology and anomaly fields at both global and regional scales [25]. The GHCN_CAMS provides global surface temperature data above 2 m since January 1948 and is periodically updated in near real-time.
The Integrated Multi-satellitE Retrievals provide the global precipitation grid dataset for the Global Precipitation Mission (IMERG) of the Global Precipitation Mission (GPM) [26]. The GPM_3IMERGM dataset is computed from observations of various passive microwave sensors and is intercalibrated with estimates from the combined Ku-band radar radiometer. It supports model validation, climate change analysis, and global water resource assessment. The monthly GPM_3IMERGM dataset is sampled at 0.1° × 0.1° and is resampled to 0.5° × 0.5° in this study.
2.4. Swarm Time-Variable Gravity Field Data
Two sets of Level-2 Swarm time-variable gravity field monthly solutions are provided by the Institute of Geodesy (IfG) at the University of Bonn [27] and the Combination Service for Time-variable Gravity Fields (COST_G) [28], respectively. These solutions were released in December 2013 and August 2014, with maximum degrees of 60 and 40, respectively. In this work, the Swarm time-variable gravity field is primarily used for a rough validation of the filled TWSA fields during the GRACE/GRACE-FO gap period. The following processing steps are applied to monthly solutions of the Swarm time-variable gravity field. First, the low-degree coefficients are replaced with estimates from Satellite Laser Ranging (SLR). Then, the mean values of the corresponding degrees from the ITSG-Grace2018 time-variable gravity field over 2004.000–2009.999 are subtracted to obtain Swarm TWSAs with the same reference time baseline as the JPL mascon solution to be filled. Subsequently, a 750 km Gaussian smoothing [29] is applied, and the ICE-6G_D model [30] is used for Glacial Isostatic Adjustment (GIA) correction. Finally, the global 0.5° × 0.5° Swarm TWSA is produced through spherical harmonic synthesis.
3. Methodology
3.1. BEAST Piecewise Detrending Algorithm
Due to the impacts of human activities and climate change, there is a long-term trend in the GRACE/GRACE-FO TWSA time series, often not fully captured by hydrological and meteorological data. Therefore, when constructing a model “connecting” driving data with the TWSA series, it is necessary to first remove the trend from the TWSA series [16,18]. The model is then built using hydrological and meteorological data along with the de-trended TWSA field to predict the de-trended series during the GRACE/GRACE-FO gap period. After re-adding the trend component TrendGRACE, one can obtain the complete filled solution TWSApredicted for the GRACE/GRACE-FO gap period:
As mentioned before, a common detrending approach is to directly subtract the long-term linear trend over the entire study period [16,18]. However, the time series from different grids of the TWSA field often exhibit multiple piecewise increasing or decreasing trends. Suppose these piecewise trends are not adequately subtracted. In that case, hydrological and meteorological data may fail to fully map the de-trended TWSA series, leading to significant biases in the final gap-filling results. To address this, we propose to use the BEAST algorithm to subtract multiple piecewise trends from the TWSA series, rather than a single long-term trend as in traditional methods. Specifically, for the time series , BEAST decomposes it into seasonal component S, trend component T, their abrupt change points, and noise term εi:
where εi represents the observation noise that follows a Gaussian distribution, with an assumed unknown variance of σ2; the parameter Θs implicitly includes the positions and numbers of abrupt change points in the seasonal component, the order of the seasonal harmonic functions, and the coefficients of the sine and cosine terms; the parameter ΘT implicitly includes the positions and numbers of abrupt change points in the trend component, and the coefficients of each trend segment. Furthermore, restructuring (4), we can get , where xM characterizes the structure of the time series model, i.e., the positions and numbers of abrupt change points in the trend and seasonal components, and the order of the seasonal harmonic functions, while βM represents the estimable coefficients of the piecewise trend and seasonal components given the model structure M. Equation (4) can be rewritten as
In BEAST, both the structure parameters xM of the time series model and the estimable coefficients βM are random. A hybrid Markov Chain Monte Carlo (MCMC) sampler generates random samples for the i-th iteration of posterior inference [22]. By probabilistically representing all potential models, the estimates of all models are then weighted and averaged. Ultimately, the Bayesian average estimate and variance of the time series model are as follows:
When applying BEAST to model the TWSA series, the number of abrupt change points for both seasonal and trend components is set not to exceed five, and the polynomial degree for trend fitting is set to one, which corresponds to a linear trend. We evaluated the correlation between five types of driving data and the global TWSAs with BEAST piecewise linear detrending or traditional long-term detrending. It is worth noting that there are different time lags between the five types of driving data and the TWSA field. The maximum correlation coefficient is used as the criterion to determine the optimal time lag between them, and the maximum correlation coefficient at the optimal lag is used to represent the correlation between each type of driving data and the TWSA series.
Figure 1 presents the correlation coefficients between the driving data and the TWSAs with BEAST piecewise linear detrending and long-term detrending, where the third column shows the difference between the two sets of correlation coefficients. Table 1 lists the global average correlation coefficients between the driving data and the TWSAs with BEAST piecewise and long-term detrending, as well as the number and proportion of global grids where the former outperforms the latter. The higher the correlation coefficient between model inputs and outputs, the easier it is to construct the model, and the higher the final prediction accuracy. Among these, SWSA, CWSC, and P are positively correlated with TWSAs, meaning that an increase in the former is associated with an increase in the latter; T and ET are negatively correlated with the TWSA field, meaning that an increase in the former leads to a decrease in the latter, and vice versa.
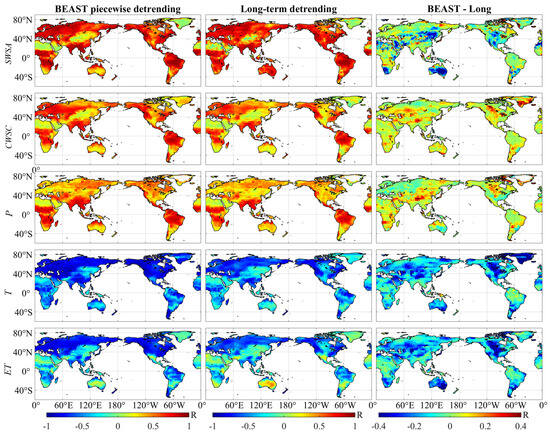
Figure 1.
The correlation coefficients between driving data (SWSA, CWSC, P, T and ET) and TWSAs with BEAST piecewise detrending (left) or long-term detrending (middle). The right column represents the difference between the left column and the middle column, namely the improved degree of correlation coefficient when using BEAST piecewise detrending, compared with using long-term detrending. One should note that the first three variables (SWSA, CWSC and P) positively correlate with TWSAs, while the last two variables (T and ET) are negatively correlated.

Table 1.
The global statistics of correlation coefficients between driving data and TWSAs using BEAST piecewise detrending or long-term detrending.
As can be seen from Figure 1 and Table 1, after BEAST piecewise detrending, the global average positive correlation coefficient between TWSAs and SWSAs (0.59) is comparable to that of the long-term detrending (0.61), and it is superior in 53.2% of the global grid cells. The global average positive correlation coefficients with CWSC and P are significantly higher than those after long-term detrending, being superior in 90.7% and 74.7% of the global grid cells, respectively. Similarly, the global average negative correlation coefficients with T and ET are also significantly higher, being superior in 96.6% and 96.4% of the global grid cells, respectively. In summary, after processing with the BEAST piecewise detrending algorithm, the correlation between the model inputs (hydrological and meteorological driving data) and the model outputs (detrended TWSA) is significantly improved, which is beneficial for reducing the difficulty of model construction and subsequently enhancing the accuracy of filling the missing values during the GRACE/GRACE-FO gap period.
3.2. GMDH Algorithm for Filling the Gap
The GMDH algorithm proposed by Ivakhnenko [21] is a heuristic self-organizing method for studying relationships between variables, which can adaptively estimate interrelationships in data and select the optimal structure of a model or network. Like feedforward multi-layer neural networks, GMDH employs a multi-layer conceptual structure, hence it is also known as a polynomial neural network. As shown in Figure 2, the driving data set is imported into the input layer. GMDH automatically selects input variables within the hidden layers during the model construction process, ultimately achieving a hierarchical polynomial regression with the necessary complexity.
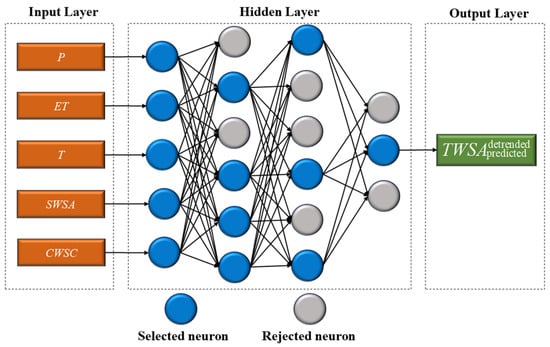
Figure 2.
A self-organization GMDH neural network structure diagram for filling the GRACE/GRACE-FO gap.
The basic concept of the GMDH polynomial model is similar to animal evolution or plant breeding, following the principle of natural selection. The multi-layer criterion is to retain well-hidden layers for several generations and eventually produce the best network structure. In GMDH, the relationship between input and output variables is represented through the Volterra series of the Kolmogorov–Gabor polynomial,
where y(t) represents the output variable, X(x1, x2, …, xm) denotes the input variables, and A(a1, a2, …, am) signifies the coefficients of the model. From (7), it is evident that the combination of any vector pair is a complex high-dimensional problem. Therefore, we employ the heuristic self-organizing GMDH model, which first pairs variables that may affect the system and sets thresholds to eliminate variables that cannot achieve a certain performance level. In this paper, the maximum layer number of the GMDH model is preset to 5, with a maximum number of neurons per layer of 15. The specific construction process of the self-organizing GMDH model is as follows [31]:
Step 1: Generate combinations of input variables for each layer. In each network layer, all combinations of the output variables from the previous layer are used as input. The number of combinations per layer is
where m is the number of input variables, and r is typically set to 2.
Step 2: Eliminate suboptimal variable combinations from each layer. Regression analysis is performed on the input data of the current layer to calculate the local optimal solution for that layer. The root mean square (RMS) is used as the criterion to eliminate suboptimal elements from each layer [32].
where represents the output value of the i-th element in the k-th layer at time t.
Step 3: Compare the index values generated by the current layer with the next layer. If there is no improvement, terminate the development of the next layer; otherwise, repeat Step 1 and Step 2 until the matching upper limit conditions are met, and then recombine all valid elements of each layer into the best GMDH polynomial model.
The basic process of using the GMDH algorithm to fill the missing values in the TWSA field during the GRACE/GRACE-FO mission gap is as follows: (1) At the mascon grid level, first determine the optimal time delay between the driving data (SWSA, CWSC, P, T, and ET) and the target data (TWSA) based on the maximum correlation coefficient; (2) input the driving data during the GRACE/GRACE-FO mission period, corrected with the optimal time delay, to best match the de-trended TWSA series, and then construct the GMDH polynomial model; (3) based on the constructed GMDH model and the driving data during the gap period, predict the de-trended TWSA field during the gap period and then re-add the removed segmental trends to finally obtain the filled result for the missing values during the gap period.
4. Results
4.1. Filling the Simulated Gap
First, we treated the GRACE-FO period of 2019, which consists of 12 months of mascon solutions, as a simulated gap. We utilized the proposed BEAST + GMDH algorithm to fill this gap. Two filling schemes were chosen as comparisons. (1) MLR [16,17]: A multiple linear regression is performed on the non-gap driving data and the long-term detrended TWSA series. Then, based on the constructed regression model and the driving data during the gap period, a de-trended filling result for the gap period is generated. By re-adding the trend, the MLR-filled TWSA field for the gap period is obtained; (2) SSA [12]: No detrending of the TWSA series and no driving data are required. Instead, a trajectory matrix is constructed directly from the non-gap TWSA series. This matrix is then decomposed and reconstructed to extract different components of the time series for prediction. This paper adopts the iterative SSA filling scheme proposed by Yi and Sneeuw [12], where the hyperparameters M (ranging from 12 to 72 months with an interval of 12) and K (ranging from 1 to 12 with an interval of 2) therein are determined through cross-validation.
Using the actual mascon solutions as reference values, Figure 3 presents the correlation coefficients (R), Nash–Sutcliffe efficiency (NSE), and normalized root mean square error (NRMSE) of the three filling schemes (MLR, SSA, and BEAST + GMDH) for the simulated missing values. The R and NSE of the BEAST + GMDH filling results are significantly higher than those of MLR and SSA, while the NRMSE is considerably lower. In most regions, the correlation coefficients between the filled results of the three schemes and the true values are above 0.85, but the filling effects are not ideal in some areas, mainly in deserts and arid regions. This is because the TWSA signals in these regions are very weak, with a low signal-to-noise ratio. Due to the impact of ice and snow in Greenland, it is difficult for hydrological and meteorological driving data to correctly recover the long-term detrended Greenland ice mass loss signal, as shown in Figure 3a–c. SSA, based solely on the self-correlation of the time series, can partially recover the Greenland signal, as shown in Figure 3d–f. The BEAST + GMDH filling results in Greenland are significantly better than the previous two, as shown in Figure 3g–i, mainly due to BEAST’s correct estimation of the piecewise trends, making the driving data only need to predict the seasonal terms, greatly reducing the prediction difficulty.
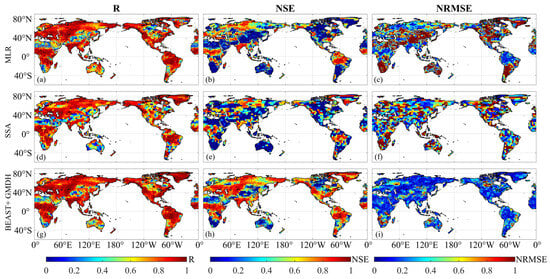
Figure 3.
Accuracy statistics of three gap-filling schemes to fill the simulated TWSA gap in 2019.
Furthermore, the filling results of the three schemes at the basin level were evaluated. Figure 4 shows the TWSA filling results of the three schemes in 50 basins, and Table 2 lists the average accuracy statistics of the filling results of the three schemes in 50 basins. Overall, the BEAST + GMDH filling results match the reference true values best and are significantly better than MLR and SSA. In the Brazos, Congo, Mackenzie, and Parana basins, MLR can correctly recover the seasonal variations of the basin TWSAs based on driving data, but cannot successfully recover the remaining short-term trends (after subtracting the long-term trend term). In the Elbe, Euphrates, Irrawaddy, Oder, Wisla, and Tarim basins, the filling results of SSA deviate significantly from the reference true value, as SSA only relies on the self-correlation of the time series and cannot reflect the actual hydrological and meteorological change information.
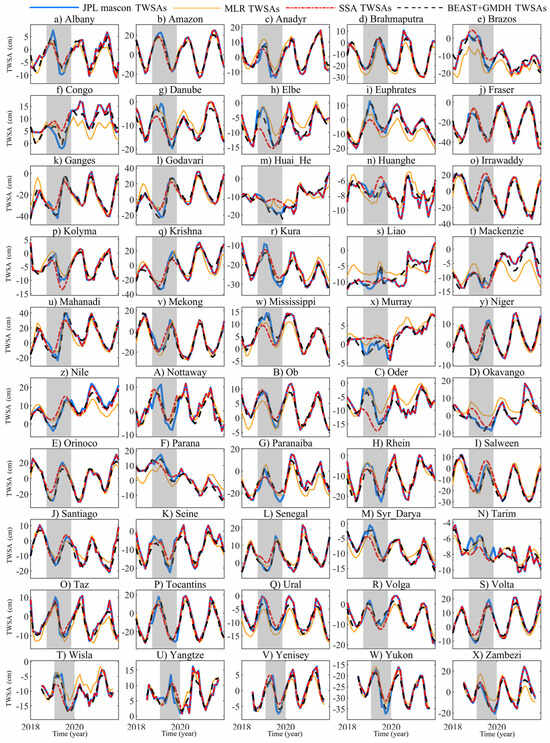
Figure 4.
Filling results of the simulated TWSA gap of three schemes, at the basin level.

Table 2.
The averaged accuracy statistics of three filling schemes at 50 basins.
4.2. Filling the GRACE/GRACE-FO Gap: Comparison with GLDAS and Swarm Solutions
The BEAST + GMDH scheme is utilized to fill the monthly missing TWSAs during the GRACE/GRACE-FO gap period. The filling results are shown in Figure 5, with GLDAS TWSAs, COST_G, and IFG Swarm TWSAs provided as comparisons. Overall, the TWSAs filled by BEAST + GMDH have a globally consistent distribution pattern with the Swarm TWSA field, especially in areas with stronger signals, such as the Amazon, Ganges, and Congo river basins.
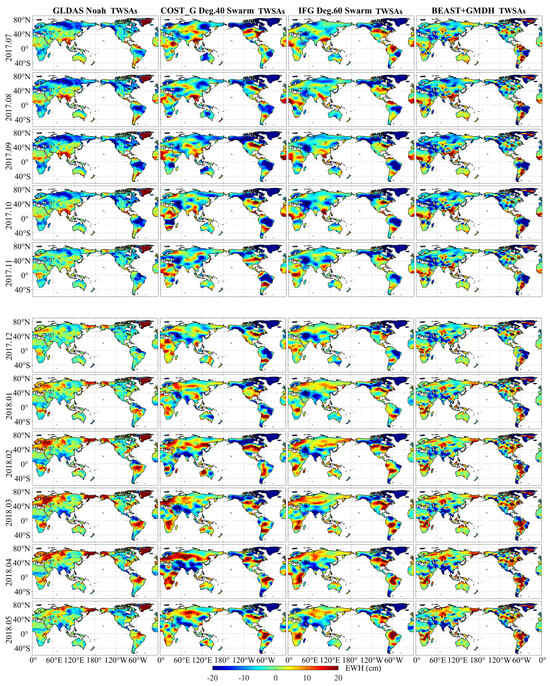
Figure 5.
The TWSAs gap-filled by BEAST + GMDH: comparison with GLDAS TWSAs, COST_G, and IFG Swarm TWSAs.
Furthermore, we analyzed the filling results of the BEAST + GMDH scheme at the basin level. Considering the limited spatial resolution of the Swarm time-variable gravity field, based on the balance between basin signals and scale, a total of 14 large basins were selected for evaluation. Figure 6 presents the TWSA time series of the 14 basins. The filling results of BEAST + GMDH generally agree well with the Swarm TWSA series, especially regarding seasonal variations. In the Ganges and Yukon River basins, the GRACE/GRACE-FO TWSA series and the Swarm TWSA series show significant differences, and the specific reasons need further investigation. Table 3 provides the correlation between the filling results of BEAST + GMDH in the 14 basins and other estimates. In most basins, the correlation coefficient between the filling results of BEAST + GMDH and the Swarm estimates is above 0.80, and the correlation coefficient with the GLDAS estimates is above 0.90, which verifies the reliability and correctness of the filling results.
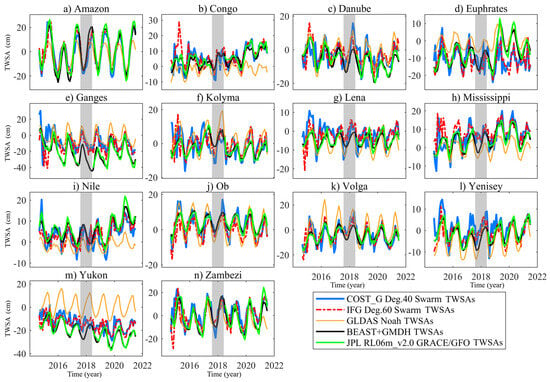
Figure 6.
The TWSA series of 15 basins during the GRACE/GRACE-FO gap filled by BEAST + GMDH: comparison with GLDAS TWSAs, COST_G Swarm TWSAs, and IFG Swarm TWSAs.

Table 3.
The correlation coefficients between the BEAST + GMDH gap-filled results and other gap-filled results.
4.3. Filling the GRACE/GRACE-FO Gap: Comparison with the Previous Literature
Firstly, we assessed the consistency of the TWSAs filled by BEAST + GMDH during the gap period with the filling results from the previous literature [17,18,33], as shown in Figure 7. Among these, Mo et al. [18] filled the gap period TWSAs of the JPL RL06 mascon based on hydrological and meteorological data using BCNNs, with the resolution of their filling results being 1° × 1°, which was then resampled to 0.5° × 0.5°; Li et al. [17] tested the performance of various data-driven methods combined with hydrological and meteorological data and climate indices and eventually determined PCA-LS-MLR as the best filling scheme, filling the gap period missing values of the CSR RL06 mascon; Zhang et al. [33] used the “abcd” hydrological model, temperature-based snowfall components, and linear corrections to simulate runoff generation, snowfall changes, and long-term trend components, respectively, and eventually constructed an empirical hydrological model to fill the gap period missing values of the JPL RL06 mascon. As can be seen from Figure 7, the filling results of BEAST + GMDH generally align well with the filling results of Zhang et al. [33] and Mo et al. [18], but there are differences in some regions with the filling results of Li et al. [17]. It is speculated that the inherent differences between the CSR and JPL mascon solutions cause this.
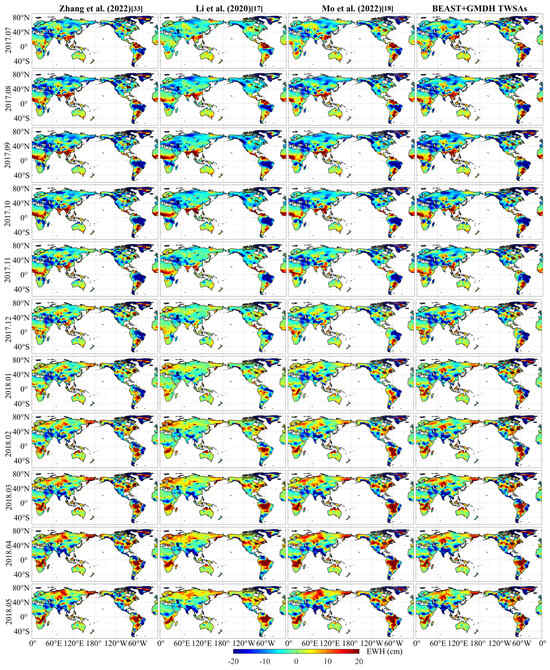
Figure 7.
The GRACE/GRACE-FO gap filled by BEAST + GMDH: comparison with the other literature’s filling results [17,18,33].
Figure 8 presents the global 50 basins’ TWSA time series filled by BEAST + GMDH and the other literature’s methods, and Table 4 lists the averaged correlation coefficients between the filling results of this work and the other literature’s results in the 50 basins. BEAST + GMDH aligns very well with the filling results of Zhang et al. [33], Li et al. [17], and Mo et al. [18] in the vast majority of basins, with averaged correlation coefficients above 0.90, further verifying the reasonableness of the filling results in this paper. It is worth noting that in basins such as the Yukon, Tarim, and Huanghe, the CSR and JPL mascon solutions show significant differences. This also explains why the correlation coefficient between the JPL mascon series filled by BEAST + GMDH and the filling results of Zhang et al. [33] and Mo et al. [18] is higher than that with the filling results of Li et al. [17] (as shown in Table 4).
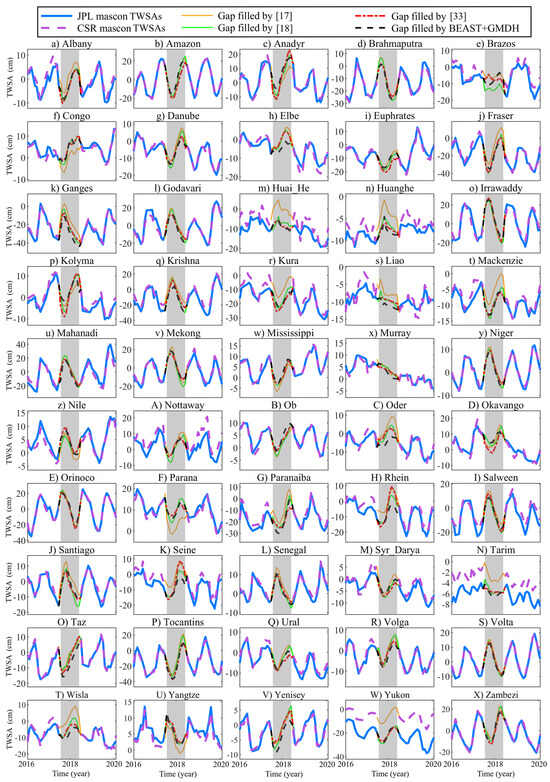
Figure 8.
The TWSA time series of 50 basins gap-filled by BEAST + GMDH: comparison with the other literature’s filling results [17,18,33].

Table 4.
The averaged correlation coefficients between the BEAST + GMDH gap-filled results and those in the previous literature at 50 basins.
5. Conclusions
Utilizing satellite gravity data from GRACE and GRACE-FO to study large-scale mass transport on the Earth’s surface has always been a research focus in geodesy, geophysics, hydrology, glaciology, and oceanography. However, the 11-month gap between the two satellite missions disrupts the continuity of the TWSA time series and may introduce biases or uncertainties in practical geoscience applications. Based on hydrological and meteorological data-driven approaches, this paper successfully fills the monthly TWSA field missing values during the gap period between GRACE and GRACE-FO using the BEAST + GMDH algorithm. Addressing the issue of driving data failing to capture the trends in the TWSA series fully, this paper proposes pre-processing the TWSA series with the BEAST algorithm to piece-wisely detrend it, significantly enhancing the correlation between the driving data and the TWSA series, reducing the difficulty of missing value filling, and thus improving the filling accuracy. The TWSAs filled by BEAST + GMDH during the GRACE/GRACE-FO gap aligns well with the Swarm satellite-inferred TWSAs, hydrological model, and the other literature’s filling results in terms of spatial distribution patterns and basin TWSA series, validating the reliability of the filling results. Future research will focus on reconstructing the TWSAs before the GRACE era and using the reconstructed results to assess long-term trend changes at global and regional scales.
Author Contributions
Conceptualization, N.Q. and Z.Y. (Zhaojin Yan); methodology, N.Q.; software, N.Q. and Y.F.; validation, Z.L. (Zhengwen Yan), J.G. and L.Y.; formal analysis, Z.Y. (Zhengwen Yan); investigation, L.Y.; resources, L.Y.; data curation, Y.F.; writing—original draft preparation, N.Q.; writing—review and editing, N.Q. and Y.F.; visualization, N.Q.; supervision, J.G.; project administration, J.G.; funding acquisition, N.Q., J.G. and Z.Y (Zhaojin Yan). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities under grant 2024ZDPYCH1003, the Natural Science Foundation of Jiangsu Province under grant number BK20241665, and the National Natural Science Foundation of China under Grants 42274020, 42274021, and 42304027.
Data Availability Statement
The JPL RL06 mascon solutions can be accessed at https://grace.jpl.nasa.gov/data/get-data/jpl_global_mascons (accessed on 1 August 2023). The GLDAS hydrological model data is available at https://ldas.gsfc.nasa.gov/gldas (accessed on 1 August 2023). The global temperature grid dataset CHCN_CAMS used in the study is available via https://www.psl.noaa.gov/data/gridded/data.ghcncams.html (accessed on 1 August 2023). The precipitation dataset GPM_3IMERGM can be accessed at https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGM_06 (accessed on 1 August 2023). The IfG and COST_G Swarm time-variable gravity fields are available at https://icgem.gfz-potsdam.de/sl/temporal (accessed on 1 August 2023). The GRACE/GRACE-FO gap filled by BEAST + GMDH can be accessed at https://doi.org/10.13140/RG.2.2.31377.40803 (accessed on 1 October 2024).
Acknowledgments
We would like to thank Wei Feng for providing the GRACE MATLAB Toolbox (GRAMAT) [34], Li et al. [17], Mo et al. [18] and Zhang et al. [33] for making their gap-filling results available, and Taikan Oki for providing basin boundaries. Gratitude is also extended to the anonymous reviewers for their constructive comments and suggestions to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feng, W.; Wang, C.; Mu, D.; Zhong, M.; Zhong, Y.; Xu, H. Groundwater storage variations in the North China Plain from GRACE with spatial constraints. Chin. J. Geophys. 2017, 60, 1630–1642. [Google Scholar]
- Ran, J.; Ditmar, P.; Klees, R.; Farahani, H.H. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. J. Geod. 2018, 92, 299–319. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Ma, M. Improving Spatial Resolution of GRACE-Derived Water Storage Changes Based on Geographically Weighted Regression Downscaled Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4261–4275. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Chen, W.; Zhang, X.; Hsu, H. An improved GRACE monthly gravity field solution by modeling the non-conservative acceleration and attitude observation errors. J. Geod. 2016, 90, 503–523. [Google Scholar] [CrossRef]
- Yang, T.; Yu, H.; Wang, Y. An efficient low-pass-filtering algorithm to de-noise global GRACE data. Remote Sens. Environ. 2022, 283, 113303. [Google Scholar] [CrossRef]
- Yan, Z.; Ran, J.; Xiao, Y.; Xu, Z.; Wu, H.; Deng, X.-L.; Du, L.; Zhong, M. The Temporal Improvement of Earth’s Mass Transport Estimated by Coupling GRACE-FO With a Chinese Polar Gravity Satellite Mission. J. Geophys. Res. Solid. Earth 2023, 128, e2023JB027157. [Google Scholar] [CrossRef]
- Xu, T.; Mu, D.; Yan, H.; Guo, J.; Yin, P. The causes of contemporary sea level rise over recent two decades: Progress and challenge. Acta Geod. Cartogr. Sin. 2022, 51, 1294. [Google Scholar]
- Sun, A.Y.; Scanlon, B.R.; Save, H.; Rateb, A. Reconstruction of GRACE total water storage through automated machine learning. Water Resour. Res. 2021, 57, e2020WR028666. [Google Scholar] [CrossRef]
- Yao, C.; Shum, C.K.; Luo, Z.; Li, Q.; Lin, X.; Xu, C.; Zhang, Y.; Chen, J.; Huang, Q.; Chen, Y. An optimized hydrological drought index integrating GNSS displacement and satellite gravimetry data. J. Hydrol. 2022, 614, 128647. [Google Scholar] [CrossRef]
- Yan, Z.; Luan, Y.; Ran, J.; Shum, C.K.; Zeng, Z.; Qian, N.; Zhang, Y.; Smith, P.; Pan, X.; Huang, Z. Optimal Design of a Third Pair of Gravity Satellites to Augment Two Existing Polar Pairs to Enhance Earth’s Temporal Gravity Field Recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 14145–14160. [Google Scholar] [CrossRef]
- Lück, C.; Kusche, J.; Rietbroek, R.; Löcher, A. Time-variable gravity fields and ocean mass change from 37 months of kinematic Swarm orbits. Solid. Earth 2018, 9, 323. [Google Scholar] [CrossRef]
- Yi, S.; Sneeuw, N. Filling the data gaps within GRACE missions using singular spectrum analysis. J. Geophys. Res. Solid. Earth 2021, 126, e2020JB021227. [Google Scholar] [CrossRef]
- Wang, F.; Shen, Y.; Chen, Q.; Wang, W. Bridging the gap between GRACE and GRACE follow-on monthly gravity field solutions using improved multichannel singular spectrum analysis. J. Hydrol. 2021, 594, 125972. [Google Scholar] [CrossRef]
- Richter, H.M.P.; Lück, C.; Klos, A.; Sideris, M.G.; Rangelova, E.; Kusche, J. Reconstructing GRACE-type time-variable gravity from the Swarm satellites. Sci. Rep. 2021, 11, 1117. [Google Scholar] [CrossRef]
- Yang, X.; You, W.; Tian, S.; Jiang, Z.; Wan, X. A Two-Step Linear Model to Fill the Data Gap Between GRACE and GRACE-FO Terrestrial Water Storage Anomalies. Water Resour. Res. 2023, 59, e2022WR034139. [Google Scholar] [CrossRef]
- Sun, Z.; Long, D.; Yang, W.; Li, X.; Pan, Y. Reconstruction of GRACE data on changes in total water storage over the global land surface and 60 basins. Water Resour. Res. 2020, 56, e2019WR026250. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lueck, C. Comparison of Data-Driven Techniques to Reconstruct (1992–2002) and Predict (2017–2018) GRACE-Like Gridded Total Water Storage Changes Using Climate Inputs. Water Resour. Res. 2020, 56, e2019WR026551. [Google Scholar] [CrossRef]
- Mo, S.; Zhong, Y.; Forootan, E.; Mehrnegar, N.; Yin, X.; Wu, J.; Feng, W.; Shi, X. Bayesian convolutional neural networks for predicting the terrestrial water storage anomalies during GRACE and GRACE-FO gap. J. Hydrol. 2022, 604, 127244. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; He, Y. Bridging the data gap between GRACE and GRACE-FO using artificial neural network in Greenland. J. Hydrol. 2022, 608, 127614. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, S.; He, H.; Yang, K.; Ma, L.; Li, J. Reconstructing GRACE-like TWS anomalies for the Canadian landmass using deep learning and land surface model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102404. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. The Group Method of Data Handling-A Rival of the Method of Stochastic Approximation. Sov. Autom. Control 1968, 1, 43–55. [Google Scholar]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid. Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Fan, Y.; van den Dool, H. A global monthly land surface air temperature analysis for 1948–present. J. Geophys. Res. Atmos. 2008, 113, D01103. [Google Scholar] [CrossRef]
- Huffman, G. GPM L3 IMERG Final 1 month 0.1 degree × 0.1 degree precipitation V03. 2015. [Google Scholar] [CrossRef]
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef]
- Jäggi, A.; Meyer, U.; Lasser, M.; Jenny, B.; Lopez, T.; Flechtner, F.; Dahle, C.; Förste, C.; Mayer-Gürr, T.; Kvas, A. International Combination Service for Time-Variable Gravity Fields (COST-G) Start of Operational Phase and Future Perspectives. In Beyond 100: The Next Century in Geodesy: Proceedings of the IAG General Assembly, Montreal, QC, Canada, 8–18 July 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 57–65. [Google Scholar]
- da Encarnacao, J.T.; Visser, P.; Arnold, D.; Bezdek, A.; Doornbos, E.; Ellmer, M.; Guo, J.; van den IJssel, J.; Iorfida, E.; Jäggi, A. Description of the multi-approach gravity field models from Swarm GPS data. Earth Syst. Sci. Data 2020, 12, 1385–1417. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid. Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Tsai, T.-M.; Yen, P.-H. GMDH algorithms applied to turbidity forecasting. Appl. Water Sci. 2017, 7, 1151–1160. [Google Scholar] [CrossRef]
- Qian, N.; Chang, G.; Gao, J. Smoothing for continuous dynamical state space models with sampled system coefficients based on sparse kernel learning. Nonlinear Dyn. 2020, 100, 3597–3610. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Dong, Q.; Wang, Z.; Zhang, H.; Liu, X. Bridging the gap between GRACE and GRACE-FO using a hydrological model. Sci. Total Environ. 2022, 822, 153659. [Google Scholar] [CrossRef] [PubMed]
- Feng, W. GRAMAT: A comprehensive Matlab toolbox for estimating global mass variations from GRACE satellite data. Earth Sci. Inform. 2019, 12, 389–404. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).