A HRWS SAR Motion Compensation Method with Multichannel Phase Correction
Abstract
1. Introduction
- The inconsistent motion errors of multiple channels can be compensated by estimating and compensating for phase errors of all channels. It improves the imaging quality of HRWS SAR with inconsistent motion errors in multiple channels. Furthermore, since the proposed method is based on BP imaging and sub-image reconstruction, it can inherit the advantages of dealing with nonlinear trajectories and implementing image domain-weighted reconstruction.
- The channel phase errors can be corrected while compensating for the motion errors, as the phase errors of multiple channels are estimated simultaneously. It simplifies the steps of channel phase errors estimation.
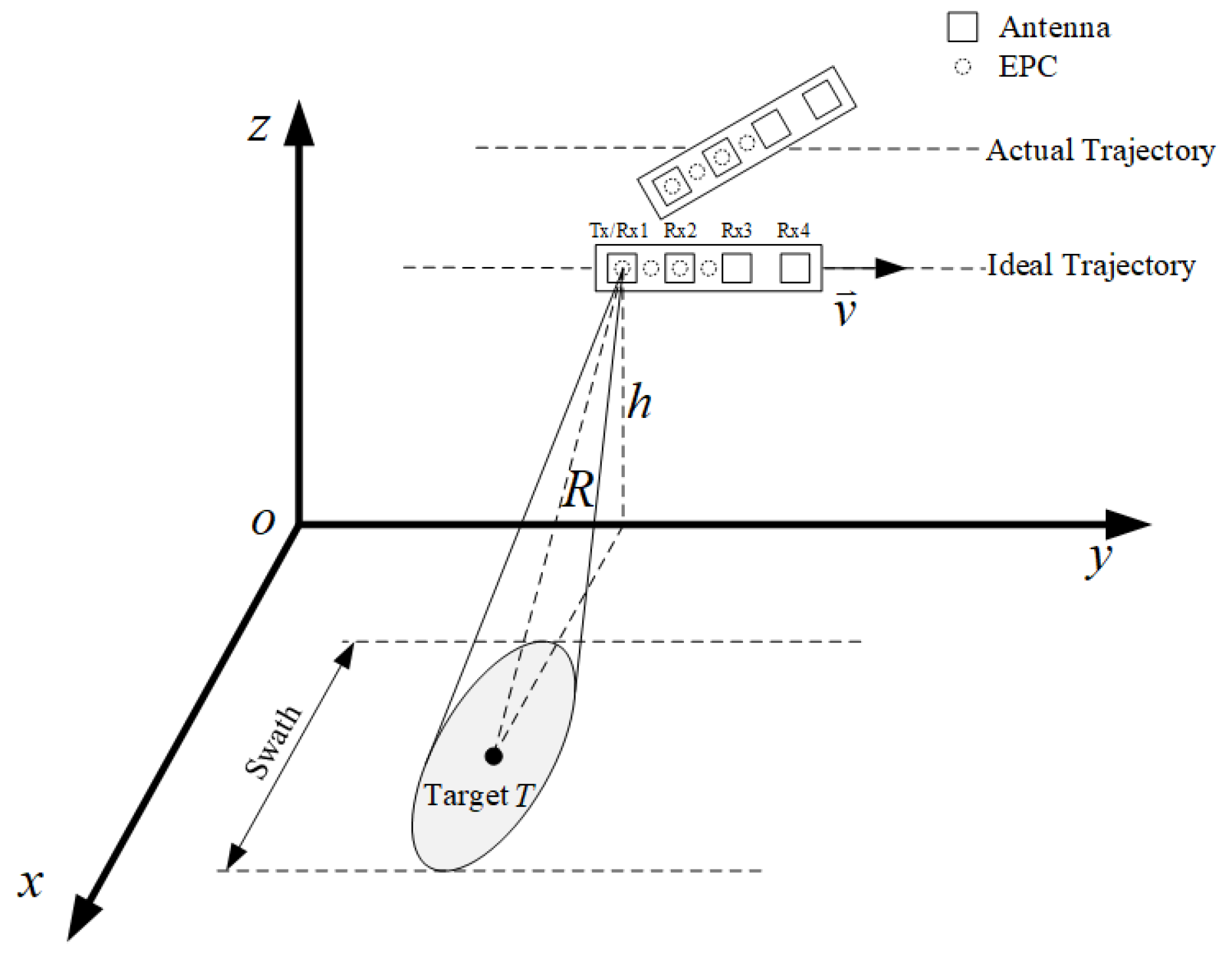
2. Reconstruction Signal with Motion Errors
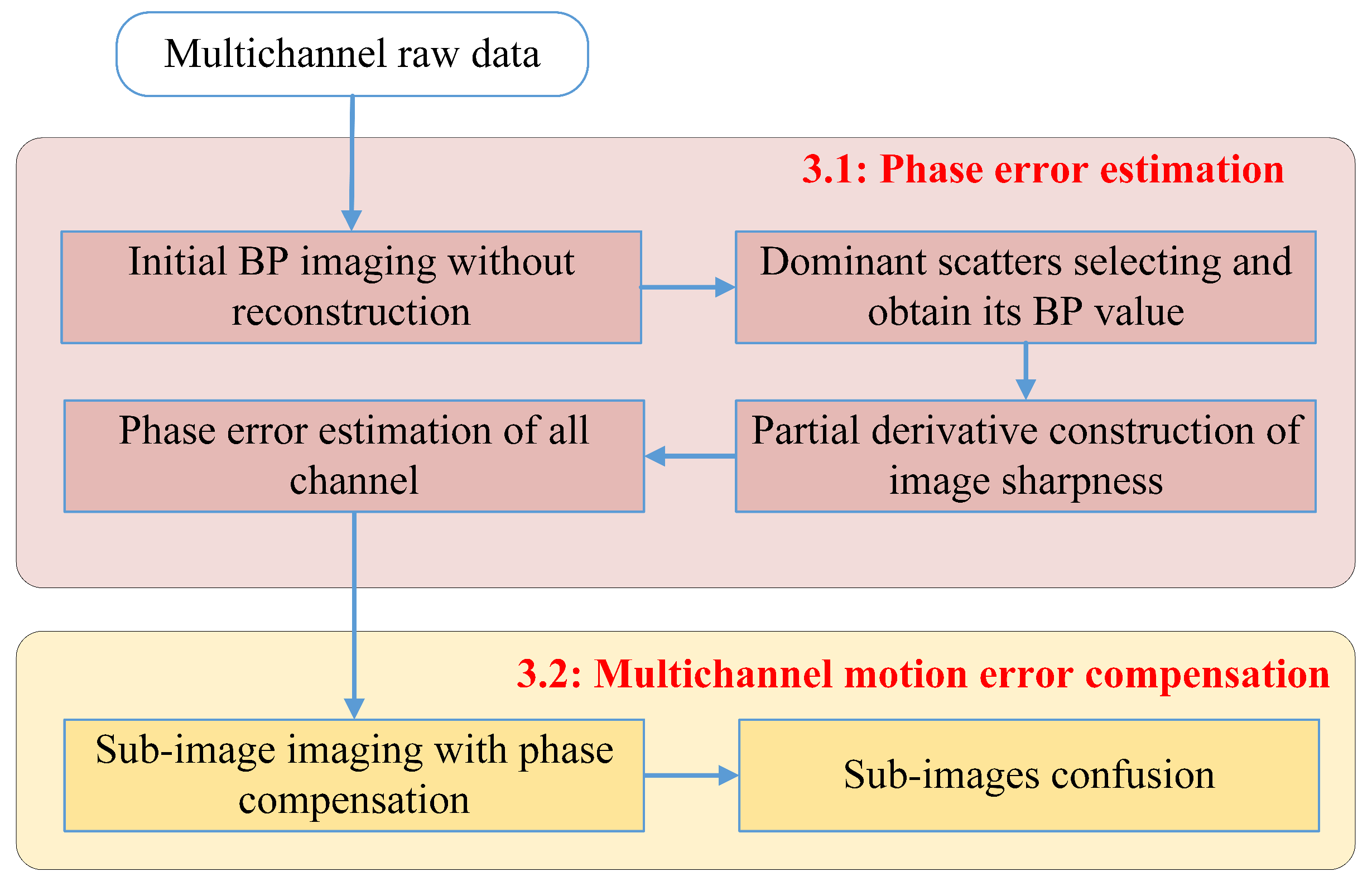
3. Multichannel SAR Motion Compensation Method
3.1. Phase Errors Estimation
| Algorithm 1. Multichannel Phase Estimating via Maximum Sharpness |
| Inputs: Multichannel SAR echo signal s |
| Step1: Process multichannel echoes using BP algorithm to obtain preliminary imaging results |
| Step2: Select dominant scatters from the preliminary image |
| Step3: Derive the image sharpness of the selected region |
| Step4: Construct the gradient of the objective function |
| Step5: Obtain the jth estimated phase by conjugate gradient method |
| Step6: Repeat step 5 when |
| Outputs: compensation phase |
3.2. Multichannel Motion Errors Compensation
4. Experiments
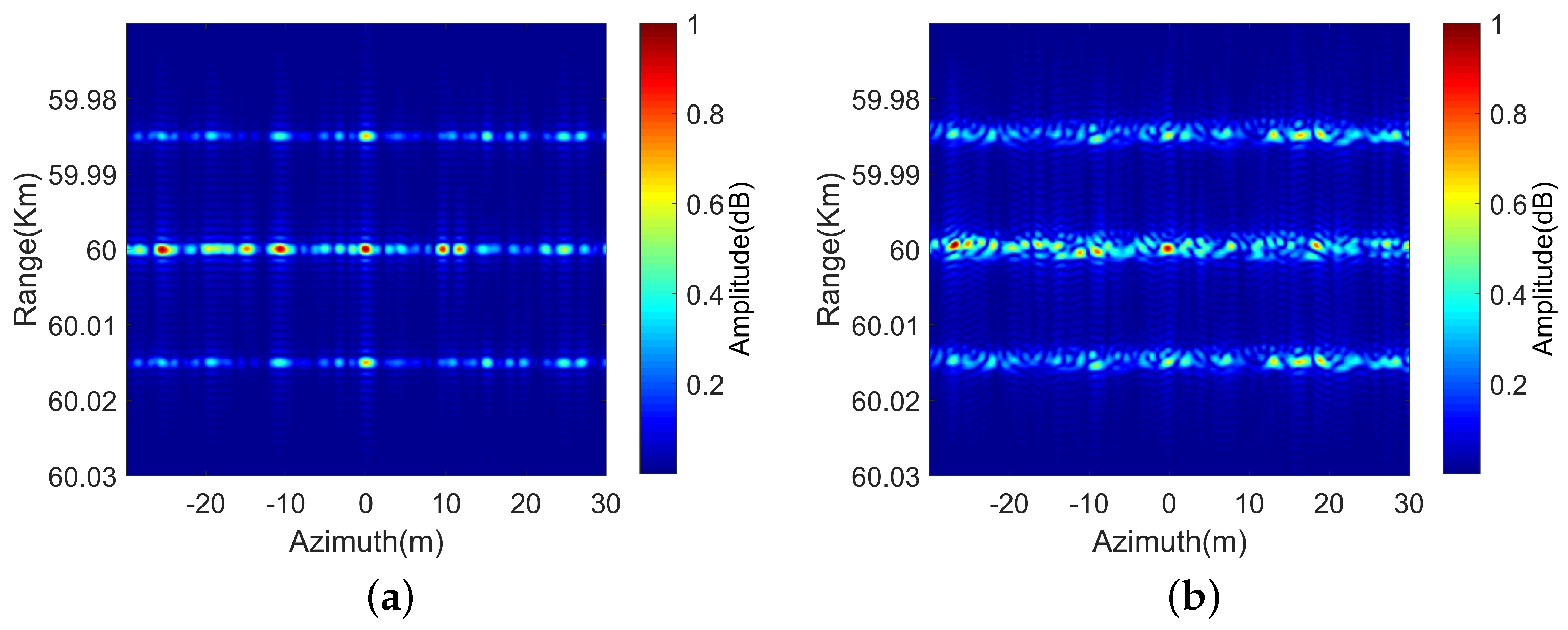
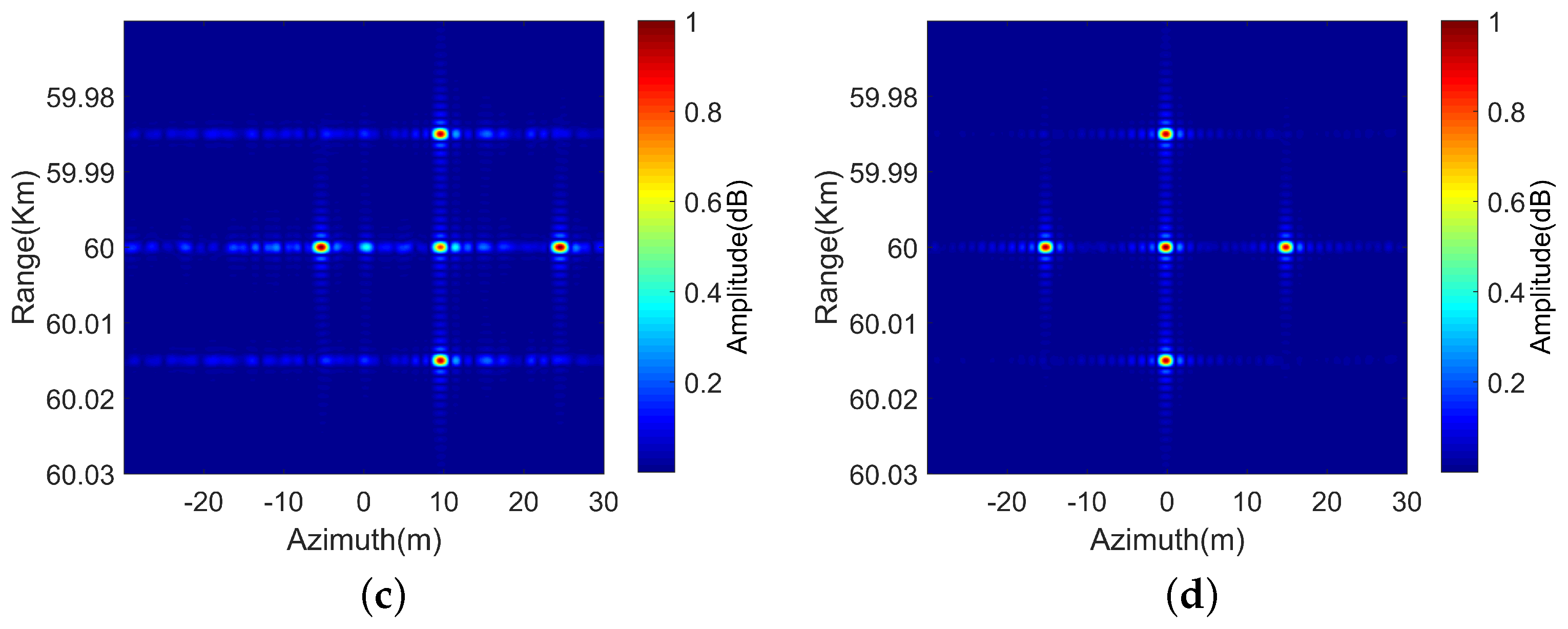
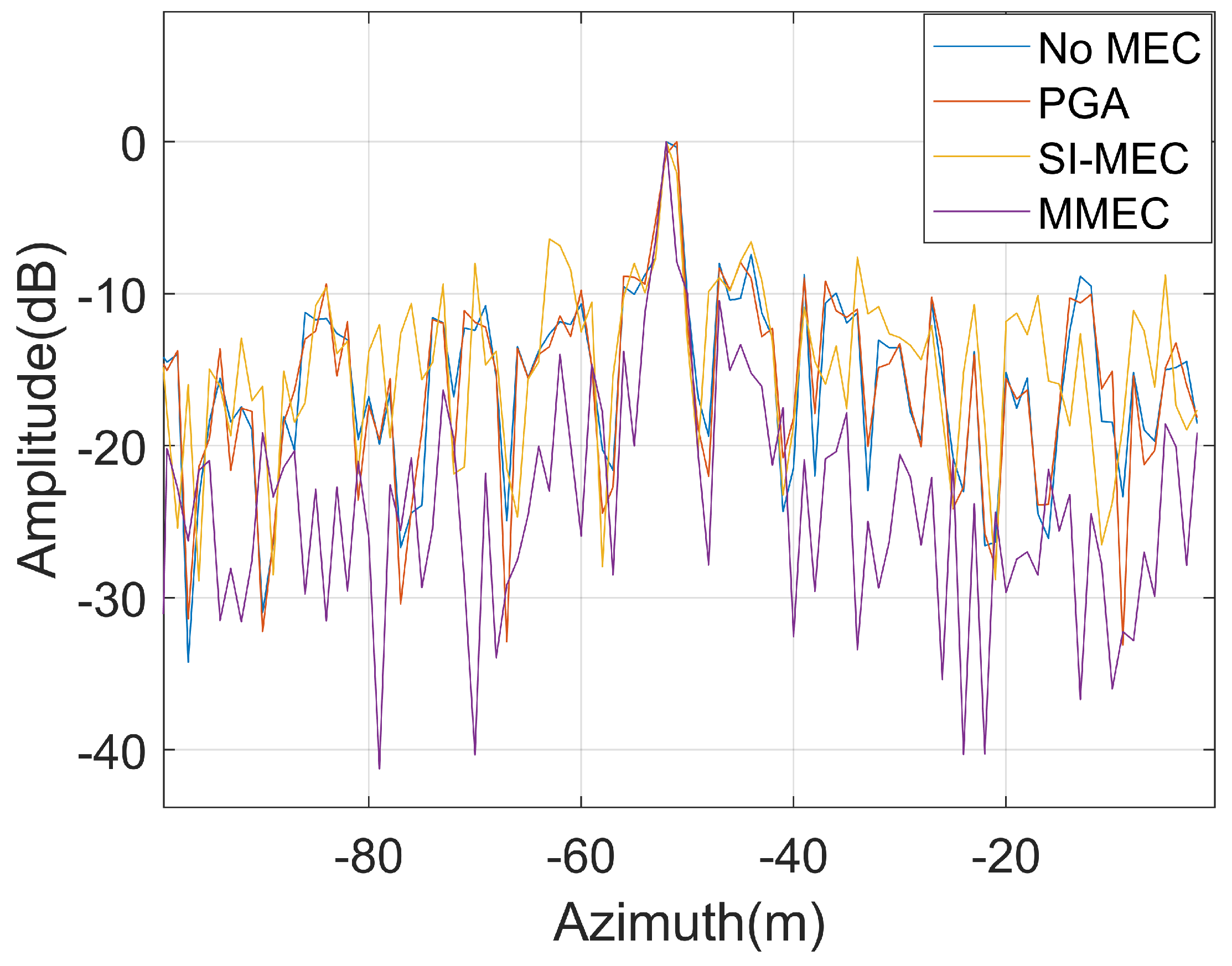
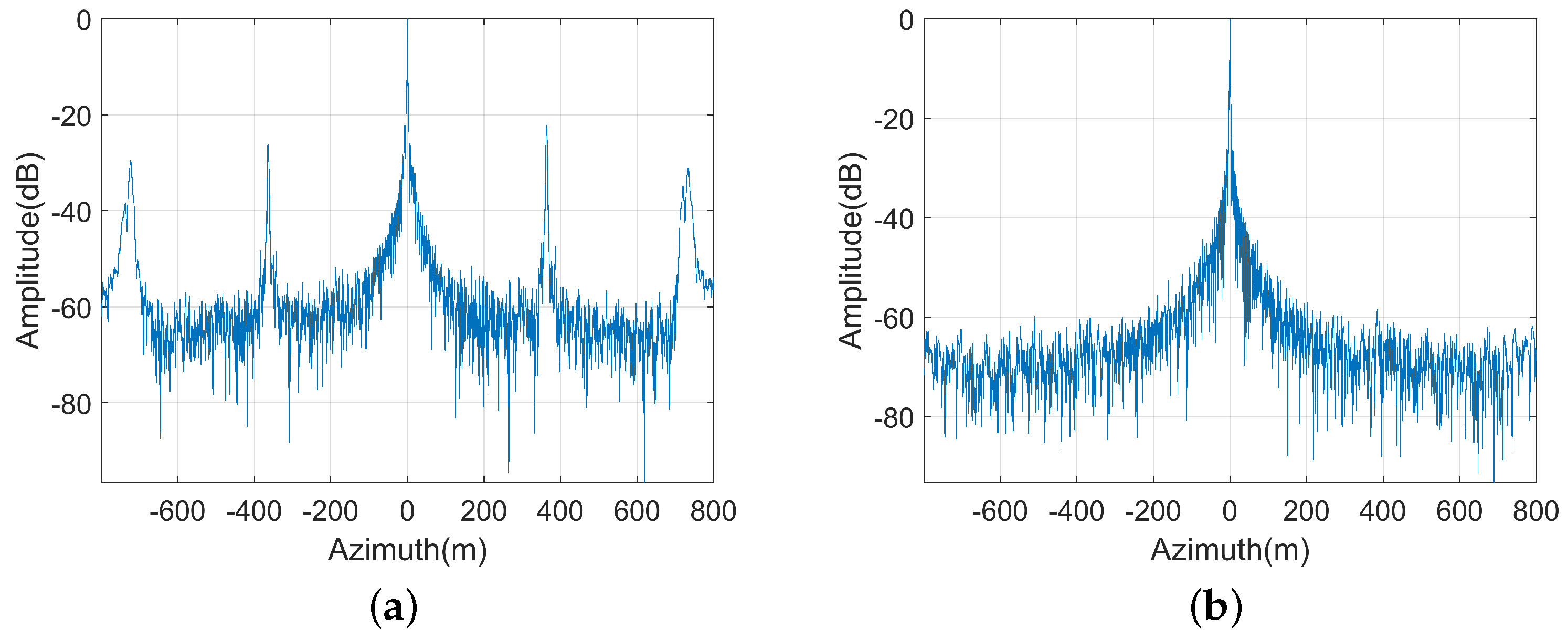
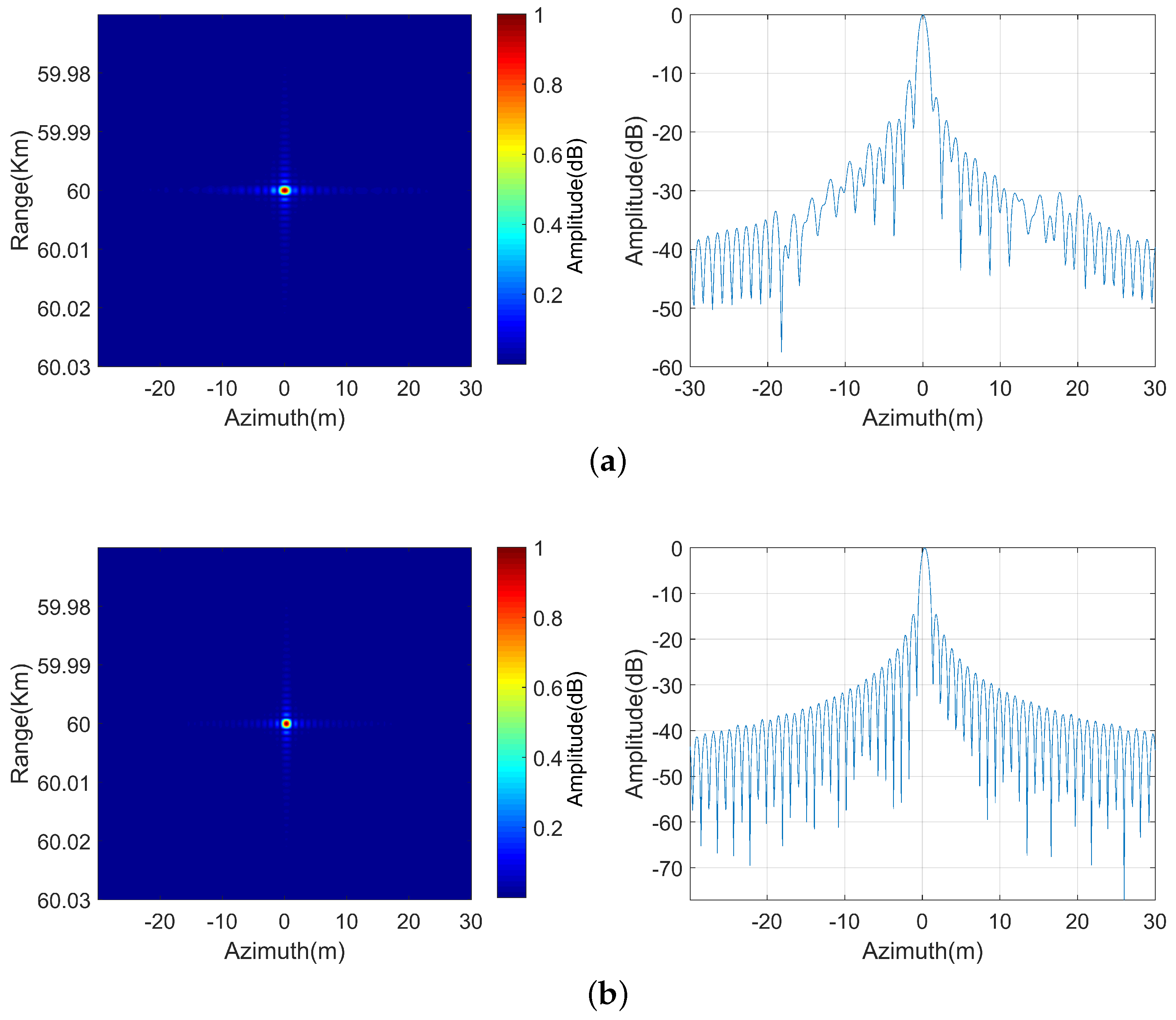
4.1. Point Target Simulation
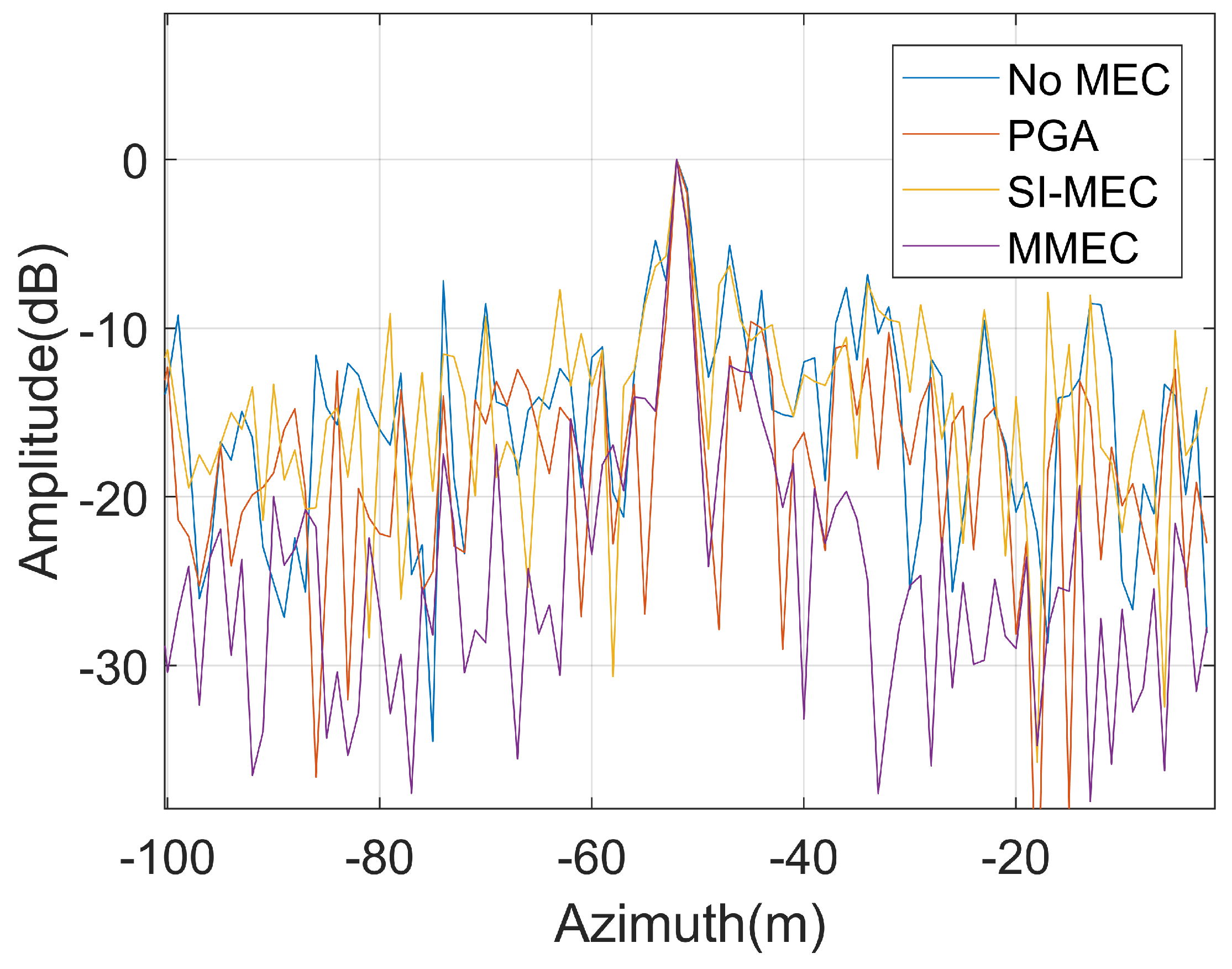
4.2. Complex Scene Simulation
5. Discussion
5.1. Performance under Channel Phase Errors
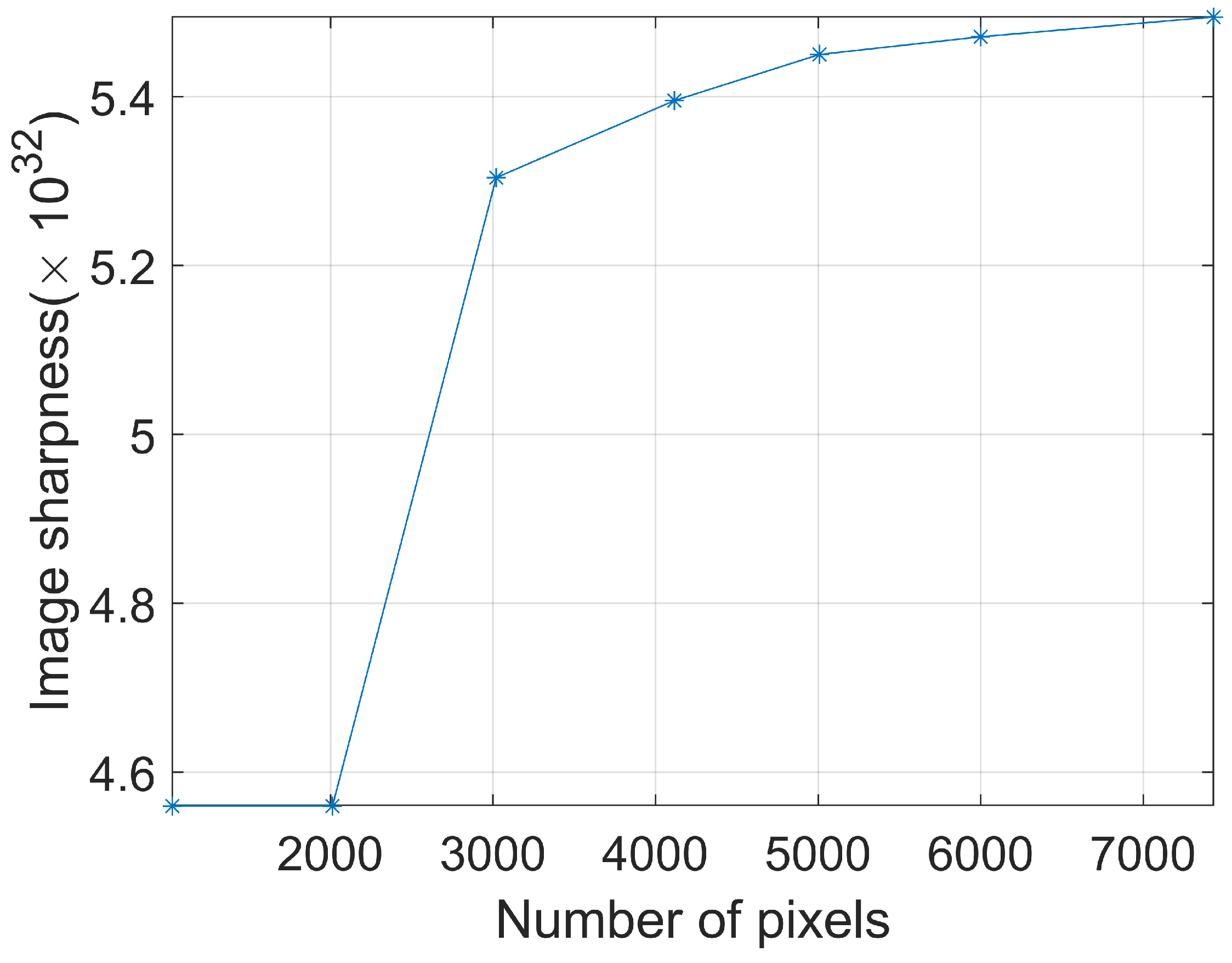
5.2. The Area Selecting for Estimation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Y.; Sun, B.; Li, J. An Image-Domain Signal Model for Azimuth Multichannel Reconstruction and Its Applications. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, Y.; Zhang, X. Accuracy Improvement of High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar Imaging with Low Pule Repetition Frequency. Remote Sens. 2023, 15, 3811. [Google Scholar] [CrossRef]
- Xu, Z.; Lu, P.; Cai, Y.; Li, J.; Yang, T.; Wu, Y.; Wang, R. An Efficient Channel Imbalance Estimation Method Based on Subadditivity of Linear Normed Space of Sub-Band Spectrum for Azimuth Multichannel SAR. Remote Sens. 2023, 15, 1561. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M. A Novel Doppler Chirp Rate and Baseline Estimation Approach in the Time Domain Based on Weighted Local Maximum-Likelihood for an MC-HRWS SAR System. IEEE Geosci. Remote Sens. Lett. 2017, 14, 299–303. [Google Scholar] [CrossRef]
- Li, B.; Sun, G.C.; Xing, M.; Hu, Y.; Guo, L.; Bao, Z. Clutter suppression via subspace projection for spaceborne HRWS multichannel SAR system. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1538–1542. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. SAR signal reconstruction from non-uniform displaced phase centre sampling. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 1763–1766. [Google Scholar]
- Cai, Y.; Lu, P.; Li, B.; Li, J.; Chen, Y.; Wang, Y.; Nan, Y.; Wang, R.; Wu, Y. An efficient phase error calibration method for azimuth multichannel SAR based on least spectrum difference. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Li, N.; Zhang, H.; Zhao, J.; Wu, L.; Guo, Z. An Azimuth Signal-Reconstruction Method Based on Two-Step Projection Technology for Spaceborne Azimuth Multi-Channel High-Resolution and Wide-Swath SAR. Remote Sens. 2021, 13, 4988. [Google Scholar] [CrossRef]
- Sikaneta, I.; Cerutti-Maori, D.; Klare, J.; Gierull, C. Comparison of multi-channel high-resolution wide-swath SAR processing methods. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3834–3837. [Google Scholar]
- Tang, J.; Deng, Y.; Wang, R.; Zhao, S.; Li, N.; Wang, W. A weighted backprojection algorithm for azimuth multichannel SAR imaging. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1265–1269. [Google Scholar] [CrossRef]
- Guo, J.; Chen, J.; Li, C.; Yang, W. An airborne multi-channel SAR imaging method with motion compensation. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 8554–8557. [Google Scholar]
- Zhang, T.; Liao, G.; Li, Y.; Gu, T.; Zhang, T.; Liu, Y. A two-stage time-domain autofocus method based on generalized sharpness metrics and AFBP. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Thompson, D.G.; Bates, J.S.; Arnold, D.V. Extending the phase gradient autofocus algorithm for low-altitude stripmap mode SAR. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No. 99CH36249), Waltham, MA, USA, 22 April 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 36–40. [Google Scholar]
- Zhang, L.; Qiao, Z.; Xing, M.d.; Yang, L.; Bao, Z. A robust motion compensation approach for UAV SAR imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Yang, L.; Xing, M.; Zhang, L.; Sheng, J.; Bao, Z. Entropy-based motion error correction for high-resolution spotlight SAR imagery. IET Radar Sonar Navig. 2012, 6, 627–637. [Google Scholar] [CrossRef]
- Potsis, A.; Reigber, A.; Mittermayer, J.; Moreira, A.; Uzunoglou, N. Sub-aperture algorithm for motion compensation improvement in wide-beam SAR data processing. Electron. Lett. 2001, 37, 1–2. [Google Scholar] [CrossRef]
- Kennedy, T. Strapdown inertial measurement units for motion compensation for synthetic aperture radars. IEEE Aerosp. Electron. Syst. Mag. 1988, 3, 32–35. [Google Scholar] [CrossRef]
- Kim, J.W.; Hwang, I.J.; Jo, H.W.; Kim, G.; Yoo, J.S.; Yu, J.W. Phase error compensation in fourier domain for fast autofocus of spotlight SAR. In Proceedings of the 2017 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), San Diego, CA, USA, 9–14 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 31–32. [Google Scholar]
- Kim, J.W.; Kim, Y.D.; Yeo, T.D.; Khang, S.T.; Yu, J.W. Fast Fourier-Domain Optimization Using Hybrid L1−/Lp-Norm for Autofocus in Airborne SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7934–7954. [Google Scholar] [CrossRef]
- Zeng, T.; Wang, R.; Li, F. SAR Image Autofocus Utilizing Minimum-Entropy Criterion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1552–1556. [Google Scholar] [CrossRef]
- Xi, L.; Guosui, L.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Morrison, R.L.; Do, M.N.; Munson, D.C. SAR image autofocus by sharpness optimization: A theoretical study. IEEE Trans. Image Process. 2007, 16, 2309–2321. [Google Scholar] [CrossRef]
- Schulz, T.J. Optimal sharpness function for SAR autofocus. IEEE Signal Process. Lett. 2006, 14, 27–30. [Google Scholar] [CrossRef]
- Ash, J.N. An Autofocus Method for Backprojection Imagery in Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 104–108. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. SAR minimum-entropy autofocus using an adaptive-order polynomial model. IEEE Geosci. Remote Sens. Lett. 2006, 3, 512–516. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Zhou, Z. Minimum-entropy phase adjustment for ISAR. IEE Proc. Radar Sonar Navig. 2004, 151, 203–209. [Google Scholar] [CrossRef]
- Kragh, T.J.; Kharbouch, A.A. Monotonic iterative algorithm for minimum-entropy autofocus. In Proceedings of the Adaptive Sensor Array Processing (ASAP) Workshop, Lexington, MA, USA, 6–7 June 2006; Volume 40, pp. 1147–1159. [Google Scholar]
- Guo, J.; Chen, J.; Liu, W.; Li, C.; Yang, W. An Improved Airborne Multichannel SAR Imaging Method with Motion Compensation and Range-Variant Channel Mismatch Correction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5414–5423. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Qiu, J.; Zhou, Y.; Wang, R. A Novel Motion Compensation Scheme for 2-D Multichannel SAR Systems with Quaternion Posture Calculation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 9350–9360. [Google Scholar] [CrossRef]
- Huang, H.; Huang, P.; Liu, X.; Xia, X.G.; Deng, Y.; Fan, H.; Liao, G. A Novel Channel Errors Calibration Algorithm for Multichannel High-Resolution and Wide-Swath SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–19. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.; Pu, L.; Zhang, T.; Shi, J.; Wei, S. A High-Precision Motion Errors Compensation Method Based on Sub-Image Reconstruction for HRWS SAR Imaging. Remote Sens. 2022, 14, 1033. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE Geosci. Remote Sens. Lett. 2004, 1, 260–264. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.; Wang, Y.; Li, L.; Pu, L.; Shi, J.; Wei, S. Unambiguous Reconstruction for Multichannel Nonuniform Sampling SAR Signal Based on Image Fusion. IEEE Access 2020, 8, 71558–71571. [Google Scholar] [CrossRef]
- Jun, S.; Zhang, X.; Yang, J. Principle and methods on bistatic SAR signal processing via time correlation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3163–3178. [Google Scholar] [CrossRef]
- Wei, S.; Zhou, L.; Zhang, X.; Shi, J. Fast back-projection autofocus for linear array SAR 3-D imaging via maximum sharpness. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018. [Google Scholar]
- Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.; Zhan, X.; Pu, L.; Zhang, T.; Shi, J.; Wei, S. A Novel Sub-Image Local Area Minimum Entropy Reconstruction Method for HRWS SAR Adaptive Unambiguous Imaging. Remote Sens. 2021, 13, 3115. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Wavelength | 0.031 m |
| Bandwidth | 150 MHz |
| Sampling frequency | 210 MHz |
| Squint angle | 0° |
| PRF | 700 Hz |
| Synthetic aperture length | 987 m |
| Distance between channel | 1 m |
| Number of channels | 4 |
| Speed | 1900 m/s |
| Height | 20 Km |
| Method | No-MEC | PGA [18] | SI-MEC [31] | MMEC |
|---|---|---|---|---|
| PSLR (dB) | −9.15 | −13.12 | −11.88 | −13.26 |
| ISLR (dB) | 5.98 | 8.52 | −2.42 | −9.93 |
| Method | NO MEC | PGA | SI-MEC | MMEC |
|---|---|---|---|---|
| Image entropy | 12.29 | 12.29 | 12.38 | 11.77 |
| Image sharpness | 3.63 × | 3.82 × | 3.0 × | 5.45 × |
| Method | NO MEC | PGA | SI-MEC | MMEC |
|---|---|---|---|---|
| Image entropy | 12.38 | 12.38 | 12.47 | 11.71 |
| Image sharpness | 3.50 × | 3.67 × | 2.90 × | 5.49 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Deng, M.; He, J.; Wang, B.; Zhang, S.; Liu, X.; Wei, S. A HRWS SAR Motion Compensation Method with Multichannel Phase Correction. Remote Sens. 2024, 16, 3544. https://doi.org/10.3390/rs16193544
Zhou L, Deng M, He J, Wang B, Zhang S, Liu X, Wei S. A HRWS SAR Motion Compensation Method with Multichannel Phase Correction. Remote Sensing. 2024; 16(19):3544. https://doi.org/10.3390/rs16193544
Chicago/Turabian StyleZhou, Liming, Minglong Deng, Jing He, Bing Wang, Shengmiao Zhang, Xuanyu Liu, and Shunjun Wei. 2024. "A HRWS SAR Motion Compensation Method with Multichannel Phase Correction" Remote Sensing 16, no. 19: 3544. https://doi.org/10.3390/rs16193544
APA StyleZhou, L., Deng, M., He, J., Wang, B., Zhang, S., Liu, X., & Wei, S. (2024). A HRWS SAR Motion Compensation Method with Multichannel Phase Correction. Remote Sensing, 16(19), 3544. https://doi.org/10.3390/rs16193544






