Performance Analysis of Moving Target Shadow Detection in Video SAR Systems
Abstract
1. Introduction
2. Mechanisms of ViSAR Moving Target Shadow Formation and Shadow Models
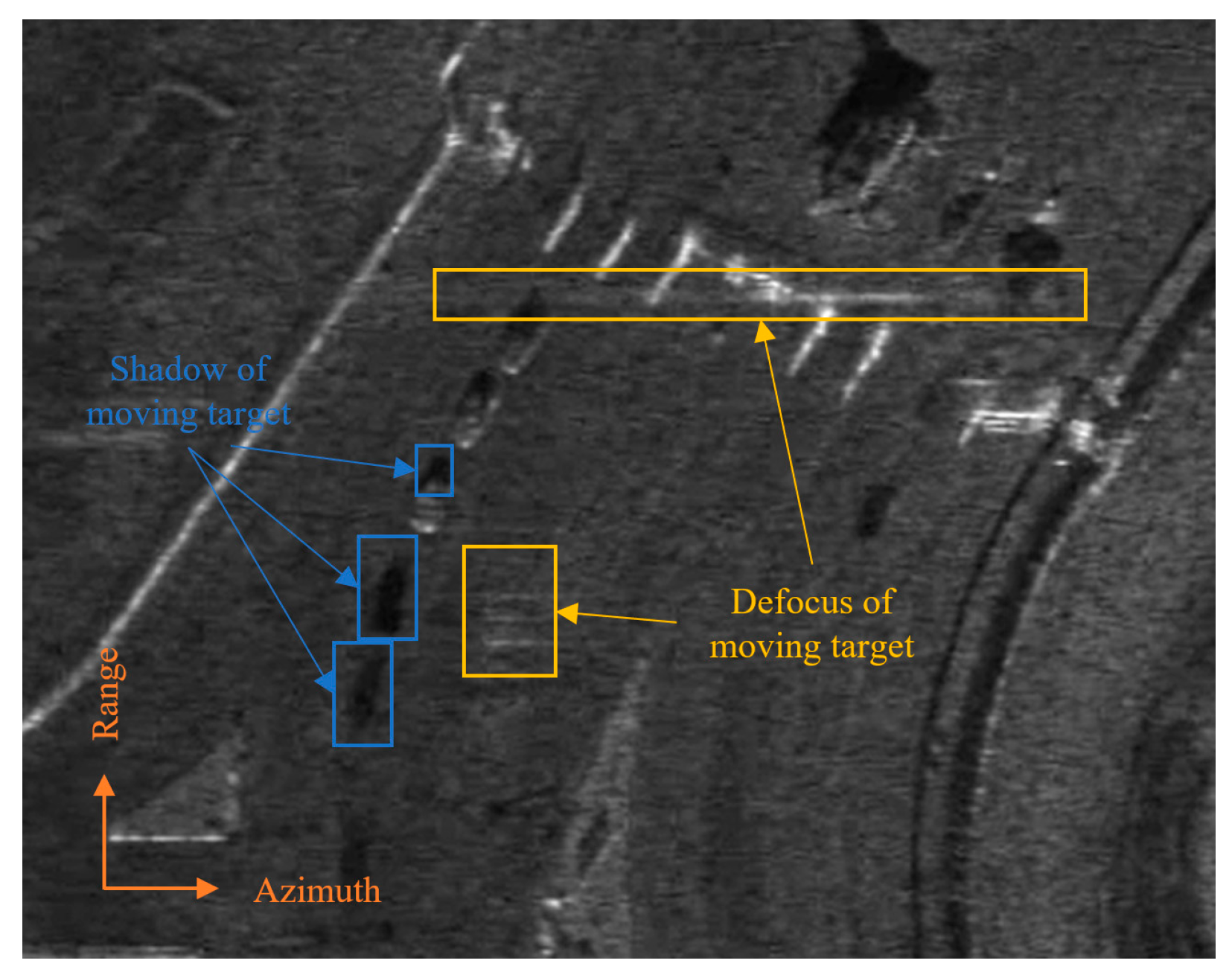
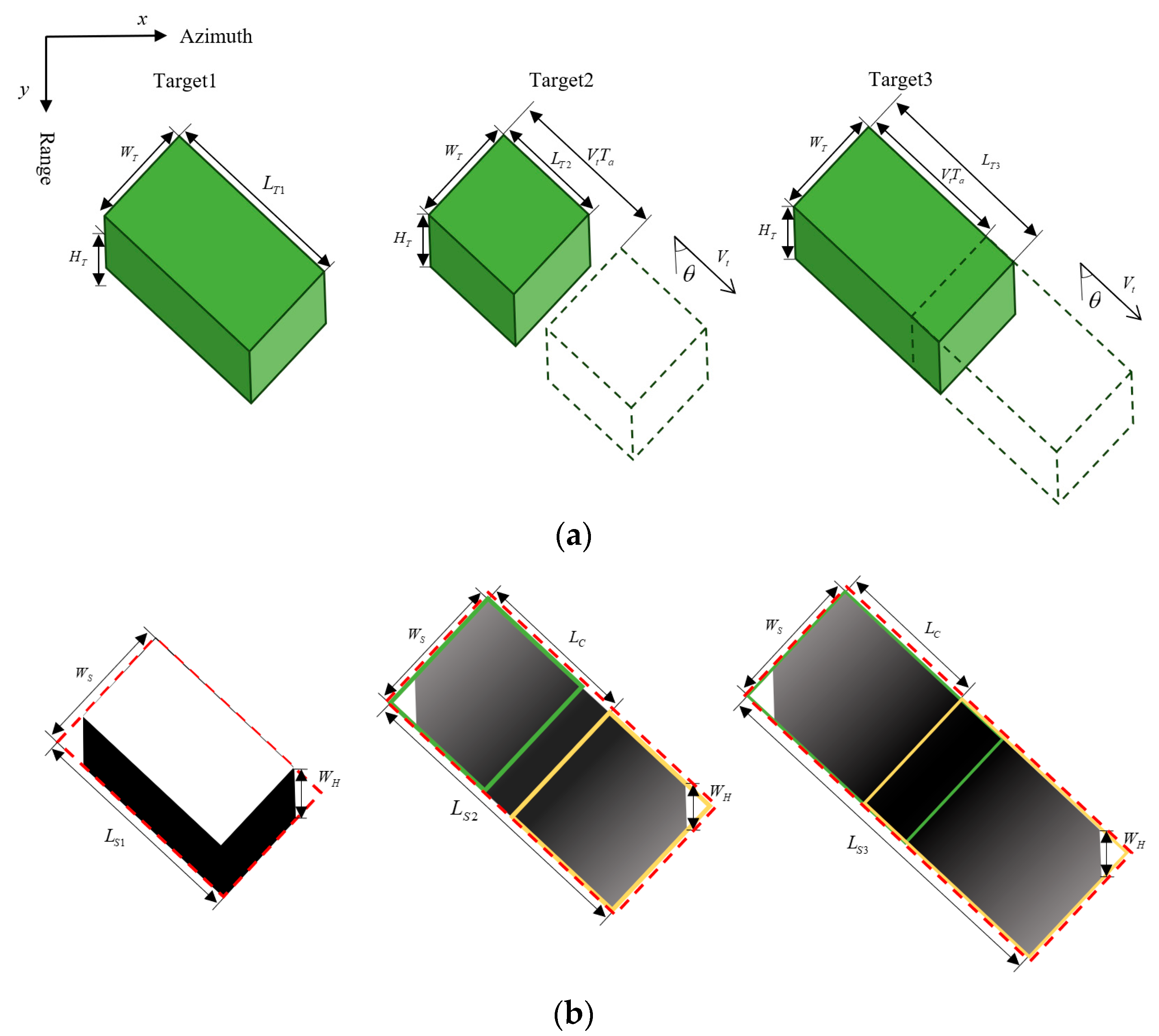
2.1. Formation of Two Types of Moving Target Shadows
- (1)
- Type I shadow,
- (2)
- Type II shadow,
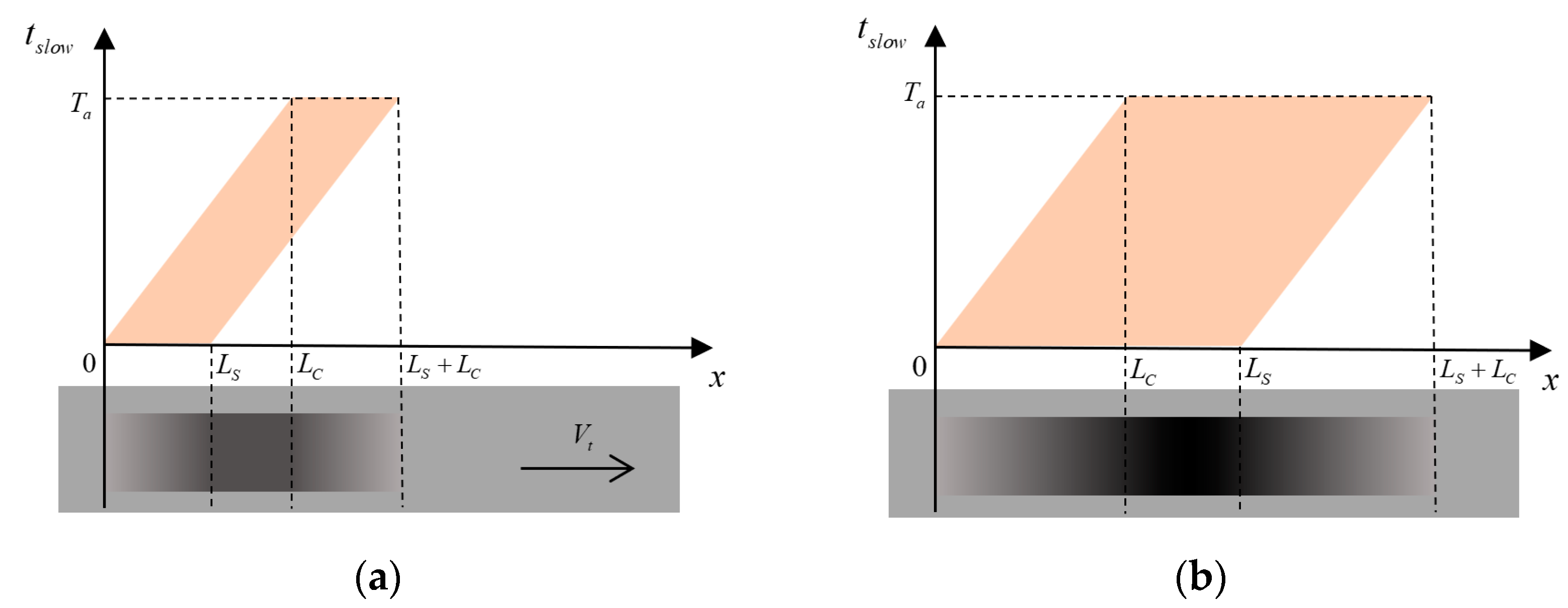
2.2. Signal-to-Clutter Ratio of Moving Target Shadows
- (1)
- Type I shadow,
- (2)
- Type II shadows,
- (1)
- Type I shadows
- (2)
- Type II shadows
3. Experiment and Analysis of Dynamic Target Shadow Characteristics in ViSAR System
3.1. Maximum Detectable Speed of Moving Targets
3.2. Minimum Clutter Backscatter Coefficient
3.3. Effective Shadow Pixel Count for Dynamic Targets
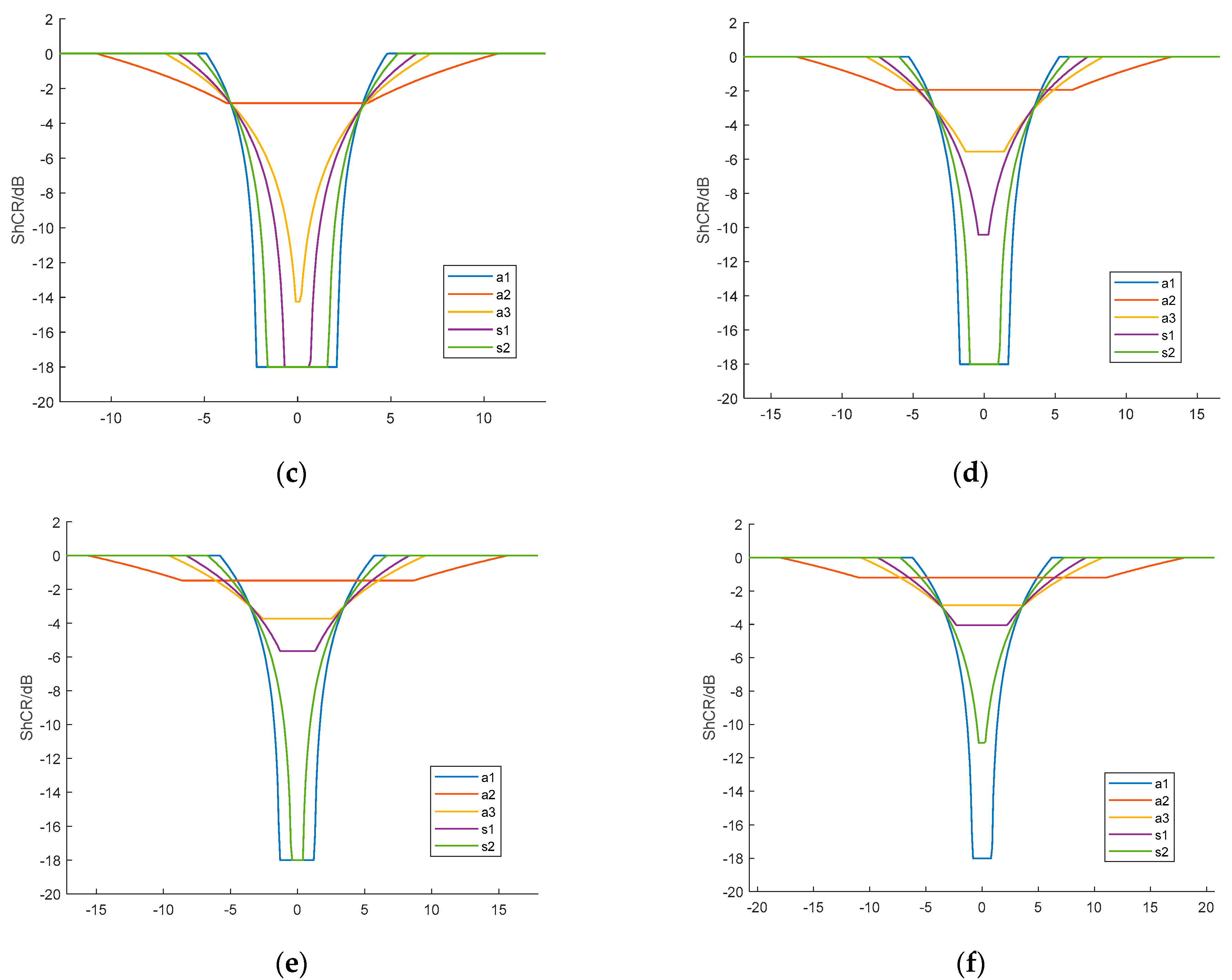
3.4. Analysis of Typical ViSAR System Moving Target Shadow Characteristics
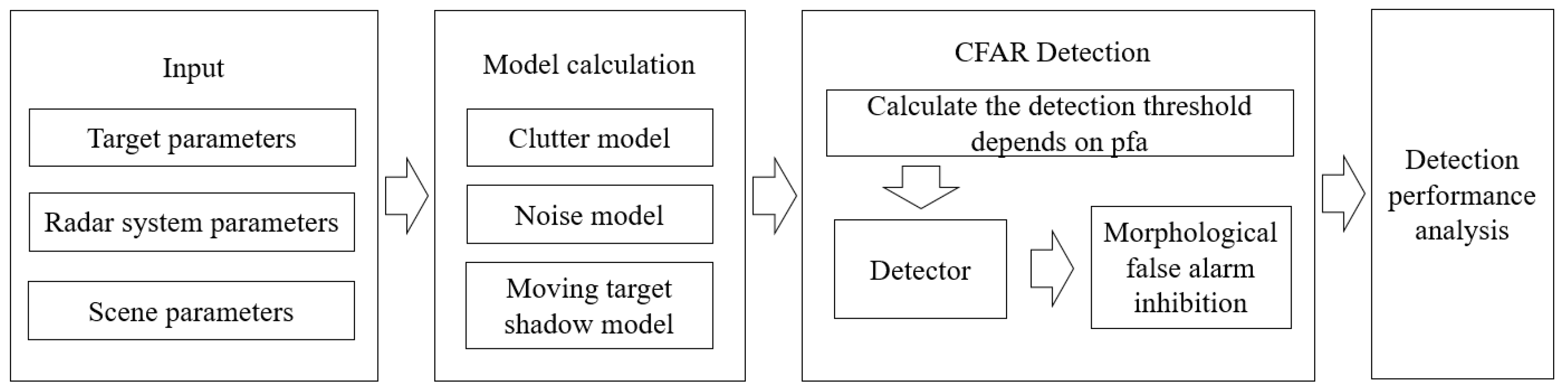
4. ViSAR Moving Target Shadow Detection Simulation Experiment
4.1. Experimental Method
4.2. Analysis of Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Soumekh, M. Synthetic Aperture Radar Signal. In Processing with MATLAB Algorithms; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Wu, B.; Gao, Y.; Ghasr, M.T.; Zougui, R. Resolution-Based Analysis for Optimizing Subaperture measurements in Circular SAR Imaging. IEEE Trans. Instrum. Meas. 2018, 67, 2804–2811. [Google Scholar] [CrossRef]
- He, Z.; Chen, X.; Yi, T.; He, F.; Dong, Z.; Zhang, Y. Moving target shadow analysis and detection for ViSAR imagery. Remote Sens. 2021, 13, 3012. [Google Scholar] [CrossRef]
- Palm, S.; Wahlen, A.; Stanko, S.; Pohl, N.; Wellig, P.; Stilla, U. Real-time onboard processing and ground-based monitoring of FMCW-SAR videos. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2–6 June 2014; pp. 1–4. [Google Scholar]
- Wallace, H.B. Development of a video SAR for FMV through clouds. In Proceedings of the Open Architecture/Open Business Model Net-Centric Systems and Defense Transformation, Baltimore, MD, USA, 21–23 April 2015; pp. 64–65. [Google Scholar]
- Raynal, A.M.; Bickel, D.L.; Doerry, A.W. Stationary and Moving Target Shadow Characteristics in Synthetic Aperture Radar. In Proceedings of the SPIE Defense + Security.Radar Sensor Technology XVIII, Baltimore, MD, USA, 5–7 May 2014. [Google Scholar]
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Boston, MA, USA; London, UK, 1995. [Google Scholar]
- Yang, X.; Shi, J.; Zhou, Y.; Wang, C.; Hu, Y.; Zhang, X.; Wei, S. Ground moving target tracking and refocusing using shadow in video-SAR. Remote Sens. 2020, 12, 3083. [Google Scholar] [CrossRef]
- Raynal, A.M.; Doerry, A.W.; Miller, J.A.; Bishop, E.E.; Horndt, V. Shadow Probability of Detection and False Alarm for Median-Filtered SAR Imagery; Sandia National Lab: Albuquerque, NM, USA; General Atomics Aeronautical Systems, Inc.: San Diego, CA, USA, 2014. [Google Scholar]
- Shi, H.Y.; Hou, Z.T.; Guo, X.H.; Li, J.W. Moving Targets Indication Method in Single High Resolution SAR Imagery Based on Shadow Detection. Signal Process 2012, 28, 1706–1713. [Google Scholar]
- Yamaoka, T.; Suwa, K.; Hara, T.; Nakano, Y. Radar Video Generated from Synthetic Aperture Radar Image. In Proceedings of the International Conference on modern Circuits and Systems Technologies (IGARSS), Beijing, China, 10–15 July 2016; pp. 4582–4585. [Google Scholar]
- Damini, A.; Mantle, V.; Davidson, G. A new approach to coherent change detection in VideoSAR imagery using stack averaged coherence. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–5. [Google Scholar]
- Wang, X.; Tian, T.; Tian, J. Shadow detection method of VideoSAR Moving Object based on Background modeling. J. Intell. Syst. 2022, 17, 10. [Google Scholar]
- Ding, J.S. Focusing Algorithms and Moving Target Detection Based on Video SAR. J. Radars 2020, 9, 321–334. [Google Scholar]
- Skolnik, M.I. Radar Handbook, 2nd ed.; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Novak, L.M. Optimal target designation techniques. IEEE Trans. Aerosp. Electron. Syst. 1981, AES–17, 676–684. [Google Scholar] [CrossRef]
- Wells, L.; Sorensen, K.; Doerry, A.; Remund, B. Developments in SAR and IFSAR systems and technologies at sandia national laboratories. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 8–15 March 2003; pp. 1085–1095. [Google Scholar]
- Cerutti-Maori, D.; Klare, J.; Brenner, A.R.; Ender, J.H. Wide-area traffic monitoring with the SAR/GMTI system PAMIR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3019–3030. [Google Scholar] [CrossRef]
- Xueyan, K.; Ruliang, Y. An Effective Imaging method of moving Targets in Airborne SAR Real Data. J. Test. meas. Technol. 2004, 18, 214–218. [Google Scholar]
- Oliver, C. Understanding Synthetic Aperture Radar Images; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]
- Tang, F.; Ji, Y.; Zhang, Y.; Dong, Z.; Wang, Z.; Zhang, Q.; Zhao, B.; Gao, H. Drifting ionospheric scintillation simulation for L-band geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 852–854. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, Z.; Zhang, Y.; Tang, F.; Mao, W.; Zhao, H.; Xu, Z.; Zhang, Q.; Zhao, B.; Gao, H. Equatorial Ionospheric Scintillation Measurement in Advanced Land Observin the minimum size of overlapg Satellite (ALOS) Phased Array-Type L-Band Synthetic Aperture Radar (PALSAR) Observations. Engineering 2024. ahead of print. [Google Scholar] [CrossRef]
- Bangham, J.A.; Pye, C.J.; Impey, S.J.; Aldridge, R.V. Multiscale median and morphological filters used for 2D pattern recognition. In Proceedings of the IEE Colloquium on Morphological and Nonlinear Image Processing Techniques, London, UK, 10 June 1993; pp. 511–513. [Google Scholar]







| Parameters | Values | |
|---|---|---|
| System parameters | Frequency (GHz) | 35 |
| Resolution (m) | 0.5 | |
| Platform altitude (km) | 600 | |
| Platform velocity (m/s) | 7556 | |
| Synthetic aperture time (s) | 0.63 | |
| Viewing angle (°) | 40 | |
| Target parameters | Target velocity (m/s) | 3, 6, 9, 12, 15, 18 |
| Target length (m) | 8 |
| Parameters | Values | |
|---|---|---|
| System parameters | Center frequency (GHz) | 35 |
| Resolution (m) | 0.5 | |
| Platform altitude (km) | 600 | |
| Platform velocity (m/s) | 7556 | |
| Synthetic aperture time (s) | 0.63 | |
| Viewing angle (°) | 40 | |
| Target parameters | Target velocity (m/s) | 10 |
| Target length (m) | 2, 4, 6, 8, 10, 12 |
| Parameters | Airborne System a1 | Airborne System a2 | Airborne System a3 | Spaceborne System s1 | Spaceborne System s2 | |
|---|---|---|---|---|---|---|
| System parameters | Frequency (GHz) | 235 | 35 | 35 | 35 | 35 |
| Resolution (m) | 0.2 | 0.5 | 0.5 | 0.5 | 0.5 | |
| Platform altitude (km) | 4 | 8 | 8 | 600 | 400 | |
| Platform velocity (m/s) | 80 | 40 | 80 | 7556 | 7667 | |
| Synthetic aperture time (s) | 0.23 | 2.42 | 1.21 | 0.96 | 0.63 | |
| Incident angle (°) | 40 | |||||
| Target parameters | Target velocity (m/s) | 10 | ||||
| Critical size (m) | 2.1 | 22.3 | 11.2 | 8.9 | 5.8 | |
| Shadow area length (m) | 9.1 | 29.3 | 18.2 | 15.9 | 12.8 | |
| Shadow area width (m) | 5.6 | 5.6 | 5.6 | 5.6 | 5.6 | |
| Pure shadow length (m) | 4.5 | 0 | 0 | 0 | 0.2 | |
| Shadow area pixel count | 1277 | 657 | 407 | 355 | 287 | |
| Effective shadow pixel count | 392 | 0 | 154 | 154 | 154 | |
| ViSAR System | 3 | 6 | 9 | 12 | 15 | 18 | |
|---|---|---|---|---|---|---|---|
| a1 | 392 | 392 | 392 | 392 | 392 | 392 | 392 |
| a2 | 154 | 154 | 0 | 0 | 0 | 0 | 51 |
| a3 | 154 | 154 | 154 | 154 | 0 | 0 | 103 |
| s1 | 154 | 154 | 154 | 154 | 154 | 0 | 128 |
| s2 | 154 | 154 | 154 | 154 | 154 | 154 | 154 |
| ViSAR System | Small Vehicles | Medium-Sized Vehicles | Large Vehicles | |
|---|---|---|---|---|
| a1 | 114 | 170 | 392 | 232 |
| a2 | 0 | 0 | 0 | 0 |
| a3 | 0 | 72 | 154 | 78 |
| s1 | 0 | 72 | 154 | 78 |
| s2 | 44 | 72 | 154 | 93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, B.; Yu, A.; Tong, W.; He, Z. Performance Analysis of Moving Target Shadow Detection in Video SAR Systems. Remote Sens. 2024, 16, 1825. https://doi.org/10.3390/rs16111825
Wei B, Yu A, Tong W, He Z. Performance Analysis of Moving Target Shadow Detection in Video SAR Systems. Remote Sensing. 2024; 16(11):1825. https://doi.org/10.3390/rs16111825
Chicago/Turabian StyleWei, Boxu, Anxi Yu, Wenhao Tong, and Zhihua He. 2024. "Performance Analysis of Moving Target Shadow Detection in Video SAR Systems" Remote Sensing 16, no. 11: 1825. https://doi.org/10.3390/rs16111825
APA StyleWei, B., Yu, A., Tong, W., & He, Z. (2024). Performance Analysis of Moving Target Shadow Detection in Video SAR Systems. Remote Sensing, 16(11), 1825. https://doi.org/10.3390/rs16111825






