Measuring Tilt with an IMU Using the Taylor Algorithm
Abstract
1. Introduction
2. Micro-Electro-Mechanical System Errors
- —proof mass;
- —dumping coefficient;
- k—spring constant;
- —force.
2.1. Calibration Techniques
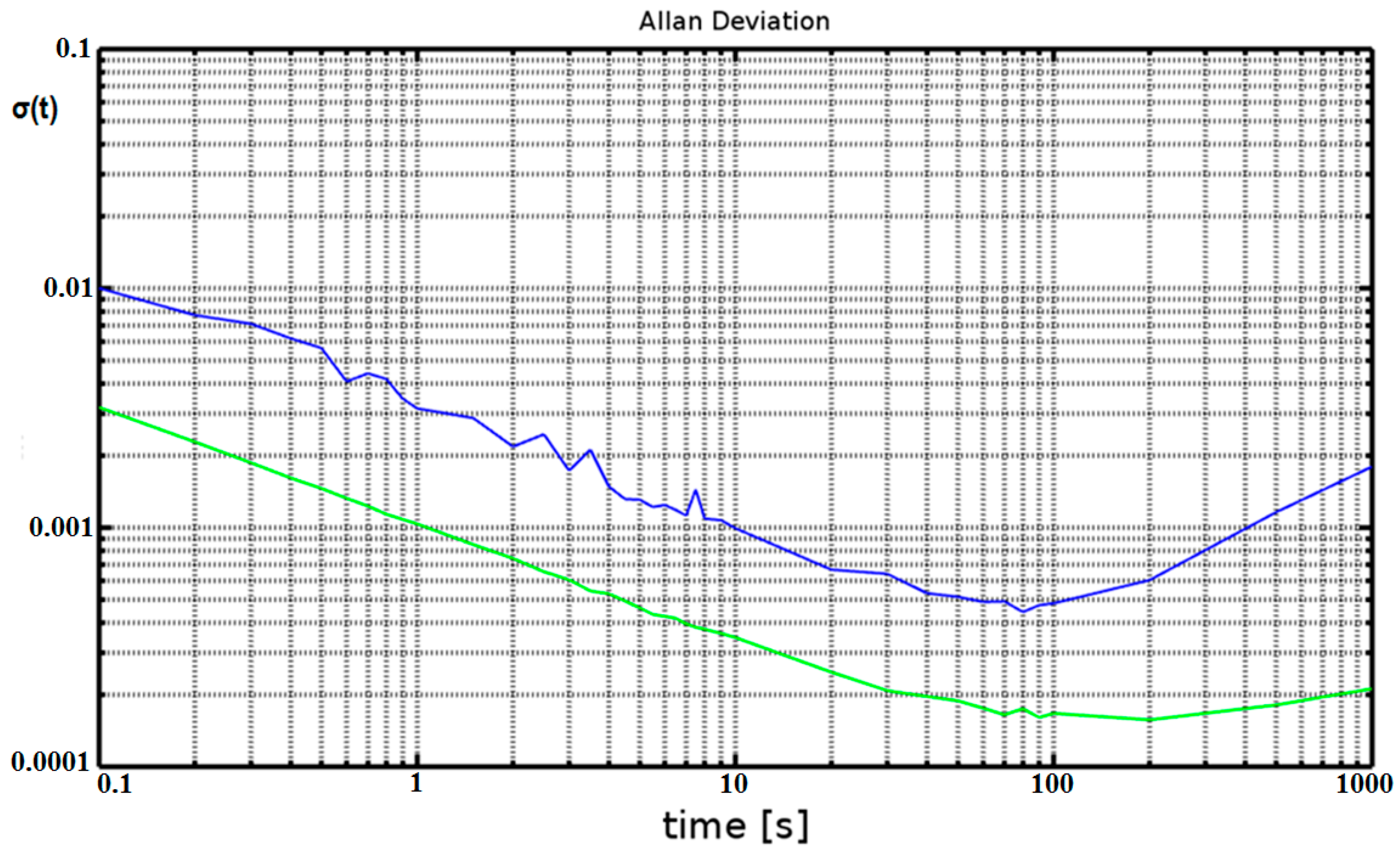
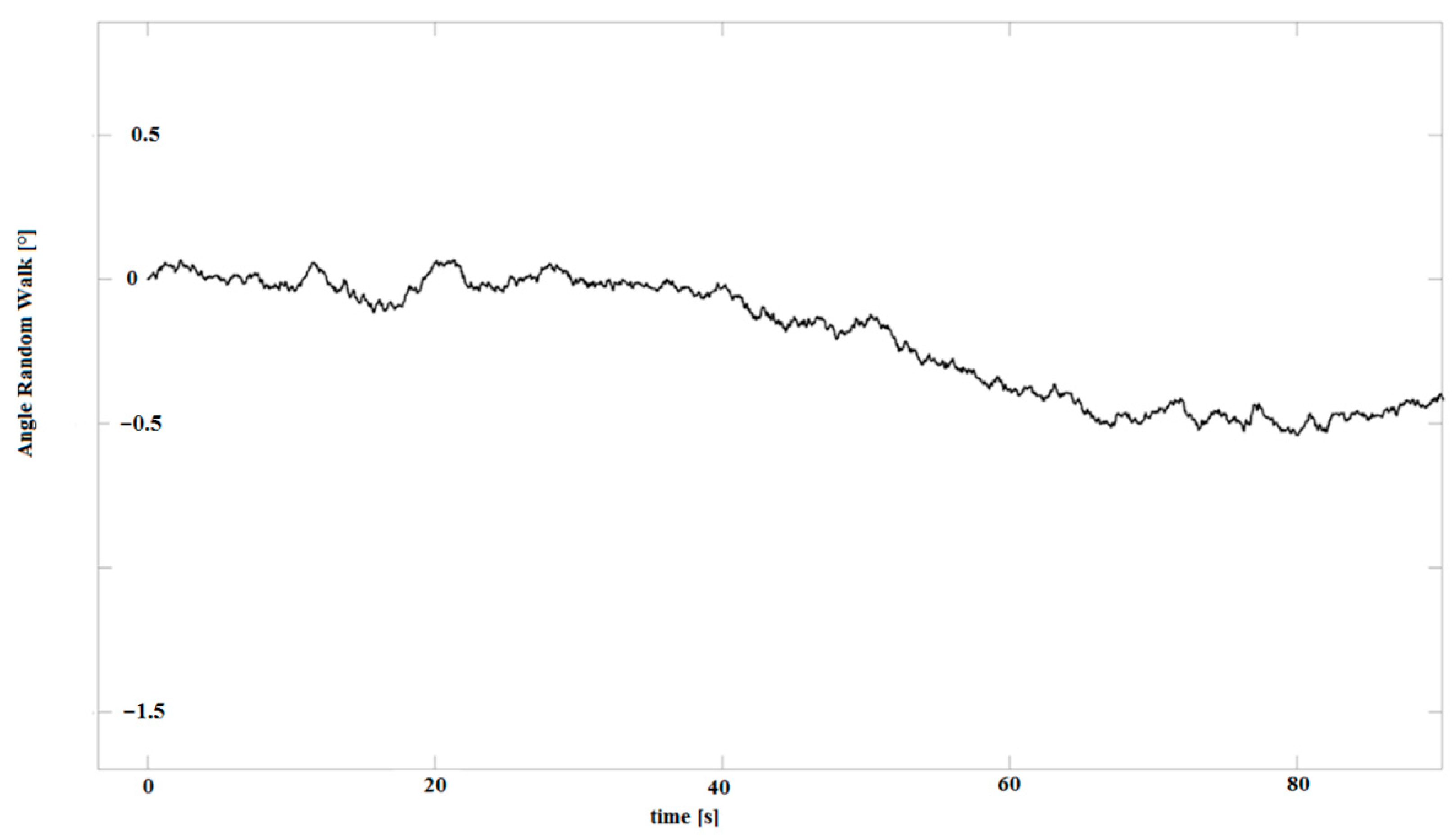
2.2. Errors Accumulated over Time
3. Problem Definition
3.1. Principle of Equivalence as the Main Problem of Inertial Navigation
3.2. Cumulative Error Correction
| Algorithm 1: Representation of the impact of angle error on overall fusion performance |
| = 10°; = 30°; = 0 ; = 0 ; = 0 ; = 10.000° = 30.000° °; ° = 0.001 G [;=0.001 G ; = 0.001 G []; = 10.043° = 30.021° |
4. Materials and Methods
4.1. New Pitch, Roll, and Accelerometer Bias Estimation Incremental Method
4.2. Numerical Example
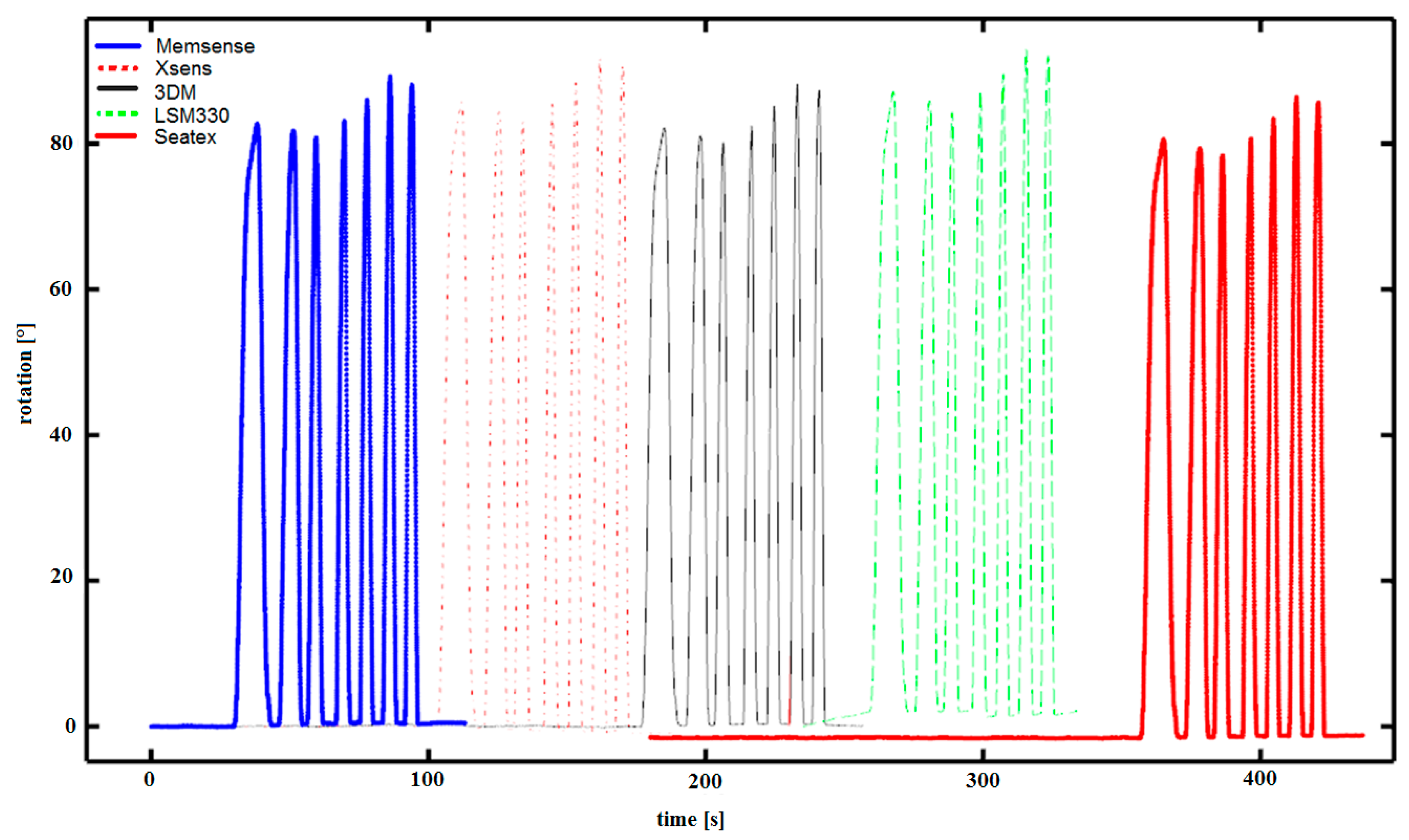
4.3. Algorithm Verification Using Simulation
| Algorithm 2: Algorithm test pseudocode representation |
| %initialization = 30; = 10; = 0.005; = 0.002; = 0.003; for i = 1:5 end ; |
4.4. Algorithm Verification Using the Side Effect of New Method—Simulation
| Algorithm 3: Proposed algorithm’s side effect test pseudocode representation |
| for j = 1:1000 %add random noise = 30°; = 10°; = = 0.002 + ; = 0.003 + ; for i = 1:5 end end |
5. Results
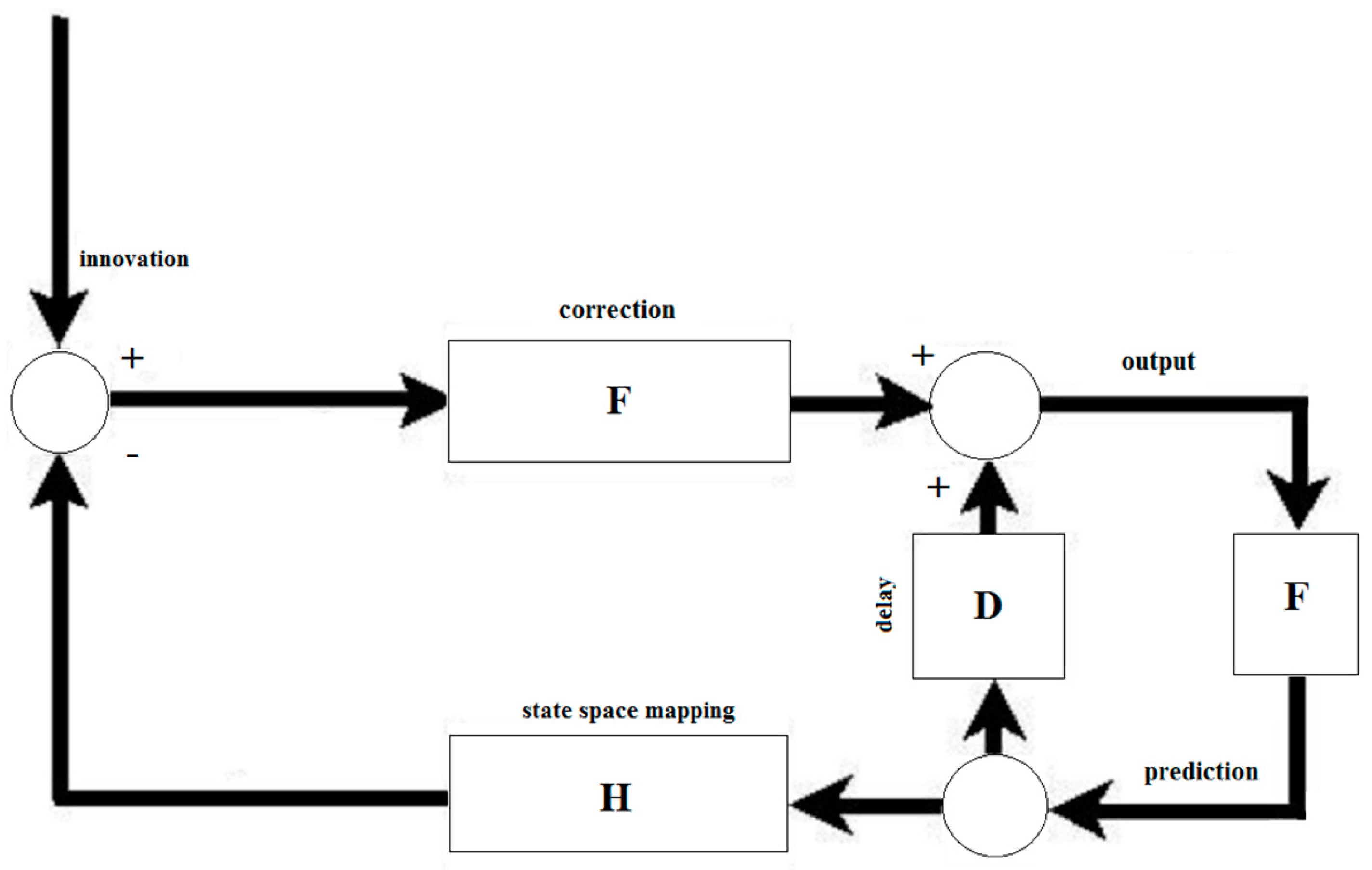
Integration of Proposed Algorithm with Kalman Sensor Fusion Algorithm
6. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: Pseudocode representation of the Kalman filter fusion process |
| for i = start to end end |
- —estimation vector:
- —covariance of the observation noise (uncertainty of the measurement).
- —covariance of the process noise (uncertainty of the system model).
- —Kalman gain.
- —estimate covariance matrix (uncertainty of the state estimate).
| Algorithm A2: Pseudocode linear acceleration definition |
| //set North–East–Down vector and linear acceleration LinNoG NED = ; LinNoG = //random roll and pitch = randn(1); = randn(1); //direct cosine matrix for roll and pitch DCM = Euler2DCM( × deg2rad, × deg2rad, 0); BiasFromG = DCM × NED; //overall acceleration = BiasFromG + DCM × ; //reverse operation, calculate acceleration in MEMS framework NoG = ( − DCM × NED); //calculate above linear acceleration, inverse operation LinNoG = = inv(DCM) × ( − DCM × NED); |
- NED—North–East–Down framework;
- DCM—direct cosine matrix;
- deg2rad = pi/180;
- rad2deg = 180/pi;
- LinNoG—linear acceleration without gravitational component (may be biased).
| Algorithm A3: Pseudocode representation of the proposed algorithm |
| function = asolve_bias(, ,, ) |
| Algorithm A4: Pseudocode representation of integration of the proposed algorithm and Kalman algorithm |
| Initialize , , and //uncertainty of the state estimate //uncertainty of the system model //uncertainty of the measurement for i = start to :end read Xsens MEMS sensor , , %%%%%%%%%%%%%%%%%%integration with asolve_bias from Algorithm 3 for i = 1:5 end ; End |
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Demkowicz, J. Autonomous Vehicle Navigation in Dense Urban Area in Global Positioning Context. In Proceedings of the 2018 11th International Conference on Human System Interaction (HSI), Gdansk, Poland, 4–6 July 2018. [Google Scholar]
- ASG-EUPOS. EUPOS, System Description. Reference Stations. Available online: http://www.asgeupos.pl/ (accessed on 17 February 2024).
- Yeong, J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: London, UK, 2013. [Google Scholar]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS/GNSS Principles and Applications; Artech House: London, UK, 2017. [Google Scholar]
- Woodman, O.J. An Introduction to Inertial Navigation; University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Demkowicz, J.; Bikonis, K. Study of Array of MEMS Inertial Measurements Units Under Quasi-Stationary and Dynamic Conditions. Pol. Marit. Res. 2021, 28, 150–155. [Google Scholar] [CrossRef]
- Demkowicz, J.; Bikonis, K. MEMS Technology Quality Requirements as Applied to Multibeam Echosounder. Pol. Marit. Res. 2018, 25, 59–64. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behaviour; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Azizi, T.; Kerr, G. Application of Stability Theory in Study of Local Dynamics of Nonlinear Systems. J. Appl. Math. Phys. 2020, 8, 1180–1192. [Google Scholar] [CrossRef]
- Quinchia, A.G.; Falco, G.; Falletti, E.; Dovis, F.; Ferrer, C. A Comparison between Different Error Modeling of MEMS Applied to GPS/INS Integrated Systems. Sensors 2013, 13, 9549–9588. [Google Scholar] [CrossRef] [PubMed]
- Demkowicz, J. MEMS Gyro in the Context of Inertial Positioning. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 247–251. [Google Scholar]
- Poddar, S.; Kumar, V.; Kumar, A. A comprehensive overview of inertial sensor calibration techniques. J. Dyn. Syst. Meas. Control 2017, 139, 011006. [Google Scholar] [CrossRef]
- Ru, X.; Gu, N.; Shang, H.; Zhang, H. MEMS Inertial Sensor Calibration Technology: Current Status and Future Trends. Micromachines 2022, 13, 879. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, P.; Syed, Z.; Niu, X.; El-Sheimy, N. A Standard Testing and Calibration Procedure for Low Cost MEMS Inertial Sensors and Units. J. Navig. 2008, 61, 323–336. [Google Scholar] [CrossRef]
- Syed, Z.; Aggarwal, P.; Goodall, C.; Niu, X.; El-Sheimy, N. A New Multi-Position Calibration Method for MEMS Inertial Navigation Systems. Meas. Sci. Technol. 2007, 18, 1897–1907. [Google Scholar] [CrossRef]
- Bekkeng, J.K. Calibration of a Novel MEMS Inertial Reference Unit. IEEE Trans. Instrum. Meas. 2009, 58, 1967–1974. [Google Scholar] [CrossRef]
- Wang, B.; Ren, Q.; Deng, Z.; Fu, M. A Self-Calibration Method for Nonorthogonal Angles Between Gimbals of Rotational Inertial Navigation System. IEEE Trans. Ind. Electron. 2015, 62, 2353–2362. [Google Scholar] [CrossRef]
- Łuczak, S.; Zams, M.; Dabrowski, B.; Kusznierewicz, Z. Tilt Sensor with Recalibration Feature Based on MEMS Accelerometer. Sensors 2022, 22, 1504. [Google Scholar] [CrossRef] [PubMed]
- IEEE Recommended Practice for Inertial Sensor Test Equipment Instrumentation Data Acquisition and Analysis. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=10423 (accessed on 31 March 2011).
- Dong, X.; Huang, X.; Du, G.; Huang, Q.; Huang, Y.; Huang, Y.; Lai, P. Calibration Method of Accelerometer Based on Rotation Principle Using Double Turntable Centrifuge. Micromachines 2022, 13, 62. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Dover Books on Electrical Engineering; Courier Corporation: North Chelmsford, MA, USA, 2005. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering with MATLAB Exercises, 3rd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1997. [Google Scholar]
- Abdolkarimi, E.S.; Mosavi, M.R. A low-cost integrated MEMS-based INS/GPS vehicle navigation system with challenging conditions based on an optimized IT2FNN in occluded environments. GPS Solut. 2020, 24, 108. [Google Scholar] [CrossRef]
- Sayed, A.H. Adaptive Filters; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- IEEE Std 952-1997; IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros. IEEE: New York, NY, USA, 1998.
- Shultz Kenneth, S. Measurement Theory in Action; Taylor & Francis Ltd.: Abingdon, UK, 2020. [Google Scholar]
- MX IMU Product Specification & User Guide Document Number: DOC00295 Document Revision: E MEMSENSE.COM 888.668.8743, USA. Available online: https://www.memsense.com/assets/docs/uploads//mx/DOC00295_Rev-D_MX-IMU_PSUG.pdf (accessed on 29 July 2024).
- MTi-G User Manual and Technical Documentation, Xsens Technologies B.V., France. Available online: https://www.movella.com/products/xsens (accessed on 23 December 2023).
- Quick Start Guide to the 3DMGX3 Soft & Hard Iron Calibration. Available online: https://www.microstrain.com (accessed on 17 February 2024).
- LSM330DLC, iNEMO Inertial Module, 3-axis Accelerometer and 3-axis Gyroscope, Data Sheet, STMicroelectronics. 2016. Available online: https://www.st.com/resource/en/datasheet/dm00037200.pdf (accessed on 29 July 2024).
- Kongsberg Seatex MRU-5 Manual, Copyright© Kongsberg Seatex AS. 2008, Norway. Available online: http://linux.geodatapub.com/shipwebpages/survey%20gear/Multibeam/EM1002%20-%20Powell/manuals/mru%20and%20h%20install%20manual.pdf (accessed on 29 July 2024).
- Sas-Uhrynowski, A. Absolute Gravity Measurements in Poland; Cartography Monographic Series; Institute of Geodesy: Warsaw, Poland, 2002; ISBN 83-916216-2-6. Available online: http://bc.igik.edu.pl/Content/30/PDF/SM_3_15028_8391621626.pdf (accessed on 17 February 2024).


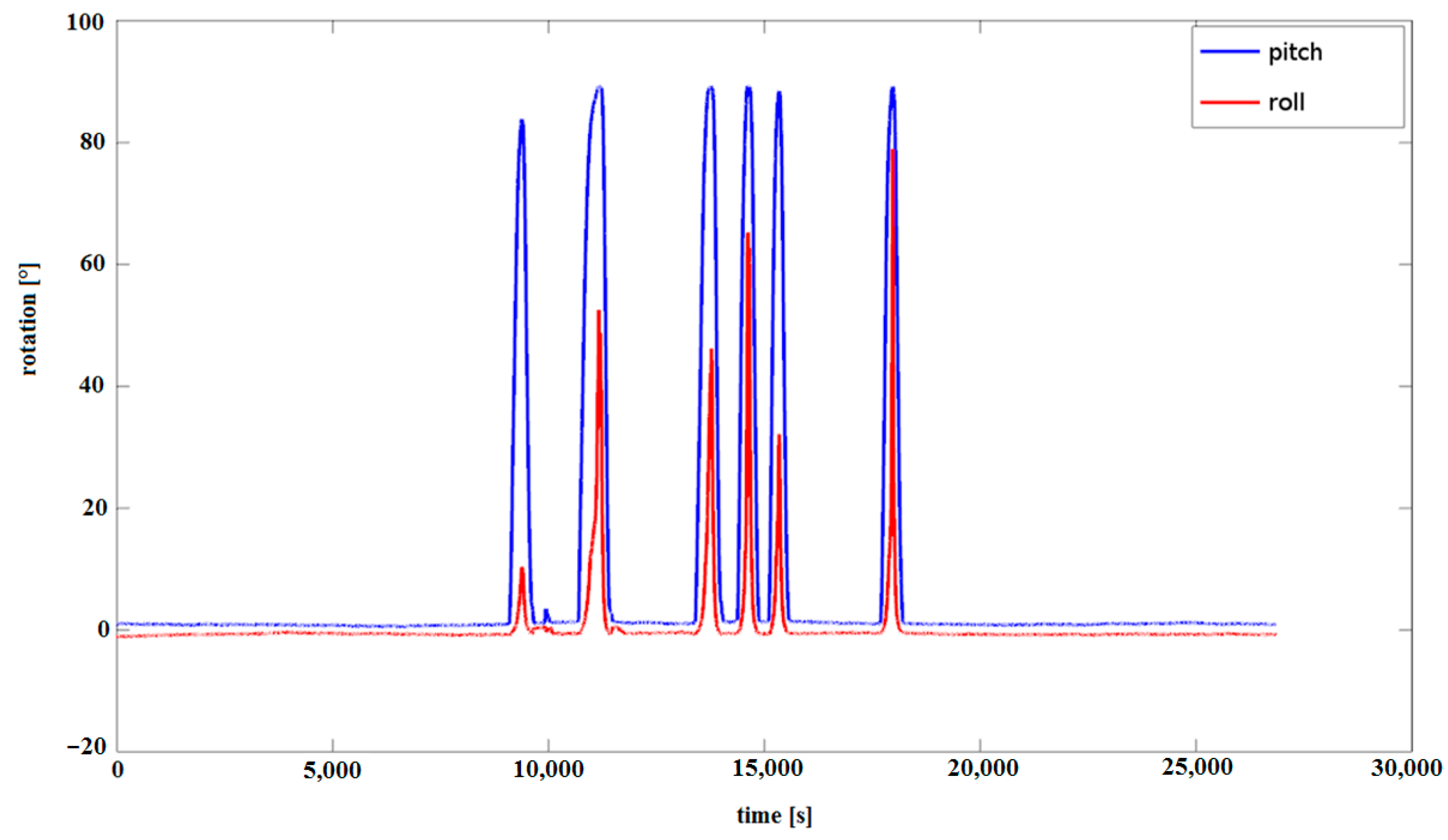

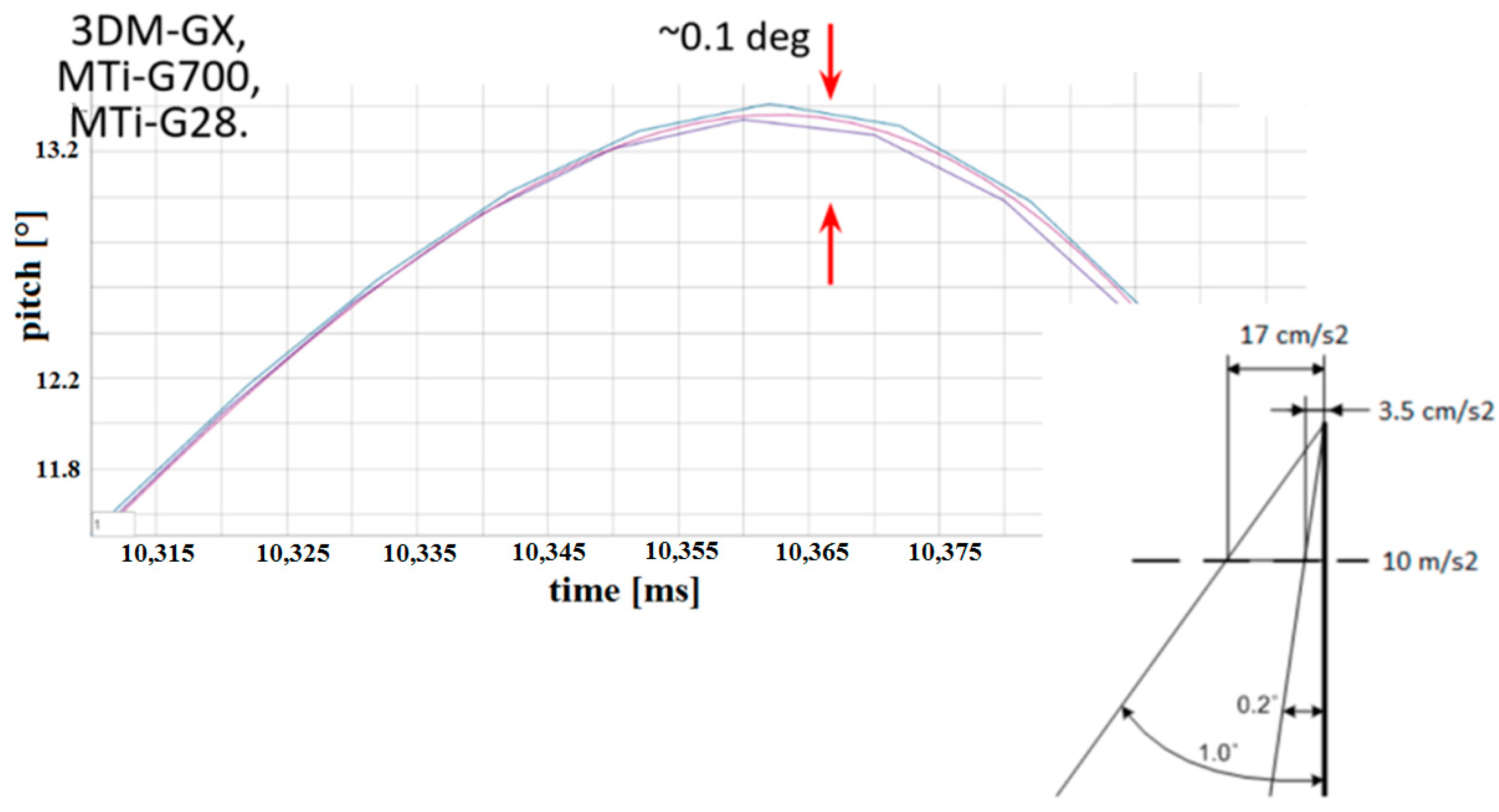
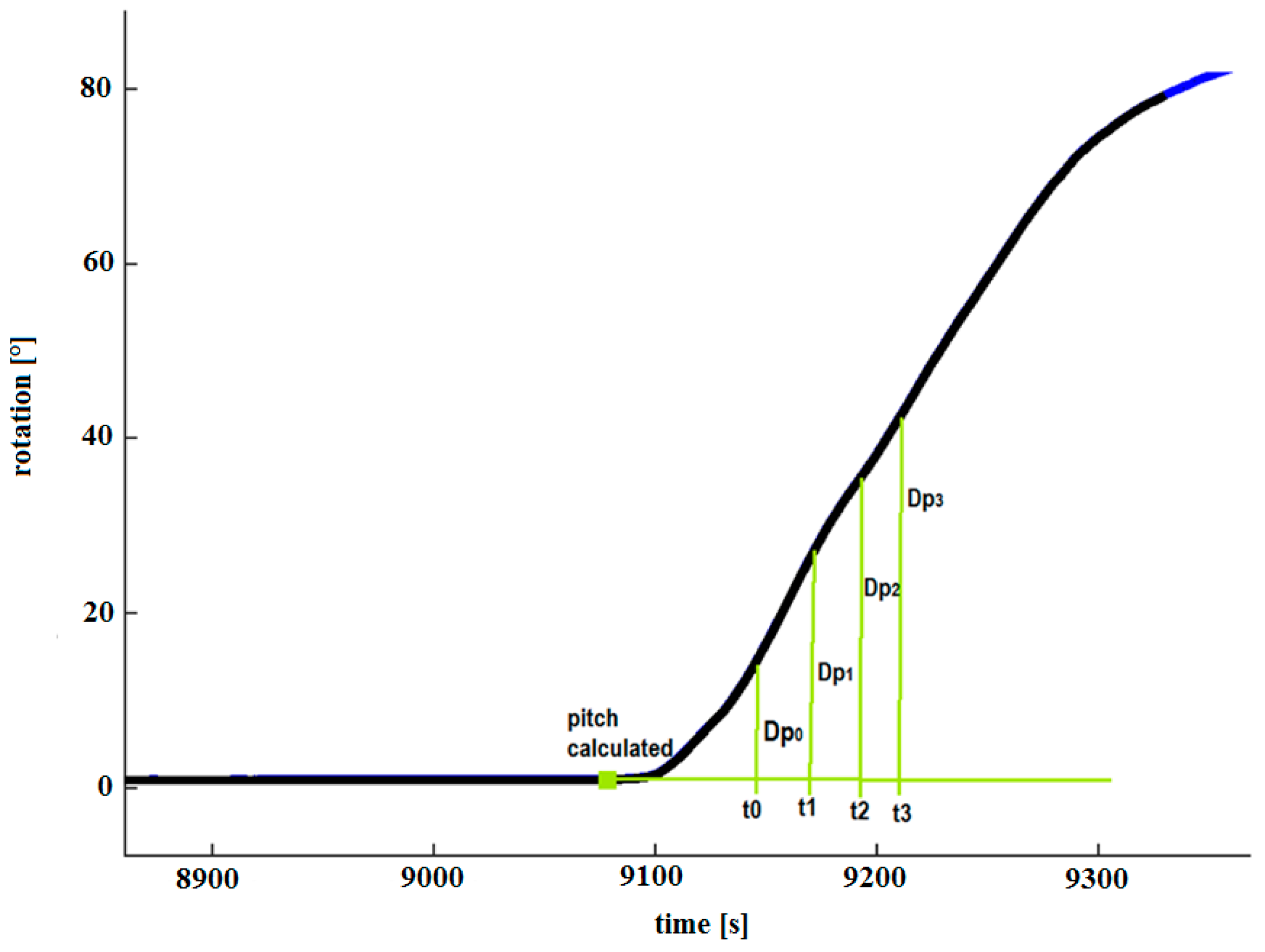
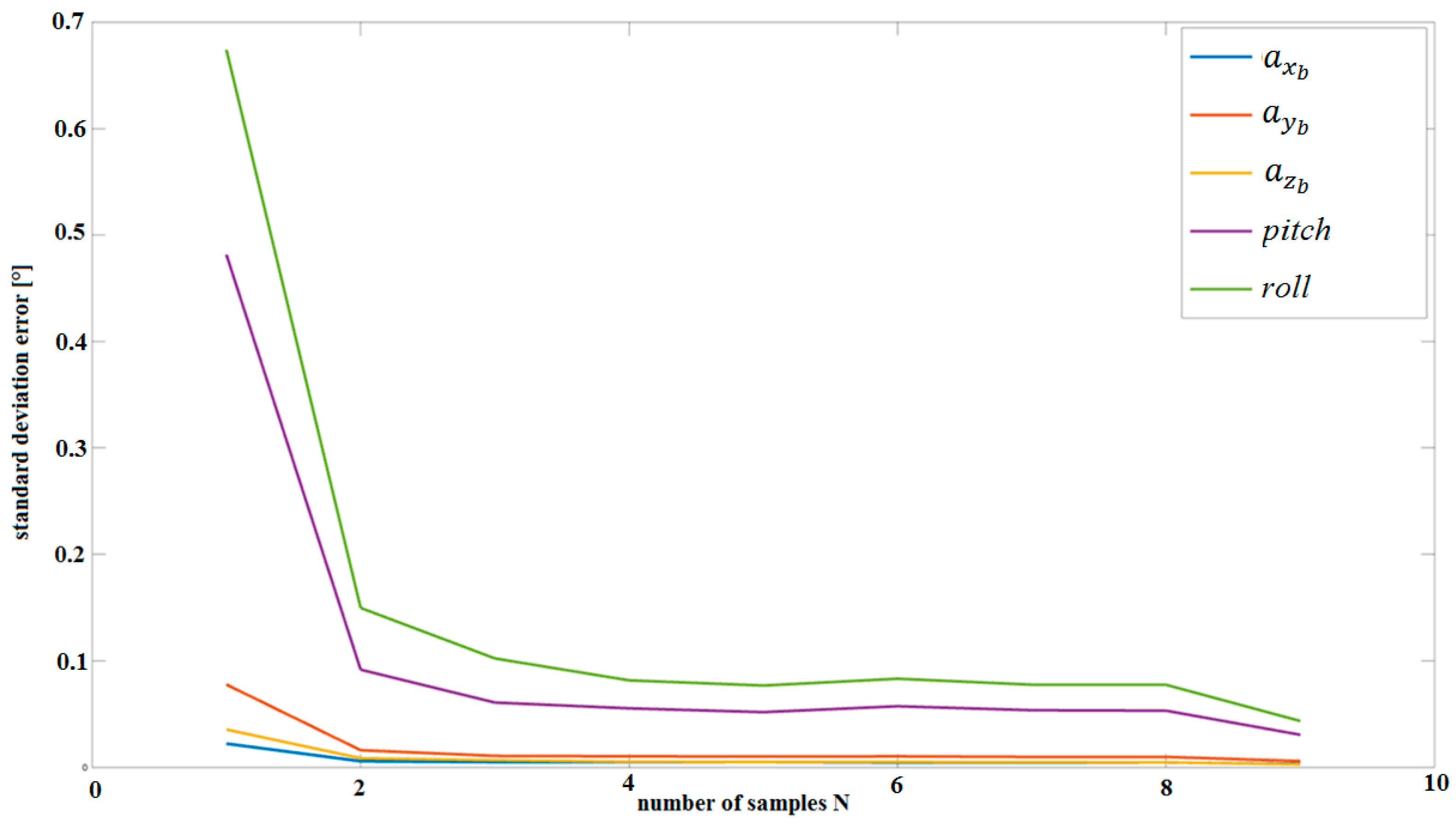
| Accelerometer Dynamic Accuracy | LSM330DLC | LSM330DLC Array |
|---|---|---|
| Bias stability deviation error [m/s2] | 4.4372 × 10−4 | 1.57224 × 10−4 |
| Variance | 4.06215 × 10−4 | 4.66665 × 10−5 |
| Standard error [m/s2] | 0.020154 | 0.006831 |
| Bias [m/s2] | 0.050850 | 0.211349 |
| Pitch/Roll Error [°] | ] | INS Error after 10 s [m] |
|---|---|---|
| 1.0 | 0.17 | 8.5 |
| 0.1 | 0.017 | 0.85 |
| 0.01 | 0.0017 | 0.085 |
| 0.001 | 0.00017 | 0.0085 |
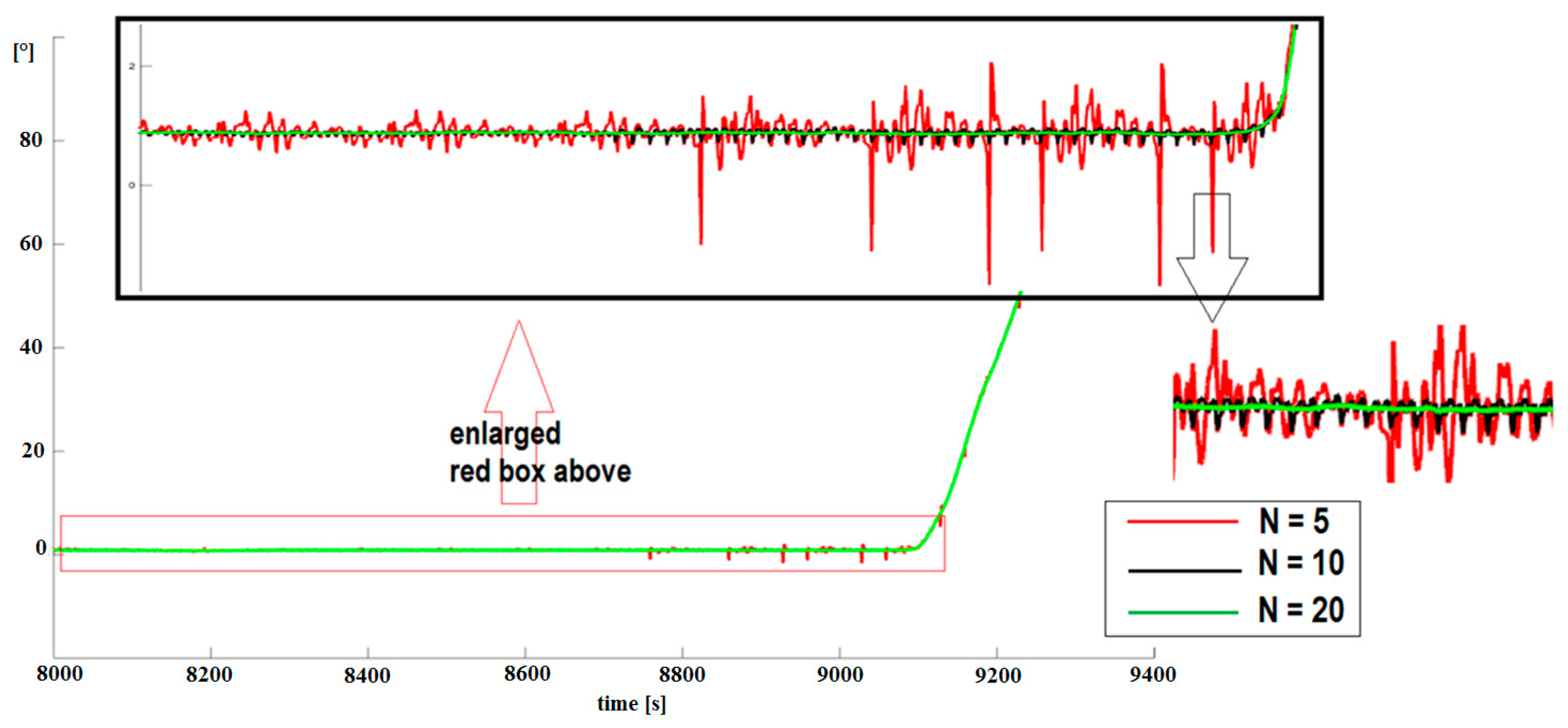
| Number of Samples N | [°] | [°] | ] | ] | ] |
|---|---|---|---|---|---|
| 2 | 0.481 | 0.674 | 0.022 | 0.077 | 0.035 |
| 3 | 0.0917 | 0.149 | 0.0058 | 0.016 | 0.0086 |
| 4 | 0.0609 | 0.102 | 0.005 | 0.0108 | 0.0067 |
| 5 | 0.055 | 0.0817 | 0.0049 | 0.01045 | 0.0053 |
| 6 | 0.0519 | 0.076 | 0.005 | 0.01018 | 0.005 |
| 7 | 0.057 | 0.083 | 0.0045 | 0.010 | 0.005 |
| 8 | 0.0536 | 0.0777 | 0.00455 | 0.0098 | 0.0049 |
| 9 | 0.053 | 0.077 | 0.00467 | 0.0098 | 0.0048 |
| 24 | 0.0305 | 0.0435 | 0.00327 | 0.0059 | 0.0028 |
| Algorithm | Pitch STD [°] |
|---|---|
| Kalman algorithm | 0.202 |
| Proposed algorithm | 0.05625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demkowicz, J. Measuring Tilt with an IMU Using the Taylor Algorithm. Remote Sens. 2024, 16, 2800. https://doi.org/10.3390/rs16152800
Demkowicz J. Measuring Tilt with an IMU Using the Taylor Algorithm. Remote Sensing. 2024; 16(15):2800. https://doi.org/10.3390/rs16152800
Chicago/Turabian StyleDemkowicz, Jerzy. 2024. "Measuring Tilt with an IMU Using the Taylor Algorithm" Remote Sensing 16, no. 15: 2800. https://doi.org/10.3390/rs16152800
APA StyleDemkowicz, J. (2024). Measuring Tilt with an IMU Using the Taylor Algorithm. Remote Sensing, 16(15), 2800. https://doi.org/10.3390/rs16152800







