Oceanic Mesoscale Eddy Fitting Using Legendre Polynomial Surface Fitting Model Based on Along-Track Sea Level Anomaly Data
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Region and Data
2.2. Methods
2.2.1. Cubic B-Spline Curve (One-Dimensional)
2.2.2. Bicubic Quasi-Uniform B-Spline Surface (Two-Dimensional)
2.2.3. Legendre Polynomials (One-Dimensional)
2.2.4. Legendre Polynomial Surfaces (Two-Dimensional)
2.2.5. Cross-Validation
- Randomly divide the existing data samples into 10 subsets;
- Select one subset as the validation set and the remaining nine subsets as the training set;
- Vary the orders of Legendre polynomials in the east–west and north–south directions in the training set, and obtain models trained with different combinations of orders;
- Import the validation set data into each model and record the mean absolute errors (MAEs) of the validation set data under different combinations of orders of Legendre polynomials;
- Repeat the process by iteratively selecting each of the nine training subsets as the validation set and the original validation set as the training set, thus obtaining new validation and training sets;
- Repeat the cross-validation process 10 times in total. Calculate the average MAE for each combination of orders of Legendre polynomials obtained from the 10 cross-validation iterations.
- Compare the average MAE values for different combinations of orders, and select the combination with the smallest MAE as the optimal combination of orders.
3. Results
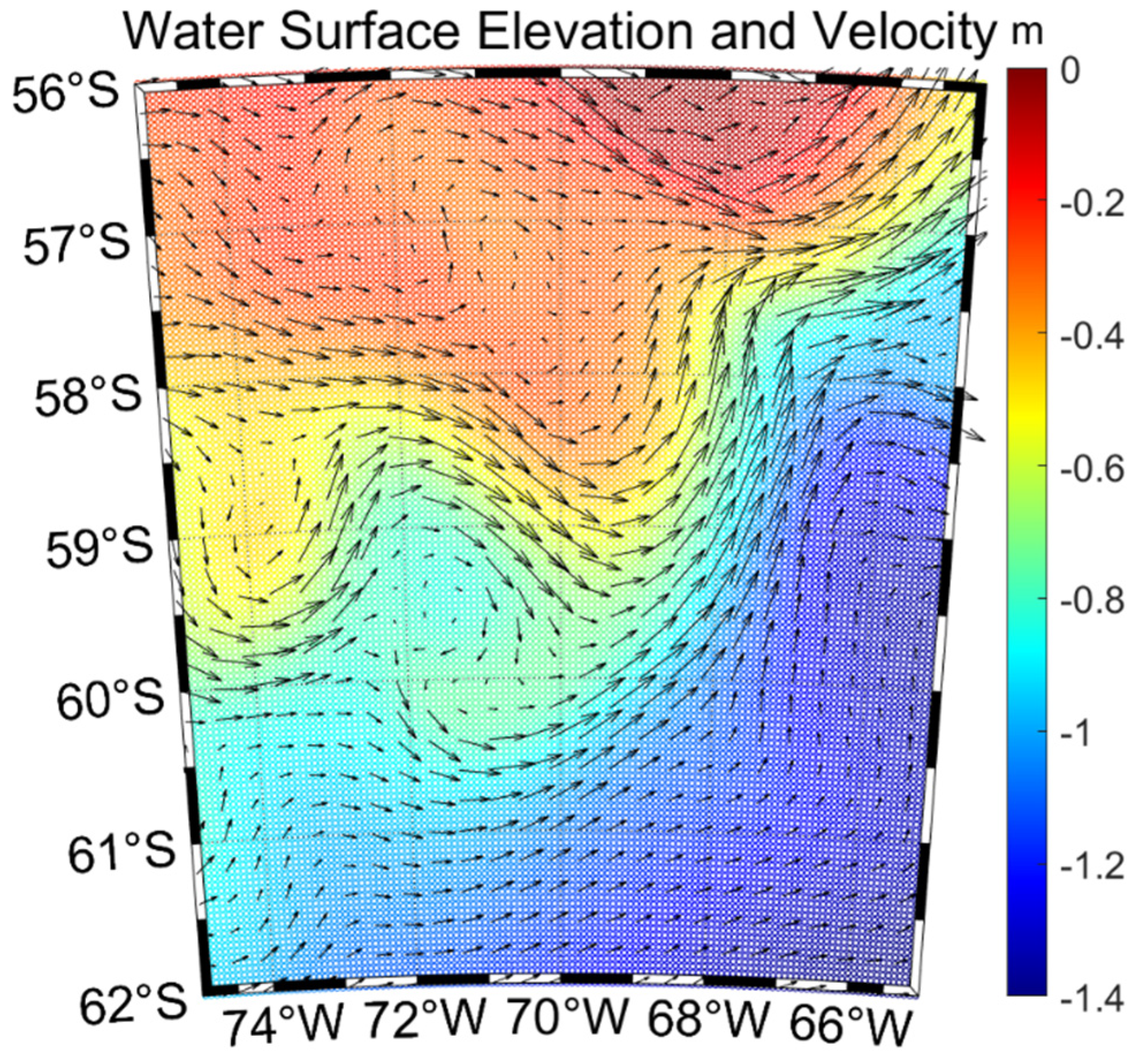
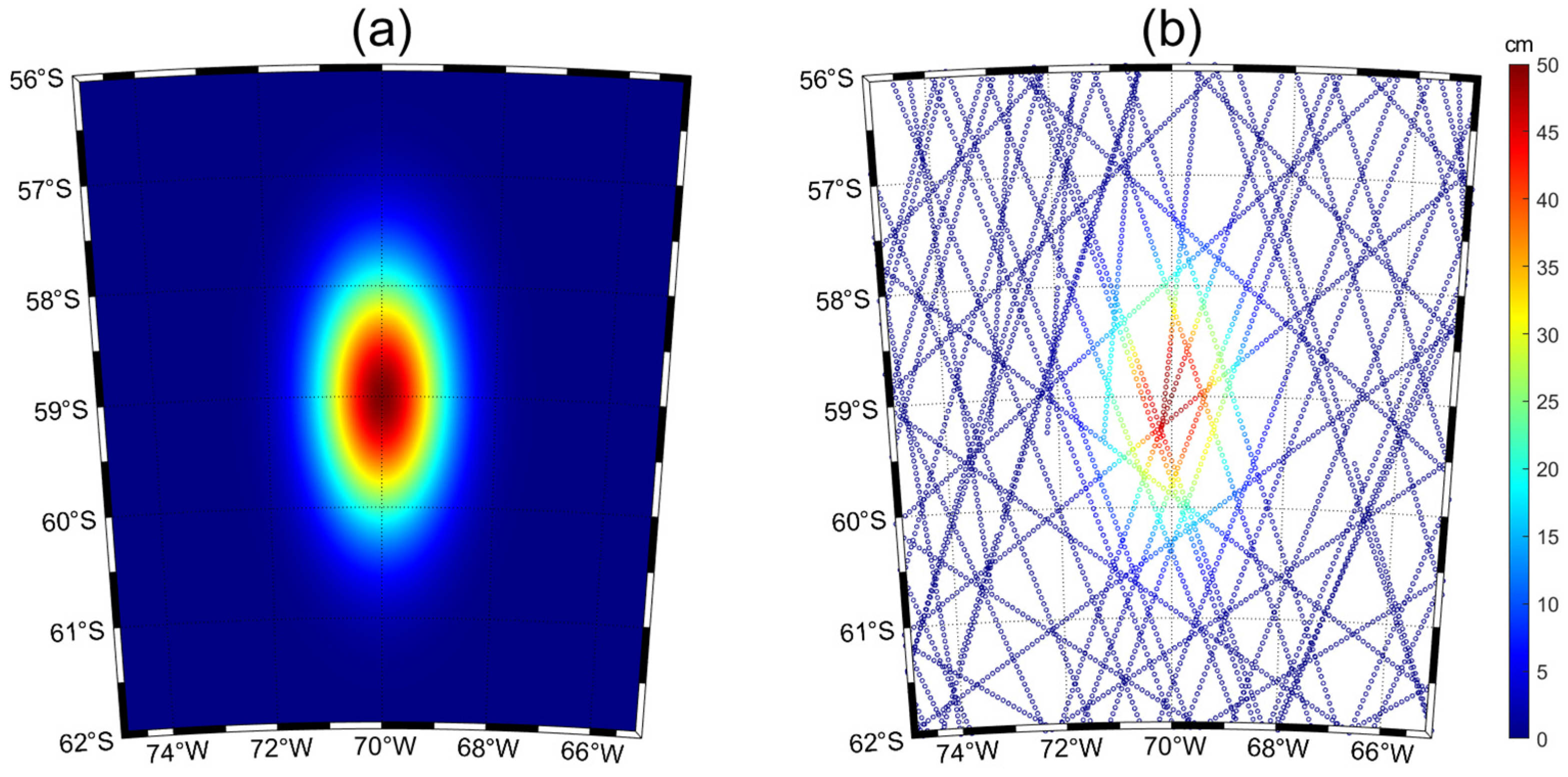
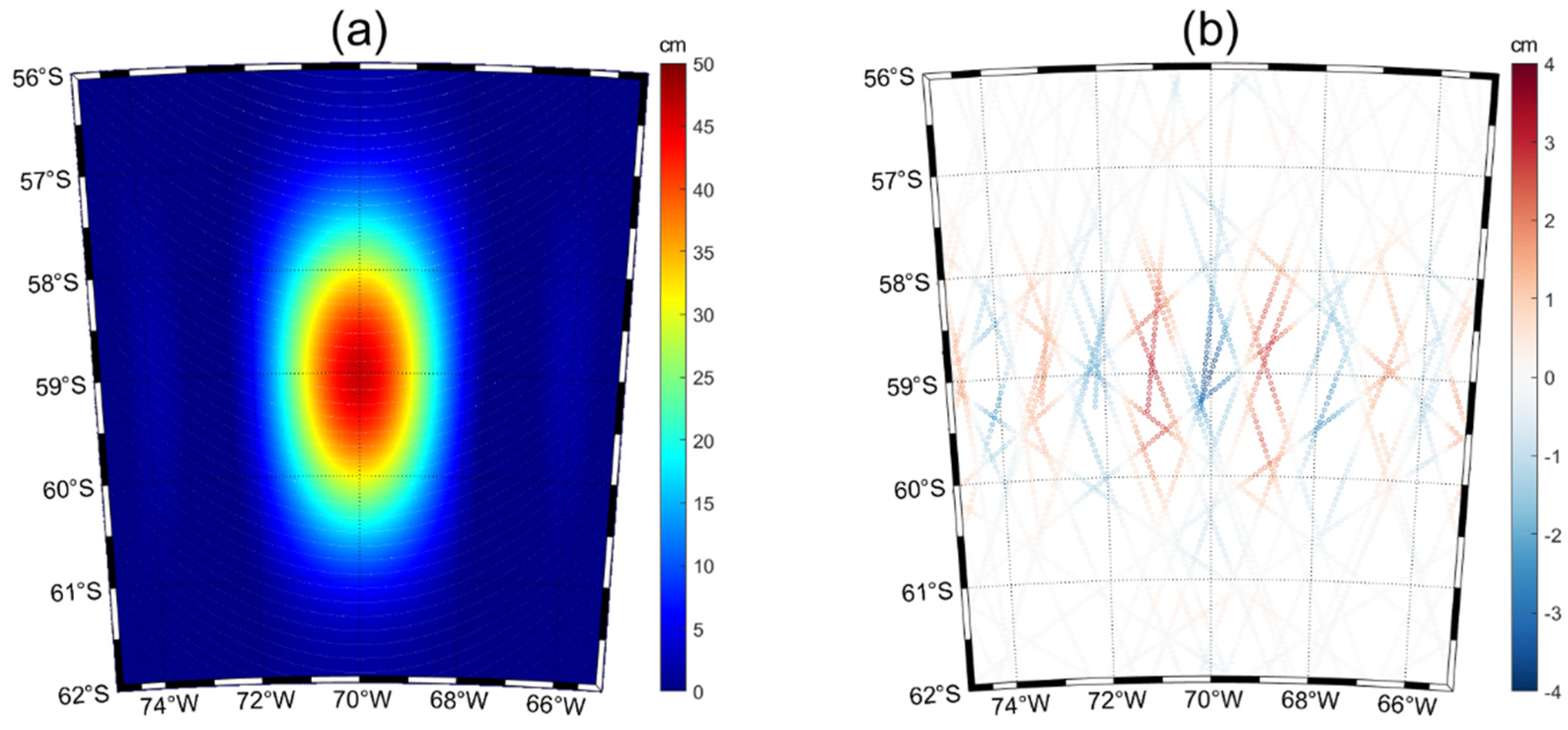
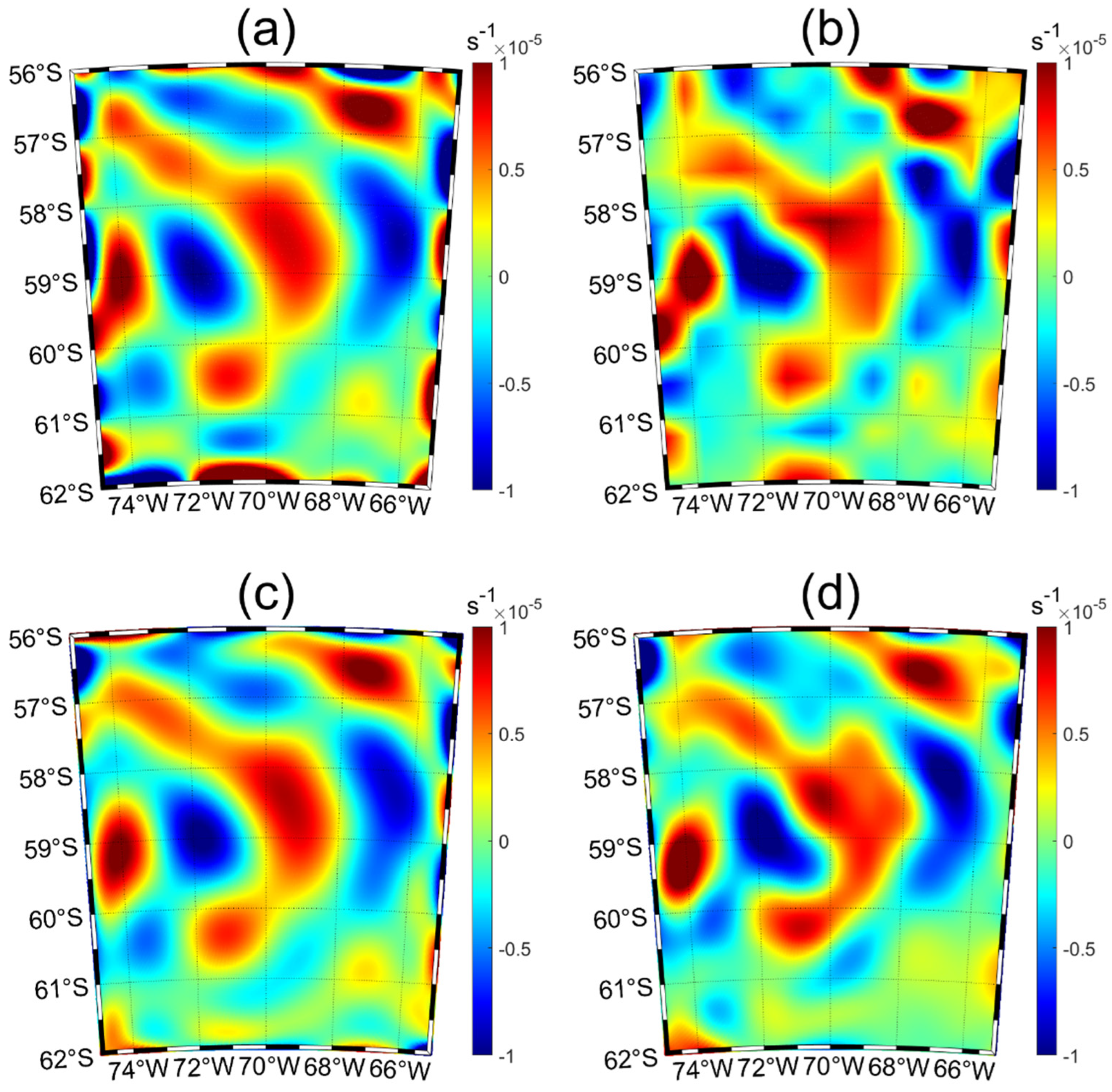
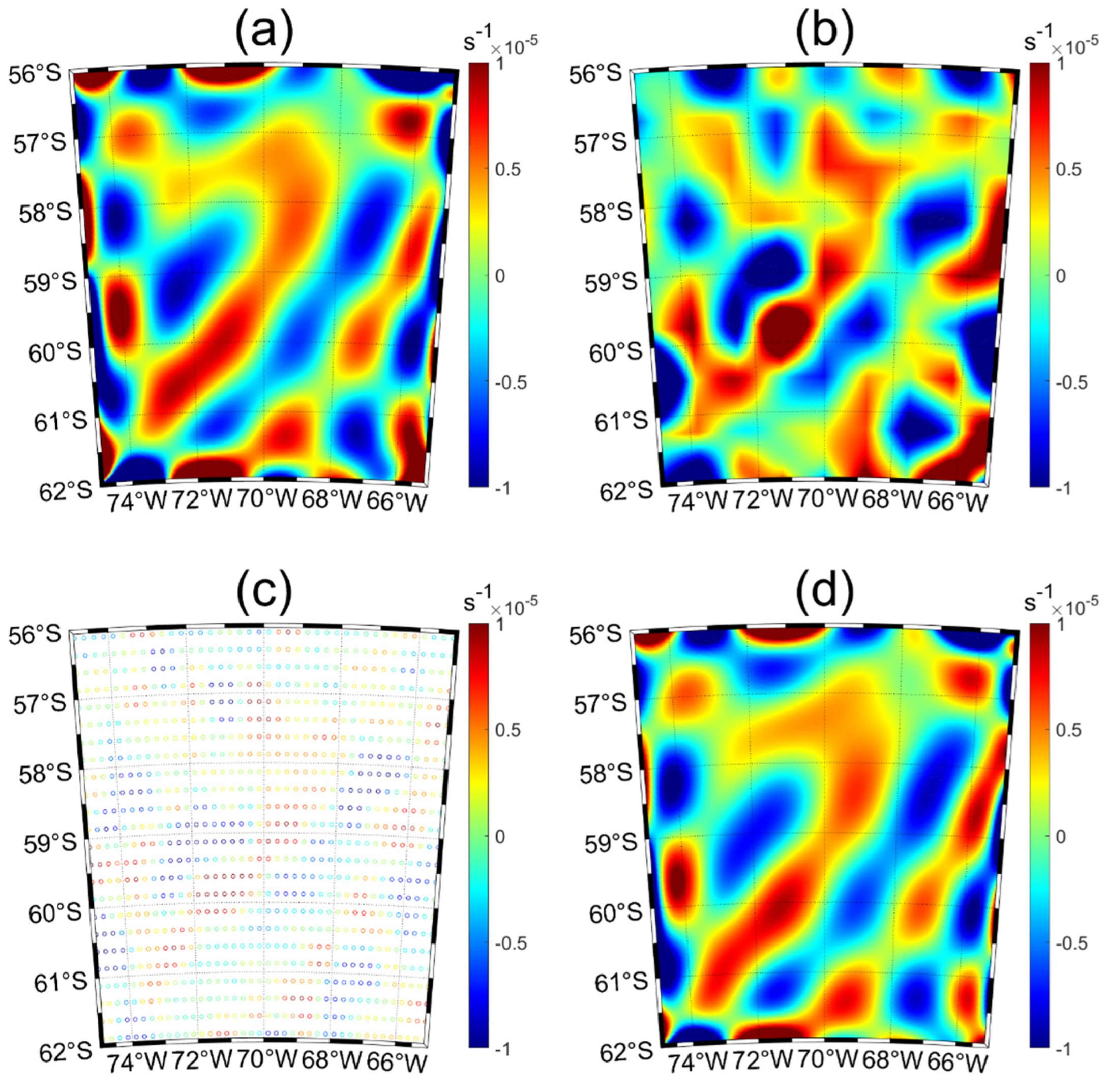
3.1. Comparison of Static Model Bicubic B-Spline Surface Fitting and Legendre Polynomial Surface Fitting
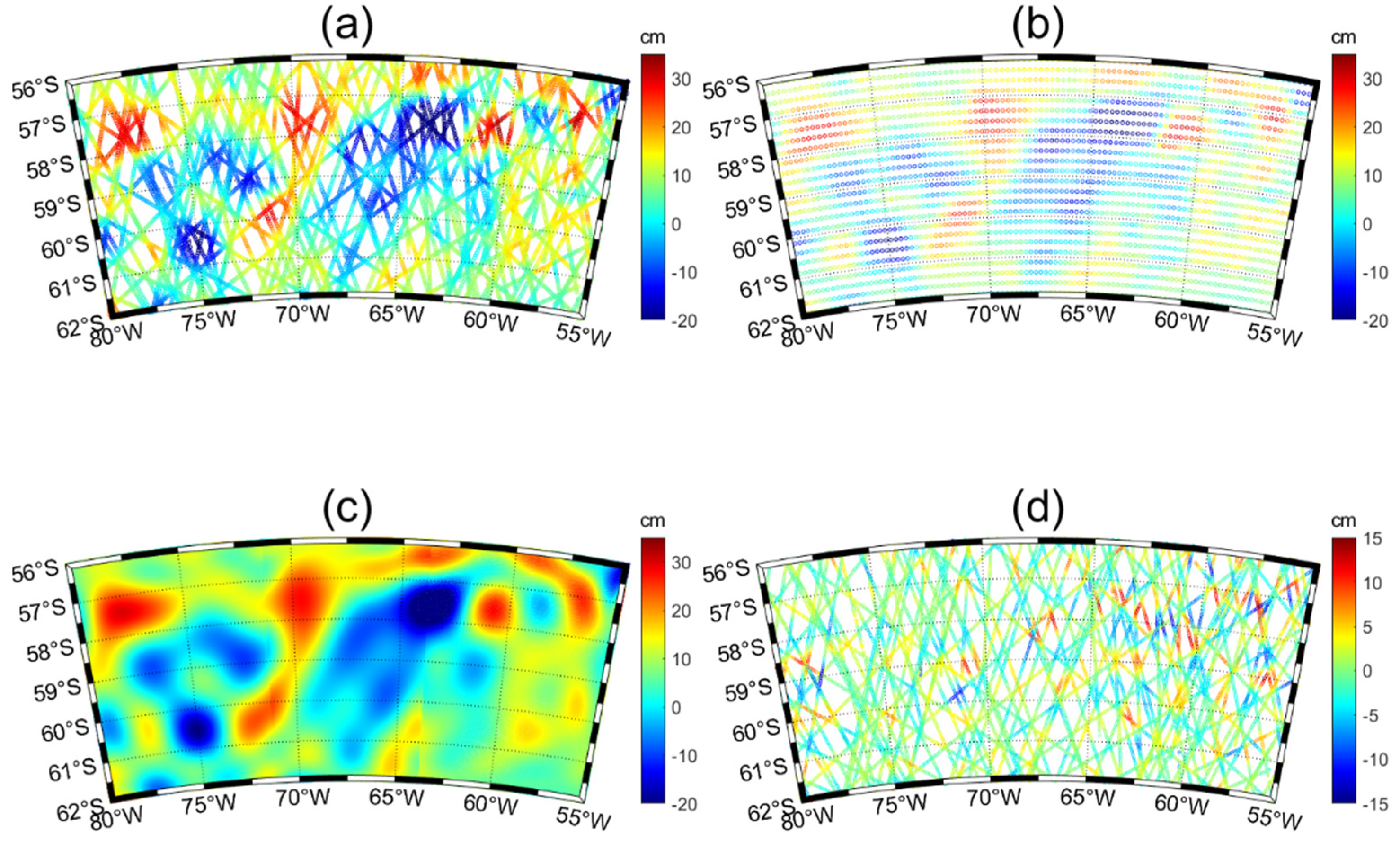
3.2. Comparison of Bicubic B-Spline Surface Fitting and Legendre Polynomial Surface Fitting for Actual Measurement Data
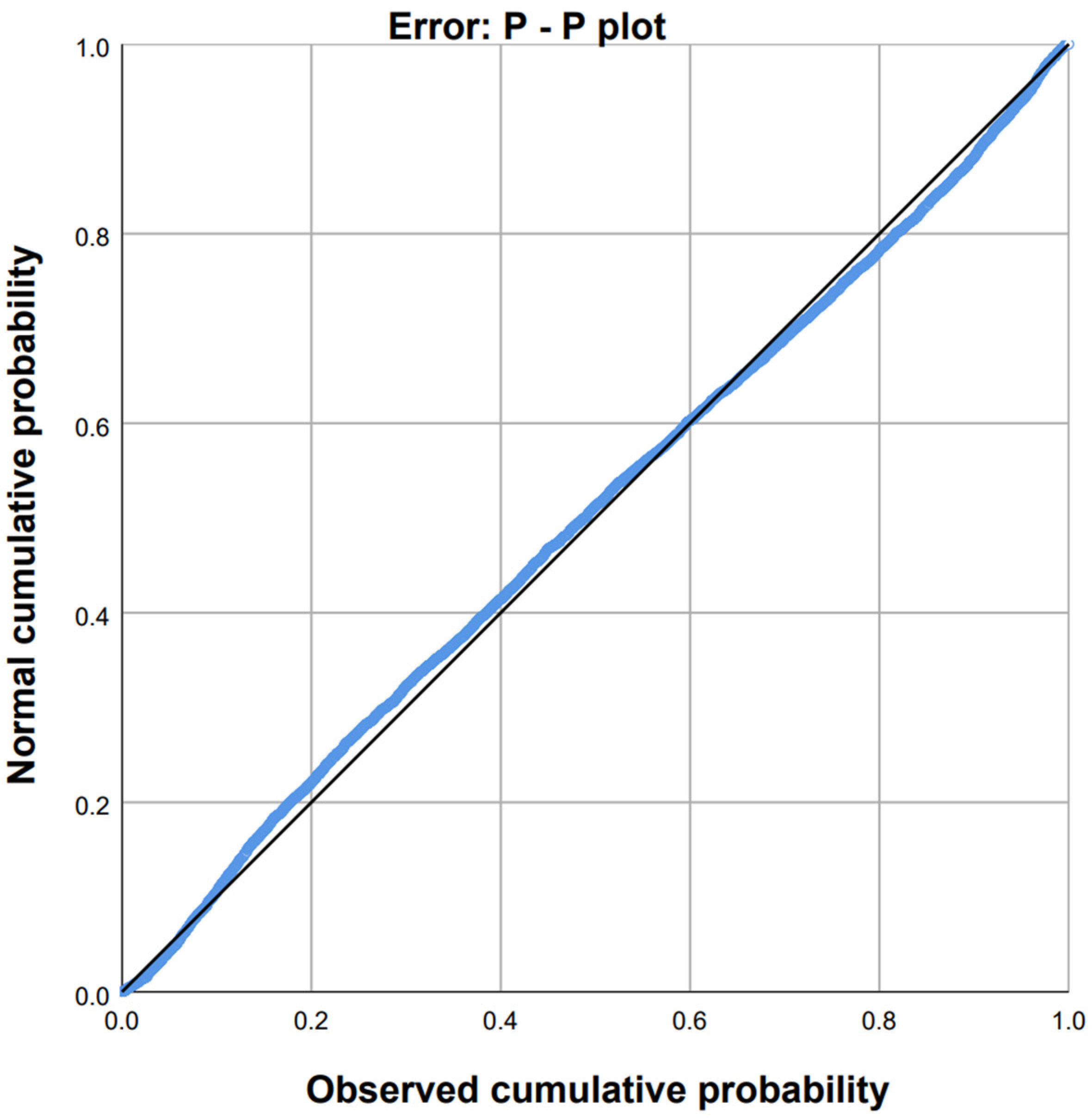
3.3. Hypothesis Testing
3.4. Comparative Analysis of Grid Data and Along-Track Data
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koriche, S.A.; Nandini-Weiss, S.D.; Prange, M.; Singarayer, J.S.; Arpe, K.; Cloke, H.L.; Schulz, M.; Bakker, P.; Leroy, S.A.G.; Coe, M. Impacts of Variations in Caspian Sea Surface Area on Catchment-Scale and Large-Scale Climate. J. Geophys. Res. Atmos. 2021, 126, e2020JD034251. [Google Scholar] [CrossRef]
- Global Warming Focus. Climate Modeling; Studies from Russian Academy of Science in the Area of Climate Modeling Described (Simulation of the Spatiotemporal Variability of the World Ocean Sea Surface Hight by the INM Climate Models); NewsRX LLC: Atlanta, GA, USA, 2016. [Google Scholar]
- Peng, F.; Deng, X. Improving precision of high-rate altimeter sea level anomalies by removing the sea state bias and intra-1-Hz covariant error. Remote Sens. Environ. 2020, 251, 112081. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, N.; Zhou, L.; Liu, K.; Wang, H. The Surface and Three-dimensional Characteristics of Mesoscale Eddies: A Review. Adv. Earth Sci. 2020, 35, 568–580. [Google Scholar] [CrossRef]
- Yu, R.; Xu, H.; Liu, B. Analysis of Spatial and Temporal Variation of Sea Level in South China Sea Based on Satellite Altimeter Data. J. Ocean. Technol. 2021, 1–9. (In Chinese) [Google Scholar]
- Baiyang, C.; Lingling, X.; Quanan, Z.; Lei, Z.; Lei, W.; Baoxin, F.; Zipeng, Y. Seasonal variability of mesoscale eddies in the Banda Sea inferred from altimeter data. Acta Oceanol. Sin. 2021, 39, 11–20. [Google Scholar]
- Yongcan, Z.; Yue, F.; Shuangwen, S.; Libao, G.; Yang, Y.; Guijun, G. Seasonal variation of mesoscale eddy intensity in the global ocean. Acta Oceanol. Sin. 2024, 43, 48–58. [Google Scholar]
- Yang, Y.; Liang, X.S. The intrinsic nonlinear multiscale interactions among the mean flow, low frequency variability and mesoscale eddies in the Kuroshio region. Sci. China Earth Sci. 2019, 62, 595–608. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, C.; Mcgillicuddy, D.J.; Liu, Y.; Barnes, B.B.; Kourafalou, V.H. Mesoscale eddies in the Gulf of Mexico: A three-dimensional characterization based on global HYCOM. Deep-Sea Res. Part II 2024, 215, 105380. [Google Scholar] [CrossRef]
- Bowen, S.; Baofu, L.; Jingyu, Y.; Yuqi, Z.; Shuo, Z. Seasonal variation of atmospheric coupling with oceanic mesoscale eddies in the North Pacific Subtropical Countercurrent. Acta Oceanol. Sin. 2022, 41, 109–118. [Google Scholar]
- Greaser, S.R.; Subrahmanyam, B.; Trott, C.B.; Stork, H.L.R. Interactions Between Mesoscale Eddies and Synoptic Oscillations in the Bay of Bengal During the Strong Monsoon of 2019. J. Geophys. Res. Ocean. 2020, 125, e2020JC016772. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, H.; Chen, X.; Zhou, M. A Gaussian Function Model of Mesoscale Eddy Temperature Anomalies and Research of Spatial Distribution Characteristics. Remote Sens. 2024, 16, 1716. [Google Scholar] [CrossRef]
- Xu, L.; Gao, M.; Zhang, Y.; Guo, J.; Lv, X.; Zhang, A. Oceanic Mesoscale Eddies Identification Using B-Spline Surface Fitting Model Based on Along-Track SLA Data. Remote Sens. 2022, 14, 5713. [Google Scholar] [CrossRef]
- Wyrtki, K.; Magaard, L.; Hager, J. Eddy energy in the oceans. J. Geophys. Res. (1896–1977) 1976, 81, 2641–2646. [Google Scholar] [CrossRef]
- Adams, D.K.; Mcgillicuddy, D.J.; Zamudio, L.; Thurnherr, A.M.; Liang, X.; Rouxel, O.; German, C.R.; Mullineaux, L.S. Surface-Generated Mesoscale Eddies Transport Deep-Sea Products from Hydrothermal Vents. Science 2011, 332, 580–583. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Deng, K.; Nie, T.; Ren, K.; Song, J. Overview on ocean mesoscale eddy detection and identification based on machine learning. Comput. Eng. Sci. 2021, 43, 2115–2125. [Google Scholar]
- Zhang, Z. Submesoscale Dynamic Processes in the South China Sea. Ocean.-Land-Atmos. Res. 2024, 3, 45. [Google Scholar] [CrossRef]
- Weifang, J.; Chujin, L.; Junyang, H.; Qicheng, M.; Haibin, L.; Yuntao, W.; Feilong, L.; Xiaoyan, C.; Xiaohui, L. Modulation Effect of Mesoscale Eddies on Sequential Typhoon-Induced Oceanic Responses in the South China Sea. Remote Sens. 2020, 12, 3059. [Google Scholar] [CrossRef]
- Mcgillicuddy, D.J.; Anderson, L.A.; Bates, N.R.; Bibby, T.; Buesseler, K.O.; Carlson, C.A.; Davis, C.S.; Ewart, C.; Falkowski, P.G.; Goldthwait, S.A.; et al. Eddy/Wind Interactions Stimulate Extraordinary Mid-Ocean Plankton Blooms. Science 2007, 316, 1021–1026. [Google Scholar] [CrossRef] [PubMed]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Siegel, D.A.; Granata, T.C.; Michaels, A.F.; Dickey, T.D. Mesoscale eddy diffusion, particle sinking, and the interpretation of sediment trap data. J. Geophys. Res. Ocean. 1990, 95, 5305–5311. [Google Scholar] [CrossRef]
- Fan, L.-L.; Wang, B.; Lv, X.-Q. Cotidal Charts near Hawaii Derived from TOPEX/Poseidon Altimetry Data. J. Atmos. Ocean. Technol. 2011, 28, 606–614. [Google Scholar] [CrossRef]
- Duo, Z.; Wang, W.; Wang, H. Oceanic Mesoscale Eddy Detection Method Based on Deep Learning. Remote Sens. 2019, 11, 1921. [Google Scholar] [CrossRef]
- Li, Z.; Cai, Z.; Liu, Z.; Wang, X.; Hu, J. A novel identification method for unrevealed mesoscale eddies with transient and weak features-Capricorn Eddies as an example. Remote Sens. Environ. 2022, 274, 112981. [Google Scholar]
- Cox, M.G. The Numerical Evaluation of B-Splines. IMA J. Appl. Math. 1972, 10, 134–149. [Google Scholar] [CrossRef]
- de Boor, C. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- de Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized Bidirectional B-Spline Parameterization Motion Planning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 406–419. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The Nurbs Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Dierckx, P. Curve and surface fitting with splines. Choice Rev. Online 1993, 31, 31–2162. [Google Scholar]
- Lorch, E.R. Review: Tables of associated Legendre functions. Bull. Am. Math. Soc. 1946, 52, 224–225. [Google Scholar] [CrossRef]
- Geisser, S. A Predictive Approach to the Random Effect Model. Biometrika 1974, 61, 101–107. [Google Scholar] [CrossRef]
- Rao, C.R.; Wu, Y. Linear model selection by cross-validation. J. Stat. Plan. Inference 2009, 128, 231–240. [Google Scholar] [CrossRef]
- Devroye, L.; Wagner, T.J. Distribution-free performance bounds for potential function rules. IEEE Trans. Inf. Theory 1979, 25, 601–604. [Google Scholar] [CrossRef]
- Geisser, S. The Predictive Sample Reuse Method with Applications. J. Am. Stat. Assoc. 1975, 70, 320–328. [Google Scholar] [CrossRef]
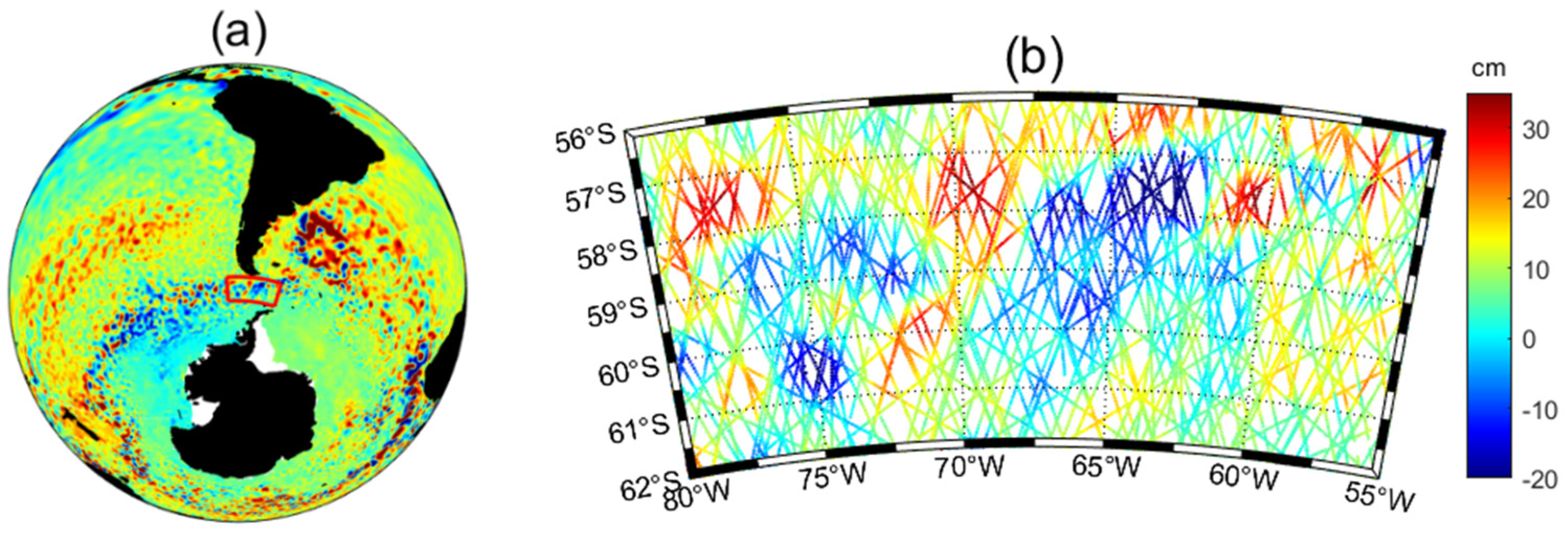


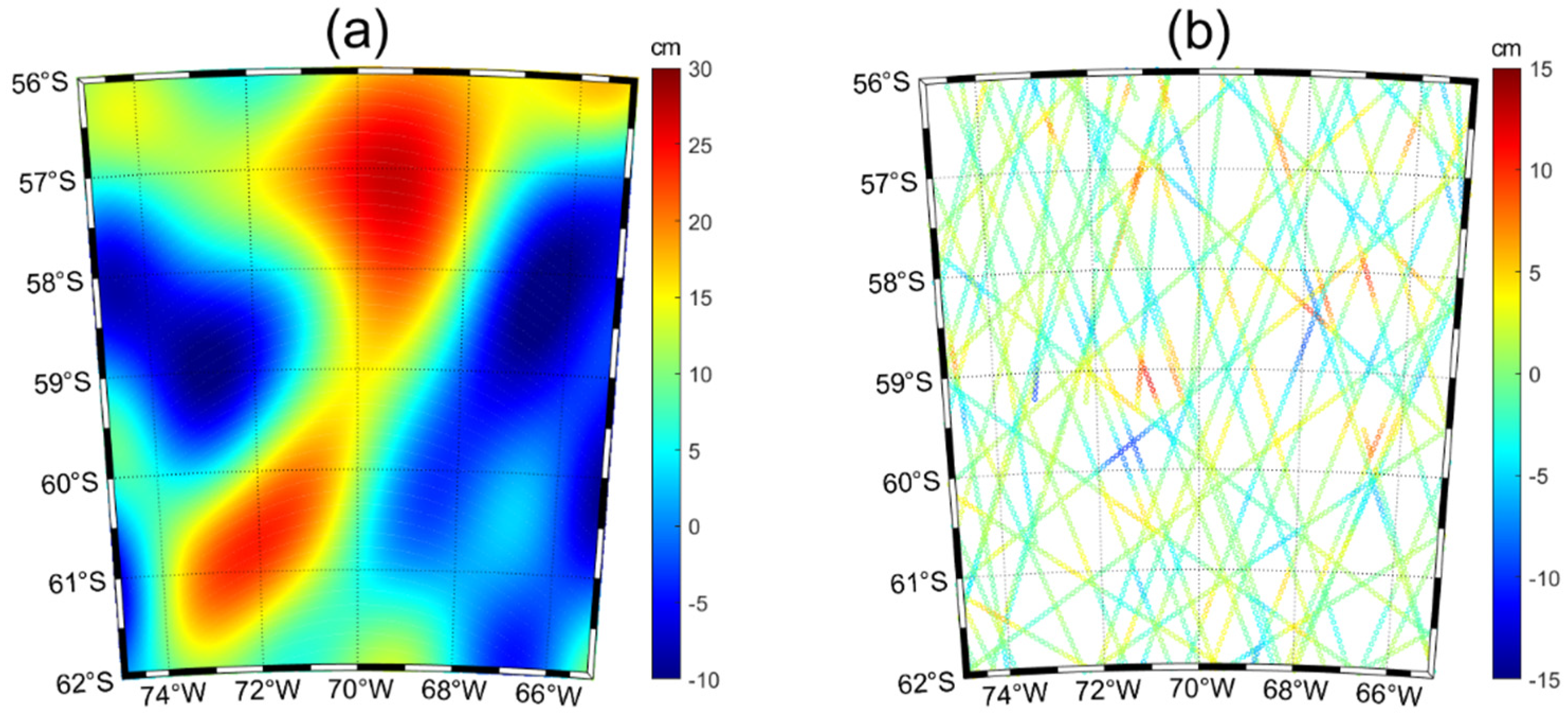

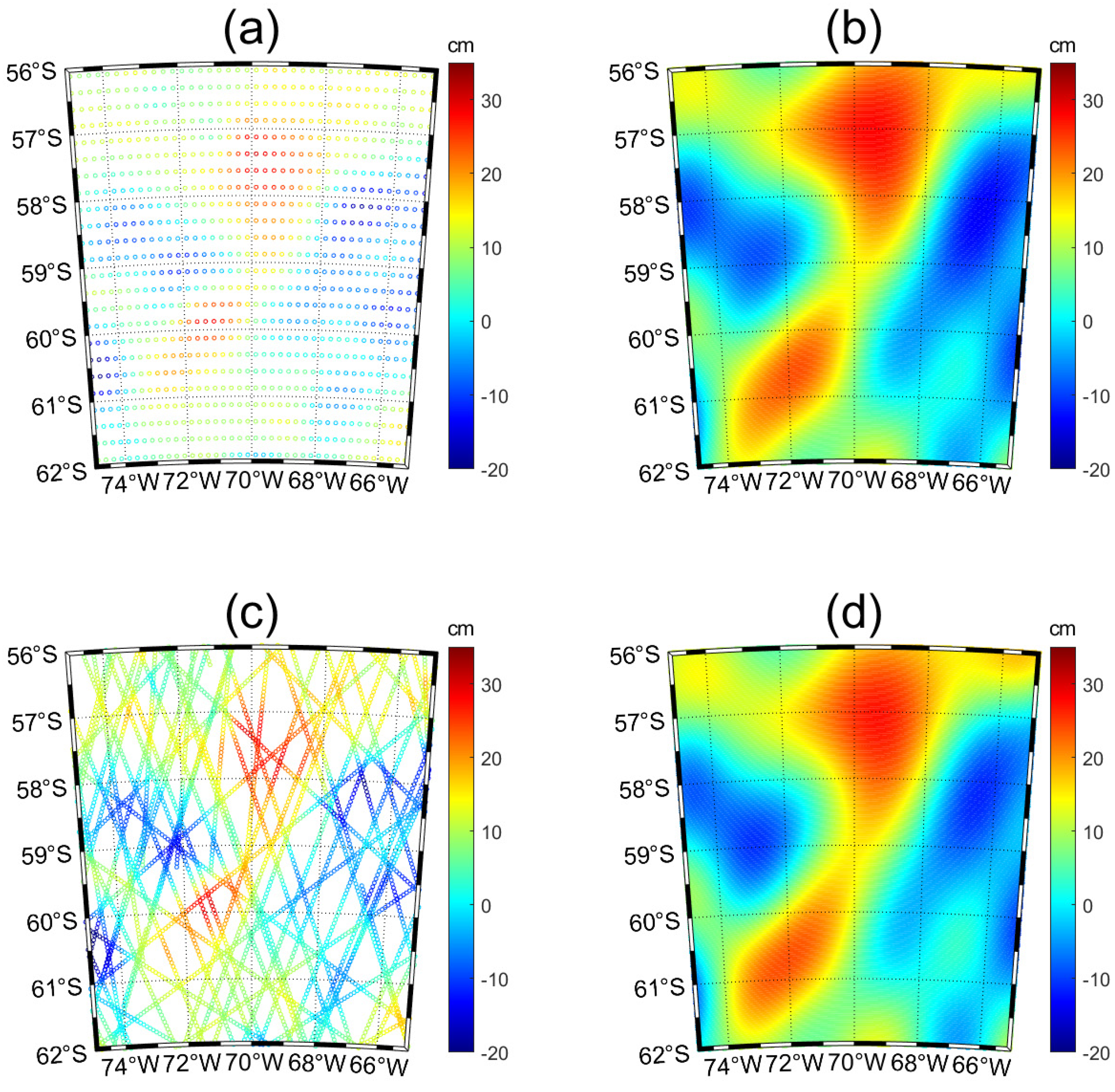

| Sample | Regional Scope | Longitude and Latitude Range | Timer Series | Level |
|---|---|---|---|---|
| SLA | Antarctic Circumpolar Current | 56°S–62°S 55°W–80°W | 20220301000000—20220313235959 | 3 |
| Days | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Legendre | 2.25 | 0.63 | 0.49 | 1.21 | 0.33 | 0.33 | 0.32 | 0.31 | 0.30 |
| B-spline | 1.90 | 0.15 | 0.11 | 0.90 | 0.04 | 0.05 | 0.04 | 0.04 | 0.04 |
| data Volume | 2608 | 3097 | 3439 | 3863 | 4427 | 5113 | 5695 | 5933 | 6454 |
| Signal-to-Noise Ratio | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | |
| Legendre | 0.30 | 0.44 | 0.65 | 0.87 | 1.08 | 1.35 | 1.55 | 1.81 | 2.05 |
| B-spline | 0.04 | 0.27 | 0.51 | 0.75 | 1.03 | 1.29 | 1.51 | 1.72 | 2.04 |
| Days | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Legendre | 4.43 | 3.16 | 2.65 | 3.10 | 2.14 | 2.35 | 2.40 | 2.42 | 2.58 |
| B-spline | 4.03 | 2.23 | 2.15 | 2.83 | 2.16 | 2.24 | 2.30 | 2.35 | 2.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, C.; Zhang, Y.; Shi, J.; Lv, X. Oceanic Mesoscale Eddy Fitting Using Legendre Polynomial Surface Fitting Model Based on Along-Track Sea Level Anomaly Data. Remote Sens. 2024, 16, 2799. https://doi.org/10.3390/rs16152799
Kong C, Zhang Y, Shi J, Lv X. Oceanic Mesoscale Eddy Fitting Using Legendre Polynomial Surface Fitting Model Based on Along-Track Sea Level Anomaly Data. Remote Sensing. 2024; 16(15):2799. https://doi.org/10.3390/rs16152799
Chicago/Turabian StyleKong, Chunzheng, Yibo Zhang, Jie Shi, and Xianqing Lv. 2024. "Oceanic Mesoscale Eddy Fitting Using Legendre Polynomial Surface Fitting Model Based on Along-Track Sea Level Anomaly Data" Remote Sensing 16, no. 15: 2799. https://doi.org/10.3390/rs16152799
APA StyleKong, C., Zhang, Y., Shi, J., & Lv, X. (2024). Oceanic Mesoscale Eddy Fitting Using Legendre Polynomial Surface Fitting Model Based on Along-Track Sea Level Anomaly Data. Remote Sensing, 16(15), 2799. https://doi.org/10.3390/rs16152799






