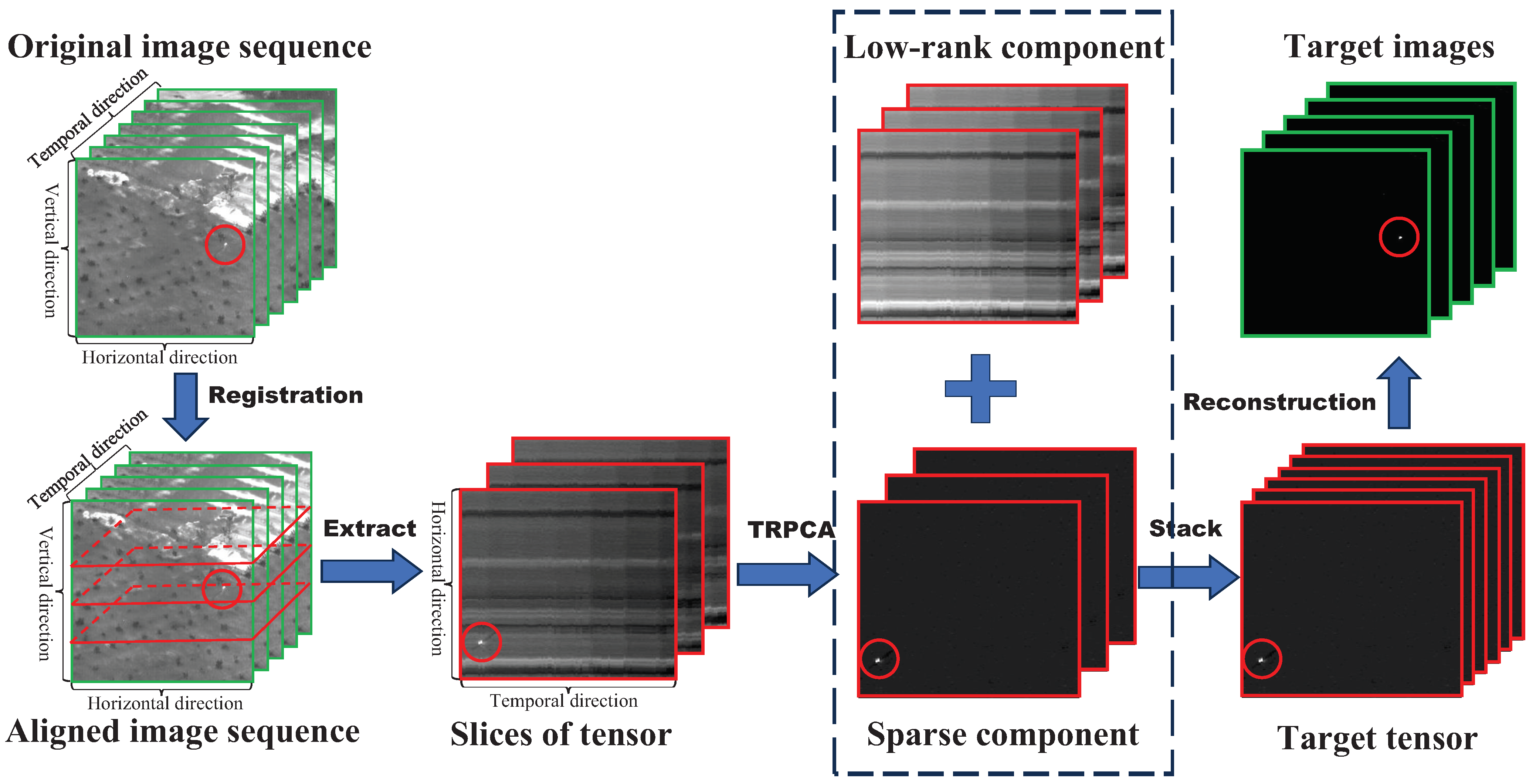
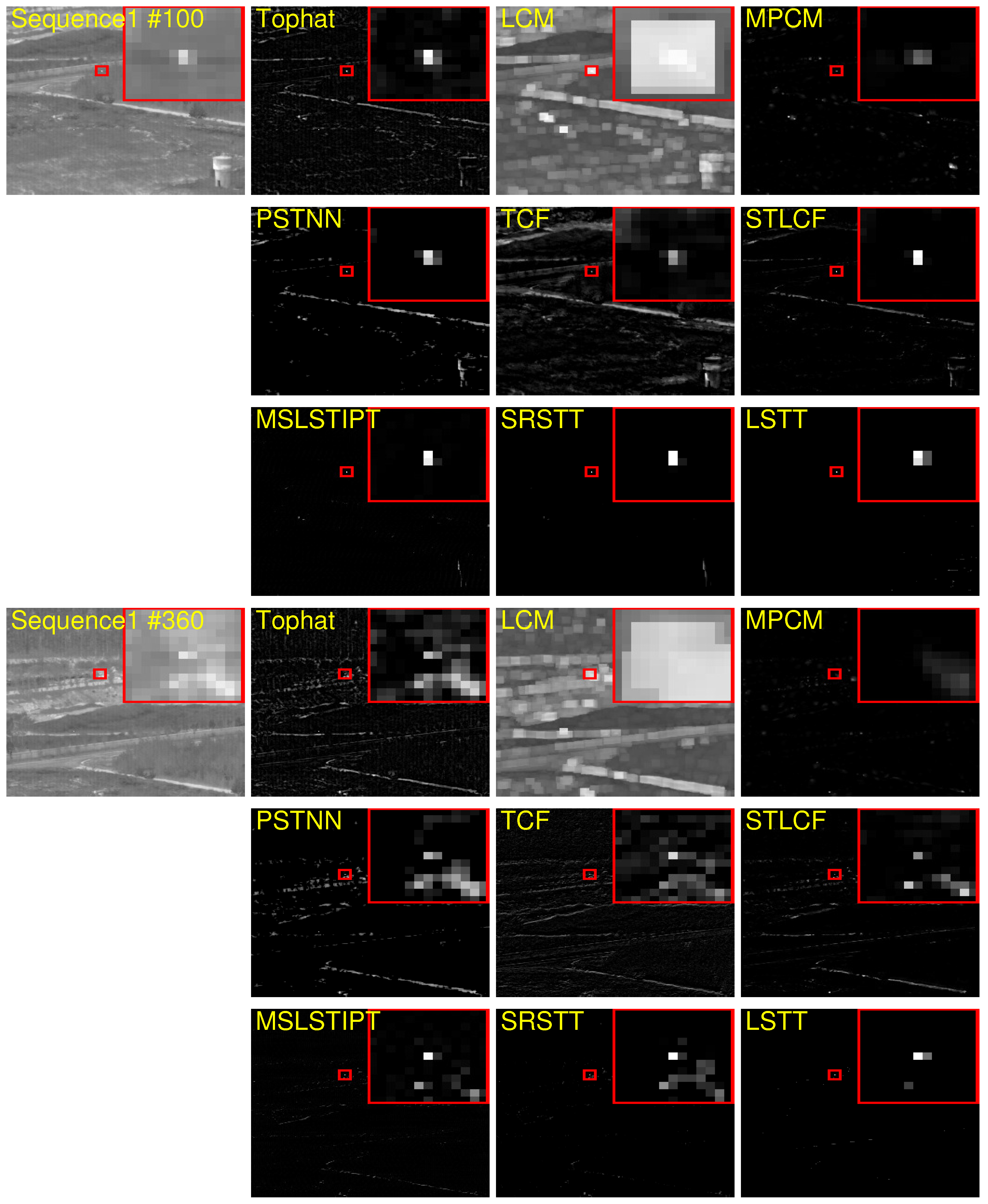
In this section, we propose a long-term spatial–temporal tensor (LSTT) model for infrared small target detection under dynamic background. The overall flow of the proposed LSTT model is presented in
Figure 2. First, by obtaining
L successive frames from the original image sequence (OIS), image registration can be used to obtain the aligned image sequence (AIS), which is then stacked to construct a third-order tensor. Second, several horizontal slices of the tensor are extracted to construct a new long-term spatiotemporal tensor. Then, using TRPCA, the new tensors are decomposed into their low-rank and sparse components. Finally, all of the decomposed sparse components are superimposed into a target tensor, from which the small moving targets of each frame are reconstructed.
2.1. Image Registration
For static backgrounds or slowly changing scenes, the background pixels of adjacent frames possess correlation and similarity in the temporal dimension. However, when the camera platform moves the whole background moves as well, and the similarity of the background pixels in the time dimension is destroyed. In this case, image registration is required, such as the image sequences in [
4]. In this paper, we mainly consider the problem of infrared small target detection under dynamic background conditions.
For the sake of simplicity, we can consider the case in which the camera only moves in translation, which was the case in [
4]. Then, we can use the pure translational model to align the inter-frame images.
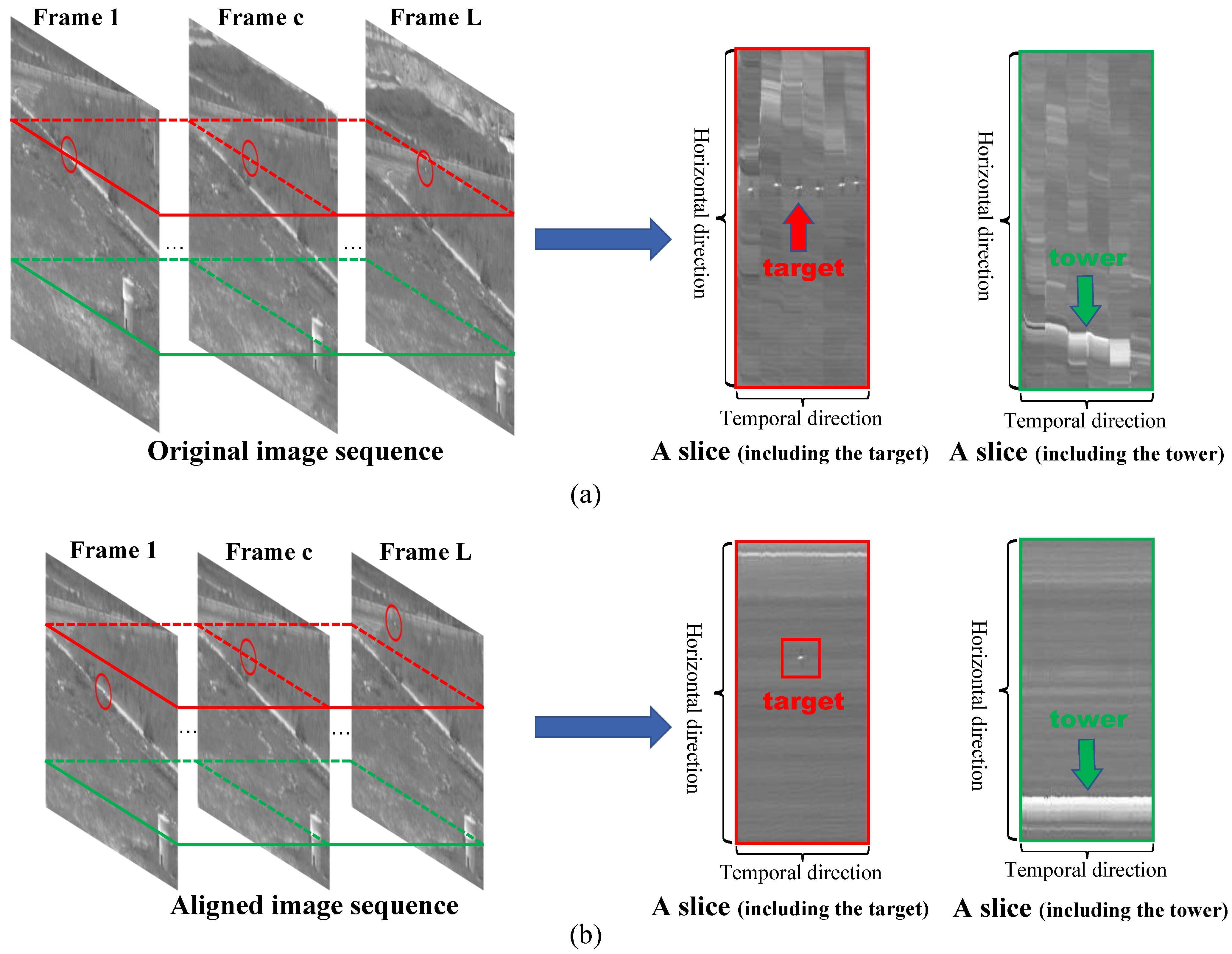
Figure 3 shows the process of image registration. Given an original image sequence, we select successive
L frames
and determine the reference frame
. From frame 1 to frame
L, the target in the red circle gradually flies away and the background in the image changes, which can be clearly seen from the white tower in the lower right corner.
Figure 4a shows that the unaligned background has no continuity or similarity in the temporal dimension. In this case, it is necessary to use image registration for spatial alignment of the adjacent frames. We use scale-invariant feature transform (SIFT) points [
50] for image registration. First, we calculate SIFT points on each frame and reference frame; then, the feature points are matched and the transformation matrix is calculated based on these points. In the case of the pure translational model, it is only necessary to calculate the amount of translation
between each frame and the reference frame. Finally, all of the images are aligned with their reference frames and the AIS with shared overlapping areas is obtained, as shown in
Figure 3b.
Figure 4 illustrates the necessity of image registration under the dynamic background of a real infrared image sequence dataset [
4].
Figure 4a shows horizontal slices of the original image sequence tensor, from which it can be seen that there is no continuity or similarity in the background parts of the slices.
Figure 4b presents the horizontal slices of tensor formed by the aligned image sequence; the background parts of the slices have local spatial similarity and temporal continuity, exhibiting a clear and strong low-rank property. From
Figure 3 and
Figure 4, it can be seen that there are trees, roads, and a white tower in the background of the original images, which poses many difficulties for small target detection. However, observing the slices of the aligned tensors in
Figure 4b, the pixel grayscale values exhibit consistency and similarity in the temporal direction. The original complex background becomes smoother and simpler, while the dim target becomes more prominent, greatly reducing the difficulty of target detection. This is the key that enables us to detect small targets from the perspective of the original image with respect to the slice while being able to utilize long-term multi-frame information in the time domain.
2.2. Long-Term Spatial–Temporal Tensor Model
Given an infrared image sequence, we choose successive
L frames
and then stack them as a tensor
with size
:
where
is the original infrared image tensor and
are the background tensor, target tensor, and noise tensor obtained by decomposition, respectively.
After image registration, the aligned image sequence (AIS) is obtained, denoted as
(
). Then, the AIS is stacked as a tensor
with size
:
where
is the aligned image tensor and
are the background tensor, target tensor, and noise tensor, respectively.
As shown in
Figure 2, the aligned image tensor
is cut into slices along the horizontal direction. Each slice is a 2D image, with one dimension being the time direction. The figure shows the intensity of horizontal spatial pixels over time. Unlike other methods that consider the entire STT [
38,
48,
49], we consider the horizontal slices of tensor
in (
2). Without considering the noise
, the
ith horizontal slice is denoted by
. Then, a new tensor
is formed by directly stacking
r consecutive slices:
where the slice number
and
p is a positive integer. In this way, the horizontal slice
of tensor
is converted into a frontal slice of the new tensor
. The proposed long-term spatial–temporal tensor (LSTT) model is as follows:
where
, and
and
are the low-rank background component and sparse target component of tensor
, respectively. Then, the problem of detecting an infrared small moving target is transformed into the decomposition and recovery of the sparse target component from
.
The new model confers two major advantages: (a) the background component of the constructed model is more consistent with the characteristics of the low-rank condition, and (b) the features of the target, background, and clutter in the slices are more obvious and better distinguished, which greatly helps in separating small targets from complex backgrounds.
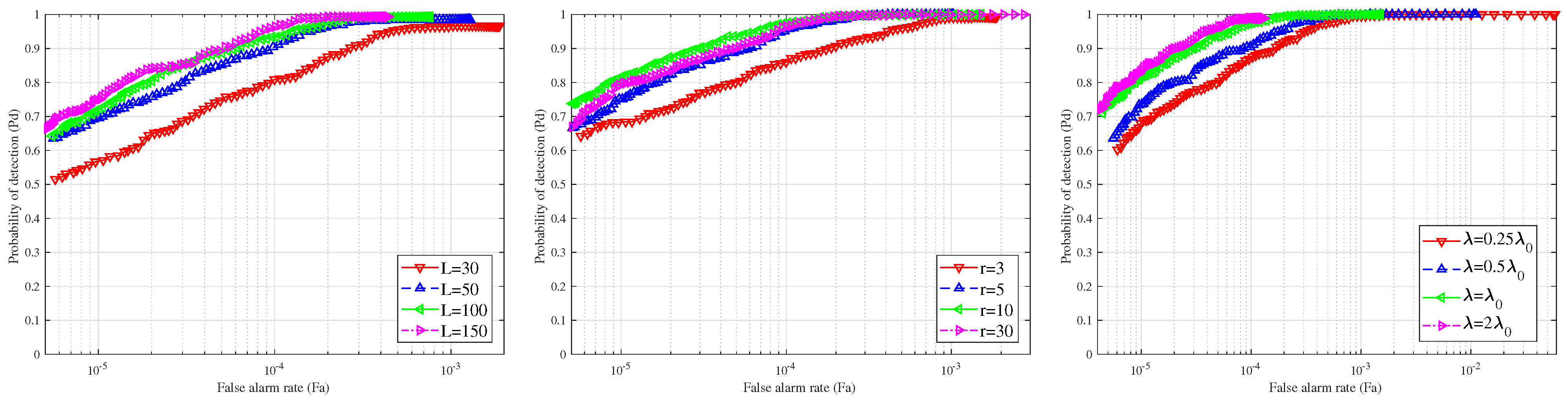
Figure 5 shows the low-rank property of the original image sequence tensor
(the first row) and the aligned image sequence tensor
(the second row). The third row shows the singular values of the horizontal/lateral/frontal slices, where the horizontal coordinate is in logarithmic form. Their values rapidly decrease and converge to zero. In particular, it is clear that the singular values of the horizontal/lateral slices of
(red) are larger and decrease faster than those of
(green). These results indicate that the background components of the horizontal/lateral slices of
are more consistent with the low-rank property. It is worth mentioning that some amount of fixed strong noise or static clutter in each frame can be converted into bright lines in the horizontal or lateral slices. Therefore, these are decomposed into the low-rank background component during the process of recovering the low-rank and sparse components in order to successfully separate the small target.
On the other hand, the dim target makes up only a small part of the overall image (less than
) [
8,
44]. Thus, the target part is obviously sparse. Therefore, based on the proposed LSTT model, the detection of an infrared moving small target can be transformed into the optimization problem of recovering the low-rank and sparse components from the constructed tensor
:
where
is the tensor rank of
,
denotes the
norm, and
is a regularization parameter.
The constrained optimization problem (
5) is hard to solve directly. In particular, how to approximate the tensor rank of
is a key problem. Based on different tensor decomposition methods such as CP decomposition and Tucker decomposition, different definitions of tensor rank can be obtained [
51,
52]. While the CP rank and Tucker rank are popular, their minimization problems can be NP-hard. The tensor nuclear norm (TNN) is commonly used for tensor rank substitution [
33,
52,
53,
54]. Unfortunately, it has the disadvantage of assigning equal weight to different singular values, resulting in bias [
12,
48]. Inspired by [
55,
56], we propose using the partial tubal nuclear norm (PTNN) of the low-rank background component to avoid this problem. For a tensor
, the PTNN is defined as follows:
where
is the partial matrix nuclear norm [
31],
denotes a tensor obtained by taking the Fast Fourier Transform (FFT) along the third dimension of
[
55], and
, with
denoting the
jth largest singular value.
In addition, as the
norm is computationally difficult to solve, it can be replaced by the
norm. In order to accelerate convergence speed and reduce the time consumption of the whole algorithm, the reweighted scheme in [
48,
57] was adopted. We combine the
norm of the sparse target component with a weighted tensor
, defined as follows:
where
is a positive constant used to avoid having a zero denominator and
k represents the
kth iteration. Then, the optimization problem (
5) can be converted to
where ⊙ is the Hadamard product.
2.3. Model Solution
To solve (
8), it is necessary to transform the constrained optimization problem into an unconstrained optimization problem. The augmented Lagrangian function of (
8) is provided as follows [
58,
59]:
where
is a penalty factor,
is the Frobenius norm,
is the inner product, and
is the Lagrange multiplier. Because the minimizer of
is hard to find directly, we can update
and
alternately using ADMM [
58]. The solution procedure consists of the following iteration subproblems of update variables:
Let
; then, the optimization problem in (
10) becomes
The tensor optimization problem in (
11) can be decomposed into
r independent matrix optimization problems in the Fourier transform domain [
55,
56], which are fortunately solvable by partial singular value thresholding (PSVT) [
31]. The PSVT operator is described below (please see [
55] for more details).
(PSVT [
31]): Let
and
;
can be decomposed by singular value decomposition (SVD), while
, where
are the singular vector matrices corresponding to the
t maximum singular values and
corresponds to the
th smallest singular values. Then, the optimal solution of the minimization problem
can be solved with the PSVT operator
where
,
, and
is the soft shrinkage operator [
60].
The subproblem in (
15) can be handled using the soft shrinkage operator [
60]:
(3) Updating :
can be updated by (
7).
Therefore, the entire process of solving (
8) is described in Algorithm 1.
| Algorithm 1 Solve (8) using ADMM |
- 1:
Input: , parameter - 2:
Initialization: - 3:
While not converge do - 4:
Update by the PSVT operator - 5:
Update by Equation ( 16) - 6:
Update by Equation ( 7) - 7:
Update by Equation ( 17) - 8:
Update by Equation ( 18) - 9:
Check the conditions for convergence -
or - 10:
Update - 11:
end while - 12:
Output:
|
2.4. Target Detection Procedure
Figure 2 shows the whole process of the proposed LSTT model. The steps of the proposed LSTT method are as follows:
(1) Considering an image sequence of frames , we choose L successive frames .
(2) After these L images are aligned by image registration, the aligned image sequence (AIS) is stacked to obtain the aligned image tensor ().
(3) We select r successive horizontal slices of sequentially and stack them to form a new tensor .
(4) The new tensor is decomposed into low-rank background components and sparse target components via Algorithm 1.
(5) The target tensor and background tensor are obtained by separately superimposing all of the decomposed sparse components and low-rank components .
(6) The target image of each frame is reconstructed from the target tensor
, then the moving small target in each frame is separated from the corresponding target image
using simple threshold segmentation:
where
is in the range
; if
, then pixel
is considered to be a target pixel.