A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression
Abstract
1. Introduction
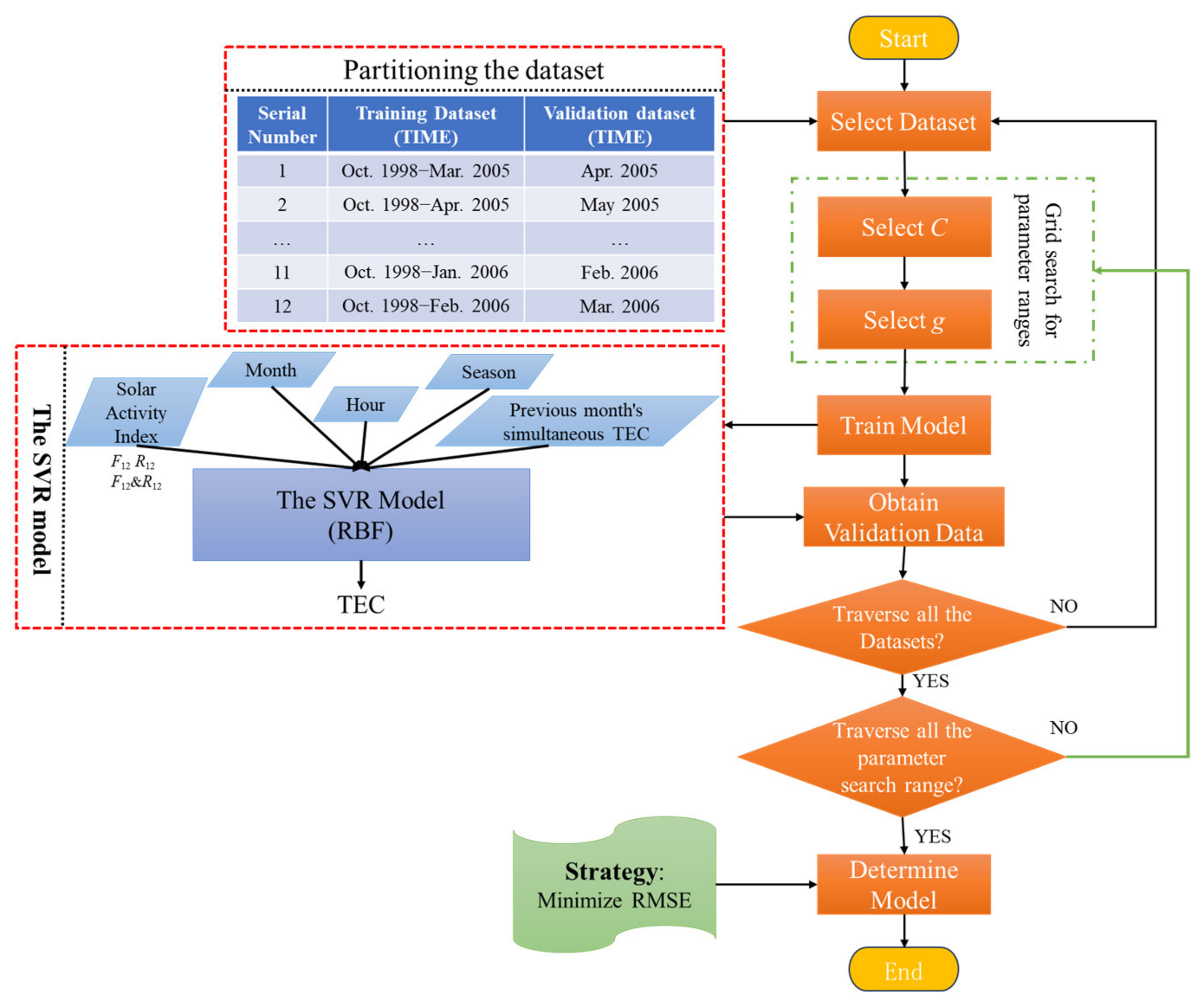
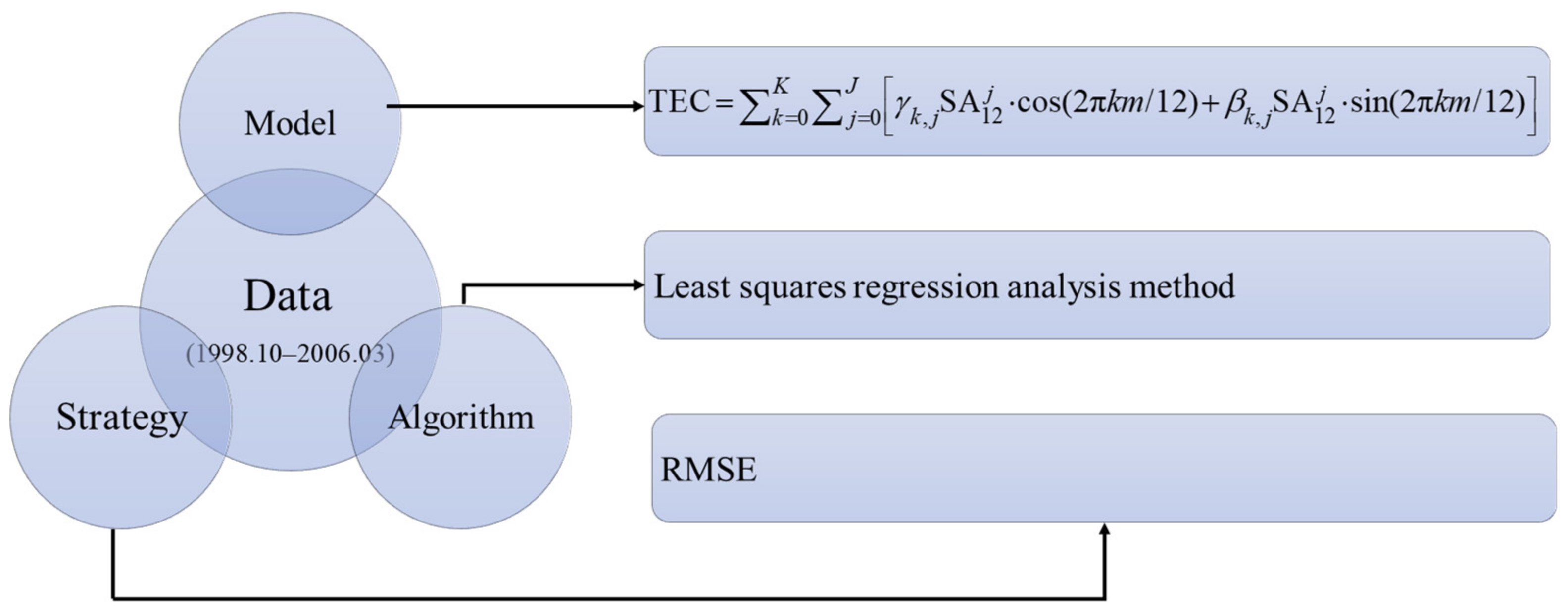
2. Methodology
- (1)
- Data Collection and Dataset Splitting: Gather and divide the required data into training and validation datasets.
- (2)
- Defining Model Inputs, Outputs, and Hyperparameter Set: In this modeling process, the inputs mainly include solar activity indices, month, hour, season, and the TEC value of the same hour in the previous month. The output is the median TEC value at the corresponding time. The hyperparameters are the values of C and g in the model.
- (3)
- Training the Model Using the SVR Method: Determine the specific hyperparameters C and g values.
- (4)
- Setting Model Evaluation Strategy: Evaluate the model using the root mean square error (RMSE) evaluation metric. The formula for RMSE is:where TEC′ represents the model’s predictions, TEC represents the observed values, and N is the total amount of data considered.
3. Data
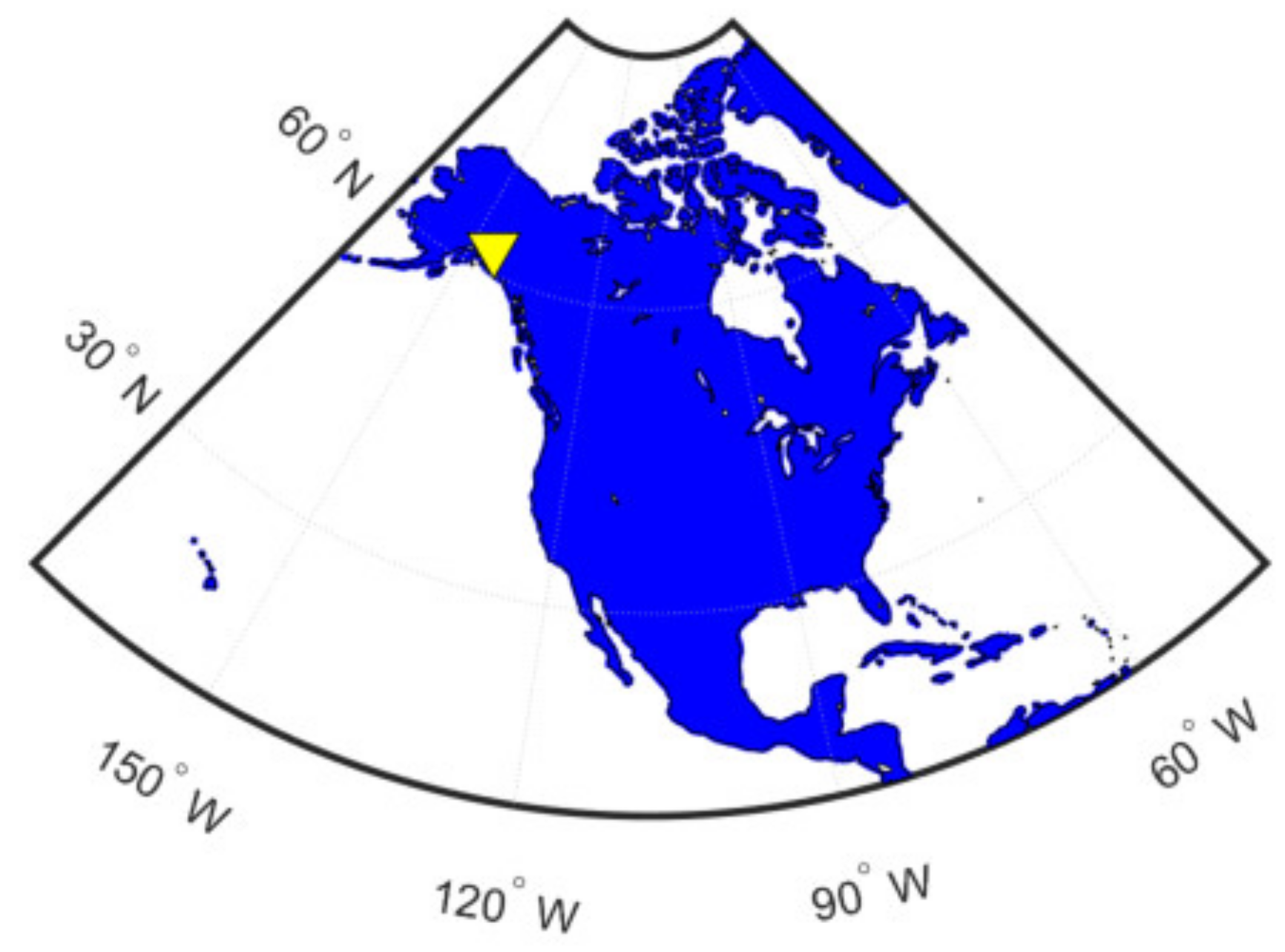
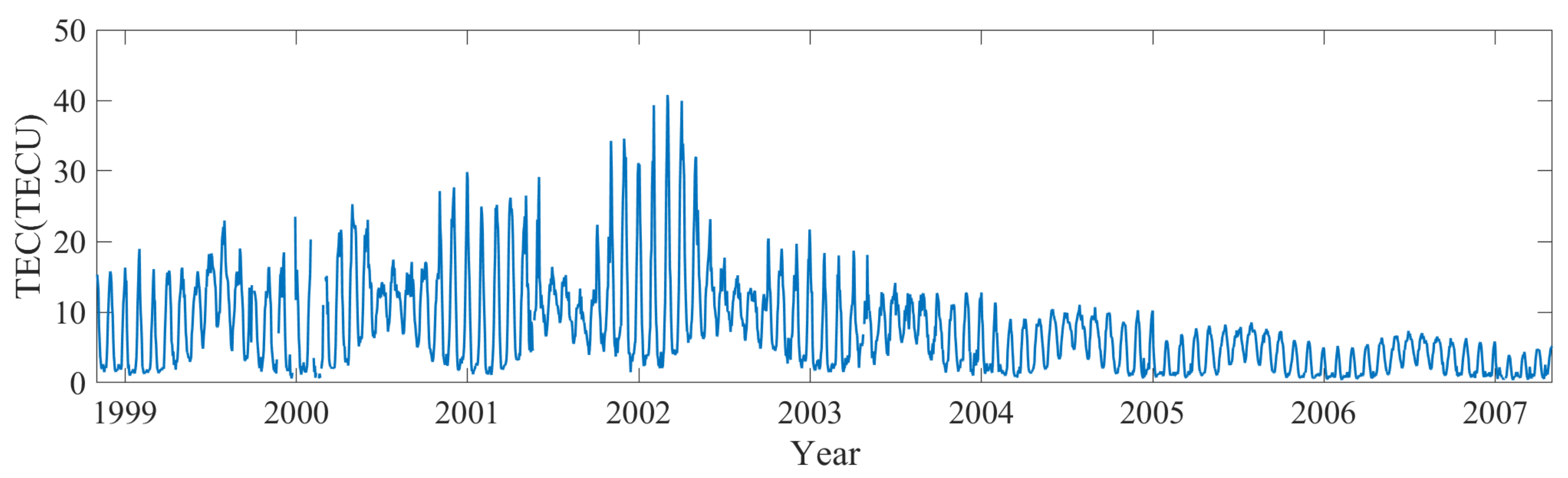
3.1. TEC Observations
3.2. Solar Activity Index
4. Modeling
5. Discussion
5.1. Comparison Models
5.1.1. The IRI Model
5.1.2. The SML Model
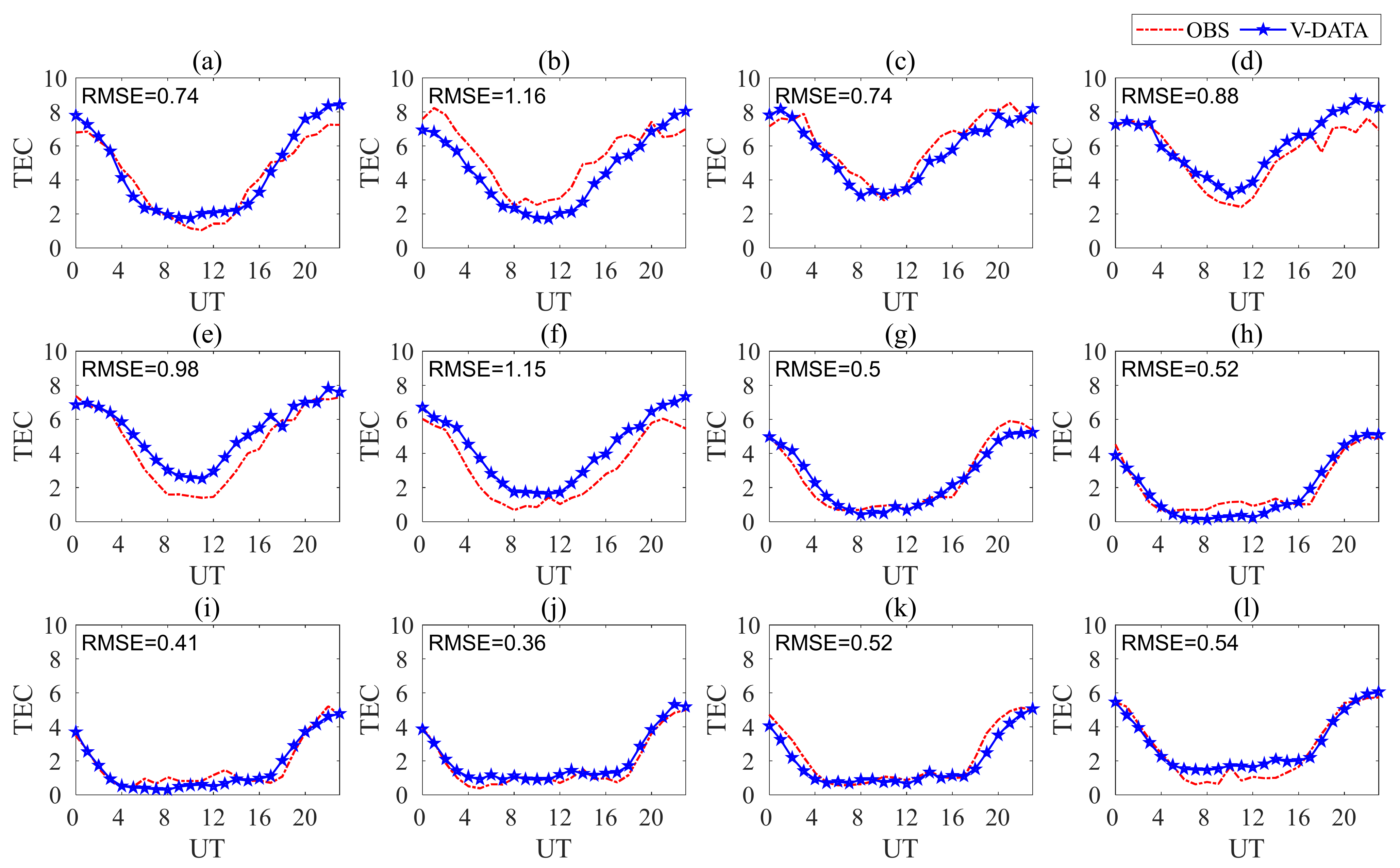
5.2. Test Results
- (1)
- All four models can fit the diurnal variation trend of TEC, but their fitting capabilities vary;
- (2)
- The CCIR and the URSI models overestimate TEC values around UT = 0;
- (3)
- December 2006 and January 2007, the SML model predicted negative values around UT = 5, which is counterintuitive.
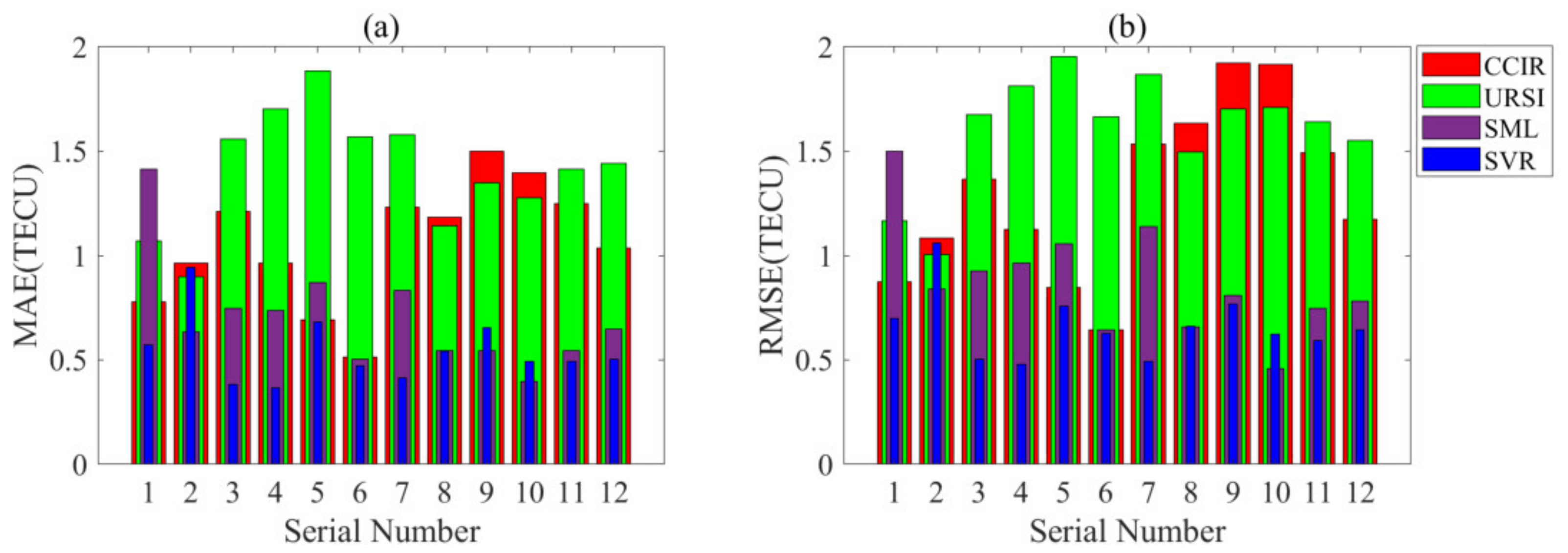
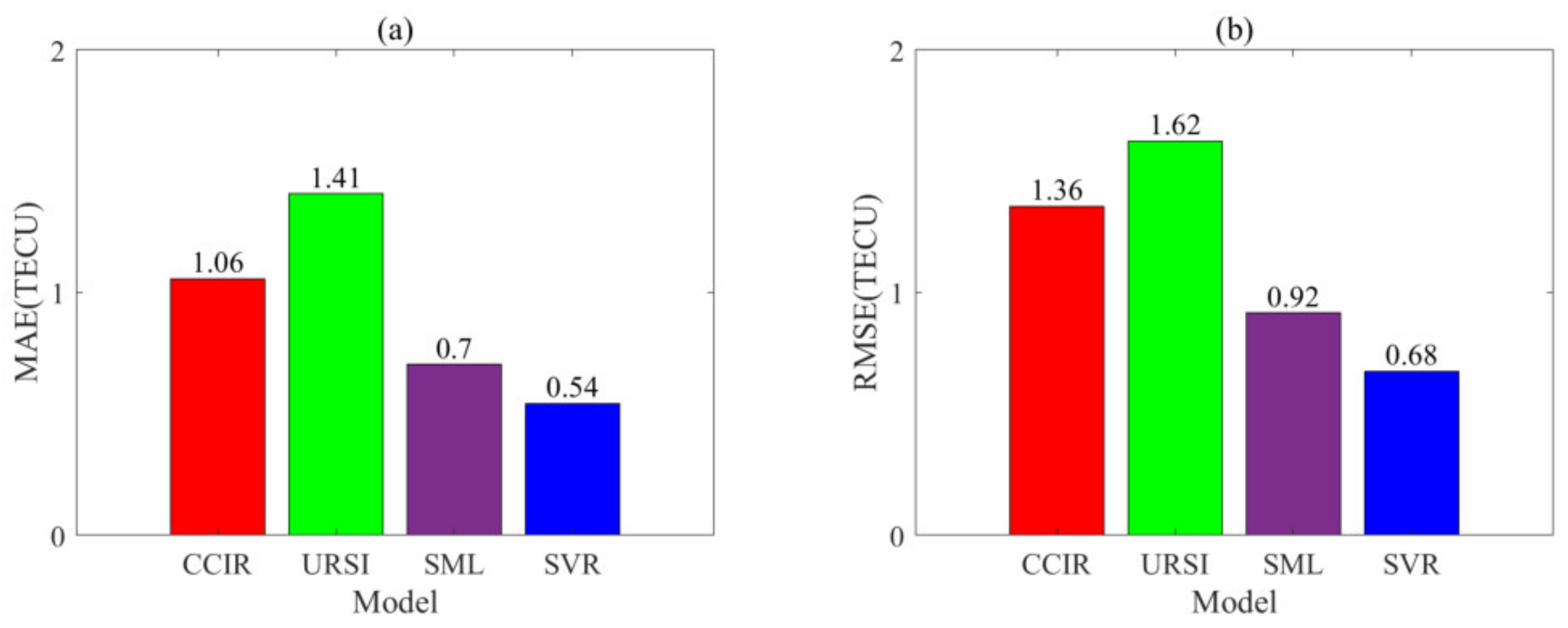
- (1)
- Within the twelve months, the CCIR model had the most significant prediction error for four months, the URSI model for seven months, and the SML model for one month.
- (2)
- From the perspective of MAE, in May 2006, the SVR model had a larger MAE than the URSI and SML models, and in January 2007 and February 2007, the SVR model had a larger MAE than the SML model. Except for these months, the SVR model had the most petite MAE for the remaining months.
- (3)
- From the perspective of RMSE, in May 2006, the SVR model had a larger RMSE than the URSI and SML models, and in January 2007 and February 2007, the SVR model had a larger RMSE than the SML model. Except for these months, the SVR model had the smallest RMSE for the remaining months.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ware, R.H.; Fulker, D.W.; Stein, S.A.; Anderson, D.N.; Avery, S.K.; Clark, R.D.; Droegemeier, K.K.; Kuettner, J.P.; Minster, J.B.; Sorooshian, S. SuomiNet: A Real–Time National GPS Network for Atmospheric Research and Education. Bull. Am. Meteorol. Soc. 2000, 81, 677–694. [Google Scholar] [CrossRef]
- Komjathy, A.; Yang, Y.M.; Meng, X.; Verkhoglyadova, O.; Mannucci, A.J.; Langley, R.B. Review and perspectives: Understanding natural-hazards-generated ionospheric perturbations using GPS measurements and coupled modeling. Radio Sci. 2016, 51, 951–961. [Google Scholar] [CrossRef]
- Klobuchar, J. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Prieto-Cerdeira, R.; Orús Pérez, R.; Breeuwer, E.; Lucas-Rodriguez, R.; Falcone, M. Performance of the Galileo Single-Frequency Ionospheric Correction During In-Orbit Validation. GPSworld 2014, 25, 53–58. [Google Scholar]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Liu, L.; Wan, W.; Chen, Y.; Le, H. Solar activity effects of the ionosphere: A brief review. Chin. Sci. Bull. 2011, 56, 1202–1211. [Google Scholar] [CrossRef]
- Priyadarshi, S. A Review of Ionospheric Scintillation Models. Surv. Geophys. 2015, 36, 295–324. [Google Scholar] [CrossRef] [PubMed]
- Dao, T.; Harima, K.; Carter, B.; Currie, J.; McClusky, S.; Brown, R.; Rubinov, E.; Choy, S. Regional Ionospheric Corrections for High Accuracy GNSS Positioning. Remote Sens. 2022, 14, 2463. [Google Scholar] [CrossRef]
- Pietrella, M.; Pezzopane, M.; Zolesi, B.; Cander, L.R.; Pignalberi, A. The Simplified Ionospheric Regional Model (SIRM) for HF Prediction: Basic Theory, Its Evolution and Applications. Surv. Geophys. 2020, 41, 1143–1178. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, T.; Li, W.; Zhao, Z.; Han, B.; Wang, K. A new global TEC empirical model based on fusing multi-source data. GPS Solut. 2022, 27, 20. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D.; Andonov, B.; Pashova, L. Global TEC maps based on GNSS data: 1. Empirical background TEC model. J. Geophys. Res. Space Phys. 2013, 118, 4594–4608. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Kong, J.; Zhou, C.; Liu, L.; Shan, L.; Guo, Z. An Updated Experimental Model of IG₁₂ Indices Over the Antarctic Region via the Assimilation of IRI2016 With GNSS TEC. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1700–1717. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the International Standard for the Ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere Model: A Review and Description of an Ionospheric Benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Yang, C.; Zheng, Y.; Fu, H. A Machine Learning-Based Method for Modeling TEC Regional Temporal-Spatial Map. Remote Sens. 2022, 14, 5579. [Google Scholar] [CrossRef]
- Weng, J.; Liu, Y.; Wang, J. A Model-Assisted Combined Machine Learning Method for Ionospheric TEC Prediction. Remote Sens. 2023, 15, 2953. [Google Scholar] [CrossRef]
- Xia, G.; Liu, Y.; Wei, T.; Wang, Z.; Huang, W.; Du, Z.; Zhang, Z.; Wang, X.; Zhou, C. Ionospheric TEC forecast model based on support vector machine with GPU acceleration in the China region. Adv. Space Res. 2021, 68, 1377–1389. [Google Scholar] [CrossRef]
- Yang, D.; Fang, H.; Liu, Z. Completion of Global Ionospheric TEC Maps Using a Deep Learning Approach. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030326. [Google Scholar] [CrossRef]
- Mallika, I.L.; Ratnam, D.V.; Ostuka, Y.; Sivavaraprasad, G.; Raman, S. Implementation of Hybrid Ionospheric TEC Forecasting Algorithm Using PCA-NN Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 371–381. [Google Scholar] [CrossRef]
- Kaselimi, M.; Voulodimos, A.; Doulamis, N.; Doulamis, A.; Delikaraoglou, D. Deep Recurrent Neural Networks for Ionospheric Variations Estimation Using GNSS Measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5800715. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, L.; Pan, Y.; Zhang, D. Prediction of Carbon Emissions Level in China’s Logistics Industry Based on the PSO-SVR Model. Mathematics 2024, 12, 1980. [Google Scholar] [CrossRef]
- Shi, Y.; Li, J.; Lv, J.; Ma, D. Monitoring and Prediction of Mining Subsidence Based on SBAS-InSAR and Improved Support Vector Regression. Remote Sens. Inf. 2021, 36, 6–12. [Google Scholar]
- Available online: http://digisonde.com/digisonde.html (accessed on 12 May 2022).
- Wang, J.; Shi, Y.; Yang, C. Investigation of Two Prediction Models of Maximum Usable Frequency for HF Communication Based on Oblique- and Vertical-Incidence Sounding Data. Atmosphere 2022, 13, 1122. [Google Scholar] [CrossRef]
- Wang, J.; Feng, F.; Bai, H.-m.; Cao, Y.-B.; Chen, Q.; Ma, J.-g. A regional model for the prediction of M(3000)F2 over East Asia. Adv. Space Res. 2020, 65, 2036–2051. [Google Scholar] [CrossRef]
- Xu, T.; Wu, Z.-S.; Wu, J.; Wu, J. Solar cycle variation of the monthly median foF2 at Chongqing station, China. Adv. Space Res. 2008, 42, 213–218. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Wintoft, P. The variability of solar EUV: A multiscale comparison between sunspot number, 10.7cm flux, LASP MgII index, and SOHO/SEM EUV flux. J. Atmos. Sol. Terr. Phys. 2011, 73, 1708–1714. [Google Scholar] [CrossRef]
- Mielich, J.; Bremer, J. Long-term trends in the ionospheric F2 region with different solar activity indices. Ann. Geophys. 2013, 31, 291–303. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, M.L.; Wan, W.; Liu, L.; Ning, B. Modeling M(3000)F2 based on empirical orthogonal function analysis method. Radio Sci. 2008, 43, 1–8. [Google Scholar] [CrossRef]
- Tang, F.; Wu, Y.; Zhou, Y.; Gobinath, R. Hybridizing Grid Search and Support Vector Regression to Predict the Compressive Strength of Fly Ash Concrete. Adv. Civ. Eng. 2022, 2022, 360191. [Google Scholar] [CrossRef]
- He, R.; Li, M.; Zhang, Q.; Zhao, Q. A Comparison of a GNSS-GIM and the IRI-2020 Model Over China Under Different Ionospheric Conditions. Space Weather 2023, 21, e2023SW003646. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Q.; Shi, Y.; Yang, C. A Prediction Method of Ionospheric hmF2 Based on Machine Learning. Remote Sens. 2023, 15, 3154. [Google Scholar] [CrossRef]

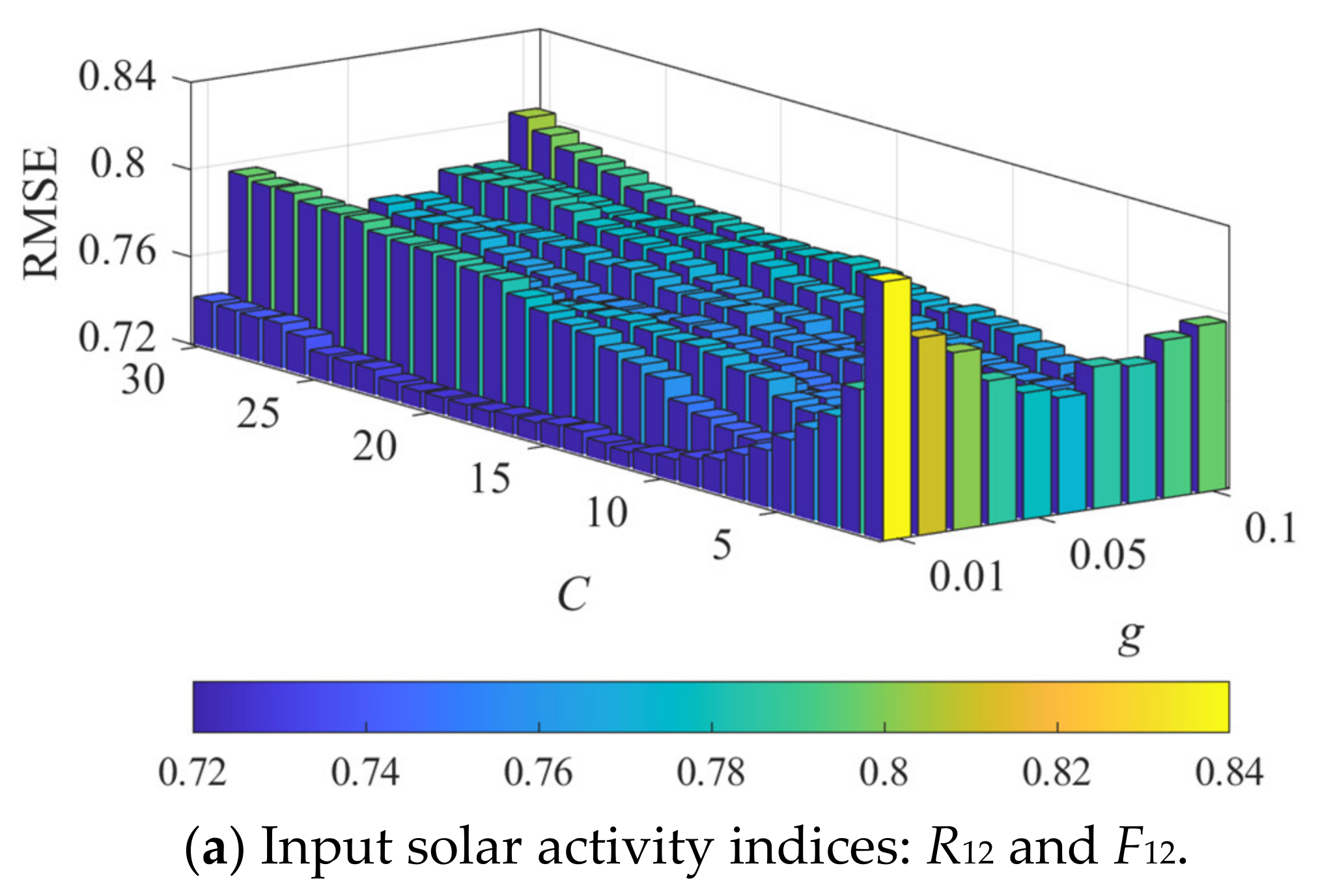



| Solar Activity Indices | RMSEMIN | CRMSEMIN | gRMSEMIN |
|---|---|---|---|
| R12 and F12 | 0.727 | 12 | 0.01 |
| R12 | 0.708 | 12 | 0.01 |
| F12 | 0.730 | 12 | 0.07 |
| Options | Implication | Selection |
|---|---|---|
| Ne Topside | The model of electron density in the topside ionosphere | NeQuick |
| FoF2 Model | The model of FoF2 | CCIR or URSI-88 |
| FoF2 Storm | The model for calculating FoF2 during a storm | OFF |
| hmF2 Model | The model of hmF2 | M3000F2 |
| Bottomside Thickness B0 | The model of the F2 bottom side region | Bil-2000 |
| F1 Model | The model of F1 layer | Scotto-1997-no-L |
| D | The model of D layer | IRI-1990 |
| Te | The model of electron temperature | TBT-2012 |
| Ion Comp Model | The model of densities and composition | DS95/DY85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Men, X.; Wang, J. A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression. Remote Sens. 2024, 16, 2701. https://doi.org/10.3390/rs16152701
Yu Q, Men X, Wang J. A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression. Remote Sensing. 2024; 16(15):2701. https://doi.org/10.3390/rs16152701
Chicago/Turabian StyleYu, Qiao, Xiaobin Men, and Jian Wang. 2024. "A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression" Remote Sensing 16, no. 15: 2701. https://doi.org/10.3390/rs16152701
APA StyleYu, Q., Men, X., & Wang, J. (2024). A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression. Remote Sensing, 16(15), 2701. https://doi.org/10.3390/rs16152701








