Power Allocation Scheme for Multi-Static Radar to Stably Track Self-Defense Jammers
Abstract
1. Introduction
- (1)
- We establish a jamming signal model, an echo model, and a measurement model of multi-static radar. The BCRLB of joint time delay and Doppler frequency is derived to characterize the tracking accuracy. In addition, the SINR of each radar is used as an optimization function to characterize the detection accuracy. As a result, the limited power resources of the multi-static radar network are allocated efficiently to minimize the worst BCRLB and optimize the detection probability.
- (2)
- We propose a multi-objective optimization algorithm to solve the power allocation problem of multi-static radar. The BCRLB and detection probability of each radar are simultaneously used as the optimization index, with varying weight coefficients assigned based on their significance. In order to maintain the target track continuity, these weight coefficients are dynamically adjusted according to the target detection probability across multiple frames.
- (3)
- Simulation results show that the proposed algorithm can achieve good tracking performance and detection performance compared with three other algorithms. For targets with low detection probability across multiple frames, the proposed algorithm adjusts its weight coefficient to improve the detection probability in the next frame, thereby ensuring target track continuity. In addition, two target reflection models are used to verify the effectiveness of the proposed algorithm.
2. System Model
2.1. Jamming Signal Model
2.2. Radar Signal Model
2.3. Motion Mode and Measurement Model
3. Bayesian Cramér–Rao Lower Bound
4. Power Allocation Algorithm
4.1. Power Allocation Model
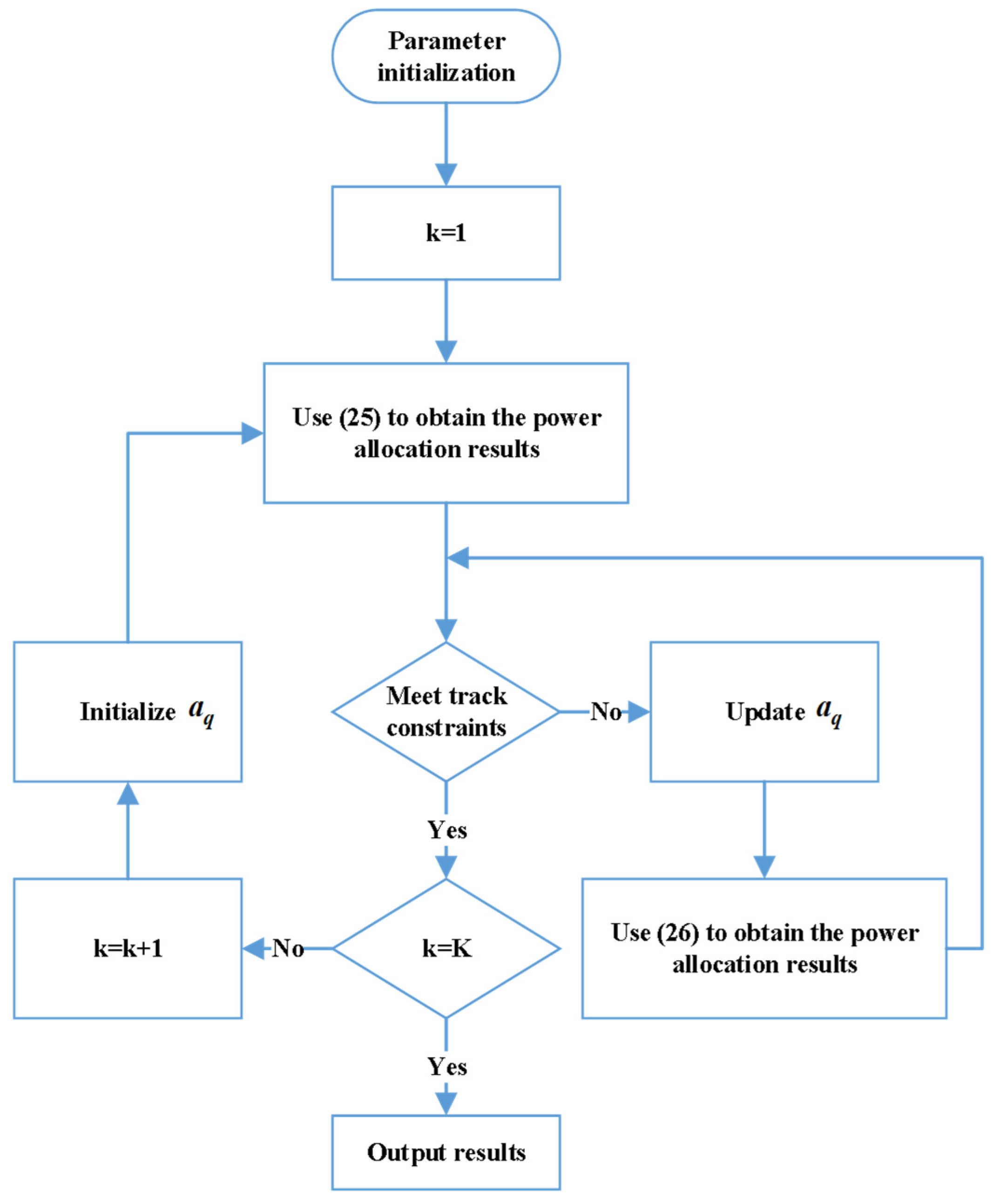
4.2. Multi-Objective Optimization Algorithm
- Step 1.
- For parameter initialization, take all corresponding weight coefficients as 0, and k = 1.
- Step 2.
- Use (34) to obtain the power distribution results. If these meet the track continuity constraint, go to step 5. Otherwise, go to step 3.
- Step 3.
- Select the jammers that do not meet the track constraint, and take the corresponding weight coefficient as 100. For the remaining jammers, the corresponding weight coefficient is 0.
- Step 4.
- Substitute the weight coefficient into (35). Record the obtained power distribution result as . If it meets the track continuity constraint, go to step 5. Otherwise, go to step 3.
- Step 5.
- If k is equal to the maximum number of frames K, output the optimal power allocation result. Otherwise, , and then go to step 2.
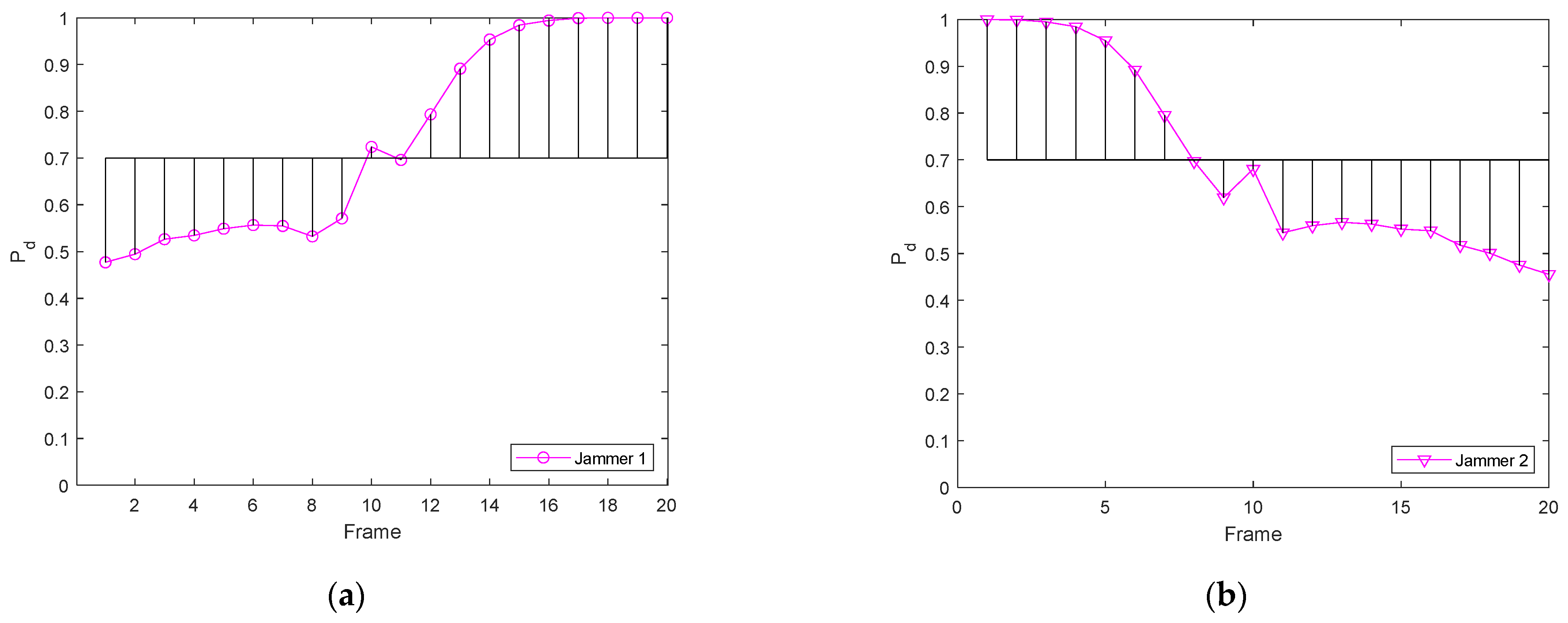
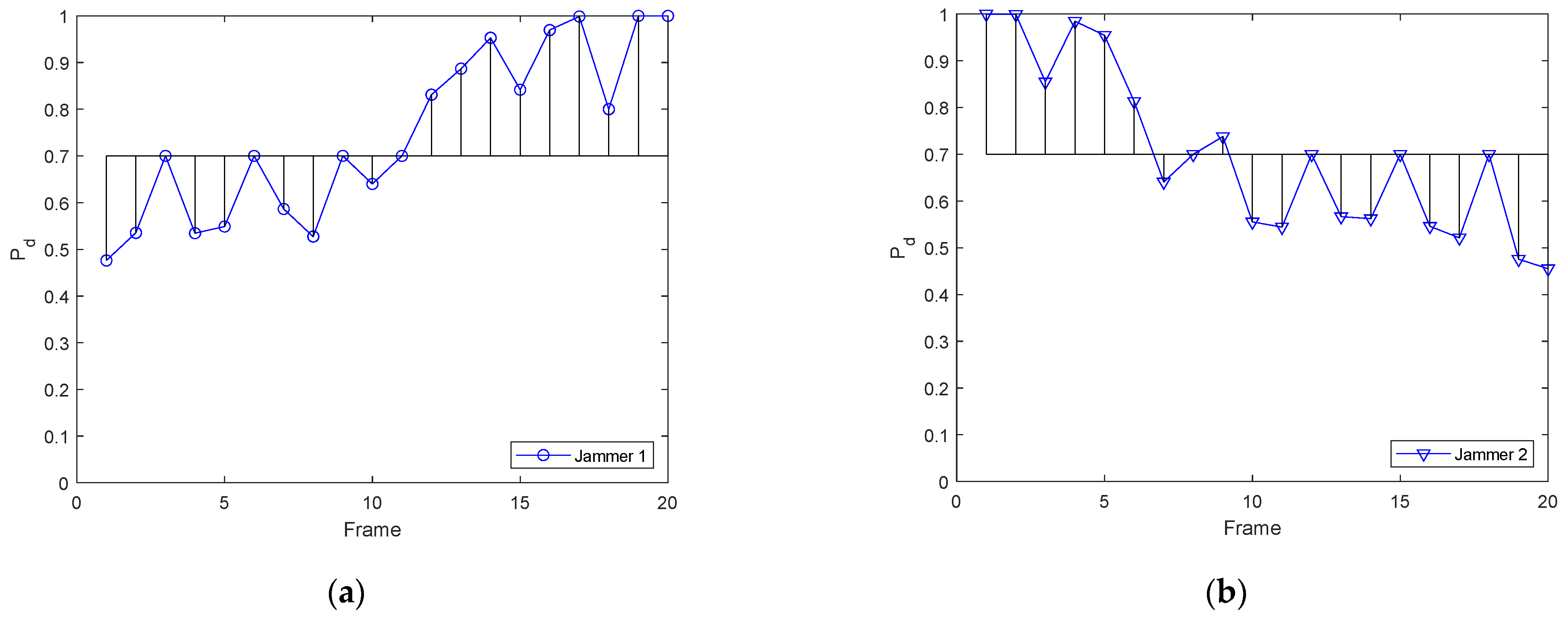
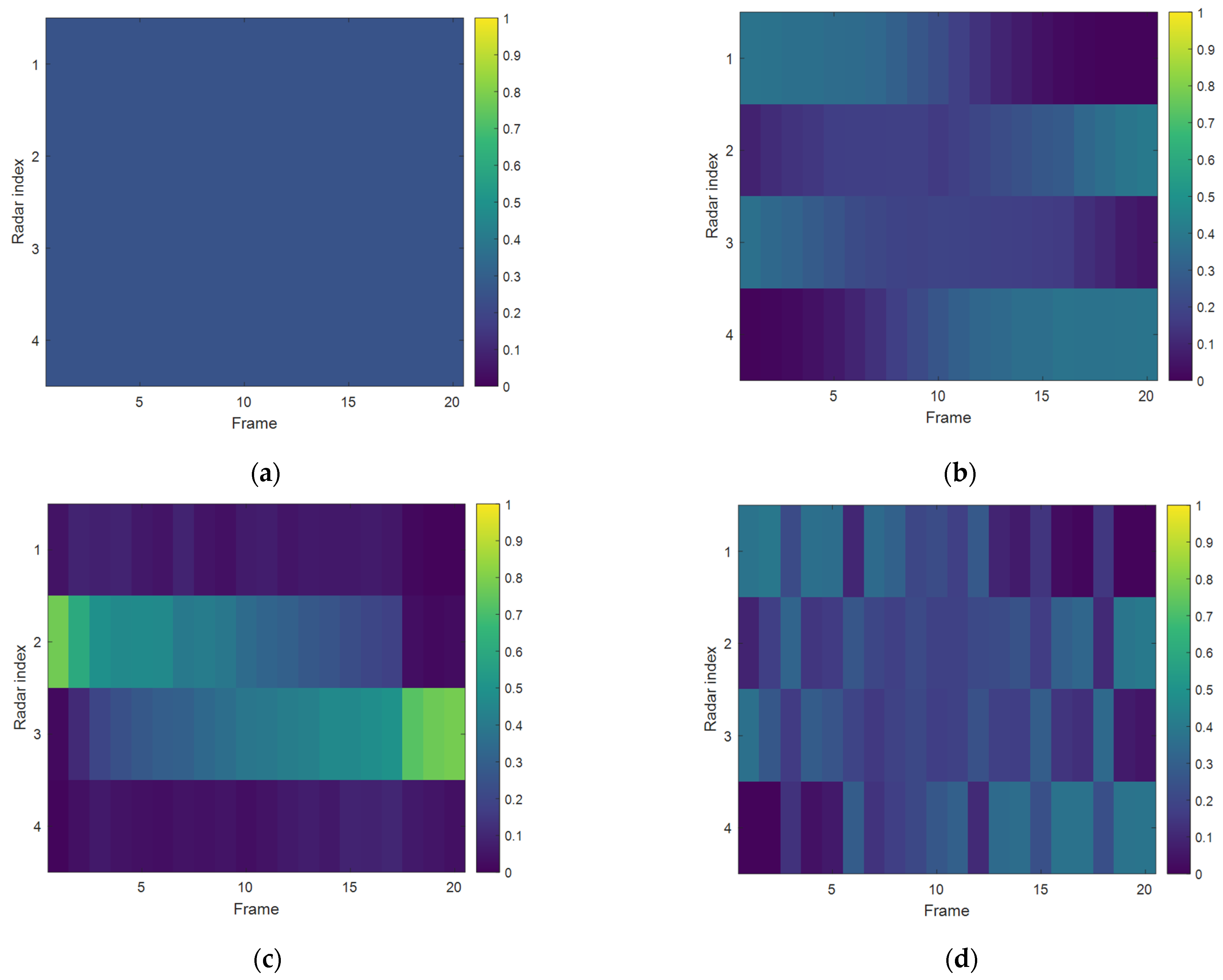
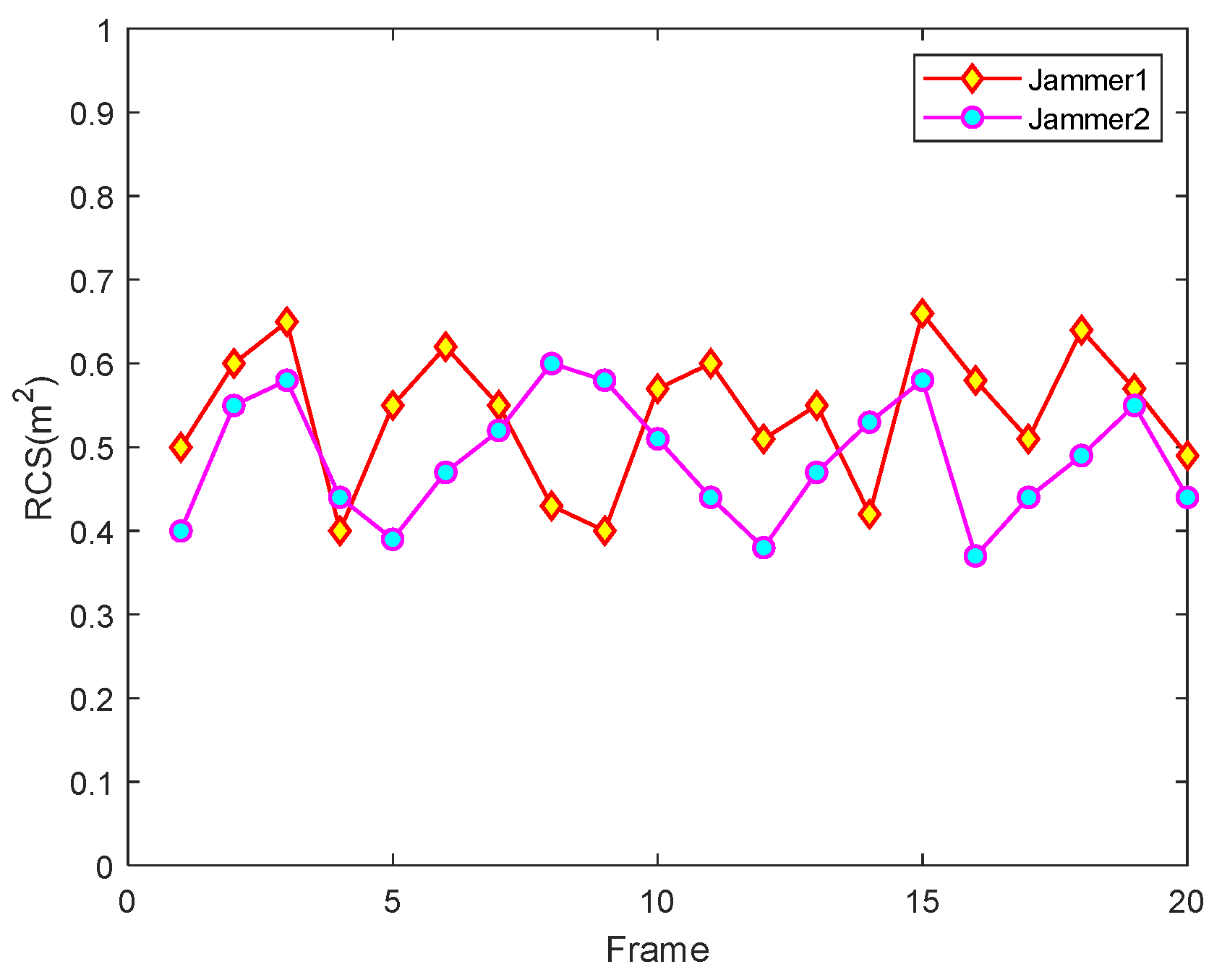
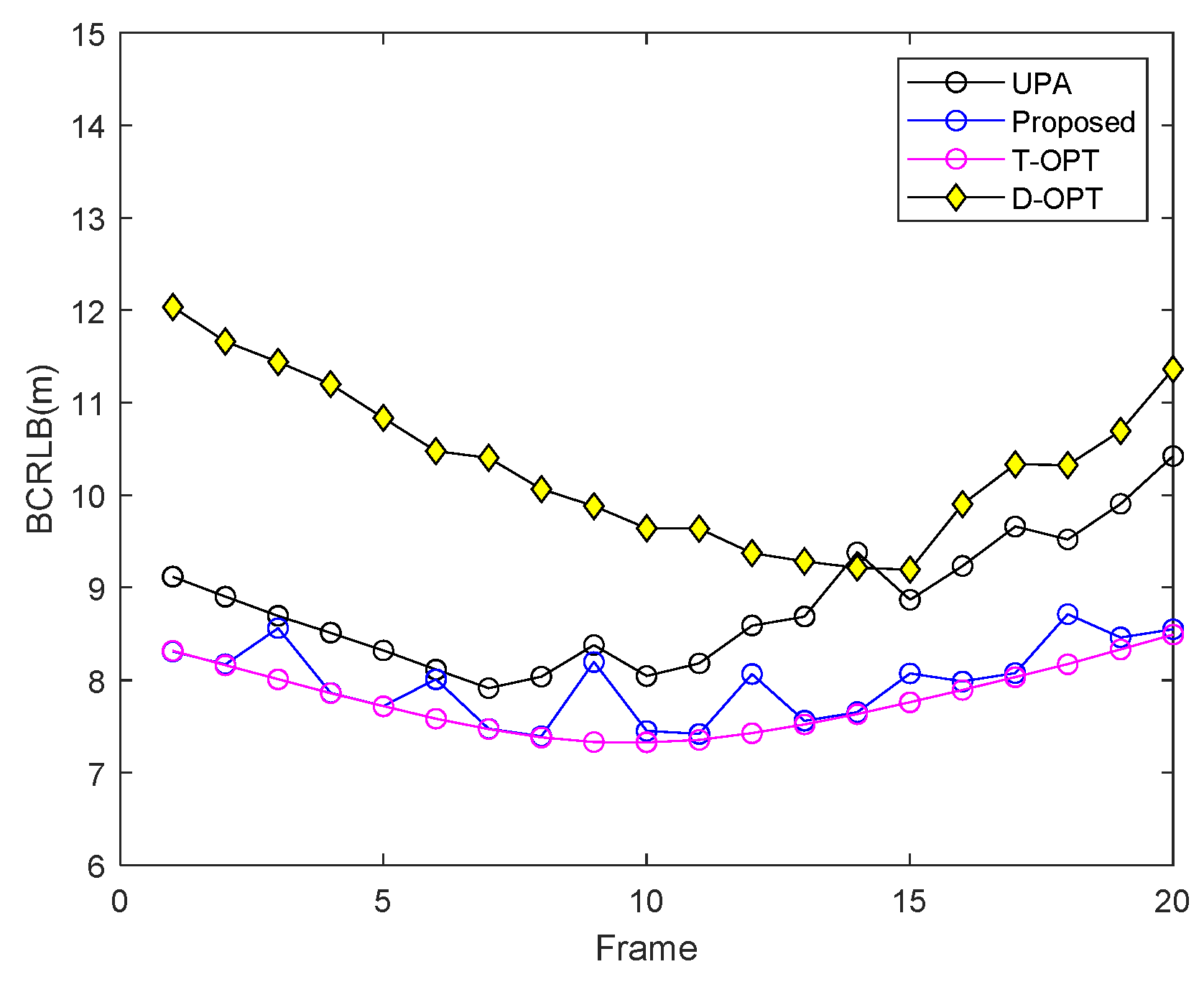
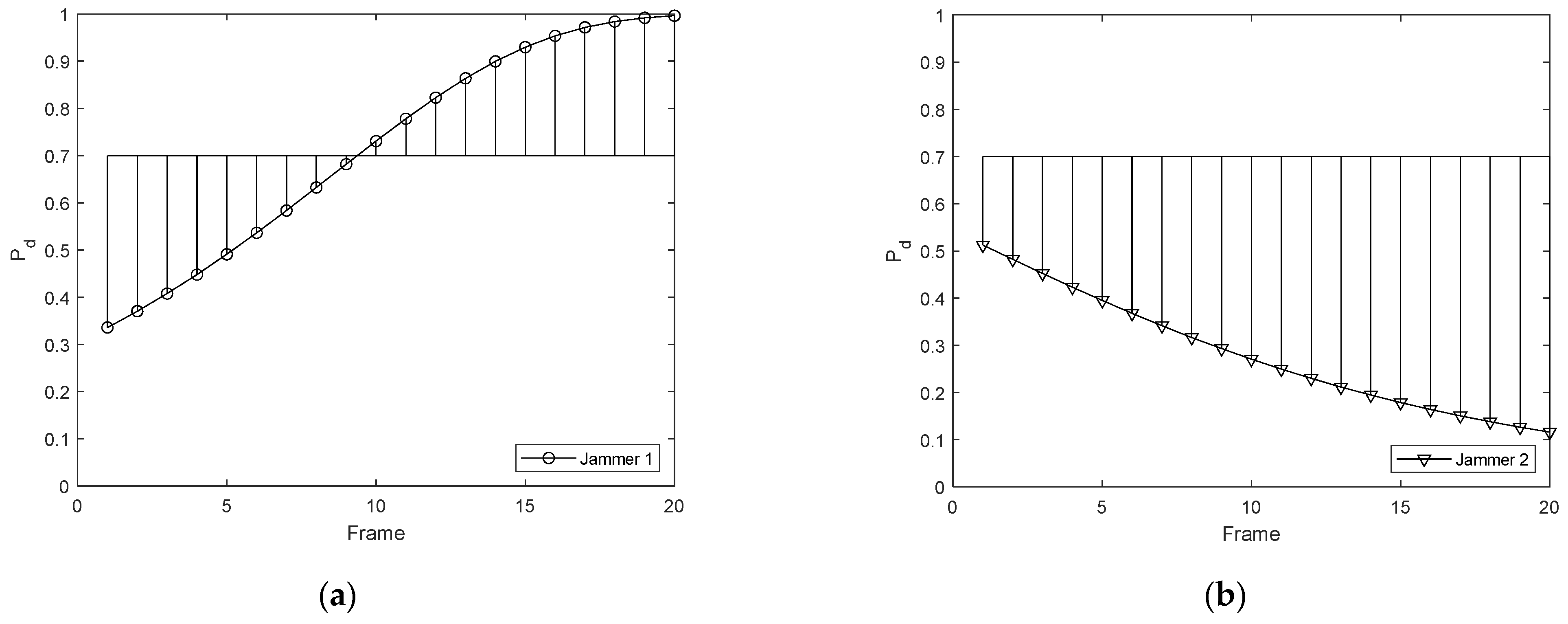
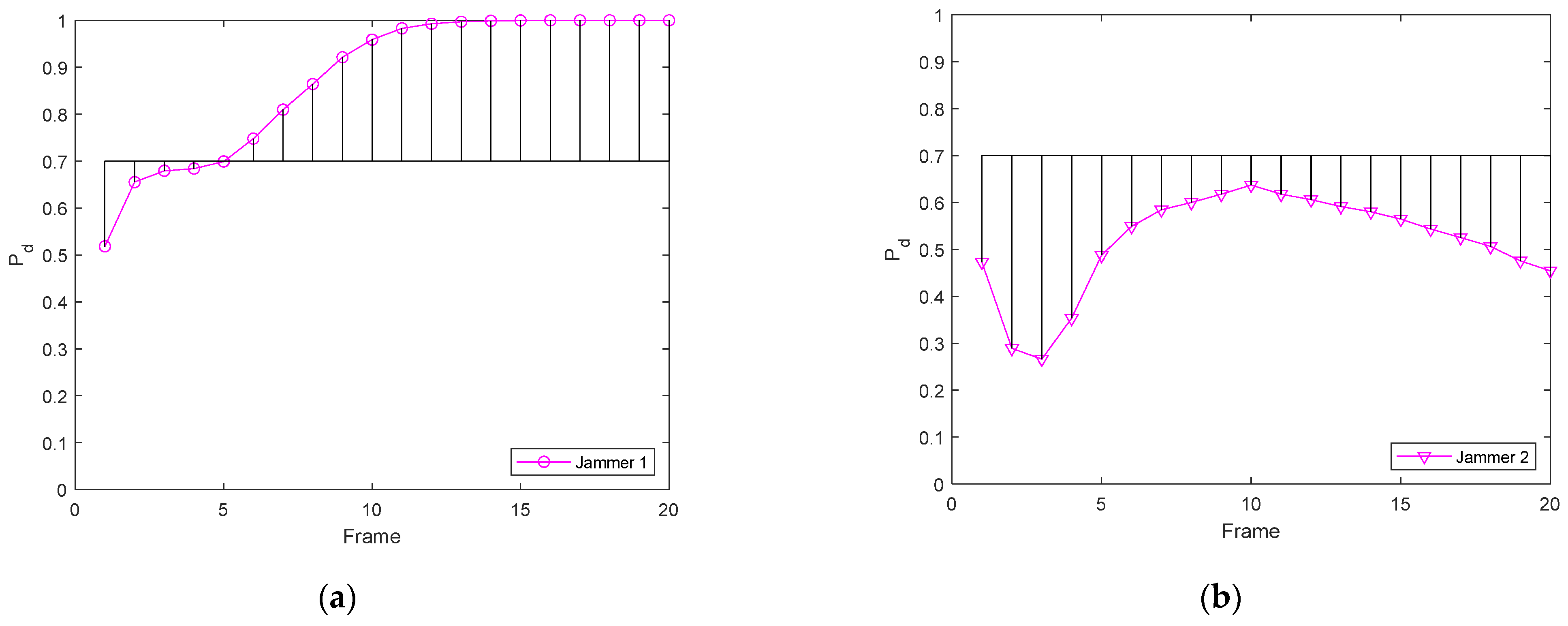
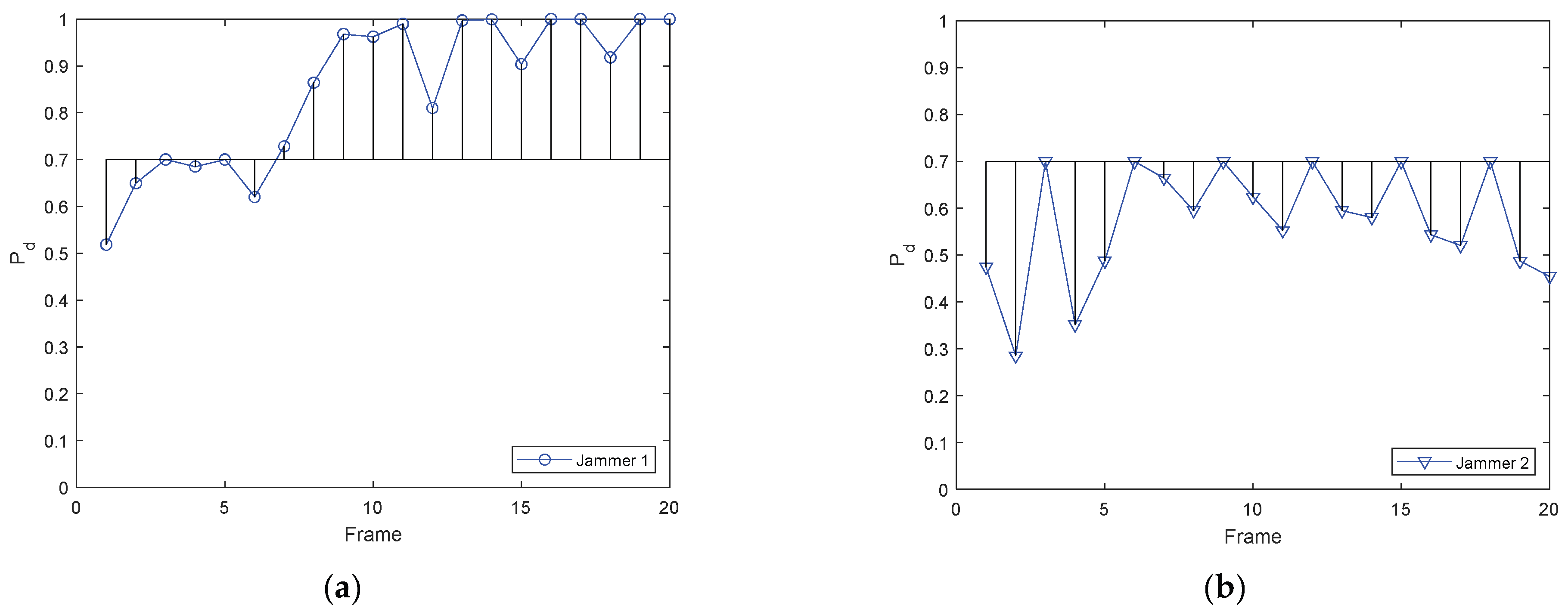
5. Simulations and Results
5.1. Simulation Scenario 1
5.2. Simulation Scenario 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J.W.; Zhang, Y.H.; Liao, G.S.; So, C. Resolving Range Ambiguity via Multiple-Input Multiple-Output Radar with Element-Pulse Coding. IEEE Trans. Signal Process. 2020, 68, 2770–2783. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.S.; Xu, J.W.; Zhang, Y.H.; Liao, B. Transceive Beamforming with Accurate Nulling in FDA-MIMO Radar for Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4145–4159. [Google Scholar] [CrossRef]
- Lan, L.; Rosamilia, M.; Aubry, A.; De Maio, A.; Liao, G.S.; Xu, J.W. Adaptive Target Detection with Polarimetric FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2204–2220. [Google Scholar] [CrossRef]
- Darzikolaei, M.A.; Mollaei, M.R.K.; Najimi, M. An effective PSO-based power allocation for target tracking in MIMO radar with widely separated antennas. Phys. Commun. 2022, 51, 101544. [Google Scholar] [CrossRef]
- Zheng, G.M.; Song, Y.W.; Liu, Y.B.; Chen, G. Search-free range and angle estimation for bistatic VHF-FDA-MIMO radar in complex terrain. Signal Process. 2023, 212, 109163. [Google Scholar] [CrossRef]
- Cong, J.Y.; Wang, X.P.; Lan, X.; Huang, M.X.; Wan, L.T. Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network. Remote Sens. 2021, 13, 1956. [Google Scholar] [CrossRef]
- Tang, B.; Li, J.; Zhang, Y.; Tang, J. Design of MIMO radar waveform covariance matrix for Clutter and Jamming suppression based on space time adaptive processsing. Signal Process. 2016, 121, 60–69. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liao, G.S.; Xu, J.W.; Lan, L. Mainlobe Deceptive Jammer Suppression Based on Quadratic Phase Coding in FDA-MIMO Radar. Remote Sens. 2022, 14, 5831. [Google Scholar] [CrossRef]
- Wu, J.L.; Shi, C.G.; Zhang, W.W.; Zhou, J.J. Joint Beamforming Design and Power Control Game for a MIMO Radar System in the Presence of Multiple Jammers. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 759–773. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Q.L.; Xie, J.W. Joint resource optimization for a distributed MIMO radar when tracking multiple targets in the presence of deception jamming. Signal Process. 2022, 200, 108641. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, J.W.; Ding, Z.; So, H.C. Target Localization with Jammer Removal Using Frequency Diverse Array. IEEE Trans. Veh. Technol. 2020, 69, 11685–11696. [Google Scholar] [CrossRef]
- Yi, W.; Yuan, Y.; Hoseinnezhad, R.; Kong, L.J. Resource Scheduling for Distributed Multi-Target Tracking in Netted Colocated MIMO Radar Systems. IEEE Trans. Signal Process. 2020, 68, 1602–1617. [Google Scholar] [CrossRef]
- Liu, W.J.; Liu, J.; Li, H.; Du, Q.L.; Wang, Y.L. Multichannel Signal Detection Based on Wald Test in Subspace Interference and Gaussian Noise. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1370–1381. [Google Scholar] [CrossRef]
- Yi, W.; Li, S.Q.; Wang, B.L.; Hoseinnezhad, R.; Kong, L.J. Computationally Efficient Distributed Multi-Sensor Fusion with Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2020, 68, 241–256. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Sensor Selection in Distributed Multiple-Radar Architectures for Localization: A Knapsack Problem Formulation. IEEE Trans. Signal Process. 2012, 60, 247–260. [Google Scholar] [CrossRef]
- Wang, X.R.; Hassanien, A.; Amin, M.G. Dual-Function MIMO Radar Communications System Design Via Sparse Array Optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1213–1226. [Google Scholar] [CrossRef]
- Ma, B.T.; Chen, H.W.; Sun, B.; Xiao, H.T. A Joint Scheme of Antenna Selection and Power Allocation for Localization in MIMO Radar Sensor Networks. IEEE Commun. Lett. 2014, 18, 2225–2228. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Xie, J.W.; Zhang, Z.J.; Lu, W.L. Joint Subarray Selection and Power Allocation for Cognitive Target Tracking in Large-Scale MIMO Radar Networks. IEEE Syst. J. 2020, 14, 2569–2580. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Z.J.; Lu, W.L.; Xie, J.W. Joint Target Assignment and Power Allocation in Multiple Distributed MIMO Radar Networks. IEEE Syst. J. 2021, 15, 694–704. [Google Scholar] [CrossRef]
- Yan, J.K.; Liu, H.W.; Pu, W.Q.; Zhou, S.H.; Liu, Z.; Bao, Z. Joint Beam Selection and Power Allocation for Multiple Target Tracking in Netted Colocated MIMO Radar System. IEEE Trans. Signal Process. 2016, 64, 6417–6427. [Google Scholar] [CrossRef]
- Yan, J.K.; Liu, H.W.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous Multibeam Resource Allocation Scheme for Multiple Target Tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Chen, H.W.; Ta, S.Y.; Sun, B. Cooperative Game Approach to Power Allocation for Target Tracking in Distributed MIMO Radar Sensor Networks. IEEE Sens. J. 2015, 15, 5423–5432. [Google Scholar] [CrossRef]
- Deligiannis, A.; Panoui, A.; Lambotharan, S.; Chambers, J.A. Game-Theoretic Power Allocation and the Nash Equilibrium Analysis for a Multistatic MIMO Radar Network. IEEE Trans. Signal Process. 2017, 65, 6397–6408. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using. MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Zhang, G.S.; Xie, J.W.; Zhang, H.W.; Li, Z.J.; Qi, C. Dynamic Antenna Selection for Colocated MIMO Radar. Remote Sens. 2022, 14, 2912. [Google Scholar] [CrossRef]
- Shi, C.G.; Wang, Y.J.; Salous, S.; Zhou, J.J.; Yan, J.K. Joint Transmit Resource Management and Waveform Selection Strategy for Target Tracking in Distributed Phased Array Radar Network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2762–2778. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Z.; Ding, L.; Yan, J. Multidomain Resource Allocation for Asynchronous Target Tracking in Heterogeneous Multiple Radar Networks with Nonideal Detection. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2016–2033. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, T.; Yi, W.; Kong, L.J. A GDOP-Based Performance Description of TOA Localization with Uncertain Measurements. Remote Sens. 2022, 14, 910. [Google Scholar] [CrossRef]
- He, Q.A.; Blum, R.S.; Haimovich, A.M. Noncoherent MIMO Radar for Location and Velocity Estimation: More Antennas Means Better Performance. IEEE Trans. Signal Process. 2010, 58, 3661–3680. [Google Scholar] [CrossRef]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef]
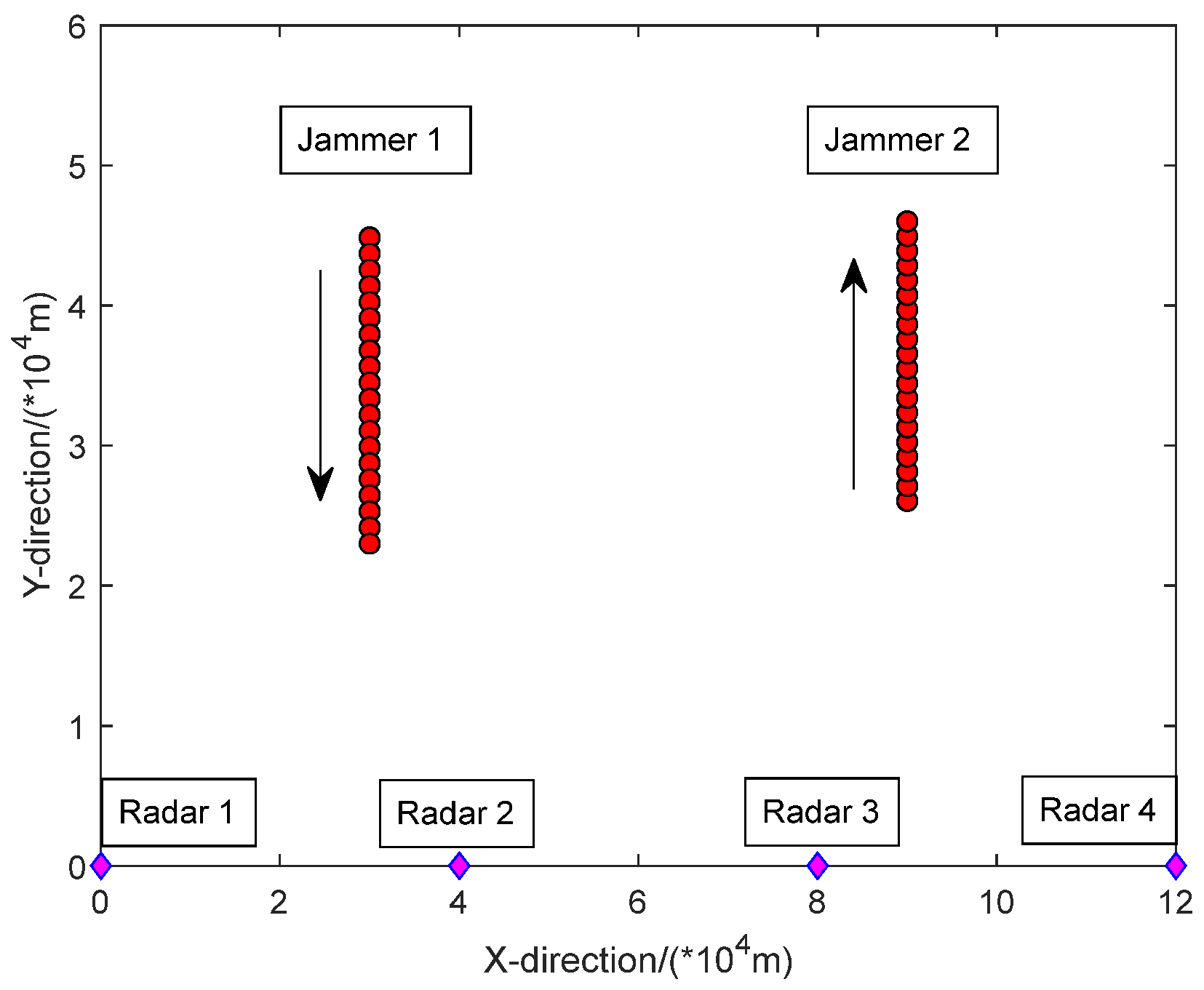


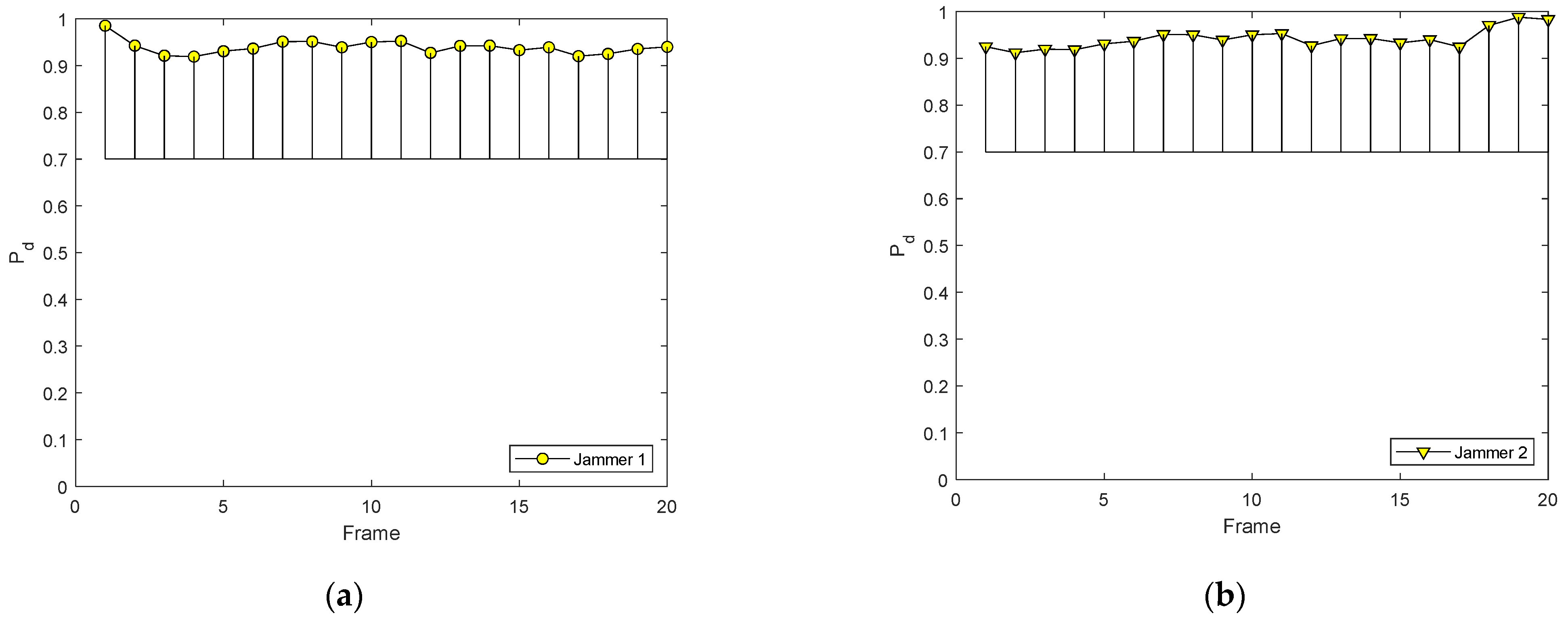
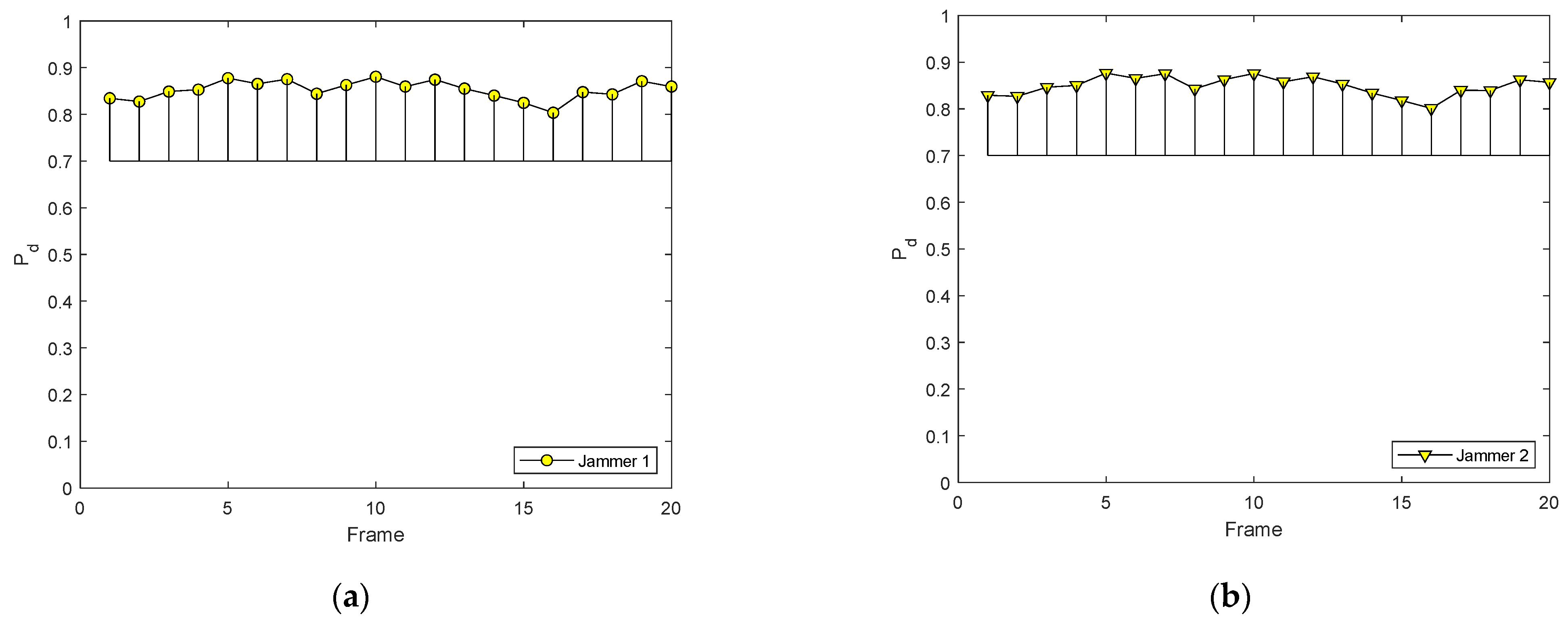

| Target Index | Position/km | Velocity/(m·s−1) |
|---|---|---|
| 1 | (30, 46) | (0, −230) |
| 2 | (90, 25) | (0, 210) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Xie, J.; Zhang, H.; Feng, W.; Liu, M.; Qin, C. Power Allocation Scheme for Multi-Static Radar to Stably Track Self-Defense Jammers. Remote Sens. 2024, 16, 2699. https://doi.org/10.3390/rs16152699
Zhang G, Xie J, Zhang H, Feng W, Liu M, Qin C. Power Allocation Scheme for Multi-Static Radar to Stably Track Self-Defense Jammers. Remote Sensing. 2024; 16(15):2699. https://doi.org/10.3390/rs16152699
Chicago/Turabian StyleZhang, Gangsheng, Junwei Xie, Haowei Zhang, Weike Feng, Mingjie Liu, and Cong Qin. 2024. "Power Allocation Scheme for Multi-Static Radar to Stably Track Self-Defense Jammers" Remote Sensing 16, no. 15: 2699. https://doi.org/10.3390/rs16152699
APA StyleZhang, G., Xie, J., Zhang, H., Feng, W., Liu, M., & Qin, C. (2024). Power Allocation Scheme for Multi-Static Radar to Stably Track Self-Defense Jammers. Remote Sensing, 16(15), 2699. https://doi.org/10.3390/rs16152699






