Adaptive Background Endmember Extraction for Hyperspectral Subpixel Object Detection
Abstract
1. Introduction
- An adaptive scale constraint is introduced into the process of background endmember dictionary learning to achieve the simultaneous extraction of the background spectral endmembers and their quantities.
- A novel background endmember extraction method based on adaptive background endmember dictionary learning is proposed to improve the detection abilities of pixel reconstruction-based subpixel detectors for small objects.
2. Related Works
2.1. SACE
2.2. hCEM
2.3. SPSMF
2.4. PALM
2.5. CSCR
2.6. HSPRD
3. Subpixel Object Detection Model
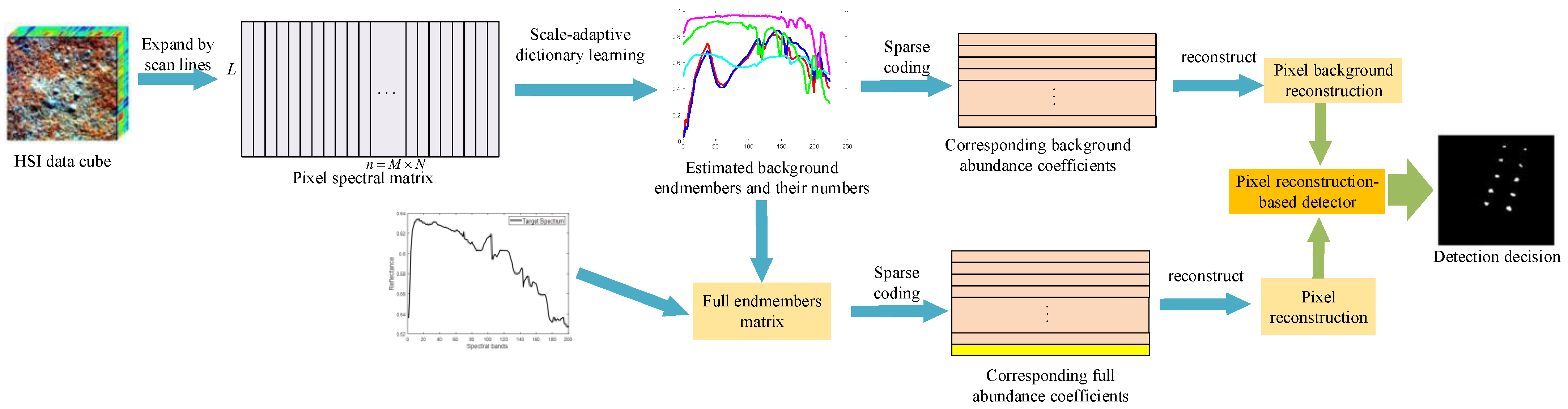
4. Adaptive Dictionary Learning-Based Background Endmember Extraction
| Algorithm 1 Adaptive dictionary learning-based background endmember extraction (ADLBEE) |
| Input: Original HSI , regularization parameters and |
| Number of iterations |
| Output: background endmember matrix |
| 1 Initialization: Set initial values , The initial background endmember matrix is generated randomly |
| 2 Repeat cycle |
| 3 |
| 4 Repeat cycle |
| 5 Solve Equation (22) to obtain at |
| 6 Substitute into Equation (23) to obtain |
| 7 |
| 8 Until the objective Function (21) converges |
| 9 |
| 10 Substitute into Equation (20) to obtain by gradient descent method |
| 11 |
| 12 Until converges or |
| 13 |
| 14 Return background endmembers |
5. Subpixel Object Detection with Pixel Reconstruction Detection Operator
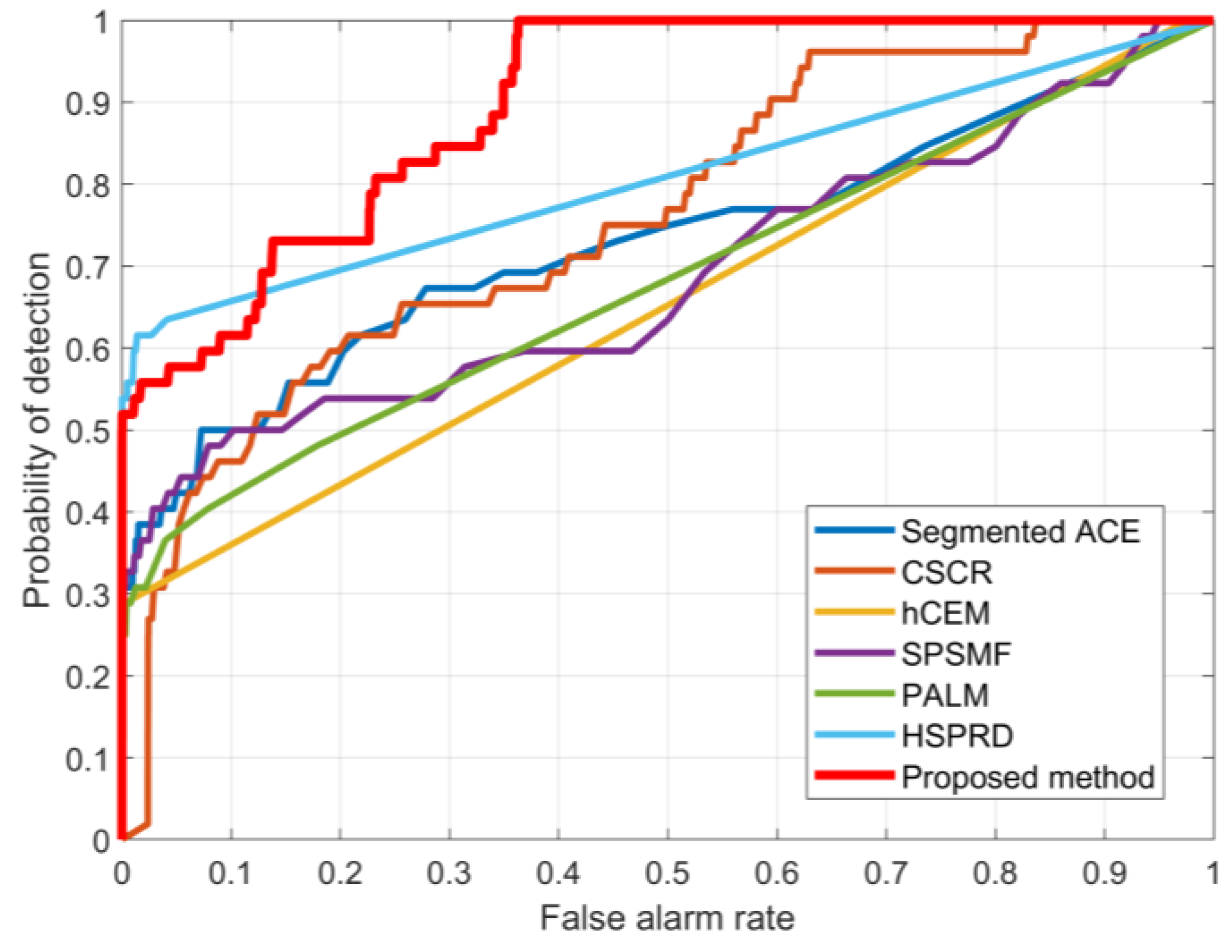
6. Experiments with Real-World Data
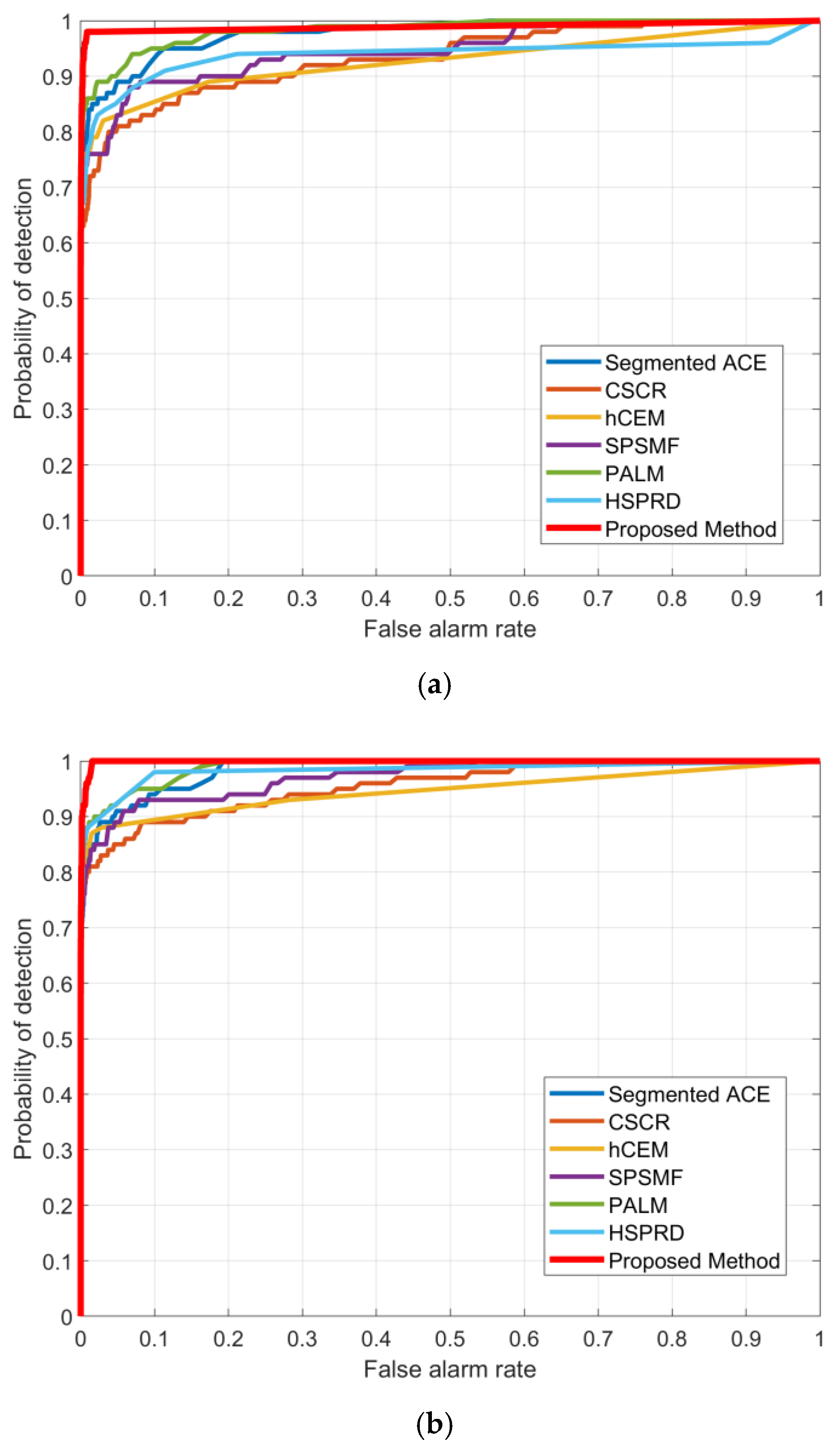
6.1. Evaluation Indicators
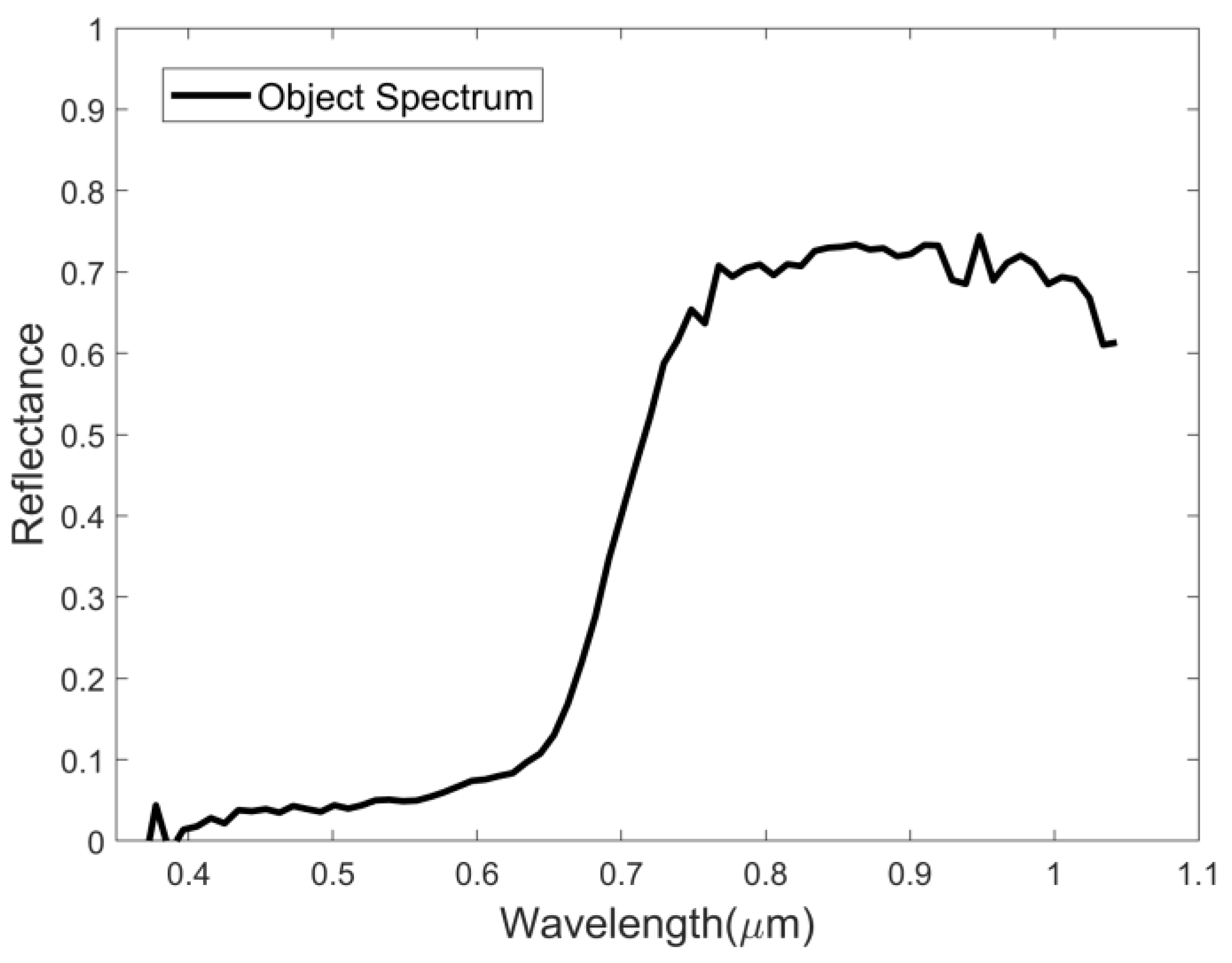
6.2. Experiment with Simulated Data
6.3. Experiment with Real-World Data
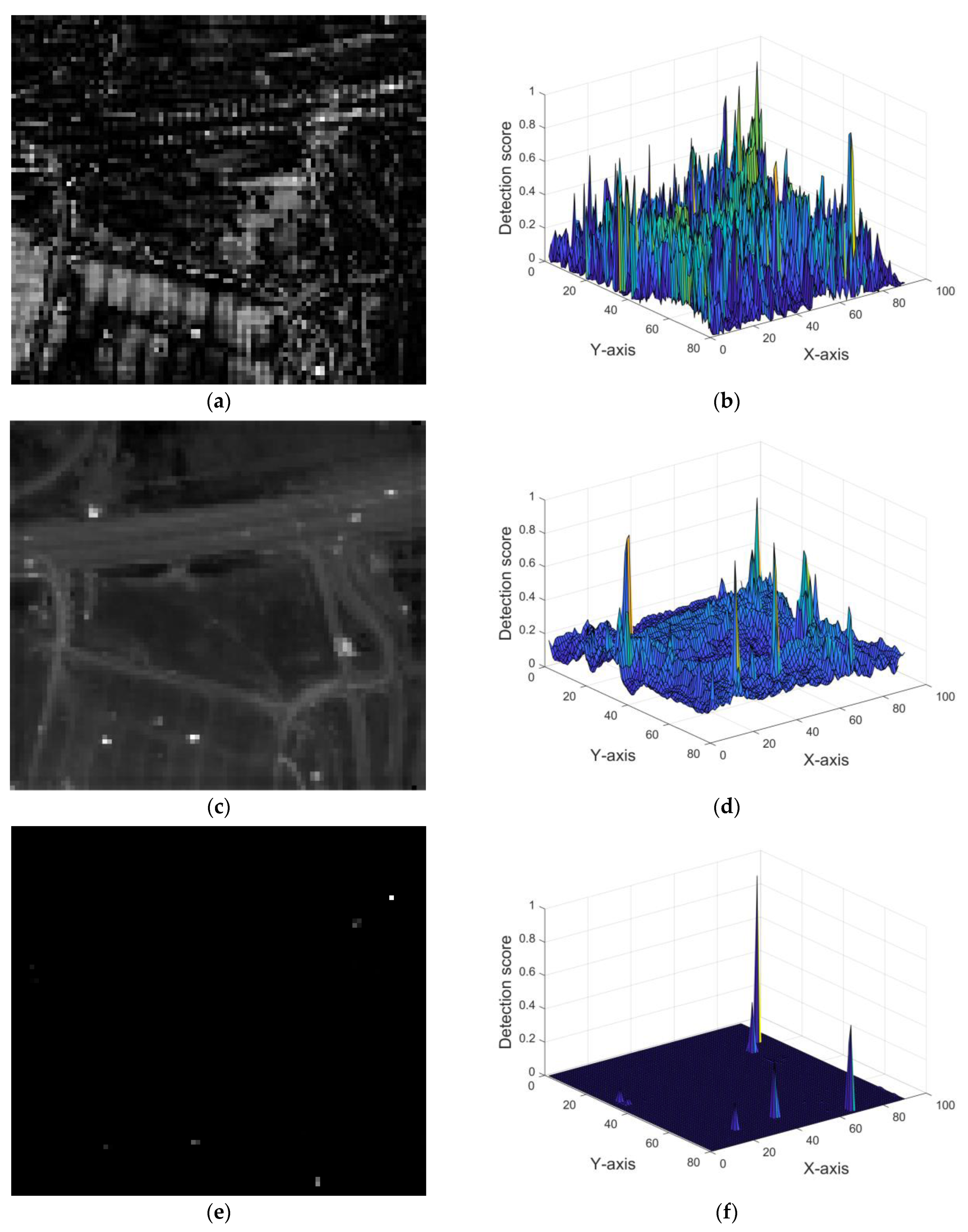
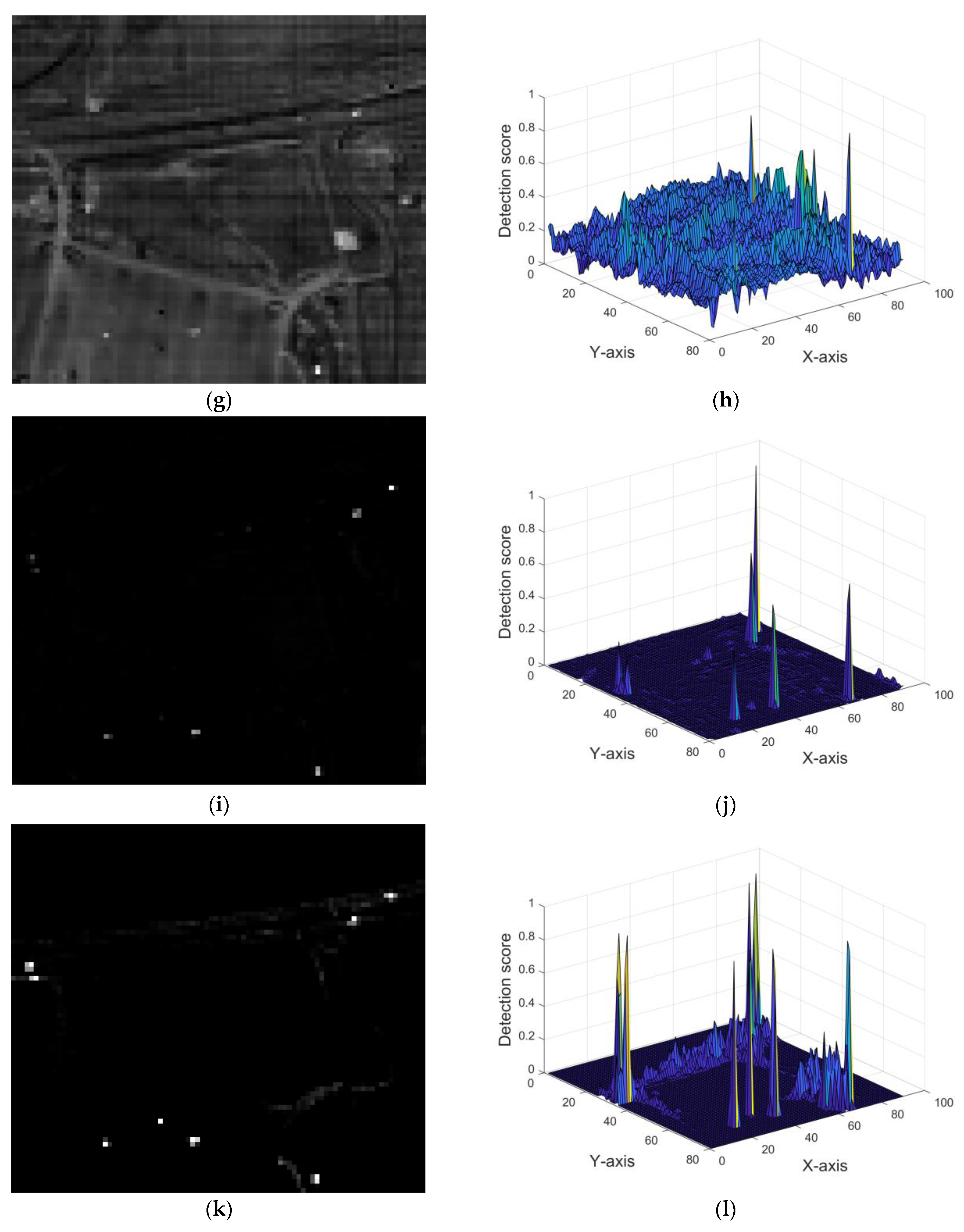
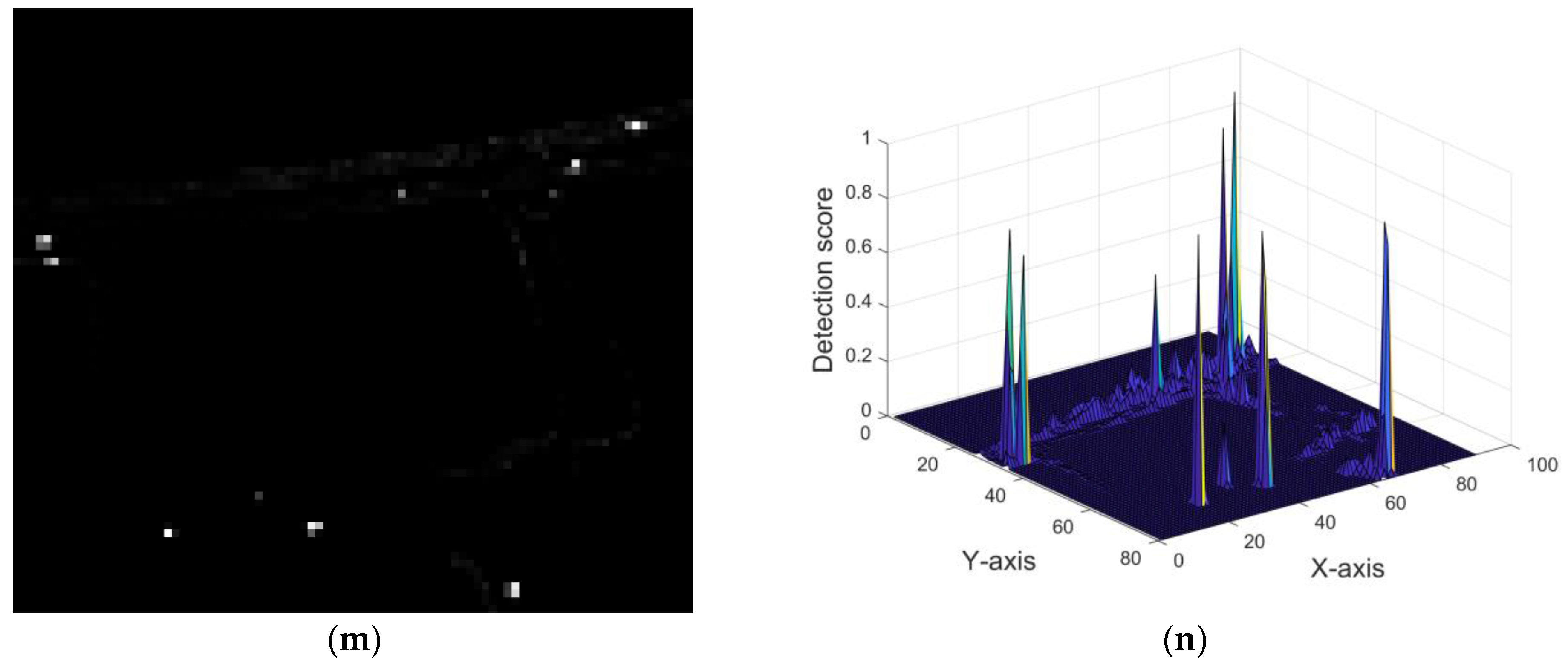
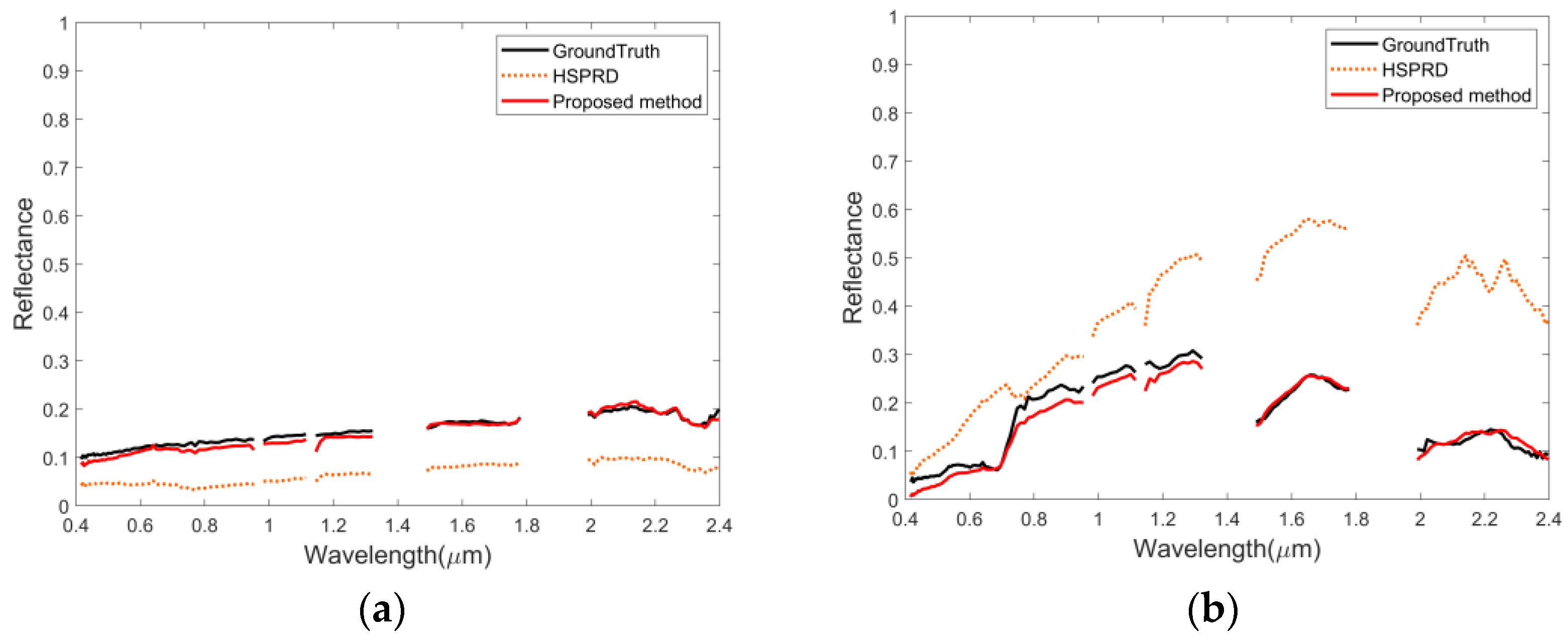
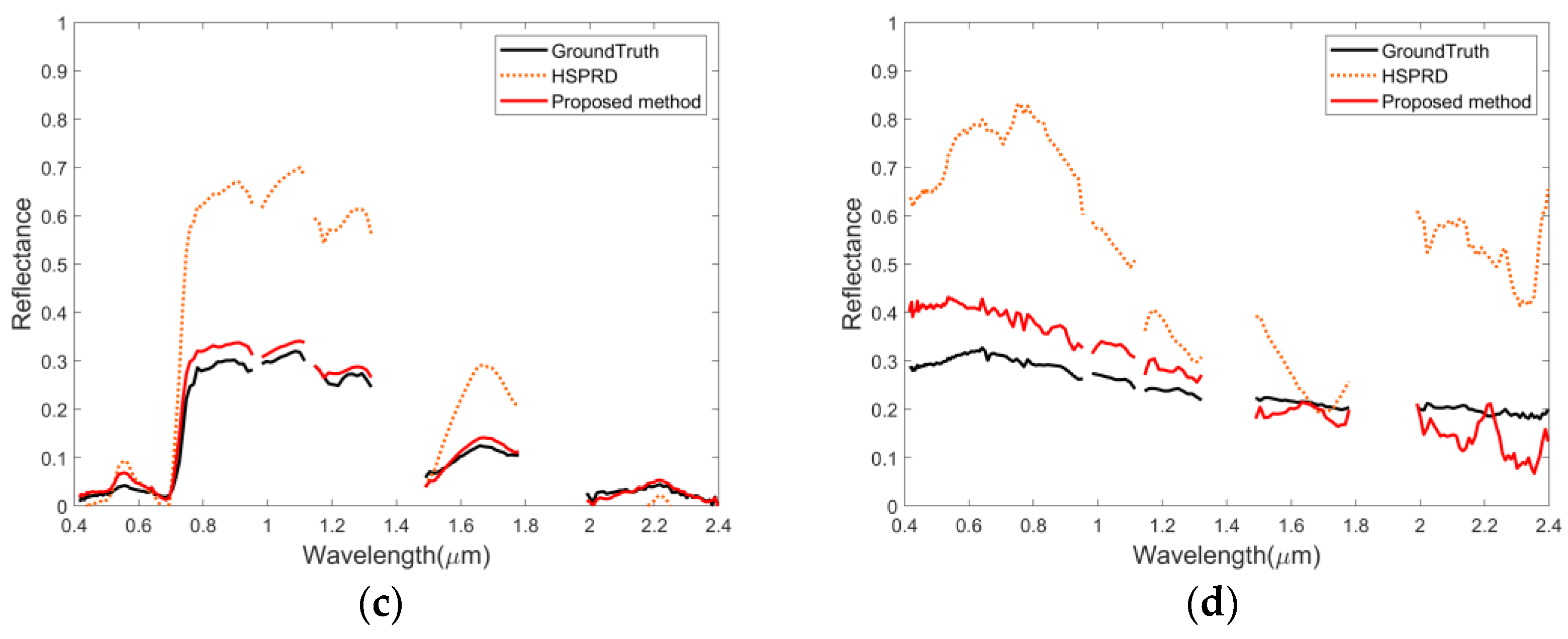
6.3.1. Urban Dataset
6.3.2. MUUFL Gulfport Dataset
6.3.3. HOSD Dataset
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, Z.; Pan, B.; Xu, X.; Li, T.; Shi, Z. LiCa: Label-indicate-conditional-alignment domain generalization for pixel-wise hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5519011. [Google Scholar] [CrossRef]
- Kang, X.; Zhu, Y.; Duan, P.; Li, S. Two-Dimensional Spectral Representation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–9. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. Learning Single Spectral Abundance for Hyperspectral Subpixel Target Detection. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Xie, C.; Fan, Z.; Duan, Q.; Zhang, D.; Jiang, L.; Wei, X.; Hong, D.; Li, G.; Zeng, X.; et al. Hyperspectral Anomaly Detection Using Deep Learning: A Review. Remote Sens. 2022, 14, 1973. [Google Scholar] [CrossRef]
- Shao, Y.; Li, Y.; Li, L.; Wang, Y.; Yang, Y.; Ding, Y.; Zhang, M.; Liu, Y.; Gao, X. RANet: Relationship Attention for Hyperspectral Anomaly Detection. Remote Sens. 2023, 15, 5570. [Google Scholar] [CrossRef]
- Liu, S.; Li, Z.; Wang, G.; Qiu, X.; Liu, T.; Cao, J.; Zhang, D. Spectral–Spatial Feature Fusion for Hyperspectral Anomaly Detection. Sensors 2024, 24, 1652. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Du, B.; Dong, Y.; Zhang, L. Target Detection with Spatial-Spectral Adaptive Sample Generation and Deep Metric Learning for Hyperspectral Imagery. IEEE Trans. Multimed. 2023, 25, 6538–6550. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, P.; Kang, X.; Mo, Y.; Li, S. Feature-Band-Based Unsupervised Hyperspectral Underwater Target Detection Near the Coastline. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5510410. [Google Scholar] [CrossRef]
- Shekhar, C.; Sharma, A.; Preet, P.; Negi, H.S.; Chowdhury, P.R.; Satyawali, P.K. Mixed and Sub-Pixel Target Detection Using Space Borne Hyper-Spectral Imaging Data: Analysis and Challenges. In Proceedings of the 2023 International Conference on Machine Intelligence for GeoAnalytics and Remote Sensing (MIGARS), Hyderabad, India, 27–29 January 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Ma, X.; Kang, X.; Qin, H.; Wang, W.; Ren, G.; Wang, J.; Liu, B. A Lightweight Hybrid Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513714. [Google Scholar] [CrossRef]
- Li, R.; Pan, B.; Xu, X.; Li, T.; Shi, Z. Towards Convergence: A Gradient-Based Multiobjective Method with Greedy Hash for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509114. [Google Scholar] [CrossRef]
- Chang, C.-I. Hyperspectral Target Detection: Hypothesis Testing, Signal-to-Noise Ratio, and Spectral Angle Theories. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5505223. [Google Scholar] [CrossRef]
- Ling, Q.; Li, K.; Li, Z.; Lin, Z.; Wang, J. Hyperspectral Detection and Unmixing of Subpixel Target Using Iterative Constrained Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1049–1063. [Google Scholar] [CrossRef]
- Chen, B.; Liu, L.; Zou, Z.; Shi, Z. Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sens. 2023, 15, 3223. [Google Scholar] [CrossRef]
- Chang, C.I.; Ma, K.Y. Band Sampling of Kernel Constrained Energy Minimization Using Training Samples for Hyperspectral Mixed Pixel Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522721. [Google Scholar] [CrossRef]
- Jiao, J.; Gong, Z.; Zhong, P. Dual-Branch Fourier-Mixing Transformer Network for Hyperspectral Target Detection. Remote Sens. 2023, 15, 4675. [Google Scholar] [CrossRef]
- Guo, T.; Luo, F.; Duan, Y.; Huang, X.; Shi, G. Rethinking Representation Learning-Based Hyperspectral Target Detection: A Hierarchical Representation Residual Feature-Based Method. Remote Sens. 2023, 15, 3608. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooley, T.; Jacobson, J. Is there a best hyperspectral detection algorithm? In Proceedings of the SPIE Defense, Security, and Sensing, Orlando, FL, USA, 13–17 April 2009. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Jiao, C.; Yang, B.; Wang, Q.; Wang, G.; Wu, J. Discriminative Multiple-Instance Hyperspectral Subpixel Target Characterization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5521420. [Google Scholar] [CrossRef]
- Glenn, T.C. Context-Dependent Detection in Hyperspectral Imagery; University of Florida: Gainesville, FL, USA, 2013. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L.; McWhorter, L.T. Adaptive subspace detectors. IEEE Trans. Signal Process. 2001, 49, 1–16. [Google Scholar] [CrossRef]
- Capobianco, L.; Garzelli, A.; Camps-Valls, G. Target Detection With Semisupervised Kernel Orthogonal Subspace Projection. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3822–3833. [Google Scholar] [CrossRef]
- Broadwater, J.; Chellappa, R. Hybrid Detectors for Subpixel Targets. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1891–1903. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Du, B.; Zhong, Y. Hybrid Detectors Based on Selective Endmembers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2633–2646. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, B. Combined sparse and collaborative representation for hyperspectral target detection. Pattern Recognit. 2015, 48, 3904–3916. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. Background joint sparse representation for hyperspectral image subpixel anomaly detection. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1528–1531. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Song, X.; Zou, L.; Wu, L. Detection of Subpixel Targets on Hyperspectral Remote Sensing Imagery Based on Background Endmember Extraction. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2365–2377. [Google Scholar] [CrossRef]
- Xiaorui, S.; Lingda, W.; Hongxing, H. Blind hyperspectral sparse unmixing based on online dictionary learning. In Proceedings of the SPIE Conference on Image and Signal Processing for Remote Sensing, Berlin, Germany, 10–13 September 2018. [Google Scholar] [CrossRef]
- Cotter, S.F.; Rao, B.D.; Engan, K.; Kreutz-Delgado, K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M. Sparse and redundant modeling of image content using an image-signature-dictionary. SIAM J. Imaging Sci. 2008, 1, 228–247. [Google Scholar] [CrossRef]
- Lu, C.; Shi, J.; Jia, J. Scale Adaptive Dictionary Learning. IEEE Trans. Image Process. 2014, 23, 837–847. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical Suppression Method for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 330–342. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Guo, T.; Luo, F.; Zhang, L.; Zhang, B.; Zhou, X. Learning Structurally Incoherent Background and Target Dictionaries for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3521–3533. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Jiao, C.; Chen, C.; McGarvey, R.G.; Bohlman, S.; Jiao, L.; Zare, A. Multiple instance hybrid estimator for hyperspectral target characterization and sub-pixel target detection. ISPRS J. Photogramm. Remote Sens. 2018, 146, 235–250. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Ghamisi, P. Hyperspectral Remote Sensing Benchmark Database for Oil Spill Detection with an Isolation Forest-Guided Unsupervised Detector. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5509711. [Google Scholar] [CrossRef]












| Method | AUC | ||
|---|---|---|---|
| SNR = 25 dB | SNR = 30 dB | SNR = 35 dB | |
| SACE | 0.9777 | 0.9848 | 0.9871 |
| SPSMF | 0.9478 | 0.9720 | 0.9862 |
| CSCR | 0.9339 | 0.9563 | 0.9684 |
| PALM | 0.9832 | 0.9897 | 0.9932 |
| hCEM | 0.9268 | 0.9462 | 0.9807 |
| HSPRD | 0.9383 | 0.9830 | 0.9969 |
| Proposed | 0.9891 | 0.9989 | 0.9990 |
| Method | SACE | SPSMF | CSCR | PALM | hCEM | HSPRD | Proposed |
|---|---|---|---|---|---|---|---|
| AUC | 0.8620 | 0.9916 | 0.9971 | 0.9962 | 0.9564 | 0.9965 | 0.9999 |
| Endmember | Asphalt | Grass | Trees | Roofs | Mean |
|---|---|---|---|---|---|
| HSPRD | 0.2958 | 0.1404 | 0.1865 | 0.2117 | 0.2086 |
| Proposed method | 0.0591 | 0.1016 | 0.0755 | 0.1142 | 0.0876 |
| Method | SACE | SPSMF | CSCR | PALM | hCEM | HSPRD | Proposed |
|---|---|---|---|---|---|---|---|
| AUC | 0.7295 | 0.7471 | 0.7600 | 0.6797 | 0.6518 | 0.8085 | 0.8987 |
| Method | SACE | SPSMF | CSCR | PALM | hCEM | HSPRD | Proposed |
|---|---|---|---|---|---|---|---|
| AUC | 0.5570 | 0.9284 | 0.9687 | 0.6814 | 0.4882 | 0.6601 | 0.9732 |
| Method | SACE | SPSMF | CSCR | PALM | hCEM | HSPRD | Proposed |
|---|---|---|---|---|---|---|---|
| Time (s) | 90.7 | 66.8 | 3024.1 | 257.4 | 17.4 | 1258.7 | 1028.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Song, X.; Bai, B.; Chen, Z. Adaptive Background Endmember Extraction for Hyperspectral Subpixel Object Detection. Remote Sens. 2024, 16, 2245. https://doi.org/10.3390/rs16122245
Yang L, Song X, Bai B, Chen Z. Adaptive Background Endmember Extraction for Hyperspectral Subpixel Object Detection. Remote Sensing. 2024; 16(12):2245. https://doi.org/10.3390/rs16122245
Chicago/Turabian StyleYang, Lifeng, Xiaorui Song, Bin Bai, and Zhuo Chen. 2024. "Adaptive Background Endmember Extraction for Hyperspectral Subpixel Object Detection" Remote Sensing 16, no. 12: 2245. https://doi.org/10.3390/rs16122245
APA StyleYang, L., Song, X., Bai, B., & Chen, Z. (2024). Adaptive Background Endmember Extraction for Hyperspectral Subpixel Object Detection. Remote Sensing, 16(12), 2245. https://doi.org/10.3390/rs16122245






