Hyperspectral Image Classification Based on Multi-Scale Convolutional Features and Multi-Attention Mechanisms
Abstract
1. Introduction
- This method employs multi-scale convolutional kernels to capture features at different scales in HSIs. By using the multi-scale convolutional kernels, the model can adapt and capture detail and structural information on these different scales, helping to retain more information and thus improving the ability to identify complex land cover environments.
- Multiple attention mechanisms based on the pyramid squeeze attention and multi-head self-attention mechanism are introduced to enhance the modeling capabilities of the perception and utilization of critical information in HSIs. By using multiple attention mechanisms, the redundant or secondary information present in HSIs is filtered to improve the modeling efficiency and comprehensively capture the image features.
- The systematic combination of the multi-scale CNNs and multiple attention mechanisms can fully and efficiently exploit the spectral and spatial features in HSIs, thereby significantly improving the classification performance. The experiments conducted on three public datasets demonstrate the superior performance of the proposed method.
2. Materials and Methods
2.1. HSI Data Pre-Processing
2.2. Multi-Scale Convolutional Feature Extraction
2.3. Feature Enhancement Based on Pyramid Squeeze Attention
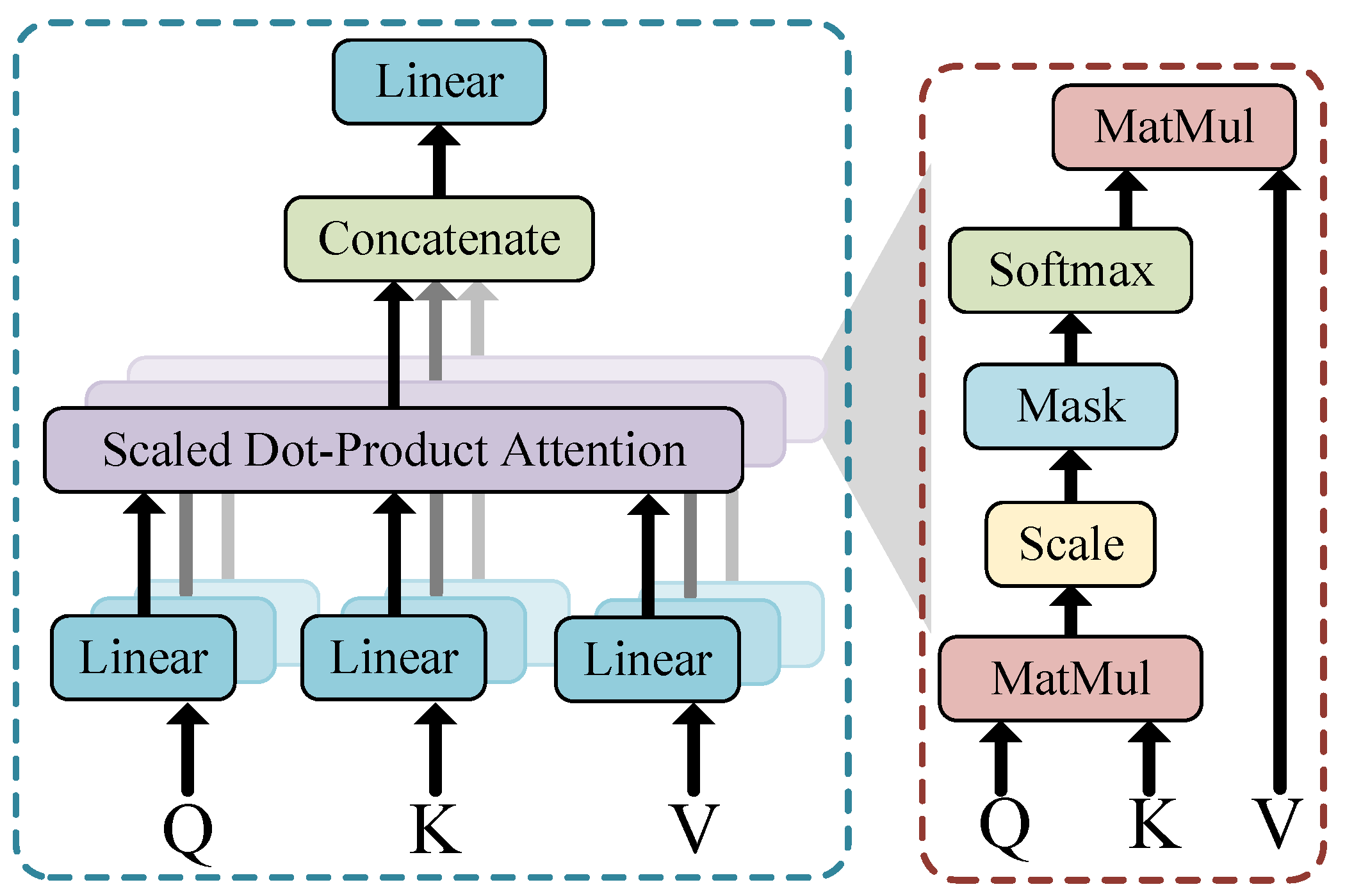
2.4. Transformer Encoder
| Algorithm 1 The proposed MSCF-MAM method. |
Input: HSI data , ground truth , batch size = 64, the PCA bands , patch size , epoch number , learning rate = , and the training sample rate . Output: Predicted labels of the test dataset. 1: Perform PCA transformation to obtain . 2: Create sample patches from , then partition them into training and testing sets. 3: for to e do 4: Perform multi-scale 3D convolution block to obtain multi-scale convolutional features. 5: Flatten multi-scale 3D convolutional features into 2D feature maps. 7: Concatenate the learnable tokens to create feature tokens and embed position information into the tokens. 9: Input the first token into the linear layer. 10: Use the softmax function to identify the labels. 11: end for 12: Utilize the test dataset along with the trained model to obtain predicted labels. |
3. Experiments and Results
3.1. Dataset Description
3.2. Experimental Setting
3.3. Quantitative and Visual Classification Results
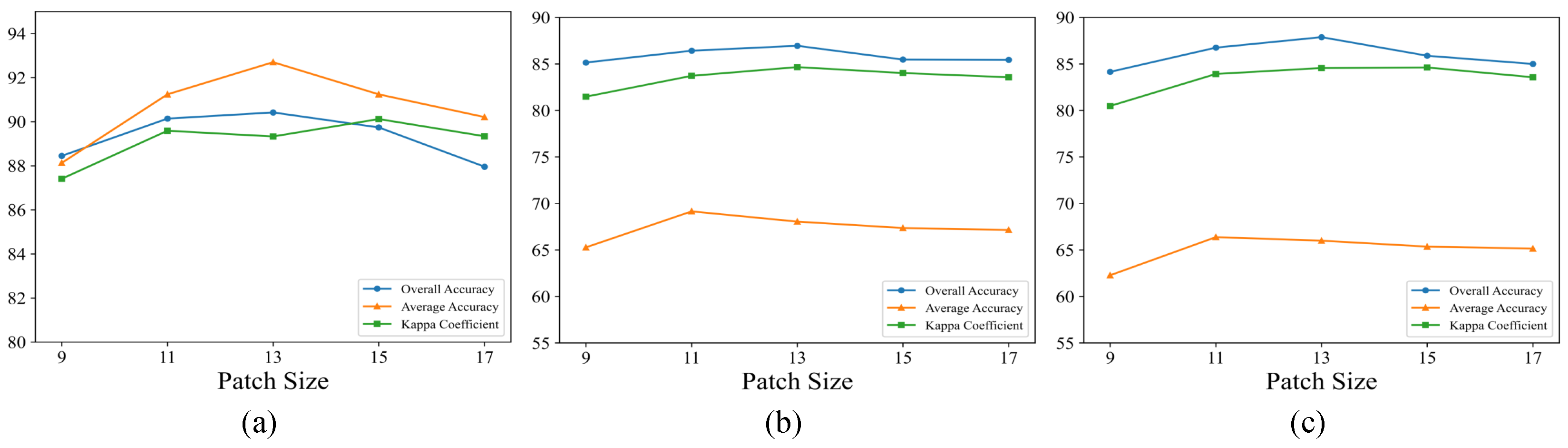
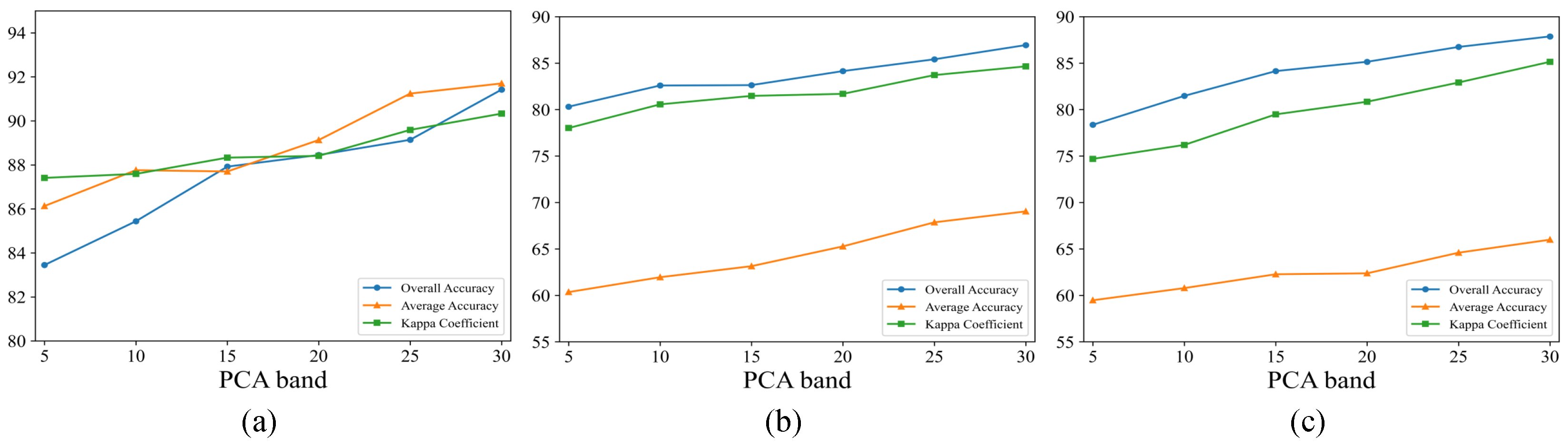
3.4. Parameter Analysis
3.5. Ablation Analysis
3.6. Comparison of Computational Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HSI | Hyperspectral image |
| CNN | Convolutional neural network |
| MHSA | Multi-head self-attention |
| PSA | Pyramid squeeze attention |
| ML | Machine learning |
| PCA | Principal component analysis |
| SVM | Support vector machine |
| MP | Morphological profile |
| DL | Deep learning |
| TE | Transformer encoder |
| GCN | Graph convolutional network |
| GAN | Generative adversarial network |
| DFFN | Deep feature fusion network |
| SE | Squeeze and excitation |
| Kappa coefficient | |
| OA | Overall accuracy |
| AA | Average accuracy |
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, J.; Zhang, Y.; Wei, Z.; Chanussot, J. Recent Developments in Parallel and Distributed Computing for Remotely Sensed Big Data Processing. Proc. IEEE 2021, 109, 1282–1305. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral–Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Khanal, S.; Kc, K.; Fulton, J.P.; Shearer, S.; Ozkan, E. Remote Sensing in Agriculture—Accomplishments, Limitations, and Opportunities. Remote Sens. 2020, 12, 3783. [Google Scholar] [CrossRef]
- Soppa, M.A.; Silva, B.; Steinmetz, F.; Keith, D.; Scheffler, D.; Bohn, N.; Bracher, A. Assessment of Polymer Atmospheric Correction Algorithm for Hyperspectral Remote Sensing Imagery over Coastal Waters. Sensors 2021, 21, 4125. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A Review of Machine Learning in Processing Remote Sensing Data for Mineral Exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Virtriana, R.; Riqqi, A.; Anggraini, T.S.; Fauzan, K.N.; Ihsan, K.T.N.; Mustika, F.C.; Suwardhi, D.; Harto, A.B.; Sakti, A.D.; Deliar, A.; et al. Development of Spatial Model for Food Security Prediction Using Remote Sensing Data in West Java, Indonesia. ISPRS Int. J. Geo-Inf. 2022, 11, 284. [Google Scholar] [CrossRef]
- Dremin, V.; Marcinkevics, Z.; Zherebtsov, E.; Popov, A.; Grabovskis, A.; Kronberga, H.; Geldnere, K.; Doronin, A.; Meglinski, I.; Bykov, A. Skin Complications of Diabetes Mellitus Revealed by Polarized Hyperspectral Imaging and Machine Learning. IEEE Trans. Med. Imaging 2021, 40, 1207–1216. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral Imaging for Military and Security Applications: Combining Myriad Processing and Sensing Techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Y.; Li, B. SISLU-Net: Spatial Information-Assisted Spectral Information Learning Unmixing Network for Hyperspectral Images. Remote Sens. 2023, 15, 817. [Google Scholar] [CrossRef]
- Sun, L.; Wu, F.; He, C.; Zhan, T.; Liu, W.; Zhang, D. Weighted Collaborative Sparse and L1/2 Low-Rank Regularizations with Superpixel Segmentation for Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2020, 19, 5500405. [Google Scholar] [CrossRef]
- Sun, L.; Cao, Q.; Chen, Y.; Zheng, Y.; Wu, Z. Mixed Noise Removal for Hyperspectral Images Based on Global Tensor Low-Rankness and Nonlocal SVD-Aided Group Sparsity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506617. [Google Scholar] [CrossRef]
- Sun, L.; He, C.; Zheng, Y.; Wu, Z.; Jeon, B. Tensor Cascaded-Rank Minimization in Subspace: A Unified Regime for Hyperspectral Image Low-Level Vision. IEEE Trans. Image Process. 2022, 32, 100–115. [Google Scholar] [CrossRef] [PubMed]
- Diao, W.; Zhang, F.; Sun, J.; Xing, Y.; Zhang, K.; Bruzzone, L. ZeRGAN: Zero-Reference GAN for Fusion of Multispectral and Panchromatic Images. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8195–8209. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Cheng, Q.; Chen, Z. Hyperspectral Image Super-Resolution Method Based on Spectral Smoothing Prior and Tensor Tubal Row-Sparse Representation. Remote Sens. 2022, 14, 2142. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2013, 31, 34–44. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Q.; Chen, Y.; Zheng, Y.; Wu, Z.; Fu, L.; Jeon, B. CRNet: Channel-enhanced Remodeling-based Network for Salient Object Detection in Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5618314. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, Q.; Sun, L.; Wu, Z.; Pan, C.; Jeon, B. Joint Classification of Hyperspectral and Lidar Data Using a Hierarchical CNN and Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5500716. [Google Scholar] [CrossRef]
- Sun, L.; Fang, Y.; Chen, Y.; Huang, W.; Wu, Z.; Jeon, B. Multi-Structure KELM with Attention Fusion Strategy for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539217. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A Review of Change detection in Multitemporal Hyperspectral Images: Current Techniques, Applications, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear Versus Nonlinear PCA for the Classification of Hyperspectral Data based on the Extended Morphological Profiles. IEEE Geosci. Remote Sens. Lett. 2011, 9, 447–451. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the Random Forest Framework for Classification of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local Manifold Learning-based K-Nearest-Neighbor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of Hyperspectral Data from Urban Areas Based on Extended Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of Hyperspectral Images by Using Extended Morphological Attribute Profiles and Independent Component Analysis. IEEE Geosci. Remote Sens. Lett. 2010, 8, 542–546. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Jia, S.; Shen, L.; Li, Q. Gabor Feature-based Collaborative Representation for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1118–1129. [Google Scholar] [CrossRef]
- Fang, S.; Li, X.; Tian, S.; Chen, W.; Zhang, E. Multi-Level Feature Extraction Networks for Hyperspectral Image Classification. Remote Sens. 2024, 16, 590. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative Adversarial Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised Hyperspectral Image Classification Based on Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2017, 15, 212–216. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J.; Pla, F. Capsule Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2145–2160. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Hao, S.; Wang, W.; Salzmann, M. Geometry-Aware Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2448–2460. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale Dynamic Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, B.; Liu, J. Hyperspectral Image Classification via Spatial Shuffle-Based Convolutional Neural Network. Remote Sens. 2023, 15, 3960. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Zhao, L.; Yi, J.; Li, X.; Hu, W.; Wu, J.; Zhang, G. Compact Band Weighting Module Based on Attention-Driven for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9540–9552. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 7 May 2024).
- Sun, L.; Zhang, H.; Zheng, Y.; Wu, Z.; Ye, Z.; Zhao, H. MASSFormer: Memory-Augmented Spectral-Spatial Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516415. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, X.; Chen, Y.; Lin, Z. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5518615. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral Image Classification Using Group-Aware Hierarchical Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539014. [Google Scholar] [CrossRef]
- Yang, A.; Li, M.; Ding, Y.; Hong, D.; Lv, Y.; He, Y. GTFN: GCN and transformer fusion with spatial-spectral features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 6600115. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Q.; Zhang, G.; Jia, X.; Yin, J. CAT: Center Attention Transformer with Stratified Spatial-Spectral Token for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5615415. [Google Scholar] [CrossRef]
- Zou, J.; He, W.; Zhang, H. Lessformer: Local-enhanced spectral-spatial transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5535416. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Y.; Tu, B.; Li, Q.; Li, W. Spatial–spectral transformer with cross-attention for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537415. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Haut, J.M.; Du, Q.; Plaza, A. Spectral–Spatial Morphological Attention Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503615. [Google Scholar] [CrossRef]
- Ouyang, E.; Li, B.; Hu, W.; Zhang, G.; Zhao, L.; Wu, J. When Multigranularity Meets Spatial–Spectral Attention: A Hybrid Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5524916. [Google Scholar] [CrossRef]
- Fang, Y.; Ye, Q.; Sun, L.; Zheng, Y.; Wu, Z. Multi-Attention Joint Convolution Feature Representation with Lightweight Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513814. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-borne hyperspectral remote sensing: From observation and processing to applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]

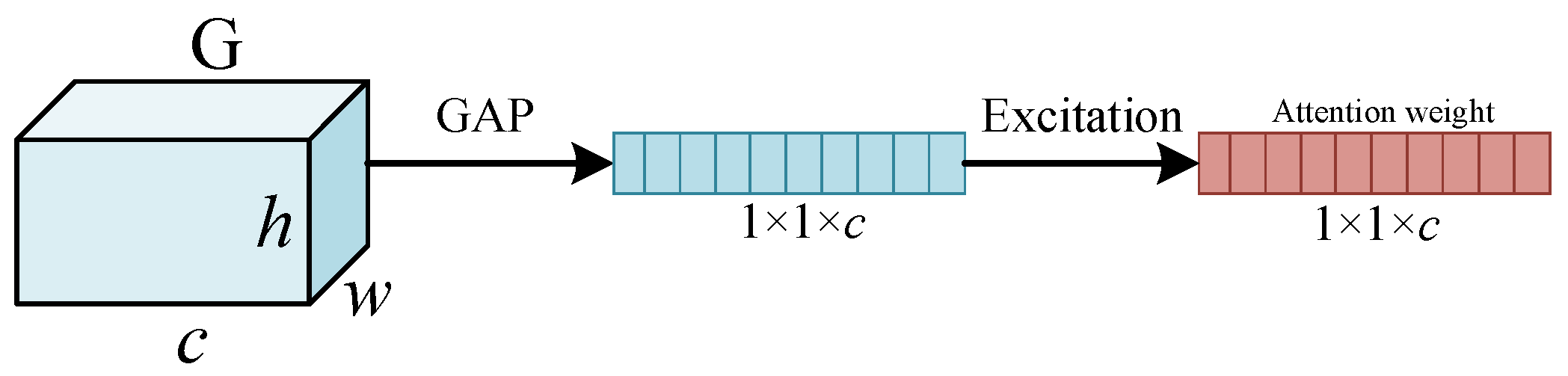
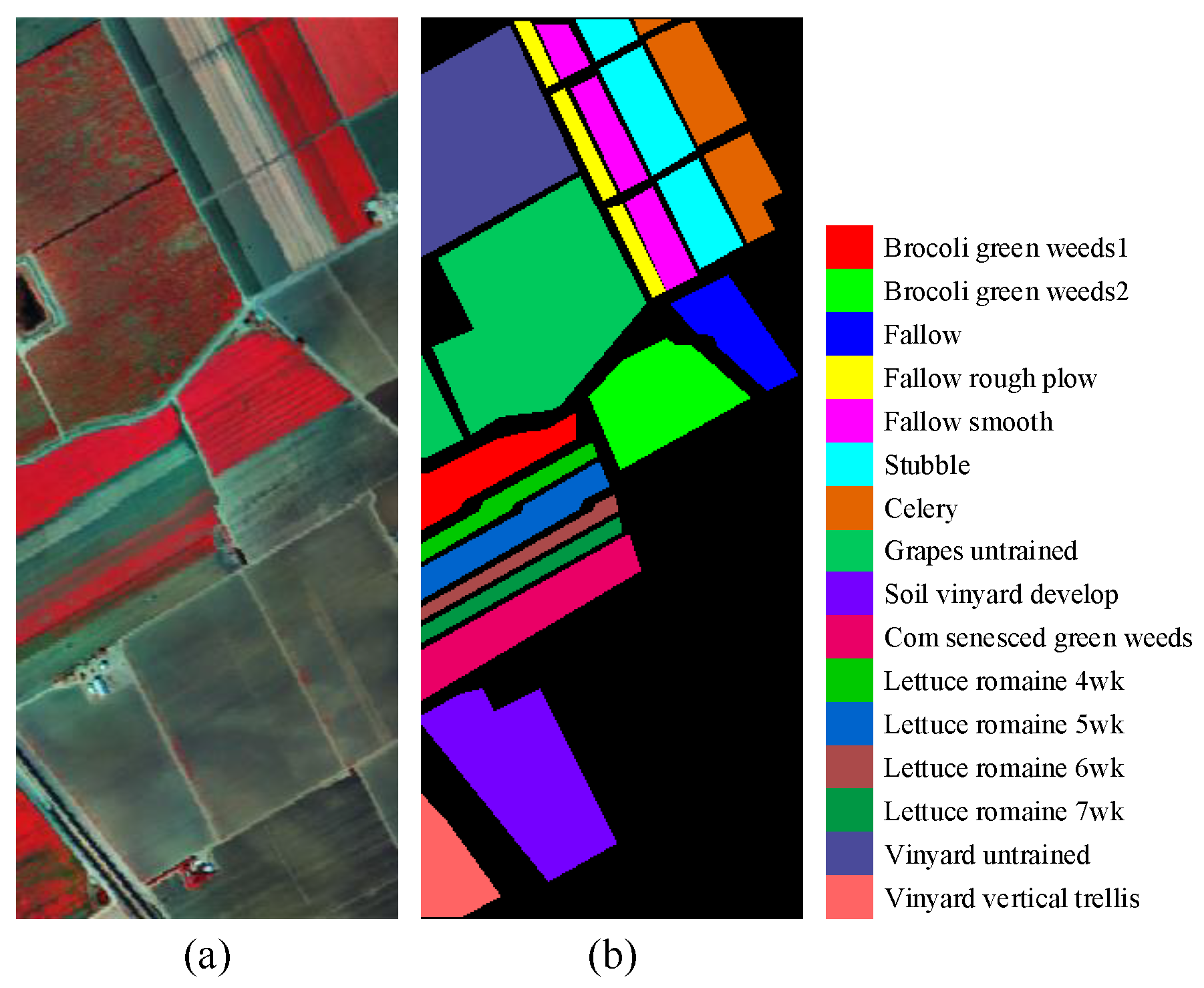
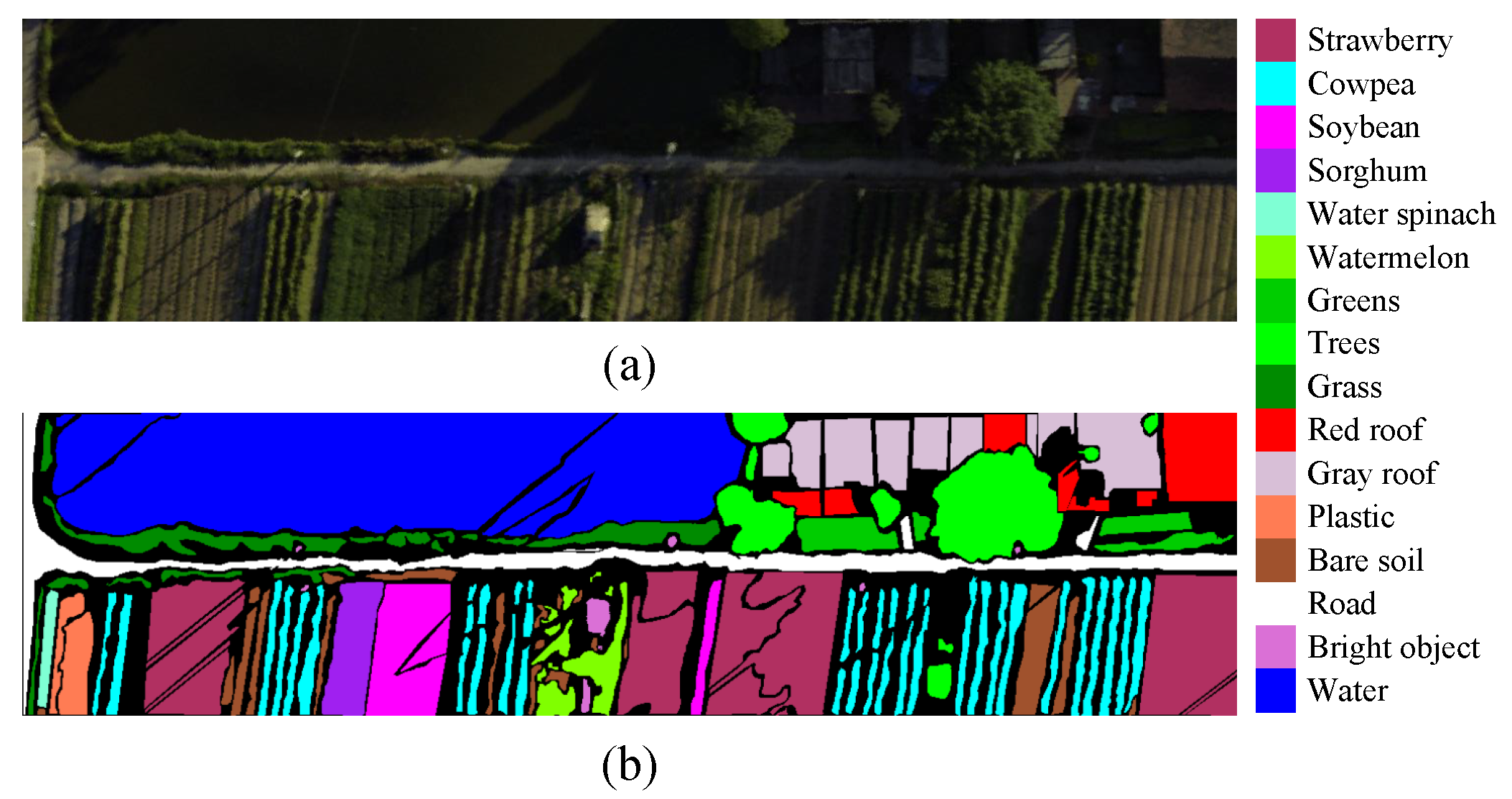




| NO. | SV | HC | HH | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Class Name | Training | Test | Class Name | Training | Test | Class Name | Training | Test | |
| C01 | Brocoli green weeds1 | 2 | 2007 | Strawberry | 45 | 44,690 | Red roof | 14 | 14,027 |
| C02 | Brocoli green weeds2 | 4 | 3722 | Cowpea | 23 | 22,730 | Road | 4 | 3508 |
| C03 | Fallow | 2 | 1974 | Soybean | 10 | 10,277 | Bare soil | 22 | 21,799 |
| C04 | Fallow rough plow | 1 | 1393 | Sorghum | 5 | 5348 | Cotton | 163 | 163,122 |
| C05 | Fallow smooth | 3 | 2675 | Water spinach | 1 | 1199 | Cotton firewood | 6 | 6212 |
| C06 | Stubble | 4 | 3955 | Watermelon | 5 | 4528 | Rape | 45 | 44,512 |
| C07 | Celery | 4 | 3575 | Greens | 6 | 5897 | Chinese cabbage | 24 | 24,079 |
| C08 | Grapes untrained | 11 | 11,260 | Trees | 18 | 17,960 | Pakchoi | 4 | 4050 |
| C09 | Soil vinyard develop | 6 | 6197 | Grass | 9 | 9460 | Cabbage | 11 | 10,808 |
| C10 | Com senesced green weeds | 3 | 3275 | Red roof | 10 | 10,506 | Tuber mustard | 12 | 12,382 |
| C11 | Lettuce romaine 4 wk | 1 | 1067 | Gray roof | 17 | 16,894 | Brassica parachinensis | 11 | 11,004 |
| C12 | Lettuce romaine 5 wk | 2 | 1925 | Plastic | 4 | 3675 | Brassica chinensis | 9 | 8945 |
| C13 | Lettuce romaine 6 wk | 1 | 915 | Bare soil | 9 | 9107 | Small brassica chinensis | 22 | 22,485 |
| C14 | Lettuce romaine 7 wk | 1 | 1069 | Road | 19 | 18,541 | Lactuca sativa | 7 | 7349 |
| C15 | Vinyard untrained | 7 | 7261 | Bright object | 1 | 1135 | Celture | 1 | 1001 |
| C16 | Vinyard vertical trellis | 2 | 1805 | Water | 75 | 75,326 | Film covered lettuce | 7 | 7255 |
| C17 | Romaine lettuce | 3 | 3007 | ||||||
| C18 | Carrot | 3 | 3214 | ||||||
| C19 | White radish | 9 | 8703 | ||||||
| C20 | Garlic sprout | 4 | 3482 | ||||||
| C21 | Broad bean | 1 | 1327 | ||||||
| C22 | Tree | 4 | 4036 | ||||||
| - | Total | 54 | 54,075 | Total | 257 | 257,273 | Total | 386 | 386,307 |
| NO. | SVM [24] | 1-D CNN [43] | 3-D CNN [46] | DFFN [48] | HybirdSN [47] | MorghAT [60] | GAHT [55] | SSFTT [54] | MSCF-MAM |
|---|---|---|---|---|---|---|---|---|---|
| C01 | 65.25 ± 5.10 | 62.77 ± 24.44 | 97.70 ± 1.96 | 97.12 ± 1.06 | 98.23 ± 1.65 | 80.72 ± 3.70 | 99.05 ± 1.26 | 96.47 ± 1.81 | 97.82 ± 1.60 |
| C02 | 86.24 ± 4.27 | 98.52 ± 3.26 | 93.18 ± 8.58 | 90.78 ± 3.00 | 99.41 ± 0.51 | 93.23 ± 6.35 | 99.80 ± 0.27 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| C03 | 53.70 ± 8.23 | 54.26 ± 5.98 | 32.69 ± 5.48 | 51.00 ± 6.26 | 83.32 ± 8.59 | 83.42 ± 6.97 | 53.45 ± 0.50 | 99.52 ± 0.46 | 99.87 ± 0.14 |
| C04 | 84.11 ± 4.07 | 86.86 ± 9.25 | 97.96 ± 1.29 | 96.72 ± 2.79 | 51.54 ± 4.60 | 93.36 ± 6.18 | 97.60 ± 1.86 | 75.78 ± 12.93 | 85.83 ± 9.70 |
| C05 | 80.09 ± 6.14 | 87.48 ± 7.85 | 96.95 ± 0.34 | 85.44 ± 2.79 | 94.12 ± 8.15 | 86.25 ± 9.87 | 96.10 ± 1.58 | 93.41 ± 3.85 | 93.44 ± 2.71 |
| C06 | 97.09 ± 0.86 | 99.40 ± 0.22 | 98.93 ± 0.75 | 84.32 ± 6.57 | 94.55 ± 3.14 | 97.88 ± 1.97 | 99.90 ± 0.17 | 99.99 ± 0.02 | 98.68 ± 1.39 |
| C07 | 93.68 ± 1.47 | 98.89 ± 0.27 | 99.69 ± 0.23 | 81.40 ± 4.67 | 100.00 ± 0.00 | 96.26 ± 0.66 | 98.40 ± 0.46 | 99.87 ± 0.24 | 99.99 ± 0.02 |
| C08 | 50.80 ± 7.64 | 55.63 ± 4.29 | 77.16 ± 12.58 | 70.75 ± 9.13 | 86.61 ± 3.67 | 77.16 ± 7.95 | 83.31 ± 3.28 | 85.04 ± 0.48 | 88.25 ± 2.46 |
| C09 | 97.32 ± 1.23 | 97.04 ± 2.45 | 99.95 ± 0.05 | 95.39 ± 2.66 | 98.94 ± 1.51 | 98.08 ± 1.70 | 99.87 ± 0.23 | 100.00 ± 0.00 | 99.92 ± 0.13 |
| C10 | 77.59 ± 6.59 | 81.57 ± 5.86 | 29.79 ± 10.26 | 81.15 ± 1.08 | 94.12 ± 3.67 | 85.10 ± 3.48 | 88.87 ± 2.37 | 96.42 ± 0.69 | 95.70 ± 1.23 |
| C11 | 56.10 ± 7.28 | 57.16 ± 28.62 | 60.63 ± 4.33 | 38.43 ± 12.02 | 46.86 ± 5.77 | 37.52 ± 7.22 | 92.02 ± 3.99 | 98.57 ± 3.03 | 99.19 ± 1.75 |
| C12 | 92.36 ± 2.96 | 97.24 ± 2.54 | 94.91 ± 5.60 | 95.42 ± 7.93 | 60.92 ± 6.32 | 61.05 ± 10.69 | 99.98 ± 0.03 | 96.32 ± 3.08 | 99.03 ± 1.12 |
| C13 | 46.78 ± 4.15 | 41.33 ± 19.65 | 50.10 ± 1.86 | 94.90 ± 4.10 | 83.86 ± 14.04 | 90.04 ± 1.53 | 94.27 ± 5.28 | 87.28 ± 11.22 | 86.95 ± 8.88 |
| C14 | 75.97 ± 2.71 | 81.09 ± 7.66 | 82.73 ± 6.32 | 85.68 ± 2.11 | 80.51 ± 6.17 | 82.30 ± 8.48 | 66.56 ± 3.61 | 67.72 ± 16.67 | 78.99 ± 9.00 |
| C15 | 49.86 ± 10.52 | 59.19 ± 5.15 | 43.84 ± 10.63 | 71.83 ± 2.15 | 72.32 ± 16.36 | 84.43 ± 1.55 | 66.56 ± 3.61 | 50.14 ± 7.52 | 61.02 ± 8.02 |
| C16 | 75.35 ± 3.64 | 72.82 ± 3.64 | 47.22 ± 7.33 | 57.40 ± 2.45 | 90.66 ± 0.23 | 47.73 ± 7.41 | 80.72 ± 2.01 | 98.91 ± 0.73 | 98.55 ± 0.40 |
| OA (%) | 69.52 ± 3.45 | 75.91 ± 2.00 | 74.61 ± 1.81 | 77.70 ± 2.77 | 85.40 ± 2.53 | 82.16 ± 0.96 | 87.94 ± 0.39 | 87.81 ± 1.05 | 90.44 ± 1.86 |
| AA (%) | 72.89 ± 4.04 | 75.94 ± 4.34 | 71.87 ± 3.00 | 77.98 ± 4.58 | 79.83 ± 8.19 | 79.24 ± 1.65 | 89.37 ± 1.74 | 90.33 ± 1.21 | 92.70 ± 1.99 |
| × 100 | 67.15 ± 3.02 | 73.21 ± 2.22 | 73.28 ± 2.60 | 75.15 ± 3.20 | 83.72 ± 2.85 | 80.11 ± 1.02 | 86.54 ± 0.45 | 86.39 ± 1.18 | 89.33 ± 2.08 |
| NO. | SVM [24] | 1-D CNN [43] | 3-D CNN [46] | DFFN [48] | HybirdSN [47] | MorghAT [60] | GAHT [55] | SSFTT [54] | MSCF-MAM |
|---|---|---|---|---|---|---|---|---|---|
| C01 | 92.73 ± 0.57 | 77.58 ± 8.49 | 82.08 ± 7.40 | 78.05 ± 10.67 | 97.69 ± 1.77 | 94.05 ± 2.23 | 90.97 ± 3.01 | 94.29 ± 2.28 | 95.79 ± 3.32 |
| C02 | 53.70 ± 9.23 | 58.08 ± 4.92 | 65.86 ± 4.83 | 50.08 ± 2.08 | 82.56 ± 3.46 | 80.37 ± 1.19 | 85.41 ± 4.28 | 86.77 ± 6.65 | 92.69 ± 3.47 |
| C03 | 60.10 ± 5.16 | 64.28 ± 3.21 | 58.76 ± 2.39 | 55.78 ± 7.58 | 67.54 ± 2.00 | 67.67 ± 8.22 | 69.79 ± 4.26 | 79.79 ± 5.03 | 72.83 ± 4.49 |
| C04 | 46.54 ± 14.01 | 40.75 ± 11.11 | 41.12 ± 14.21 | 49.89 ± 6.54 | 99.08 ± 0.75 | 72.63 ± 7.86 | 91.30 ± 6.91 | 92.53 ± 6.76 | 94.49 ± 2.74 |
| C05 | 15.67 ± 9.06 | 14.65 ± 8.69 | 15.48 ± 3.38 | 22.89 ± 5.01 | 21.18 ± 8.69 | 21.07 ± 4.42 | 17.29 ± 5.31 | 26.56 ± 11.93 | 23.86 ± 2.33 |
| C06 | 13.21 ± 4.08 | 12.74 ± 3.96 | 16.71 ± 2.71 | 10.72 ± 3.63 | 33.83 ± 2.67 | 31.99 ± 3.29 | 31.56 ± 4.50 | 47.91 ± 8.81 | 50.68 ± 2.10 |
| C07 | 65.77 ± 5.27 | 61.49 ± 4.68 | 53.29 ± 3.44 | 61.87 ± 7.68 | 64.53 ± 0.24 | 80.43 ± 4.35 | 67.46 ± 3.89 | 82.99 ± 3.76 | 73.93 ± 4.59 |
| C08 | 45.72 ± 5.25 | 46.82 ± 3.02 | 55.69 ± 2.29 | 72.24 ± 4.98 | 74.08 ± 2.28 | 74.35 ± 3.06 | 72.42 ± 1.28 | 67.40 ± 9.73 | 75.96 ± 7.06 |
| C09 | 16.86 ± 12.37 | 16.97 ± 15.19 | 17.71 ± 4.29 | 17.36 ± 4.93 | 43.63 ± 1.85 | 25.42 ± 1.96 | 33.04 ± 7.92 | 60.17 ± 5.40 | 63.79 ± 2.66 |
| C10 | 26.21 ± 6.29 | 25.98 ± 4.13 | 29.71 ± 4.61 | 33.31 ± 5.73 | 82.08 ± 4.16 | 53.95 ± 9.60 | 87.78 ± 10.65 | 91.21 ± 5.11 | 95.80 ± 1.68 |
| C11 | 25.17 ± 6.32 | 41.70 ± 11.05 | 48.94 ± 5.44 | 44.38 ± 12.19 | 85.30 ± 4.86 | 90.55 ± 10.41 | 95.59 ± 0.75 | 94.78 ± 3.49 | 89.07 ± 3.86 |
| C12 | 12.10 ± 4.47 | 10.09 ± 5.27 | 12.64 ± 3.27 | 15.26 ± 3.32 | 31.84 ± 0.97 | 38.37 ± 9.05 | 42.62 ± 7.76 | 45.91 ± 1.92 | 52.22 ± 6.36 |
| C13 | 13.51 ± 6.78 | 14.62 ± 5.84 | 14.82 ± 3.27 | 20.00 ± 5.85 | 38.54 ± 4.03 | 51.03 ± 11.41 | 51.60 ± 7.08 | 42.51 ± 6.42 | 46.51 ± 3.14 |
| C14 | 74.04 ± 4.21 | 69.38 ± 3.94 | 71.58 ± 2.98 | 71.60 ± 2.84 | 77.04 ± 5.11 | 72.19 ± 11.77 | 88.72 ± 2.11 | 86.51 ± 5.71 | 88.71 ± 4.82 |
| C15 | 11.19 ± 15.11 | 12.62 ± 5.24 | 38.01 ± 6.75 | 57.17 ± 8.79 | 44.11 ± 1.98 | 24.94 ± 9.03 | 10.29 ± 4.54 | 29.91 ± 7.96 | 37.94 ± 3.67 |
| C16 | 98.06 ± 0.64 | 92.53 ± 7.22 | 99.54 ± 0.70 | 98.26 ± 1.00 | 99.58 ± 0.26 | 98.64 ± 0.06 | 99.04 ± 0.42 | 98.51 ± 1.10 | 99.40 ± 0.49 |
| OA (%) | 60.27 ± 3.28 | 57.41 ± 3.01 | 65.06 ± 1.19 | 62.86 ± 3.95 | 83.06 ± 1.04 | 77.09 ± 1.15 | 83.19 ± 1.71 | 85.80 ± 1.40 | 86.94 ± 0.47 |
| AA (%) | 40.37 ± 9.54 | 39.42 ± 3.53 | 53.51 ± 5.54 | 48.04 ± 4.21 | 62.04 ± 1.13 | 52.91 ± 2.41 | 60.95 ± 1.92 | 67.67 ± 2.12 | 68.04 ± 1.40 |
| × 100 | 53.93 ± 6.11 | 49.49 ± 3.44 | 58.05 ± 3.09 | 55.48 ± 5.33 | 80.06 ± 1.23 | 72.98 ± 1.50 | 80.29 ± 2.00 | 83.35 ± 1.61 | 84.65 ± 0.57 |
| NO. | SVM [24] | 1-D CNN [43] | 3-D CNN [46] | DFFN [48] | HybirdSN [47] | MorghAT [60] | GAHT [55] | SSFTT [54] | MSCF-MAM |
|---|---|---|---|---|---|---|---|---|---|
| C01 | 74.93 ± 2.42 | 55.11 ± 10.49 | 79.64 ± 2.65 | 82.58 ± 11.98 | 91.35 ± 3.18 | 92.35 ± 3.53 | 95.81 ± 1.09 | 86.95 ± 5.70 | 96.93 ± 0.59 |
| C02 | 33.81 ± 11.23 | 18.65 ± 16.10 | 56.64 ± 6.45 | 33.67 ± 5.66 | 36.95 ± 5.34 | 45.44 ± 9.67 | 54.84 ± 9.60 | 59.96 ± 10.47 | 61.92 ± 8.05 |
| C03 | 93.24 ± 2.16 | 91.11 ± 2.49 | 92.71 ± 1.56 | 96.32 ± 0.77 | 87.95 ± 2.31 | 92.99 ± 0.74 | 89.16 ± 3.94 | 91.50 ± 3.56 | 93.43 ± 3.95 |
| C04 | 98.61 ± 1.01 | 96.44 ± 0.66 | 99.28 ± 0.14 | 99.72 ± 0.11 | 98.87 ± 0.89 | 98.32 ± 0.67 | 99.33 ± 0.32 | 99.02 ± 0.32 | 98.42 ± 1.77 |
| C05 | 25.67 ± 10.04 | 19.43 ± 6.83 | 25.48 ± 4.38 | 22.76 ± 4.76 | 42.22 ± 5.85 | 51.07 ± 14.42 | 46.16 ± 12.27 | 62.80 ± 4.48 | 56.84 ± 6.85 |
| C06 | 87.75 ± 0.92 | 82.44 ± 6.19 | 88.11 ± 1.35 | 88.31 ± 0.95 | 92.65 ± 0.58 | 96.11 ± 1.32 | 91.57 ± 2.91 | 93.13 ± 4.02 | 93.98 ± 1.02 |
| C07 | 75.46 ± 3.27 | 53.65 ± 13.73 | 80.44 ± 3.05 | 66.96 ± 12.94 | 70.37 ± 2.92 | 76.99 ± 4.68 | 78.14 ± 2.29 | 85.52 ± 4.82 | 92.98 ± 2.77 |
| C08 | 35.16 ± 9.25 | 29.91 ± 4.96 | 30.80 ± 10.21 | 30.06 ± 9.05 | 36.29 ± 5.15 | 37.32 ± 4.67 | 45.25 ± 3.97 | 34.02 ± 3.24 | 34.32 ± 4.99 |
| C09 | 83.21 ± 4.16 | 62.99 ± 17.45 | 86.64 ± 1.88 | 84.63 ± 4.37 | 90.43 ± 2.64 | 94.45 ± 0.75 | 98.99 ± 0.50 | 91.90 ± 3.58 | 96.12 ± 1.45 |
| C10 | 10.31 ± 8.29 | 9.79 ± 4.18 | 49.51 ± 9.50 | 44.77 ± 4.46 | 50.07 ± 7.87 | 70.02 ± 7.49 | 79.07 ± 7.18 | 84.89 ± 3.18 | 87.84 ± 1.72 |
| C11 | 14.47 ± 14.32 | 16.53 ± 15.19 | 17.38 ± 3.94 | 16.00 ± 12.52 | 50.62 ± 10.83 | 51.03 ± 8.04 | 46.48 ± 10.84 | 66.00 ± 3.88 | 68.03 ± 7.70 |
| C12 | 50.48 ± 8.47 | 26.08 ± 10.44 | 52.64 ± 4.64 | 47.23 ± 3.45 | 58.78 ± 10.41 | 55.59 ± 7.25 | 65.06 ± 2.24 | 58.39 ± 7.43 | 58.95 ± 4.28 |
| C13 | 56.19 ± 6.28 | 46.49 ± 5.88 | 68.71 ± 0.44 | 65.89 ± 6.13 | 78.81 ± 2.93 | 72.39 ± 6.31 | 75.36 ± 4.71 | 70.43 ± 10.58 | 72.40 ± 5.30 |
| C14 | 36.89 ± 6.15 | 31.37 ± 11.33 | 30.91 ± 13.94 | 44.36 ± 12.92 | 60.83 ± 5.28 | 66.45 ± 7.12 | 78.94 ± 4.31 | 72.61 ± 5.27 | 73.45 ± 9.92 |
| C15 | 11.23 ± 10.04 | 15.11 ± 9.13 | 12.17 ± 8.29 | 10.54 ± 11.05 | 45.50 ± 3.68 | 41.93 ± 11.61 | 41.17 ± 3.61 | 50.07 ± 4.09 | 56.85 ± 3.00 |
| C16 | 83.89 ± 3.64 | 85.19 ± 11.56 | 90.33 ± 1.50 | 89.04 ± 3.08 | 80.50 ± 9.70 | 88.30 ± 7.18 | 95.96 ± 1.65 | 88.74 ± 4.59 | 90.59 ± 2.03 |
| C17 | 23.58 ± 11.03 | 12.95 ± 8.63 | 16.60 ± 2.94 | 16.40 ± 4.03 | 34.94 ± 6.54 | 40.44 ± 3.90 | 40.16 ± 2.27 | 40.15 ± 4.22 | 48.09 ± 10.79 |
| C18 | 16.54 ± 10.24 | 10.34 ± 5.59 | 10.27 ± 10.47 | 17.40 ± 6.45 | 34.60 ± 10.29 | 46.56 ± 7.33 | 36.91 ± 1.62 | 52.33 ± 7.34 | 65.50 ± 4.93 |
| C19 | 45.18 ± 6.35 | 23.84 ± 7.03 | 49.69 ± 10.32 | 15.11 ± 9.84 | 70.33 ± 3.54 | 74.41 ± 11.44 | 73.09 ± 10.91 | 81.00 ± 8.41 | 79.61 ± 5.31 |
| C20 | 14.71 ± 8.66 | 12.40 ± 13.70 | 28.04 ± 14.29 | 22.89 ± 15.53 | 28.44 ± 4.75 | 75.33 ± 4.46 | 81.01 ± 4.29 | 43.28 ± 3.29 | 50.27 ± 2.27 |
| C21 | 13.90 ± 13.45 | 10.10 ± 8.17 | 12.64 ± 4.57 | 17.29 ± 12.14 | 19.82 ± 5.89 | 21.71 ± 2.55 | 19.86 ± 10.87 | 24.24 ± 3.56 | 30.30 ± 2.65 |
| C22 | 21.54 ± 12.36 | 15.19 ± 13.78 | 24.64 ± 8.36 | 25.21 ± 12.47 | 56.55 ± 5.18 | 51.84 ± 8.15 | 69.87 ± 10.53 | 73.47 ± 3.48 | 72.88 ± 3.00 |
| OA (%) | 73.52 ± 5.28 | 69.52 ± 2.92 | 79.09 ± 1.19 | 77.38 ± 1.73 | 82.44 ± 0.76 | 85.09 ± 0.78 | 86.34 ± 0.62 | 86.74 ± 1.00 | 87.87 ± 0.60 |
| AA (%) | 45.52 ± 9.04 | 42.77 ± 6.82 | 54.91 ± 3.42 | 51.90 ± 3.54 | 55.77 ± 2.47 | 59.14 ± 1.60 | 62.16 ± 2.16 | 64.29 ± 1.54 | 65.99 ± 0.48 |
| × 100 | 67.90 ± 5.02 | 60.42 ± 4.80 | 73.05 ± 2.28 | 75.15 ± 3.20 | 77.68 ± 0.95 | 81.07 ± 0.96 | 82.66 ± 0.79 | 83.05 ± 1.44 | 84.55 ± 0.80 |
| Cases | Component | Indicators | ||||||
|---|---|---|---|---|---|---|---|---|
| 3D Conv1 | 3D Conv2 | 3D Conv3 | PSA | TE | OA (%) | AA (%) | ||
| 1 | √ | ✕ | ✕ | √ | √ | 87.74 | 88.13 | 87.58 |
| 2 | √ | √ | ✕ | √ | √ | 89.12 | 90.43 | 88.71 |
| 3 | √ | √ | √ | ✕ | √ | 86.78 | 87.21 | 86.58 |
| 4 | √ | √ | √ | √ | ✕ | 89.23 | 90.33 | 88.24 |
| 5 | √ | √ | √ | √ | √ | 90.44 | 92.70 | 89.33 |
| Methods | SV | HC | HH | FLOPs (M) | Params (M) | |||
|---|---|---|---|---|---|---|---|---|
| Training (s) | Test (s) | Training (s) | Test (s) | Training (s) | Test (s) | |||
| 1-D CNN [43] | 4.17 | 5.72 | 3.45 | 7.68 | 4.84 | 11.69 | 277.46 | 0.12 |
| 3-D CNN [46] | 8.53 | 4.97 | 40.49 | 21.50 | 58.37 | 25.76 | 1728.97 | 0.16 |
| DFFN [48] | 15.90 | 10.01 | 74.63 | 44.05 | 124.21 | 54.86 | 1328.13 | 0.42 |
| HybridSN [47] | 6.65 | 9.18 | 10.08 | 19.41 | 13.57 | 38.82 | 3252.56 | 4.84 |
| MorghAT [60] | 26.33 | 23.38 | 95.46 | 37.63 | 136.51 | 50.34 | 2725.21 | 0.20 |
| GAHT [55] | 17.02 | 10.05 | 77.98 | 39.25 | 110.22 | 47.58 | 3046.75 | 0.97 |
| SSFTT [54] | 1.93 | 3.36 | 8.65 | 19.32 | 5.64 | 15.75 | 781.38 | 0.16 |
| MSCF-MAM | 3.26 | 4.98 | 11.64 | 21.94 | 12.06 | 26.20 | 2551.71 | 0.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Zhao, G.; Xia, X.; Xie, Y.; Fang, C.; Sun, L.; Wu, Z.; Pan, C. Hyperspectral Image Classification Based on Multi-Scale Convolutional Features and Multi-Attention Mechanisms. Remote Sens. 2024, 16, 2185. https://doi.org/10.3390/rs16122185
Sun Q, Zhao G, Xia X, Xie Y, Fang C, Sun L, Wu Z, Pan C. Hyperspectral Image Classification Based on Multi-Scale Convolutional Features and Multi-Attention Mechanisms. Remote Sensing. 2024; 16(12):2185. https://doi.org/10.3390/rs16122185
Chicago/Turabian StyleSun, Qian, Guangrui Zhao, Xinyuan Xia, Yu Xie, Chenrong Fang, Le Sun, Zebin Wu, and Chengsheng Pan. 2024. "Hyperspectral Image Classification Based on Multi-Scale Convolutional Features and Multi-Attention Mechanisms" Remote Sensing 16, no. 12: 2185. https://doi.org/10.3390/rs16122185
APA StyleSun, Q., Zhao, G., Xia, X., Xie, Y., Fang, C., Sun, L., Wu, Z., & Pan, C. (2024). Hyperspectral Image Classification Based on Multi-Scale Convolutional Features and Multi-Attention Mechanisms. Remote Sensing, 16(12), 2185. https://doi.org/10.3390/rs16122185








