HyperKon: A Self-Supervised Contrastive Network for Hyperspectral Image Analysis
Abstract
1. Introduction
- HyperKon: a hyperspectral-native CNN backbone that can learn useful representations from large amounts of unlabeled data.
- EnHyperSet-1: an EnMAP dataset curated for use in precision agriculture and other deep learning projects.
- Hyperspectral perceptual loss: a novel perceptual loss function minimizing errors in the spectral domain.
- Demonstration that the representations learned by HyperKon improve performance in hyperspectral downstream tasks.
2. Materials and Methods
2.1. Dataset
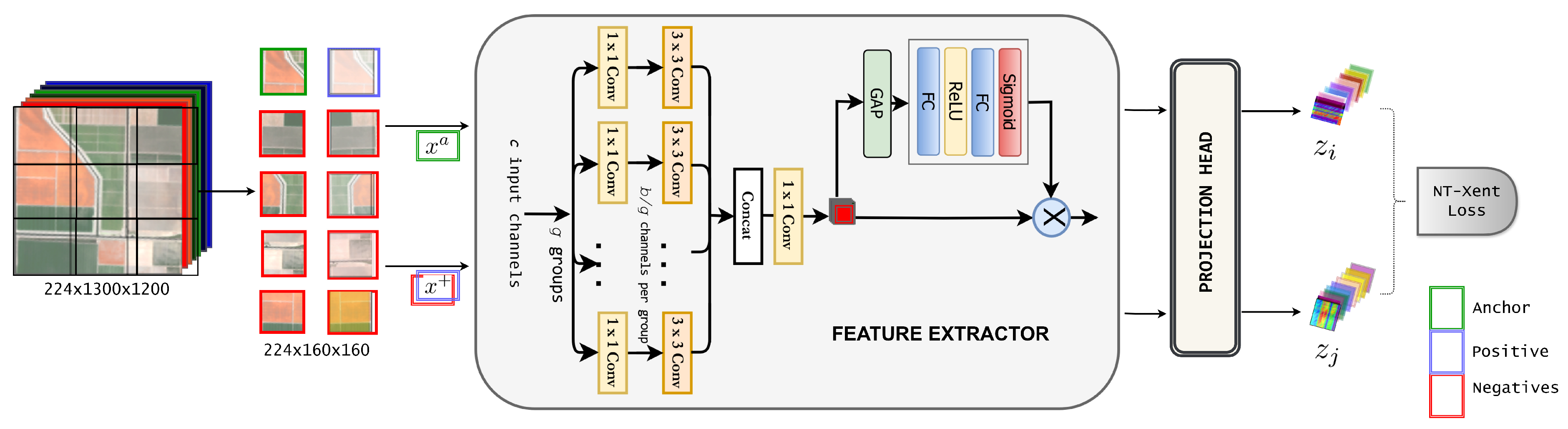
2.2. Hyperspectral Backbone Architecture
2.3. Contrastive Learning
2.3.1. Self-Supervised Contrastive Loss
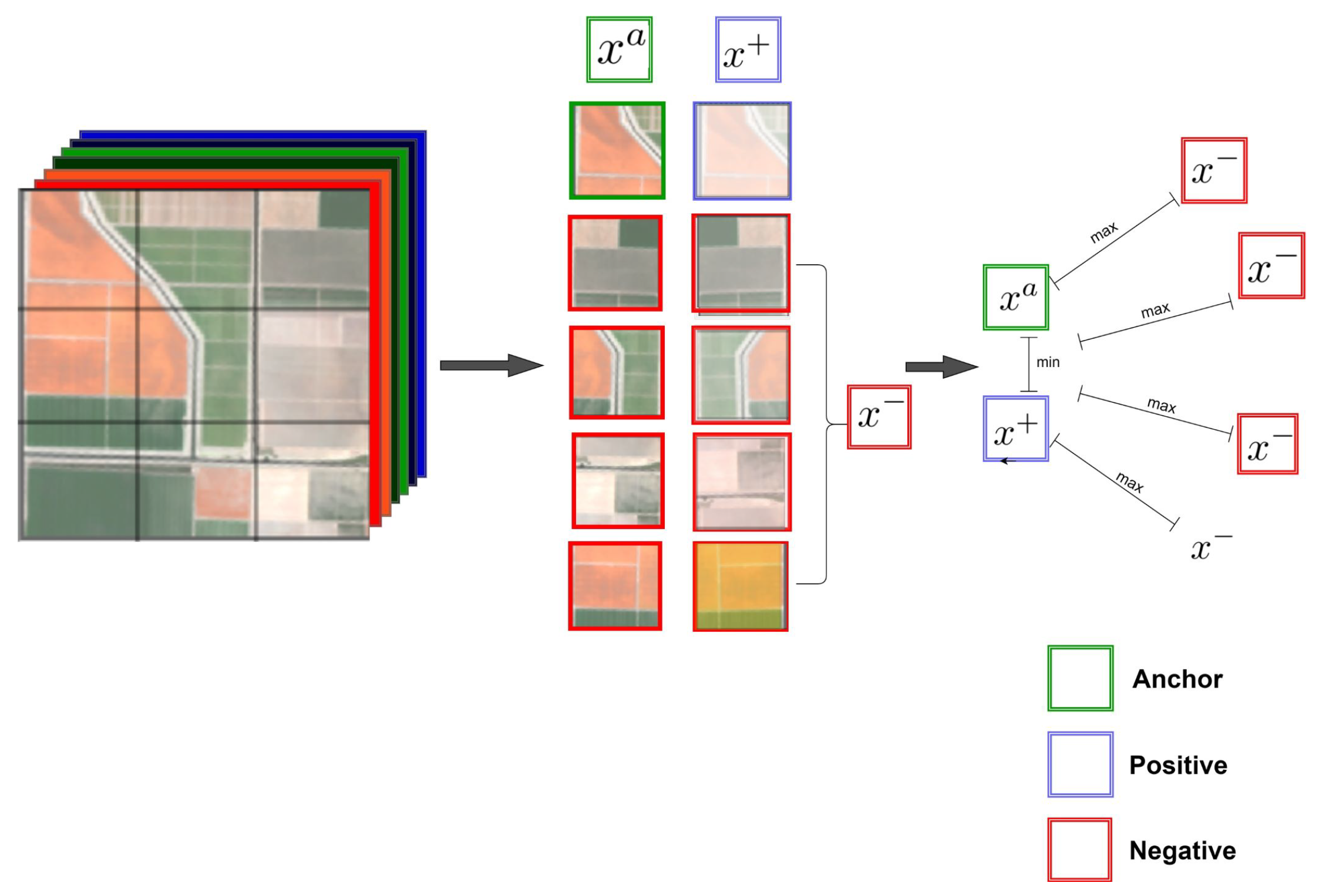
2.3.2. HSI Contrastive Sampling
2.4. Hyperspectral Perceptual Loss
3. Results
3.1. Ablation Study
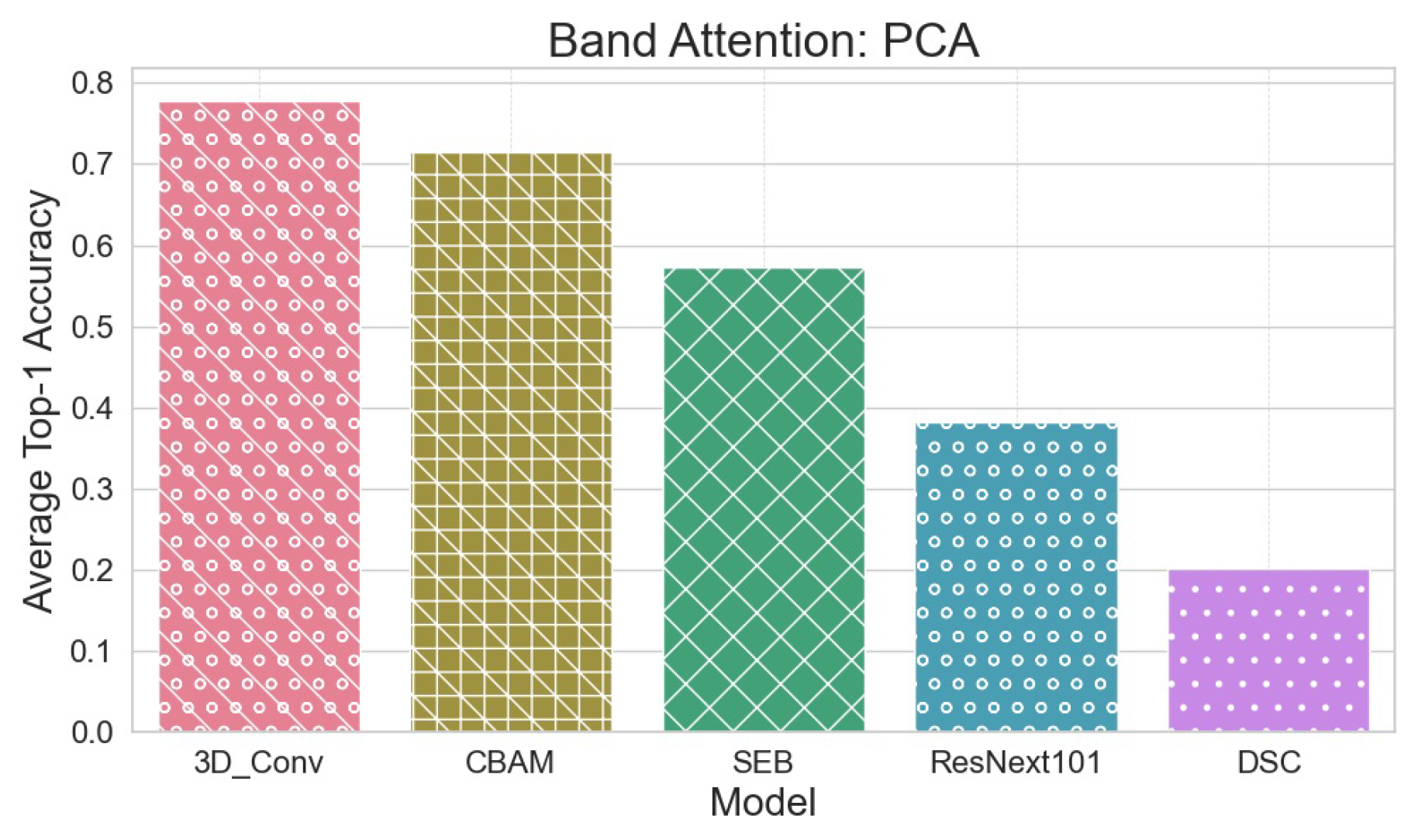
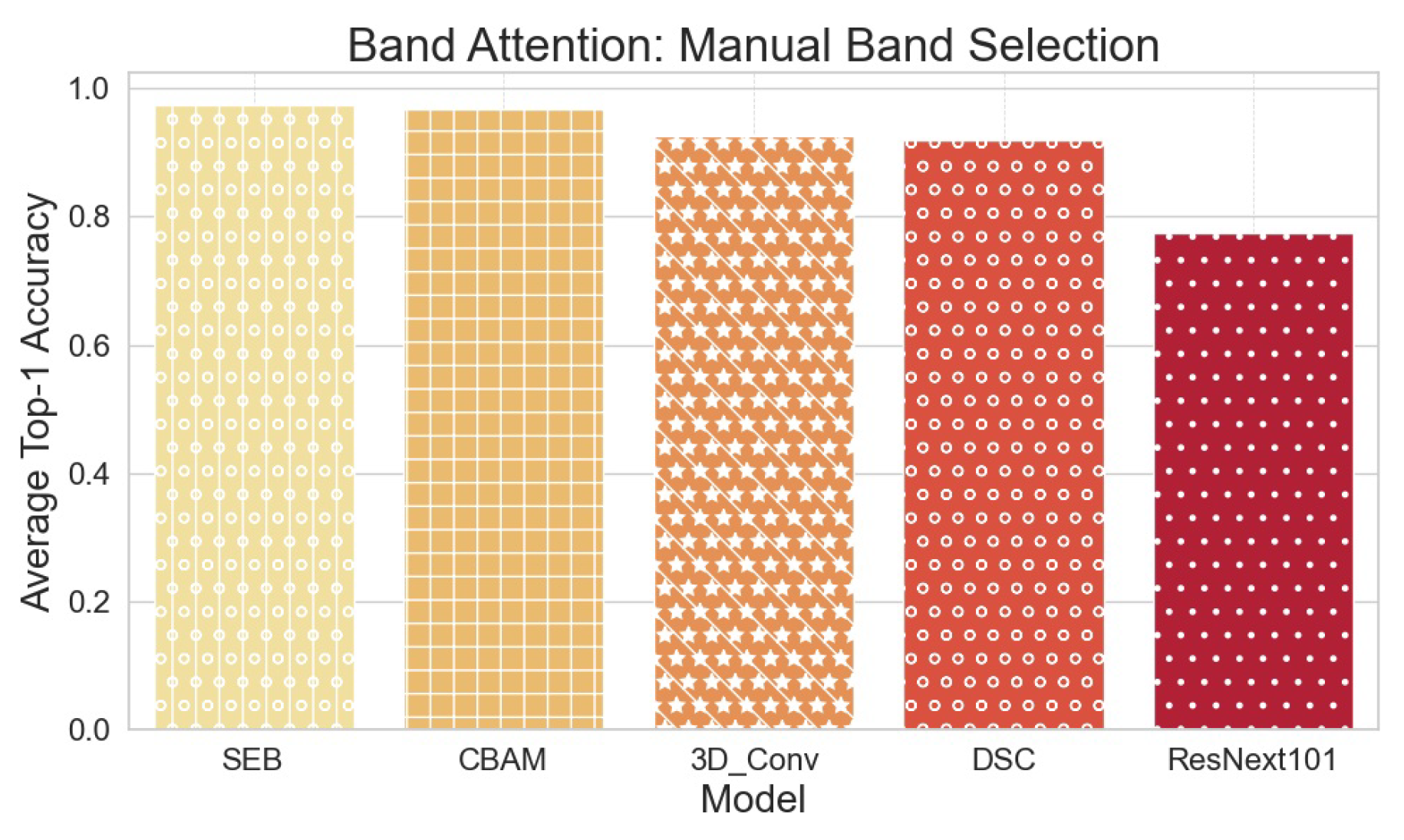
Band Attention
3.2. Super-Resolution
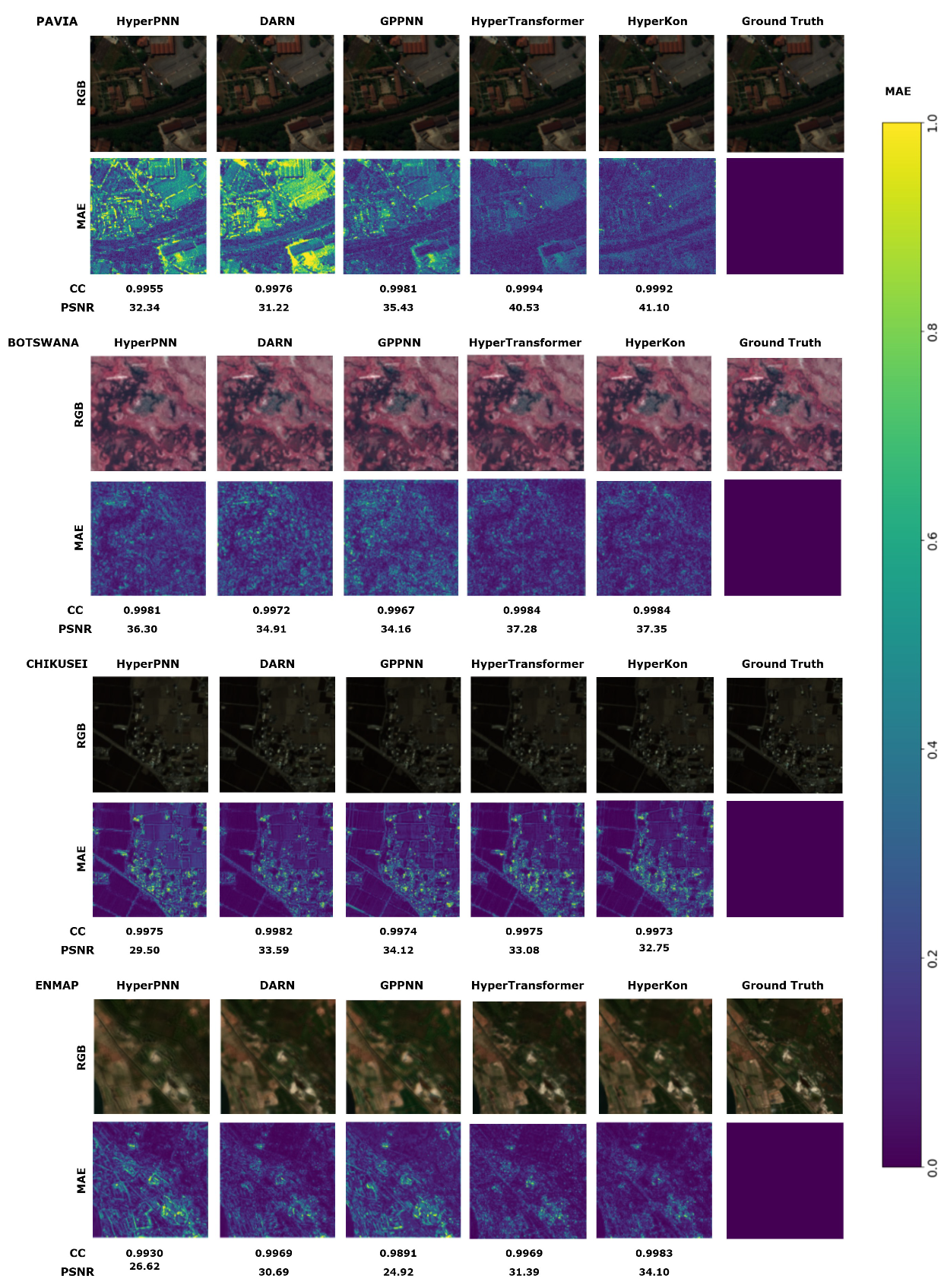
| Pavia Center Dataset | |||||
|---|---|---|---|---|---|
| Method | CC↑ | SAM↓ | RMSE↓ | ERGAS↓ | PSNR↑ |
| HySure [52] | 0.966 | 6.13 | 1.8 | 3.77 | 35.91 |
| HyperPNN [49] | 0.967 | 6.09 | 1.67 | 3.82 | 36.7 |
| PanNet [53] | 0.968 | 6.36 | 1.83 | 3.89 | 35.61 |
| Darn [45] | 0.969 | 6.43 | 1.56 | 3.95 | 37.3 |
| HyperKite [27] | 0.98 | 5.61 | 1.29 | 2.85 | 38.65 |
| SIPSA [54] | 0.948 | 5.27 | 2.38 | 4.52 | 33.65 |
| GPPNN [50] | 0.963 | 6.52 | 1.91 | 4.05 | 35.36 |
| HyperTransformer [51] | 0.9881 | 4.1494 | 0.9862 | 0.5346 | 40.9525 |
| HyperKon | 0.9883 | 3.9551 | 0.9369 | 0.5152 | 41.9808 |
| Botswana Dataset | Chikusei Dataset | Pavia Dataset | ||||
|---|---|---|---|---|---|---|
| Metric | RGB-Native | HS-Native | RGB-Native | HS-Native | RGB-Native | HS-Native |
| CC↑ | 0.9104 | 0.9411 | 0.9801 | 0.9777 | 0.9881 | 0.9883 |
| SAM↓ | 3.1459 | 2.5798 | 2.2547 | 2.4192 | 4.1494 | 3.9551 |
| RMSE↓ | 0.0233 | 0.0193 | 0.0123 | 0.0131 | 0.0098 | 0.0093 |
| ERGAS↓ | 0.6753 | 0.5249 | 0.8662 | 0.9193 | 0.5346 | 0.5152 |
| PSNR↑ | 27.3925 | 29.4128 | 36.8861 | 36.2889 | 40.9525 | 41.9808 |
3.3. Transfer Learning Capability of HyperKon
3.4. Model Efficiency Analysis
4. Discussion
4.1. Architectural Considerations
4.2. Self-Supervised Learning for Hyperspectral Data
4.3. Transfer Learning and Downstream Task Performance
4.4. Hyperspectral Perceptual Loss
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MAE | Mean Absolute Error |
| RMSE | Root-Mean-Square Error |
| PSNR | Peak Signal-to-Noise Ratio |
| CC | Correlation Coefficient |
| SAM | Spectral Angle Mapper |
| ERGAS | Erreur Relative Globale Adimensionnelle de Synthèse |
| CNN | Convolutional Neural Network |
| DSC | Depthwise Separable Convolutions |
| SEB | Squeeze and Excitation Block |
| CBAM | Convolutional Block Attention Module |
| PCA | Principal Component Analysis |
| HSI | Hyperspectral image |
| NT-Xent | Normalized Temperature-Scaled Cross Entropy |
| HSPL | HyperSpectral Perceptual Loss |
| RSFM | Remote Sensing Foundation Model |
| EnMAP | Environmental Mapping and Analysis Program |
References
- Cheng, C.; Zhao, B. Prospect of application of hyperspectral imaging technology in public security. In Proceedings of the International Conference on Applications and Techniques in Cyber Security and Intelligence ATCI 2018: Applications and Techniques in Cyber Security and Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 299–304. [Google Scholar]
- Brisco, B.; Brown, R.; Hirose, T.; McNairn, H.; Staenz, K. Precision agriculture and the role of remote sensing: A review. Can. J. Remote. Sens. 1998, 24, 315–327. [Google Scholar] [CrossRef]
- da Lomba Magalhães, M.J. Hyperspectral Image Fusion—A Comprehensive Review. Master’s Thesis, University of Eastern Finland, Kuopio, Finland, 2022. [Google Scholar]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Signoroni, A.; Savardi, M.; Baronio, A.; Benini, S. Deep learning meets hyperspectral image analysis: A multidisciplinary review. J. Imaging 2019, 5, 52. [Google Scholar] [CrossRef]
- Shi, C.; Sun, J.; Wang, L. Hyperspectral image classification based on spectral multiscale convolutional neural network. Remote. Sens. 2022, 14, 1951. [Google Scholar] [CrossRef]
- Bouchoucha, R.; Braiek, H.B.; Khomh, F.; Bouzidi, S.; Zaatour, R. Robustness assessment of hyperspectral image CNNs using metamorphic testing. Inf. Softw. Technol. 2023, 162, 107281. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote. Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning deep hierarchical spatial–spectral features for hyperspectral image classification based on residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, B.; Sun, L.; Zhan, T.; Tang, S. 3-D channel and spatial attention based multiscale spatial–spectral residual network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 4311–4324. [Google Scholar] [CrossRef]
- Li, C.; Qiu, Z.; Cao, X.; Chen, Z.; Gao, H.; Hua, Z. Hybrid dilated convolution with multi-scale residual fusion network for hyperspectral image classification. Micromachines 2021, 12, 545. [Google Scholar] [CrossRef]
- Gbodjo, Y.J.E.; Ienco, D.; Leroux, L.; Interdonato, R.; Gaetano, R.; Ndao, B. Object-based multi-temporal and multi-source land cover mapping leveraging hierarchical class relationships. Remote. Sens. 2020, 12, 2814. [Google Scholar] [CrossRef]
- Li, Q.; Zhong, R.; Du, X.; Du, Y. TransUNetCD: A hybrid transformer network for change detection in optical remote-sensing images. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5622519. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–28 October 2018; pp. 3–19. [Google Scholar]
- Hong, D.; Zhang, B.; Li, X.; Li, Y.; Li, C.; Yao, J.; Yokoya, N.; Li, H.; Ghamisi, P.; Jia, X.; et al. SpectralGPT: Spectral remote sensing foundation model. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5227–5244. [Google Scholar] [CrossRef]
- Manas, O.; Lacoste, A.; Giró-i Nieto, X.; Vazquez, D.; Rodriguez, P. Seasonal contrast: Unsupervised pre-training from uncurated remote sensing data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9414–9423. [Google Scholar]
- He, X.; Chen, Y.; Huang, L.; Hong, D.; Du, Q. Foundation model-based multimodal remote sensing data classification. IEEE Trans. Geosci. Remote. Sens. 2023, 62, 5502117. [Google Scholar] [CrossRef]
- Guo, X.; Lao, J.; Dang, B.; Zhang, Y.; Yu, L.; Ru, L.; Zhong, L.; Huang, Z.; Wu, K.; Hu, D.; et al. Skysense: A multi-modal remote sensing foundation model towards universal interpretation for earth observation imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2024; pp. 27672–27683. [Google Scholar]
- Yan, Z.; Li, J.; Li, X.; Zhou, R.; Zhang, W.; Feng, Y.; Diao, W.; Fu, K.; Sun, X. RingMo-SAM: A foundation model for segment anything in multimodal remote-sensing images. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Dong, H.; Ma, W.; Wu, Y.; Zhang, J.; Jiao, L. Self-supervised representation learning for remote sensing image change detection based on temporal prediction. Remote. Sens. 2020, 12, 1868. [Google Scholar] [CrossRef]
- Hou, S.; Shi, H.; Cao, X.; Zhang, X.; Jiao, L. Hyperspectral imagery classification based on contrastive learning. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y.; He, X. Spectral–spatial masked transformer with supervised and contrastive learning for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Hu, X.; Li, T.; Zhou, T.; Liu, Y.; Peng, Y. Contrastive learning based on transformer for hyperspectral image classification. Appl. Sci. 2021, 11, 8670. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Cwiek, M.; Zak, L.; Lakota, T.; Tulczyjew, L.; Kawulok, M. Towards on-board hyperspectral satellite image segmentation: Understanding robustness of deep learning through simulating acquisition conditions. Remote. Sens. 2021, 13, 1532. [Google Scholar] [CrossRef]
- Storch, T.; Honold, H.P.; Chabrillat, S.; Habermeyer, M.; Tucker, P.; Brell, M.; Ohndorf, A.; Wirth, K.; Betz, M.; Kuchler, M.; et al. The EnMAP imaging spectroscopy mission towards operations. Remote. Sens. Environment 2023, 294, 113632. [Google Scholar] [CrossRef]
- Bandara, W.G.C.; Valanarasu, J.M.J.; Patel, V.M. Hyperspectral pansharpening based on improved deep image prior and residual reconstruction. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2020; pp. 1597–1607. [Google Scholar]
- Wu, P.; Cui, Z.; Gan, Z.; Liu, F. Three-dimensional resnext network using feature fusion and label smoothing for hyperspectral image classification. Sensors 2020, 20, 1652. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26–30 June 2016; pp. 770–778. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Ohri, K.; Kumar, M. Review on self-supervised image recognition using deep neural networks. Knowl.-Based Syst. 2021, 224, 107090. [Google Scholar] [CrossRef]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar]
- Caron, M.; Misra, I.; Mairal, J.; Goyal, P.; Bojanowski, P.; Joulin, A. Unsupervised learning of visual features by contrasting cluster assignments. Adv. Neural Inf. Process. Syst. 2020, 33, 9912–9924. [Google Scholar]
- Le-Khac, P.H.; Healy, G.; Smeaton, A.F. Contrastive representation learning: A framework and review. IEEE Access 2020, 8, 193907–193934. [Google Scholar] [CrossRef]
- Purushwalkam, S.; Gupta, A. Demystifying contrastive self-supervised learning: Invariances, augmentations and dataset biases. Adv. Neural Inf. Process. Syst. 2020, 33, 3407–3418. [Google Scholar]
- Robinson, J.; Chuang, C.Y.; Sra, S.; Jegelka, S. Contrastive learning with hard negative samples. arXiv 2020, arXiv:2010.04592. [Google Scholar]
- Li, W.; Feng, F.; Li, H.; Du, Q. Discriminant analysis-based dimension reduction for hyperspectral image classification: A survey of the most recent advances and an experimental comparison of different techniques. IEEE Geosci. Remote. Sens. Mag. 2018, 6, 15–34. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature extraction for hyperspectral image classification: A review. Int. J. Remote. Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, F. Review on graph learning for dimensionality reduction of hyperspectral image. Geo-Spat. Inf. Sci. 2020, 23, 98–106. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote. Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Ungar, S.G.; Pearlman, J.S.; Mendenhall, J.A.; Reuter, D. Overview of the earth observing one (EO-1) mission. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 1149–1159. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; Tecnical Report SAL-2016-05-27; University Tokyo: Tokyo, Japan, 2016; Volume 5. [Google Scholar]
- Zheng, Y.; Li, J.; Li, Y.; Guo, J.; Wu, X.; Chanussot, J. Hyperspectral pansharpening using deep prior and dual attention residual network. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 8059–8076. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, H.; Kadambi, G.R.; Kishore, J.; Shuttleworth, J.; Manikandan, J. Quality metrics evaluation of hyperspectral images. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, 40, 1221–1226. [Google Scholar] [CrossRef]
- Deborah, H.; Richard, N.; Hardeberg, J.Y. A comprehensive evaluation of spectral distance functions and metrics for hyperspectral image processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 3224–3234. [Google Scholar] [CrossRef]
- Chaithra, C.; Taranath, N.; Darshan, L.; Subbaraya, C. A Survey on Image Fusion Techniques and Performance Metrics. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), IEEE, Coimbatore, India, 29–31 March 2018; pp. 995–999. [Google Scholar]
- He, L.; Zhu, J.; Li, J.; Plaza, A.; Chanussot, J.; Li, B. HyperPNN: Hyperspectral pansharpening via spectrally predictive convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2019, 12, 3092–3100. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J.; Zhao, Z.; Sun, K.; Liu, J.; Zhang, C. Deep gradient projection networks for pan-sharpening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 21–25 June 2021; pp. 1366–1375. [Google Scholar]
- Bandara, W.G.C.; Patel, V.M. HyperTransformer: A textural and spectral feature fusion transformer for pansharpening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1767–1777. [Google Scholar]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote. Sens. 2014, 53, 3373–3388. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Lee, J.; Seo, S.; Kim, M. Sipsa-net: Shift-invariant pan sharpening with moving object alignment for satellite imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 21–25 June 2021; pp. 10166–10174. [Google Scholar]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote. Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.; Lu, X.; Wu, S. Spectral–spatial attention network for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2019, 58, 3232–3245. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote. Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Heo, B.; Yun, S.; Han, D.; Chun, S.; Choe, J.; Oh, S.J. Rethinking spatial dimensions of vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 11936–11945. [Google Scholar]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral image transformer classification networks. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Zhou, Y. Quantum-Inspired Spectral-Spatial Pyramid Network for Hyperspectral Image Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 9925–9934. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Ayush, K.; Uzkent, B.; Meng, C.; Tanmay, K.; Burke, M.; Lobell, D.; Ermon, S. Geography-aware self-supervised learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10181–10190. [Google Scholar]
- Ou, X.; Liu, L.; Tan, S.; Zhang, G.; Li, W.; Tu, B. A hyperspectral image change detection framework with self-supervised contrastive learning pretrained model. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 7724–7740. [Google Scholar] [CrossRef]
- Loncan, L.; de Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote. Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Liang, T.; Glossner, J.; Wang, L.; Shi, S.; Zhang, X. Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing 2021, 461, 370–403. [Google Scholar] [CrossRef]
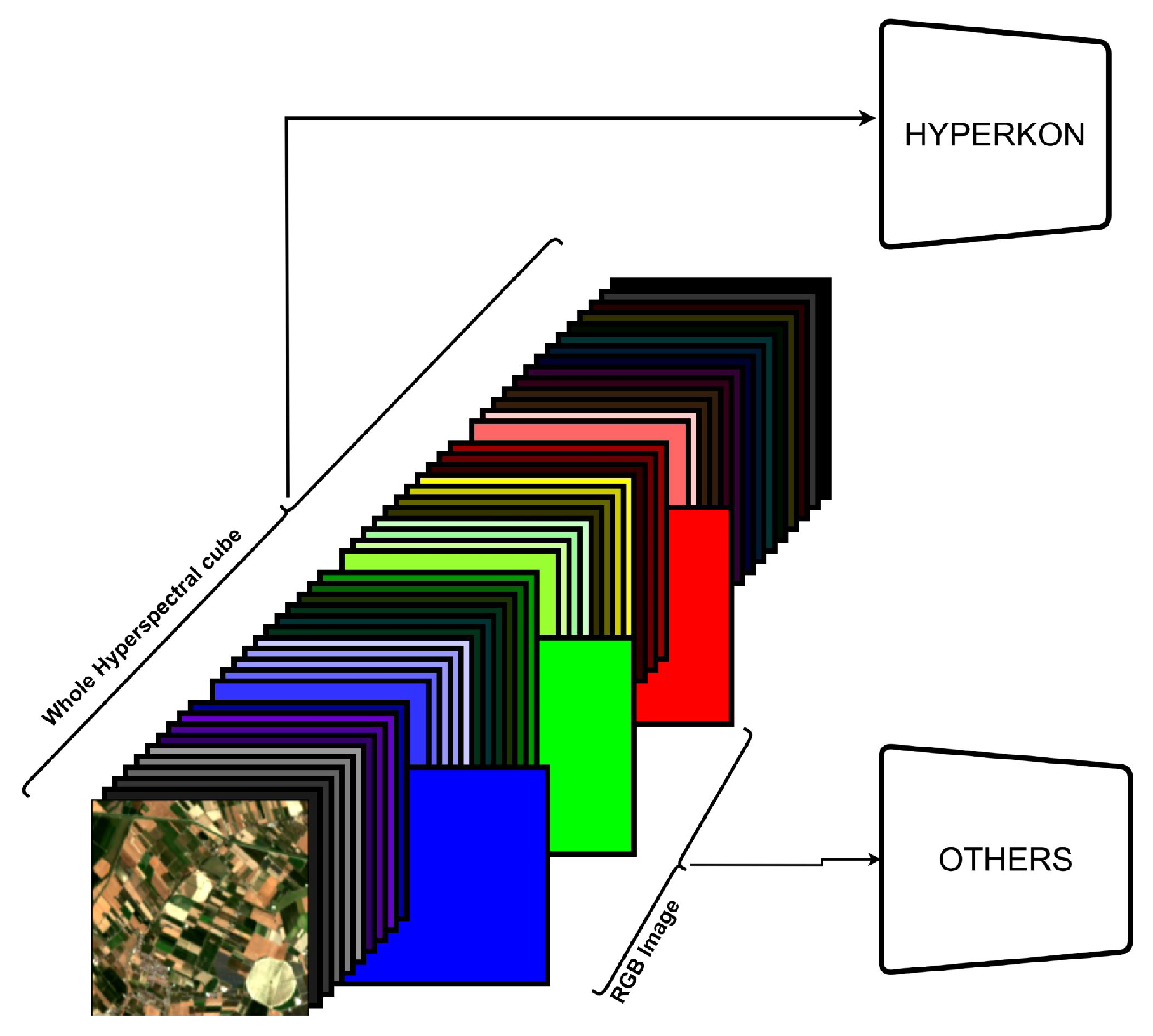


| Dataset | Number of Bands | Size | Spectral Range | Number of Images | Spatial Resolution | Imaging Location | Platform Type |
|---|---|---|---|---|---|---|---|
| Indian Pines | 200 | 145 × 145 | 400–2500 nm | 1 | 30 m | Indiana, USA | Airborne |
| Pavia Centre | 102 | 1096 × 1096 | 430–860 nm | 1 | 1.3 m | Pavia, Italy | Airborne |
| Salinas | 204 | 512 × 217 | 360–2500 nm | 1 | 3.7 m | Salinas Valley, CA, USA | Airborne |
| Harvard | 31 | 1392 × 1040 | 420–720 nm | 50 | - | Harvard, USA | Airborne |
| Botswana | 145 | 1476 × 256 | 400–2500 nm | 1 | 30 m | Botswana | Airborne |
| Chikusei | 100 | 2517 × 2335 | 263–1018 nm | 1 | 2.5 m | Chikusei, Japan | Airborne |
| EnHyperSet-1 | 224 | 1300 × 1200 | 420–2450 nm | 800 | 30 m | Global, on demand | Spaceborne |
| Datasets | Metrics | SSAN [56] | SSRN [57] | RvT [58] | HiT [59] | SSFTT [60] | QSSPN-3 [61] | HyperKon |
|---|---|---|---|---|---|---|---|---|
| IP | OA(%) | 89.46 | 91.85 | 83.85 | 90.59 | 96.35 | 95.87 | 98.77 |
| AA(%) | 85.99 | 81.51 | 79.67 | 86.71 | 89.99 | 96.40 | 97.82 | |
| Kappa(%) | 88.04 | 90.73 | 81.68 | 89.27 | 95.82 | 95.34 | 98.60 | |
| Params. | 148.83 K | 735.88 K | 10.78 M | 49.60 M | 148.50 K | 910.50 K | 5.54 M | |
| FLOPs | 7.88 M | 212.48 M | 17.83 M | 345.88 M | 3.66 M | 34.54 M | 1.27 G | |
| PU | OA(%) | 99.15 | 99.63 | 97.37 | 99.43 | 99.52 | 99.71 | 99.89 |
| AA(%) | 98.70 | 99.29 | 95.86 | 99.09 | 99.20 | 99.43 | 99.76 | |
| Kappa(%) | 98.87 | 99.51 | 96.52 | 99.24 | 99.36 | 99.61 | 99.86 | |
| Params. | 94.63 K | 396.99 K | 9.77 M | 42.41 M | 148.03 K | 609.16 K | 4.08 M | |
| FLOPs | 5.57 M | 108.04 M | 16.83 M | 190.85 M | 3.66 M | 10.25 M | 370.59 M | |
| SA | OA(%) | 98.92 | 99.31 | 98.11 | 99.38 | 99.53 | 99.66 | 100.00 |
| AA(%) | 99.33 | 99.70 | 98.83 | 99.70 | 99.72 | 99.81 | 100.00 | |
| Kappa(%) | 98.80 | 99.23 | 97.90 | 99.31 | 99.47 | 99.63 | 100.00 | |
| Params. | 149.71 K | 750 K | 10.82 M | 50 M | 148.50 K | 926.90 K | 5.62 M | |
| FLOPs | 7.97 M | 216.84 | 17.80 M | 354.42 M | 3.66 M | 35.87 M | 1.32 G |
| Indian Pines | Pavia University | Salinas | |||
|---|---|---|---|---|---|
| Class | Acc. (%) | Class | Acc. (%) | Class | Acc. (%) |
| Alfalfa | 100.00 | Asphalt | 100.00 | Broccoli_green_weeds_1 | 100.00 |
| Corn-notill | 99.72 | Meadows | 100.00 | Broccoli_green_weeds_2 | 100.00 |
| Corn-mintill | 99.16 | Gravel | 100.00 | Fallow | 100.00 |
| Corn | 100.00 | Trees | 99.87 | Fallow_rough_plow | 100.00 |
| Grass-pasture | 99.59 | Painted metal sheets | 100.00 | Fallow_smooth | 100.00 |
| Grass-trees | 100.00 | Bare Soil | 100.00 | Stubble | 100.00 |
| Grass-pasture-mowed | 100.00 | Bitumen | 99.85 | Celery | 100.00 |
| Hay-windrowed | 100.00 | Self-blocking bricks | 99.95 | Grapes_untrained | 100.00 |
| Oats | 95.00 | Shadows | 99.58 | Soil_vinyard_develop | 100.00 |
| Soybean-notill | 99.69 | Corn_senesced_green | 100.00 | ||
| Soybean-mintill | 99.80 | Lettuce_romaine_4wk | 100.00 | ||
| Soybean-clean | 99.49 | Lettuce_romaine_5wk | 100.00 | ||
| Wheat | 100.00 | Lettuce_romaine_6wk | 100.00 | ||
| Woods | 99.29 | Lettuce_romaine_7wk | 100.00 | ||
| Buildings-grass-trees-drives | 100.00 | Vinyard_untrained | 100.00 | ||
| Stone-steel-towers | 100.00 | Vinyard_vertical | 100.00 | ||
| Performance Metrics | |||||
| Total training time (s) | 2346.18 | Total training time (s) | 9251.00 | Total training time (s) | 12,172.18 |
| Total test time (s) | 52.07 | Total test time (s) | 513.87 | Total test time (s) | 294.16 |
| Avg. inference time (s) | 0.0009 | Avg. inference time (s) | 0.0009 | Avg. inference time (s) | 0.0010 |
| Throughput (samples/s) | 1088.39 | Throughput (samples/s) | 1078.45 | Throughput (samples/s) | 1038.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayuba, D.L.; Guillemaut, J.-Y.; Marti-Cardona, B.; Mendez, O. HyperKon: A Self-Supervised Contrastive Network for Hyperspectral Image Analysis. Remote Sens. 2024, 16, 3399. https://doi.org/10.3390/rs16183399
Ayuba DL, Guillemaut J-Y, Marti-Cardona B, Mendez O. HyperKon: A Self-Supervised Contrastive Network for Hyperspectral Image Analysis. Remote Sensing. 2024; 16(18):3399. https://doi.org/10.3390/rs16183399
Chicago/Turabian StyleAyuba, Daniel La’ah, Jean-Yves Guillemaut, Belen Marti-Cardona, and Oscar Mendez. 2024. "HyperKon: A Self-Supervised Contrastive Network for Hyperspectral Image Analysis" Remote Sensing 16, no. 18: 3399. https://doi.org/10.3390/rs16183399
APA StyleAyuba, D. L., Guillemaut, J.-Y., Marti-Cardona, B., & Mendez, O. (2024). HyperKon: A Self-Supervised Contrastive Network for Hyperspectral Image Analysis. Remote Sensing, 16(18), 3399. https://doi.org/10.3390/rs16183399







