An Ensemble Machine Learning Model to Estimate Urban Water Quality Parameters Using Unmanned Aerial Vehicle Multispectral Imagery
Abstract
1. Introduction
2. Materials and Methods
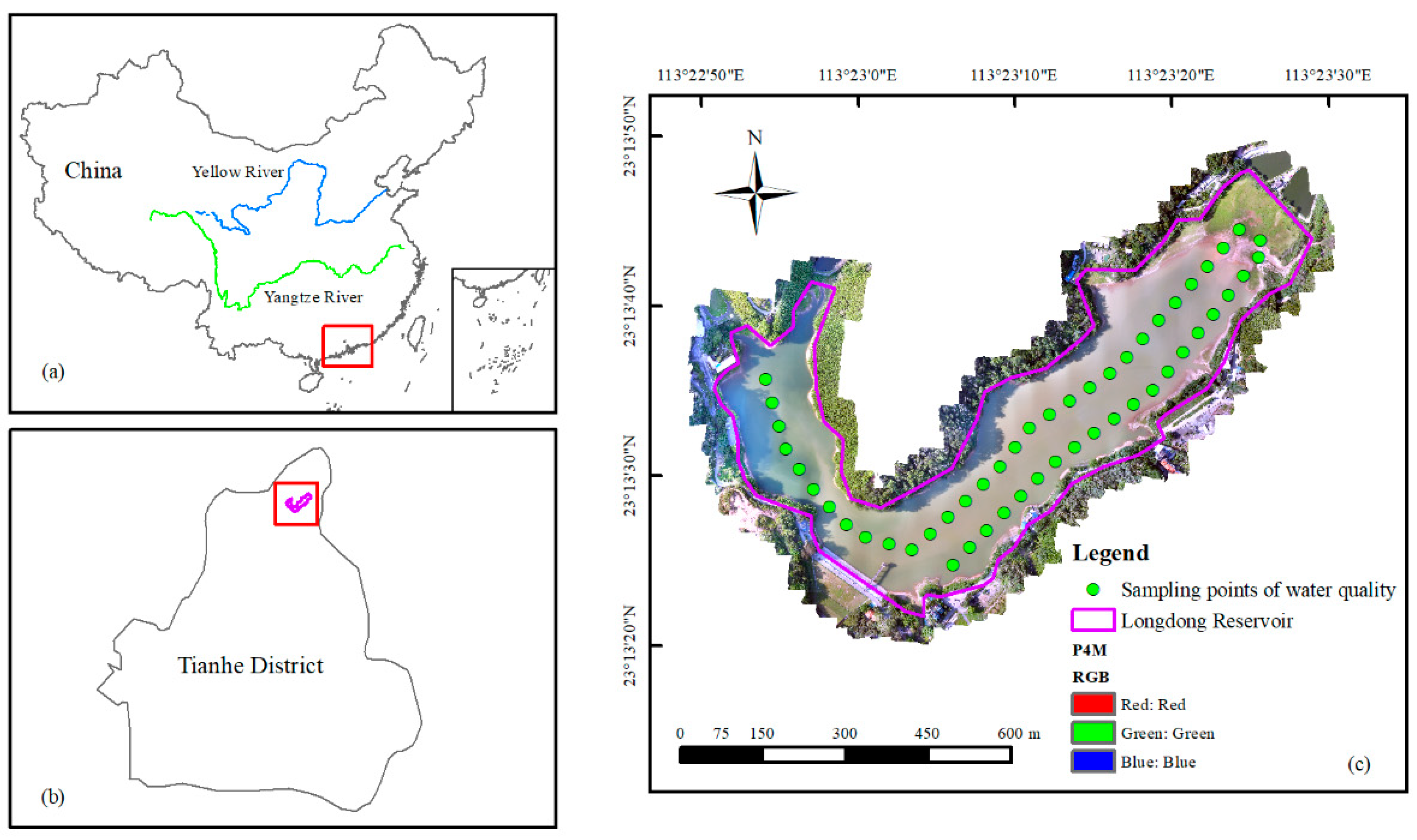
2.1. Study Area
2.2. Method
2.2.1. Multispectral Data Collection and Preprocessing
2.2.2. Water Sample Collection and Measurement
2.2.3. Oversampling of WQPs Samples Based on SMOTE
- (1)
- Divide one of the datasets into five equal parts and calibrate them into five categories (I, II, III, IV, and V) according to the WQP ranges;
- (2)
- According to the five categories, divide the whole dataset into the training dataset (referred to as T-I) and validation dataset (referred to as V-I) according to the ratio of 3:1 using the stratified random sampling method;
- (3)
- Execute the same processing for the remaining four datasets.
2.2.4. Feature Band Selection Based on Feature Combination and Genetic Algorithm (FC-GA)
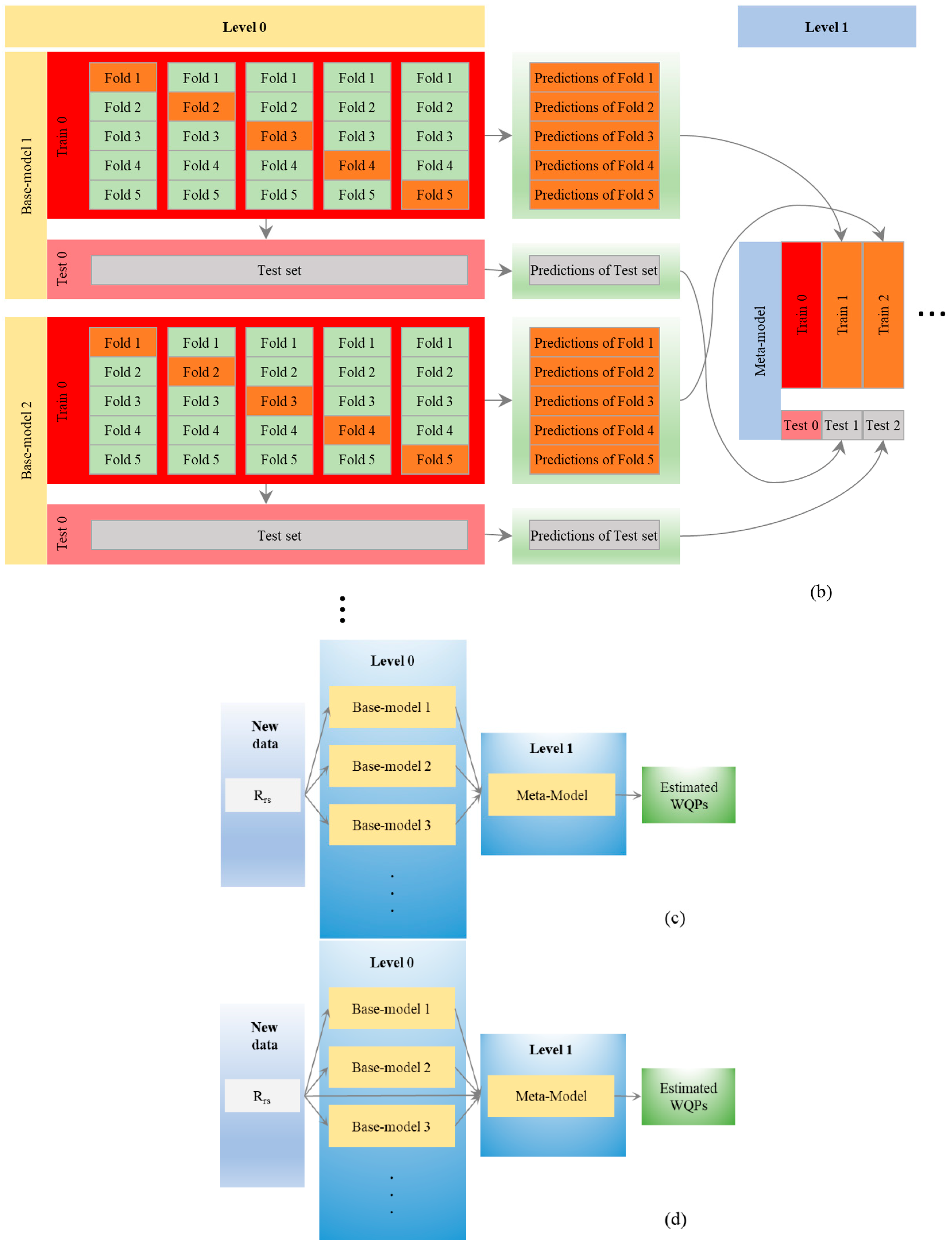
2.2.5. Ensemble Machine Learning (EML) Algorithm
- (a)
- The T-III dataset is divided into five datasets, four of which are used for training, and the remaining one is used for prediction to perform a 5-fold cross-validation.
- (b)
- The datasets divided in (a) are used for the training and prediction of one type of base-model, and the prediction results are obtained after 5 cycles. The 5 predictions are vertically combined into 1 column to form a column vector with the same number of columns as .
- (c)
- Steps (a) and (b) are repeated in all the selected base-models to obtain the same number of column vectors as the number of columns of .
- (d)
- The base-model is trained using the entire T-III dataset and then the V-III dataset is predicted to form with the same number of columns as .
- (e)
- Input to the meta-model trained on finally yields , which is the predicted TN.
2.2.6. Performance Evaluation
3. Results
3.1. Statistical Analysis of Water Quality Samples
3.2. Feature Band Selection Results
3.3. Analysis of ML Models and EML Model Results
3.3.1. Comparison of Different Models for Water Quality Estimation
3.3.2. Comparative Analysis of OAP and NOAP Estimation
3.4. Reversal Results of Spatial and Temporal Distribution of WQPs
4. Discussion
4.1. Performance of the FC-GA Method
4.2. Performance of EML Models
4.3. Temporal and Spatial Variations of Water Quality
4.4. Challenges and Opportunities
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albert, J.S.; Destouni, G.; Duke-Sylvester, S.M.; Magurran, A.E.; Oberdorff, T.; Reis, R.E.; Winemiller, K.O.; Ripple, W.J. Scientists′ warning to humanity on the freshwater biodiversity crisis. Ambio 2021, 50, 85–94. [Google Scholar] [CrossRef]
- Faghihinia, M.; Xu, Y.; Liu, D.; Wu, N. Freshwater biodiversity at different habitats: Research hotspots with persistent and emerging themes. Ecol. Indic. 2021, 129, 107926. [Google Scholar] [CrossRef]
- Li, J.; Ianaiev, V.; Huff, A.; Zalusky, J.; Ozersky, T.; Katsev, S. Benthic invaders control the phosphorus cycle in the world′s largest freshwater ecosystem. Proc. Natl. Acad. Sci. USA 2021, 118, e2008223118. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.; Sun, H.; Wu, X.; Li, J.; Wang, Z.; Tong, H.; Feng, J. Water availability may not constrain vegetation growth in Northern Hemisphere. Agric. Water Manag. 2024, 291, 108649. [Google Scholar] [CrossRef]
- Ma, T.; Sun, S.; Fu, G.; Hall, J.W.; Ni, Y.; He, L.; Yi, J.; Zhao, N.; Du, Y.; Pei, T.; et al. Pollution exacerbates China′s water scarcity and its regional inequality. Nat. Commun. 2020, 11, 650. [Google Scholar] [CrossRef] [PubMed]
- Messager, M.L.; Lehner, B.; Cockburn, C.; Lamouroux, N.; Pella, H.; Snelder, T.; Tockner, K.; Trautmann, T.; Watt, C.; Datry, T. Global prevalence of non-perennial rivers and streams. Nature 2021, 594, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Giri, S. Water quality prospective in Twenty First Century: Status of water quality in major river basins, contemporary strategies and impediments: A review. Environ. Pollut. 2021, 271, 116332. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zhang, Y.; Bing, H.; Peng, J.; Dong, F.; Gao, J.; Arhonditsis, G.B. Characterizing the river water quality in China: Recent progress and on-going challenges. Water Res. 2021, 201, 117309. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, Z.; Chen, X.; Lai, C. Fast simulation and prediction of urban pluvial floods using a deep convolutional neural network model. J. Hydrol. 2023, 624, 129945. [Google Scholar] [CrossRef]
- Wang, J.; Fu, Z.; Qiao, H.; Liu, F. Assessment of eutrophication and water quality in the estuarine area of Lake Wuli, Lake Taihu, China. Sci. Total Environ. 2019, 650, 1392–1402. [Google Scholar] [CrossRef]
- Xu, H.; Paerl, H.W.; Qin, B.; Zhu, G.; Hall, N.S.; Wu, Y. Determining Critical Nutrient Thresholds Needed to Control Harmful Cyanobacterial Blooms in Eutrophic Lake Taihu, China. Environ. Sci. Technol. 2015, 49, 1051–1059. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.C.; Michalak, A.M.; Pahlevan, N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature 2019, 574, 667–670. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Liu, G.; Wang, Q.; Wen, Z.; Lyu, L.; Du, Y.; Sha, L.; Fang, C. Quantification of lake clarity in China using Landsat OLI imagery data. Remote Sens. Environ. 2020, 243, 111800. [Google Scholar] [CrossRef]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Bownik, A.; Wlodkowic, D. Advances in real-time monitoring of water quality using automated analysis of animal behaviour. Sci. Total Environ. 2021, 789, 147796. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Guo, H.; Huang, J.J.; Tian, S.; Xu, W.; Mai, Y. An ensemble machine learning model for water quality estimation in coastal area based on remote sensing imagery. J. Environ. Manag. 2022, 323, 116187. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Tian, S.; Huang, J.J.; Zhu, X.; Wang, B.; Zhang, Z. Performance of deep learning in mapping water quality of Lake Simcoe with long-term Landsat archive. J. Photogramm. Remote Sens. 2022, 183, 451–469. [Google Scholar] [CrossRef]
- Saranathan, A.M.; Smith, B.; Pahlevan, N. Per-Pixel Uncertainty Quantification and Reporting for Satellite-Derived Chlorophyll-a Estimates via Mixture Density Networks. Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Do, T.-N.; Nguyen, D.-M.T.; Ghimire, J.; Vu, K.-C.; Do Dang, L.-P.; Pham, S.-L.; Pham, V.-M. Assessing surface water pollution in Hanoi, Vietnam, using remote sensing and machine learning algorithms. Environ. Sci. Pollut. Res. 2023, 30, 82230–82247. [Google Scholar] [CrossRef]
- Maciel, D.A.; Faria Barbosa, C.C.; Leao de Moraes Novo, E.M.; Flores Junior, R.; Begliomini, F.N. Water clarity in Brazilian water assessed using Sentinel-2 and machine learning methods. J. Photogramm. Remote Sens. 2021, 182, 134–152. [Google Scholar] [CrossRef]
- Shen, H.; Wu, J.; Cheng, Q.; Aihemaiti, M.; Zhang, C.; Li, Z. A Spatiotemporal Fusion Based Cloud Removal Method for Remote Sensing Images With Land Cover Changes. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 862–874. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Shi, K.; Zhang, Y.; Li, N.; Wang, W.; Huang, X.; Qin, B. Monitoring water quality using proximal remote sensing technology. Sci. Total Environ. 2022, 803, 149805. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Pyo, J.; Kwon, Y.-H.; Duan, H.; Cho, K.H.; Park, Y. Drone-based hyperspectral remote sensing of cyanobacteria using vertical cumulative pigment concentration in a deep reservoir. Remote Sens. Environ. 2020, 236, 111517. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Jiang, D.; Matsushita, B.; Pahlevan, N.; Gurlin, D.; Lehmann, M.K.; Fichot, C.G.; Schalles, J.; Loisel, H.; Binding, C.; Zhang, Y.; et al. Remotely estimating total suspended solids concentration in clear to extremely turbid waters using a novel semi-analytical method. Remote Sens. Environ. 2021, 258, 112386. [Google Scholar] [CrossRef]
- Li, S.; Chen, F.; Song, K.; Liu, G.; Tao, H.; Xu, S.; Wang, X.; Wang, Q.; Mu, G. Mapping the trophic state index of eastern lakes in China using an empirical model and Sentinel-2 imagery data. J. Hydrol. 2022, 608, 127613. [Google Scholar] [CrossRef]
- Lai, L.; Zhang, Y.; Cao, Z.; Liu, Z.; Yang, Q. Algal biomass mapping of eutrophic lakes using a machine learning approach with MODIS images. Sci. Total Environ. 2023, 880, 163357. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Werther, M.; Odermatt, D.; Simis, S.G.H.; Gurlin, D.; Lehmann, M.K.; Kutser, T.; Gupana, R.; Varley, A.; Hunter, P.D.; Tyler, A.N.; et al. A Bayesian approach for remote sensing of chlorophyll-a and associated retrieval uncertainty in oligotrophic and mesotrophic lakes. Remote Sens. Environ. 2022, 283, 113295. [Google Scholar] [CrossRef]
- He, Y.; Lu, Z.; Wang, W.; Zhang, D.; Zhang, Y.; Qin, B.; Shi, K.; Yang, X. Water clarity mapping of global lakes using a novel hybrid deep-learning-based recurrent model with Landsat OLI images. Water Res. 2022, 215, 118241. [Google Scholar] [CrossRef]
- Li, L.; Gu, M.; Gong, C.; Hu, Y.; Wang, X.; Yang, Z.; He, Z. An advanced remote sensing retrieval method for urban non-optically active water quality parameters: An example from Shanghai. Sci. Total Environ. 2023, 880, 163389. [Google Scholar] [CrossRef] [PubMed]
- Qun′ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, G.; Huang, G. Evaluation of the cost-effectiveness of Green Infrastructure in climate change scenarios using TOPSIS. Urban For. Urban Green. 2021, 64, 127287. [Google Scholar] [CrossRef]
- Liu, C.; Xing, C.; Hu, Q.; Wang, S.; Zhao, S.; Gao, M. Stereoscopic hyperspectral remote sensing of the atmospheric environment: Innovation and prospects. Earth-Sci. Rev. 2022, 226, 103958. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, S.; Gao, C. Dynamic simulation and comprehensive evaluation of the water resources carrying capacity in Guangzhou city, China. Ecol. Indic. 2022, 135, 108528. [Google Scholar] [CrossRef]
- Shafiee, S.; Mroz, T.; Burud, I.; Lillemo, M. Evaluation of UAV multispectral cameras for yield and biomass prediction in wheat under different sun elevation angles and phenological stages. Comput. Electron. Agric. 2023, 210, 107874. [Google Scholar] [CrossRef]
- Yao, C.; Sun, Z.; Lu, S. Reducing BRDF Effects on the Estimation of Leaf Biochemical Parameters Using the Nonpolarized Reflectance Factor in the Hemispheric Space. Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Daniels, L.; Eeckhout, E.; Wieme, J.; Dejaegher, Y.; Audenaert, K.; Maes, W.H. Identifying the Optimal Radiometric Calibration Method for UAV-Based Multispectral Imaging. Remote Sens. 2023, 15, 2909. [Google Scholar] [CrossRef]
- Svensgaard, J.; Jensen, S.M.; Christensen, S.; Rasmussen, J. The importance of spectral correction of UAV-based phenotyping with RGB cameras. Field Crops Res. 2021, 269, 108177. [Google Scholar] [CrossRef]
- Tang, Y.; Pan, Y.; Zhang, L.; Yi, H.; Gu, Y.; Sun, W. Efficient Monitoring of Total Suspended Matter in Urban Water Based on UAV Multi-spectral Images. Water Resour. Manag. 2023, 37, 2143–2160. [Google Scholar] [CrossRef]
- Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
- Cai, J.; Meng, L.; Liu, H.; Chen, J.; Xing, Q. Estimating Chemical Oxygen Demand in estuarine urban rivers using unmanned aerial vehicle hyperspectral images. Ecol. Indic. 2022, 139, 108936. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms-A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
- Lemaitre, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 17. [Google Scholar]
- Rivera, W.A.; Xanthopoulos, P. A priori synthetic over-sampling methods for increasing classification sensitivity in imbalanced data sets. Expert Syst. Appl. 2016, 66, 124–135. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Cao, Z.; Hu, M.; Xue, K.; Chen, X.; Ma, R. Development of remote sensing algorithm for total phosphorus concentration in eutrophic lakes: Conventional or machine learning? Water Res. 2022, 215, 118213. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, P.; Meng, F.; Yang, X.; Xu, J.; Cui, Y. Estimation algorithm for chlorophyll-a concentrations in water from hyperspectral images based on feature derivation and ensemble learning. Ecol. Inform. 2022, 71, 101783. [Google Scholar] [CrossRef]
- Rocha, A.D.; Groen, T.A.; Skidmore, A.K. Spatially-explicit modelling with support of hyperspectral data can improve prediction of plant traits. Remote Sens. Environ. 2019, 231, 111200. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carre, G.; Garcia Marquez, J.R.; Gruber, B.; Lafourcade, B.; Leitao, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Martinez, F.; Pilar Frias, M.; Dolores Perez, M.; Jesus Rivera, A. A methodology for applying k-nearest neighbor to time series forecasting. Artif. Intell. Rev. 2019, 52, 2019–2037. [Google Scholar] [CrossRef]
- De′ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bentejac, C.; Csorgo, A.; Martinez-Munoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Hu, X.; Weng, Q. Estimating impervious surfaces from medium spatial resolution imagery using the self-organizing map and multi-layer perceptron neural networks. Remote Sens. Environ. 2009, 113, 2089–2102. [Google Scholar] [CrossRef]
- Rajadurai, H.; Gandhi, U.D. A stacked ensemble learning model for intrusion detection in wireless network. Neural Comput. Appl. 2022, 34, 15387–15395. [Google Scholar] [CrossRef]
- Wang, R. Significantly Improving the Prediction of Molecular Atomization Energies by an Ensemble of Machine Learning Algorithms and Rescanning Input Space: A Stacked Generalization Approach. J. Phys. Chem. C 2018, 122, 8868–8873. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the aboveground biomass of coniferous forest in Northeast China using spectral variables, land surface temperature and soil moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef] [PubMed]
- Kwon, S.; Seo, I.W.; Noh, H.; Kim, B. Hyperspectral retrievals of suspended sediment using cluster-based machine learning regression in shallow waters. Sci. Total Environ. 2022, 833, 155168. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a Few Examples: A Survey on Few-shot Learning. Acm. Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Emadi, M.; Taghizadeh-Mehrjardi, R.; Cherati, A.; Danesh, M.; Mosavi, A.; Scholten, T. Predicting and Mapping of Soil Organic Carbon Using Machine Learning Algorithms in Northern Iran. Remote Sens. 2020, 12, 2234. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, C.; Akbar, A.; Xue, Y.; Zhou, Y. Spectral and Spatial Feature Integrated Ensemble Learning Method for Grading Urban River Network Water Quality. Remote Sens. 2021, 13, 4591. [Google Scholar] [CrossRef]
- Rahman, M.; Chen, N.; Elbeltagi, A.; Islam, M.M.; Alam, M.; Pourghasemi, H.R.; Tao, W.; Zhang, J.; Tian, S.; Faiz, H.; et al. Application of stacking hybrid machine learning algorithms in delineating multi-type flooding in Bangladesh. J. Environ. Manag. 2021, 295, 113086. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Lao, Z.; Liang, Y.; Sun, J.; He, X.; Deng, T.; He, W.; Fan, D.; Gao, E.; Hou, Q. Evaluating optically and non-optically active water quality and its response relationship to hydro-meteorology using multi-source data in Poyang Lake, China. Ecol. Indic. 2022, 145, 109675. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa Yield Prediction Using UAV-Based Hyperspectral Imagery and Ensemble Learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Asteris, P.G.; Mohammed, A.S.; Alexakis, D.E.; Mamou, A.; Armaghani, D.J. Introducing stacking machine learning approaches for the prediction of rock deformation. Transp. Geotech. 2022, 34, 100756. [Google Scholar] [CrossRef]
- Werther, M.; Spyrakos, E.; Simis, S.G.H.; Odermatt, D.; Stelzer, K.; Krawczyk, H.; Berlage, O.; Hunter, P.; Tyler, A. Meta-classification of remote sensing reflectance to estimate trophic status of inland and nearshore waters. J. Photogramm. Remote Sens. 2021, 176, 109–126. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Nguyen, H.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Cao, J.; Hou, Z.-Y.; Li, Z.-K.; Zheng, B.-H.; Chu, Z.-S. Spatiotemporal dynamics of phytoplankton biomass and community succession for driving factors in a meso-eutrophic lake. J. Environ. Manag. 2023, 345, 118693. [Google Scholar] [CrossRef]
- Zou, W.; Zhu, G.; Xu, H.; Zhu, M.; Qin, B.; Zhang, Y.; Bi, Y.; Liu, M.; Wu, T. Elucidating phytoplankton limiting factors in lakes and reservoirs of the Chinese Eastern Plains ecoregion. J. Environ. Manag. 2022, 318, 115542. [Google Scholar] [CrossRef]
- Laura Sanchez, M.; Izaguirre, I.; Zagarese, H.; Romina Schiaffino, M.; Castro Berman, M.; Lagomarsino, L.; Chaparro, G.; Balina, S.; Solange Vera, M.; Spence Cheruvelil, K. Drivers of planktonic chlorophyll a in pampean shallow lakes. Ecol. Indic. 2023, 146, 109834. [Google Scholar] [CrossRef]
- Zeng, C.; Richardson, M.; King, D.J. The impacts of environmental variables on water reflectance measured using a lightweight unmanned aerial vehicle (UAV)-based spectrometer system. J. Photogramm. Remote Sens. 2017, 130, 217–230. [Google Scholar] [CrossRef]
- Li, X.; Huang, T.; Ma, W.; Sun, X.; Zhang, H. Effects of rainfall patterns on water quality in a stratified reservoir subject to eutrophication: Implications for management. Sci. Total Environ. 2015, 521, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Z.; Li, Z.; Ma, W.; Nie, X. Response of organic carbon in drainage ditch water to rainfall events in Zoige Basin in the Qinghai-Tibet Plateau. J. Hydrol. 2019, 579, 124187. [Google Scholar] [CrossRef]
- Wang, P.; Chen, B.; Yuan, R.; Li, C.; Li, Y. Characteristics of aquatic bacterial community and the influencing factors in an urban river. Sci. Total Environ. 2016, 569, 382–389. [Google Scholar] [CrossRef]
- Yeh, C.-S.; Wang, R.; Chang, W.-C.; Shih, Y.-H. Synthesis and characterization of stabilized oxygen-releasing CaO2 nanoparticles for bioremediation. J. Environ. Manag. 2018, 212, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Feng, J.; Wang, Y. Chlorophyll a predictability and relative importance of factors governing lake phytoplankton at different timescales. Sci. Total Environ. 2019, 648, 472–480. [Google Scholar] [CrossRef]
- Bonelli, A.G.; Vantrepotte, V.; Jorge, D.S.F.; Demaria, J.; Jamet, C.; Dessailly, D.; Mangin, A.; d’Andon, O.F.; Kwiatkowska, E.; Loisel, H. Colored dissolved organic matter absorption at global scale from ocean color radiometry observation: Spatio-temporal variability and contribution to the absorption budget. Remote Sens. Environ. 2021, 265, 112637. [Google Scholar] [CrossRef]








| Evaluation Indicator | Method | Chla | SD | CODMn | TN | TP |
|---|---|---|---|---|---|---|
| R2 | FC-GA | 0.77 | 0.72 | 0.76 | 0.55 | 0.70 |
| PC | 0.72 | 0.62 | 0.62 | 0.50 | 0.19 | |
| RFE | 0.73 | 0.82 | 0.76 | 0.28 | 0.56 | |
| RMSE | FC-GA | 2.53 | 10.38 | 0.22 | 0.19 | 0.10 |
| PC | 2.80 | 12.01 | 0.29 | 0.21 | 0.17 | |
| RFE | 2.75 | 8.22 | 0.22 | 0.25 | 0.13 | |
| VIF_min | FC-GA | 1.17 | 2.61 | 3.88 | 1.62 | 1.28 |
| PC | 62.49 | 51.05 | * | 67.23 | * | |
| RFE | 3.28 | 1.04 | 3.13 | 2.48 | 1.56 | |
| VIF_max | FC-GA | 9.49 | 9.65 | 7.04 | 8.04 | 2.63 |
| PC | * | * | * | * | * | |
| RFE | 36.65 | 56.94 | 22.07 | 11.16 | 17.62 |
| WQPs | ML | |
|---|---|---|
| Base-Model | Mate-Model | |
| Chla | NNR, LightGBM, BRR, | NNR |
| SD | SVR, NNR, MLP, BRR | SVR |
| CODMn | RF, NNR, CART | MLP |
| TN | NNR, LightGBM, RF, CART | MLP |
| TP | LightGBM | LightGBM |
| WQPs | Evaluation Indicators | BRR | SVR | NNR | CART | RF | LightGBM | MLP | EML-1 | EML-2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Chla | R2 | 0.74 | 0.78 | 0.81 | 0.72 | 0.73 | 0.78 | 0.66 | 0.86 | 0.83 |
| RMSE (mg m−3) | 2.69 | 2.51 | 2.30 | 2.82 | 2.74 | 2.48 | 3.11 | 2.02 | 2.16 | |
| MRE/% | 23.71 | 19.98 | 19.03 | 21.62 | 24.80 | 19.71 | 24.51 | 13.66 | 14.87 | |
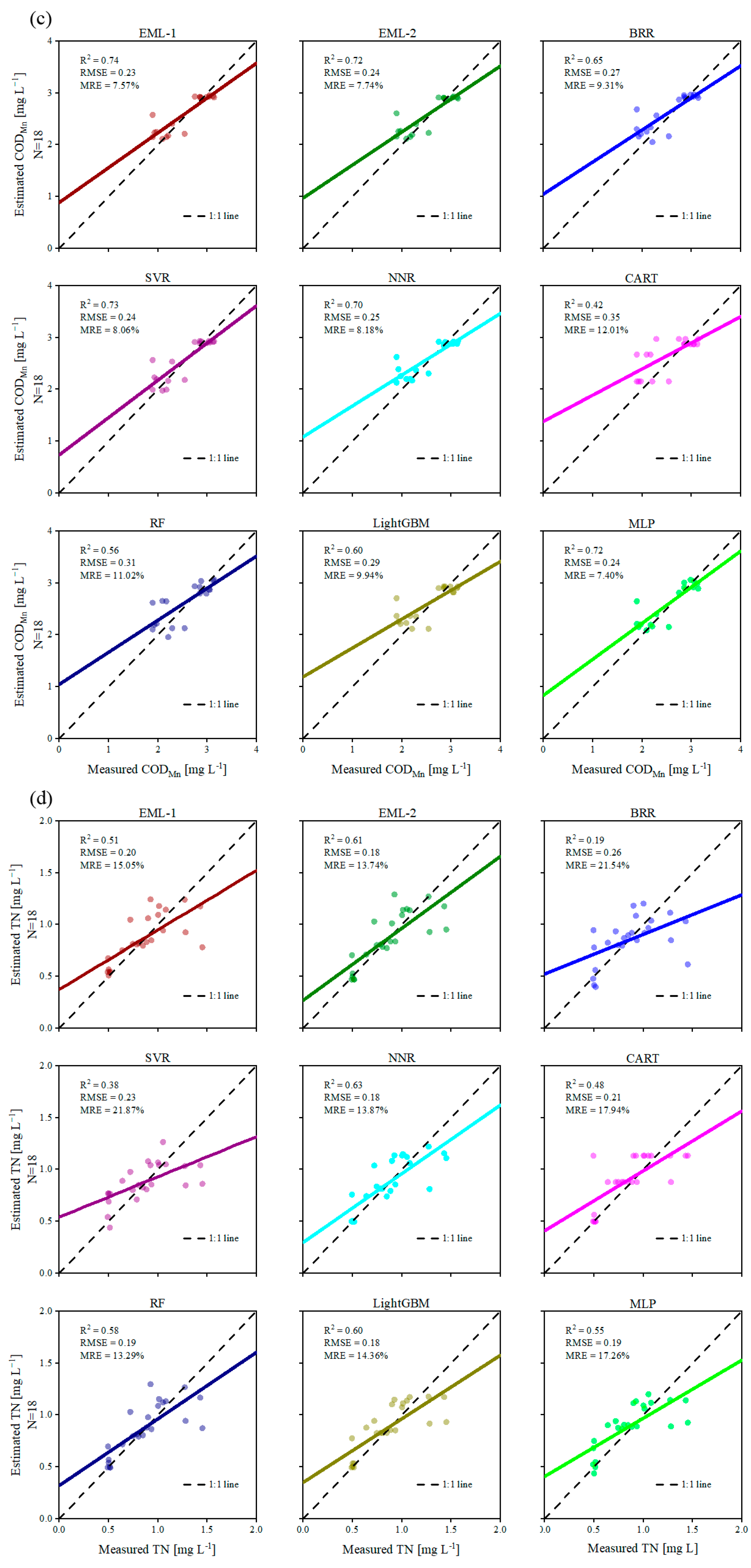
| CODMn | R2 | 0.65 | 0.73 | 0.70 | 0.42 | 0.56 | 0.60 | 0.72 | 0.74 | 0.72 |
| RMSE/ (mg L−1) | 0.27 | 0.24 | 0.25 | 0.35 | 0.31 | 0.29 | 0.24 | 0.23 | 0.24 | |
| MRE/% | 9.31 | 8.06 | 8.18 | 12.01 | 11.02 | 9.94 | 7.40 | 7.57 | 7.74 | |
| SD | R2 | 0.52 | 0.53 | 0.73 | 0.73 | 0.81 | 0.60 | 0.58 | 0.89 | 0.90 |
| RMSE/ (cm) | 13.52 | 13.37 | 10.13 | 10.15 | 8.56 | 12.36 | 12.55 | 6.51 | 6.14 | |
| MRE/% | 37.08 | 34.07 | 24.09 | 27.71 | 21.69 | 28.68 | 30.75 | 19.35 | 16.34 | |
| TN | R2 | 0.19 | 0.38 | 0.63 | 0.48 | 0.58 | 0.60 | 0.55 | 0.51 | 0.61 |
| RMSE/ (mg L−1) | 0.26 | 0.23 | 0.18 | 0.21 | 0.19 | 0.18 | 0.19 | 0.20 | 0.18 | |
| MRE/% | 21.54 | 21.87 | 13.87 | 17.94 | 13.29 | 14.36 | 17.26 | 15.05 | 13.74 | |
| TP | R2 | 0.24 | 0.50 | 0.54 | 0.29 | 0.62 | 0.76 | -1.05 | 0.74 | 0.83 |
| RMSE/ (mg L−1) | 0.16 | 0.13 | 0.13 | 0.16 | 0.12 | 0.09 | 0.27 | 0.10 | 0.08 | |
| MRE/% | 87.40 | 150.65 | 38.27 | 39.74 | 32.03 | 47.90 | 127.16 | 42.06 | 22.29 |
| Methods | Chla | CODMn | SD | TN | TP |
|---|---|---|---|---|---|
| ML | 1.86 | 0.19 | 10.80 | 0.12 | 0.056 |
| EML | 1.30 | 0.17 | 4.65 | 0.13 | 0.042 |
| WQPs | Class (AR) | ||
|---|---|---|---|
| Low | Medium | High | |
| Chla | 1.14 | 1.07 | 1.68 |
| SD | 6.89 | 2.76 | 4.31 |
| CODMn | 0.26 | 0.14 | 0.12 |
| TN | 0.09 | 0.10 | 0.19 |
| TP | 0.013 | 0.056 | 0.063 |
| WQPs | Model | 0 ≤ μ ≤ 0.2 Very Good | 0.2 < μ ≤ 0.3 Good | 0.3 < μ ≤ 0.4 Middle | 0.4 < μ ≤ 0.5 General | μ > 0.5 Poor | Proportion of μ ≤ 0.5 |
|---|---|---|---|---|---|---|---|
| OAPs | MLP | 19 | 5 | 3 | 2 | 7 | 0.81 |
| BRR | 16 | 6 | 5 | 3 | 6 | 0.83 | |
| CART | 17 | 7 | 5 | 2 | 5 | 0.86 | |
| NNR | 21 | 5 | 5 | 2 | 3 | 0.92 | |
| LightGBM | 16 | 13 | 1 | 2 | 4 | 0.89 | |
| RF | 21 | 5 | 2 | 3 | 5 | 0.86 | |
| SVR | 18 | 9 | 2 | 3 | 4 | 0.89 | |
| EML-1 | 27 | 4 | 2 | 1 | 2 | 0.94 | |
| EML-2 | 27 | 3 | 3 | 1 | 2 | 0.94 | |
| NOAPs | MLP | 37 | 5 | 6 | 2 | 8 | 0.86 |
| BRR | 34 | 7 | 2 | 3 | 12 | 0.79 | |
| CART | 37 | 11 | 4 | 1 | 5 | 0.91 | |
| NNR | 42 | 6 | 2 | 2 | 6 | 0.90 | |
| LightGBM | 43 | 4 | 5 | 1 | 5 | 0.91 | |
| RF | 42 | 4 | 3 | 6 | 3 | 0.95 | |
| SVR | 33 | 4 | 6 | 3 | 12 | 0.79 | |
| EML-1 | 44 | 2 | 3 | 2 | 7 | 0.88 | |
| EML-2 | 46 | 3 | 4 | 3 | 2 | 0.97 |
| Parameters | OAPs | NOAPs | |||
|---|---|---|---|---|---|
| Chla | SD | CODMn | TN | TP | |
| EML-1 | 13.66% | 19.35% | 7.57% | 15.05% | 42.06% |
| EML-2 | 14.87% | 16.34% | 7.74% | 13.74% | 22.29% |
| Season | Chla | SD | CODMn | TN | TP | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | std | Mean | std | Mean | std | Mean | std | Mean | std | |
| rainy | 12.97 | 1.64 | 45.22 | 5.60 | 2.15 | 0.15 | 1.09 | 0.07 | 0.120 | 0.030 |
| dry | 7.89 | 2.10 | 56.16 | 6.93 | 2.28 | 0.14 | 0.98 | 0.21 | 0.068 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Jiang, J.; Deng, Z.; Wu, D.; Wang, F.; Lai, C.; Wang, Z.; Chen, X. An Ensemble Machine Learning Model to Estimate Urban Water Quality Parameters Using Unmanned Aerial Vehicle Multispectral Imagery. Remote Sens. 2024, 16, 2246. https://doi.org/10.3390/rs16122246
Lei X, Jiang J, Deng Z, Wu D, Wang F, Lai C, Wang Z, Chen X. An Ensemble Machine Learning Model to Estimate Urban Water Quality Parameters Using Unmanned Aerial Vehicle Multispectral Imagery. Remote Sensing. 2024; 16(12):2246. https://doi.org/10.3390/rs16122246
Chicago/Turabian StyleLei, Xiangdong, Jie Jiang, Zifeng Deng, Di Wu, Fangyi Wang, Chengguang Lai, Zhaoli Wang, and Xiaohong Chen. 2024. "An Ensemble Machine Learning Model to Estimate Urban Water Quality Parameters Using Unmanned Aerial Vehicle Multispectral Imagery" Remote Sensing 16, no. 12: 2246. https://doi.org/10.3390/rs16122246
APA StyleLei, X., Jiang, J., Deng, Z., Wu, D., Wang, F., Lai, C., Wang, Z., & Chen, X. (2024). An Ensemble Machine Learning Model to Estimate Urban Water Quality Parameters Using Unmanned Aerial Vehicle Multispectral Imagery. Remote Sensing, 16(12), 2246. https://doi.org/10.3390/rs16122246








