Variable Doppler Starting Point Keystone Transform for Radar Maneuvering Target Detection
Abstract
1. Introduction
1.1. Review
1.2. Motivation
- The compensation flexibility of KT is improved by transforming the Doppler ambiguity compensation function from an integer form to a fractional form, allowing the compensation bands to be adjusted as needed.
- The HBVE in sinc interpolation is efficiently addressed by defining the effective gain portion in compensation Doppler bands as new bands through changing their connection points.
- The efficiency of KT in compensating for NDFRs is significantly improved by adjusting the compensation band to cover a NDFR, reducing the calculation times from two to one when the NDFR spans two compensation Doppler bands.
2. Comprehensive Analysis of Issues in KT
2.1. Signal Model and Keystone Transform
2.1.1. Signal Model
2.1.2. Keystone Transform
2.2. Issues of “Half-Blind-Velocity” Effect
2.2.1. Sinc Interpolation
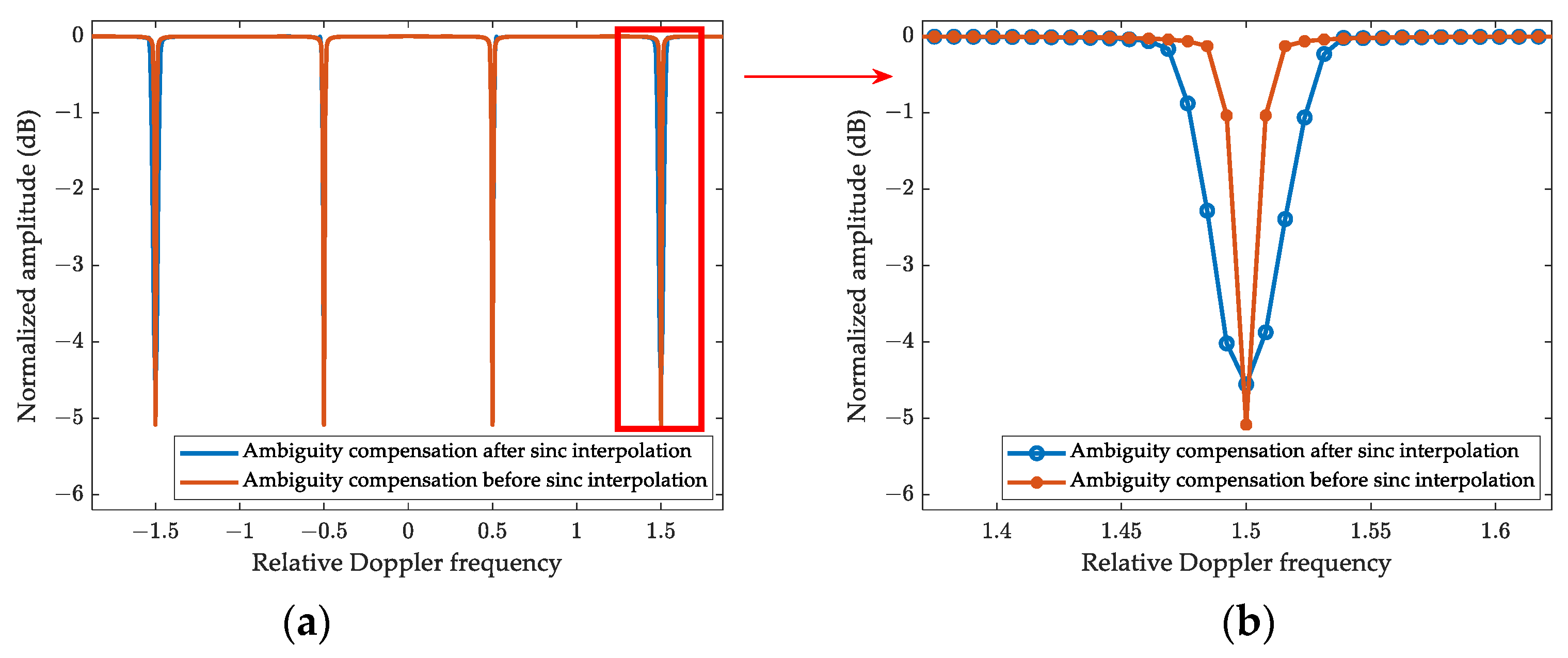
2.2.2. “Half-Blind-Velocity” Effect
| Parameter | Symbol | Value |
|---|---|---|
| Carrier Frequency | 500 MHz | |
| Bandwidth | B | 20 MHz |
| Pulse duration | 4 | |
| Pulse repetition frequency | 1 KHz | |
| Sampling rate | 160 MHz | |
| Fast-time frequency sampling points | L | 4096 |
| Integrated pulse number | N | 128 |
| Number of points in sinc interpolation, CZT and Doppler filtering | M | 128 |
2.2.3. Existing Methods to Address the HBVE
2.3. Issues Related to Narrow Doppler Frequency Range
2.3.1. Chirp-z Transform
2.3.2. Narrow Doppler Frequency Range
3. The Proposed VDSPKT Method
3.1. VDSPKT Implemented by Sinc Interpolation (VDSPKT-SI)
3.2. VDSPKT Implemented by CZT (VDSPKT-CZT)
4. Simulation Experiments
4.1. Effectiveness in Addressing the HBVE
4.1.1. Effectiveness for HBV Points
4.1.2. Effectiveness in Solving the HBVE
4.1.3. Computational Complexity
4.2. The Effectiveness of VDSPKT-CZT
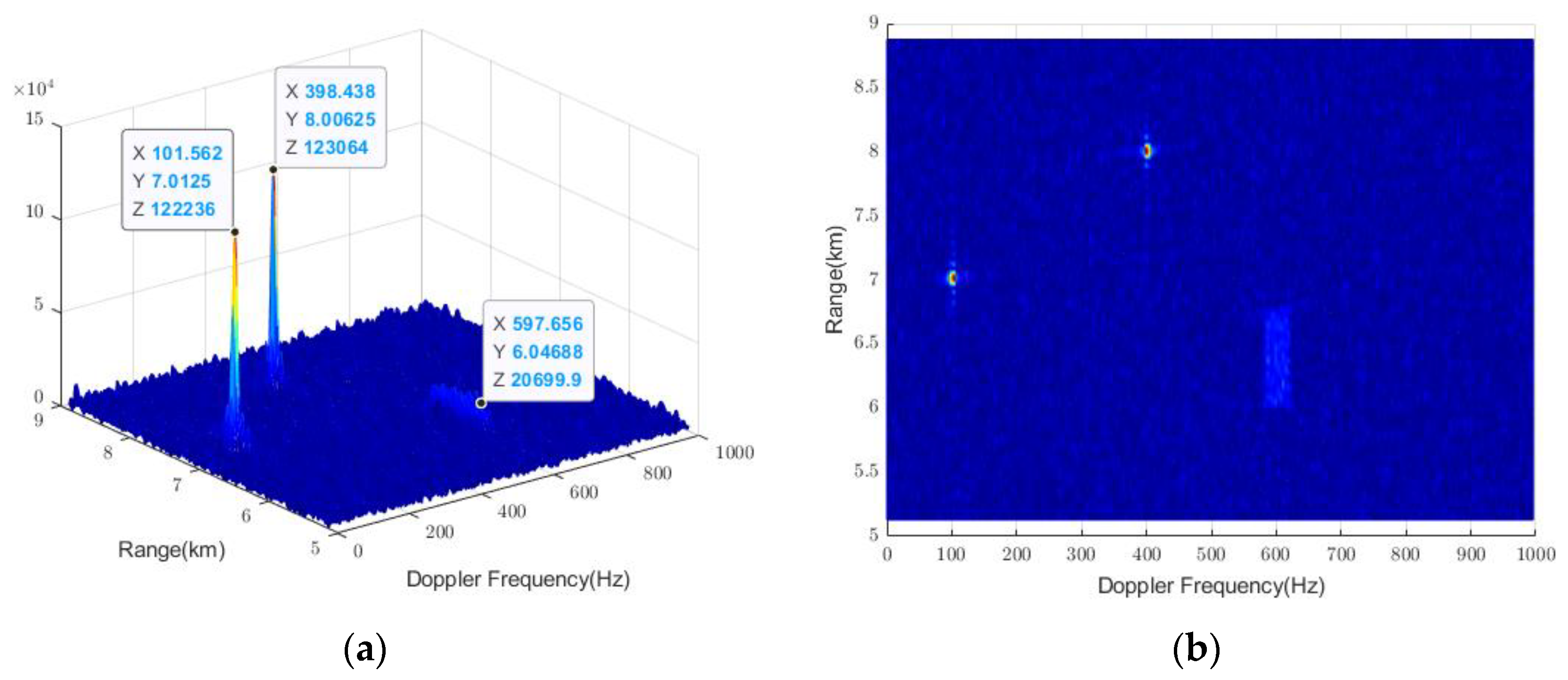
5. Verification with Real Radar Data
5.1. Effectiveness in Addressing the HBVE
5.2. The Effectiveness of VDSPKT-CZT
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Guan, J.; Zheng, J.; Zhang, Y.; Yu, X. Radar Fast Long-Time Coherent Integration via TR-SKT and Robust Sparse FRFT. J. Syst. Eng. Electron. 2023, 34, 1116–1129. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, Z.; Cui, G.; Yeo, T.S. Coherent Integration and Parameter Estimation for High-Speed Target Detection With Bistatic MIMO Radar. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, J.; Du, X.; Liu, Q.H. Radar High-Speed Maneuvering Target Detection Based on Three-Dimensional Scaled Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2821–2833. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.-G.; Ma, J.-T.; Ma, J. Long-Time Coherent Integration for Weak Maneuvering Target Detection and High-Order Motion Parameter Estimation Based on Keystone Transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Liu, H.; Liao, G.; Liu, Z.; Liu, Q.H. Radar High-Speed Target Detection Based on the Frequency-Domain Deramp-Keystone Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 285–294. [Google Scholar] [CrossRef]
- Kong, L.; Li, X.; Cui, G.; Yi, W.; Yang, Y. Coherent Integration Algorithm for a Maneuvering Target with High-Order Range Migration. IEEE Trans. Signal Process. 2015, 63, 4474–4486. [Google Scholar] [CrossRef]
- Tian, J.; Cui, W.; Wu, S. A Novel Method for Parameter Estimation of Space Moving Targets. IEEE Geosci. Remote Sens. Lett. 2014, 11, 389–393. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.-G.; Wu, Y.; Bao, Z. Robust Ground Moving-Target Imaging Using Deramp–Keystone Processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Carlson, B.D.; Evans, E.D.; Wilson, S.L. Search Radar Detection and Track with the Hough Transform. I. System Concept. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 102–108. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L.; Yang, X. Computationally Efficient Coherent Detection and Parameter Estimation Algorithm for Maneuvering Target. Signal Process. 2019, 155, 130–142. [Google Scholar] [CrossRef]
- Jin, K.; Li, G.; Lai, T.; Jin, T.; Zhao, Y. A Novel Long-Time Coherent Integration Algorithm for Doppler-Ambiguous Radar Maneuvering Target Detection. IEEE Sens. J. 2020, 20, 9394–9407. [Google Scholar] [CrossRef]
- Sadjadi, F. New Comparative Experiments in Range Migration Mitigation Methods Using Polarimetric Inverse Synthetic Aperture Radar Signatures of Small Boats. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0613–0616. [Google Scholar]
- Wan, R.; Song, Y.; Mu, T.; Wang, Z. Moving Target Detection Using the 2D-FFT Algorithm for Automotive FMCW Radars. In Proceedings of the 2019 International Conference on Communications, Information System and Computer Engineering (CISCE), Haikou, China, 5–7 July 2019; IEEE: Haikou, China, 2019; pp. 239–243. [Google Scholar]
- Yu, J.; Xu, J.; Peng, Y. Performance Analysis of Long-Time Coherent Integration for Moving Targets. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xian, China, 26–30 October 2009; IEEE: Xian, China, 2009; pp. 197–200. [Google Scholar]
- Wang, D.; Bao, Q.; Niu, Z.; Chen, Z. Long Time Coherent Integration Method for Frequency Agile Radar. In Proceedings of the 2014 11th European Radar Conference, Rome, Italy, 8–10 October 2014; IEEE: Rome, Italy, 2014; pp. 553–556. [Google Scholar]
- Wang, G. The Minimum Entropy Criterion of Range Alignment in ISAR Motion Compensation; IET: Edinburgh, UK, 1997; pp. 236–239. [Google Scholar]
- Chen, C.-C.; Andrews, H. Target-Motion-Induced Radar Imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, AES-16, 2–14. [Google Scholar] [CrossRef]
- Delisle, G.Y.; Wu, H. Moving Target Imaging and Trajectory Computation Using ISAR. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 887–899. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier Transform for Radar Target Detection (II): Blind Speed Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier Transform for Radar Target Detection (III): Optimality and Fast Implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.-G.; Peng, S.-B.; Yu, J.; Peng, Y.-N.; Qian, L.-C. Radar Maneuvering Target Motion Estimation Based on Generalized Radon-Fourier Transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Sun, Z.; Cui, G.; Yeo, T.S. Multi-Frame Integration Method for Radar Detection of Weak Moving Target. IEEE Trans. Veh. Technol. 2021, 70, 3609–3624. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A Fast Maneuvering Target Motion Parameters Estimation Algorithm Based on ACCF. IEEE Signal Process. Lett. 2015, 22, 270–274. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Detection of Maneuvering Target with Complex Motions Based on ACCF and FRFT. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 0017–0020. [Google Scholar]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. SAR Imaging of Moving Targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Jungang, Y.; Xiaotao, H.; Tian, J.; Thompson, J.; Zhimin, Z. New Approach for SAR Imaging of Ground Moving Targets Based on a Keystone Transform. IEEE Geosci. Remote Sens. Lett. 2011, 8, 829–833. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.-G.; Peng, Y.-N. Doppler Keystone Transform: An Approach Suitable for Parallel Implementation of SAR Moving Target Imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.-G.; Peng, Y.-N. Doppler Keystone Transform for SAR Imaging of Moving Targets. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; pp. 716–719. [Google Scholar]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for Single Channel SAR Ground Moving Target Imaging and Motion Parameter Estimation. IET Radar Sonar Navig. 2007, 1, 59–66. [Google Scholar] [CrossRef]
- Shi, H.; Liu, Y.; Guo, J.; Liu, M. ISAR Autofocus Imaging Algorithm for Maneuvering Targets Based on Deep Learning and Keystone Transform. J. Syst. Eng. Electron. 2020, 31, 1178–1185. [Google Scholar] [CrossRef]
- Huo, K.; Liu, Y.; Hu, J.; Jiang, W.; Li, X. A Novel Imaging Method for Fast Rotating Targets Based on the Segmental Pseudo Keystone Transform. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1464–1472. [Google Scholar] [CrossRef]
- Li, Y.; Xing, M.; Su, J.; Quan, Y.; Bao, Z. A New Algorithm of ISAR Imaging for Maneuvering Targets with Low SNR. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 543–557. [Google Scholar] [CrossRef]
- Zhang, S.-s.; Zeng, T.; Long, T.; Yuan, H.-p. Dim Target Detection Based on Keystone Transform. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 889–894. [Google Scholar]
- Zhu, D.; Li, Y.; Zhu, Z. A Keystone Transform Without Interpolation for SAR Ground Moving-Target Imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Huang, L.; Yang, R. Low Complexity Keystone Transform without Interpolation for Dim Moving Target Detection. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; pp. 1745–1748. [Google Scholar]
- Shan, T.; Liu, S.; Zhang, Y.D.; Amin, M.G.; Tao, R.; Feng, Y. Efficient Architecture and Hardware Implementation of Coherent Integration Processor for Digital Video Broadcast-based Passive Bistatic Radar. IET Radar Sonar Navig. 2016, 10, 97–106. [Google Scholar] [CrossRef]
- Kirkland, D. Imaging Moving Targets Using the Second-Order Keystone Transform. IET Radar Sonar Navig. 2011, 5, 902–910. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Tang, J.; Peng, Y. An Improved Keystone-Transform Based Method for Long-Time Coherent Integration of Radar Target. Radar Sci. Technol. 2008, 6, 454–458. [Google Scholar]
- Hong, Y.; Gao, M.; Wang, J.; Qin, G. The Suppression and Elimination of Half Blind Velocity Effect Associated with Keystone Transform. J. Electron. Inf. Technol. 2014, 36, 175–180. [Google Scholar] [CrossRef]
- Sun, Q.; Shan, T.; Feng, Y.; He, S.; Bai, X.; Zhang, H. A Frequency Domain Clutter Suppression Approach for Passive Radar. IEEE Sens. J. 2024, 24, 14916–14929. [Google Scholar] [CrossRef]
















| Target Number | Initial Range | Radial Velocity | Doppler Centroid |
|---|---|---|---|
| 1 | 8 km | 120 m/s | 400 Hz |
| 2 | 7 km | 30 m/s | 100 Hz |
| 3 | 6 km | −120 m/s | −400 Hz |
| Parameter | Symbol | Value |
|---|---|---|
| Carrier Frequency | 674 MHz | |
| Bandwidth | B | 7.56 MHz |
| Pulse repetition frequency | 612 Hz | |
| Baseband sampling rate | 9 MHz | |
| Fast-time frequency sampling points | L | 128 |
| Integrated pulse number | N | 1024 |
| Number of points in sinc interpolation, CZT and Doppler filtering | M | 1024 |
| Target equivalent radial velocity | v | −136 m/s |
| Doppler Centroid | −305.5 Hz |
| Parameter | Symbol | Value |
|---|---|---|
| Carrier Frequency | 554 MHz | |
| Bandwidth | B | 7.56 MHz |
| Pulse repetition frequency | 1 kHz | |
| Baseband sampling rate | 10 MHz | |
| Fast-time frequency sampling points | L | 128 |
| Integrated pulse number | N | 4096 |
| Number of points in sinc interpolation, CZT and Doppler filtering | M | 4096 |
| Target Number | Initial Range | Equivalent Radial Velocity | Doppler Centroid |
|---|---|---|---|
| 1 | 0.35 km | 14.3 m/s | 26.4 Hz |
| 2 | 1.05 km | −20.9 m/s | −38.6 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Feng, Y.; Qiao, X.; Wang, T.; Shan, T. Variable Doppler Starting Point Keystone Transform for Radar Maneuvering Target Detection. Remote Sens. 2024, 16, 2129. https://doi.org/10.3390/rs16122129
Jia W, Feng Y, Qiao X, Wang T, Shan T. Variable Doppler Starting Point Keystone Transform for Radar Maneuvering Target Detection. Remote Sensing. 2024; 16(12):2129. https://doi.org/10.3390/rs16122129
Chicago/Turabian StyleJia, Wei, Yuan Feng, Xingshuai Qiao, Tianrun Wang, and Tao Shan. 2024. "Variable Doppler Starting Point Keystone Transform for Radar Maneuvering Target Detection" Remote Sensing 16, no. 12: 2129. https://doi.org/10.3390/rs16122129
APA StyleJia, W., Feng, Y., Qiao, X., Wang, T., & Shan, T. (2024). Variable Doppler Starting Point Keystone Transform for Radar Maneuvering Target Detection. Remote Sensing, 16(12), 2129. https://doi.org/10.3390/rs16122129







