Scenario-Based Simulation of Impervious Surfaces for Detecting the Effects of Landscape Patterns on Urban Waterlogging
Abstract
1. Introduction
2. Materials and Methods
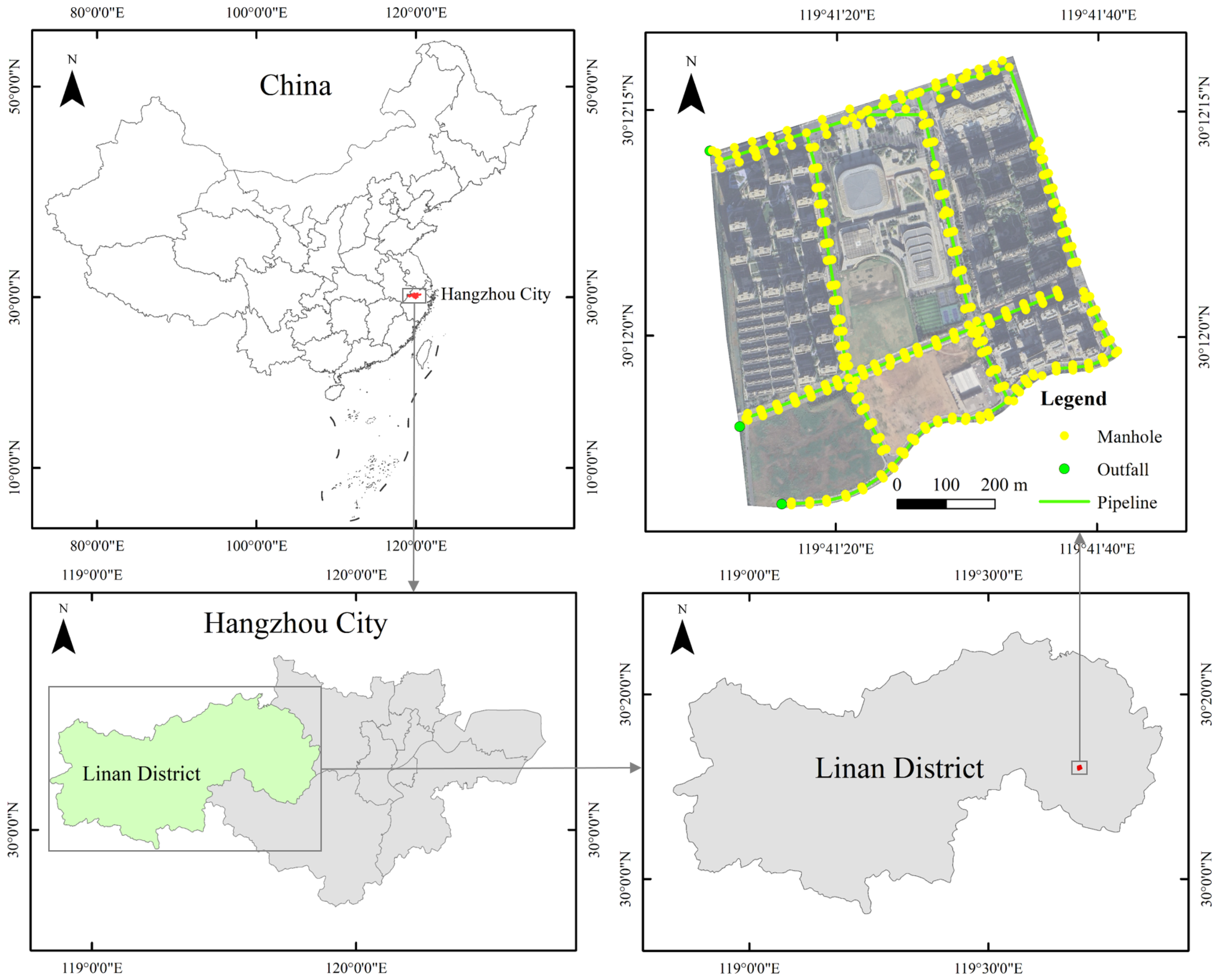
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. Data Sources and Pre-Processing
2.2.2. Designed Rainfall Events
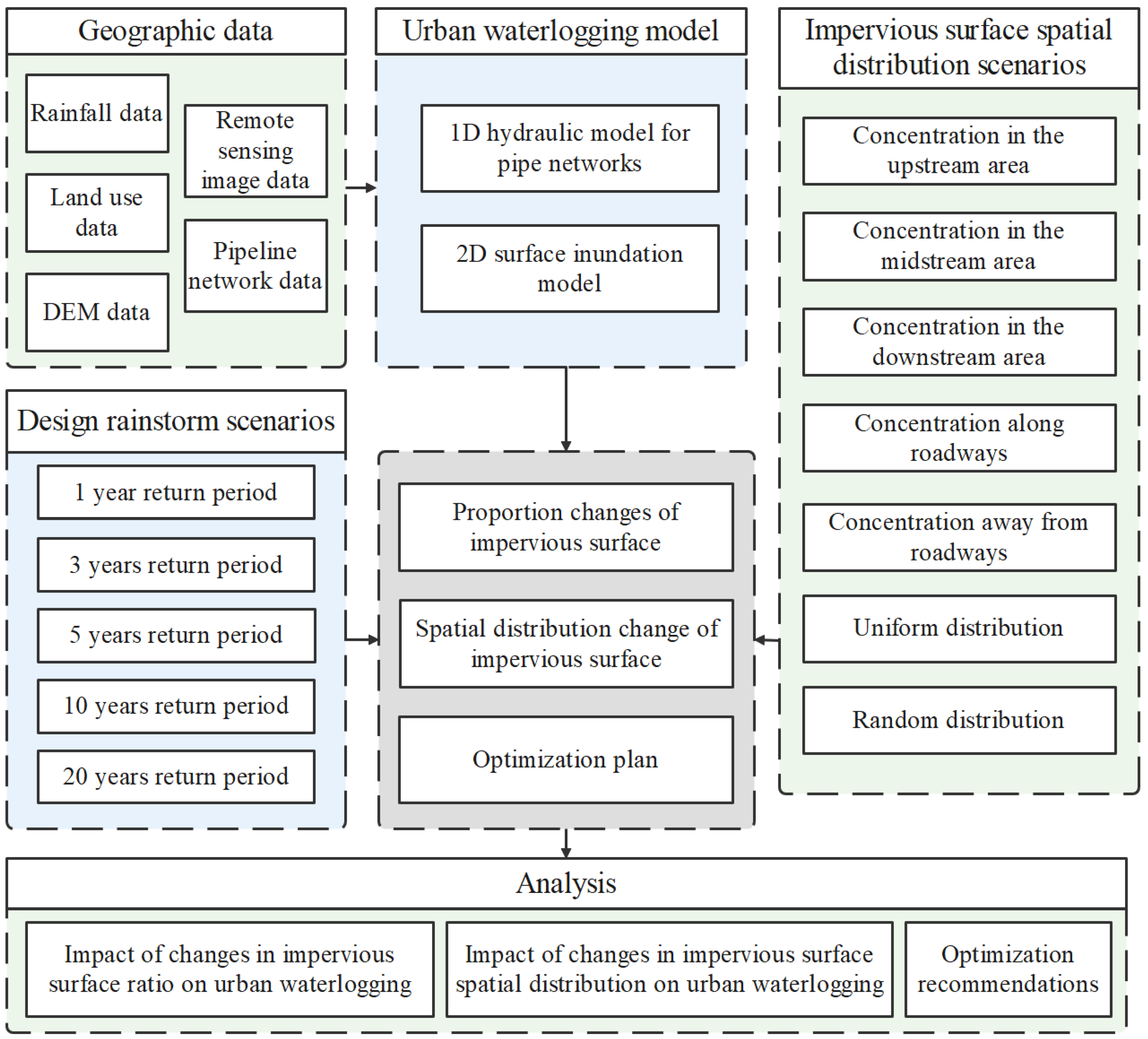
2.3. Overall Flow
2.4. Model Construction
2.5. Scenario Design for the Spatial Distribution of Impervious Surfaces
2.6. Optimization Plan for Impervious Surfaces
3. Results
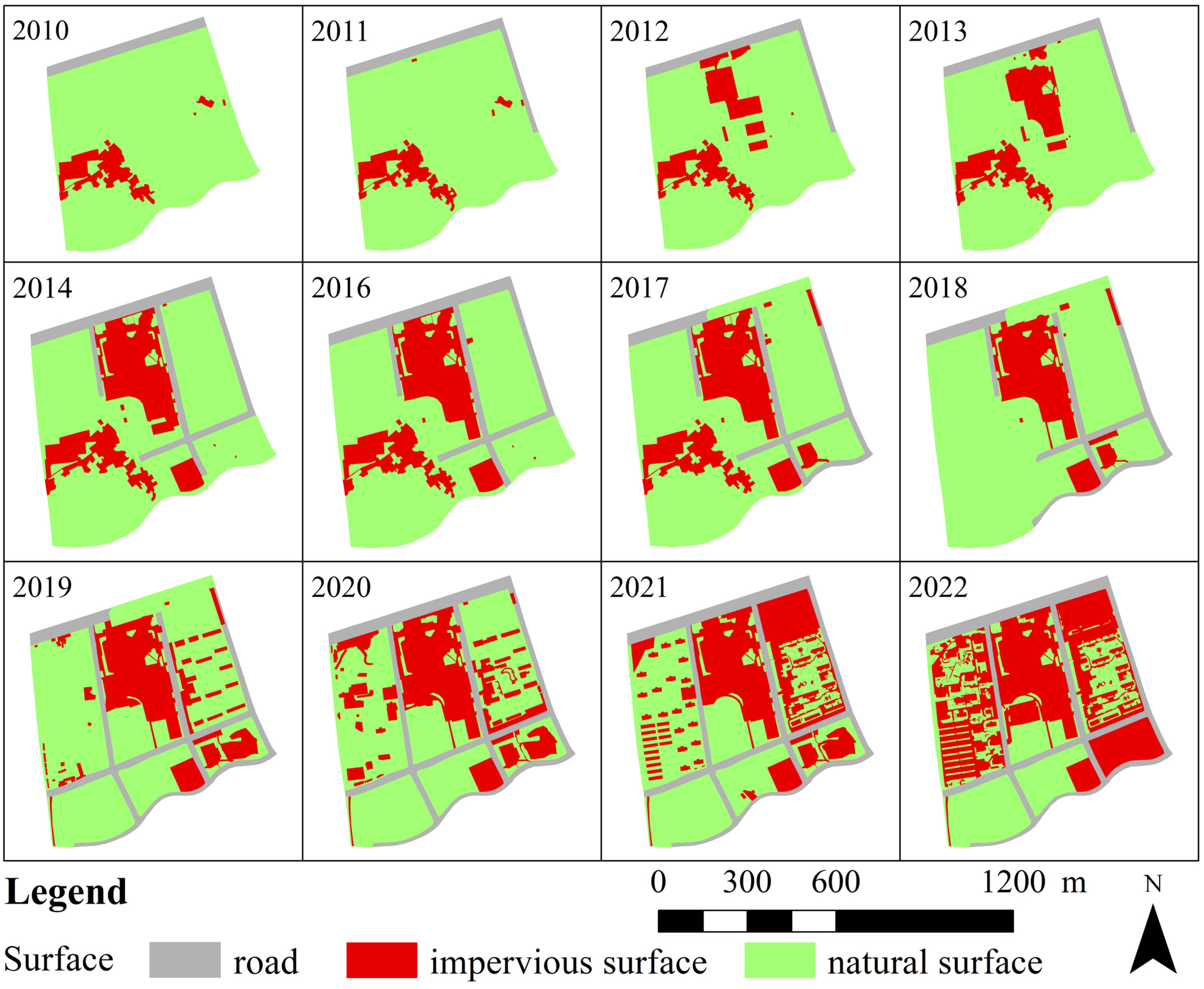
3.1. Proportion Changes in Impervious Surfaces
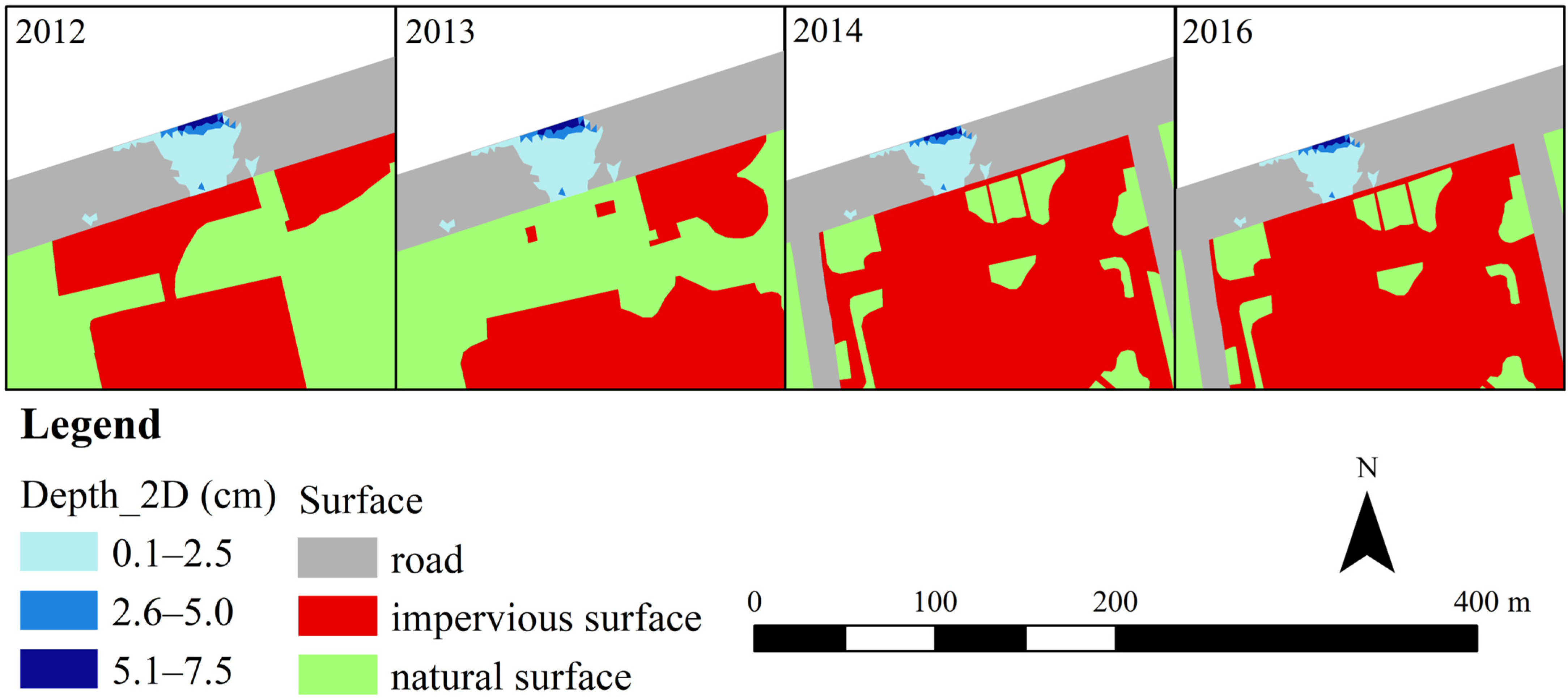
3.2. Spatial Distribution Changes in Impervious Surfaces
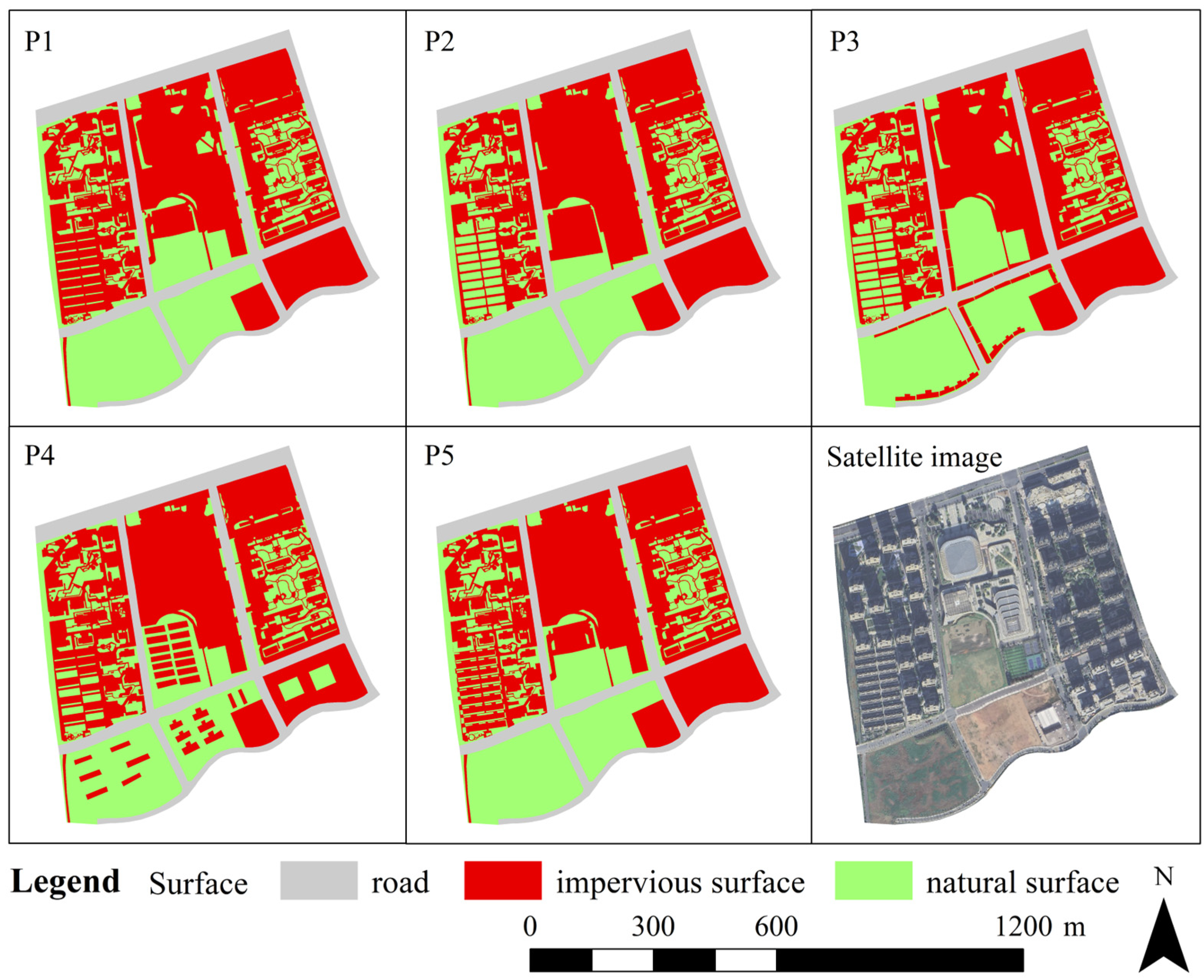
3.3. Impervious Surface Optimization Plan Design
4. Discussion
4.1. Urban Waterlogging Characteristics with Different Impervious Surfaces Ratios
4.2. Urban Waterlogging Characteristics under Different Spatial Distributions of Impervious Surfaces
4.3. Optimization Plans and Suggestions
4.4. Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hermanns, T.; Li, Q. Sustainability Impact Assessment of Land Use Changes in the Anthropocene. In The Anthropocene Debate and Political Science; Routledge: London, UK, 2018; ISBN 978-1-351-17412-1. [Google Scholar]
- El Kasri, J.; Lahmili, A.; Soussi, H.; Jaouda, I.; Bentaher, M. Trend Analysis of Meteorological Variables: Rainfall and Temperature. Civ. Eng. J. 2021, 7, 1868–1879. [Google Scholar] [CrossRef]
- Broekx, S.; Smets, S.; Liekens, I.; Bulckaen, D.; De Nocker, L. Designing a Long-Term Flood Risk Management Plan for the Scheldt Estuary Using a Risk-Based Approach. Nat. Hazards 2011, 57, 245–266. [Google Scholar] [CrossRef]
- Garcia, E.S.; Loáiciga, H.A. Sea-Level Rise and Flooding in Coastal Riverine Flood Plains. Hydrol. Sci. J. 2014, 59, 204–220. [Google Scholar] [CrossRef]
- Güneralp, B.; Güneralp, İ.; Liu, Y. Changing Global Patterns of Urban Exposure to Flood and Drought Hazards. Glob. Environ. Change 2015, 31, 217–225. [Google Scholar] [CrossRef]
- Smit, W. Urbanization in the Global South. In Oxford Research Encyclopedia of Global Public Health; Oxford University Press: Oxford, UK, 2021; ISBN 978-0-19-063236-6. [Google Scholar]
- Gu, C. Urbanization: Processes and Driving Forces. Sci. China Earth Sci. 2019, 62, 1351–1360. [Google Scholar] [CrossRef]
- Bai, X.; Shi, P.; Liu, Y. Society: Realizing China’s Urban Dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef]
- Pan, Y.; Teng, T.; Wang, S.; Wang, T. Impact and Mechanism of Urbanization on Urban Green Development in the Yangtze River Economic Belt. Ecol. Indic. 2024, 158, 111612. [Google Scholar] [CrossRef]
- McCarthy, M.P.; Best, M.J.; Betts, R.A. Climate Change in Cities Due to Global Warming and Urban Effects. Geophys. Res. Lett. 2010, 37, 2010GL042845. [Google Scholar] [CrossRef]
- Moazzam, M.F.U.; Rahman, G.; Munawar, S.; Tariq, A.; Safdar, Q.; Lee, B.-G. Trends of Rainfall Variability and Drought Monitoring Using Standardized Precipitation Index in a Scarcely Gauged Basin of Northern Pakistan. Water 2022, 14, 1132. [Google Scholar] [CrossRef]
- Wang, C.; Geng, L.; Rodríguez-Casallas, J.D. How and When Higher Climate Change Risk Perception Promotes Less Climate Change Inaction. J. Clean. Prod. 2021, 321, 128952. [Google Scholar] [CrossRef]
- Campagnolo, L.; De Cian, E. Distributional Consequences of Climate Change Impacts on Residential Energy Demand across Italian Households. Energy Econ. 2022, 110, 106020. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human Contribution to More-Intense Precipitation Extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Rohith, A.N.; Sudheer, K.P. A Novel Safe-Fail Framework for the Design of Urban Stormwater Drainage Infrastructures with Minimal Failure and Flood Severity. J. Hydrol. 2023, 627, 130393. [Google Scholar] [CrossRef]
- Liang, X.-Z. Extreme Rainfall Slows the Global Economy. Nature 2022, 601, 193–194. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, Y.; Zhang, C.; Tian, Y.; Guo, Z. Urban Flooding Prediction Method Based on the Combination of LSTM Neural Network and Numerical Model. Int. J. Environ. Res. Public Health 2023, 20, 1043. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; Guo, G.; Zhang, H.; Tarolli, P. Explicit the Urban Waterlogging Spatial Variation and Its Driving Factors: The Stepwise Cluster Analysis Model and Hierarchical Partitioning Analysis Approach. Sci. Total Environ. 2021, 763, 143041. [Google Scholar] [CrossRef]
- Cheng, T.; Xu, Z.; Hong, S.; Song, S. Flood Risk Zoning by Using 2D Hydrodynamic Modeling: A Case Study in Jinan City. Math. Probl. Eng. 2017, 2017, e5659197. [Google Scholar] [CrossRef]
- Huang, H.; Lei, X.; Liao, W.; Zuo, X.; Wang, H. A Novel Multi-Strategy Hydrological Feature Extraction (MHFE) Method to Improve Urban Waterlogging Risk Prediction, a Case Study of Fuzhou City in China. Sci. Total Environ. 2023, 904, 165834. [Google Scholar] [CrossRef]
- Ma, B.; Wu, Z.; Hu, C.; Wang, H.; Xu, H.; Yan, D. Process-Oriented SWMM Real-Time Correction and Urban Flood Dynamic Simulation. J. Hydrol. 2022, 605, 127269. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.; Wang, H.; Li, Z.; Yang, Z.; Shao, W.; Ding, X.; Weng, B.; Yu, Y.; Yan, D. Urban Flood Inundation and Damage Assessment Based on Numerical Simulations of Design Rainstorms with Different Characteristics. Sci. China E Technol. Sci. 2020, 63, 2292–2304. [Google Scholar] [CrossRef]
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Inundation Simulation for Urban Drainage Basin with Storm Sewer System. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, M.; Ma, Z.; Zhang, Z.; Yue, S.; Xiao, D.; Zhu, Z.; Wen, Y.; Lü, G. An Online Participatory System for SWMM-Based Flood Modeling and Simulation. Environ. Sci. Pollut. Res. 2022, 29, 7322–7343. [Google Scholar] [CrossRef] [PubMed]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Sensitivity of Peak Flow to the Change of Rainfall Temporal Pattern Due to Warmer Climate. J. Hydrol. 2018, 560, 546–559. [Google Scholar] [CrossRef]
- Xu, T.; Xie, Z.; Jiang, F.; Yang, S.; Deng, Z.; Zhao, L.; Wen, G.; Du, Q. Urban Flooding Resilience Evaluation with Coupled Rainfall and Flooding Models: A Small Area in Kunming City, China as an Example. Water Sci. Technol. 2023, 87, 2820–2839. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Cao, J.; Xu, R. Optimizing Low Impact Development for Stormwater Runoff Treatment: A Case Study in Yixing, China. Water 2023, 15, 989. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, H.; Liu, G.; Huang, M.; Xie, Z. Composite Scheme of Comprehensive Improvement for Urban Rivers. IOP Conf. Ser. Earth Environ. Sci. 2020, 546, 032005. [Google Scholar] [CrossRef]
- Chen, J.; Chang, K.; Karacsonyi, D.; Zhang, X. Comparing Urban Land Expansion and Its Driving Factors in Shenzhen and Dongguan, China. Habitat. Int. 2014, 43, 61–71. [Google Scholar] [CrossRef]
- Xu, T.; Xie, Z.; Zhao, F.; Li, Y.; Yang, S.; Zhang, Y.; Yin, S.; Chen, S.; Li, X.; Zhao, S.; et al. Permeability Control and Flood Risk Assessment of Urban Underlying Surface: A Case Study of Runcheng South Area, Kunming. Nat. Hazards 2022, 111, 661–686. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; Tarolli, P. Investigating the Role of Green Infrastructure on Urban WaterLogging: Evidence from Metropolitan Coastal Cities. Remote Sens. 2021, 13, 2341. [Google Scholar] [CrossRef]
- Basnet, K.; Chettri, K.; Parajuli, G.; Bhandari, A. Hydrological and Hydraulic Analyses of Urban Storm Water Drainage System of Major Area of Pokhara, Nepal. J. Innov. Eng. Educ. 2020, 3, 78–91. [Google Scholar] [CrossRef]
- Jiang, W.; Yu, J. Impact of Rainstorm Patterns on the Urban Flood Process Superimposed by Flash Floods and Urban Waterlogging Based on a Coupled Hydrologic–Hydraulic Model: A Case Study in a Coastal Mountainous River Basin within Southeastern China. Nat. Hazards 2022, 112, 301–326. [Google Scholar] [CrossRef]
- Deb, D.; Schneider, P.; Dudayev, Z.; Emon, A.; Areng, S.S.; Mozumder, M.M.H. Perceptions of Urban Pollution of River Dependent Rural Communities and Their Impact: A Case Study in Bangladesh. Sustainability 2021, 13, 13959. [Google Scholar] [CrossRef]
- Ning, Y.-F.; Zhang, J.-T.; Huang, J.-H.; Long, H.-F.; Huang, Q.-S. Systematic Treatment of Urban River Pollution. IOP Conf. Ser. Earth Environ. Sci. 2020, 446, 032021. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Jiang, L.; Huang, X.; Huang, D.; Dai, W.; Cai, Z.; Wang, D. Water Quality Status Response to Multiple Anthropogenic Activities in Urban River. Environ. Sci. Pollut. Res. 2023, 30, 3440–3452. [Google Scholar] [CrossRef]
- Ministry of Water Resources. Statistical Bulletin of Flood and Drought Disasters in China. Available online: http://www.mwr.gov.cn/sj/tjgb/zgshzhgb/ (accessed on 6 April 2024).
- Lin’an District Bureau of Statistics. Statistical Bulletin of National Economic and Social Development in Lin’an District of Hangzhou City in 2022. Available online: https://www.linan.gov.cn/art/2023/4/6/art_1229252926_4155359.html?eqid=85e8e9d800006c6a000000046435ac40 (accessed on 6 April 2024).
- Liao, D.; Zhu, H.; Zhou, J.; Wang, Y.; Sun, J. Study of the Natural Rainstorm Moving Regularity Method for Hyetograph Design. Theor. Appl. Climatol. 2019, 138, 1311–1321. [Google Scholar] [CrossRef]
- Keifer, C.J.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1332-1–1332-25. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Zhang, C. The Effect of Design Rainfall Patterns on Urban Flooding Based on the Chicago Method. Int. J. Environ. Res. Public Health 2023, 20, 4245. [Google Scholar] [CrossRef]
- Silveira, A.L.L.d. Cumulative Equations for Continuous Time Chicago Hyetograph Method. RBRH 2016, 21, 646–651. [Google Scholar] [CrossRef]
- Pan, C.; Wang, X.; Liu, L.; Huang, H.; Wang, D. Improvement to the Huff Curve for Design Storms and Urban Flooding Simulations in Guangzhou, China. Water 2017, 9, 411. [Google Scholar] [CrossRef]
- Krvavica, N.; Rubinić, J. Evaluation of Design Storms and Critical Rainfall Durations for Flood Prediction in Partially Urbanized Catchments. Water 2020, 12, 2044. [Google Scholar] [CrossRef]
- Gong, Y.; Li, X.; Zhai, D.; Yin, D.; Song, R.; Li, J.; Fang, X.; Yuan, D. Influence of Rainfall, Model Parameters and Routing Methods on Stormwater Modelling. Water Resour. Manag. 2018, 32, 735–750. [Google Scholar] [CrossRef]
- Peng, H.-Q.; Liu, Y.; Gao, X.-L.; Wang, H.-W.; Chen, Y.; Cai, H.-Y. Calculation of Intercepted Runoff Depth Based on Stormwater Quality and Environmental Capacity of Receiving Waters for Initial Stormwater Pollution Management. Environ. Sci. Pollut. Res. 2017, 24, 24681–24689. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ng, S.T.; Dao, J.; Zhou, S.; Xu, F.J.; Xu, X.; Zhou, Z. BIM-GIS-DCEs Enabled Vulnerability Assessment of Interdependent Infrastructures—A Case of Stormwater Drainage-Building-Road Transport Nexus in Urban Flooding. Autom. Constr. 2021, 125, 103626. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Hou, H.; Chen, Y.; Fan, J.; Wang, P.; Hu, T. Analyzing Spatial Variance of Urban Waterlogging Disaster at Multiple Scales Based on a Hydrological and Hydrodynamic Model. Nat. Hazards 2022, 114, 1915–1938. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, L.; Liu, J. Hydrodynamic Modelling and Flood Risk Analysis of Urban Catchments under Multiple Scenarios: A Case Study of Dongfeng Canal District, Zhengzhou. Int. J. Environ. Res. Public Health 2022, 19, 14630. [Google Scholar] [CrossRef] [PubMed]
- Sidek, L.M.; Jaafar, A.S.; Majid, W.H.A.W.A.; Basri, H.; Marufuzzaman, M.; Fared, M.M.; Moon, W.C. High-Resolution Hydrological-Hydraulic Modeling of Urban Floods Using InfoWorks ICM. Sustainability 2021, 13, 10259. [Google Scholar] [CrossRef]
- Çirağ, B.; Firat, M. Two-Dimensional (2D) Flood Analysis and Calibration of Stormwater Drainage Systems Using Geographic Information Systems. Water Sci. Technol. 2023, 87, 2577–2596. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Lee, D. Urban Green Space Arrangement for an Optimal Landscape Planning Strategy for Runoff Reduction. Land 2021, 10, 897. [Google Scholar] [CrossRef]
- Mei, C.; Shi, H.; Liu, J.; Song, T.; Wang, J.; Gao, X.; Wang, H.; Li, M. Analyzing Urban Form Influence on Pluvial Flooding via Numerical Experiments Using Random Slices of Actual City Data. J. Hydrol. 2024, 633, 130916. [Google Scholar] [CrossRef]
- Li, H.; Wang, Q.; Li, M.; Zang, X.; Wang, Y. Identification of Urban Waterlogging Indicators and Risk Assessment Based on MaxEnt Model: A Case Study of Tianjin Downtown. Ecol. Indic. 2024, 158, 111354. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.; Feng, Q.; Yu, T.; Engel, B.A. Analyzing the Impacts of Topographic Factors and Land Cover Characteristics on Waterlogging Events in Urban Functional Zones. Sci. Total Environ. 2023, 904, 166669. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, Y.; Fu, Y.; Li, L. Spatiotemporal Variance Assessment of Urban Rainstorm Waterlogging Affected by Impervious Surface Expansion: A Case Study of Guangzhou, China. Sustainability 2018, 10, 3761. [Google Scholar] [CrossRef]
- Lu, D.; Song, K.; Zang, S.; Jia, M.; Du, J.; Ren, C. The Effect of Urban Expansion on Urban Surface Temperature in Shenyang, China: An Analysis with Landsat Imagery. Environ. Model. Assess. 2015, 20, 197–210. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, W.; Wen, Y.; Qiu, S. Evaluating the Association between Morphological Characteristics of Urban Land and Pluvial Floods Using Machine Learning Methods. Sustain. Cities Soc. 2023, 99, 104891. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting Future Urban Waterlogging-Prone Areas by Coupling the Maximum Entropy and FLUS Model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, Y.; Fu, Y. Optimization of Impervious Surface Space Layout for Prevention of Urban Rainstorm Waterlogging: A Case Study of Guangzhou, China. J. Environ. Res. Public Health 2019, 16, 3613. [Google Scholar] [CrossRef]



| Type | Resolution (m) | Date | Data Source |
|---|---|---|---|
| DEM | 2 | - | Surveying and Mapping Department of Lin’an |
| Rainfall data | - | 31 July 2022 | National Meteorological Science Data Center “http://data.cma.cn/” (accessed on 30 May 2024) |
| 13 September 2022 | |||
| Pipeline network data | - | - | Urban Administration of Lin’an |
| Multi-temporal high-resolution remote sensing images | 0.27 | 30 June 2010 | Google Earth |
| 8 June 2011 | |||
| 20 September 2012 | |||
| 15 November 2013 | |||
| 16 December 2014 | |||
| 9 February 2016 | |||
| 18 May 2017 | |||
| 29 March 2018 | |||
| 16 October 2019 | |||
| 5 March 2020 | |||
| 19 January 2021 | |||
| Aerial images | 0.2 | March 2022 | Aerial photography |
| Surface | Routine Parameter | Surface Type | Runoff Model | Initial Loss/mm | Fixed Runoff Coefficient | Initial Infiltration Rate (mm/h) | Stable Infiltration Rate (mm/h) | Decay Rate Coefficient (1/h) |
|---|---|---|---|---|---|---|---|---|
| Road | 0.02 | Impervious | Fixed | 1.5 | 0.9 | - | - | - |
| Impervious surface | 0.02 | Impervious | Fixed | 1.5 | 0.85 | - | - | - |
| Natural surface | 0.035 | Pervious | Horton | 2.8 | - | 76 | 4 | 2 |
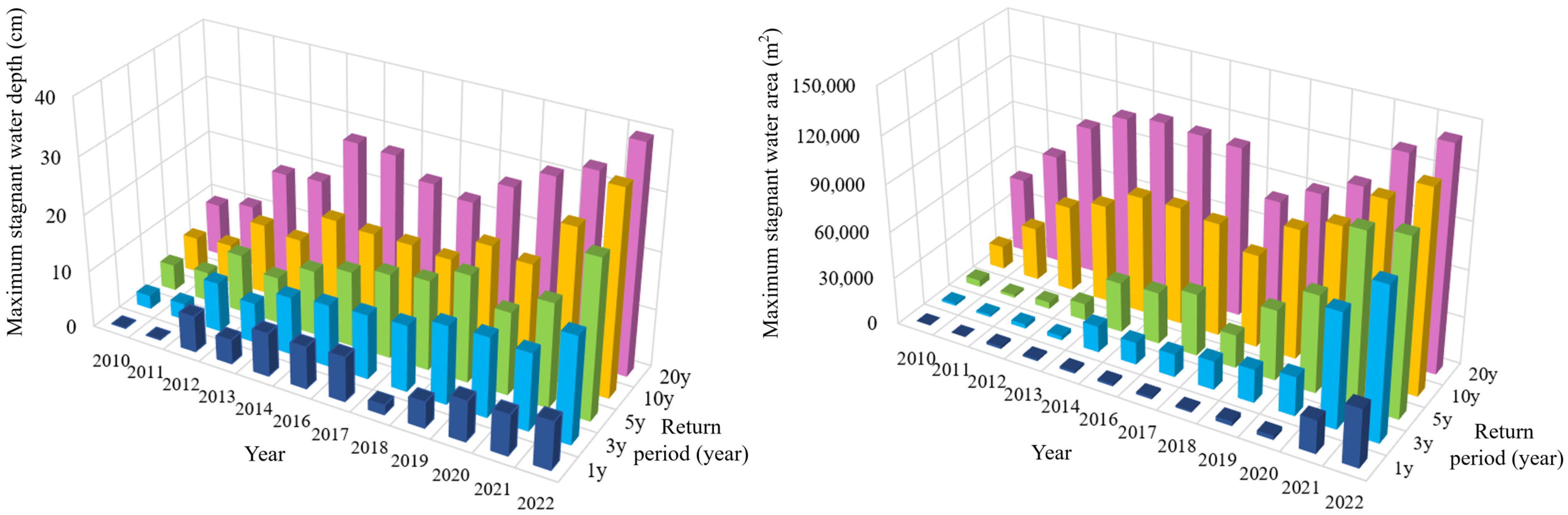
| Year | Maximum Stagnant Water Depth in Each Return Period/cm | Stagnant Water Area in Each Return Period/m2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 year | 3 years | 5 years | 10 years | 20 years | 1 year | 3 years | 5 years | 10 years | 20 years | |
| 2010 | 0 | 2.4 | 4.6 | 6.3 | 9.3 | 0 | 1392.64 | 4334.15 | 14824.61 | 48,403.20 |
| 2011 | 0 | 2.9 | 5.2 | 6.9 | 10.8 | 0 | 1369.44 | 1777.32 | 33,973.52 | 70,384.74 |
| 2012 | 6.3 | 8.7 | 10.3 | 12.5 | 18.6 | 1705.52 | 2624.06 | 4268.83 | 55,145.45 | 95,111.17 |
| 2013 | 4.2 | 7.1 | 8.2 | 11.7 | 19.1 | 1185.09 | 2633.47 | 10,695.72 | 62,557.18 | 107,174.93 |
| 2014 | 7.5 | 10.2 | 11.4 | 17.1 | 27.6 | 1568.29 | 16,808.32 | 31,866.56 | 74,803.97 | 110,935.19 |
| 2016 | 7.3 | 10.9 | 13.2 | 16.6 | 27.2 | 1568.29 | 14,110.16 | 32,964.96 | 75,010.02 | 109,173.85 |
| 2017 | 7.7 | 11.3 | 14.8 | 16.6 | 24.0 | 1483.35 | 14,513.36 | 39,615.86 | 71,905.11 | 107,714.62 |
| 2018 | 1.6 | 11.6 | 15.7 | 16.0 | 22.6 | 1125.50 | 18,145.58 | 21,042.07 | 58,920.57 | 80,676.55 |
| 2019 | 4.5 | 13.7 | 18.7 | 20.3 | 27.0 | 2836.62 | 20,980.50 | 44,646.99 | 82,133.27 | 92,412.86 |
| 2020 | 7.0 | 13.9 | 14.4 | 19.1 | 30.6 | 2650.14 | 24,643.08 | 61,711.58 | 91,511.86 | 103,580.09 |
| 2021 | 7.0 | 13.4 | 18.1 | 27.3 | 33.3 | 21,078.53 | 72,602.58 | 107,832.98 | 114,098.09 | 130,042.46 |
| 2022 | 8.2 | 18.5 | 27.6 | 35.5 | 39.6 | 36,688.73 | 96,311.57 | 111,739.52 | 128,098.60 | 142,068.38 |
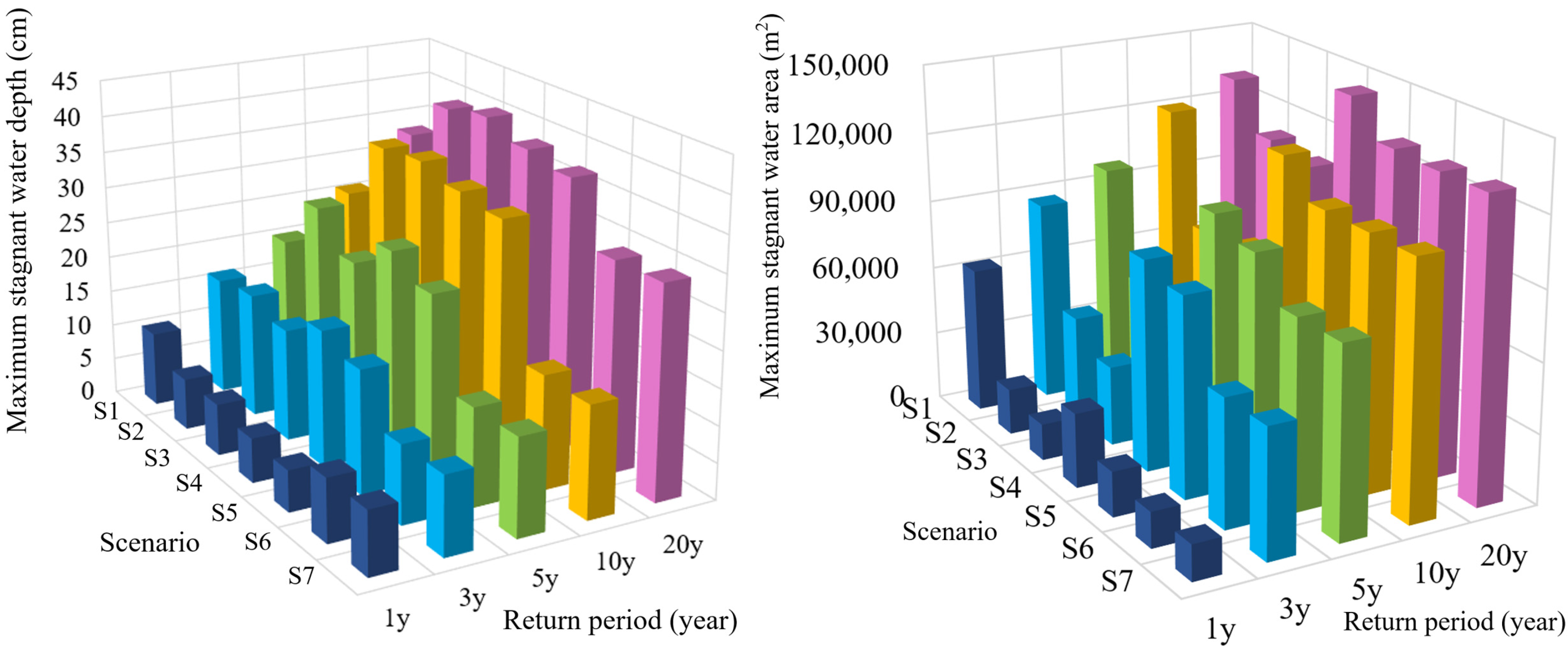
| Scenario | Maximum Stagnant Water Depth in Each Return Period/cm | Stagnant Water Area in Each Return Period/m2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 year | 3 years | 5 years | 10 years | 20 years | 1 year | 3 years | 5 years | 10 years | 20 years | |
| S1 | 10.3 | 16.3 | 20.3 | 25.9 | 33.1 | 63,162.10 | 87,385.05 | 98,403.94 | 120,506.20 | 131,055.38 |
| S2 | 7.1 | 17.2 | 28.0 | 35.0 | 39.2 | 19,838.47 | 45,883.28 | 55,408.38 | 73,746.77 | 111,156.39 |
| S3 | 7.1 | 15.5 | 23.2 | 35.7 | 40.4 | 15,741.54 | 34,560.03 | 44,561.49 | 75,383.69 | 107,019.20 |
| S4 | 6.1 | 18.8 | 27.8 | 34.2 | 38.4 | 32,003.44 | 91,172.91 | 105,178.51 | 124,910.79 | 145,389.95 |
| S5 | 5.7 | 17.0 | 25.1 | 33.3 | 37.2 | 19,333.79 | 86,186.77 | 98,191.78 | 110,242.08 | 130,735.65 |
| S6 | 8.7 | 10.8 | 13.5 | 15.7 | 29.1 | 15,303.08 | 55,183.68 | 81,605.45 | 110,060.51 | 129,569.95 |
| S7 | 8.7 | 10.8 | 13.4 | 15.4 | 29.2 | 15,303.08 | 55,154.42 | 81,638.16 | 109,898.50 | 129,616.97 |
| Plan | Maximum Stagnant Water Depth in Each Return Period/cm | Stagnant Water Area in Each Return Period/m2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 year | 3 years | 5 years | 10 years | 20 years | 1 year | 3 years | 5 years | 10 years | 20 years | |
| P1 | 8.2 | 18.5 | 27.6 | 35.5 | 39.6 | 36,688.73 | 96,311.57 | 111,739.52 | 128,098.60 | 142,068.38 |
| P2 | 7.1 | 18.3 | 28.1 | 35.4 | 39.5 | 32,217.19 | 90,575.56 | 104,762.43 | 123,353.35 | 140,012.86 |
| P3 | 7.0 | 15.1 | 22.8 | 32.9 | 37.8 | 32,918.31 | 89,037.38 | 103,430.89 | 120,266.93 | 136,420.80 |
| P4 | 8.2 | 17.5 | 26.6 | 35.1 | 39.3 | 36,864.19 | 95,800.20 | 110,749.82 | 126,898.30 | 139,796.53 |
| P5 | 8.9 | 18.4 | 26.1 | 32.9 | 36.9 | 36,577.89 | 95,835.23 | 110,619.33 | 128,047.53 | 137,729.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hou, H.; Zhang, Y.; Huang, R.; Hu, T. Scenario-Based Simulation of Impervious Surfaces for Detecting the Effects of Landscape Patterns on Urban Waterlogging. Remote Sens. 2024, 16, 2130. https://doi.org/10.3390/rs16122130
Li J, Hou H, Zhang Y, Huang R, Hu T. Scenario-Based Simulation of Impervious Surfaces for Detecting the Effects of Landscape Patterns on Urban Waterlogging. Remote Sensing. 2024; 16(12):2130. https://doi.org/10.3390/rs16122130
Chicago/Turabian StyleLi, Jiahui, Hao Hou, Yindong Zhang, Ruolin Huang, and Tangao Hu. 2024. "Scenario-Based Simulation of Impervious Surfaces for Detecting the Effects of Landscape Patterns on Urban Waterlogging" Remote Sensing 16, no. 12: 2130. https://doi.org/10.3390/rs16122130
APA StyleLi, J., Hou, H., Zhang, Y., Huang, R., & Hu, T. (2024). Scenario-Based Simulation of Impervious Surfaces for Detecting the Effects of Landscape Patterns on Urban Waterlogging. Remote Sensing, 16(12), 2130. https://doi.org/10.3390/rs16122130









