Design of Scanning Units for the Underwater Circumferential-Scanning LiDAR Based on Pyramidal-Shaped Reflectors and a Rapid Detection Method for Target Orientation
Abstract
1. Introduction
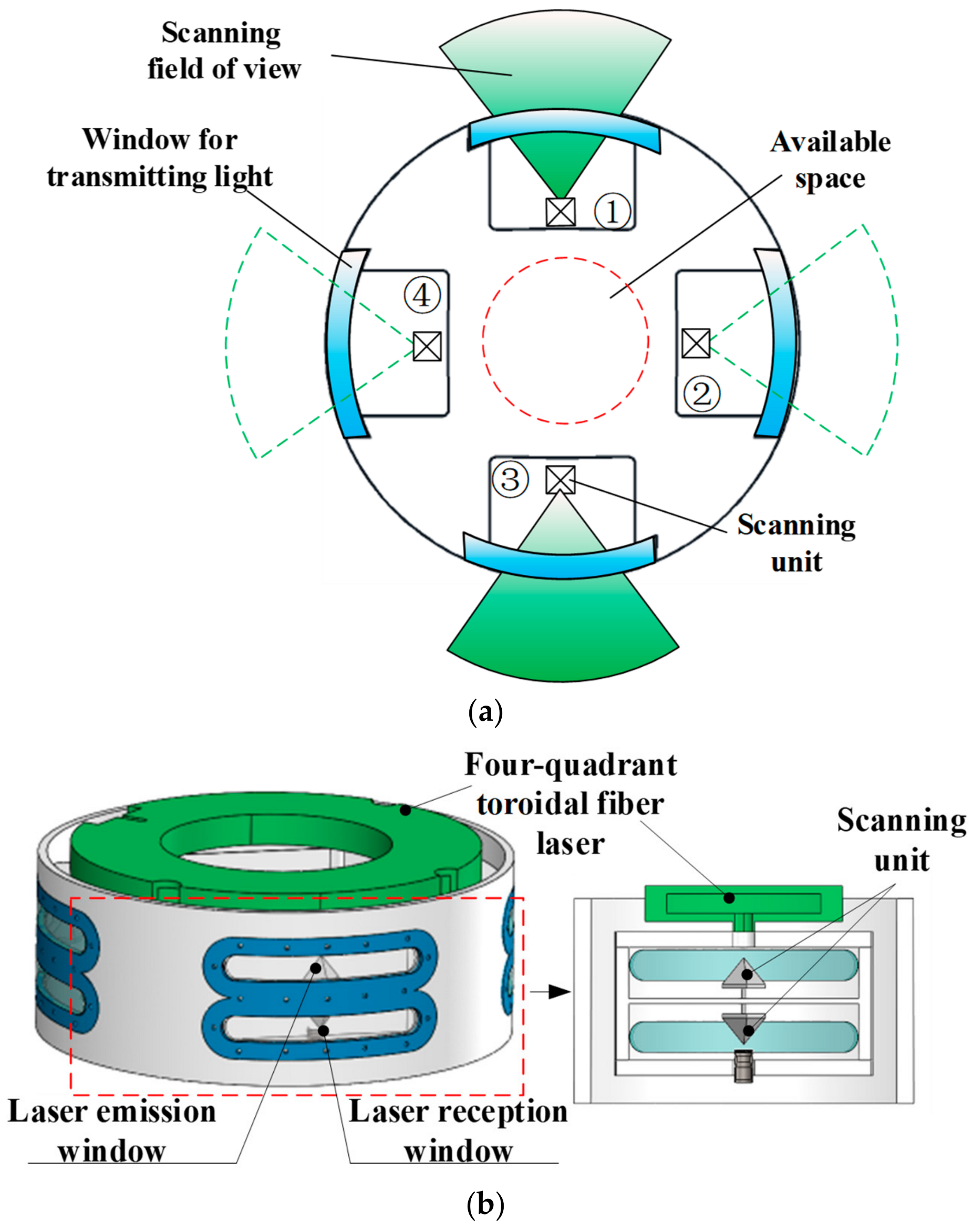
2. Design and Optimization of Scanning Unit Based on the Pyramidal-Shaped Reflector
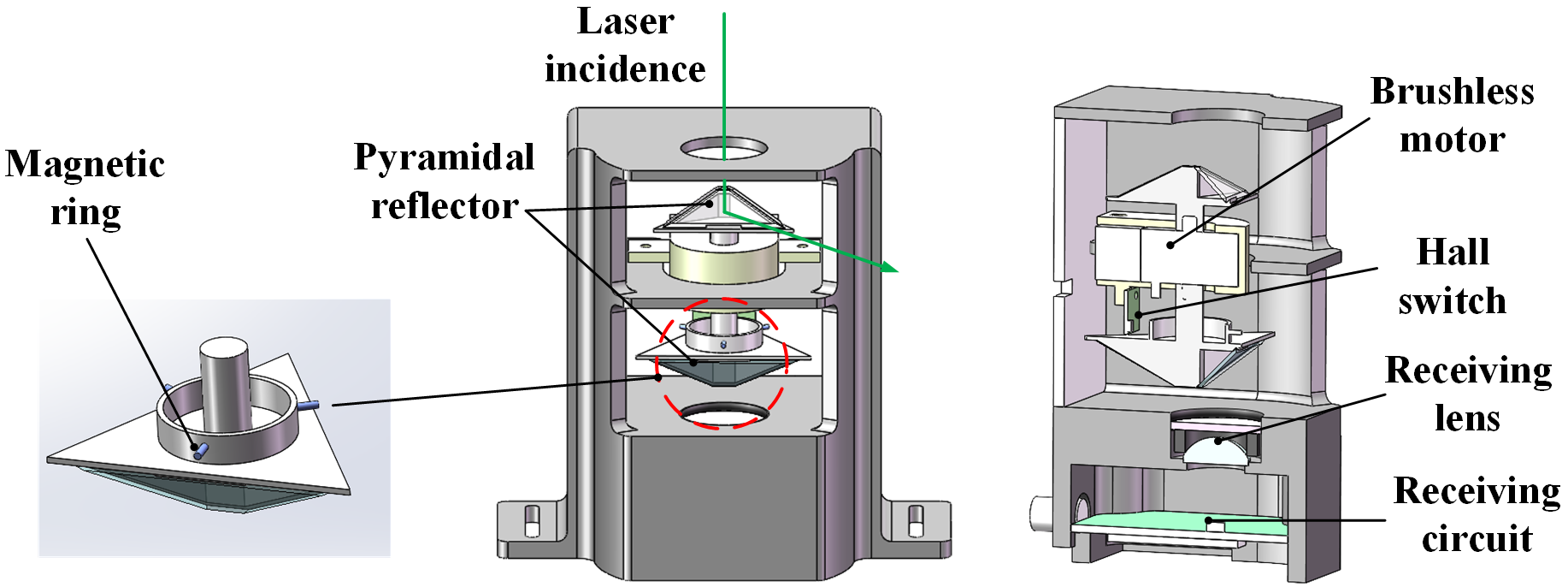
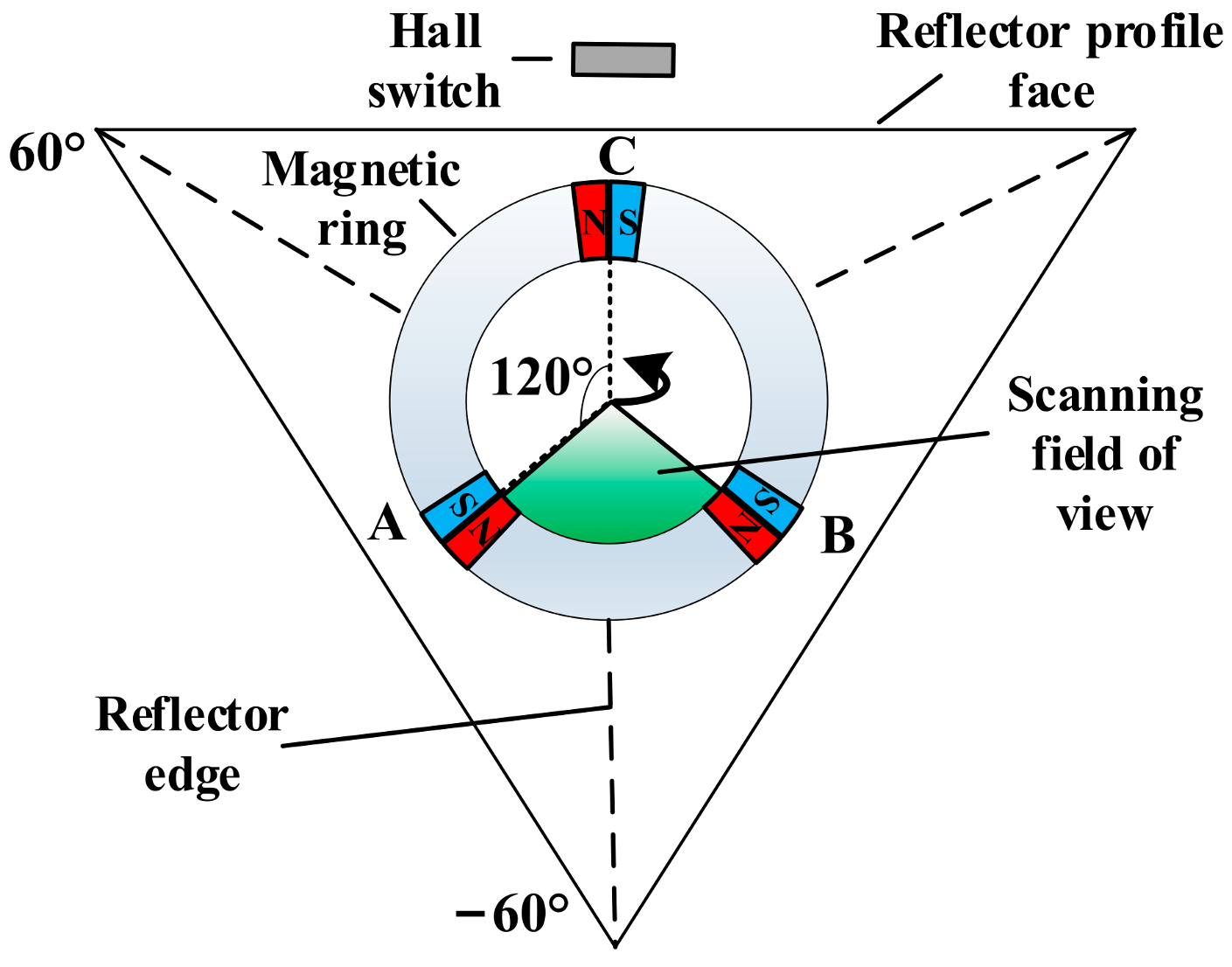
2.1. Design of the Scanning Unit
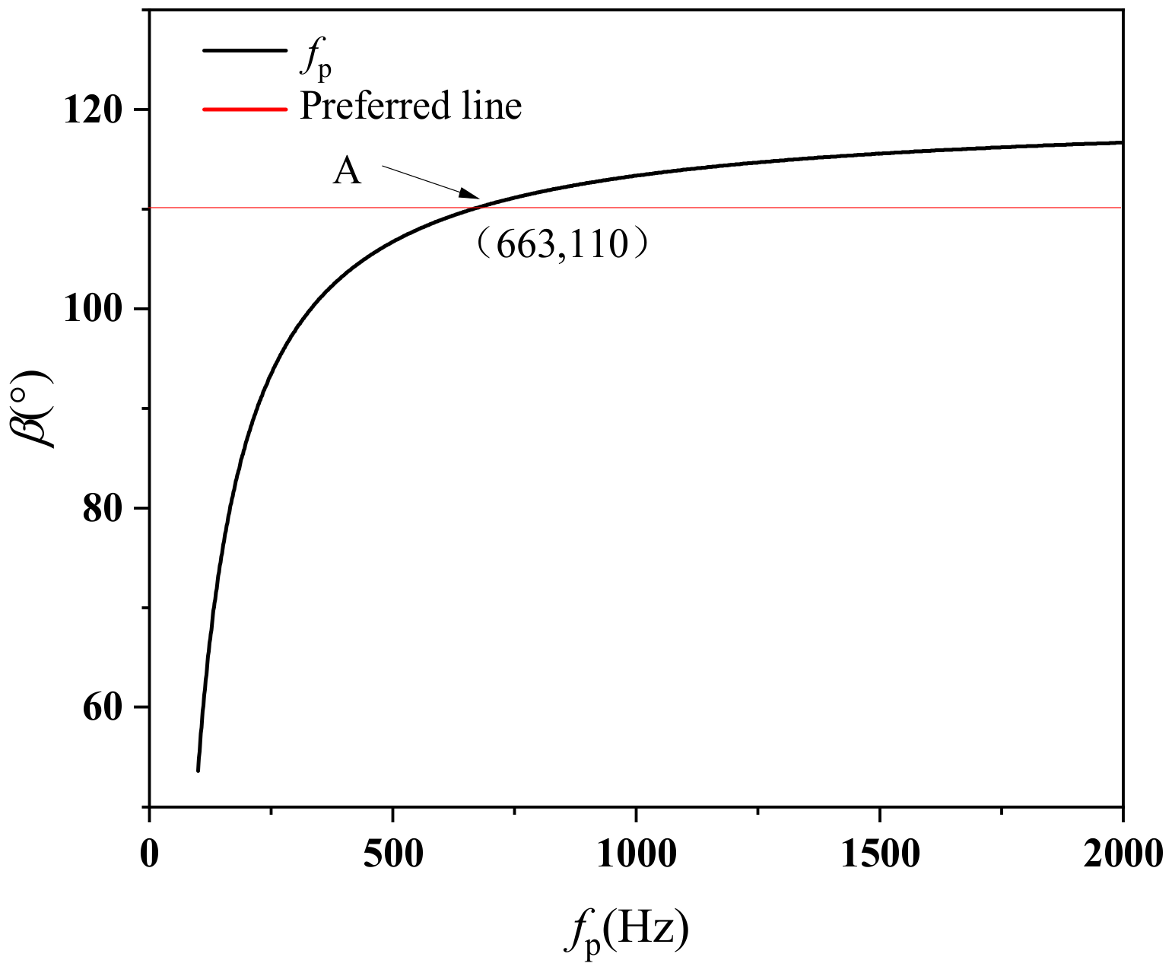
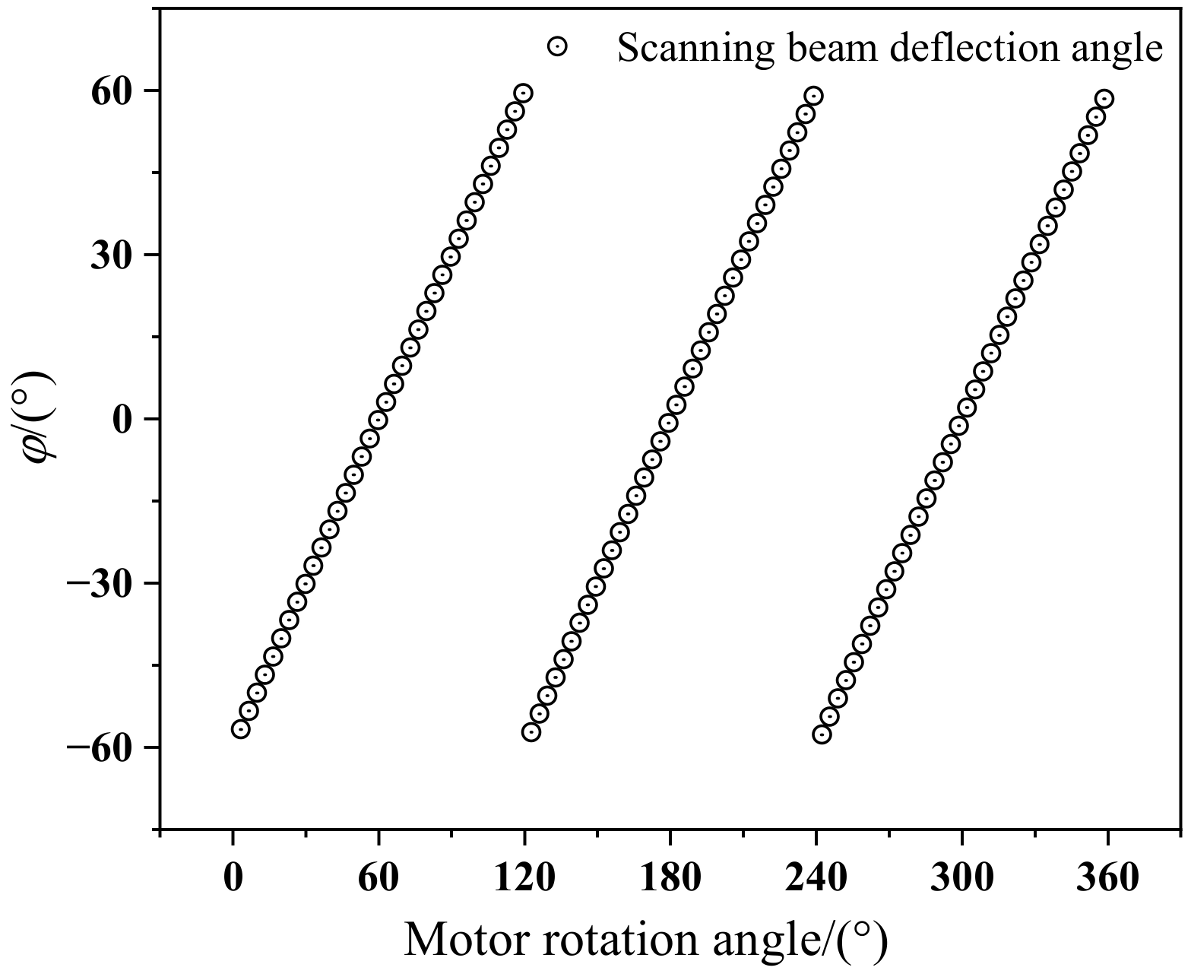
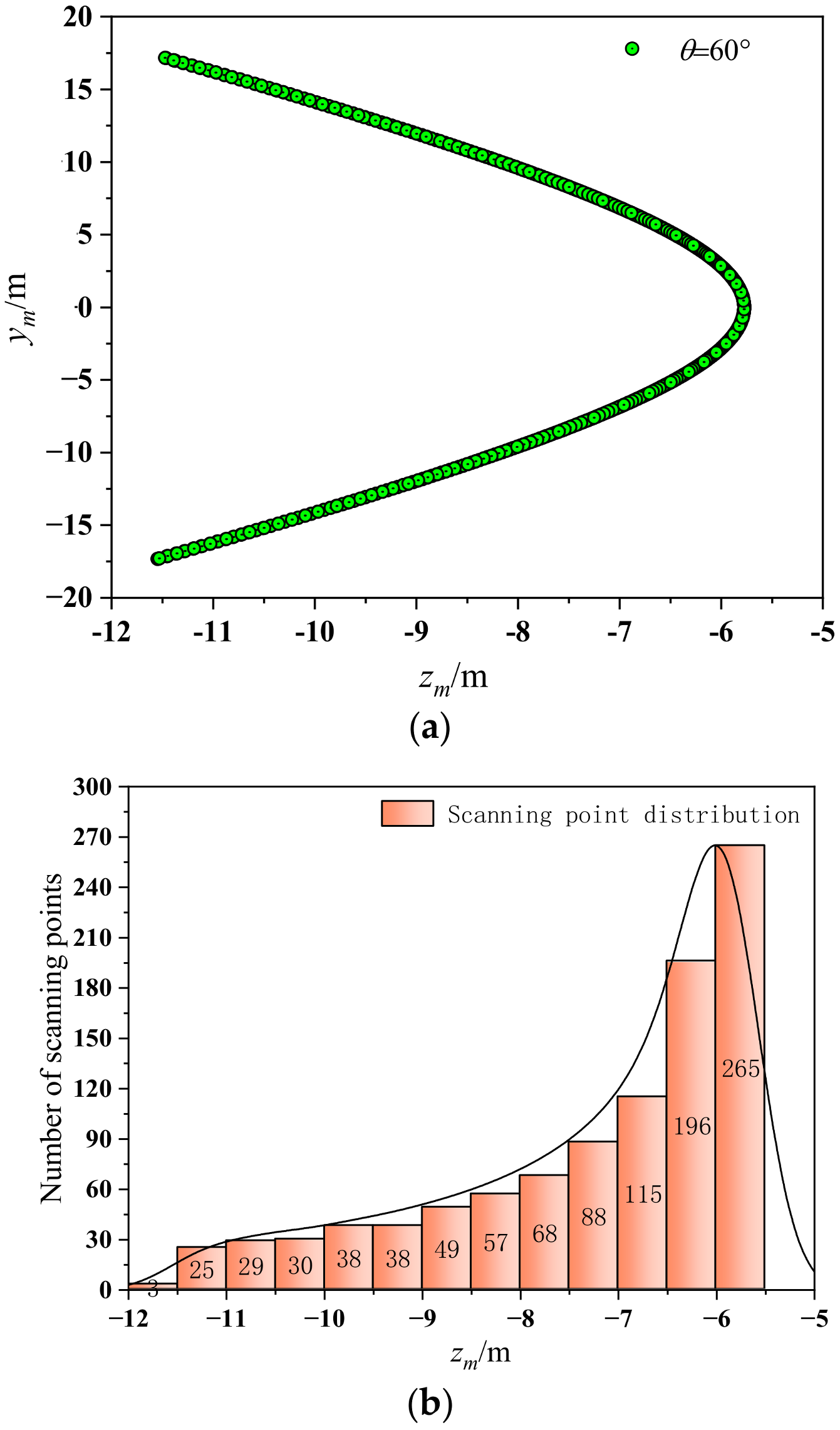
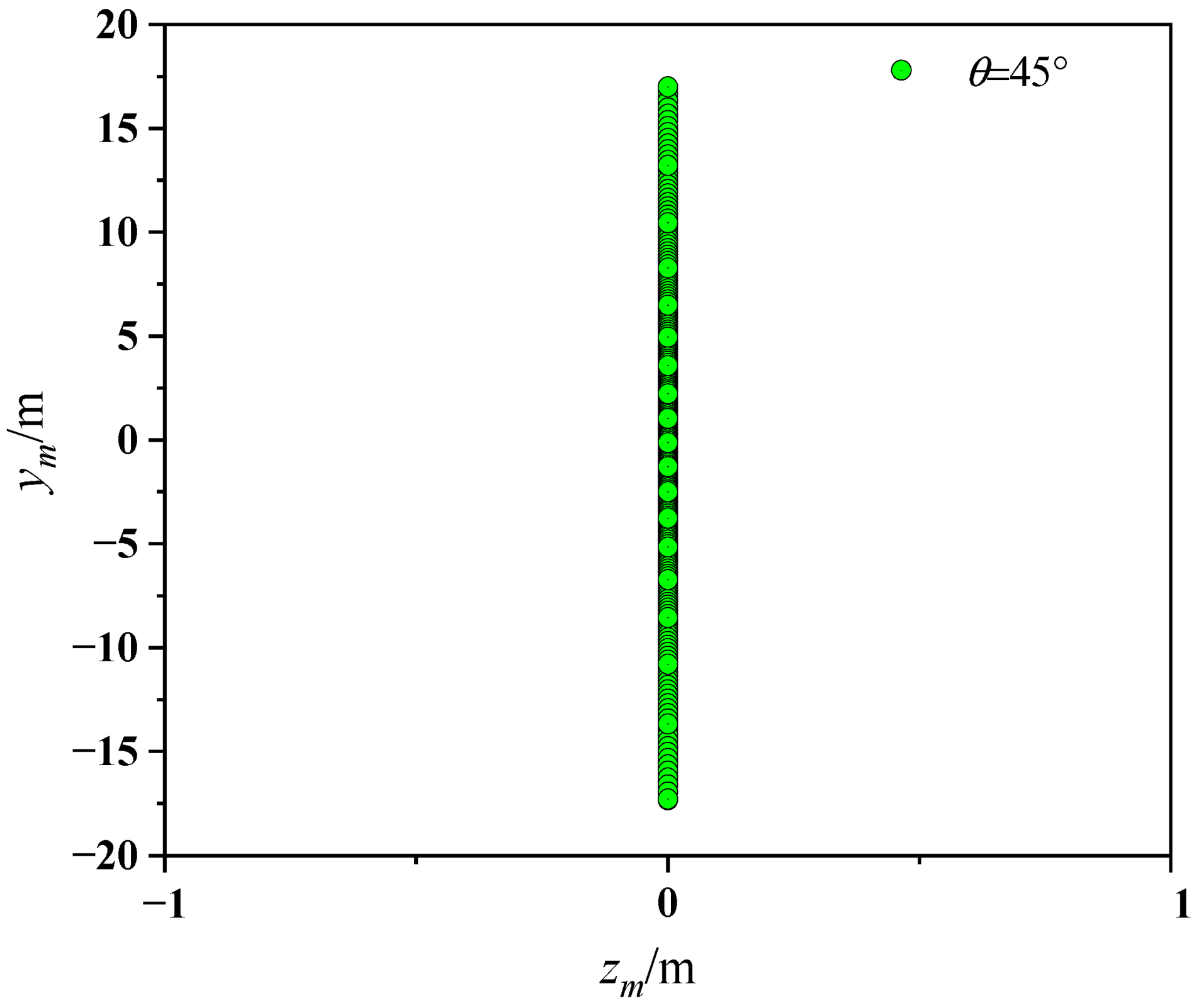
2.2. Multi-Parameter Optimization Design for Pyramidal Reflector
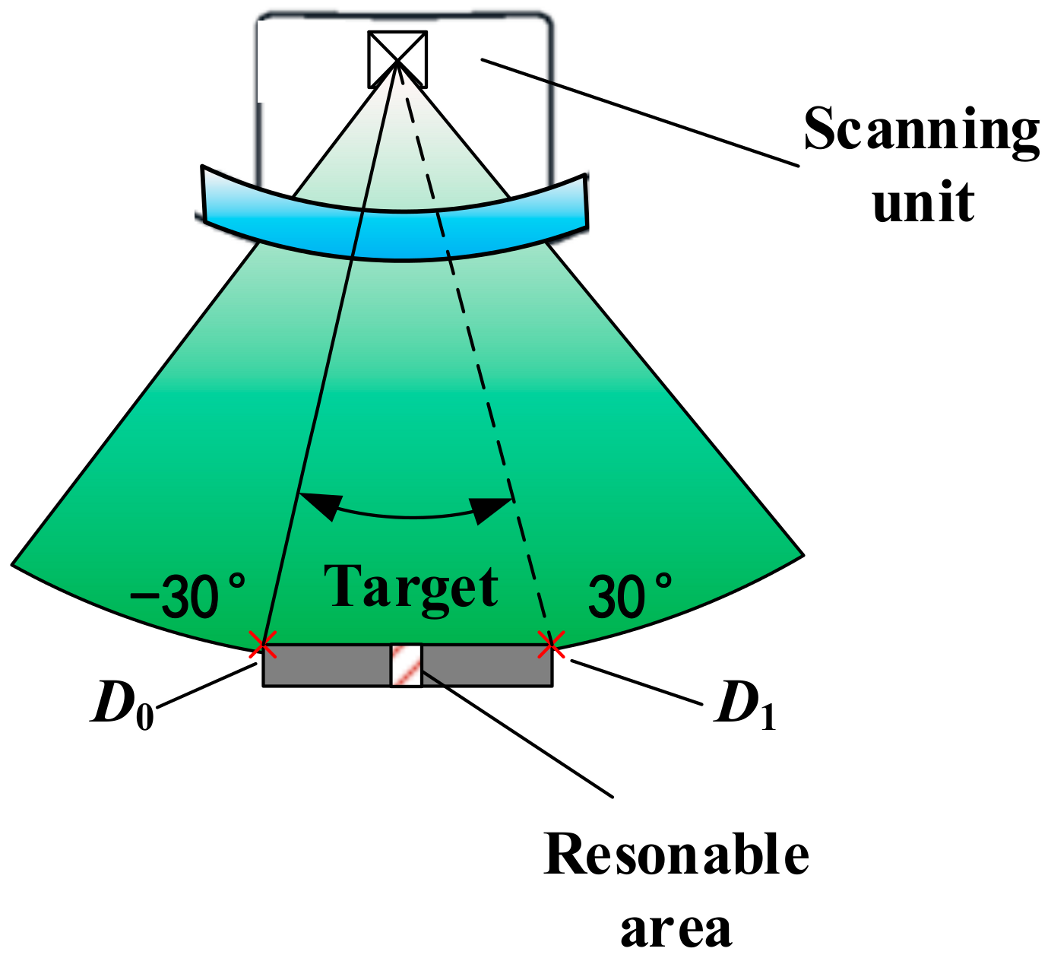
3. FPGA-Based Fast Detection Method for Target Orientation
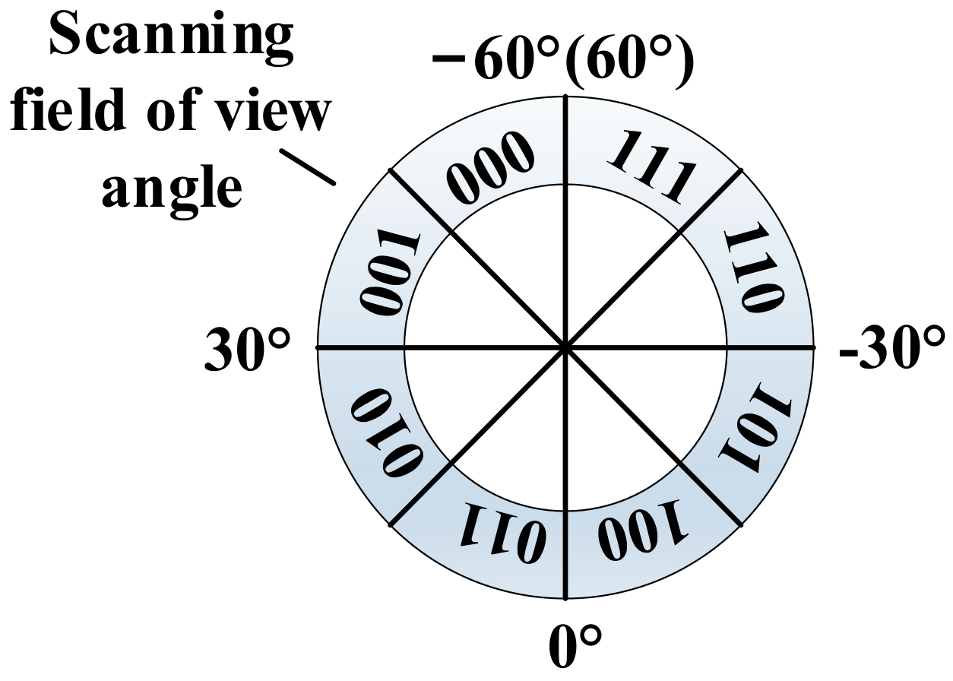
3.1. Principles for Target Orientation Detection and Design of the Magneto-Electric Detection Modules
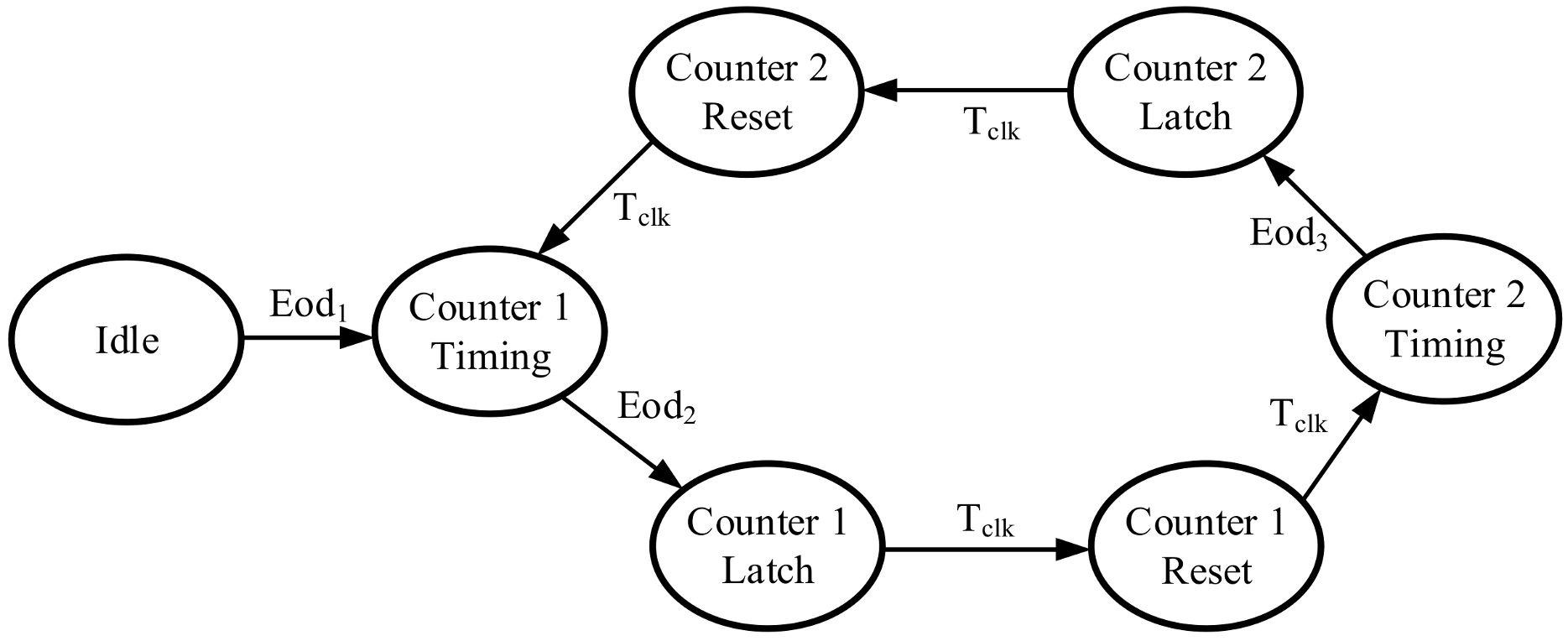
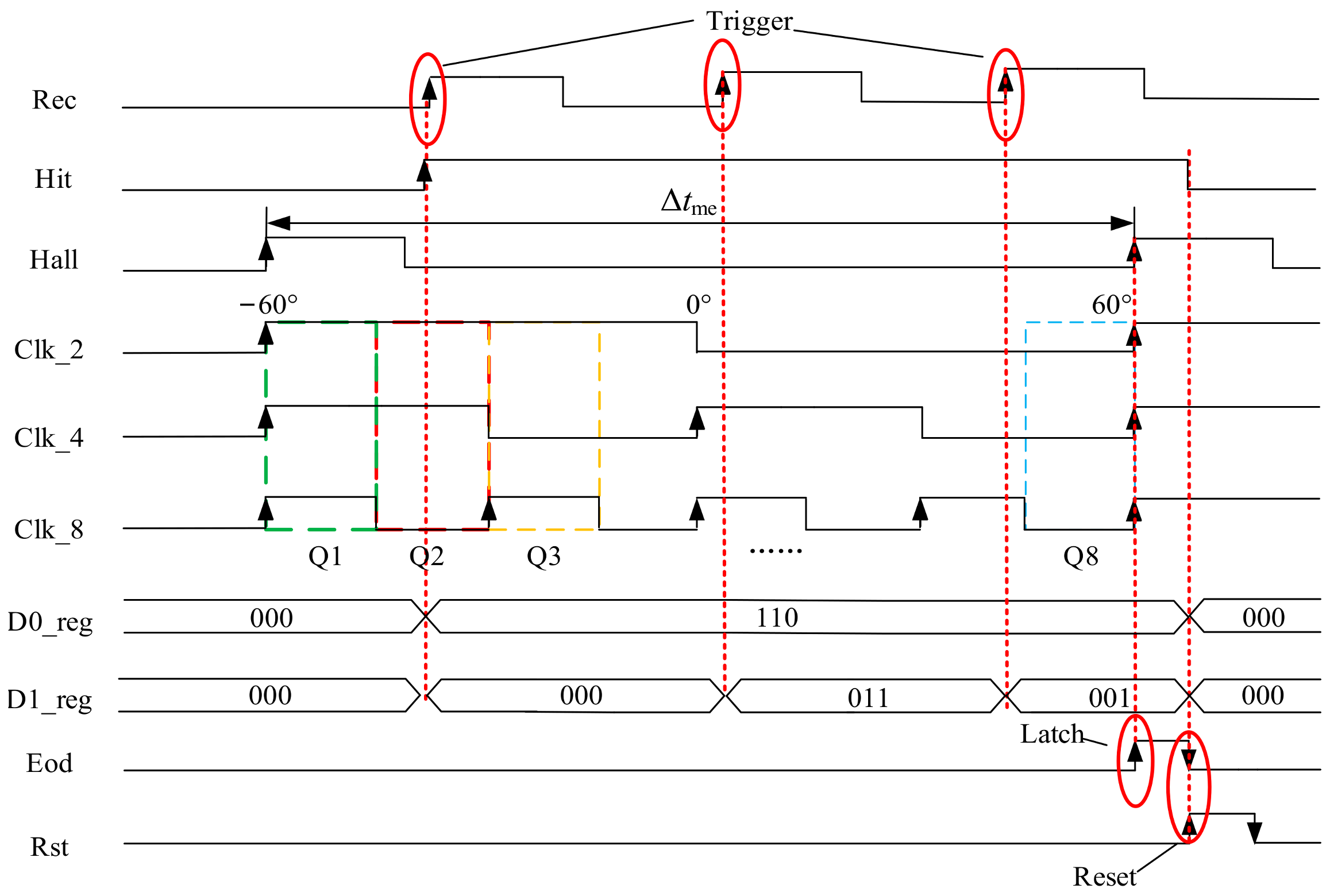
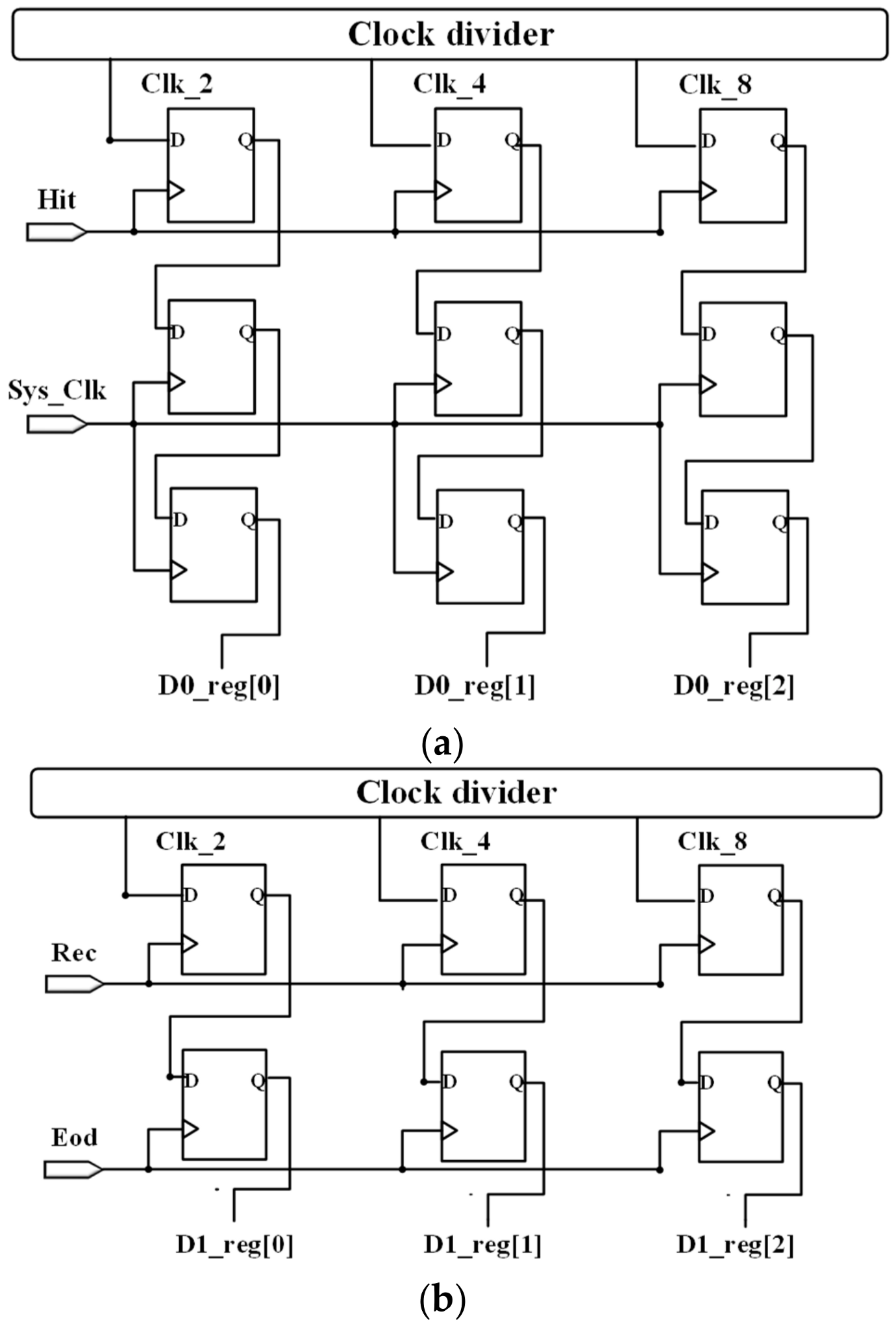
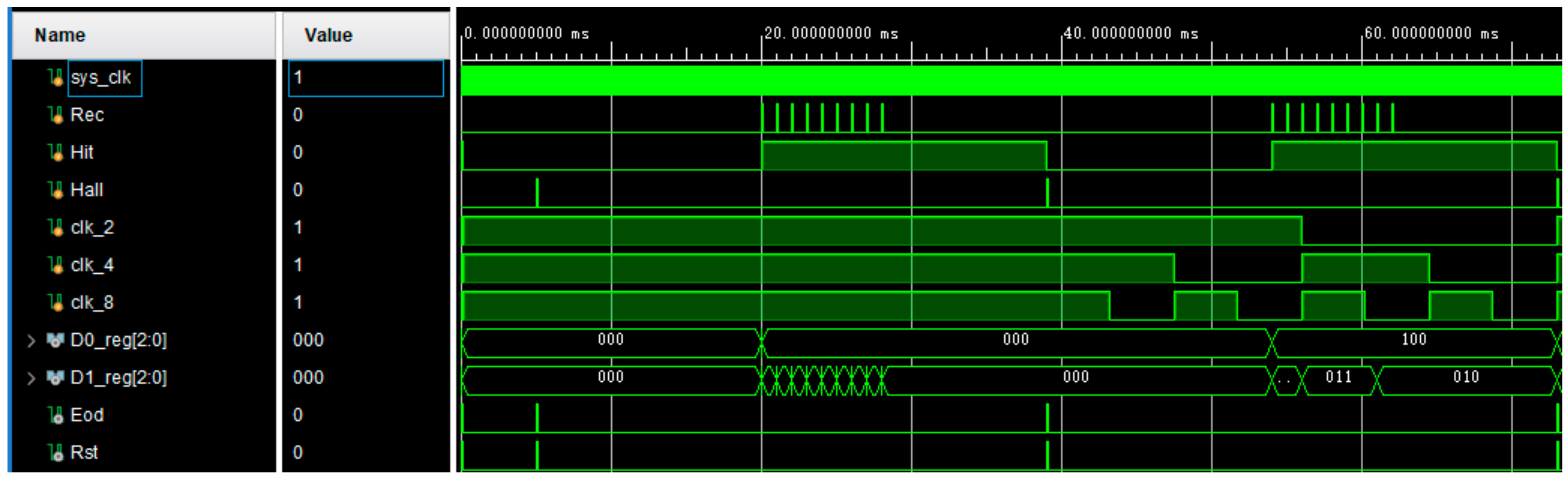
3.2. FPGA-Based Rapid Detection Method for Target Orientation
4. Experiment Results and Analysis
4.1. Air Test
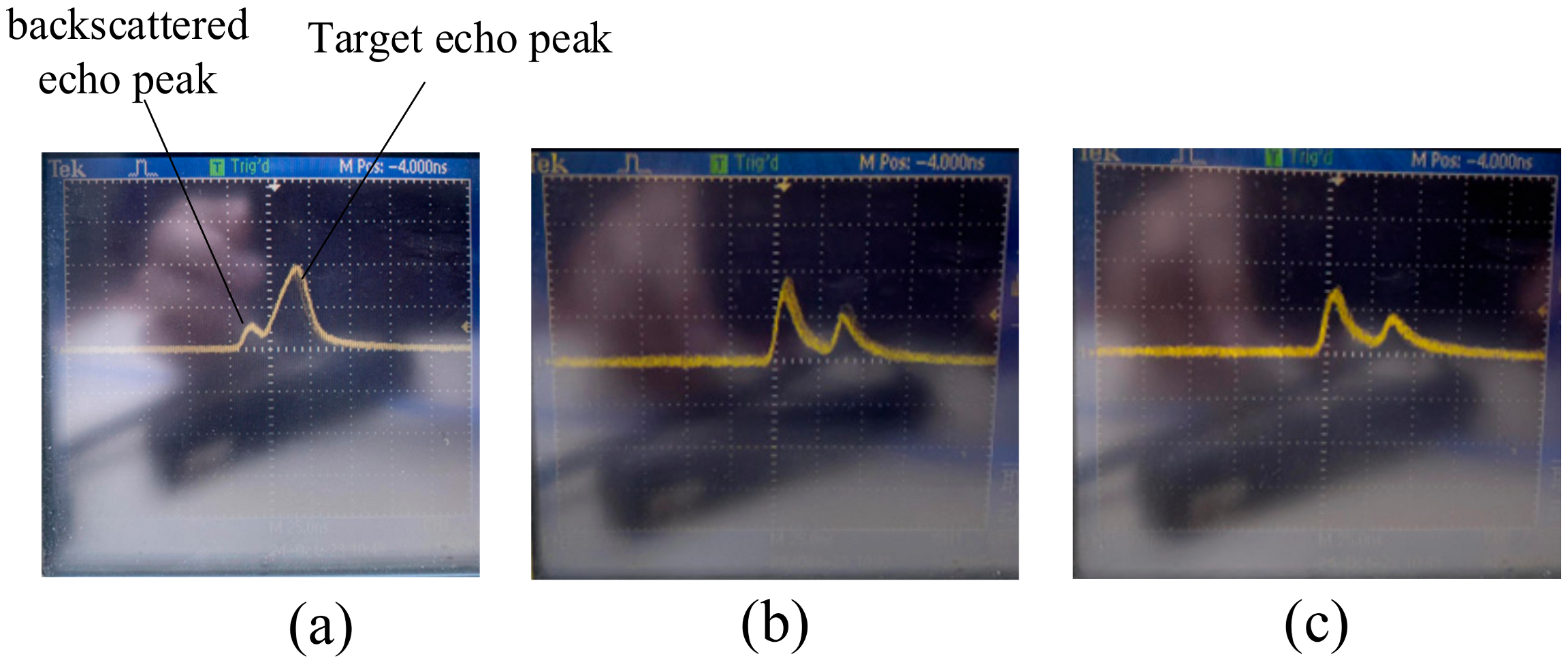
4.2. Pool Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, Z.; Zha, B.; Zhou, Y.; Huang, J.; Xuchen, Y.; Zhang, H. Single-Stage Adaptive Multi-Scale Point Cloud Noise Filtering Algorithm Based on Feature Information. Remote Sens. 2022, 14, 367. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Peng, X.; Yin, Y.; Li, A.; Wu, J.; Gao, B.Z. Structured light field 3D imaging. Opt. Express 2016, 24, 20324–20334. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.L.; Zhang, H.; Zha, B.T.; Ding, L.B. Trajectory correction and position error analysis of underwater laser scanning. Opt. Laser Technol. 2022, 153, 108136. [Google Scholar] [CrossRef]
- Li, Z.-P.; Ye, J.-T.; Huang, X.; Jiang, P.-Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-photon imaging over 200 km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Maccarone, A.; McCarthy, A.; Ren, X.; Warburton, R.E.; Wallace, A.M.; Moffat, J.; Petillot, Y.; Buller, G.S. Underwater depth imaging using time-correlated single-photon counting. Opt. Express 2015, 23, 33911–33926. [Google Scholar] [CrossRef] [PubMed]
- Pokorny, P. One-mirror and two-mirror three-dimensional optical scanners position and accuracy of laser beam spot. Appl. Optics 2014, 53, 2730–2740. [Google Scholar] [CrossRef] [PubMed]
- Keskin, A.; Baykal, Y. Scintillation and BER analysis of cosine and cosine-hyperbolic-Gaussian beams in turbulent ocean. Appl. Opt. 2021, 60, 7054–7063. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; Drummond, K.; McCarthy, A.; Steinlehner, U.K.; Tachella, J.; Garcia, D.A.; Pawlikowska, A.; Lamb, R.A.; Henderson, R.K.; McLaughlin, S.; et al. Submerged single-photon LiDAR imaging sensor used for real-time 3D scene reconstruction in scattering underwater environments. Opt. Express 2023, 31, 16690–16708. [Google Scholar] [CrossRef]
- Shangguan, M.; Weng, Z.; Lin, Z.; Lee, Z.; Yang, Z.; Sun, J.; Wu, T.; Zhang, Y.; Wen, C. Day and night continuous high-resolution shallow-water depth detection with single-photon underwater lidar. Opt. Express 2023, 31, 43950–43962. [Google Scholar] [CrossRef]
- Macdonald, I.R.; Chu, J.S.; Reilly, F.F.; Blincow, M.; Olivier, D. Deep-ocean use of the SM2000 laser line scan-ner on submarine NR-1 demonstrates system potential for industry and basic science. In Challenges of Our Changing Global Environment, Proceedings of the OCEANS ’95 MTS/IEEE, San Diego, CA, USA, 9–12 October 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 1, pp. 555–565. [Google Scholar]
- Fournier, G.R.; Bonnier, D.; Forand, J.L.; Pace, P.W. LUCIE ROV mounted laser imaging system. In Proceedings of the Ocean Optics XI. SPIE, San Diego, CA, USA, 20–22 July 1992; Volume 1750, pp. 443–452. [Google Scholar]
- Steinvall, O.; Andersson, P.; Elmquist, M. Image Quality for Range-Gated Systems during Different Ranges Atmospheric Conditions; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; p. 639607. [Google Scholar]
- Fuchse, T. Conceptual Design of the CZMIL Data Acquisition System (DAS): Integrating a New Bathymetric LiDAR with a Commercial Spectrometer and Metric Camera for Coastal Mapping Applications. In Proceedings of the SPIE7695, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVI, Orlando, FL, USA, 5–9 April 2010; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Zeng, X.; Xia, M.; Cheng, Z.; Li, L.; Chen, J.; Du, P.; Yang, K. A small-size pulsed lidar designed for obstacles detection in natural underwater environment. In AOPC 2015: Optical and Optoelectronic Sensing and Imaging Technology; SPIE: Bellingham, WA, USA, 2015; Volume 9674, pp. 381–386. [Google Scholar]
- Maccarone, A.; Della Rocca, F.M.; McCarthy, A.; Henderson, R.; Buller, G.S. Three-dimensional imaging of stationary and moving targets in turbid underwater environments using a single-photon detector array. Opt. Express 2019, 27, 28437–28456. [Google Scholar] [CrossRef] [PubMed]
- Zha, B.T.; Yuan, H.L.; Ma, S.J.; Chen, G.S. Influence of single-beam expanding scanning laser circumferential detection system parameters on detection capability. Acta Phys. Sin. 2019, 68, 79–88. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Zhang, H.; Zha, B.T. Simulation of underwater LiDAR echo on the basis of bidirectional reflectance distribution function. Acta Photonica Sin. 2016, 45, 59–64. [Google Scholar]
- Chen, S.S.; Zhang, H.; Xu, X.B. Echo characteristic of planar target in pulsed LiDAR detection. Acta Armamentarii 2018, 39, 1095–1102. [Google Scholar]
- Gan, L.; Zhang, H. Underwater laser autonomous scanning short-range orientation detection method on the basis of fluid-driven. Chin. J. Lasers 2019, 46, 0304004. [Google Scholar]
- Cheng, Z.; Yang, K.; Han, J.; Zhou, Y.; Sun, L.; Li, W.; Xia, M. Improved time-of-flight range acquisition technique in underwater LiDAR experiments. Appl. Opt. 2015, 54, 5715–5725. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Zha, B.; Zhang, H. Parameter Optimization of Geometrically Truncated Ranging LiDAR System. Infrared Laser Eng. 2018, 47, 97–102. [Google Scholar]
- Tan, Y.Y.; Zhang, H.; Zha, B.T. Underwater single beam circumferentially scanning detection system using range-gated receiver and adaptive filter. J. Mod. Opt. 2017, 64, 1648–1656. [Google Scholar] [CrossRef]
- Zhong, K.; Su, W.; Peng, B.; Huang, S. Design of 4f emission optical system for underwater laser peripheral scanning. Infrared Laser Eng. 2021, 50, 199–210. [Google Scholar]
- Xu, X.; Zhang, L.; Yang, J.; Cao, C.; Wang, W.; Ran, Y.; Tan, Z.; Luo, M. A Review of Multi-Sensor Fusion SLAM Systems Based on 3D LIDAR. Remote Sens. 2022, 14, 2835. [Google Scholar] [CrossRef]
- Xu, G.; Zha, B.; Yuan, H.; Zheng, Z.; Zhang, H. Underwater four-quadrant dual-beam circumferential scanning laser fuze using nonlinear adaptive backscatter filter based on pauseable SAF-LMS algorithm. Def. Technol. 2023, in press. [Google Scholar] [CrossRef]
- Xu, G.B.; Zha, B.T.; Zheng, Z.; Zhang, H. Design and modeling of small-opening cascade sync-scanning underwater LiDARs. Acta Armamentarii 2022, 43, 3162–3171. [Google Scholar]
- Gan, L.; Wang, K.; Xu, Z.; Zhang, N.; Zhang, H. Influence of periodically scanning magnetic signal characteristics on the statistical distribution of laser-magnetic composite azimuth detection. Chin. J. Sci. Instrum. 2022, 43, 235–243. [Google Scholar] [CrossRef]
- Xu, G.; Zha, B.; Xia, T.; Zheng, Z.; Zhang, H. A high-throughput vernier time-to-digital converter on FPGAs with improved resolution using a bi-time interpolation scheme. Appl. Sci. 2022, 12, 7674. [Google Scholar] [CrossRef]








| Parameter | Numerical Value |
|---|---|
| 3 | |
| 553.2 r/min | |
| 1000 Hz | |
| 3.3° | |
| β | 113.4° |
| θ | 45° |
| l | 15 mm |
| e | 2.1 mm |
| h | 10 mm |
| Spacing of the Target Plate Prototype (m) | Scanning Track Length (m) | Field of View Angle (°) |
|---|---|---|
| 0.20 | 0.61 | 113.6 |
| 0.30 | 0.91 | 113.2 |
| 0.40 | 1.22 | 113.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, B.; Xu, G.; Chen, Z.; Tan, Y.; Qin, J.; Zhang, H. Design of Scanning Units for the Underwater Circumferential-Scanning LiDAR Based on Pyramidal-Shaped Reflectors and a Rapid Detection Method for Target Orientation. Remote Sens. 2024, 16, 2131. https://doi.org/10.3390/rs16122131
Zha B, Xu G, Chen Z, Tan Y, Qin J, Zhang H. Design of Scanning Units for the Underwater Circumferential-Scanning LiDAR Based on Pyramidal-Shaped Reflectors and a Rapid Detection Method for Target Orientation. Remote Sensing. 2024; 16(12):2131. https://doi.org/10.3390/rs16122131
Chicago/Turabian StyleZha, Bingting, Guangbo Xu, Zhuo Chen, Yayun Tan, Jianxin Qin, and He Zhang. 2024. "Design of Scanning Units for the Underwater Circumferential-Scanning LiDAR Based on Pyramidal-Shaped Reflectors and a Rapid Detection Method for Target Orientation" Remote Sensing 16, no. 12: 2131. https://doi.org/10.3390/rs16122131
APA StyleZha, B., Xu, G., Chen, Z., Tan, Y., Qin, J., & Zhang, H. (2024). Design of Scanning Units for the Underwater Circumferential-Scanning LiDAR Based on Pyramidal-Shaped Reflectors and a Rapid Detection Method for Target Orientation. Remote Sensing, 16(12), 2131. https://doi.org/10.3390/rs16122131








