Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data
Abstract
1. Introduction
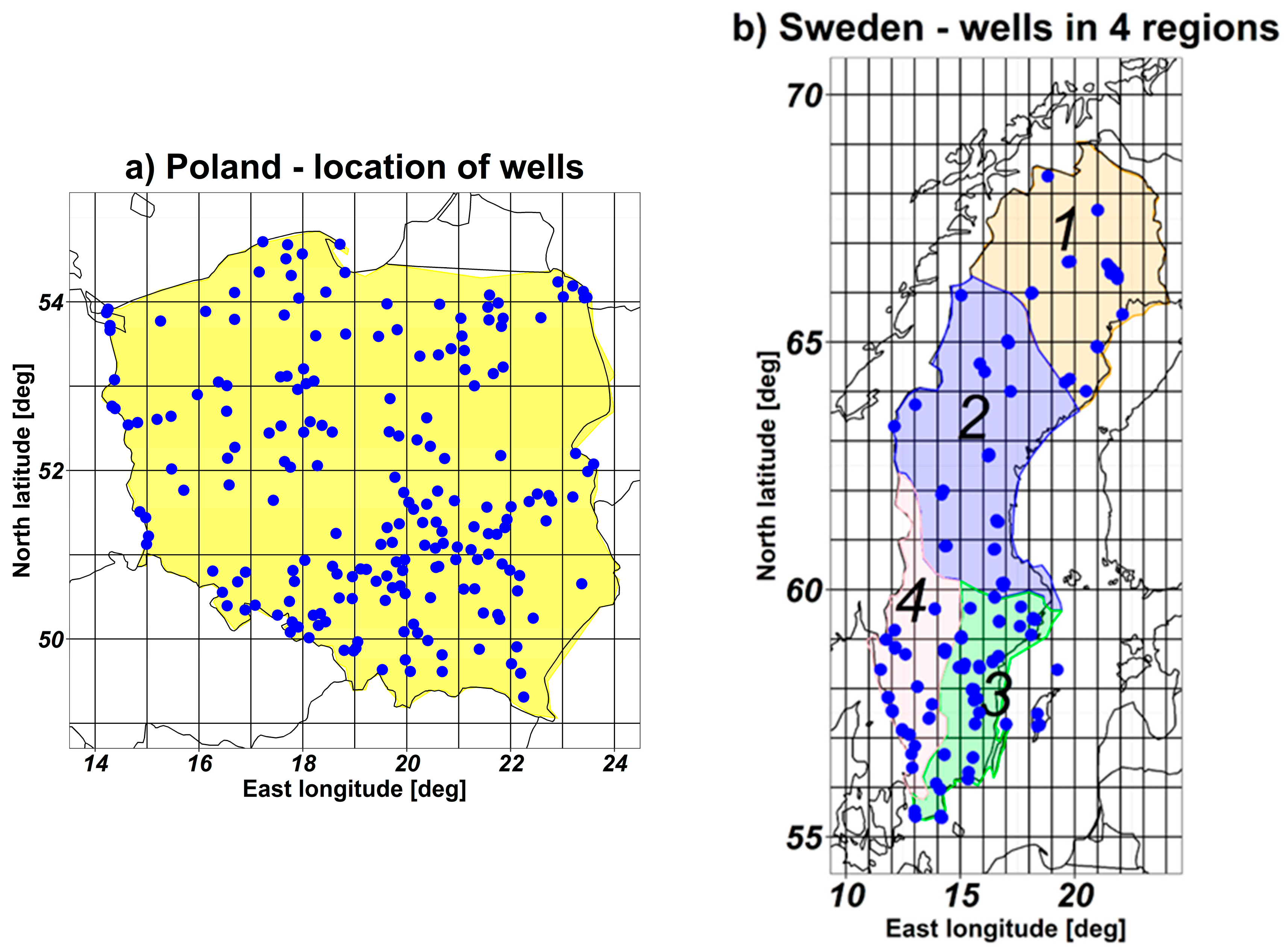
2. Study Area Description
- Region 2—between the Umeälven and Dalälven basins, where the GWS regime is still strongly governed by snowmelt in spring and autumn rainfall. According to the Köppen classification system, the predominant climate is the same as for region 1.
- Region 3—the eastern region south of Dalälven basin, where the GWS regime is governed by rainfall of the autumn–winter period and spring snowmelt. According to the Köppen classification system, the predominant climate is temperate, without a dry season and with warm summers (abbreviated Cfb, [36,37]). The region additionally has significantly lower annual average precipitation (around 600 mm/year) than region 4.
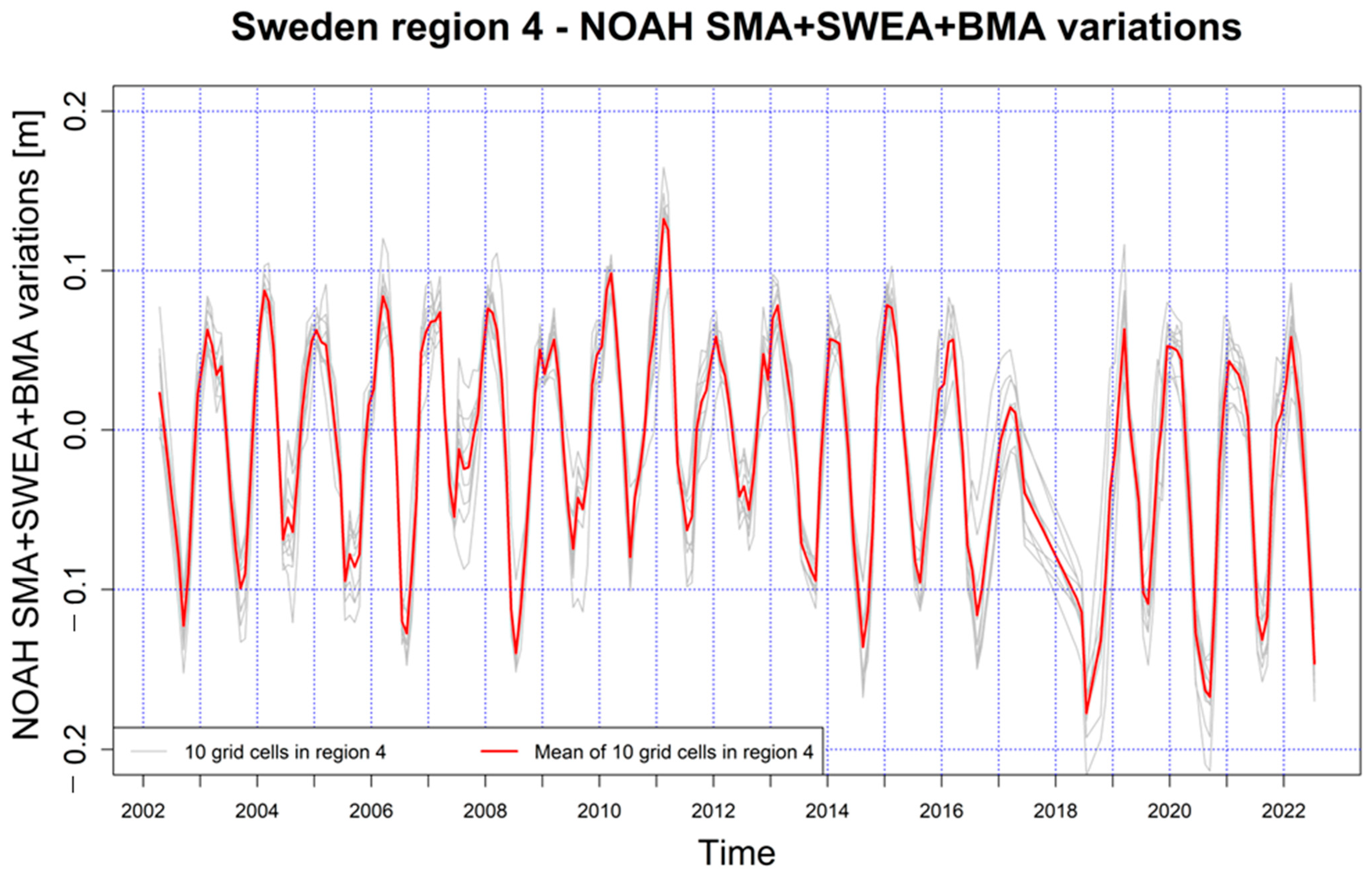
- Region 4—the western region south of Dalälven basin, where the GWS regime is mainly governed by autumn–winter rainfalls, as well as the, negligible, effect of snowmelt. According to the Köppen classification system, the predominant climate is the same as in region 3 (also as in Poland). The region additionally has significantly higher annual average precipitation (around 900 mm/year) than region 3.
3. Observational Data and Models
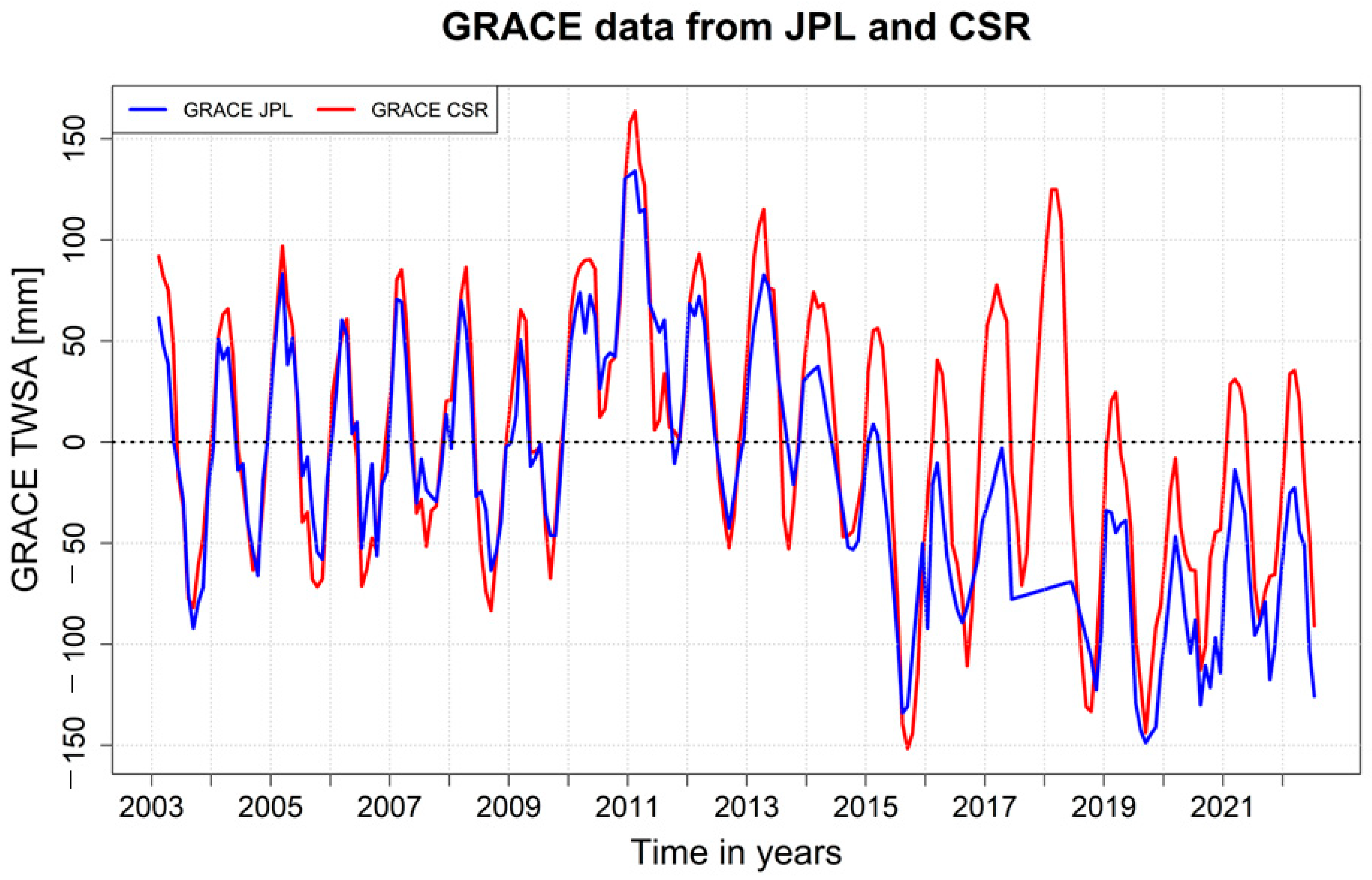
3.1. GRACE Observations
3.2. Observations in Groundwater Wells
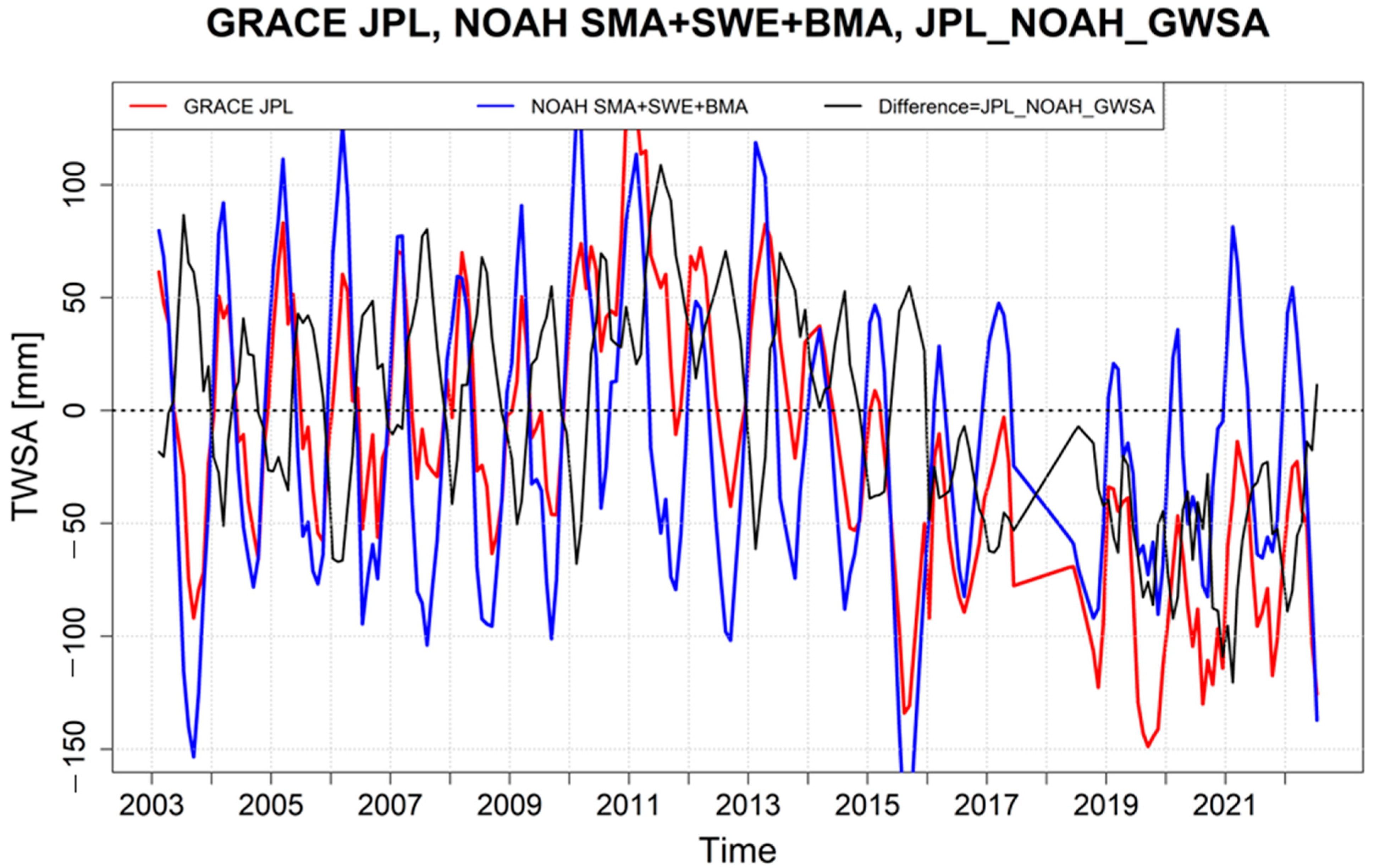
3.3. The GLDAS NOAH Model
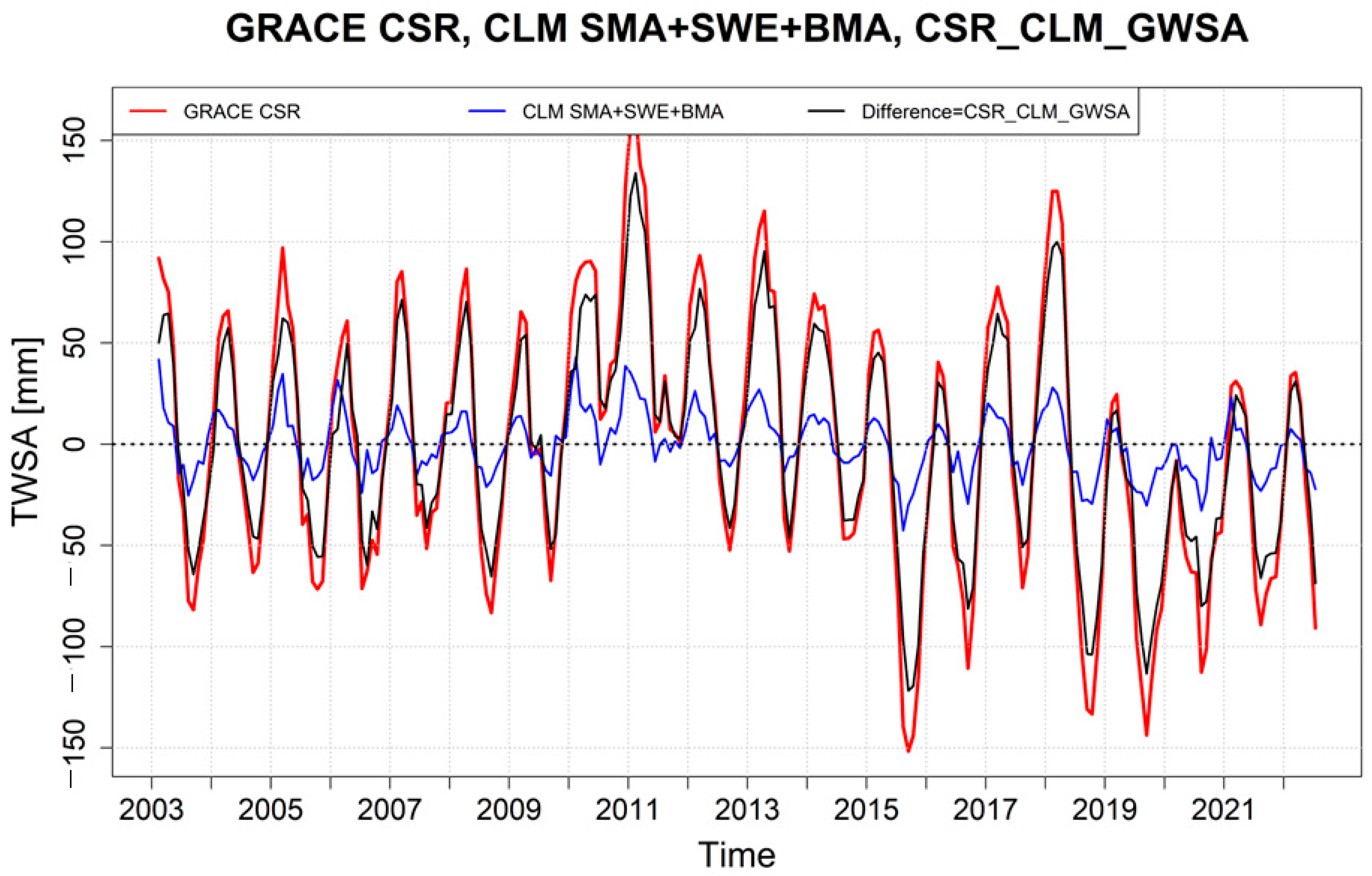
3.4. The GLDAS CLM Model
4. Theory
5. Results
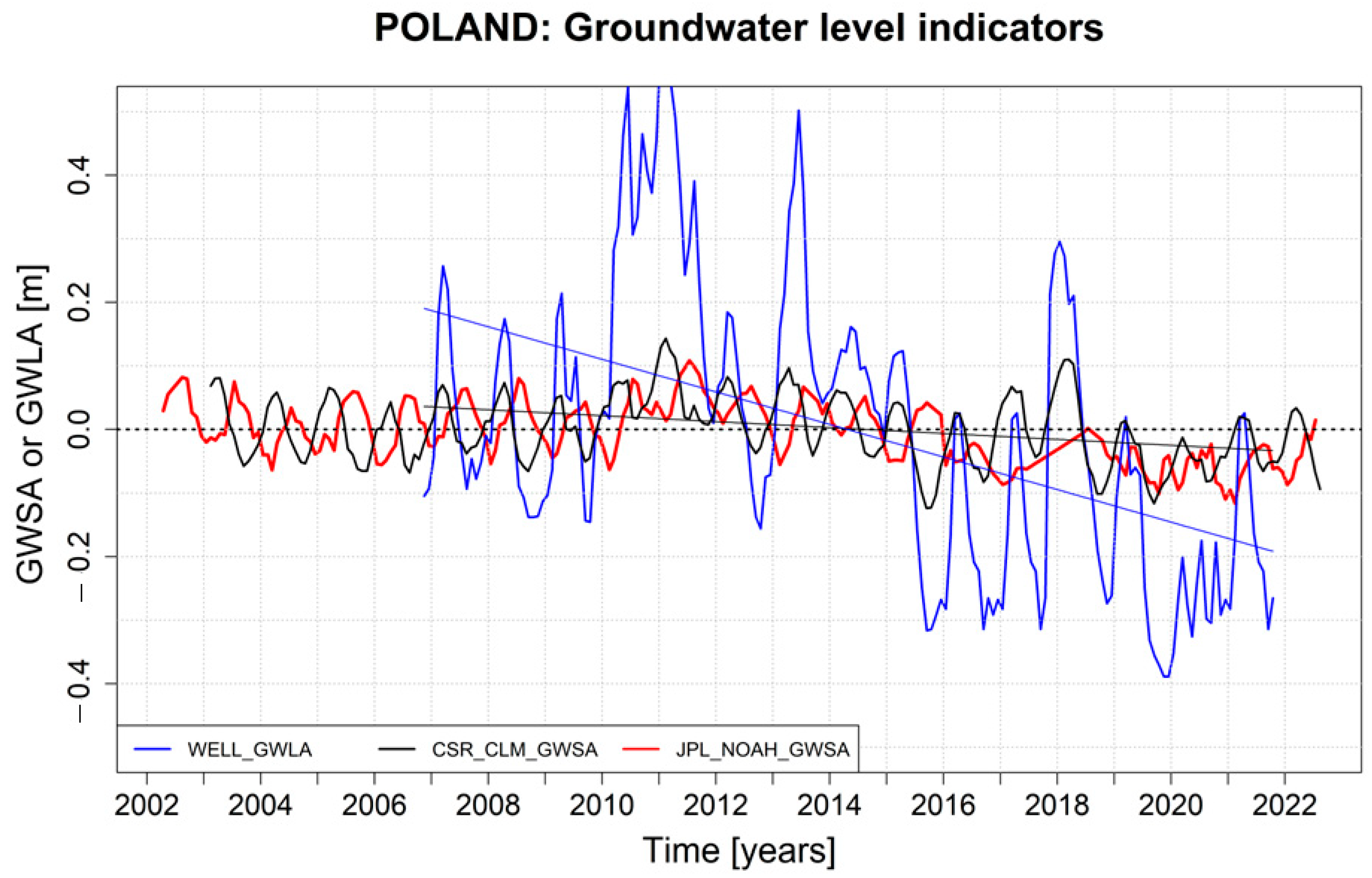
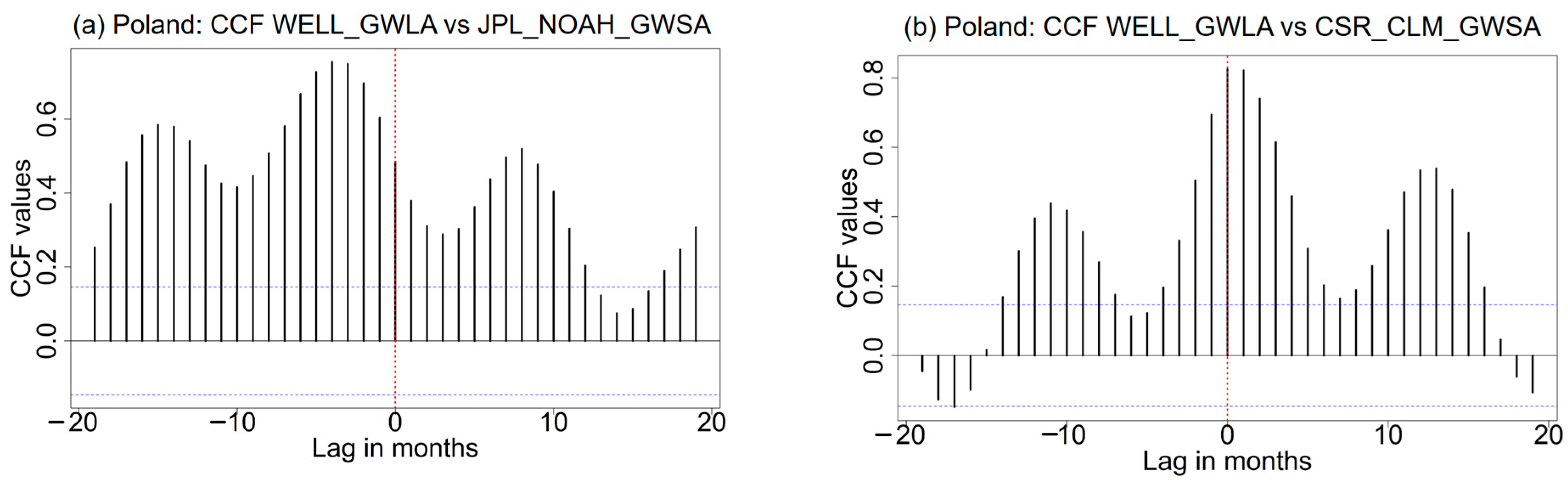
5.1. Poland
5.2. Sweden
6. Discussion
7. Conclusions
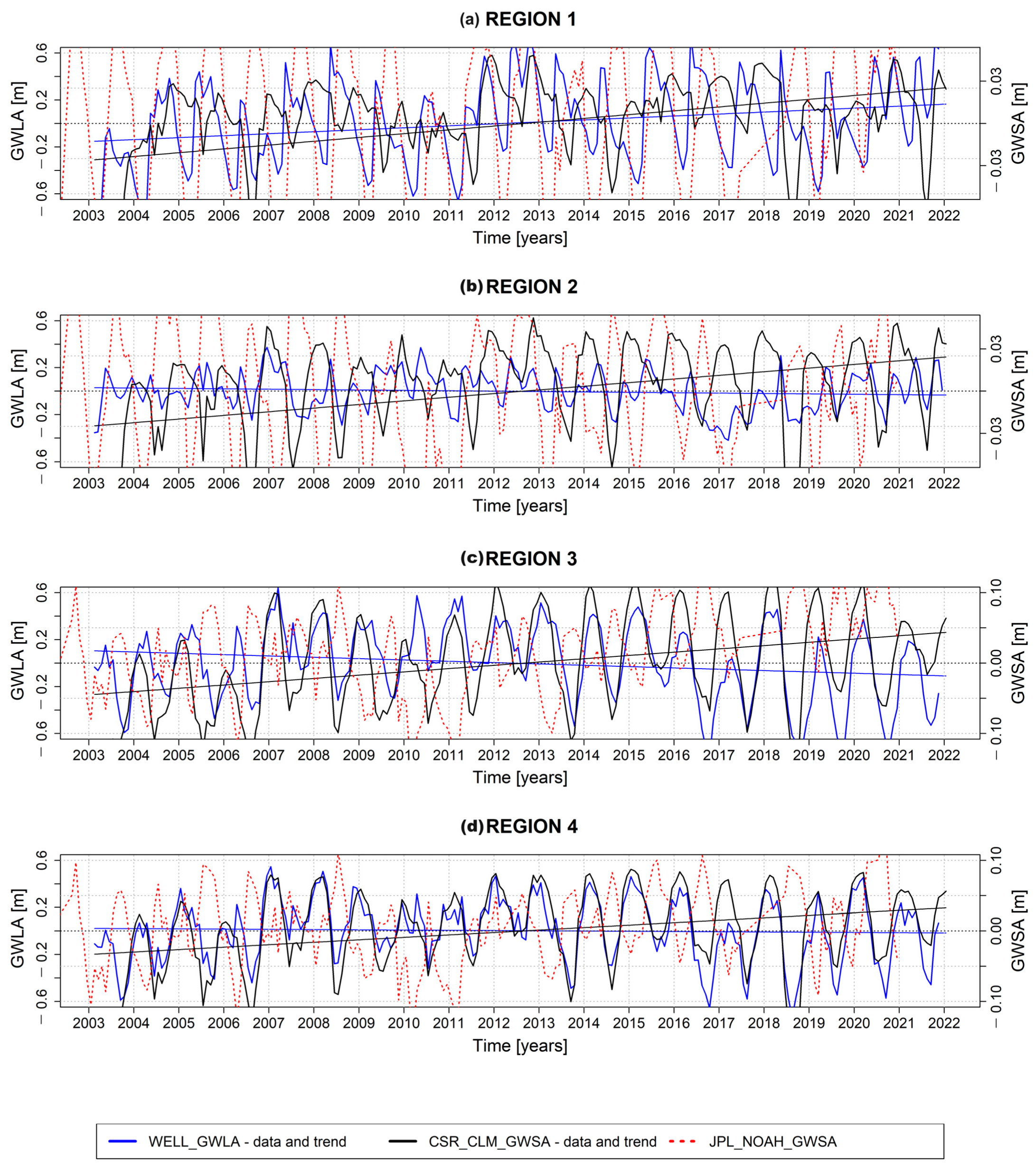
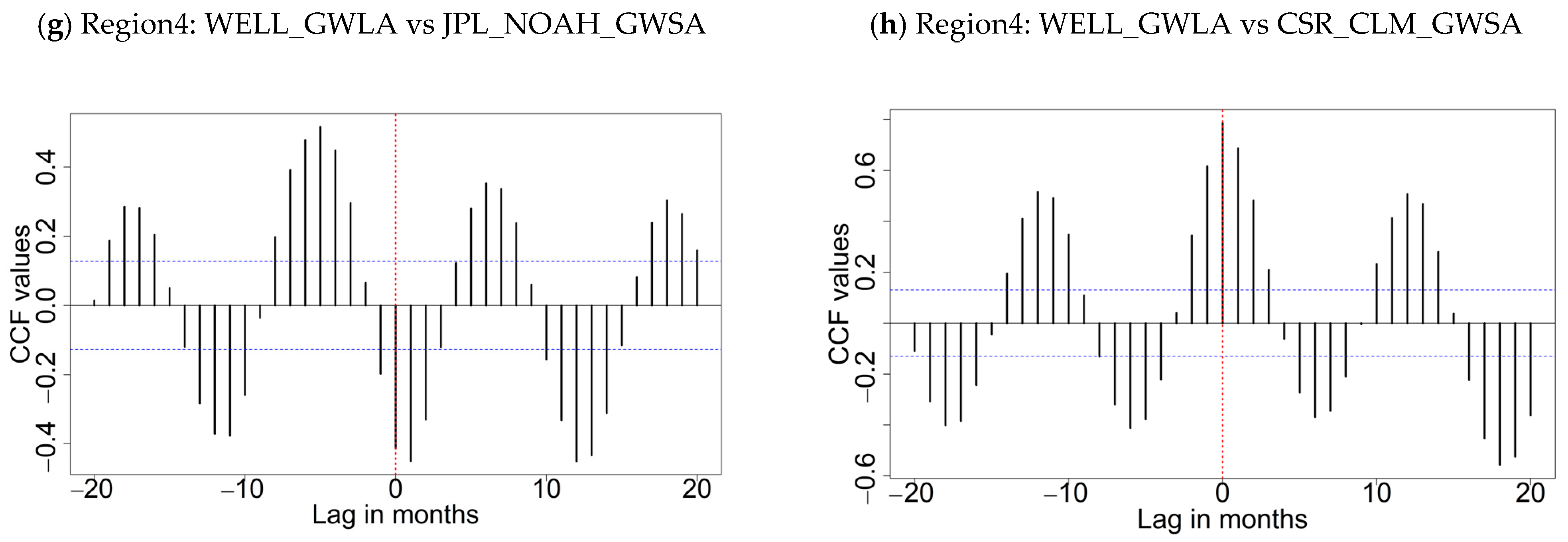
- In temperate European climate zones (Poland and south Sweden), the CSR_CLM_GWSA model showed very good agreement with changes in 387 observation wells (cross-correlation coefficient of 0.8, implying a good performance of remote sensing models in representing seasonal groundwater dynamics, including amplitudes of groundwater level). However, the JPL_NOAH_GWSA model did not show satisfactory results as the NOAH values for key water balance terms (sum of SMA, SWEA and BMA) that were subtracted from TWSA to obtain GWSA were too large compared with direct measurements, which led to the over-correction of otherwise consistent TWSA results. The use of the JPL_NOAH_GWSA model should consequently be avoided, at least under temperate conditions similar to those investigated here.
- In sub-Arctic and Arctic climate zones, our comparison involving 85 wells in northern Sweden showed that the CSR_CLM_GWSA model results were poorly correlated with ground observations (cross-correlation coefficients of 0.3 or less).
- Considering multi-annual (2003–2022) trends within the temperate climate regions, the remote sensing model indicated increasing groundwater levels in SW Sweden, whereas the region’s 59 wells indicated essentially unchanged conditions. For the 113 wells of SE Sweden, there was even disagreement on the direction of change. While the remote sensing model indicated increasing levels, the observations indicated a decreasing trend of ~10 mm/a. These discrepancies may, however, not necessarily be due to errors of the remote sensing model but may rather reflect impacts of anthropogenic pressures, which are higher near the observation wells that are often located in eskers used for water supply; consequently, this more generally emphasizes the potential significant roles of other pressures on water resources apart from climate change.
- For multi-annual groundwater trends of sub-Arctic and Arctic Sweden, the (more uncertain) remote sensing results nevertheless agree reasonably well with the groundwater well observations that show increasing groundwater levels of up to ~14 mm/a, which is consistent with reported trends of large Siberian river basins and in contrast with decreasing trends of large North American river basins.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Guppy, L.; Uyttendaele, P.; Villholth, K.G.; Smakhtin, V. Groundwater and Sustainable Development Goals: Analysis of Inter-Linkages; United Nations University Institute for Water, Environment and Health: Hamilton, ON, Canada; ISBN 9789280860924.
- Solander, K.C.; Reager, J.T.; Wada, Y.; Famiglietti, J.S.; Middleton, R.S. GRACE satellite observations reveal the severity of recent water over-consumption in the United States. Sci. Rep. 2017, 7, 8723. [Google Scholar] [CrossRef]
- Tzanakakis, V.A.; Paranychianakis, N.V.; Angelakis, A.N. Water Supply and Water Scarcity. Water 2020, 12, 2347. [Google Scholar] [CrossRef]
- Śliwińska, J.; Birylo, M.; Rzepecka, Z.; Nastula, J. Analysis of Groundwater and Total Water Storage Changes in Poland Using GRACE Observations, In-situ Data, and Various Assimilation and Climate Models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the global mass change data record: Grace follow-on instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Rzepecka, Z.; Birylo, M. Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland. Geosciences 2020, 10, 124. [Google Scholar] [CrossRef]
- Karimi, H.; Iran-Pour, S.; Amiri-Simkooei, A.; Babadi, M. A gap-filling algorithm selection strategy for GRACE and GRACE Follow-On time series based on hydrological signal characteristics of the individual river basins. J. Géod. Sci. 2023, 13, 20220129. [Google Scholar] [CrossRef]
- Shao, C.; Liu, Y. Analysis of Groundwater Storage Changes and Influencing Factors in China Based on GRACE Data. Atmosphere 2023, 14, 250. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global terrestrial water storage and drought severity under climate change. Nat. Clim. Chang. 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Sinha, D.; Syed, T.H.; Famiglietti, J.S.; Reager, J.T.; Thomas, R.C. Characterizing drought in India using GRACE observations of terrestrial water storage deficit. J. Hydrometeorol. 2017, 18, 381–396. [Google Scholar] [CrossRef]
- Cooley, S.S.; Landerer, F.W. GRACE D-103133 Gravity Recovery and Climate Experiment Follow-On (GRACE-FO) Level-3 Data Product User Handbook; NASA Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2019.
- Li, M.; Wu, P.; Ma, Z.; Lv, M.; Yang, Q.; Duan, Y. The decline in the groundwater table depth over the past four decades in China simulated by the Noah-MP land model. J. Hydrol. 2022, 607, 127551. [Google Scholar] [CrossRef]
- Birylo, M.; Rzepecka, Z.; Nastula, J. Assessment of the Water Budget from GLDAS Model. In Proceedings of the 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018. [Google Scholar] [CrossRef]
- Verma, K.; Katpatal, Y.B. Groundwater Monitoring Using GRACE and GLDAS Data after Downscaling within Basaltic Aquifer System. Groundwater 2018, 58, 143–151. [Google Scholar] [CrossRef]
- Schumacher, M.; Forootan, E.; van Dijk, A.I.J.M.; Schmied, H.M.; Crosbie, R.S.; Kusche, J.; Doell, P. Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model. Remote Sens. Environ. 2018, 204, 212–228. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2006, 15, 159–166. [Google Scholar] [CrossRef]
- Badora, D. Studium wykorzystania modelu GRACE w ocenie zmian poziomu wód gruntowych w kontekście dostępności wody dla rolnictwa w zlewni rzeki Wisły. Pol. J. Agron. 2016, 27, 21–31. [Google Scholar] [CrossRef]
- Badora, D.; Wawer, R. Review of selected geophysical methods used in the assessment of water resources for agriculture. Pol. J. Agron. 2018, 34, 23–33. [Google Scholar] [CrossRef]
- Lenczuk, A.; Klos, A.; Bogusz, J. Studying spatio-temporal patterns of vertical displacements caused by groundwater mass changes observed with GPS. Remote Sens. Environ. 2023, 292, 113597. [Google Scholar] [CrossRef]
- Taylor, C.J.; Alley, W.M. Ground-Water-Level Monitoring and the Importance of Long-Term Water-Level Data; US Geological Survey: Denver, CO, USA, 2001; Volume 1217.
- Megdal, S.B.; Gerlak, A.K.; Varady, R.G.; Huang, L. Groundwater governance in the United States: Common priorities and challenges. Groundwater 2015, 53, 677–684. [Google Scholar] [CrossRef] [PubMed]
- Araújo, R.S.; da Gloria Alves, M.; de Melo, M.T.C.; Chrispim, Z.M.; Mendes, M.P.; Júnior, G.C.S. Water resource management: A comparative evaluation of Brazil, Rio de Janeiro, the European Union, and Portugal. Sci. Total Environ. 2015, 511, 815–828. [Google Scholar] [CrossRef]
- Chinnasamy, P.; Maheshwari, B.; Prathapar, S. Understanding Groundwater Storage Changes and Recharge in Rajasthan, India through Remote Sensing. Water 2015, 7, 5547–5565. [Google Scholar] [CrossRef]
- Inoue, J.; Yamazaki, A.; Ono, J.; Dethloff, K.; Maturilli, M.; Neuber, R.; Edwards, P.; Yamaguchi, H. Additional Arctic observations improve weather and sea-ice forecasts for the Northern Sea Route. Sci. Rep. 2015, 5, 16868. [Google Scholar] [CrossRef] [PubMed]
- Duncan, B.N.; Ott, L.E.; Abshire, J.B.; Brucker, L.; Carroll, M.L.; Carton, J.; Comiso, J.C.; Dinnat, E.P.; Forbes, B.C.; Gonsamo, A.; et al. Space-Based Observations for Understanding Changes in the Arctic-Boreal Zone. Rev. Geophys. 2009, 8, e2019RG000652. [Google Scholar] [CrossRef]
- Müller, F.L.; Dettmering, D.; Bosch, W.; Seitz, F. Monitoring the Arctic Seas: How Satellite Altimetry Can Be Used to Detect Open Water in Sea-Ice Regions. Remote Sens. 2017, 9, 551. [Google Scholar] [CrossRef]
- Muskett, R.R.; Romanovsky, V.E. Groundwater storage changes in arctic permafrost watersheds from GRACE and in situ measurements. Environ. Res. Lett. 2009, 4, 045009. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Werth, S.; Ramillien, G.; Prigent, C.; Bonnet, M.P. Interannual variations of the terrestrial water storage in the Lower Ob’Basin from a multisatellite approach. Hydrol. Earth Syst. Sci. 2010, 14, 2443–2453. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, J.; Chen, Y.; Li, W. Downscaling simulation of groundwater storage in the Tarim River basin in northwest China based on GRACE data. Phys. Chem. Earth 2021, 123, 103042. [Google Scholar] [CrossRef]
- Eveborn, D.; Vikberg, E.; Thunholm, B.; Hjerne, C.E.; Gustafsson, M. Grundvattenbildning och Grundvattentillgång i Sverige; Geological Survey of Sweden: Uppsala, Sweden, 2017. [Google Scholar]
- Krogulec, E.; Zabłocki, S.; Sawicka, K. Changes in groundwater regime during vegetation period in Groundwater Dependent Ecosystems. Acta Geol. Pol. 2016, 66, 525–540. [Google Scholar] [CrossRef]
- Rzepecka, Z.; Birylo, M.; Kuczynska-Siehien, J. Analysis of groundwater level variations and water balance in the area of the Sudety mountains. Acta Geodyn. Geomater. 2017, 14, 313–321. [Google Scholar] [CrossRef]
- Ehlert, K. Avrinningsområden i Sverige. Del 1. Vattendrag till Bottenviken: Svenskt Vattenarkiv 2020. Available online: https://www.smhi.se/polopoly_fs/1.164669!/Hydrologi_82%20Avrinningsomr%C3%A5den%20i%20Sverige.%20Del%201.%20Vattendrag%20till%20Bottenviken.pdf (accessed on 10 May 2023).
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.W. Using the Köppen classification to quantify climate variation and change: An example for 1901–2010. Environ. Dev. 2013, 6, 69–79. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Sheffield, J.; Wood, E.; Sutanudjaja, E. Long-term, non-anthropogenic groundwater storage changes simulated by three global-scale hydrological models. Sci. Rep. 2019, 9, 10746. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pham, Q.B.; Rahaman, M.M.; Dang, T.D.; Anh, D.T. Improving the Resolution of GRACE Data for Spatio-Temporal Groundwater Storage Assessment. Remote Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Neves, M.C.; Nunes, L.M.; Monteiro, J.P. Evaluation of GRACE data for water resource management in Iberia: A case study of groundwater storage monitoring in the Algarve region. J. Hydrol. Reg. Stud. 2020, 32, 100734. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Huang, F.; Zhang, Y.; Zhang, D.; Chen, X. Environmental Groundwater Depth for Groundwater-Dependent Terrestrial Ecosystems in Arid/Semiarid Regions: A Review. Int. J. Environ. Res. Public Health 2019, 16, 763. [Google Scholar] [CrossRef]
- Hamm, A.; Frampton, A. Impact of lateral groundwater flow on hydrothermal conditions of the active layer in a high-Arctic hillslope setting. Cryosphere 2021, 15, 4853–4871. [Google Scholar] [CrossRef]
- Nygren, M.; Giese, M.; Barthel, R. Recent trends in hydroclimate and groundwater levels in a region with seasonal frost cover. J. Hydrol. 2021, 602, 126732. [Google Scholar] [CrossRef]
- Hachborn, E.; Berg, A.; Levison, J.; Ambadan, J.T. Sensitivity of GRACE-derived estimates of groundwater-level changes in southern Ontario, Canada. Hydrogeol. J. 2017, 25, 2391–2402. [Google Scholar] [CrossRef]
- Rateb, A.; Scanlon, B.R.; Pool, D.R.; Sun, A.; Zhang, Z.; Chen, J.; Clark, B.; Faunt, C.C.; Haugh, C.J.; Hill, M.; et al. Comparison of Groundwater Storage Changes from GRACE Satellites with Monitoring and Modeling of Major U.S. Aquifers. Water Resour. Res. 2020, 56, e2020WR027556. [Google Scholar] [CrossRef]
- Strassberg, G.; Scanlon, B.R.; Rodell, M. Comparison of Seasonal Terrestrial Water Storage Variations from GRACE with Groundwater-Level Measurements from the High Plains Aquifer (USA). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Birylo, M.; Rzepecka, Z. Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland). Remote Sens. 2023, 15, 5226. [Google Scholar] [CrossRef]
- Rodhe, A.; Lindström, G.; Dahné, J. Grundvattennivåer i Ett Förändrat Klimat; Slutrapport Från SGU-Projektet; Grundvattenbildning i Ett Förändrat Klimat; SGUs Diarienummer 60-1642; Institutionen för Geovetenskaper, Uppsala Universitet: Uppsala, Sweden, 2007. [Google Scholar]
- Nadeau, S.; Rosa, E.; Cloutier, V.; Daigneault, R.-A.; Veillette, J. A GIS-based approach for supporting groundwater protection in eskers: Application to sand and gravel extraction activities in Abitibi-Témiscamingue, Quebec, Canada. J. Hydrol. Reg. Stud. 2015, 4, 535–549. [Google Scholar] [CrossRef]
- Barthel, R.; Stangefelt, M.; Giese, M.; Nygren, M.; Seftigen, K.; Chen, D. Current understanding of groundwater recharge and groundwater drought in Sweden compared to countries with similar geology and climate. Geogr. Ann. Ser. A Phys. Geogr. 2021, 103, 323–345. [Google Scholar] [CrossRef]
- Sparrenbom, C.; Jeppsson, H.; Appelo, T.; Barmen, G.; Barth, J.; Dahlin, T.; Dahlqvist, P.; Dopson, M.; O Ericsson, L.; Fagerlund, F.; et al. Grundvattenboken; Studentlitteratur AB: Lund, Sweden, 2022. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzepecka, Z.; Birylo, M.; Jarsjö, J.; Cao, F.; Pietroń, J. Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data. Remote Sens. 2024, 16, 2104. https://doi.org/10.3390/rs16122104
Rzepecka Z, Birylo M, Jarsjö J, Cao F, Pietroń J. Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data. Remote Sensing. 2024; 16(12):2104. https://doi.org/10.3390/rs16122104
Chicago/Turabian StyleRzepecka, Zofia, Monika Birylo, Jerker Jarsjö, Feifei Cao, and Jan Pietroń. 2024. "Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data" Remote Sensing 16, no. 12: 2104. https://doi.org/10.3390/rs16122104
APA StyleRzepecka, Z., Birylo, M., Jarsjö, J., Cao, F., & Pietroń, J. (2024). Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data. Remote Sensing, 16(12), 2104. https://doi.org/10.3390/rs16122104





