Abstract
Abstract: While software-defined radars can switch their transmitted waveform on the go, they cannot transmit all waveforms at the same time, meaning they must balance the advantages and drawbacks of each configuration. Here, we propose theoretically and demonstrate experimentally the universal radar, which can apply the desired waveform in the post-processing stage after the physical measurement has been performed. This method also allows using a single measurement of a scene to design and test any other radar in complex scenarios without having to take it to the field. The method is based on post-processing the frequency response measured by a synthetically broadband stepped-frequency continuous wave radar, such as a vector network analyzer. An algorithm for overcoming distortions due to moving targets is derived as well. This approach not only provides an ultra-wideband software-only defined radar, but it also enables the acquired data from any measured site to be used for the design and analysis of almost any other future radar system, significantly cutting the time and cost of new developments. The method suggests the creation of radar raw data repositories that can be shared across diversely different radar platforms.
1. Introduction
Radar systems have been continuously developing since the early 20th century, constantly advancing into new fields and applications where remote sensing is instrumental. Modern-day requirements for automotive, the Internet of Things (IoT), healthcare monitoring, fault imaging, and numerous other applications continue to challenge radar technologies, demanding ever-improving performance. These can include better resolution, improved ability to operate in very cluttered environments, robustness to extreme multipath scenarios, and many others. The task of radar design is traditionally application-specific, both in terms of the signal processing algorithms and the hardware implementation. Only after overcoming the challenges of fabrication and validation can the final design be field-tested. Assessing performance requires numerous locations involving complicated scenarios of multiple cooperating targets, various clutter environments, and other aspects that contribute to the complexity of the measurement. Today, the data collected from such field experiments cannot be straightforwardly used for the design and testing of other radar systems, forcing every development to go through the same costly evaluation in the same real-world scenarios as did the systems that came before. Today, the diverse range of radar applications leads to the development of special hardware and software tools that optimize for the specific task at hand. However, the high cost of such development and subsequent testing is often prohibitive for new competitors entering the market.
To remove these barriers, an all-purpose ‘universal radar’ is proposed theoretically and demonstrated experimentally. This radar is capable of emulating almost any kind of radar without having to design and fabricate its hardware. Instead, the emulation is achieved with relatively simple and straightforward signal processing software. This approach allows the radar designers access to a database of raw recordings from real-world scattering scenes, enabling a considerable reduction in the development and testing time of both radar hardware requirements and algorithm performance.
In most cases, the hardware realization of radar systems is waveform-specific. In particular, radio frequency (RF) systems are optimized to transmit a pre-defined signal, such as pulsed, frequency modulated (FMCW), phase coded, or any other type of modulation, while the receiver is matched to the waveform of choice [1,2,3]. Different radars, which are constructed this way, have to trade-off between the advantages and disadvantages of the chosen waveform, such as autocorrelation and Doppler side lobe levels, Doppler sensitivity, signal-to-noise ratio (SNR) processing gain, and more [4,5,6]. To overcome these constraints, an all-purpose radar was envisioned, one that could be programmed to switch the transmitted waveform depending on the desired application. The solution came in the form of software-defined radars (SDR) [7,8,9], which operated on the technological platform developed for software-defined radios, sharing the same acronym [9,10,11,12,13,14,15]. The key idea of this approach is using fully programmable gate arrays (FPGA) and direct digital synthesis (DDS) devices to switch the operation of the hardware in such a way that would permit transmitting the desired waveform simply by swapping the software of the radar. While this approach achieves versatility at a low cost, SDR often suffers from the limited bandwidth contemporary DDS can provide (typically, below 1 GHz), as well as from waveform distortion resulting from finite digital-to-analog resolution [16,17]. To mitigate these limitations, other forms of SDR were proposed based on the Fourier synthesis technique [18,19,20], but as with all other SDR architectures, the radar still needed to transmit a chosen waveform, leading to inevitable exposure to its weaknesses. As illustrative examples, a target could remain hidden in the shade of a sidelobe [21], and the choice of non-orthogonal waveforms could lead to spectrum-sharing issues with nearby operating systems, seeing as the whole bandwidth must be broadcast at once [22]. Finally, while SDR partially addresses the problem of versatility, it does not allow for the recorded raw data to be straightforwardly reused for the design and analysis of other radar systems.
Today, the diverse range of radar applications leads to the development of special hardware and software tools that optimize for the specific challenges they must face. However, the high cost of this development and subsequent testing is often prohibitive for new competitors entering the market, and only after constructing the system can it be evaluated in the field. Such evaluation can be very cumbersome, requiring several cooperative targets (such as airplanes, helicopters, vehicles, drones, and other probable scene participants) to follow pre-defined tracks to establish ground truth for later comparison. Such tests are often time-consuming and require a lot of specialization, forcing the formation of dedicated field teams. To remove these barriers, an all-purpose ‘universal radar’ is proposed theoretically and demonstrated experimentally based on the existing Vector Network Analyzer (VNA) architecture. This system is capable of emulating almost any kind of radar without having to design and fabricate its hardware. Instead, the emulation is achieved with relatively simple and straightforward signal processing software. This approach also enables radar designers to access a database of raw recordings from real-world scattering scenes that can be used for the validation of their signal processing algorithms and hardware requirements before having the final product at hand. This method can have numerous applications in remote sensing, such as healthcare [23,24,25], biometric monitoring [26], gesture recognition [27,28,29], automotive [30,31], through-the-wall imaging [32,33,34], and any other radar-related field, including sonars, LIDAR’s, and so on.
The manuscript is organized as follows: first, a signal processing method for extracting the response of any waveform from the frequency response is proposed theoretically and verified experimentally. Specifically, static targets are detected by emulating synthetically constructed pulsed, phase-coded (Barker 13), and linear frequency modulation (LFM) waveforms, which are synthesized from the frequency response of a vector network analyzer (VNA) [35,36]. Then, the method is extended and applied to a moving target in the anechoic chamber, exploring intrinsic trade-offs. Finally, a signal processing method for overcoming Doppler distortion in raw data is derived.
2. Methods—Extracting Raw Data from the Frequency Response of Static Scenes
In the vast majority of practical scattering scenarios, the medium between the transmitting and receiving antennas of any radar system can be considered approximately linear and time-invariant (LTI) [37,38], as long as no non-linear materials are present and if the motion of scattering objects is slow enough (quasi-static) [39,40,41]. Since LTI systems are completely characterized by their frequency response (the Fourier transform of the impulse response), their measurement, including amplitude and phase, contains all the information about the scattering scene. This includes the channel’s response to any type of transmitted waveform. In particular, it holds information about the location of scatterers in the scene, the detection of which is one of the main objectives of radar systems. Proper processing of the frequency response, therefore, allows retrieving the echo of any possible radar waveform without ever having to transmit it. This measurement could be achieved by transmitting an ultra-wideband short pulse of significant energy (theoretically, a delta function), yet this would set a severe constraint on the hardware. Instead, it is more practical to transmit long pulsed envelopes of varying single-tone frequencies, which is, in fact, equivalent to discretely sampling the frequency response of the scattering scene. To achieve this, a stepped-frequency continuous wave (SFCW) radar is ideal [42], as it allows very low noise figures for the receiver owing to its instantaneous narrow bandwidth as well as the high average power that can be transmitted during long temporal pulses. These advantages, along with the ability to synthesize very large bandwidths (in some cases exceeding 40 GHz), had already brought such systems for applications in transmission line fault detection [43], ground penetrating [3], through the wall [32,33], and other applications where cost is not a significant factor. In such cases, VNAs can find use, yet their relatively high cost, along with a lack of clear understanding of how to apply them to dynamic scenarios, keeps them from being employed in broader applications. Recently, SFCW radars have gained renewed interest, with cheap, low-power systems on chip becoming readily available [44], providing a potential platform for the following method.
Consider the frequency response of a scattering scene containing several targets along with multipath ghosts, as exemplified in Figure 1a. The frequency response contains only positive angular frequencies ( and it is the Fourier transform of an analytical function, the real part of which is the impulse response of the investigated scene. To synthesize the emulated temporal echo at the receiver in response to some arbitrary emulated temporal waveform , a windowing function , which is the Fourier transform of the temporal waveform, needs to be multiplied by the frequency response and inversely transformed back into the time domain:
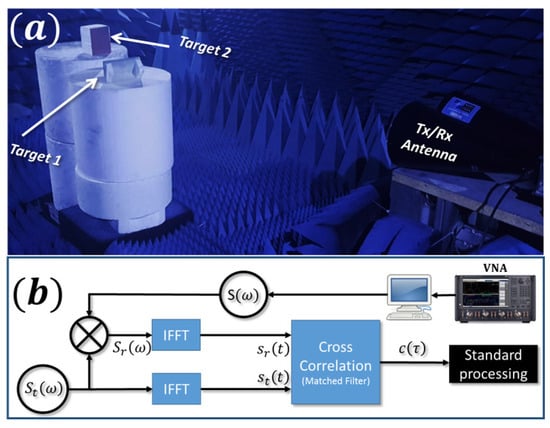
Figure 1.
(a) Experimental setup photograph. (b) Signal processing block diagram.
Note that the above temporal function is a complex analytical function, the real part of which gives the real-valued echo that would be measured at the receiver. In the remaining text, the real-part operation is not performed, seeing as the analytical signal already contains all the required information. The form of Equation (1) is intuitively understandable, seeing as for an LTI system, each frequency component experiences some attenuation and phase delay due to the propagation channel, which is completely described by the frequency response of the LTI scattering scene. It is, therefore, clear that the multiplication in Equation (1) would apply the corresponding attenuation and phase delay to all the frequency components of the transmitted waveform, with the inverse transform bringing the result back into the time domain and producing the received echo. Here, it is important to stress the difference between using the VNA in our method and ‘standard’ approaches where such systems were used to create radar images (for example, in-ground penetrating applications). In the standard case, the windowing function is unity for all frequencies, allowing for maximal bandwidth for optimal resolution. Our method, on the other hand, can achieve other desirable properties, such as low side lobe level in autocorrelation and any other waveform advantage.
Once the echo is synthesized, it can be processed in a standard way, as if it were not emulated but actually recorded by a dedicated system. Note that such effects as multipath interference, ghost targets, and more are all present in the above formulation, just as they would be if the waveforms were transmitted in the air. The first step in processing the received frame of S-parameters, often termed a pulse repetition interval (PRI) in pulsed systems, would normally be removing the carrier and decimating the remaining signal to match the range resolution that can be expected from the bandwidth of the signal. Yet, such treatment is restrictive to narrowband waveforms, seeing as the concept of carrier frequency is not well defined for broadband signals, which can nonetheless be correctly emulated by the proposed method. To account for broadband signals, the first step taken by the method is directly applying pulse compression by matched filtering, which can be achieved by cross-correlation of the echo with the transmitted waveform to detect the locations of targets:
The output of the cross-correlation can finally be compared to a threshold to determine the presence and location of objects of interest. The signal processing method described above is shown schematically in Figure 1b. Note that , the emulated signal, is completely arbitrary, with all relevant information about the scattering channel encompassed entirely in the frequency response . In practice, the frequency response is a set of discrete samples in frequency. The more points measured, the slower the maximal frame rate (inverse of the PRI) of the radar can be, and therefore, the lower its unambiguous Doppler velocity is. However, using too few points can lead to insufficient accuracy and the degradation of the cross-correlation. Assuming uniform sampling of the bandwidth, a reversed Nyquist relation holds true, where the frequency sample rate (i.e., the distance between consecutive samples in the frequency domain) determines the maximal range (time delay) of the emulated received echo . It should, however, be noted that the unambiguous range is limited by the duration of the single-tone pulse (i.e., the period of time used for sampling every frequency). Similarly, another reversed relation exists between the width of the bandwidth (i.e., the total number of points inside the bandwidth that is being sampled by the constant frequency sampling rate) and the range gate length, where the larger the bandwidth, the better the range resolution is. The final important factor is the intermediate frequency (IF) bandwidth of the SFCW radar, which is related to the inverse of the coherent single-tone pulse duration, affecting the length of the frame scan. The lower the IF frequency is, the better the SNR can be, the longer the scan time is, and the longer the unambiguous range is. At this point, it is important to stress that the versatility of the proposed method, which allows emulation of all waveform radars within the bandwidth, inherently comes at the expense of maximal frame rate (or PRF). Dedicated systems, transmitting all the bandwidth at once, will clearly have an advantage in this metric.
3. Experimental Verification—Static Targets
To validate the method proposed in the previous section, an experiment was conducted in an anechoic chamber. In the first experiment, two rectangular metallic plates of size were placed at a rather arbitrary distance of 2.2 and 2.8 m away from a simultaneously transmitting and receiving broadband (2–18 GHz) horn antenna, as shown in Figure 1a. The targets were placed approximately on the same radial line, clearing a direct line of sight between both and the radar antennas. The horn was connected to a VNA (Keysight PNA-L N5232B) with up to 20 GHz of bandwidth via broadband cables.
The frequency response of the empty room was measured by performing an sweep over a controllable bandwidth, number of sweep points, total scan time, and intermediate frequency (IF) bandwidth. This calibration procedure was mainly required for the removal of reflections coming from the antenna itself, yet the process is not necessary if a moving target indicator (MTI) filter is implemented [45]. The subsequent measurements of the frequency response from two different scenes were performed, one with a single target in the anechoic chamber and another with both targets present. The recorded frequency responses (S-parameters) were processed as described in the previous section and as shown schematically in Figure 1b. Three types of windowing functions were used for the emulation of the echoes, as prescribed by Equation (1). The chosen windows were (i) pulsed, (ii) Barker 13, and (iii) LFM, as these are some of the most commonly used waveforms. The absolute values of these frequency domain windows are plotted in Figure 2a. It is important to stress that all the processing was conducted on the same measured frequency response frame . The resulting temporal echoes were down-converted to baseband using the heterodyne technique implemented digitally in software and finally cross-correlated with the temporal waveform as in Equation (2). The result of the cross-correlation for a single metallic plate is plotted in Figure 2b, while the cross-correlation of the scattering scene containing both plates is presented in Figure 2c.
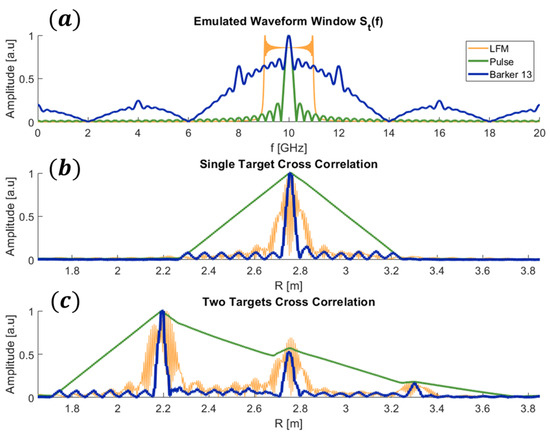
Figure 2.
(a) The absolute value of the emulated waveforms in the frequency domain. (b) Experimental result of cross-correlation with a single target in the anechoic chamber. (c) Experimental result of cross-correlation: when two targets are present in the anechoic chamber, a multipath echo is also observed.
It can be observed that for the single target, the classic shapes of the autocorrelation of each of the waveforms appear, where the width of the autocorrelation is determined by the overall bandwidth used for the processing. It can be seen from Figure 2a that the lowest bandwidth is that of the pulsed waveform, corresponding to the broadest cross-correlation in Figure 2b. It is important to note that the frequency response measurement was taken with very high SNR, owing in part to the proximity of the scattering objects as well as the absorbing nature of the anechoic chamber. Similarly, when two targets are present, the cross-correlation can be seen in Figure 2c, with an additional multipath echo appearing at a location corresponding to the distance between the two metallic plates. For the pulsed waveform, the bandwidth is insufficient to clearly distinguish these targets under low SNR conditions, while the broadband Barker 13 waveform can achieve it quite well. It should be noted that the bandwidth is not an inherent property of the waveform; rather, it was chosen differently for each to exemplify the versatility of the method, being able to emulate and, in fact, synthesize the response of different types of radars, regardless of operating band or chosen waveform.
4. Experimental Verification—Moving Target
While the first experiment shows that the method can be used to investigate static scenes, most modern radars deal with dynamic environments and moving targets. To account for these, a second experiment was conducted, where the metal plate was placed on a moving platform with controllable speed, as shown in Figure 3a. For a slowly moving target, the scene could be assumed to be approximately static during the scan of the frequency response frame (set of S-parameters) and only changing in between frames (subsequent repeats of the scan). Processing each frame as in the previous static case allows obtaining the cross-correlation, where every range gate also has a phase that depends on the serial number of the frame, stemming from the Doppler effect. The velocity of the target in any range gate can be deduced by the phase shift in between frames at that delay. The most popular process is using a fast Fourier transform (FFT) on the so-called ‘slow time’ at each range gate over a pre-defined coherent processing interval (CPI), which is a certain number of frames. Figure 3b shows the result of the output of the FFT at each range gate in what is termed the range-Doppler map, obtained using 26 frames and a frame rate of 5 per second, corresponding to the maximal unambiguous velocity of 0.143 m/s at the carrier frequency of 5.23 GHz. In essence, the output of the FFT is maximal at a bin that compensates most closely to the existing Doppler shift, as can be seen by the location of the peaks. The main target is correctly located at a distance of 1.2 m and a velocity of 7.3 mm/s away from the radar (here, positive velocity is related to a receding target). The low velocity of the plate is partially due to the speed limitations of the moving platform but also due to the constraint on the frame rate (frequency response scan time) attainable by the VNA for the given number of measured frequency response points (1000) and IF filter cut-off of 10 KHz that were chosen to obtain good SNR while collecting as much data as possible. Care was taken not to increase the CPI too much as range migration could occur, where the target moves between range bins during the CPI, causing errors in the output of the FFT. This was achieved by choosing the processing to be conducted with a bandwidth of 1 GHz around the carrier of 5.23 GHz, which was produced by an emulated pulsed waveform for simplicity. Additional clutter (stationary) echoes can be seen in Figure 3b at greater ranges, corresponding to static objects in the chamber (such as the walls and the metallic platform on which the setup was mounted).
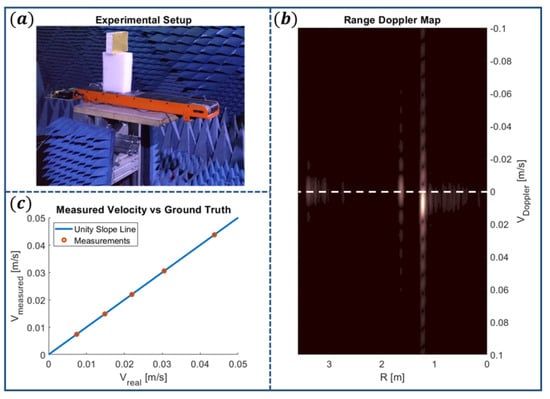
Figure 3.
(a) Photograph of the experimental setup containing a metal plate target on a conveyor moving with controllable speed. (b) Example of a Doppler range map (c) radar estimated velocity of the moving target compared with the actual speed of the plate, linear relationship shows correct estimation.
The experiment was repeated for different velocities, producing Figure 3c, showing good agreement between measured and ground truth velocities. The first point on that figure was obtained from the range-Doppler map shown in Figure 3b. It is noted that for narrowband waveforms, the frame rate serves as the de facto PRI of the radar, with unambiguous Doppler completely determined by it and the carrier frequency. To resolve ambiguities, contemporary systems often transmit staggered PRI signals, which means varying the PRI between consecutive CPIs. While this could be conducted in the field for the purpose of capturing raw data with staggered PRI, diversity can be alternatively achieved by changing the carrier frequency of the emulated pulse without having to rely on additional frames. Resolving the Doppler ambiguity can then serve to interpolate the recorded data and produce raw data containing staggered PRI frames without having to record them in the field at all. This means that the raw data from such field experiments can be used to correctly assess the performance of almost any system using staggered PRI simply by performing post-processing of the recorded frames long after the experiment was conducted.
5. Compensating Doppler-Induced Distortion of Raw Data
In the previous section, the interrogated scene was assumed to be static during the measurement of the frequency response, but the real world insists on moving fast at times, potentially causing distortions to the method described so far. To account for inter-frame motion, consider the frequency response of the observed dynamic environment , which can be broken down into contributions from static clutter and K moving targets, both real ones as well as multipath ghosts:
Assuming the SFCW radar samples the bandwidth uniformly, each frequency experiences a slightly different Doppler shift , depending on the radial velocity of the target:
where is the unmeasured static frequency response of the moving target (or multipath ghost) that would be measured if the entire bandwidth was transmitted simultaneously or if the radial velocity was zero; is the delay between transmitting the first frequency in the sampled bandwidth and the frequency , while is the time it takes to scan the whole bandwidth (frame of S-parameters). The form of the distortion to the frequency response described in Equation (4) could be understood as the phase modulation caused by each frequency due to the Doppler effect. It can be seen by substitution that the distortion term is, in fact, the frequency analog of a chirp, where the complex exponent depends quadratically on frequency. By inserting Equation (4) into Equation (1) and taking the inverse transform, the temporal effect of this distortion can be assessed. By using the fact that the inverse transform of multiplied terms is the convolution of the transformed functions, it can be deduced that the synthesized distorted echo produced by the moving target is the convolution between the statically received synthetic echo and the inverse transform of the (rearranged) frequency distortion term.
For small bandwidth () the quadratic term in Equation (5) can be neglected. The resulting transform is then proportional to a temporal Dirac delta function centered around time.
The convolution of this Dirac delta function with the undistorted temporal echo results in a shift of the emulated echo, thereby creating an error in the delay of the kth target by the amount For large bandwidth, the inverse Fourier transform in Equation (5) is that of a chirp, which is known to resemble a rectangular function. The resulting convolution thus serves to not only shift the static result in time but also to deform it, resulting in changes to the form of the cross-correlation sidelobes as well as the location and quality of the main lobe peak. This can be expected from the fact that the receiving filter is no longer matched to the deformed emulated echo .
The experiment in Section IV was repeated for varying values of target velocity, sweep time, bandwidth, and central frequency, producing the results shown in Figure 4. It should be noted that 100 sweeps of 501 S-parameter points were continuously performed over a total CPI of 6.18 [s] (). A trigger for the measurement had been placed close to the beginning of the conveyor belt, ensuring all measurements occurred within the same true range. The methods described in the previous sections were used to calculate the range of the target as a function of the parameters used, with the error indicating the absolute offset from the true range. It can be seen that the experimental results agree well with the theoretical predictions of Equation (6), where the range error is related to the delay error through the speed of light by . Note that the velocities in Figure 4a are not uniformly sampled, seeing as the conveyor belt in the experiment is non-linear. The first point in Figure 4b indicates the highest error measured for the lowest bandwidth of 10 MHz. This point is, in fact, the same as the last (topmost) point in Figure 4a, where an error of about 1.8 [m] is measured for a carrier frequency of 7 [GHz] and maximal conveyor belt velocity of 0.042 [m/s].
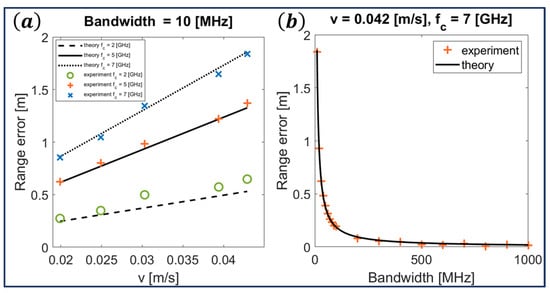
Figure 4.
Experimental verification of Equation (6) (a) range error as a function of target velocity and central frequency (b) range error as a function of radar bandwidth.
To compensate for this distortion, an estimation of the radial velocity of the kth target can be made using the coherent processing described in Section IV. For narrowband processing, the result in Equation (6) can be sufficient to ascertain the amount of error in the range. Yet, for the use of the recorded raw data for any (perhaps broadband) system, it is desirable to preprocess the frequency response frames and compensate for this Doppler distortion. It is important to stress that the abovementioned distortion is an artifact of the proposed emulation method that relies on SFCW architecture and will not be an issue for a dedicated system transmitting a constant waveform, where all the bandwidth is broadcast simultaneously. To filter out such distortions from the raw data, a prior assessment of the location of targets and their respective velocities is needed, which can be obtained from the processing steps described in the previous sections. Once the location of the targets in the frame is known, they can be isolated by a temporal filter (for example, a rectangular window of sufficient width centered around the location of the target) with the frequency response . The isolated temporal echoes can then be transformed to the frequency domain and de-chirped by multiplying each frequency by its conjugate Doppler distortion . The corrected targets can finally be summed together with the remaining clutter to obtain the corrected frequency response frame, given by
The resulting Doppler-corrected frequency response frames can now be processed using the methods described in the previous sections, providing undistorted field data that truly represent the real-world scattering scene with the moving targets of interest. The above method assumes it is possible to isolate the targets in the temporal domain, which could be challenging for nearby targets under low bandwidth conditions. In addition, if the distortion is sufficiently severe (a very fast-moving target), thresholding the cross-correlation might not detect it due to the deformation of the unmatched filter described in Equation (5), which can result in unsuccessful correction of the frame of frequency response measurements.
6. Conclusions
A universal method for emulating the operation of any kind of waveform-based radar in a recording of a real-world time-varying environment has been proposed and demonstrated. In particular, three different waveforms have been considered (pulsed, Barker 13, and LFM), producing textbook results following careful signal processing of the experimentally obtained data. In addition to detecting static targets, it was shown that moving objects can be correctly identified as well, even when moving fast relative to the effective PRF of the system, provided that corrective filtering of the Doppler-induced distortion is applied. The strength of the proposed method extends beyond an all-purpose universal radar that can turn any VNA into a broadband software-defined radar. Rather, the data collected by this type of radar can be used to design and test any kind of radar, providing designers with genuine raw data from real environments on which to test their designs and signal processing algorithms. By using this approach, the development time and cost of new platforms can be reduced significantly, alleviating the need for numerous field tests. This can be achieved since a recording of an environment can be easily used for all other platforms with the same bandwidth. A raw data repository could be created, much as is happening with image recognition and other artificial intelligence data libraries that are commonplace today.
Optimizing radar waveforms is crucial for improving the accuracy and efficiency of radar systems, enabling more precise detection and identification of objects in diverse and challenging environments. This optimization also significantly enhances the ability of radar to operate effectively in congested electromagnetic spaces, reducing interference and increasing reliability. Automotive, homeland security, healthcare, and many others are among the applications that will hopefully benefit from this approach.
Author Contributions
Conceptualization, V.K. and P.G.; methodology, V.K.; software, V.K. and E.R.; data curation, E.R. and A.K.; writing—original draft preparation, V.K. and P.G.; writing—review and editing, V.B. and T.S.; supervision, P.G.; funding acquisition, P.G., V.B. and T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Department of the Navy, Office of Naval Research Global, under ONRG award No. N62909–21–1–2038, and ERC POC Grant 101061890, ‘DeepSight’.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Levanon, N.; Mozeson, E. Radar Signals; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Skolnik, M.I. Radar Handbook; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Galati, G.; Pavan, G. Waveforms design for modern and MIMO radar. IEEE EuroCon 2013, 2013, 508–513. [Google Scholar]
- Sun, H.; Brigui, F.; Lesturgie, M. Analysis and comparison of MIMO radar waveforms. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–6. [Google Scholar]
- Yao, M.; Zhao, Z.; Chen, G.; Yang, G.; Su, F.; Li, S.; Zhang, X. Comparison of radar waveforms for a low-power vertical-incidence ionosonde. IEEE Geosci. Remote Sens. Lett. 2010, 7, 636–640. [Google Scholar] [CrossRef]
- Debatty, T. Software Defined Radar a State of the Art. In Proceedings of the 2nd International Workshop on Cognitive Information Processing, Elba, Italy, 14–16 June 2010. [Google Scholar]
- Zhang, H.; Li, L.; Wu, K. 24GHz Software-Defined Radar System for Automotive Applications. In Proceedings of the 10th European Conference on Wireless Technology, Munich, Germany, 8–10 October 2007; pp. 138–141. [Google Scholar]
- Feng, S.; Mughees, N.; Wollesen, V. Reviewing the Application and Integration of Software Defined Radios to Radar Systems. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020. [Google Scholar]
- Sadiku, M.N.O.; Akujuobi, C.M. Software-defined radio: A brief overview. IEEE Potentials 2004, 23, 14–15. [Google Scholar] [CrossRef]
- Haghighat, A. A review on essentials and technical challenges of software defined radio. In Proceedings of the IEEE Military Communications Conference MILCOM, Anaheim, CA, USA, 7–10 October 2002; Volume 1, pp. 377–382. [Google Scholar]
- Mitola, J., III. Software Radios Survey, Critical Evaluation and Future Directions; IEEE: New York, NY, USA, 1992. [Google Scholar]
- Harris, F.; Lowdermilk, W. Software defined radio: Part 22 in a series of tutorials on instrumentation and measurement. IEEE Instrum. Meas. Mag. 2010, 13, 23–32. [Google Scholar] [CrossRef]
- Catarinucci, L.; De Donno, D.; Colella, R.; Ricciato, F.; Tarricone, L. A cost-effective SDR platform for performance characterization of RFID tags. IEEE Trans. Instrum. Meas. 2012, 61, 903–911. [Google Scholar] [CrossRef]
- Wright, D.P.; Ball, E.A. Highly Portable, Low-Cost SDR Instrument for RF Propagation Studies. IEEE Trans. Instrum. Meas. 2020, 69, 5446–5457. [Google Scholar] [CrossRef]
- Pápay, Z. Numerical distortion in single-tone DDS. In Proceedings of the 8th IEEE Instrumentation and Measurement Technology Conference, Budapest, Hungary, 21–23 May 2001; Volume 2, pp. 720–724. [Google Scholar]
- Larson, D.C. High speed direct digital synthesis techniques and applications. In Proceedings of the GaAs IC Symposium. IEEE Gallium Arsenide Integrated Circuit Symposium. 20th Annual. Technical Digest 1998, Atlanta, GA, USA, 1–4 November 1998; No. 6. pp. 209–212. [Google Scholar]
- Gill, G.S. Ultra-wideband radar using Fourier synthesized waveforms. IEEE Trans. Electromagn. Compat. 1997, 39, 124–131. [Google Scholar] [CrossRef]
- Gill, G.S.; Chiang, H.F.; Hall, J. Waveform Synthesis for Ultra Wideband Radar. In Proceedings of the 1994 IEEE National Radar Conference, Atlanta, GA, USA, 29–31 March 1994; pp. 240–245. [Google Scholar]
- Rabideau, D.J. Nonlinear synthetic wideband waveforms. In Proceedings of the 2002 IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002; pp. 212–219. [Google Scholar]
- Dakai, Z.; Xiaobin, F.; Xiaoling, S.; Yinkai, L.; Min, C.; Yun, Z.; Yu, F. A method of sidelobe suppression in the specified location based on window function. Procedia Comput. Sci. 2019, 147, 84–89. [Google Scholar] [CrossRef]
- Davis, M.E. Frequency allocation challenges for ultra-wideband radars. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 12–18. [Google Scholar] [CrossRef]
- Li, C.; Lubecke, V.M.; Boric-Lubecke, O.; Lin, J. A review on recent advances in doppler radar sensors for noncontact healthcare monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2046–2060. [Google Scholar] [CrossRef]
- Lai, J.C.Y.; Xu, Y.; Gunawan, E.; Chua, E.C.-P.; Maskooki, A.; Guan, Y.L.; Low, K.-S.; Soh, C.B.; Poh, C.-L. Wireless sensing of human respiratory parameters by low-power ultrawideband impulse radio radar. IEEE Trans. Instrum. Meas. 2011, 60, 928–938. [Google Scholar] [CrossRef]
- Gu, C.; Li, C.; Lin, J.; Long, J.; Huangfu, J.; Ran, L. Instrument-based noncontact doppler radar vital sign detection system using heterodyne digital quadrature demodulation architecture. IEEE Trans. Instrum. Meas. 2010, 59, 1580–1588. [Google Scholar]
- Wang, Y.; Liu, Q.; Fathy, A.E. Simultaneous localization and respiration detection of multiple people using low cost UWB biometric pulse Doppler radar sensor. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 17–22 June 2012; pp. 31–33. [Google Scholar]
- Dekker, B.; Jacobs, S.; Kossen, A.S.; Kruithof, M.C.; Huizing, A.G. Gesture Recognition with a Low Power FMCW Radar and a Deep Convolutional Neural Network. In Proceedings of the 14th European Radar Conference, Nuremberg, Germany, 11–13 October 2017; pp. 163–166. [Google Scholar]
- Kim, Y.; Member, S.; Toomajian, B. Hand Gesture Recognition Using Micro-Doppler Signatures With Convolutional Neural Network. IEEE Access 2016, 4, 7125–7130. [Google Scholar] [CrossRef]
- Choi, J.W.; Ryu, S.J.; Kim, J.H. Short-Range Radar Based Real-Time Hand Gesture Recognition Using LSTM Encoder. IEEE Access 2019, 7, 33610–33618. [Google Scholar] [CrossRef]
- Komissarov, R.; Kozlov, V.; Filonov, D.; Ginzburg, P. Partially coherent radar unties range resolution from bandwidth limitations. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Saponara, S.; Neri, B. Radar Sensor signal acquisition and multidimensional FFT processing for surveillance applications in transport systems. IEEE Trans. Instrum. Meas. 2017, 66, 604–615. [Google Scholar] [CrossRef]
- Mahfouz, M.; Fathy, A.; Yang, Y.; Ali, E.E.H.; Badawi, A. See-through-wall imaging using ultra wideband pulse systems. In Proceedings of the 34th Applied Imagery and Pattern Recognition Workshop (AIPR’05), Washington, DC, USA, 19 October–21 December 2005; pp. 48–53. [Google Scholar]
- Ritchie, M.; Ash, M.; Chen, Q.; Chetty, K. Through Wall Radar Classification of Human Decomposition Analysis. Sensors 2016, 16, 1401. [Google Scholar] [CrossRef]
- Lee, J.S.; Nguyen, C.; Scullion, T. A novel, compact, low-cost, impulse ground-penetrating radar for nondestructive evaluation of pavements. IEEE Trans. Instrum. Meas. 2004, 53, 1502–1509. [Google Scholar] [CrossRef]
- Estrada, A. The vector network analyzer—An essential tool in modern ATE measurements. IEEE Instrum. Meas. Mag. 2012, 15, 22–26. [Google Scholar] [CrossRef]
- Marco, P.; Teppati, V.; Camarchia, V. Microwave Measurements Part1: Linear Measurements. IEEE Instrum. Meas. Mag. 2007, 10, 14–19. [Google Scholar]
- Oppenheim, A.V.; Ronald, S.W.; Buck, J.R. Discrete-Time Signal Processing; Pearson Education: Chennai, India, 2001; Volume 1, No. 21. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Kozlov, V.; Kosulnikov, S.; Vovchuk, D.; Ginzburg, P. Memory effects in scattering from accelerating bodies. Adv. Photonics 2020, 2, 1–10. [Google Scholar]
- Kozlov, V.; Kosulnikov, S.; Filonov, D.; Schmidt, A.; Ginzburg, P. Coupled micro-Doppler signatures of closely located targets. Phys. Rev. B 2019, 100, 214308. [Google Scholar] [CrossRef]
- Kozlov, V.; Vovchuk, D.; Kosulnikov, S.; Filonov, D.; Ginzburg, P. Micro-Doppler signatures of subwavelength nonrigid bodies in motion. Phys. Rev. B 2021, 104, 1–6. [Google Scholar] [CrossRef]
- Nguyen, C.; Park, J. Stepped-Frequency Radar Sensors Theory, Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Coutinho, M.S.; Novo, L.L.; de Melo, M.; de Medeiros, L.; Barbosa, D.; Alves, M.; Tarragô, V.; dos Santos, R.; Neto, H.L.; Gama, P. Machine learning-based system for fault detection on anchor rods of cable-stayed power transmission towers. Electr. Power Syst. Res. 2021, 194, 107106. [Google Scholar] [CrossRef]
- Vayyar SFCW Radar. Available online: https://www.minicircuits.com/pdfs/VTRIG-74.pdf (accessed on 29 May 2024).
- Kozlov, V.; Vovchuk, D.; Ginzburg, P. Broadband radar invisibility with time-dependent metasurfaces. Sci. Rep. 2021, 11, 1–11. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).