Enhancing Subsurface Phytoplankton Layer Detection in LiDAR Data through Supervised Machine Learning Techniques

Abstract

Phytoplankton are the foundation of marine ecosystems and play a crucial role in determining the optical properties of seawater, which are critical for remote sensing applications. However, passive remote sensing techniques are limited to obtaining data from the near surface, and cannot provide information on the vertical distribution of the subsurface phytoplankton. In contrast, active LiDAR technology can provide detailed profiles of the subsurface phytoplankton layer (SPL). Nevertheless, the large amount of data generated by LiDAR brought a challenge, as traditional methods for SPL detection often require manual inspection. In this study, we investigated the application of supervised machine learning algorithms for the automatic recognition of SPL, with the aim of reducing the workload of manual detection. We evaluated five machine learning models—support vector machine (SVM), linear discriminant analysis (LDA), a neural network, decision trees, and RUSBoost—and measured their performance using metrics such as precision, recall, and F₃ score. The study results suggest that RUSBoost outperforms the other algorithms, consistently achieving the highest F₃ score in most of the test cases, with the neural network coming in second. To improve accuracy, RUSBoost is preferred, while the neural network is more advantageous due to its faster processing time. Additionally, we explored the spatial patterns and diurnal fluctuations of SPL captured by LiDAR. This study revealed a more pronounced presence of SPL at night during this experiment, thereby demonstrating the efficacy of LiDAR technology in the monitoring of the daily dynamics of subsurface phytoplankton layers.

1. Introduction

Phytoplankton is the foundation of marine ecosystems. Dense aggregations of phytoplankton, known as phytoplankton layers [1], can be several kilometers long and range in thickness from a few centimeters to several meters, occasionally leading to harmful algal blooms [2]. These phytoplankton layers have profound effects on biogeochemical processes [3], primary productivity [4], carbon cycle [5], and climate [6] in the upper layers of the ocean. In addition, the actual distribution of phytoplankton contains important ecological information and is an indispensable part of discerning the optical properties of the ocean, which are essential for remote sensing. A comprehensive understanding of the state and stratification of phytoplankton not only deepens our understanding of its ecological role, but also refines the interpretation of remote sensing data [7]. These insights are also critical for managing ocean circulation, protecting marine ecosystems, and sustaining fisheries’ resources [8].

Traditional detection techniques, such as seawater sampling [9], the use of optical sensors [10] and acoustic systems [11], and underwater imaging [12], require in situ operations, which have shown limited efficiency and scalability for large-scale surveys. In contrast, LiDAR, as an advanced active remote sensing technology, has demonstrated its efficacy in mapping fish and zooplankton populations [13,14], detecting air bubbles [15], delineating bathymetric contours line [16], and characterizing optical water column profiles [17,18]. This capability enables LiDAR to provide comprehensive information on the diurnal variability of marine phytoplankton, contributing to a deeper understanding of the spatial and temporal distribution of phytoplankton [19], as well as the dynamics of the upper ocean [20].

In recent years, an increasing number of studies have utilized LiDAR data for internal surveys of the subsurface phytoplankton layer (SPL). Mitra and Churnside [21] estimated the optical signals from marine LiDAR by using the one-dimensional transient time-varying radiative transfer equation via the discrete ordinates method, and further investigated the influence of the SPL on different depths, thicknesses, and densities. Churnside et al. [22] conducted a comparative analysis of three different data-processing methods specifically for SPL, including manual identification, multiscale median filtering, and curve fitting applied to LiDAR profiles, all three of which require manual inspection. Hill and Zimmerman [23], in their study, emphasized the significant improvements LiDAR has brought to estimating the primary productivity of the Arctic Ocean through the combined use of active and passive remote sensing data, and pointed out its significant impact on Arctic estimations. In 2014, Churnside and Marchbanks [24] used airborne LiDAR to make sounding measurements of the subsurface phytoplankton layer in the western Arctic Ocean. Their study identified the phytoplankton layer in the Chukchi and Beaufort Seas and examined the effect of ice floes on the depth and thickness of the phytoplankton layer. A follow-up study conducted three years later in the same area showed that the average depth of the phytoplankton layer in open waters was greater than that of the layer under ice floes [25]. Zavalas et al. [26] applied an automatic classification technique of LiDAR data to the habitat classification of benthic macroalgae communities, and the result of the study proved its effectiveness. Chen et al. [27,28] introduced a novel hybrid inversion method that combined Klett LiDAR per perturbation of β_π using airborne LiDAR over the South China Sea. The inversion results of this method are in good agreement with the in situ chlorophyll-a measurements. Liu et al. [29] used airborne LiDAR to study the spatial distribution and seasonal dynamics of the subsurface phytoplankton layer in Sanya Bay, South China Sea, and gained significant insights. Recently, M. Shangguan et al. conducted a comprehensive study of diurnal continuous, high-resolution SPL in the South China Sea using single-photon underwater LiDAR technology [30,31]. These examples fully demonstrate the usefulness of LiDAR, and data processing for LiDAR is an essential step regardless of the application of LiDAR.

In the study of subsurface phytoplankton layers using LiDAR data, data processing includes data screening and calculations. Generally, each Lidar detection experiment will generate a large amount of data; however, not all LiDAR data are indicative of phytoplankton layers. Manual visual analysis to detect the physical signatures of these layers is typically required, consuming approximately 10 to 20 min for a specialist to discern a subsurface layer within an hour of LiDAR data. Consequently, there is an urgent need for an automated method to identify the phytoplankton layer to reduce the labor intensity of manual inspection. While the authors of previous studies have used spatial filtering and thresholding to detect phytoplankton, the authors of one study encountered challenges in fine-tuning the filtering parameters and threshold levels when using this approach [32]. Churnside explored the potential of supervised machine learning for locating regions containing fish [33], and found that there is no universally applicable optimal model; instead, the selection of a classifier depends on the specific goals of the research.

In the following paper, we explore the potential of using supervised machine learning algorithms to identify phytoplankton layers. The paper is organized as follows: Section 2 details the data collection and methodology; Section 3 presents the results obtained from the machine learning algorithm in detecting the phytoplankton layer; and Section 4 investigates the performance of the algorithm with respect to diurnal fluctuations in the phytoplankton layer.

2. Materials and Methods

2.1. Study Area

Our study focuses on the Gulf of Mexico, located off the southeastern coast of the North American continent, which has an ocean area of 1,507,639 km² and an average depth of 1615 m. In a study of global changes of phytoplankton concentrations over the last 20 years, while the concentrations of phytoplankton have declined along the lower latitude coasts of the Northern Hemisphere, increased concentrations have been observed in the Gulf of Mexico. The phytoplankton layer is widely distributed in the Gulf of Mexico, with 70% concentrated in shallower bays. The formation probability of phytoplankton layers is influenced by chlorophyl concentration. In the Gulf of Mexico, the layers increase when Chl is less than 6 mg/m³, and the layers with a thickness less than 5 m are mainly located 10–15 m below the water surface. Fieldwork was conducted from 24 September to 7 October 2011, in the northern Gulf of Mexico, where NOAA’s LiDAR system was utilized both during the day and at night for the detection of flying fish, fish schools, jellyfish, and plankton layers (see Figure 1). The LiDAR was mounted underneath a small twin-engine aircraft and was capable of conducting and extensive survey of the study area at an altitude of 300 m above sea level and at speeds of 80–100 m/s. Routine daytime flights were conducted at night, twice a day. For analysis purposes, the collected dataset was divided into daytime and nighttime sets based on the respective flight times, and subjected to separate data preprocessing, parameter optimization, and model training. The airborne NOAA LiDAR system consist of a frequency-modulated, continuous-wave Nd:YAG laser emitting 532 nm linearly polarized light at a repetitive frequency of 30 Hz, containing 12 ns pulses. The receiver has two channels: a co-polarized channel and a cross-polarized channel, each equipped with an optical filtering system with a 1 nm bandwidth interference filter, supplemented by a photomultiplier tube (PMT) for effective detection. Unprocessed LiDAR data were generously provided by the NOAA Chemical Sciences Laboratory.

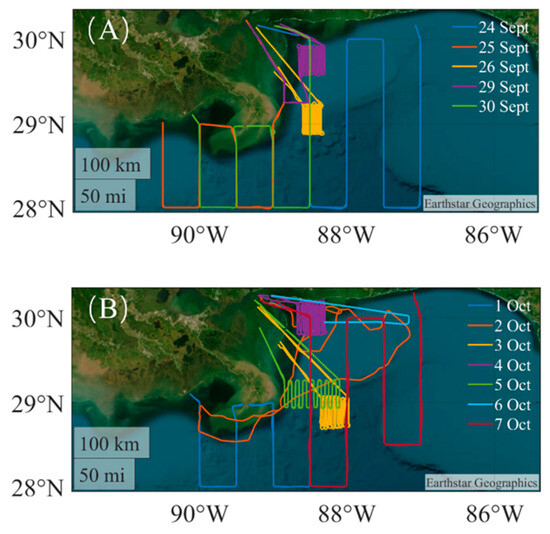
Figure 1. Flight route map for airborne LiDAR detection in the Gulf of Mexico from 24 September through to 7 October. (A) shows the flight path in September and (B) shows the flight path in October.

2.2. Data Processing

The raw data are PNG images of 1000 × 1000 pixels, and each PNG image contains four object labels: flying fish, fish schools, jellyfish, and phytoplankton layers. Data transformation is performed for each image and the four object labels are placed into a matrix where each row corresponds to four objects and each column indicates the presence of the object, and then, the data for each day are presented in separate Matlab .mat files. In our study, we prioritized the phytoplankton layer; hence, the other three object labels were ignored. For each region, the labels were divided into 1000 windows, and a region is considered to be a region of layer (ROL) if a layer label ids present in the region. Figure 2 shows an example of LiDAR data displaying a phytoplankton layer captured on the evening of 26 September at an approximate depth of 25 m.

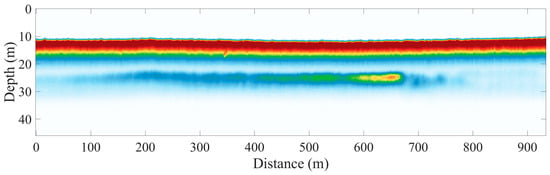
Figure 2. Example of cross-polarized channel LiDAR data from the Gulf of Mexico. The red color represents high intensity while the blue color means low intensity.

2.2.1. Data Preprocessing

Three steps are required to preprocess the converted PNG image data, which are surface detection and smoothing, surface correction, and depth adjustment. The first two steps aim to compensate for aircraft altitude variations, and the depth adjustment is to reduce the dimensionality of data and reduce the time for calculation. The cross-polarized channel data were used for both surface correction and depth adjustment since the cross polarized data provide a better contrast between the phytoplankton layer and the background water column. Water surface detection involves finding the maximum echo of each LiDAR data in the co-polarized channel and moving up to 25% of this maximal echo.

$$S_{raw}\left[m\right]={max}_n[n|y_n\left[m\right]\le 0.25·\max \left(y\left[m\right]\right)]$$

(1)

where $S_{raw}\left[m\right]$ is the surface index, $y\left[m\right]$ is the vector return value, and $y_n\left[m\right]$ is the return value within sample range n. To avoid large gaps between the identified surface locations and the neighboring data, a mean shift filter is applied for surface smoothing operations.

$$S_{smooth}\left[m\right]=\frac{1}{10}{\sum }_{l=0}^9{S}_{raw}[m-l].$$

(2)

Once the surface is found, the surface data were shifted up to the first row and the bottom were filled with 0 data to maintain the original number of rows. Surface correction enables the machine learning algorithm to interpret each row as a specific feature, correlating the LiDAR’s returned intensity with a precise depth in the water column.

Following surface correction, the dataset was condensed to 300 rows corresponding to a depth of approximately 35 m, based on the penetration depth of the LiDAR and the expected depth of the layer. The adjustment in depth is to reduce the data dimensionality, thereby simplifying the complexity of machine learning algorithm and mitigating the influence of the appended zero data from the surface correction process.

2.2.2. Parameter Adjustment

The preprocessed data were partitioned into training and test subsets, while daily data were divided into day and night datasets, which were then subsequently segmented into sets of 1000 contiguous shots. Of these, 80% of both daytime and nighttime data were randomly designated as training data, while the remaining 20% constituted the test data.

For parameter optimization for the training data, we utilized a triple cross-validation approach, which involved fine-tuning the hyperparameters of each algorithm, the undersampling ratio, and the requisite count of predicted labels for a region of layer (ROL) classification. Table 1 shows the hyperparameter setting range of machine learning algorithms. The default parameters served as the starting point for undersampling adjustments, supplemented by a grid search with an increment of 0.05 within the range [0, 0.95]. For each parameter setting, triple cross-validation was employed, the F₃ scores—outlined in Section 2.4—for each fold were documented, and the mean score calculated per grid node. The undersampling ratio yielding the highest mean F₃ score was selected for subsequent use. Hyperparameter refinement proceeded through the use of MATLAB’s Bayesian optimization function. In instances where the F₃ scores remained suboptimal post-adjustments, the default settings were reinstated. Subsequently, to curtail potential predictive inaccuracies, the threshold for layer label counts per region was modified, with the optimal label threshold derived from a spectrum ranging from 1 to 100, based on the highest mean F₃ score achieved.

Table 1. Machine Learning Algorithm Hyperparameter Setting Range.

SVM	LDA			Neural Net
Lambda	$\frac{1}{\left|S\right|}[{10}^{-5},{10}^5]$	Delta	$[{10}^{-5},{10}^5]$	Layer Size	$[10, 50]\in \mathbb{Z}$
Regulation	[ridge, lasso]	Gamma	[0, 1]	Activation	[relu, sigmoid, tanh]
FN cost	$[1,20]\in \mathbb{Z}$	FN cost	$[1,20]\in \mathbb{Z}$
Tree	RUSBoost
Max number of splits	$[1,\left|S\right|-1]\in \mathbb{Z}$	Learning cycles	$[10, 500]$
Min leaf size	$[1,⌊\left|S\right|/2⌋]\in \mathbb{Z}$	Learning rate	$[{10}^{-3},1]$
Split criterion	[gid, deviance]	Max number of splits	$[1,\left|S\right|-1]\in \mathbb{Z}$
FN cost	$[1,20]\in \mathbb{Z}$	Min leaf size	$[1,⌊\left|S\right|/2⌋]\in \mathbb{Z}$
		Split criterion	[gid, deviance]
		FN cost	$[1,20]\in \mathbb{Z}$

2.3. Supervised Machine Learning Algorithms

Supervised learning is a form of machine learning in which a model is trained using labeled sample data, enabling it to make label predictions for new, unlabeled data. The accurate training of supervised algorithms has the potential to minimize classification errors and enhance predictive precision. This study examines a selection of notable supervised machine learning algorithms, including support vector machine (SVM) [34], linear discriminant analysis (LDA) [35], neural networks [36], decision trees [37], and Random Under-Sampling Boost (RUSBoost) [38]. While SVM, LDA, and decision trees are standard classifiers, RUSBoost has been tailored for imbalanced datasets by integrating random undersampling with the AdaBoost M2 [39] boosting framework, thereby improving overall algorithmic performance. The technique of random undersampling [40], widely regarded as an effective approach to addressing dataset imbalances, has been empirically shown to yield positive results. Despite the potential for information loss due to the removal of samples from the majority class [41], this strategy reduces imbalance and shortens training durations [42]. AdaBoost, a prevalent boosting method, iteratively trains a weak learner, adjusts sample weights based on the current learner’s accuracy, and ultimately aggregates all weak learners to establish the final model.

2.4. Evaluation Indicators

The findings of this study are presented in the confusion matrix (refer to Table 2). This matrix serves as a visual representation of the classification outcomes derived from the applied classifier:

Table 2. Confusion matrix.

	Predicted Class Positive	Predicted Class Negative
True class positive	True positive, TP	false positive, FP
True class negative	False negative, FN	True negative, TN

The efficacy of the classifier’s classification capabilities is assessed through precision, recall, and F₃ score. Precision and recall represent nuanced balances between metrics that can be categorized as either “too conservative” or “too aggressive.” Originally employed within the realm of information retrieval, these metrics were introduced to ascertain the susceptibility of a model to degradation by irrelevant data. Precision is the measure of identified positive instances (layers) that are genuinely positive, reflecting the accuracy and reliability of the classifier’s predictions. Specifically, a high precision value signifies the classifier’s adeptness at avoiding the misclassification of non-layer instances as layers:

$$precision=TP/(TP+FP)$$

(3)

Recall represents the proportion of true positive instances (layers) within a sample that the classifier accurately identifies; in other words, it gauges the classifier’s competency in detecting positive cases. A higher recall value indicates enhanced capacity of the model to identify a larger subset of positive instances, with a recall of 1 indicating towards successful recognition of all layers:

$$Recall=TP/(TP+FN)$$

(4)

The F-score is a metric that amalgamates both precision and recall. It is computed based on the weighted harmonic mean of these two metrics, with the weighting relationship between precision (accuracy) and recall typically set at a 1/β ratio:

$$F_{\beta }=(1+{\beta }^2)\frac{precision\times recall}{{\beta }^2\times precision+recall}$$

(5)

In the context of this study, β was defined as 3, thereby employing the F₃ score as a solitary measure for evaluating the classifier’s performance:

$$F_3=10\frac{precision\times recall}{9\times precision+recall}$$

(6)

For the selection of the optimal model, F₃ is the primary basis of consideration, and the model that obtains the highest F₃ value is considered to be the optimal model. The next indicator considered is the recall, as it indicates the number of layers correctly identified by the algorithm out of all the layer signals. Finally, precision is considered. In addition to the three evaluation indicators, the parameter tuning time and running time of each algorithm are also counted as a comprehensive consideration of the model performance.

3. Result

In the following section, the experimental outcomes for both the daytime and nighttime datasets are presented. The section encompasses the test results and region of layer (ROL) findings alongside those obtained from cross-validation procedures.

3.1. Daytime Results

Table 3 shows the hyperparameter values for each algorithm that was calibrated using daytime data from the Gulf of Mexico. Notably, the default hyperparameters for LDA surpassed the performance of all others assessed during the tuning process, leading to the exclusive adjustment of the FN cost.

Table 3. Hyperparameter values for daytime data in the Gulf of Mexico.

SVM	LDA			Neural Net
Lambda	5.05 × 10−7	Delta	0a	Layer Size	49
Regulation	Lasso	Gamma	0a	Activation	relu
FN cost	20	FN cost	3	Undersampling	0.95
Undersampling	0	Undersampling	0.95	Label for ROL	89
Label for ROL	90	Label for ROL	60
Tree	RUSBoost
Max number of splits	1.0067	Learning cycles	55.9864
Min leaf size	323.1351	Learning rate	0.0010
Split criterion	Deviance	Max number of splits	1.0367 × 103
FN cost	20	Min leaf size	1.1993 × 103
Undersampling	0.85	Split criterion	Deviance
Label for ROL	1	FN cost	2
		Undersampling	0.5
		Label for ROL	97

Figure 3 illustrates the test prediction outcomes using daytime data from the Gulf of Mexico. The figure shows that the decision tree algorithm classified all the data as layers, whereas the neural network excelled with the highest correct identification rate of layers at approximately 22.4%. RUSBoost followed with a commendable 17.1%, while SVM, LDA, and decision tree yielded similar accuracy rates of 7.0%, 7.3%, and 6.9%, respectively. These latter three algorithms demonstrated a tendency to incorrectly label non-layer data as layers. In contrast, the neural network and RUSBoost showed a propensity to erroneously categorize layer data as non-layers. Figure 4 displays the cross-validated outcomes, where there was a slight decrease in accuracy for all algorithms, yet the ranking order of their performance persisted. The neural network still leads with an accuracy rate of 19.8%, RUSBoost ranks the second at 16.1%, and the SVM, LDA, and decision tree performances remain close to one another at 6.3%, 6.4%, and 6.1%, respectively. Despite the neural network showcasing superior accuracy in both the test and the cross-validated results, as stated in Table 4, RUSBoost achieved the highest F₃ score, with the neural network ranking second.

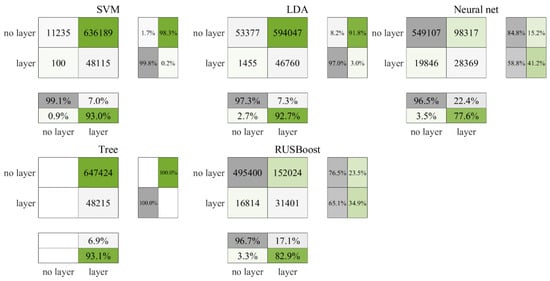
Figure 3. Test results for daytime data in the Gulf of Mexico.

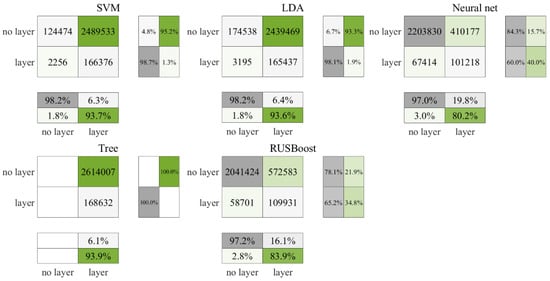
Figure 4. Cross-validation results for daytime data in the Gulf of Mexico.

Table 4. Statistics for the daytime data assessment indicators in the Gulf of Mexico.

		SVM	LDA	Neural Net	Tree	RUSBoost
Test	Precision	0.0703	0.0730	0.2239	0.0693	0.1712
	Recall	0.9979	0.9698	0.5884	1	0.6513
	F3	0.4303	0.4351	0.5060	0.4268	0.5086
Cross validation	Precision	0.0626	0.0635	0.1979	0.0606	0.1611
	Recall	0.9866	0.9811	0.6002	1	0.6519
	F3	0.3986	0.4013	0.4988	0.3921	0.4996

Figure 5 illustrates the test outcomes for the daytime ROL data from the Gulf of Mexico, and Figure 6 corresponds to the cross-validation outcomes. According to Figure 5, both the SVM and decision tree algorithms classified all data points as layers, yet they also registered the highest count of accurately identified layers, at 78 each. Following cross-validation, as depicted in Figure 6, the decision tree alone continued to categorize all data as layers, in contrast, the SVM accurately recognized 41 non-layers. In comparison, the neural network and RUSBoost demonstrated a lower accuracy in identifying layers but exhibited superior performance in correctly categorizing non-layers relative to the other algorithms. Table 5 encapsulates the ROL data results, indicating that the neural network achieved the most elevated F₃ score, with RUSBoost ranking a close second.

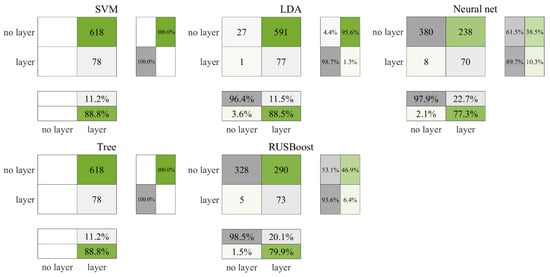
Figure 5. Test results for daytime ROL data in the Gulf of Mexico.

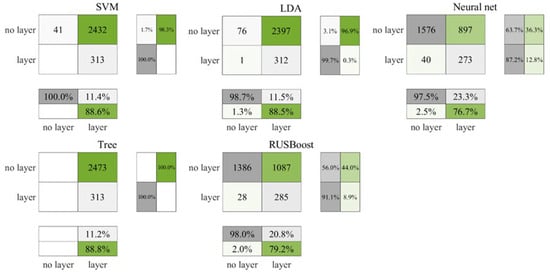
Figure 6. Cross-validation results for daytime ROL data in the Gulf of Mexico.

Table 5. Statistics on daytime ROL data assessment metrics in the Gulf of Mexico.

		SVM	LDA	Neural Net	Tree	RUSBoost
Test	Precision	0.1121	0.1153	0.2273	0.1121	0.2011
	Recall	1	0.9872	0.8974	1	0.9359
	F3	0.5579	0.5620	0.6931	0.5579	0.6854
Cross validation	Precision	0.1140	0.1152	0.2333	0.1123	0.2077
	Recall	1	0.9968	0.8722	1	0.9105
	F3	0.5627	0.5646	0.6847	0.5586	0.6804

3.2. Nighttime Results

Table 6 displays the hyperparameter settings for each algorithm, which were calibrated using nighttime data from the Gulf of Mexico. The default LDA hyperparameters surpassed the performance of all others evaluated throughout the tuning process; thus, only the FN cost underwent fine-tuning.

Table 6. Hyperparameter values for nighttime data in the Gulf of Mexico.

SVM	LDA			Neural Net
Lambda	42.4824	Delta	0a	Layer Size	44
Regulation	Lasso	Gamma	0a	Activation	tanh
FN cost	18	FN cost	5	Undersampling	0.95
Undersampling	0.95	Undersampling	0.95	Label for ROL	97
Label for ROL	1	Label for ROL	63
Tree	RUSBoost
Max number of splits	1.1258	Learning cycles	194.7356
Min leaf size	234.8988	Learning rate	0.0010
Split criterion	Deviance	Max number of splits	2.0308 × 103
FN cost	19	Min leaf size	1.0448
Undersampling	0.95	Split criterion	Deviance
Label for ROL	1	FN cost	17
		Undersampling	0.7
		Label for ROL	40

Figure 7 and Figure 8 illustrate that the precision of the prediction outcomes for nighttime data surpass those of the daytime. In the testing phase, RUSBoost accurately identified 35.2% of the layers, with a slight increase to 36.7% in the cross-validation stage. Conversely, the neural network correctly identified 24.6% of the layers in the testing phase, which slightly decreased to 23% in the cross-validation. In comparison, neither SVM nor the decision tree classified any non-layers correctly in either the testing or cross-validation phases. As indicated in Table 7, RUSBoost consistently secured higher F₃ values across both result sets.

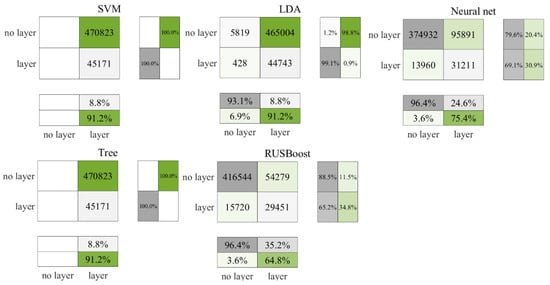
Figure 7. Test results for nighttime data in the Gulf of Mexico.

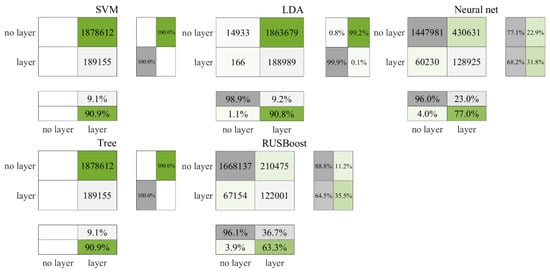
Figure 8. Cross-validation results for nighttime data in the Gulf of Mexico.

Table 7. Statistics for the nighttime data assessment indicators in the Gulf of Mexico.

		SVM	LDA	Neural Net	Tree	RUSBoost
Test	Precision	0.0875	0.0878	0.2456	0.0875	0.3517
	Recall	1	0.9905	0.6910	1	0.6520
	F3	0.4896	0.4883	0.5849	0.4896	0.6007
Cross validation	Precision	0.0915	0.0921	0.2304	0.0915	0.3669
	Recall	1	0.9991	0.6816	1	0.6450
	F3	0.5017	0.5033	0.5700	0.5017	0.5996

Figure 9 and Figure 10 present the test and cross-validation outcomes for nighttime ROL data, respectively. Echoing the patterns observed in earlier findings, RUSBoost achieved the most robust performance followed by the neural network, with both SVM and the decision tree categorizing all data as layers. During the testing phase, LDA similarly classified all data as layers, whereas the cross-validation phase showed a marginal improvement, with one non-layer data point being correctly identified. As illustrated in Figure 10, in the cross-validation phase, RUSBoost correctly identified 314 more non-layer data points than the neural network, albeit accurately identifying seven fewer layers. The neural network misclassified 50.2% of non-layer data as layers, in contrast to RUSBoost, which was found to have a lower misclassification rate of 32.3%. Consistent with previous trends, the results shown in Table 8 confirm the fact RUSBoost secured the highest F₃ score among the evaluated metrics.

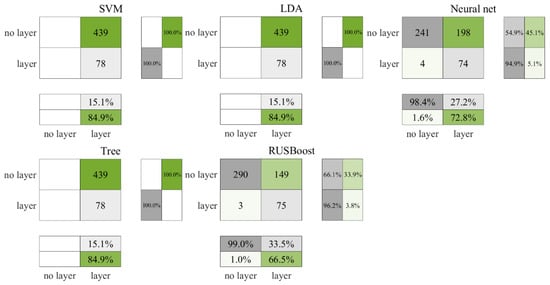
Figure 9. Test results for nighttime ROL data in the Gulf of Mexico.

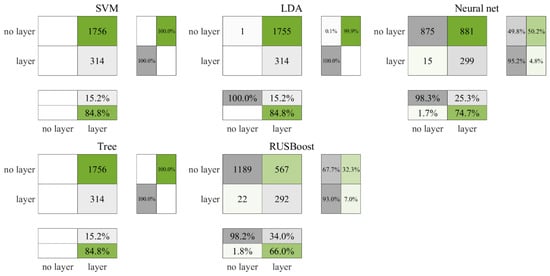
Figure 10. Cross-validation results for nighttime ROL data in the Gulf of Mexico.

Table 8. Statistics for the nighttime ROL data assessment metrics in the Gulf of Mexico.

		SVM	LDA	Neural Net	Tree	RUSBoost
Test	Precision	0.1509	0.1509	0.2721	0.1509	0.3348
	Recall	1	1	0.9487	1	0.9615
	F3	0.6399	0.6399	0.7598	0.6399	0.8099
Cross validation	Precision	0.1517	0.1518	0.2534	0.1517	0.3399
	Recall	1	1	0.9522	1	0.9299
	F3	0.6413	0.6415	0.7464	0.6413	0.7924

4. Discussion

4.1. Performance Analysis of Supervised Learning Algorithms

The findings detailed in Section 3 demonstrate that both the neural network and RUSBoost algorithms outperform the three alternative algorithms by a notable margin, with RUSBoost achieving the top F₃ score in three out of four sets of evaluation metric statistics. RUSBoost’s superior F₃ values were noted across multiple categories, except in the daytime ROL data set, where the neural network ranked highest (as confirmed by the results shown in Table 5). Furthermore, algorithms that excelled in cross-validation tended to also show strong performance with the test data. This could suggest that the LiDAR data’s regions, containing layers, possess distinctive characteristics or distribution properties. Generally, the study’s algorithms operate under the presumption of data independence, which might not align with the real-world scenario where a single layer may extend across several adjacent areas, challenging this assumption.

According to the study’s outcomes, both the neural network and RUSBoost are recommended for detecting phytoplankton layers. As illustrated by the results shown in Table 9, despite requiring the most extended total time with prolonged hyperparameter tuning phases compared to other algorithms, RUSBoost is preferred due to its accuracy, notwithstanding its longer running time. If more rapid analysis is prioritized, the neural network serves as an efficient alternative, consuming only 85% and 61% of the time required by RUSBoost for daytime and nighttime data, respectively, while still delivering similar results.

Table 9. Running time statistics for the tuning of each algorithm parameter, described in seconds (s). Training was run on a Windows system computer with 32 gigabytes of RAM.

		SVM	LDA	Neural Net	Tree	RUSBoost
Day	Undersampling	402.83	1332.85	32,332.51	7094.32	20,309.72
	Model hyperparamenters	805.80	546.98	18,304.67	2195.04	38,902.10
	ROL label tuning	120.68	30.79	807.27	14.10	1092.18
	total	1329.31	1910.61	51,444.45	9303.46	60,304
Night	Undersampling	312.25	943.29	25,127.95	4973.33	24,755.18
	Model hyperparamenters	130.11	419.55	18,344.40	503.39	41,800.17
	ROL label tuning	15.36	23.48	745.25	8.35	5916.52
	total	457.72	1386.32	44,217.60	5485.07	72,471.87

Use of the decision tree algorithm is advised against as it consistently misclassified all data as layers, besides being significantly slower, with the average run times being 8.2 and 4.5 times longer than SVM and LDA, respectively. Similarly, SVM’s tendency to classify all data as layers in three out of four cases, despite having the shortest run time, limits it from being recommended. SVM is mainly applied to small-scale datasets, and when the number of samples and classes increase, the optimization scale increases and the algorithm time consumption increases accordingly. When faced with data with imbalanced categories, SVM may fail to recognize a few classes. LDA may identify more layers accurately than RUSBoost and neural networks; however, it has a high false-positive rate for non-layers, improving recall but necessitating additional manual review. Consequently, while LDA remains an option, it is only suitable when manual verification time can be afforded.

4.2. Diurnal Variation in Phytoplankton Layers

In this study, phytoplankton layers were delineated using layer labels from LiDAR data, as cited in reference [32]. The characteristics of selected phytoplankton layer profiles are illustrated in Figure 11, with their depth and thickness details presented in Figure 12. Single-layer regions, designated as (A–D), exhibit average depths of −4.17 m, −11.80 m, −1.61 m, and −13.02 m, respectively, in addition to average thicknesses of 4.14 m, 2.80 m, 2.25 m, and 1.16 m. Profiles (E–H) reveal dual-layer regions, with average depths for the shallower and deeper layers being −1.83 m and −15.08 m, −1.78 m and −11.08 m, −1.8 m and −13.59 m, and −2.05 m and −7.51 m, correspondingly. The thicknesses for these deeper layers are noted as 1.97 m and 4.63 m, 2.07 m and 3.06 m, 2.19 m and 3.68 m, and 2.72 m and 3.34 m, respectively. A comparison of the layer labels with profile outcomes suggests an oversight of deeper layer labels particularly in regions comprising multiple layers. For instance, the results shown in Figure 11E indicate layer presence at distances beyond 4000, though there exists a significant layer within the 1000–4000 distance range at a depth of 17 m, which seems to have been overlooked in labeling.

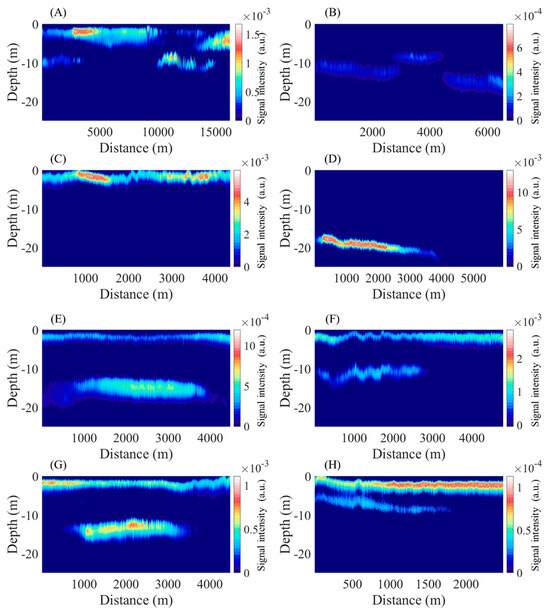
Figure 11. Example of phytoplankton layers in the Gulf of Mexico; (A–D) are single layers and (E–H) are multiple layers. The X-axis is the distance flown by the airborne lidar and the Y-axis is the depth below sea level. The color bar is the signal strength of the lidar (a.u.).

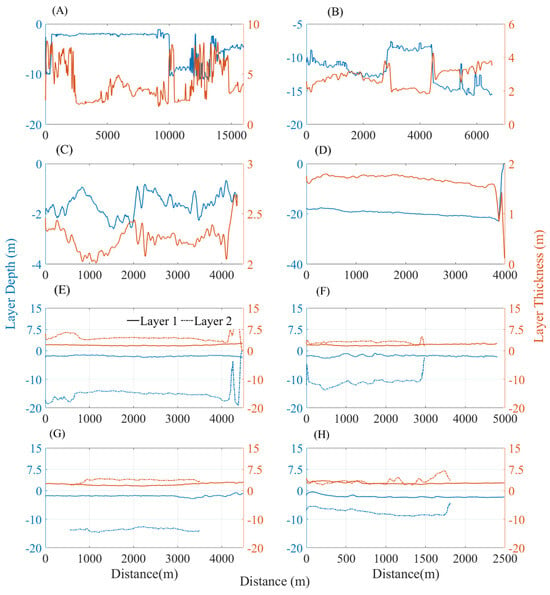
Figure 12. Depth and thickness statistics for the phytoplankton layer in the Gulf of Mexico, (A–H) correspond to (A–H) of Figure 11, respectively. Bule lines are the depth of layers and orange lines are the thickness of layers.

Despite occasional omissions in labeling, leveraging machine learning algorithms for data prediction markedly reduces the manual processing time required for depth and thickness calculations. As an illustrative case, Figure 10 shows that RUSBoost identified 1189 (57%) of the 2070 analyzed regions as non-layers. These 2070 regions represent roughly 20.6 h of LiDAR data, which would ideally require 6.9 h for manual analysis, estimated at about 20 min per hour of LiDAR data. Accordingly, the identification of the 1189 non-layered segments could potentially save about 3.9 h of analysis time.

The observations from the flight conducted on 4 October revealed significant detection of thin phytoplankton layers, with daytime LiDAR data capturing about 35% of the layers and nighttime data detecting approximately 39% of the layers. This result indicates higher efficacy in layer detection during the nighttime. The results shown in Figure 13 juxtapose the layers detected in the same geographic area both during the day and at night. Notably, a thin layer located at 30.15°S, 88.53°W, at a depth of roughly 20 m, is observable during the daytime. However, at nighttime, this layer appears elongated with an enhanced signal strength, alongside two additional layers at the same depth but with marginally weaker signal intensity. This variation is attributed to the diurnal changes affecting the phytoplankton concentration, which typically remains low in the latter part of the day but experiences significant increase after 6 p.m., according to findings cited in reference [43].

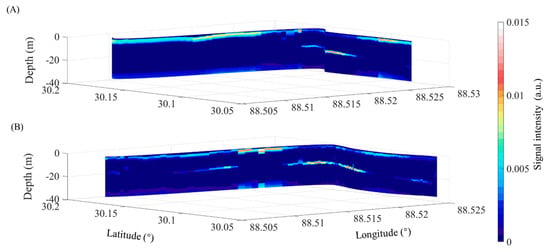
Figure 13. Comparison of daytime and nighttime detections in the same area on 4 October. (A) Layers detected by daytime flights and (B) layers detected by nighttime flights.

In shallow aquatic environments, the phytoplankton layer depth is predominantly determined by the water depth. Selph [44] discussed, in his research on phytoplankton community composition within the Gulf of Mexico, how the biomass and composition of phytoplankton vary according to depth and season. Specifically, the surface water or mixed layer is predominated by prokaryotic and cryptophytic algae, whereas diatoms are more predominant at the depth of the chlorophyll maximum in deeper waters. Moreover, the concentration of nitrate and phosphate is minimal in the mixed layer, and the distribution of these nutrients significantly influences the community composition of phytoplankton [45].

The formation of phytoplankton layers is also subject to environmental factors such as salinity, wind, internal waves, and hypoxia, with distinct formation patterns emerging in different regions [46]. Therefore, understanding the dynamics of phytoplankton layer formation necessitates further investigation into the interplay between these environmental factors and the interactions among phytoplankton, zooplankton, and fish behavior.

5. Conclusions

The findings presented in this paper illustrate the potential of applying supervised machine learning algorithms to ascertain regions likely to harbor phytoplankton layers based on LiDAR data. The data in this study were divided into daytime data and nighttime data for testing based on the time of the survey flight. Empirical evidence suggests that among the evaluated algorithms, RUSBoost garners the most commendable performance albeit one with the longest runtime. Conversely, the neural network stands out as a viable alternative should there be a premium on saving time. RUSBoost distinguished itself by accurately predicting the majority of regions with phytoplankton layers, thereby streamlining the overall data-analysis duration. Moreover, a comparative study of phytoplankton layers during the day and night unraveled an increased detection frequency at night, thus offering valuable insights. Such findings serve to augment future research directed toward deciphering phytoplankton layer formation mechanisms, as well as understanding their diurnal and seasonal fluctuations.