Block-Circulant Approximation of the Precision Matrix for Assimilating SWOT Altimetry Data
Abstract
1. Introduction
2. Approximations of the SWOT Error Covariance
2.1. Precision of Observations in the Data Assimilation Systems
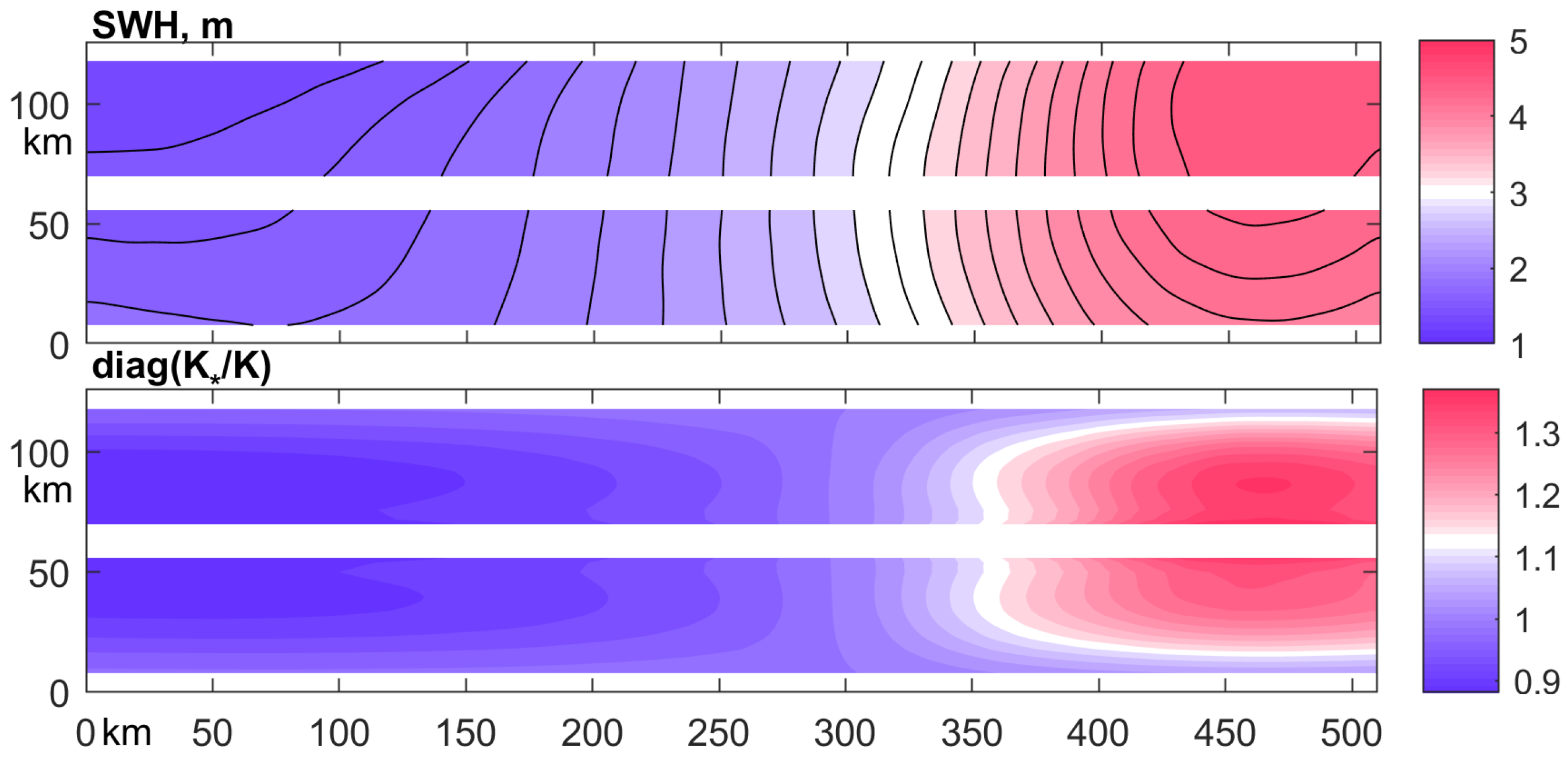
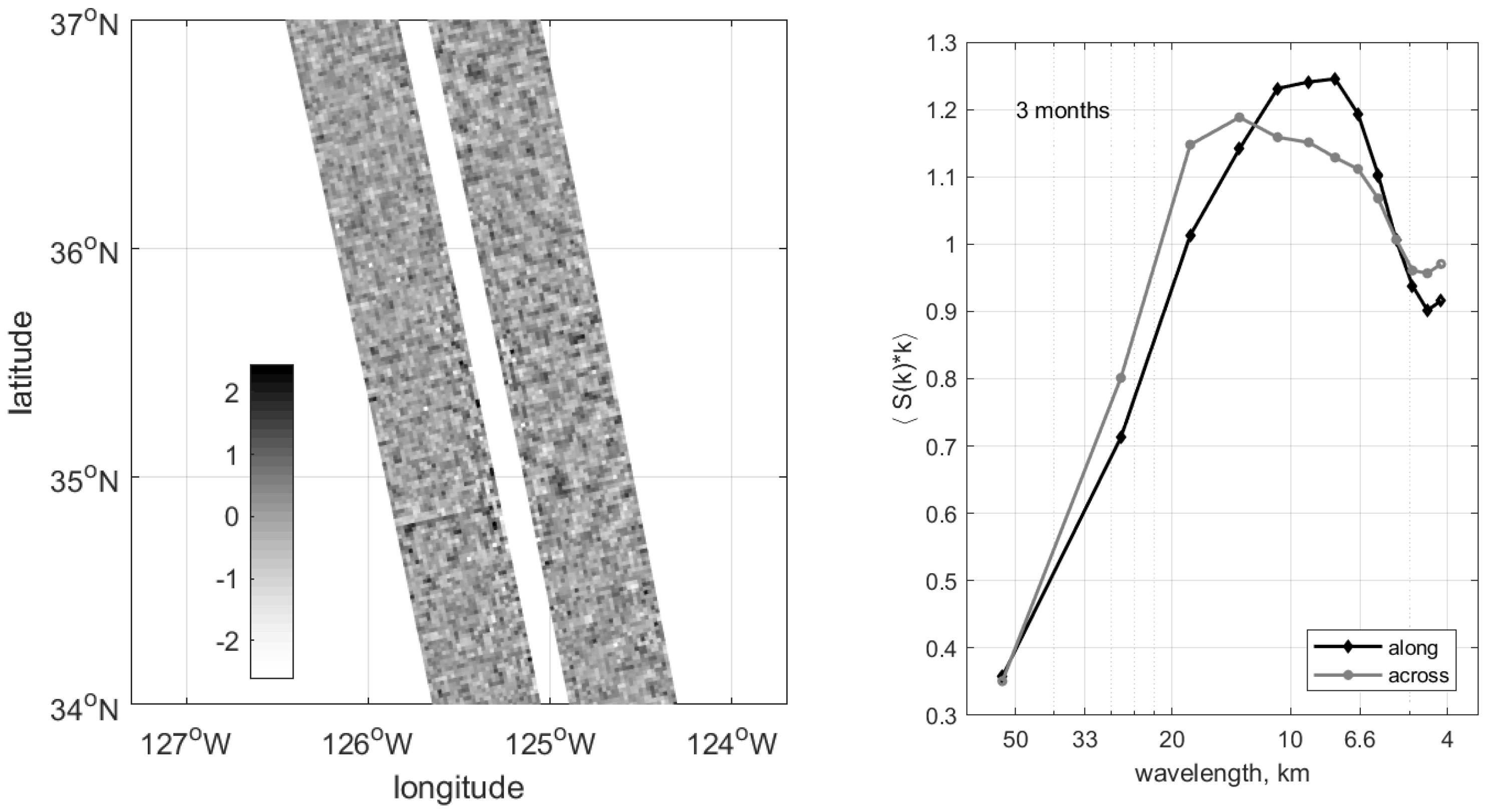
2.2. SWOT Error Covariance Model
2.3. Block-Circulant Approximation
3. Testing the BC Approximation
3.1. Ocean Simulation
3.2. Simulation of Error Statistics
3.2.1. Observation Errors
3.2.2. Background Errors
3.3. Methodology of the OSSEs
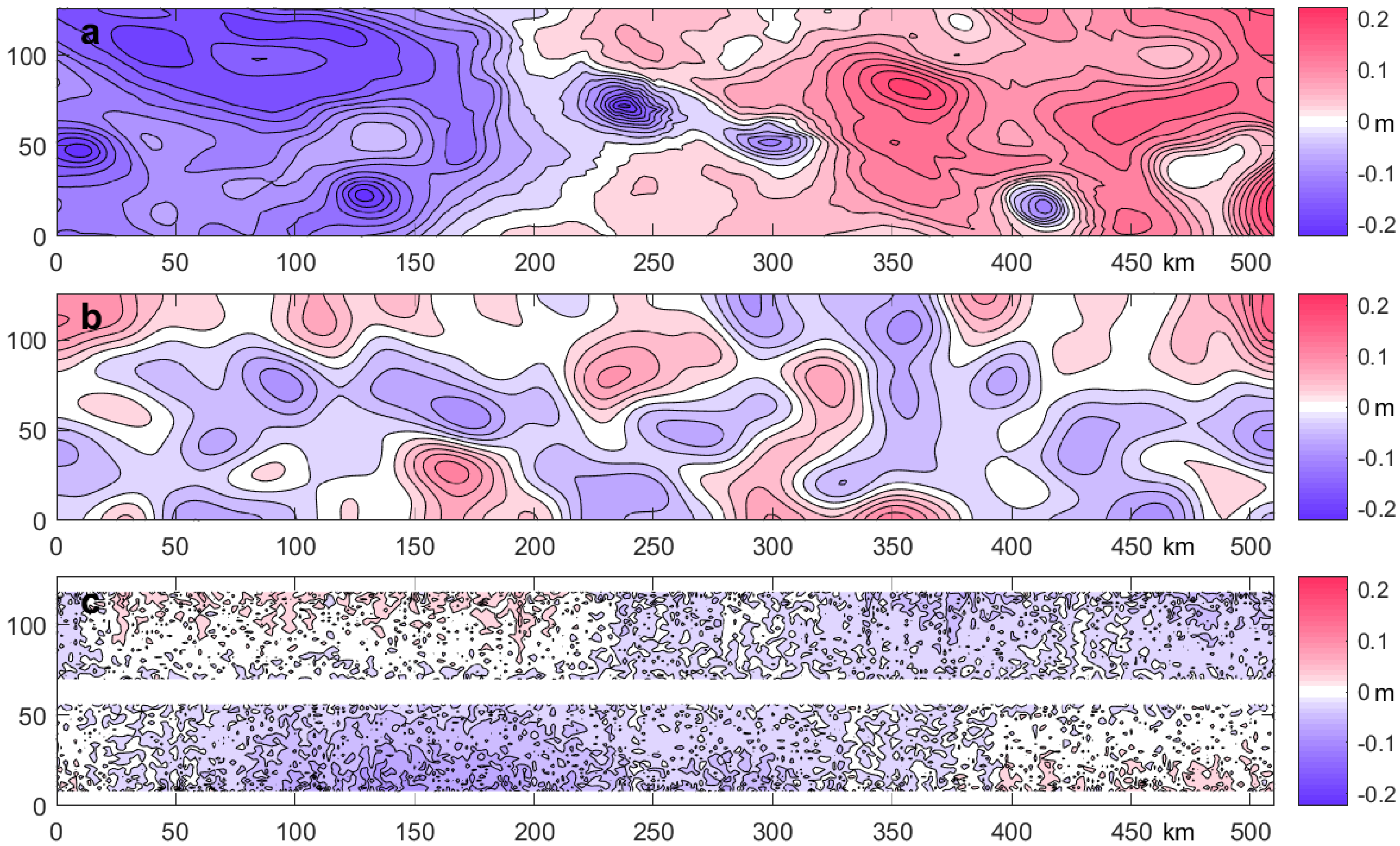
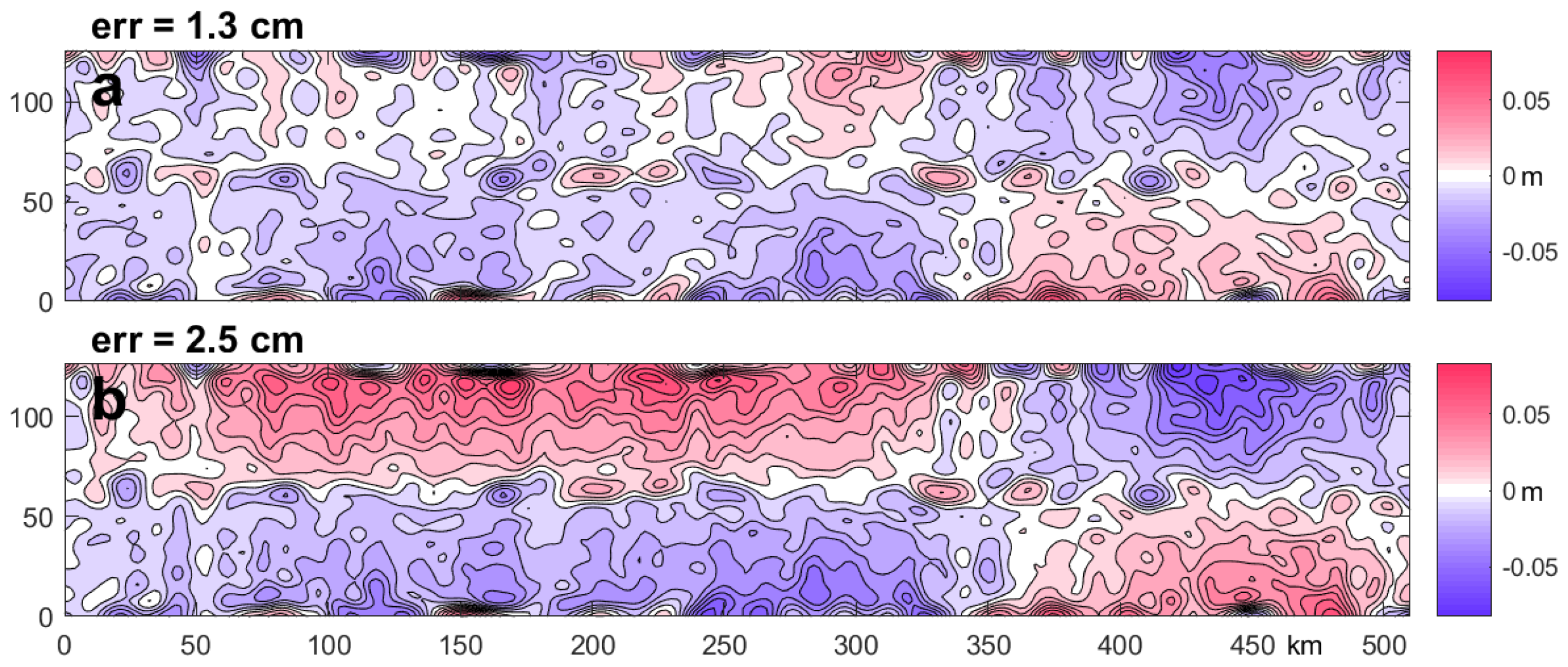
4. Results
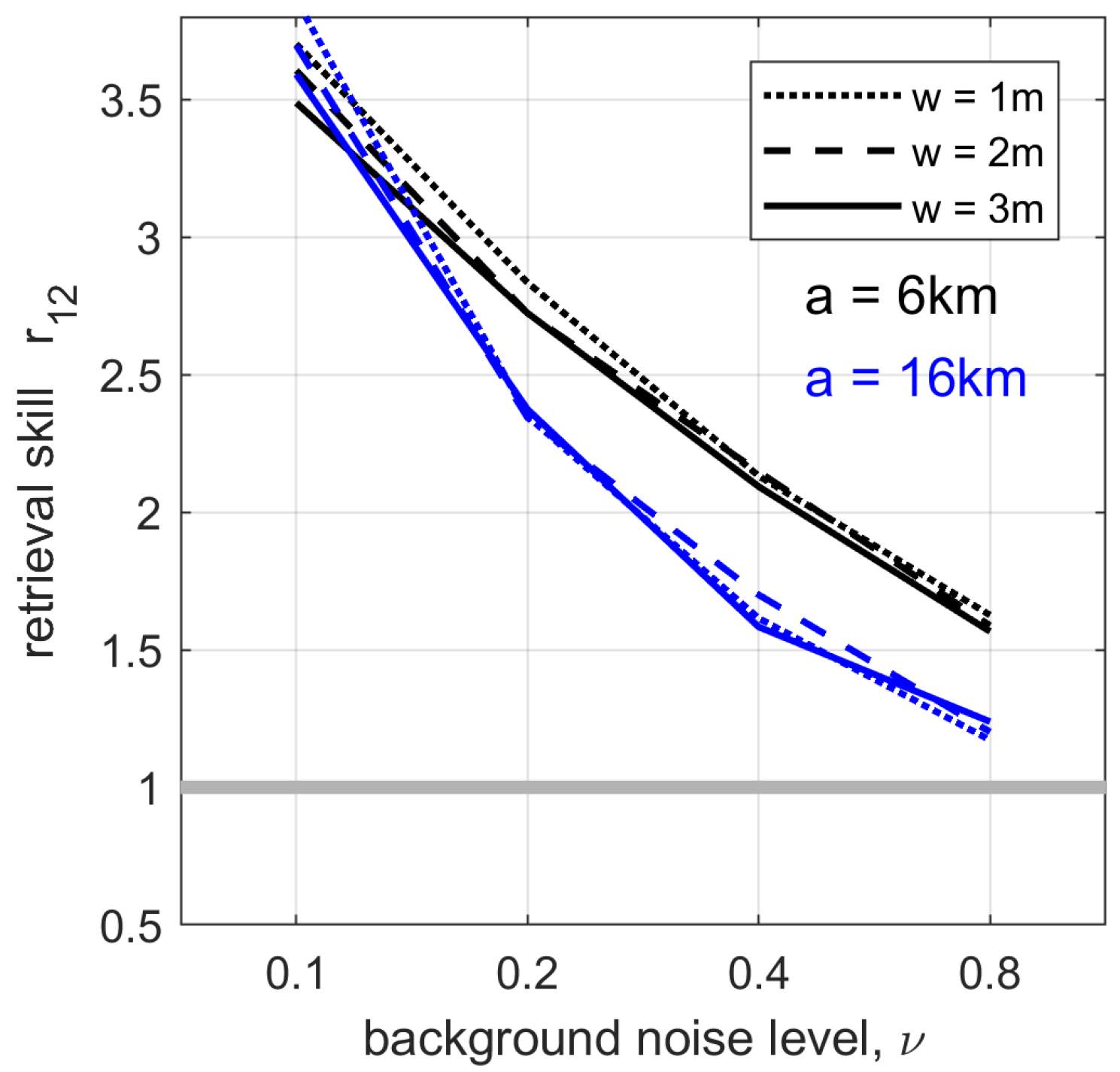
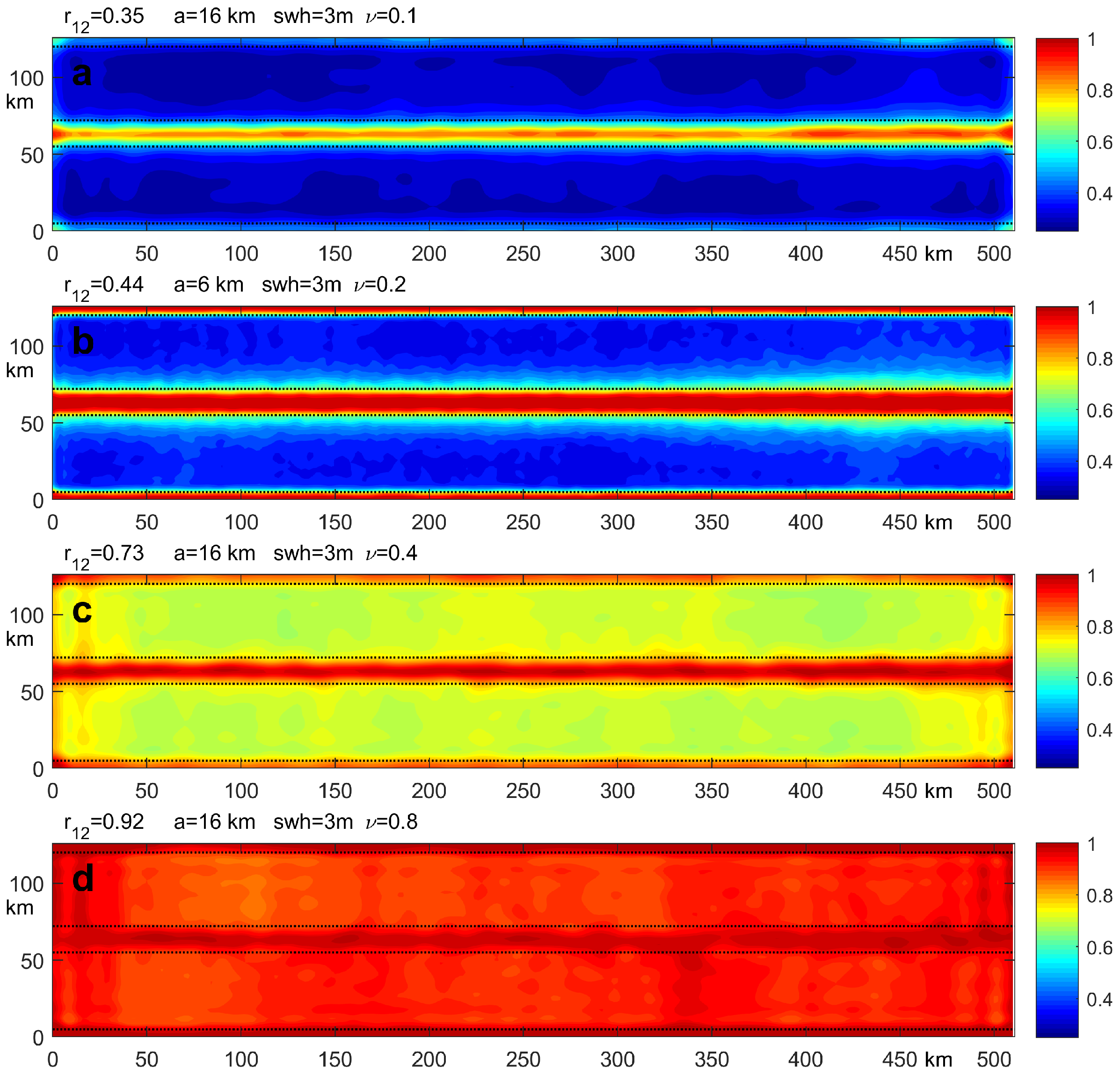
4.1. Retrieval Skill
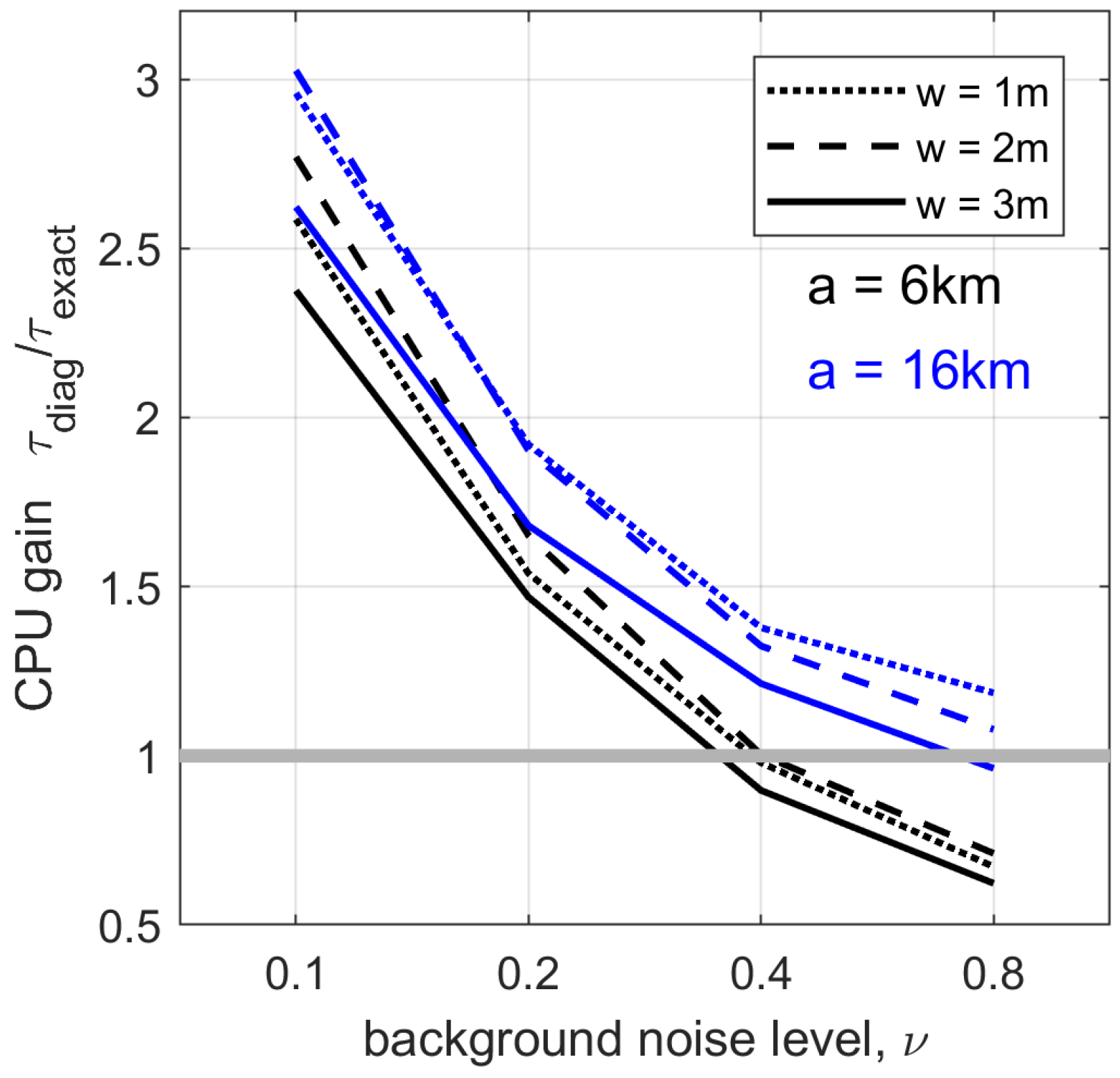
4.2. Computational Efficiency
5. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Factorization of the BC Approximation of the Precision Matrix
References
- Durand, D.; Fu, M.; Lettenemaier, L.L.; Alsdorf, D.; Rodriguers, E.; Esteban-Fernandez, D. The surface water and ocean topography mission: Observing terrestrial surface water and oceanic submesoscale eddies. Proc. IEEE 2010, 98, 766–779. [Google Scholar] [CrossRef]
- Esteban-Fernandez, D. SWOT Project: Mission Performance and Error Budget. Revision A, NASA. /JPL Tech. Rep. JPL D-79084. 2013; 83p. Available online: http://swot.jpl.nasa.gov/files/SWOT_D-79084_v5h6_SDT.pdf (accessed on 10 April 2024).
- Fu, L.L.; Pavelsky, T.; Cretaux, J.F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Sengenes, P.; Vinogradova-Shiffer, N.; Sylvestre-Baron, A.; Picot, N.; et al. The surface water and ocean topography mission: A breakthrough in radar remote sensing of the ocean and land surface water. Geophys. Res. Lett. 2023, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Ito, N.; Uematsu, A.; Yajima, Y.; Isoguchi, O. A Japanese new altimetry mission COMPIRA—Towards high temporal and spatial sampling of sea surface height. Agu Fall Meet. Abstr. 2014, 2014, OS34B-05. [Google Scholar]
- Chen, G.; Tnag, J.; Zhao, C.; Wo, S.; Yu, F.; Ma, C.; Xu, Y.; Chen, W.; Zhnag, Y.; Wi, L. Concept design of the Guanlan science mission: China’s novel contribution to space oceanography. Front. Mar. Sci. 2019, 6, 194. [Google Scholar] [CrossRef]
- SWOT Project: Product Description, Algorithm Theoretical Basis and Data, Level 2 KaRIn Low Rate Sea Surface Height Data Product, Version 1.1, 2023. Available online: https://podaac.jpl.nasa.gov/dataset/SWOT_L2_LR_SSH_1.1 (accessed on 26 May 2024).
- Dibarboure, G.; Ubelmann, C.; Flamant, B.; Briol, F.; Peral, E.; Bracher, G.; Vergara, O.; Faugère, Y.; Soulat, F.; Picot, N. Data-driven calibration algorithm and pre-launch performance simulations for the SWOT mission. Remote Sens. 2022, 14, 6070. [Google Scholar] [CrossRef]
- Gaultier, L.; Ubelmann, C.; Fu, L.-L. SWOT Simulator Documentation; Tech. Rep. 2.3.0, Jet Propulsion Laboratory; CalTech: Pasadena, CA, USA, 2017. [Google Scholar]
- Gaultier, L.; Ubelmann, C.; Fu, L.-L. The challenge of using future SWOT data for oceanic field reconstruction. J. Atm. Oceanic Tech. 2016, 33, 119–126. [Google Scholar] [CrossRef]
- Ma, C.; Guo, X.; Zhang, H.; Di, J.; Chen, G. An investigation of the influences of SWOT sampling and errors on ocean eddy observation. Remote Sens. 2020, 12, 2682. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Fu, L.-L. An observing system simulation experiment for ocean state estimation to assess the performance of the SWOT mission: Part 1—A twin experiment. J. Geophys. Res. Oceans 2019, 124, 4838–4855. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.-L.; Qui, B.; Menemenlis, D.; Farrar, J.T.; Chao, Y.; Thompson, A.F.; Flexas, M.M. An observing system simulation experiment for the calibration and validation of the SWOT sea surface height measurement using in situ platforms. J. Ocean Atm. Tech. 2018, 35, 281–297. [Google Scholar] [CrossRef]
- King, R.R.; Martin, M.J. Assimilating realistically simulated wide-swath altimeter observations in a high-resolution shelf-seas forecasting system. Ocean Sci. 2021, 17, 1701–1813. [Google Scholar] [CrossRef]
- Gaultier, L.; Ubelmann, C. SWOT Science Ocean Simulator Open Source Repository. 2022. Available online: https://github.com/SWOTsimulator/swotsimulator (accessed on 13 March 2024).
- SWOT Project: Release Note KaRIn Science Data Products, Version C. 2024. Available online: https://podaac.jpl.nasa.gov/dataset/SWOT_L2_LR_SSH_2.0 (accessed on 26 May 2024).
- Ubelmann, C.; Dibarboure, G.; Dubois, P. A cross-spectral approach to measure the error budget of the SWOT altimetry mission over the ocean. J. Ocean Atm. Tech. 2018, 35, 845–857. [Google Scholar] [CrossRef]
- Beauchamp, M.; Febvre, Q.; Georgenthum, H.; Fablet, R. 4DVarNet-SSH: End-to-end learning of variational interpolation schemes for nadir and wide-swath satellite altimetry. Geosci. Model Dev. 2023, 16, 2119–2147. [Google Scholar] [CrossRef]
- Tréboutte, A.; Carli, E.; Ballarotta, M.; Carpentier, B.; Faugère, Y.; Dibarboure, G. KaRIn noise reduction using a convolutional neural network for the SWOT ocean products. Remote Sens. 2023, 15, 2183. [Google Scholar] [CrossRef]
- SWOT Project: Release Note KaRIn Science Data Products, Version C. 2024. Available online: https://podaac.jpl.nasa.gov/dataset/SWOT_L2_LR_SSH_EXPERT_2.0 (accessed on 26 May 2024).
- Rosmond, T.; Xu, L. Development of NAVDAS-AR: Non-linear formulation and outer loop nests. Tellus 2006, 58A, 45–58. [Google Scholar] [CrossRef]
- Fletcher, S.J. Observation space variational data assimilation methods. In Data Assimilation Methods for the Geosciences; Elsevier: Amsterdam, The Netherlands, 2022; pp. 785–795. [Google Scholar] [CrossRef]
- Cummings, J.A.; Smedstad, O.M. Variational data analysis for the global ocean. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications Vol. II; Park, S.K., Xu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM Press: Philadelphia, PA, USA, 2003; 547p, Available online: https://epubs.siam.org/doi/book/10.1137/1.9780898718003 (accessed on 26 May 2024).
- Ruggiero, G.A.; Cosme, E.; Brankart, J.M.; Le Sommer, J.; Ubelmann, C. An efficient way to account for observation error correlations in the assimilation of data from the future SWOT high-resolution altimeter mission. J. Ocean Atm. Tech. 2016, 33, 2755–2768. [Google Scholar] [CrossRef]
- Yaremchuk, M.; D’Addezio, J.; Jacobs, G. Facilitating inversion of the error covariance models for the wide-swath altimeters. Remote Sens. 2020, 12, 1823. [Google Scholar] [CrossRef]
- Metref, S.; Cosme, E.; Guillou, F.L.; Sommer, J.L.; Brankart, J.-M.; Verron, J. Wide-swath altimetric satellite data assimilation with correlated error reduction. Front. Mar. Sci. 2020, 6, 822. [Google Scholar] [CrossRef]
- Yaremchuk, M. Sparse approximation of the precision matrices for the wide-swath altimeters. Remote Sens. 2022, 14, 2827. [Google Scholar] [CrossRef]
- Yaremchuk, M.; Beattie, C.; Panteleev, G.; d’Addezio, J.; Smith, S. The effect of spatially correlated errors on sea surface height retrieval from SWOT altimetry. Remote Sens. 2023, 15, 4277. [Google Scholar] [CrossRef]
- Ubelmann, C.; Fu, L.-L.; Brown, S.; Peral, E.; Esteban-Fernandez, D. The effect of atmospheric water vapor content on the performance of future wide-swath ocean altimetry measurement. J. Atmos. Ocean Technol. 2014, 31, 1446–1454. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, G.; Ma, C.; Zhao, C.; Zhang, B. The effect of differential tropospheric error on the measurement of wide-swath interferometric altimetry. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5222011. [Google Scholar] [CrossRef]
- Li, Z.; McWiliams, J.C.; Ide, K.; Farrara, J.D. A multi-scale variational data assimilation scheme: Formulation and illustration. Mon. Wea. Rev. 2015, 143, 3804–3822. [Google Scholar] [CrossRef]
- de Moraes, R.J.; Hajibeygi, H.; Jansen, J.D. A multiscale method for data assimilation. Comput. Geosci. 2020, 24, 425–442. [Google Scholar] [CrossRef]
- De Mazancourt, T.; Gerlic, D. The inverse of a block-circulant matrix. IEEE Trans. Antennas Propag. 1983, 31, 808–810. [Google Scholar] [CrossRef]
- Barron, C.N.; Kara, A.B.; Martin, P.J.; Rhodes, R.C.; Smedstad, L.F. 2006: Formulation, implementation and examination of vertical coordinate choices in the Global Navy Coastal Ocean Model (NCOM). Ocean. Model. 2006, 11, 347–375. [Google Scholar] [CrossRef]
- Helber, R.W.; Smith, S.R.; Panteleev, G.; Shriver, J.; Pickard, R. Greenland Freshwater Stability in the East Greenland Current. Deep Sea Res. 2023; in press. [Google Scholar]
- Hogan, T.F.; Liu, M.; Ridout, J.A.; Peng, M.S.; Whitcomb, T.R.; Ruston, B.C.; Reynolds, C.A.; Eckermann, S.D.; Moskaitis, J.R.; Baker, N.L.; et al. The Navy Global Environmental Model. Oceanography 2014, 27, 116–125. [Google Scholar] [CrossRef]
- Jacobs, G.; Barron, C.; Fox, D.N.; Whitmer, K.R.; Klingenberger, S.; May, D.; PBlaha, J.P. Operational altimeter sea level products. Oceanography 2002, 15, 13–21. [Google Scholar] [CrossRef]
- Jacobs, G.; Desai, S.; D’Addezio, J.; Bartels, B. SWOT cross-track error characteristics estimated from observations. Geophys. Res. Lett. 2024; under review. [Google Scholar]
- Souopgui, I.; D’Addezio, J.; Rowley, C.D.; Smith, S.R.; Jacobs, G.A.; Helber, R.W.; Yaremchuk, M.; Osborne, J. Multi-scale assimilation of simulated SWOT observations. Ocean. Model. 2020, 154, 101683. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaremchuk, M.; Beattie, C.; Panteleev, G.; D’Addezio, J. Block-Circulant Approximation of the Precision Matrix for Assimilating SWOT Altimetry Data. Remote Sens. 2024, 16, 1954. https://doi.org/10.3390/rs16111954
Yaremchuk M, Beattie C, Panteleev G, D’Addezio J. Block-Circulant Approximation of the Precision Matrix for Assimilating SWOT Altimetry Data. Remote Sensing. 2024; 16(11):1954. https://doi.org/10.3390/rs16111954
Chicago/Turabian StyleYaremchuk, Max, Christopher Beattie, Gleb Panteleev, and Joseph D’Addezio. 2024. "Block-Circulant Approximation of the Precision Matrix for Assimilating SWOT Altimetry Data" Remote Sensing 16, no. 11: 1954. https://doi.org/10.3390/rs16111954
APA StyleYaremchuk, M., Beattie, C., Panteleev, G., & D’Addezio, J. (2024). Block-Circulant Approximation of the Precision Matrix for Assimilating SWOT Altimetry Data. Remote Sensing, 16(11), 1954. https://doi.org/10.3390/rs16111954




