Monitoring Dissolved Oxygen Concentrations in the Coastal Waters of Zhejiang Using Landsat-8/9 Imagery
Abstract
1. Introduction
2. Materials and Methods
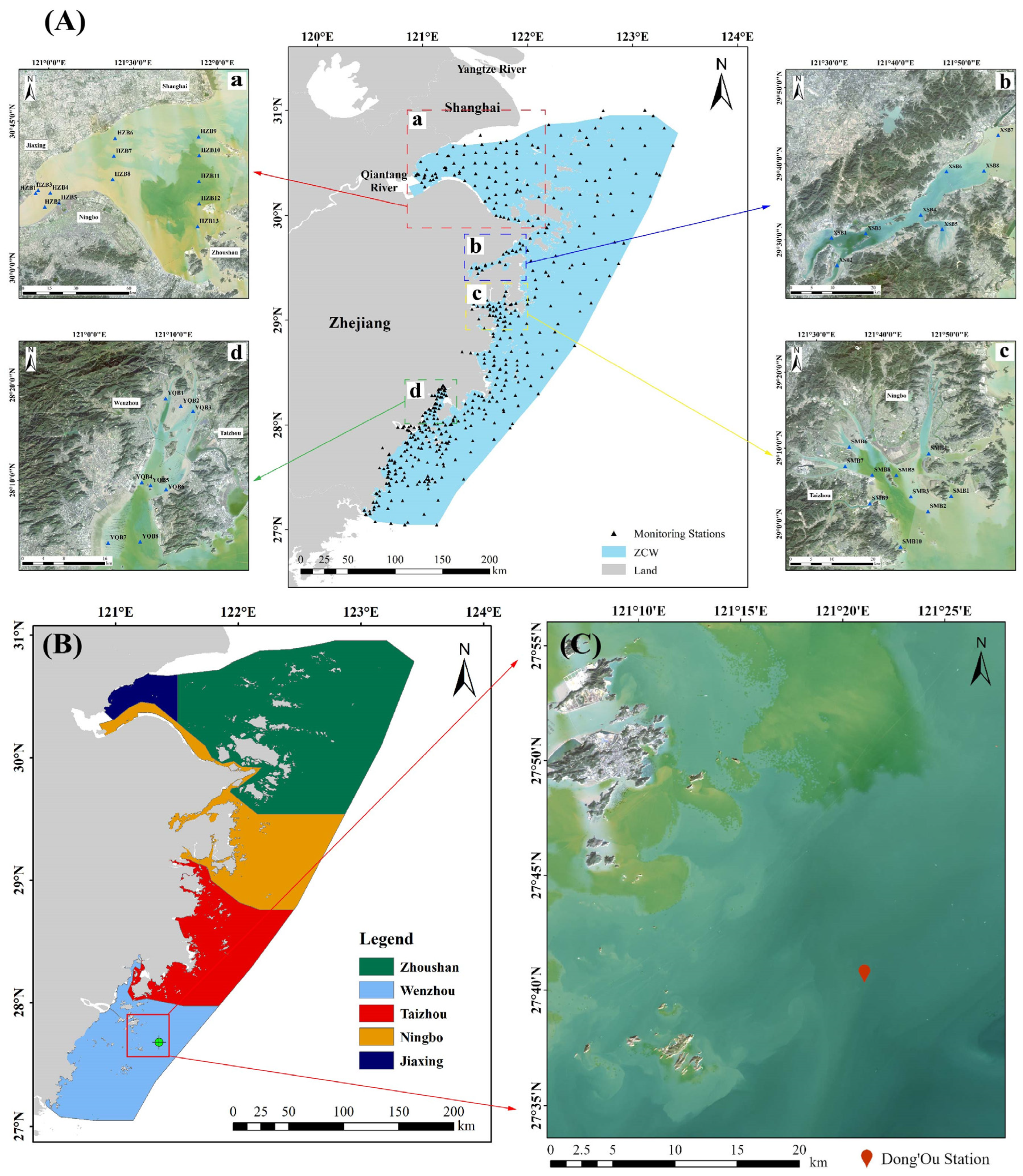
2.1. Study Area
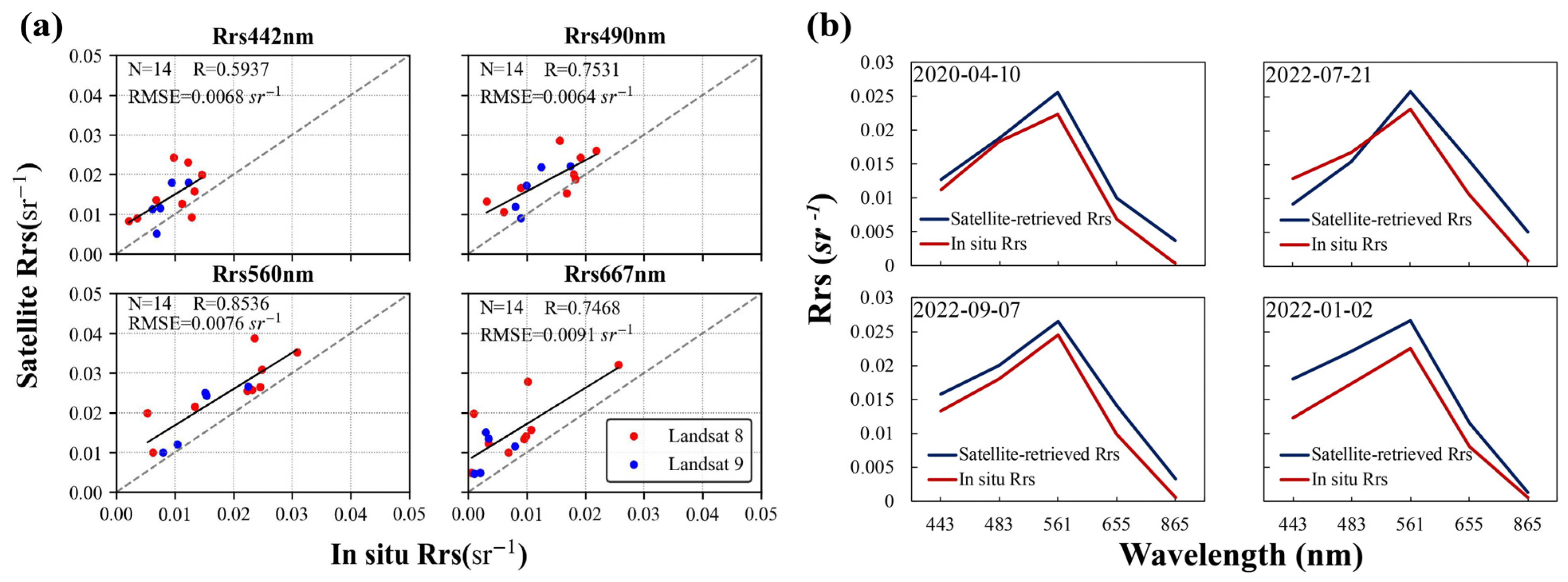
2.2. Satellite Data Acquisition and Processing
2.3. In Situ Measurement Data
2.4. Modeling Methods
2.4.1. Multiple Linear Regression
2.4.2. Model Performance Evaluation
2.4.3. MLR Hypothesis Testing
3. Results
3.1. Model Construction and Validation
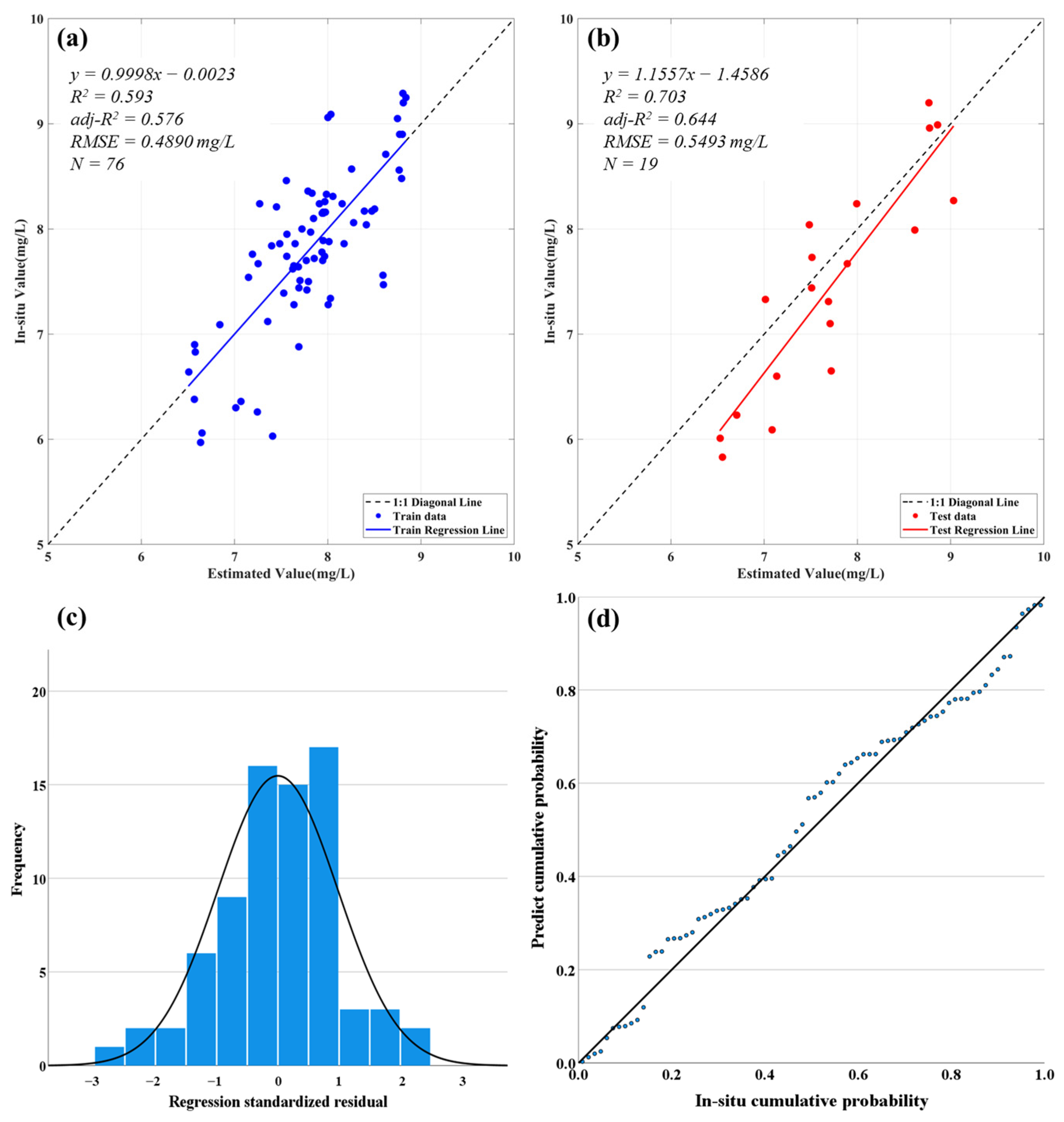
3.1.1. Model Construction
3.1.2. Model Validation
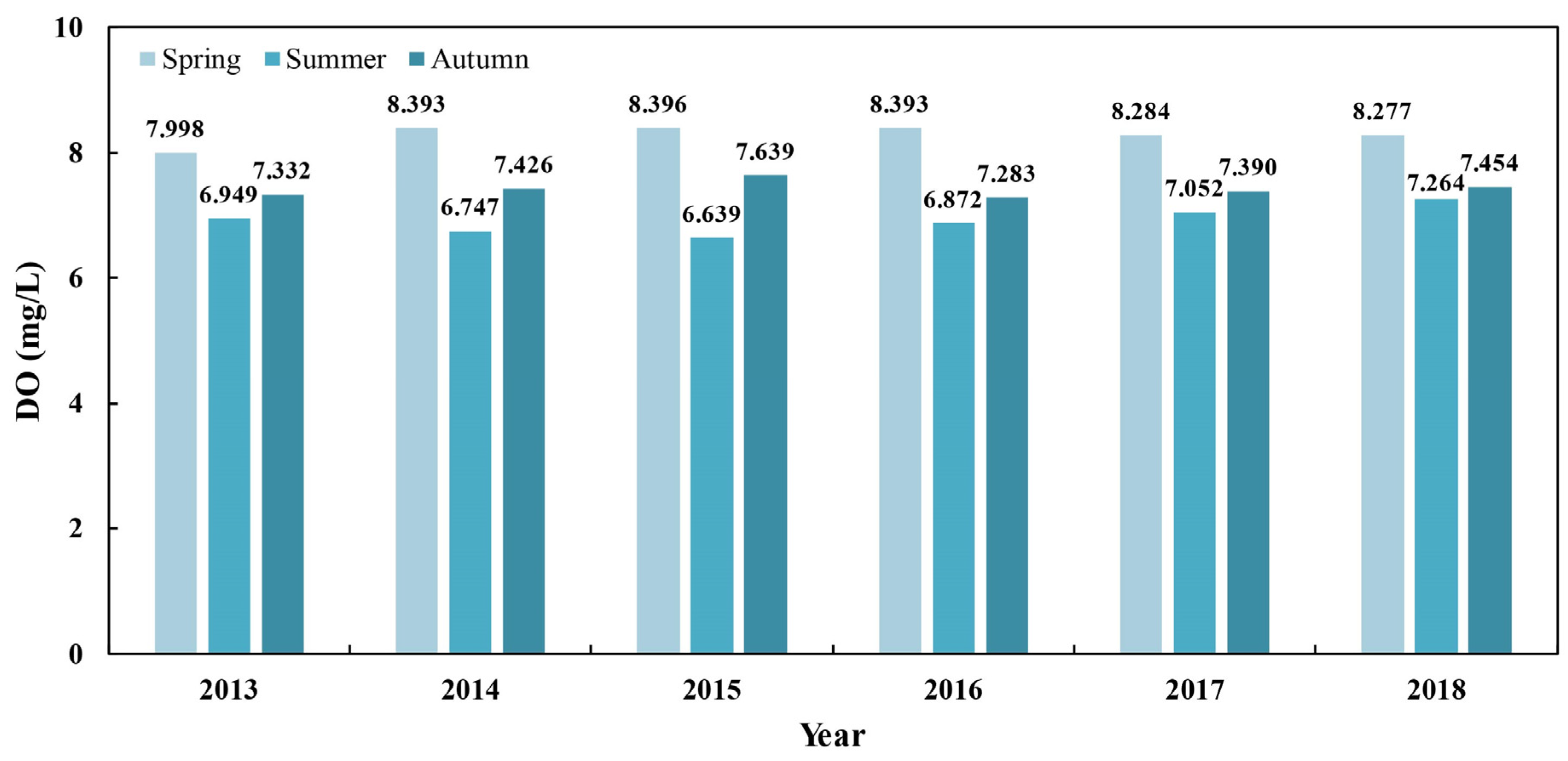
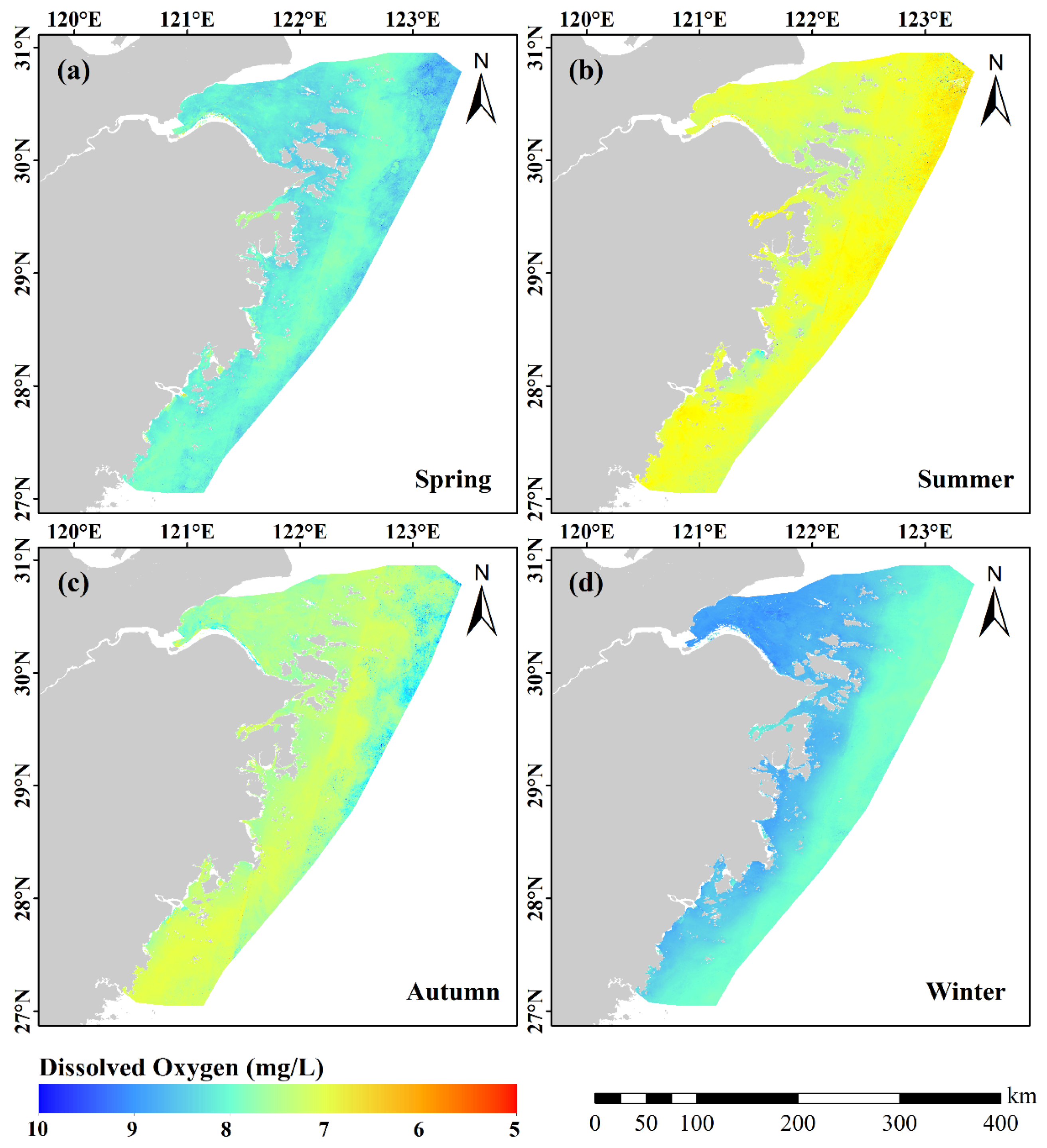
3.2. Temporal and Spatial Characteristics of DO
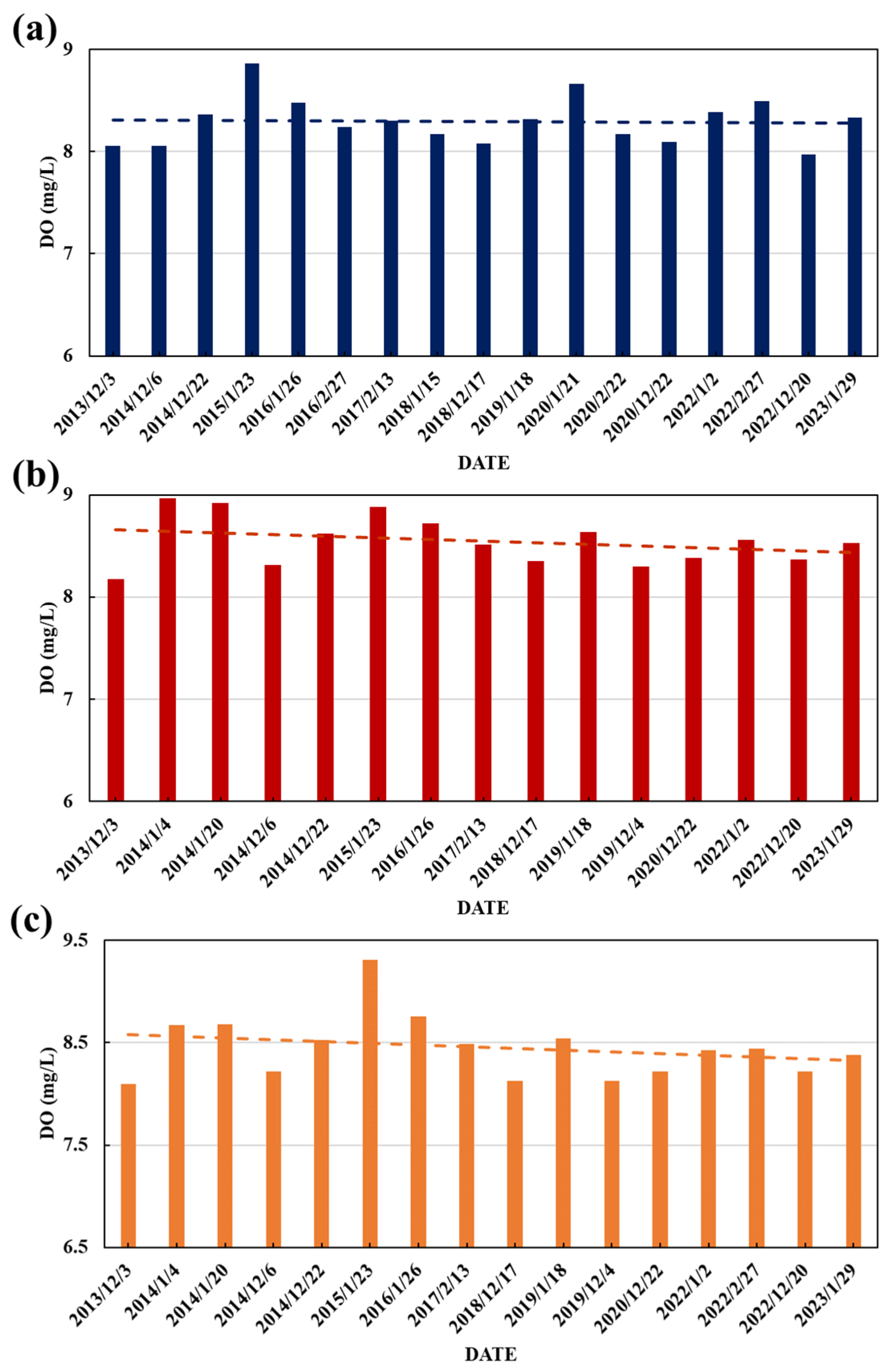
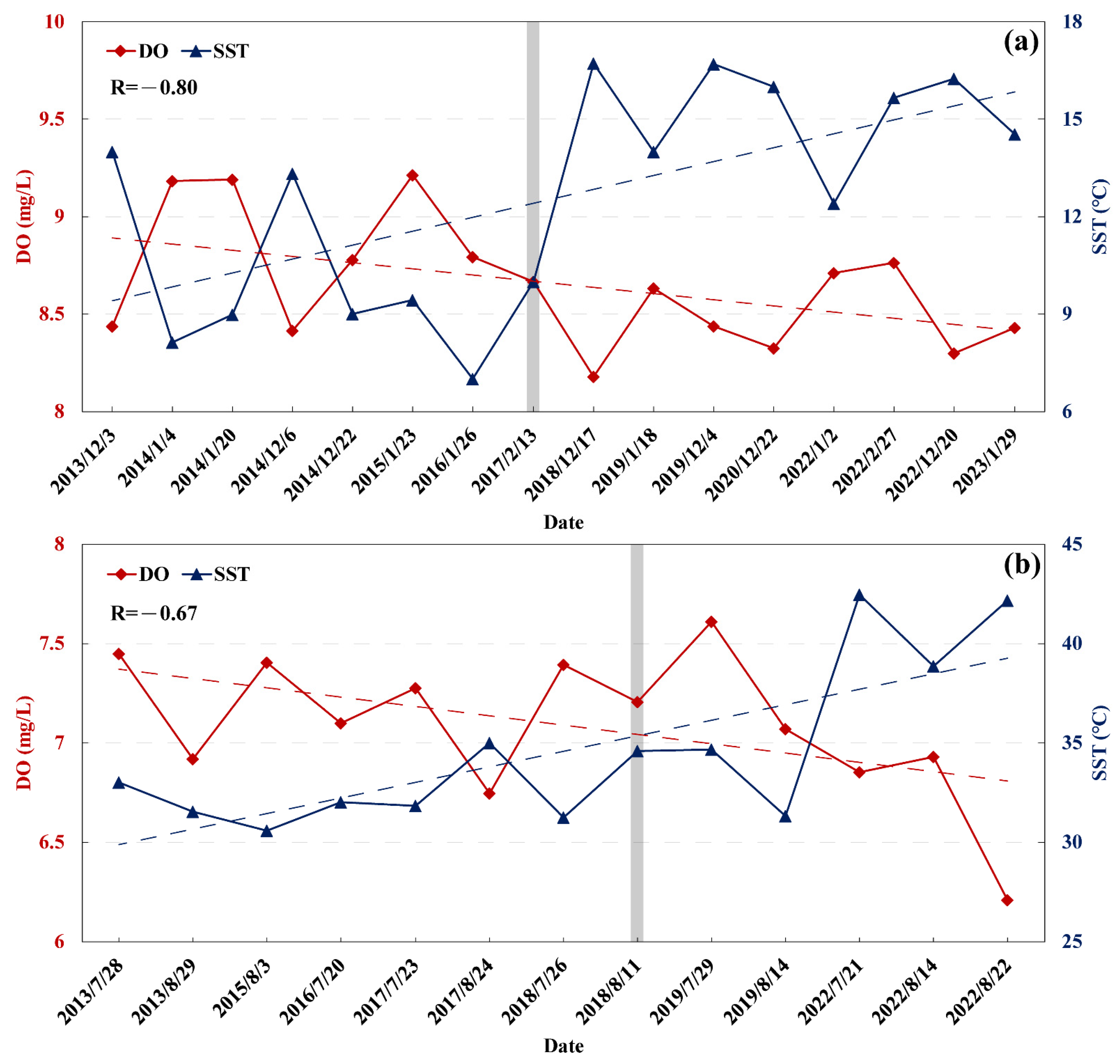
3.3. Long-Time Series Analysis
4. Discussion
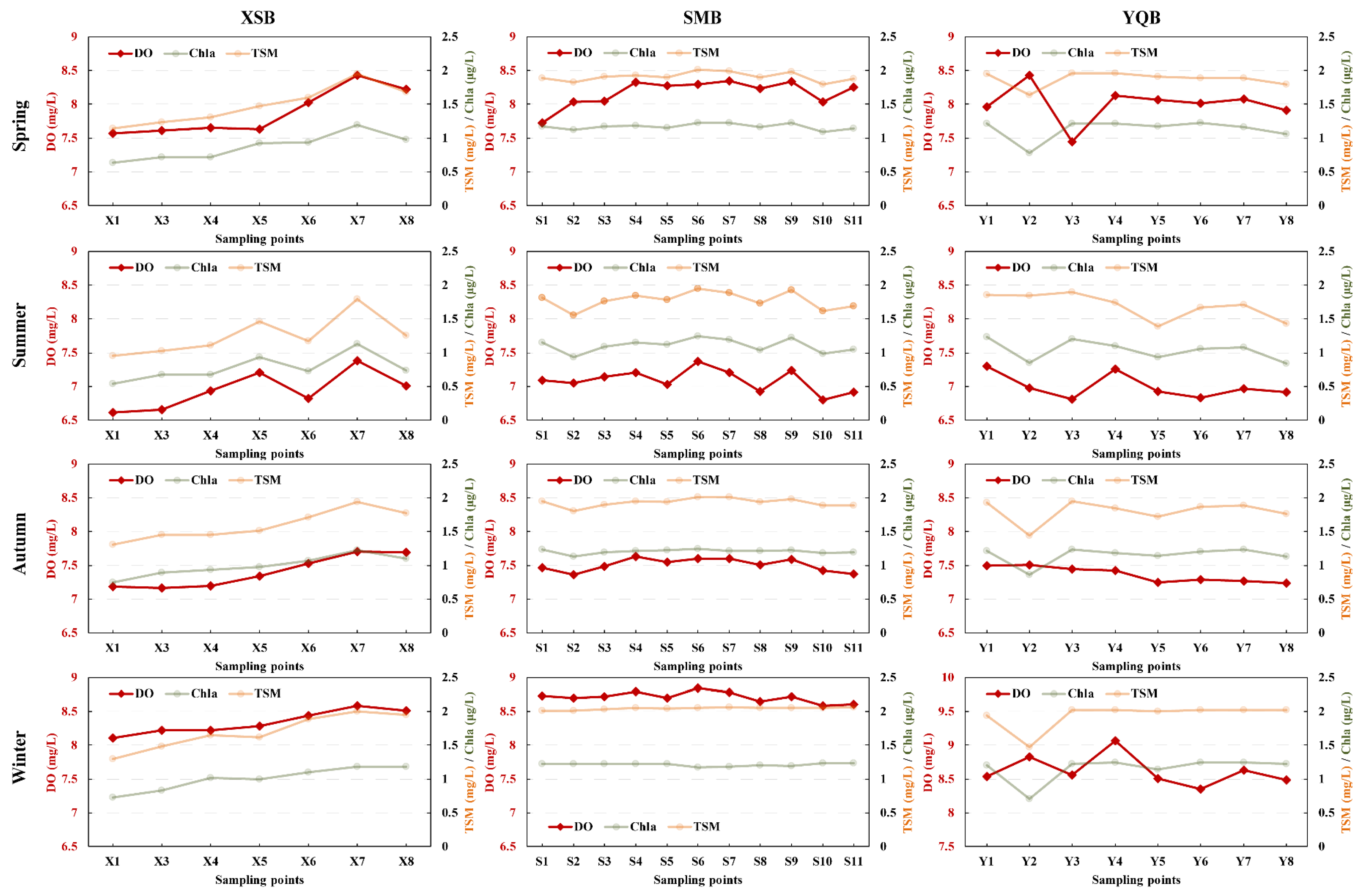
4.1. Effect of Chl-a and TSM Concentrations on DO
4.2. The Impact of Nuclear Power Plant Commissioning on DO
4.3. Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohseni, F.; Saba, F.; Mirmazloumi, S.M.; Amani, M.; Mokhtarzade, M.; Jamali, S.; Mahdavi, S. Ocean water quality monitoring using remote sensing techniques: A review. Mar. Environ. Res. 2022, 180, 105701. [Google Scholar] [CrossRef]
- Coppola, L.; Legendre, L.; Lefevre, D.; Prieur, L.; Taillandier, V.; Riquier, E.D. Seasonal and inter-annual variations of dissolved oxygenin the northwestern Mediterranean Sea (DYFAMED site). Progress. Oceanogr. 2018, 162, 187–201. [Google Scholar] [CrossRef]
- Dawson, J.; Orescanin, M.M.; Clark, R.; O’Connor, K. Spatiotemporal variability of dissolved oxygen in response to morphological state in a central California coast bar-built estuary. Estuar. Coast. Shelf Sci. 2023, 282, 108241. [Google Scholar] [CrossRef]
- Abouelsaad, O.; Matta, E.; Omar, M.; Hinkelmann, R. Numerical simulation of Dissolved Oxygen as a water quality indicator in artificial lagoons–Case lagoons—Case study El Gouna, Egypt. Reg. Stud. Mar. Sci. 2022, 56, 102697. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Cai, H.; Chai, X.; Tang, J.; Zhuo, L.; Jia, H. Summertime dissolved oxygen concentration and hypoxia in the Zhejiang coastal area. Front. Mar. Sci. 2022, 9, 1051549. [Google Scholar] [CrossRef]
- Li, D.; Zhang, J.; Huang, D.; Wu, Y.; Liang, J. Oxygen depletion off the Changjiang (Yangtze River) estuary. Sci. China Ser. D Earth Sci. 2002, 45, 1137–1146. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, B.; Chen, J.; Xia, C.; Qu, D.; Xie, L. Recognition on the forming-vanishing process and underlying mechanisms of the hypoxia of the Yangtze River estuary. Sci. China Earth Sci. 2015, 58, 628–648. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, B.; Zhang, X.; Ran, X.; Fu, M.; Sun, X.; Yu, Z. Contribution of the offshore detached Changjiang (Yangtze River) Diluted Water to the formation of hypoxia in summer. Sci. Total Environ. 2021, 764, 142838. [Google Scholar] [CrossRef]
- Guo, X.; Xu, B.; Burnett, W.C.; Wei, Q.; Nan, H.; Zhao, S.; Charette, M.A.; Lian, E.; Chen, G.; Yu, Z. Does submarine groundwater discharge contribute to summer hypoxia in the Changjiang (Yangtze) River Estuary? Sci. Total Environ. 2020, 719, 137450. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; Li, Y.; Yang, Y. Physical controls of hypoxia in waters adjacent to the Yangtze Estuary: A numerical modeling study. Mar. Pollut. Bull. 2015, 97, 349–364. [Google Scholar] [CrossRef]
- Chen, J.; Ni, X.; Mao, Z.; Wang, Y.; Liang, L.; Gong, F. Remote Sensing and Buoy Based Effect Analysis of Typhoon on Hypoxia off the Changjiang (Yangtze) Estuary. In Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2012, Edinburgh, UK, 19 October 2012; pp. 257–264. [Google Scholar]
- Qi, J.; Du, Z.; Wu, S.; Chen, Y.; Wang, Y. A spatiotemporally weighted intelligent method for exploring fine-scale distributions of surface dissolved silicate in coastal seas. Sci. Total Environ. 2023, 886, 163981. [Google Scholar] [CrossRef]
- Andréfouët, S.; Costello, M.; Rast, M.; Sathyendranath, S. Earth observations for marine and coastal biodiversity and ecosystems. Remote Sens. Environ. 2008, 112, 3297–3299. [Google Scholar] [CrossRef]
- Harvey, E.T.; Kratzer, S.; Philipson, P. Satellite-based water quality monitoring for improved spatial and temporal retrieval of chlorophyll-a in coastal waters. Remote Sens. Environ. 2015, 158, 417–430. [Google Scholar] [CrossRef]
- Zhu, B.; Bai, Y.; Zhang, Z.; He, X.; Wang, Z.; Zhang, S.; Dai, Q. Satellite remote sensing of water quality variation in a semi-enclosed bay (Yueqing Bay) under strong anthropogenic impact. Remote Sens. 2022, 14, 550. [Google Scholar] [CrossRef]
- Chen, J.; Ni, X.; Liu, M.; Chen, J.; Mao, Z.; Jin, H.; Pan, D. Monitoring the occurrence of seasonal low-oxygen events off the Changjiang Estuary through integration of remote sensing, buoy observations, and modeling. J. Geophys. Res. Ocean. 2014, 119, 5311–5322. [Google Scholar] [CrossRef]
- Li, Y.; Robinson, S.V.J.; Nguyen, L.H.; Liu, J. Satellite prediction of coastal hypoxia in the northern Gulf of Mexico. Remote Sens. Environ. 2023, 284, 113346. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Zhu, X.; Wang, B.; Tian, S.; Xu, W.; Mai, Y. A generalized machine learning approach for dissolved oxygen estimation at multiple spatiotemporal scales using remote sensing. Environ. Pollut. 2021, 288, 117734. [Google Scholar] [CrossRef]
- Chatziantoniou, A.; Spondylidis, S.C.; Stavrakidis-Zachou, O.; Papandroulakis, N.; Topouzelis, K. Dissolved oxygen estimation in aquaculture sites using remote sensing and machine learning. Remote Sens. Appl. Soc. Environ. 2022, 28, 100865. [Google Scholar] [CrossRef]
- Salas, E.A.L.; Kumaran, S.S.; Partee, E.B.; Willis, L.P.; Mitchell, K. Potential of mapping dissolved oxygen in the Little Miami River using Sentinel-2 images and machine learning algorithms. Remote Sens. Appl. Soc. Environ. 2022, 26, 100759. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Y.; He, X.; Li, T.; Jiang, Z.; Gong, F. Three stages in the variation of the depth of hypoxia in the California Current System 2003–2020 by satellite estimation. Sci. Total Environ. 2023, 874, 162398. [Google Scholar] [CrossRef]
- Kim, Y.H.; Son, S.; Kim, H.C.; Kim, B.; Park, Y.G.; Nam, J.; Ryu, J. Application of satellite remote sensing in monitoring dissolved oxygen variabilities: A case study for coastal waters in Korea. Environ. Int. 2020, 134, 105301. [Google Scholar] [CrossRef]
- Arief, M. Development of dissolved oxygen concentration extraction model using Landsat data case study: Ringgung coastal waters. Int. J. Remote Sens. Earth Sci. (IJReSES) 2015, 12, 1–12. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, D.; Bai, Y. Study of coastal water zone ecosystem health in Zhejiang Province based on remote sensing data and GIS. Acta Oceanol. Sin. 2010, 29, 27–34. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Song, Q.; Chen, S.; Hu, L.; Wang, X.; Shi, X.; Li, X.; Deng, L.; Ma, C. Introducing Two Fixed Platforms in the Yellow Sea and East China Sea Supporting Long-Term Satellite Ocean Color Validation: Preliminary Data and Results. Remote Sens. 2022, 14, 2894. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Razi, M.A.; Athappilly, K. A comparative predictive analysis of neural networks (NNs), nonlinear regression and classification and regression tree (CART) models. Expert. Syst. Appl. 2005, 29, 65–74. [Google Scholar] [CrossRef]
- Etemadi, S.; Khashei, M. Etemadi multiple linear regression. Measurement 2021, 186, 110080. [Google Scholar] [CrossRef]
- Savin, N.E. Multiple hypothesis testing. Handb. Econom. 1984, 2, 827–879. [Google Scholar]
- Loaiza, J.G.; Rangel-Peraza, J.G.; Monjardín-Armenta, S.A.; Bustos-Terrones, Y.A.; Bandala, E.R.; Sanhouse-García, A.J.; Rentería-Guevara, S.A. Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression. Water 2023, 15, 2606. [Google Scholar] [CrossRef]
- Daoud, J.I. Multicollinearity and Regression Analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar] [CrossRef]
- Wiedermann, W.; von Eye, A. Direction of effects in multiple linear regression models. Multivar. Behav. Res. 2015, 50, 23–40. [Google Scholar] [CrossRef] [PubMed]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Measurement of Total Dissolved Solids and Total Suspended Solids in Water Systems: A Review of the Issues, Conventional, and Remote Sensing Techniques. Remote Sens. 2023, 15, 3534. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H.; Song, K.; Liu, Z.; Xu, Y.; Li, Z. Remote chlorophyll-a estimates for inland waters based on a cluster-based classification. Sci. Total Environ. 2013, 444, 1–15. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Chen, Y.; Wu, J.; Stow, D.A.; Christakos, G. Space-time chlorophyll-a retrieval in optically complex waters that accounts for remote sensing and modeling uncertainties and improves remote estimation accuracy. Water Res. 2020, 171, 115403. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Tang, R.; Yan, X.; Zhou, Y.; Jiang, J.; Yu, M. The spatial-temporal consistency of chlorophyll-a and fishery resources in the water of the Zhoushan archipelago revealed by high resolution remote sensing. Front. Mar. Sci. 2022, 9, 1022375. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Lu, Y.; Jin, H.; Wang, K.; Zhang, H. Seasonal variation of DO and formation mechanism of bottom water hypoxia of Changjiang River Estuary. J. Mar. Sci. 2011, 29, 78–87. [Google Scholar]
- Shi, X.; Wang, X.; Lu, R.; Sun, X. Distribution of dissolved oxygen and pH in frequent hab area of the East China Sea in spring 2002. Oceanol. Et Limnol. Sin. 2005, 36, 404. [Google Scholar]
- Chen, J.; Pan, D.; Liu, M.; Mao, Z.; Zhu, Q.; Chen, N.; Zhang, X.; Tao, B. Relationships between long-term trend of satellite-derived chlorophyll-a and hypoxia off the Changjiang Estuary. Estuaries Coasts 2017, 40, 1055–1065. [Google Scholar] [CrossRef]
- Xiuqing, H.; Ping, Q.; Weihua, Q. Research on the evaluation method of marine ecological environment in Xiangshan Bay. Acta Oceanol. Sin. 2015, 37, 63–75. [Google Scholar]
- Qiang, Z.; Wei, C.; Jian, X.; Shao-qiao, L. Spatio-temporal characteristics of thermal discharge from Sanmen Nuclear Power Plant in winter based on field observations. Mar. Environ. Sci. 2022, 41, 847–856. [Google Scholar] [CrossRef]
- Wang, Y.S.; Lou, Z.P.; Sun, C.C.; Sun, S. Ecological environment changes in Daya Bay, China, from 1982 to 2004. Mar. Pollut. Bull. 2008, 56, 1871–1879. [Google Scholar] [CrossRef] [PubMed]
- Jin, R.; Gnanadesikan, A.; Pradal, M.-A.S.; St-Laurent, P.J.A.P. How does colored dissolved organic matter (CDOM) influence the distribution and intensity of hypoxia in coastal oceans? Authorea Prepr. 2023. [Google Scholar] [CrossRef]





| MLR Model | R2 | adj-R2 |
|---|---|---|
| Single Input | ||
| (1) DO = −1.154 × (Rrs_561/Rrs_613) − 0.069 × SST + 10.325 | 0.503 | 0.489 |
| (2) DO = 30.469 × Rrs_613 − 0.07 × SST + 8.034 | 0.573 | 0.561 |
| Multi-Input | ||
| (3) DO = 28.962 × Rrs_483 + 19.493 × Rrs_865 − 0.07 × SST + 8.193 | 0.592 | 0.575 |
| (4) DO = 1.885 × (Rrs_561/Rrs_655) − 6.29 × (Rrs_483/Rrs_655) − 0.068 × SST + 14.932 | 0.554 | 0.536 |
| (5) DO = 38.1165 × Rrs_655 + 0.88 × (Rrs_483/Rrs_613) − 0.069 × SST + 7.226 | 0.593 | 0.576 |
| Coefficient | Standard Error | t-Value | p-Value | VIF | |
|---|---|---|---|---|---|
| Intercept | 7.226 | 0.538 | 13.428 | <0.001 | |
| Rrs_655 | 38.1165 | 7.321 | 5.206 | <0.001 | 1.713 |
| Rrs_483/Rrs_613 | 0.88 | 0.415 | 2.122 | 0.037 | 1.679 |
| SST | −0.069 | 0.009 | −7.584 | <0.001 | 1.040 |
| Area | Satellite-Derived Value | In Situ Value | ||||||
|---|---|---|---|---|---|---|---|---|
| Max | Min | Max | Min | |||||
| Station | DO | Station | DO | Station | DO | Station | DO | |
| HZB | HZB2 | 9.02 | HZB5 | 6.83 | HZB4 | 9.51 | HZB4 | 7.69 |
| XSB | XSB7 | 8.59 | XSB1 | 6.62 | XSB5 | 9.27 | XSB2 | 6.60 |
| SMB | SMB3 | 8.77 | SMB9 | 6.84 | SMB6 | 9.18 | SMB7 | 7.04 |
| YQB | YQB4 | 9.06 | YQB3 | 6.81 | YQB8 | 8.85 | YQB3 | 6.60 |
| Area | Time Interval | Slope | Intercept | R2 |
|---|---|---|---|---|
| XSB | 2013–2023 | −0.002 | 8.315 | 0.0018 |
| 2013–2023 (December) | −0.0166 | 8.1617 | 0.0546 | |
| 2013–2023 (January) | −0.046 | 8.6431 | 0.1810 | |
| SMB | 2013–2023 | −0.0157 | 8.6769 | 0.0845 |
| 2013–2023 (December) | 0.0148 | 8.3012 | 0.0566 | |
| 2013–2023 (January) | −0.0811 | 9.0708 | 0.966 | |
| YQB | 2013–2023 | −0.0168 | 8.5958 | 0.0658 |
| 2013–2023 (December) | 0.0062 | 8.2142 | 0.0057 | |
| 2013–2023 (January) | −0.0765 | 8.9879 | 0.2823 |
| Spring | Summer | Autumn | Winter | ||
|---|---|---|---|---|---|
| XSB | Chl-a | 0.89 | 0.93 | 0.90 | 0.93 |
| TSM | 0.95 | 0.96 | 0.95 | 0.97 | |
| SMB | Chl-a | 0.43 | 0.81 | 0.73 | −0.64 |
| TSM | 0.59 | 0.81 | 0.86 | 0.01 | |
| YQB | Chl-a | −0.61 | 0.33 | −0.32 | −0.31 |
| TSM | −0.62 | 0.28 | −0.14 | −0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Wang, D.; Song, L.; Gong, F.; Chen, S.; Huang, J.; He, X. Monitoring Dissolved Oxygen Concentrations in the Coastal Waters of Zhejiang Using Landsat-8/9 Imagery. Remote Sens. 2024, 16, 1951. https://doi.org/10.3390/rs16111951
Dong L, Wang D, Song L, Gong F, Chen S, Huang J, He X. Monitoring Dissolved Oxygen Concentrations in the Coastal Waters of Zhejiang Using Landsat-8/9 Imagery. Remote Sensing. 2024; 16(11):1951. https://doi.org/10.3390/rs16111951
Chicago/Turabian StyleDong, Lehua, Difeng Wang, Lili Song, Fang Gong, Siyang Chen, Jingjing Huang, and Xianqiang He. 2024. "Monitoring Dissolved Oxygen Concentrations in the Coastal Waters of Zhejiang Using Landsat-8/9 Imagery" Remote Sensing 16, no. 11: 1951. https://doi.org/10.3390/rs16111951
APA StyleDong, L., Wang, D., Song, L., Gong, F., Chen, S., Huang, J., & He, X. (2024). Monitoring Dissolved Oxygen Concentrations in the Coastal Waters of Zhejiang Using Landsat-8/9 Imagery. Remote Sensing, 16(11), 1951. https://doi.org/10.3390/rs16111951






