The Atmospheric Heating Mechanism over the Tharsis Bulge of Mars and the Impact of Global Dust Storms

Abstract

Mars atmospheric dynamics are crucial for understanding its climate and weather patterns, especially over plateaus. Previous studies have explored localized atmospheric heating mechanisms over Mars plateaus only to a little extent. The local atmospheric heating dynamics over the Tharsis plateau, especially during global dust storms (GDSs), have not been quantitatively analyzed before. Based on reanalysis datasets, our analysis reveals that the central highlands of Tharsis experience ~130 K diurnal temperature fluctuations, driven by intense daytime convective activity. Surface temperature and near-surface air temperatures show fluctuations approximately 25 K and 20 K higher than those at similar latitudes, respectively. We quantify a super-adiabatic lapse rate around noon that suggests strong atmospheric instability, previously unquantified in this region. By dusk, the atmosphere stabilizes, presenting a homogenized condition. At aphelion, sensible heating and adiabatic terms control the atmospheric heating, while, at perihelion, radiative and sensible heating predominate. Notably, the onset of GDS significantly alters this dynamic, reducing the ground–air temperature gap from 17 K to 5 K and enhancing diabatic heating (adiabatic cooling) in the mid-to-lower (mid-to-upper) troposphere, with increases in radiative components up to 60 W/m².

1. Introduction

The influences of elevated terrain on weather systems and atmospheric circulations are of great interest in geosciences due to their thermal effects. The profound influence of Earth’s Qinghai–Tibetan Plateau on monsoonal activity and broader climatic systems exemplifies this, as demonstrated in multiple studies [1,2,3,4,5,6]. This phenomenon offers a valuable analogy for exploring similar atmospheric dynamics on Mars, specifically over the elevated region of the Tharsis Bulge.

The Tharsis Bulge (TB), characterized by its significant altitude, is stricken with extreme diurnal temperature changes that play a pivotal role in the heating and circulation patterns of Mars’ atmosphere. Nevertheless, despite the acknowledged significance of these processes on Earth [5,7,8,9,10], research exploring these dynamics on Martian plateaus has been constrained. Adding to the complexity, Mars shows a dynamic dust cycle that influences radiative transfer and, subsequently, atmospheric temperatures, circulation, and wave patterns [11,12,13]. The interaction between the dust cycle, water cycle, and wave activity [14] brings a unique complexity to the Martian lower atmosphere. This complexity makes the study of thermal dynamics in the Tharsis region not only innovative but vital for increasing our understanding of Martian atmospheric science.

In 1982, Kahn et al. [15] observed strong downslope flows in the boundary layers on the steep slopes of two volcanoes in the TB region. Between these peaks, in saddle-like areas, the airflow slows and undergoes a hydraulic jump, resulting in the formation of elongated clouds. Hinson and Wilson (2004) [16] noted that adiabatic cooling above TB leads to the formation of water ice clouds, with their variability modulated by thermal tides. Furthermore, the radiative forcing of these clouds reciprocally influences the tides, creating a tide–cloud coupling that produces a temperature inversion of about 30 K during the midsummer of the Northern Hemisphere (Ls = 134°–162°) above TB. Studies by Wilson et al. (2007) [17] and Benson et al. (2003) [18] highlighted diurnal and seasonal variations of water ice clouds over the TB region’s volcanoes, which are significantly more pronounced than in other regions and are accompanied by substantial radiative forcing. Montmessin et al. (2004) [19] and Wordsworth et al. (2013) [20] showed through modeling that adiabatic cooling effects lead to significantly lower temperatures in the valleys of the southern highlands compared to the global average. Long-term climate simulations indicate that, under these conditions, water ice is transported from low-lying areas to highlands across broad orbital inclinations and from poles towards the equator. These findings are significant, revealing the impacts of adiabatic (adiabatic cooling), diabatic (water ice cloud radiative heating), and atmospheric heating (affecting thermal tides) processes above TB. Our work goes further by quantifying the contributions and vertical distributions of advective, adiabatic, and diabatic terms using the thermodynamic energy equation. We aim to more comprehensively explore the heating mechanisms above the plateau, focusing on the integrated contributions of each heating component, including radiative effects of water ice clouds, and providing a more detailed examination of the associated processes.

It is also meaningful to study the relations between the plateau heating mechanism and Martian Global Dust Storms (GDSs). Actually, GDSs tend to cause net warming of the surface temperature and near-surface air temperature in low thermal inertia (TI) regions, including the middle north region of TB (Figures 1a,b and 2b in the work of Streeter et al. (2019) [21]), where strong nightside warming outweighed dayside cooling. The unique interactions between Mars topography and its atmosphere, particularly over the Tharsis Bulge, mirrors Earth’s high plateaus, where diurnal cycles significantly affect thermal behaviors [2,10]. Mars’ extreme conditions [22,23] are expected to amplify these effects, but the specific impacts of its diurnal variations on the Tharsis region remain underexplored, despite extensive analogous studies on Earth [2,10]. Additionally, the modulation of solar and infrared flux by GDSs introduces further complexity to these thermal processes [24,25], with their direct effects on regions like the Tharsis Bulge largely unexplored.

Previous research has contributed substantially to our understanding of Martian dust storms. In 1977, Toon et al. [26] investigated the physical properties of particles composing a Martian dust storm, providing foundational insights into dust composition and behavior. Clancy et al. [27,28] further utilized observations from the Mars Global Surveyor (MGS) Thermal Emission Spectrometer (TES) to study dust optical depths, particle sizes, and ice cloud formations across different latitudes and solar longitudes. Their findings provided valuable insights into the spatial and temporal variability of dust distribution and revealed the vertical distribution of dust particles in the Martian atmosphere. Afterwards, researchers have further deepened the understanding of dust using various instruments. In addition, Vasilyev et al. (2009) [29], Maattanen et al. (2013) [30], and Guzewich et al. (2014) [31] conducted detailed investigations into the vertical distribution and climatology of Martian aerosols, utilizing data from instruments aboard spacecrafts of the Visible and Infrared Mineralogical Mapping Spectrometer (OMEGA) onboard Mars Express (MEX), Spectroscopy for the Investigation of the Characteristics of the Atmosphere of Mars (SPICAM) onboard MEX, and the Compact Reconnaissance Imaging Spectrometer for Mars (CRISM) onboard Mars Reconnaissance Orbiter (MRO), respectively. These studies provided crucial insights into the dust aerosol characteristics on Mars, contributing to our understanding of Martian atmospheric processes. Recently, Smith et al. (2023) [32] examined diurnal and seasonal variations of dust optical depths observed by the Mars Environmental Dynamics Analyzer (MEDA) at Jezero Crater. Cozzolino et al. (2024) [33] developed the Micro Measurement Environment Dust (MicroMED) sensor, advancing dust monitoring capabilities. Their study offers valuable insights into short-term and long-term aerosol dynamics, complementing previous research on Martian dust storms.

Benefitting from previous excellent works [21,34,35,36,37,38,39], it is now clear that Mars GDSs block downward solar shortwave radiation during the day, leading to surface cooling, while, at night, they cause surface warming through backscatter and longwave emission. However, critical questions remain unanswered about the proportion of this radiative effect in the total non-adiabatic heating of the atmosphere, the contribution of non-adiabatic heating to atmospheric warming, how these factors change with the development of GDSs, and their vertical structure, among others. GDSs are a unique phenomenon on Mars [21,34,36,37,38,40], and the heating mechanism dominated by these storms on the plateau is also worthy of investigation. Research on the Tibetan Plateau has focused on the water-related influence on the heating mechanism of the plateau [6,9,41,42,43]. Although scientists have pointed out that dust and water cycles are somewhat similar in some respects [14], there are still significant differences in their impacts on atmospheric heating mechanisms. For example, dust contributes more to the radiative term in diabatic heating but has no contribution to the latent heat term; on the other hand, the contribution of water vapor is more concentrated on the latent heat term.

Recent advancements in Martian atmospheric data, notably through the Ensemble Mars Atmosphere Reanalysis System (EMARS), have provided unparalleled insights into the Martian atmosphere by integrating observations from various spacecraft and General Circulation Models (GCMs) [44]. These data allow for a detailed analysis of the Martian atmosphere’s interaction with topographical features such as the Tharsis Bulge [45]. The significance of topographical diversity in understanding Martian climate dynamics has also been emphasized in recent studies, such as that by Montabone et al. (2014) [46].

This research aims to deepen our understanding of the thermal dynamics atop Mars central highland, the Tharsis Bulge, using the comprehensive dataset provided by EMARS. By drawing parallels with the Qinghai–Tibetan Plateau and incorporating the unique dynamics of Martian dust, this study seeks to uncover the complex local heating mechanisms at play over the Tharsis central highland. Our focus will be on elucidating the processes that drive diurnal temperature shifts in this region and how these are influenced by Martian dust storms, which are crucial in shaping the atmosphere over plateaus.

2. Materials and Methods

In this research, we employ the residuals calculation method to obtain the atmospheric apparent heat (Q1) and the thermodynamic energy equation to distinguish the diabatic terms in the atmospheric heating process [10]. Leveraging the EMARS Version 1.0 data spanning Martian years 24 to 33, our analysis focuses on atmospheric variables during key seasonal periods, including a GDS event.

2.1. Data

Single observational datasets lack the precision and coverage necessary for this study. The current leading Martian atmospheric reanalysis datasets include EMARS [44], MACDA [46], and OpenMars [47], all of which are highly regarded. However, due to the specific needs of our research, we selected EMARS for three main reasons. First, EMARS offers the highest vertical resolution among these datasets, providing data on 28 mixed sigma–pressure levels from the surface to ~0.035 Pa, which is crucial for detailed calculations of atmospheric heating mechanisms’ vertical profiles, especially in the troposphere. In contrast, OpenMars covers 25 sigma levels up to ~100 km, and MACDA spans 25 sigma levels from 610 to 0.034 Pa on average. Second, EMARS provides a finer temporal resolution of one Martian hour, compared to two Martian hours for both OpenMars and MACDA, allowing for a better delineation of diurnal atmospheric variations.

We are pursuing the advancement of our comprehension of the Martian atmosphere by employing an intricate methodology centered around EMARS Version 1.0, established by Greybush et al. (2019) [44]. This dataset, spanning the Martian years 24 to 33 (1999 to 2017 on Earth), consists of hourly gridded atmospheric variables that encapsulate the dynamic state of Mars’ atmosphere with unprecedented detail and accuracy. EMARS represents a pioneering effort to merge sparsely distributed observational data with a sophisticated dynamic model, judiciously balancing them against their inherent uncertainties to craft an optimal representation of the Martian atmospheric state. This assimilation of remote sensing data collected from a series of Martian probes with the theoretical and computational frameworks of the Geophysical Fluid Dynamics Laboratory (GFDL) Mars Global Climate Model (MGCM) provides a holistic view of the Martian atmosphere’s state and its temporal evolution.

Central to the EMARS framework is its reliance on the Local Ensemble Transform Kalman Filter (LETKF), a data assimilation technique that ensures the meticulous integration of observational data from instruments such as the TES aboard the MGS and the MCS on the Mars Reconnaissance Orbiter (MRO). This approach allows for the precise calibration of the model’s background states by addressing discrepancies between observed data and model predictions, thus refining our understanding of Martian atmospheric processes.

In this study, we delineate the central highland (CH) region of Tharsis as encompassing 18 °S–2.57° and 123 °W–93 °W (Figure 1). This region, characterized by its elevated topography, displays marked diurnal meteorological variations. Specifically, we utilized EMARS data grid points, as shown by the red dots in Figure 1, and the average values of these data points were employed to represent the overall results for the CH region.

Here, we use the hourly wind, temperature, and pressure data in Ls = 180–360° Martian Year (MY)28 and Ls = 0–360° MY30. The dataset has 6° (lon) × 5° (lat) grids with 28 vertical levels in hybrid sigma–pressure coordinates, with 13 of these levels are in the lowest scale height (~10 km) of the atmosphere. Interactions between the land surface and the atmosphere, such as heat flux and momentum transfer, are most pronounced in this height range. The terrain following nature of the hybrid sigma–pressure system allows for a better simulation of these exchanges. In a hybrid sigma–pressure coordinate system, the “near-surface layer” refers to the lowermost levels of the atmosphere that are closely aligned with the surface, where the system behaves more like a sigma coordinate, following the terrain. Specifically, for each latitude and longitude grid point, the pressure at the k level is calculated using the following formula [44]:

$$p_k=\frac{p_{\mathrm{sfc}}(b_{k+1}-b_k)+a_{k+1}-a_k}{\mathit{ln}\left(p_{\mathrm{sfc}}{b}_{k+1}+a_{k+1}\right)-\mathit{ln}\left(p_{\mathrm{sfc}}{b}_k+a_k\right)}$$

(1)

In Equation (1), $p_{\mathrm{sfc}}$ represents the surface pressure, while $a_k$ and $b_k$ are the pressure coefficient and sigma coefficient within the hybrid sigma–pressure coordinate system provided in EMARS, respectively. In EMARS, the levels are numbered from 1 to 28 going from the top of the atmosphere to near the surface. Consequently, for the near-surface layer $p_{28}$ in question, $a_{28}=0.002,a_{29}=0,b_{28}=0.9933,\mathrm{a}\mathrm{n}\mathrm{d}{b}_{29}=1$.

Our analytical focus narrows to the atmospheric conditions during the winter season of the Northern Hemisphere’s 28th Martian year, a period marked by a significant GDS [45,48], alongside the comparative climatology of the 30th Martian year’s summer and winter seasons. This latter period, chosen for its absence of GDSs, serves as a climatic baseline, with the adjacent 29th and subsequent 31st Martian years providing additional stability without GDSs for our study. Within this framework, we delve into the examination of key atmospheric variables, including pressure; surface and near-surface air temperatures; three-dimensional wind fields; adiabatic heating (sensible, latent, and radiative heating); diabatic heating; advective term; water vapor; and dust mixing ratios. These variables are crucial for understanding the Martian atmosphere’s response to seasonal changes and dust activity, allowing for the derivation of additional physical quantities that further illuminate the intricate dynamics. By dissecting these variables within specified seasonal and temporal windows, our study seeks to elucidate the atmospheric behavior during periods of climatology and storms over the Tharsis Bulge in detail.

This study applies averaging periods of 90–180 Ls for the Northern Hemisphere summer and 270–360 Ls for the Northern Hemisphere winter on Mars, paralleling Professor Yanai’s method of averaging over four months (May–August) for Earth’s Northern Hemisphere summer [10]. We focus on atmospheric heating mechanisms, where the thermodynamic energy equation reveals that fluctuations, during Martian winter, remain meaningful and manageable (detailed in Section 3.3 and Section 3.4). This averaging filters out transient fluctuations, revealing the stable underlying seasonal characteristics that are crucial to our study. In specific domains, employing a 270–360 Ls average to represent Martian winters is a common practice in both observational [49] and simulation-based [20] Martian atmospheric studies, even used for assessing atmospheric optical depths [50], thus supporting its validity in representing both direct and indirect dust effects. However, averaging over 90-degree Ls still obscures atmospheric details on Mars due to its strong seasonal changes, unlike Earth. Therefore, this study includes an intra-seasonal analysis at 5-degree Ls intervals (Figures S1–S9) alongside seasonal averages.

In addition, the study used all the 24-h LT to perform the investigation. Strong atmospheric tides on Mars cause temperature anomalies to shift to earlier local times at lower pressures, affecting wind fields, dust, and clouds [51,52,53,54]. Given the significant influence of tides on the Martian atmosphere, which differs greatly from Earth’s, it is essential to consider the entire 24-h local time period in analyses. This comprehensive approach is necessary for accurate conclusions, as partial coverage may lead to incorrect interpretations.

2.2. Methods

In this comprehensive analysis, we elucidate the sophisticated computational methodologies employed to investigate the Martian atmospheric heat dynamics. Utilizing the seminal framework established by Yanai et al. (1994) [10], our calculations hinge on a precise formula designed to quantify the atmospheric apparent heat source, $Q_1$, integrating key atmospheric variables and dynamics. This equation

$$Q_1=c_P{\left(\frac{p}{p_0}\right)}^{\mathsf{\kappa }}\left(\frac{\partial \mathsf{\theta }}{\partial t}+v·\nabla \mathsf{\theta }+\mathsf{\omega }\frac{\partial \mathsf{\theta }}{\partial p}\right)$$

(2)

serves as the cornerstone of our computational approach, where $\mathsf{\theta }$ is the potential temperature, $v$ denotes the horizontal wind velocity, and $\mathsf{\omega }\equiv dp/dt$ represents the vertical velocity in relation to pressure $p$. The parameters are $\mathsf{\kappa }=R/c_p$, with $R$ and $c_p$ being the gas constant and specific heat at constant pressure for dry air, respectively, and $p_0=636$ Pa is the surface pressure at the mean radius [55].

Expanding upon this foundational equation, we delve into the advective, adiabatic, and diabatic contributions, derived from the thermodynamic energy equation:

$$\frac{\partial T}{\partial t}=-v·\nabla T-{\left(\frac{p}{p_0}\right)}^{\mathsf{\kappa }}\mathsf{\omega }\frac{\partial \mathsf{\theta }}{\partial p}+\frac{Q_1}{c_p}$$

(3)

where $T$ is the air temperature (K). This equation enables a nuanced analysis of the atmospheric energy balance and heat dynamics. We extend our computational rigor by vertically integrating $Q_1$, alongside the latent heat term (lheat) and the radiative term (h rad), from the Martian surface up to the tropopause, employing the integration notation introduced by Yanai et al. (1994) [10]

$$⟨⟩\equiv \frac{1}{g}{\int }_{p_T}^{p_s}\left(\right)dp$$

(4)

to ascertain the vertically integrated values of these critical thermal components.

Employing the EMARS data, our investigation encompasses a broad spectrum of variable analyses that illuminate the complex dynamics of the Martian atmosphere. The diurnal variations of surface pressure, temperature, near-surface air temperature, and dust mixing ratios within Tharsis’ central highland during distinct seasons are analyzed, which are further enriched by vertical cross-sections and time–height contour plots of potential temperature, water vapor, and dust mixing ratios to reveal vertical details.

In addition to these detailed analyses, our study also ventures into the examination of wind field streamline maps during summer and winter, complemented by time series data of vertically integrated diabatic terms (Q1, l heat, s heat, and h rad). These analyses show the seasonal changes of atmospheric heating mechanisms.

3. Results

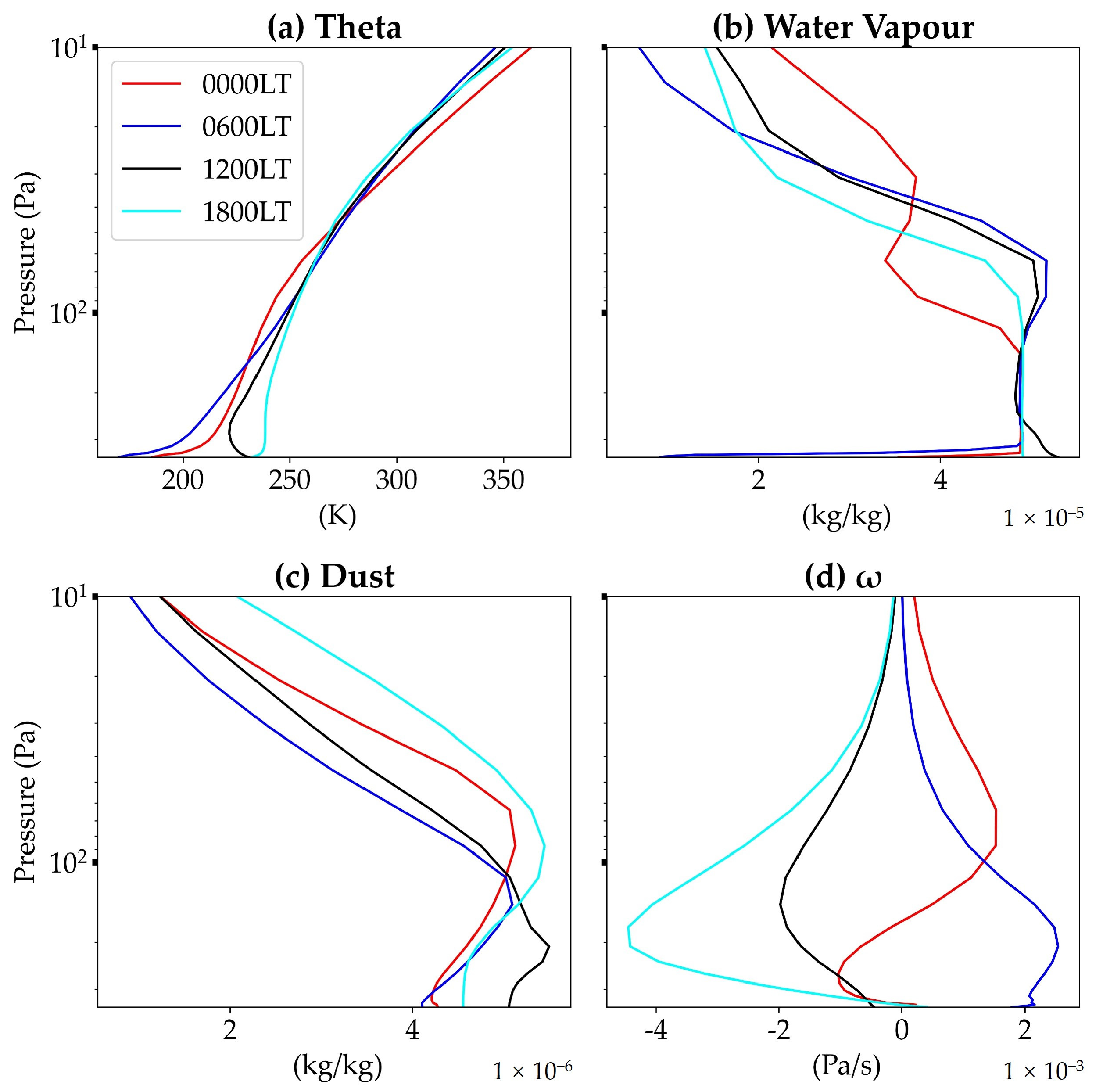
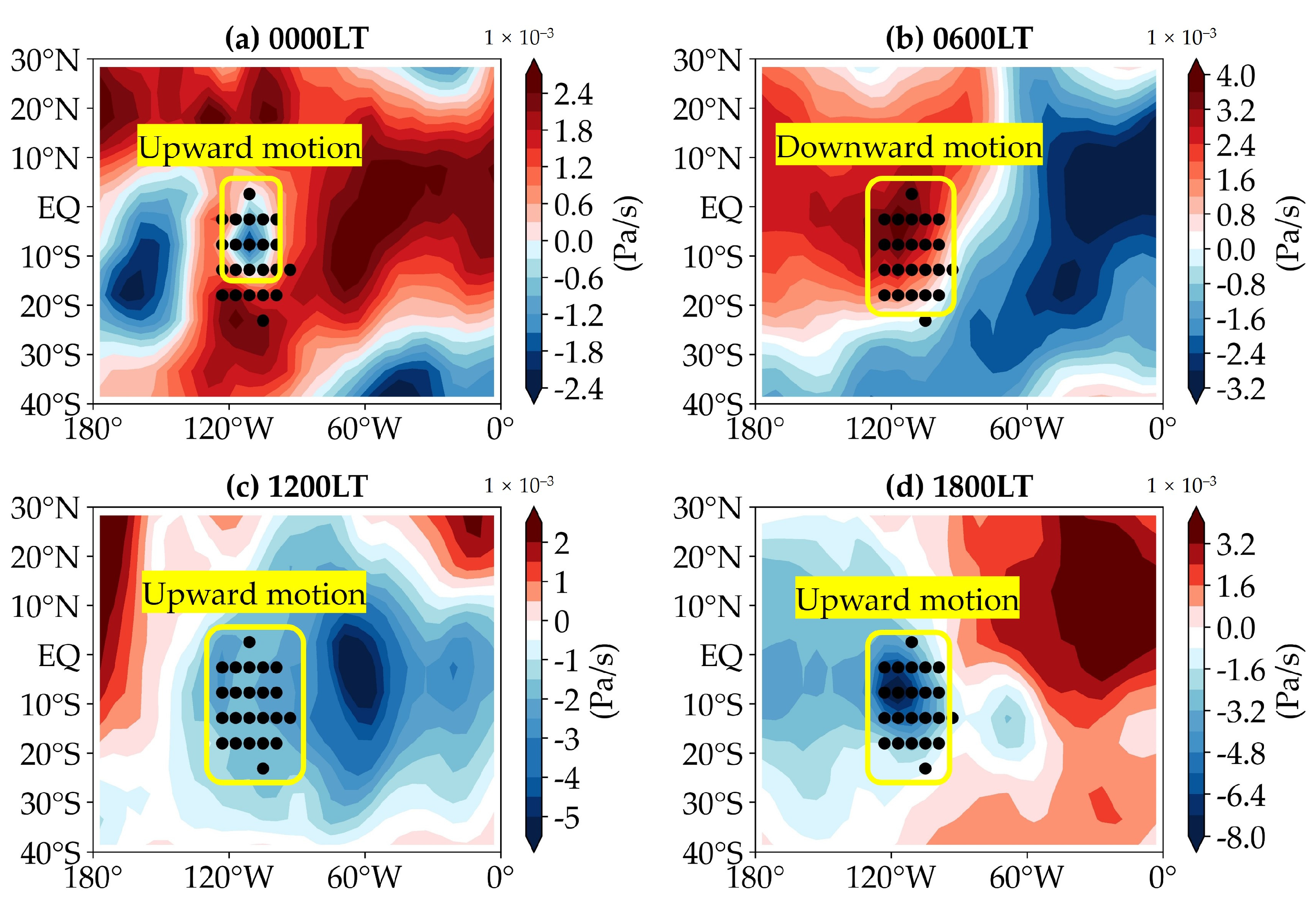
3.1. Characteristics of the Planetary Boundary Layer

Our analysis, depicted in Figure 2 and Figure 3, captures the diurnal flux in the surface and near-surface meteorological parameters during the winter season of the Northern Hemisphere (Ls = 270°–360°), which corresponds to the summertime for the CH region primarily situated in the Southern Hemisphere, for the 30th Martian year.

Firstly, we analyzed diurnal patterns in the surface pressure within the CH region (Figure 2d), which revealed a peak pressure at the local midnight (0000LT, 105 °W) and a minimum pressure at 1600LT, with the diurnal amplitude approximating 12.5 Pa. As the highest plateau on Mars, CH has a significantly lower pressure than the surrounding areas (Figure 2d), accompanied by relatively higher diurnal variations of the surface temperature, the air temperature at the lowest atmospheric level, and the differential between surface and air temperatures, shown in Figure 2a–c. These degrees of temperature differences and moisture characteristics are among the possible factors influencing the unique heating mechanisms of the atmosphere above CH, as discussed in subsequent sections.

Notably, surface temperatures exhibit a rapid ascent post-sunrise at 0600LT, achieving a zenith after noon (1300LT), followed by a gradual decline to the lowest point just prior to the next sunrise (0500LT). Conversely, the surface air temperature begins its ascent at 0700LT, reaching its peak after noon (1500LT) and then diminishing until the next sunrise (0600LT). The observed average diurnal temperature range on the plateau’s surface is ~130 K, in contrast to the relatively lower range of ~105 K in the comparison areas at the same latitude. The discrepancy in the amplitude and phase of surface and air temperature shifts culminates in diurnal fluctuations in the temperature differential between the ground and the air, with a disparity peak reaching up to 50 K around noon and a minimum of approximately −2 K at night.

The diurnal variations of the ground surface temperature (TS), near-surface air temperature (TA), TS-TA, surface pressure, and water vapor mass mixing ratio are generally stable in the 30th Martian year’s Northern Hemisphere winter (Figure S1). Conventional perspectives suggest that surface temperature variations in the Tharsis region do not significantly differ from those in other areas, which has led to less focus on this region. To investigate this, we conducted comparative experiments with four regions at the same latitude as the CH region, as depicted in Figure 1. However, our research has identified previously unrecognized features in the surface temperature differences within the CH region, including diurnal variations that exceed those of other regions at similar latitudes. Our findings, detailed in Figure 2, show that the central highlands of Tharsis undergo diurnal surface temperature differences of approximately 25 K and near-surface air temperature fluctuations around 20 K greater than those observed in adjacent plains. Such pronounced diurnal temperature differences are significant enough to cause atmospheric water vapor to manifest in distinctly different phases, such as water vapor and water ice, across latitudes.

We also found that a deep mixing layer extends from the surface to 200 Pa, as Figure 3a shows in the evening (1800LT), with a super-adiabatic lapse rate layer indicating strong instability during midday (0600LT). At dusk (1800LT), the boundary layer mixing is optimal, with the mixed layer reaching greater heights than at other times: potential temperature below ~200 Pa (Figure 3a), water vapor below ~80 Pa (Figure 3b), and dust below ~250 Pa (Figure 3c) show almost no variation with the altitude. During the evening transition, the boundary layer exhibits optimal mixing and reaches its peak altitude due to residual daytime heating and the onset of nocturnal cooling. This period is characterized by a significant reduction in surface temperature inversion, which normally suppresses vertical motion. Consequently, the weakened inversion coupled with the persisting thermal energy from the ground facilitates greater vertical mixing. Additionally, evening conditions often involve increased wind shear, which introduces mechanical turbulence, further enhancing the vertical uplift. Collectively, these factors contribute to a notably higher ascent rate in the mixed layer’s vertical wind speed (Figure 3d), allowing for a more pronounced and efficient mixing of atmospheric constituents.

Notably, when analyzing within the season at intervals of 5 Ls, we found that the potential temperature, water vapor, dust, and vertical velocity profiles at 1800LT were more stable compared to other times (Figure S2). This is characterized by a well-developed mixed layer near the surface and upward vertical wind speeds.

Figure 4 presents the vertical time profiles of potential temperature, water vapor mixing ratio, and dust mixing ratio during 0000LT, 0600LT, 1200LT, and 1800LT of the 30th Martian winter in the CH region. The profiles in Figure 4a,b reveal that the mixing layer in the evening is significantly more developed than in the early morning. Correspondingly, the water vapor and dust in the evening (Figure 4d,f) show a more pronounced barotropic structure within the height range of the mixing layer compared to the early morning (Figure 4c,e).

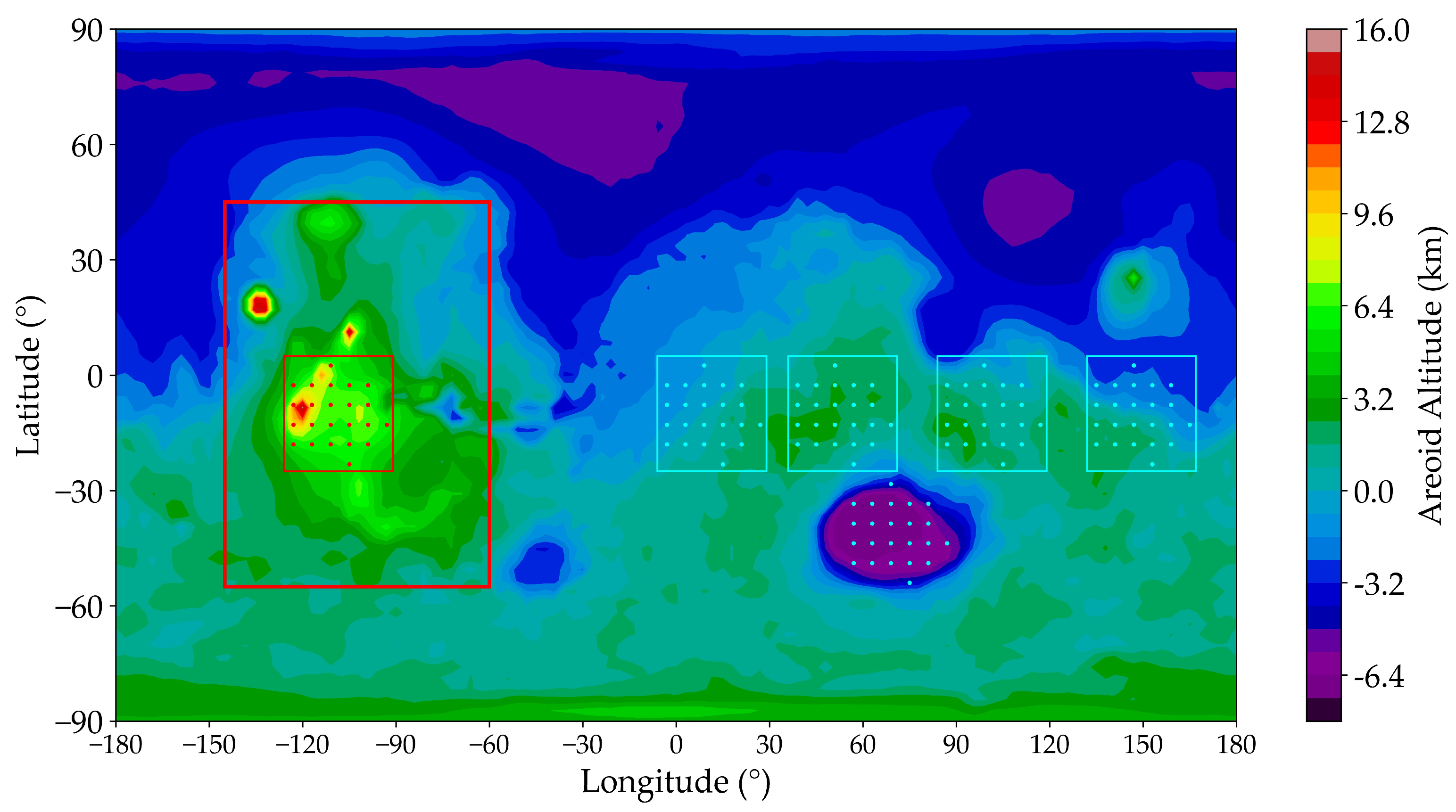
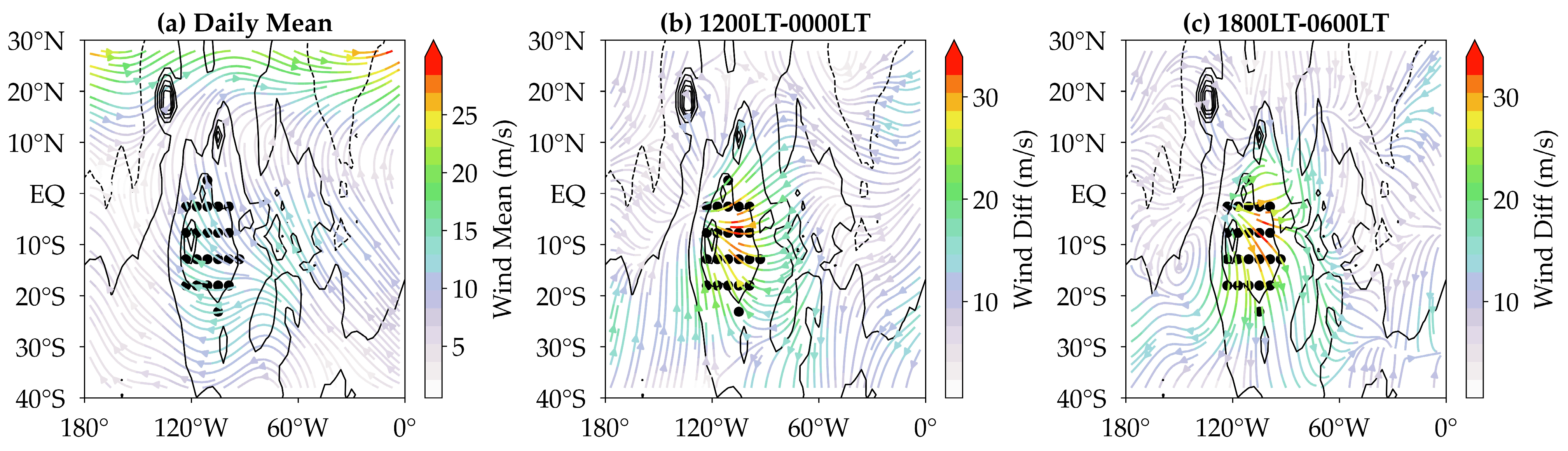
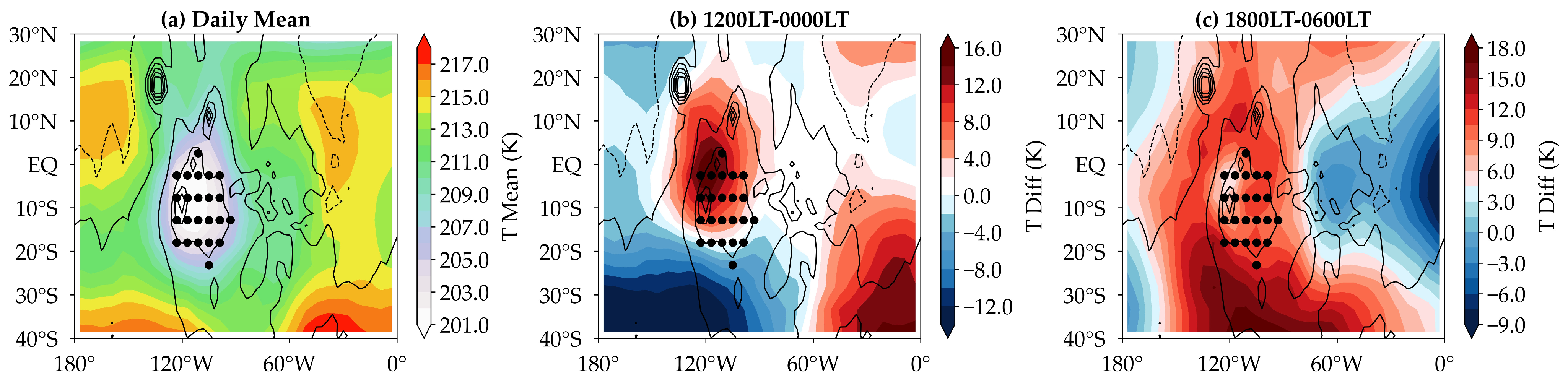
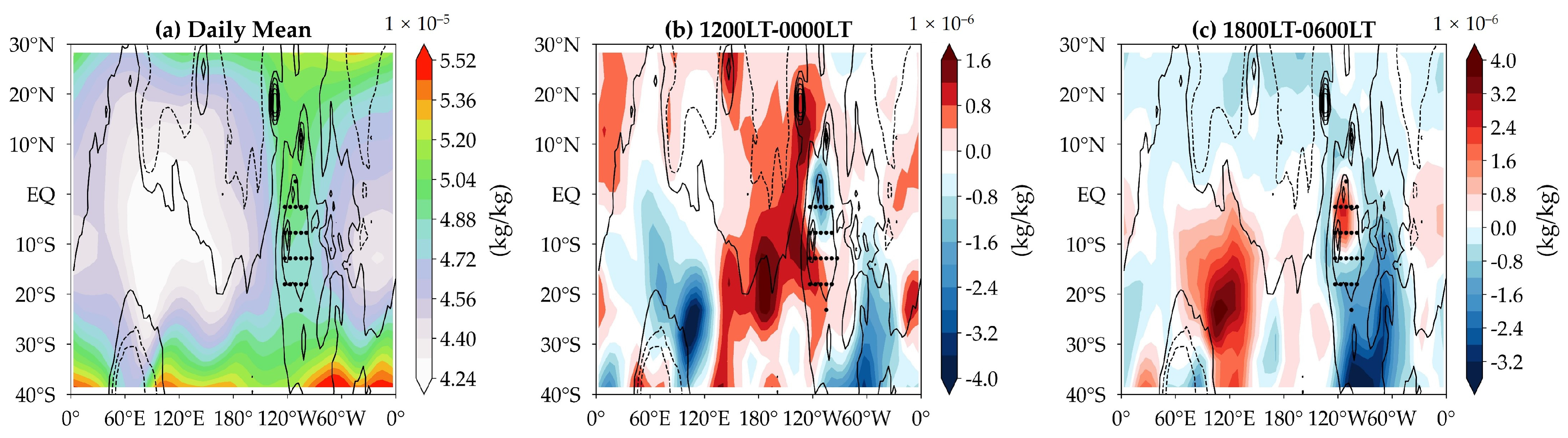
3.2. Basic Analysis of Large-Scale Wind, Pressure, Temperature Fields, and Dust Distribution Characteristics

In this section, we succinctly describe the mean large-scale fields and their diurnal variations in the CH region during the Northern Hemisphere winter. The large-scale characteristics of horizontal flow, temperature, and dust distributions around the highlands and their vicinity are discerned through seasonal mean maps, facilitating qualitative discussions.

We adopted the methodology of utilizing averages and differences between measurements at 0000LT and 1200LT (corresponding to local noon and midnight at Tharsis) to characterize the diurnal temperature averages and variations over the TB region. This approach is inspired by Yanai’s meaningful work on diurnal temperature cycles over Earth’s Tibetan Plateau [10]. Yanai employed the coldest temperature recorded at 0600LT and the peak temperature at 1800LT, marking a consistent 12-h interval. In contrast, based on Martian conditions near TB, we selected 0000LT for near-minimal temperatures and 1200LT for maximal temperatures for two primary reasons. Firstly, the gradual decline in nighttime temperatures on Mars, as evidenced in Figure 2a, shows minimal temperature variation between 0000LT and the lowest point at 0500LT. Secondly, the significant temperature differences on Mars do not align with a 12-h cycle as they typically do on Earth, necessitating a methodological adjustment. Therefore, our selection of 0000LT and 1200LT, spaced exactly 12 h apart not only aligns with the natural diurnal rhythm but also adheres to Yanai’s methodological precedent. This optimized approach was chosen to reflect the unique Martian environmental conditions rather than adhering strictly to terrestrial time points of noon and midnight.

Streamline and isotach analysis at 150 Pa clearly reveals the topographic and thermal effects of the CH region on a large-scale flow. The most prominent feature in the mean circulation during this period is the deflection of a northward flow around the CH region (with the wind direction tending to follow the contours of CH’s southern topography), with wind speeds over the highlands slightly exceeding those in the surrounding areas (Figure 5a and Figure S3a). Combining the 5 Ls interval analysis (Figure S3b) and seasonal average daily mean vector difference fields (Figure 5b) reveals a wind convergence center in the northwestern CH region at 1200LT compared to 0000LT. This convergence center migrates northward from the western CH region (~270 Ls) to the northwestern CH region (~350 Ls) (Figure S3b). Regarding the wind field differences over CH, the wind direction at 1200LT compared to 0000LT shifts from northeasterly (~270 Ls) to southerly (~360 Ls) (Figure S3b). The wind at 1800LT compared to 0600LT shows slight fluctuations in the winter but generally remains northwesterly (Figure S3c). Notably, both cases exhibit significantly stronger wind speeds over CH during the daytime compared to nighttime, with a greater increase than in the surrounding regions. These characteristics are also roughly observable in the seasonal average maps (Figure 5b,c).

We also found the thermal influence of the highlands evident in the distribution of pressure and temperature near the surface of the highlands. During winter, a vast cold high is present at an altitude of 150 Pa over the highlands (Figure 6a), with a deep structure extending from 250 Pa to approximately 30 Pa that is generally stable in winter (Figure S4a). Furthermore, we observe a significant temperature difference of ~12 K between 1200LT and 0000LT at a similar altitude range over the northwestern corner of the highlands (Figure 6b) generally stable in the northwestern CH (Figure S4b), corresponding to the enhanced daytime influx of air over the northwestern highlands mentioned in Figure 5b. It is noteworthy that there is also a temperature difference of ~−6 K between 1800LT and 0600LT (Figure 6c), moving from the northwestern CH (~270 Ls) to western CH (~360 Ls) (Figure S4c).

Figure 7a–c present the mean distribution and diurnal difference fields of the water vapor mixing ratio at 150 Pa. Notably, within the longitudinal range of the CH region at low latitudes, the water vapor mixing is significantly higher than in other regions at the same latitude (Figure 7a), especially in late winter (Figure S5a). The combination of the 5 Ls interval analysis (Figure S5b) and seasonal average daily mean vector difference fields (Figure 7b) reveals a center of negative water vapor values at 1200LT relative to 0000LT in the northern CH region, exhibiting significant seasonal fluctuations (Figure S5b). In contrast, a center of positive water vapor values is observed at 1800LT relative to 0600LT in the same region (Figure 7c), which are stronger and more stable compared to the negative center mentioned earlier (Figure S5c).

In addition to stronger diurnal variations of near-surface water vapor over the CH region compared to similar latitudes (Figure 2e), we also observed higher daily average water vapor levels in this region (Figure 7a). These characteristics of water vapor are likely linked to water ice clouds, which are predominantly composed of fine ice crystals that can sublimate under certain conditions. The modeling studies by Montmessin [19] and Wordsworth [20] showed that adiabatic cooling can significantly reduce temperatures in the valleys of the southern highlands below the global average, leading to the transport of water ice from low-lying areas to elevated regions and from the poles towards the equator. The changes in water vapor over the TB region are likely caused by the phase change of water ice clouds transported from other areas.

In Figure 8a–d, we present the mean vertical velocities ω at 150 Pa during the nocturnal (0000LT), early morning (0600LT), midday (1200LT), and evening (1800LT) periods of the 30th Martian winter. The diurnal variation in vertical velocity over the highlands is pronounced, with most of the highlands experiencing downward mean vertical motions at midnight and early morning and upward motions at noon and evening. However, two areas warrant attention.

At midnight (0000LT), localized upward motions were observed over the northern CH region. Subsequently, intense subsidence occurred over the northwestern CH region in the early morning hours (0600LT); this subsidence dissipated around noon (1200LT) and gradually transitioned into an upward motion, reaching its peak by late afternoon (1800LT). This pronounced vertical motion variability in the CH region is attributed to the significant diurnal temperature contrast between the land and the atmosphere. The upward air currents over CH at 0000LT, 1200LT, and 1800LT and the downward air current over CH at 0600LT exhibit slight seasonal fluctuations in intensity but remain consistent in direction (Figure S6).

Vertical updrafts are crucial for dust transport processes; hence, the region of frequent dust maxima near Arsia Mons (8°21′S 120°05′W) around 1500LT (Figure S7d) may be associated with the upward air motion over CH shown in Figure 8.

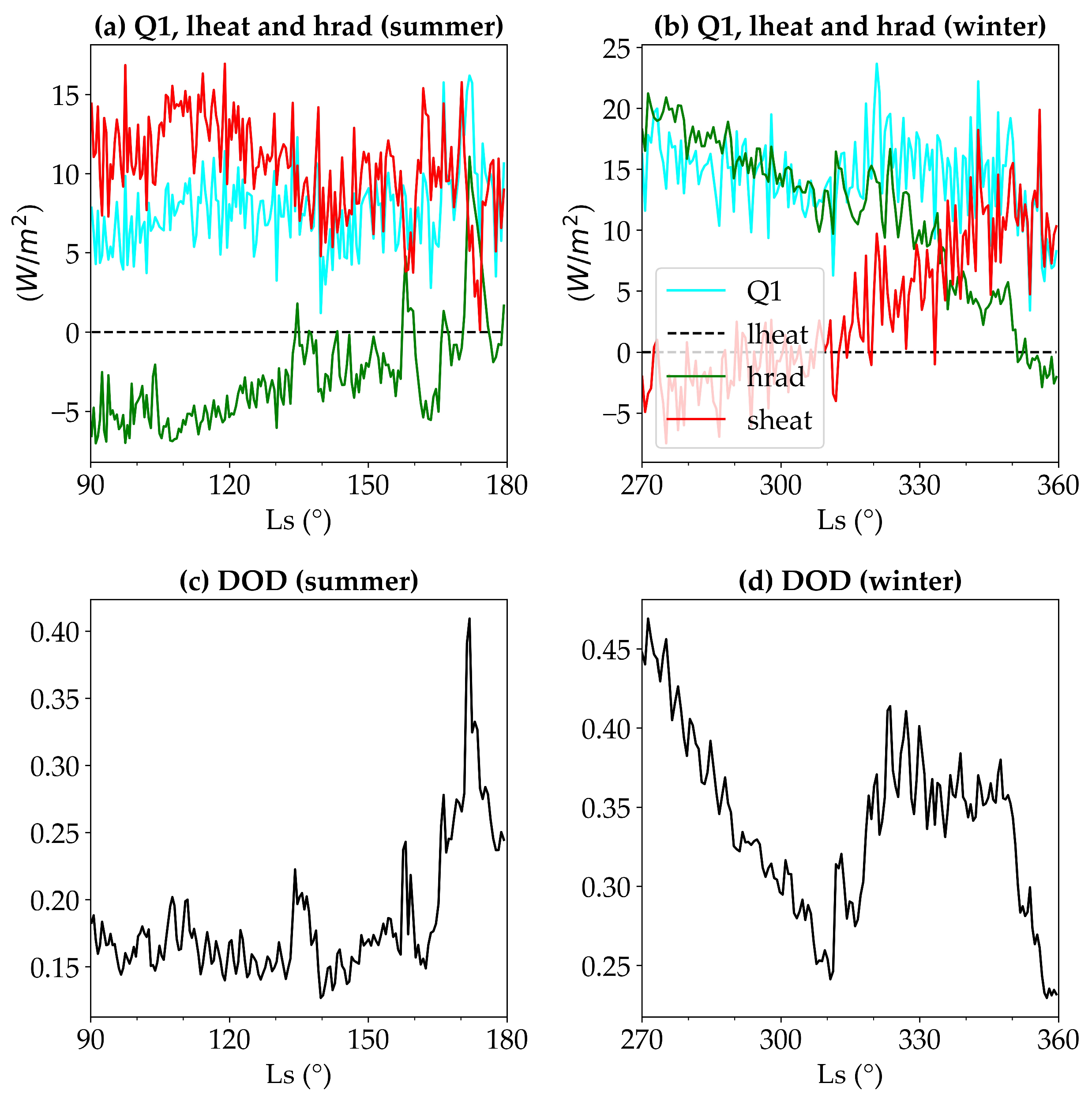
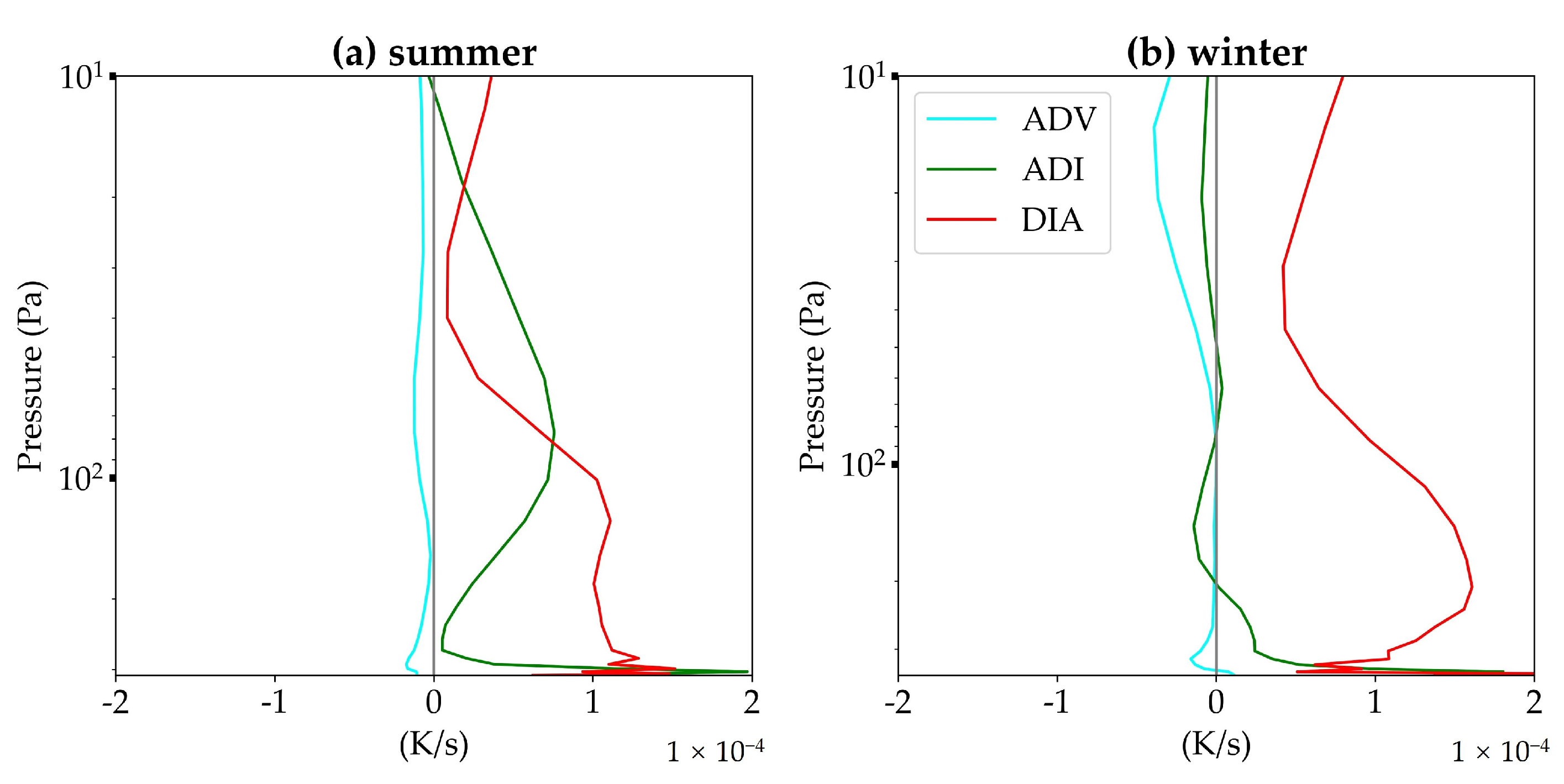
3.3. Plateau Heating Mechanism on Tharsis

We examined the diurnal mean and vertically integrated atmospheric apparent heat source Q1, including its latent and radiative components, in pursuit of elucidating the seasonal variations and dust-related mechanisms of atmospheric heating in the CH region on Mars across two distinct seasons. The sensible heat component was deduced by subtracting the latter two from Q1. As depicted in Figure 9a, during the Northern Hemisphere’s summer, Q1 is predominantly governed by the sensible heat component, maintaining a stable presence around 10 $\mathrm{W}/{\mathrm{m}}^2$. However, Q1 also exhibits corresponding increases in conjunction with significant peaks in the radiative component (e.g., around Ls = 173°).

In 270–360° Ls, when the CH region predominantly resides in the Southern Hemisphere, the radiative component is mostly negative and highly correlated with the dust opacity (DOD) time series (Figure 9c). Figure 9b illustrates that, in the Northern Hemisphere’s winter, Q1 is dominated by the radiative component, but as the radiative heating diminishes towards the end of winter, it is compensated for by an increase in sensible heat, thereby stabilizing the overall Q1. In 90–180° Ls, the correlation between the radiative component and DOD is less consistent; initially, both decline together, but in the latter half, the DOD briefly increases while the radiative component continues to fall (Figure 9d). Unlike Earth, where latent and sensible heat predominantly drive Q1 variations [1,2,43,56], on Mars, the combination of radiative and sensible heat takes precedence, with the radiative component assuming greater importance and the latent heat being negligible. This is attributed partly to the arid state of the Martian atmosphere and partly to the extensive radiative effects of Martian dust.

In both summer and winter of the Northern Hemisphere, we present key time series to corroborate the role of sensible heat heating on the Martian plateaus. These series include diurnal mean surface temperatures, near-surface air temperatures (the closest atmospheric pressure level to the surface), and the surface–air temperature difference over the CH region (Figure 10). The surface–air temperature difference in the CH region on Mars does not exhibit significant seasonal variations; yet, with an average value of approximately 15 degrees, it significantly exceeds that of the Tibetan Plateau on Earth during the same periods (averaging about 3–7 degrees, as shown in Yanai’s Figure 14 [10]). This suggests that sensible heat transport in the CH region is possibly stronger than that over the Tibetan Plateau, underscoring the importance of sensible heating on Mars. Furthermore, we find that, even under conditions of near-constant surface–air temperature differences, the sensible heat component still dynamically balances with the radiative component to some extent, contributing to the stabilization of Q1. These findings, in conjunction with the intense diurnal variations in surface temperatures (Figure 2a), indicate that surface conditions on the plateaus are conducive to dry convective heat transfer.

We analyzed each term of the thermodynamic energy equation (see Equation (3)) to gain a deeper understanding of the boundary layer structure. This analysis accounts for local temporal changes in temperature and encompasses horizontal thermal advection, adiabatic heating, and diabatic heating terms from left to right. Figure 11 presents the average vertical profiles of the terms of the thermodynamic energy equation over the CH region during the summer and winter in the Northern Hemisphere. Within the Martian atmospheric boundary layer, the advection term over the CH region is notably less significant than that over the Tibetan Plateau, consistently contributing negatively, remaining stable, and being significantly smaller relative to the other two terms; hence, it is not discussed further. Figure 11a shows that, during the Northern Hemisphere summer, atmospheric heating is primarily driven by intense diabatic and adiabatic processes, both of which consistently dominate throughout the season (Figure S8a). During winter (Figure 11b), from the surface to 100 Pa, diabatic heating intensifies further, while adiabatic heating induced by vertical motion weakens to the same magnitude as adiabatic heating caused by advection. Throughout this period, atmospheric heating in the mid-to-lower troposphere is consistently dominated by diabatic processes (Figure S8b).

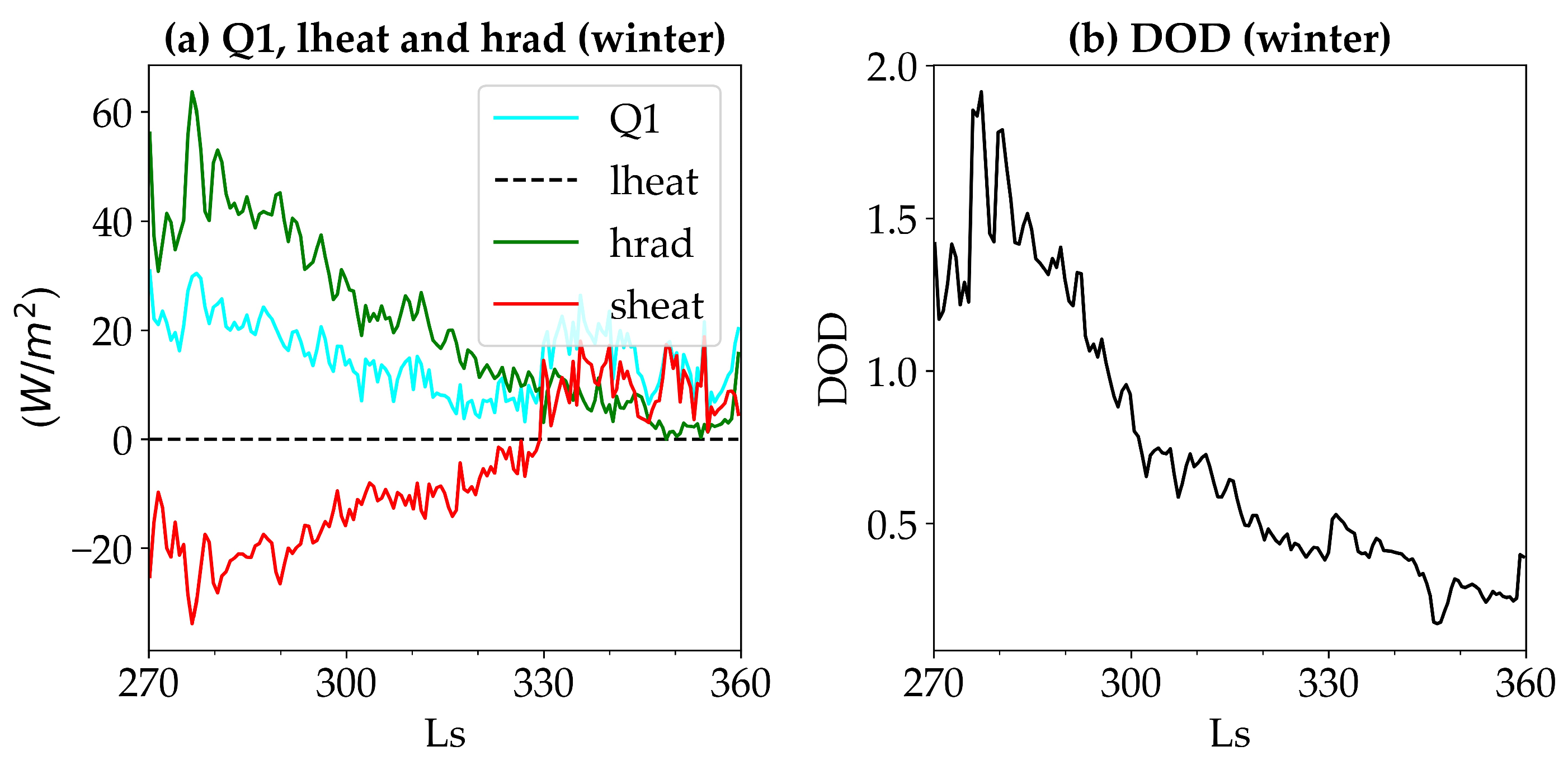
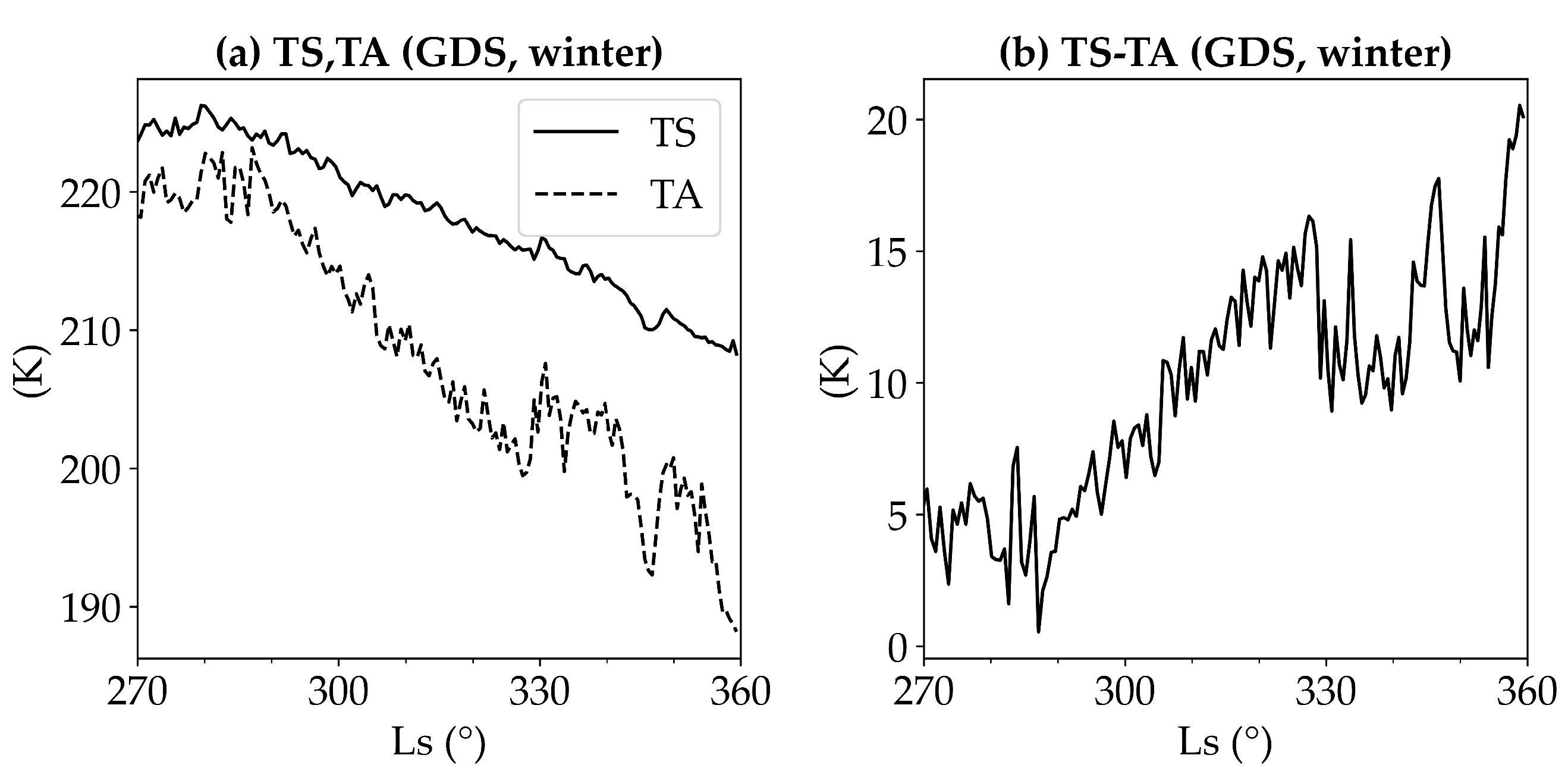
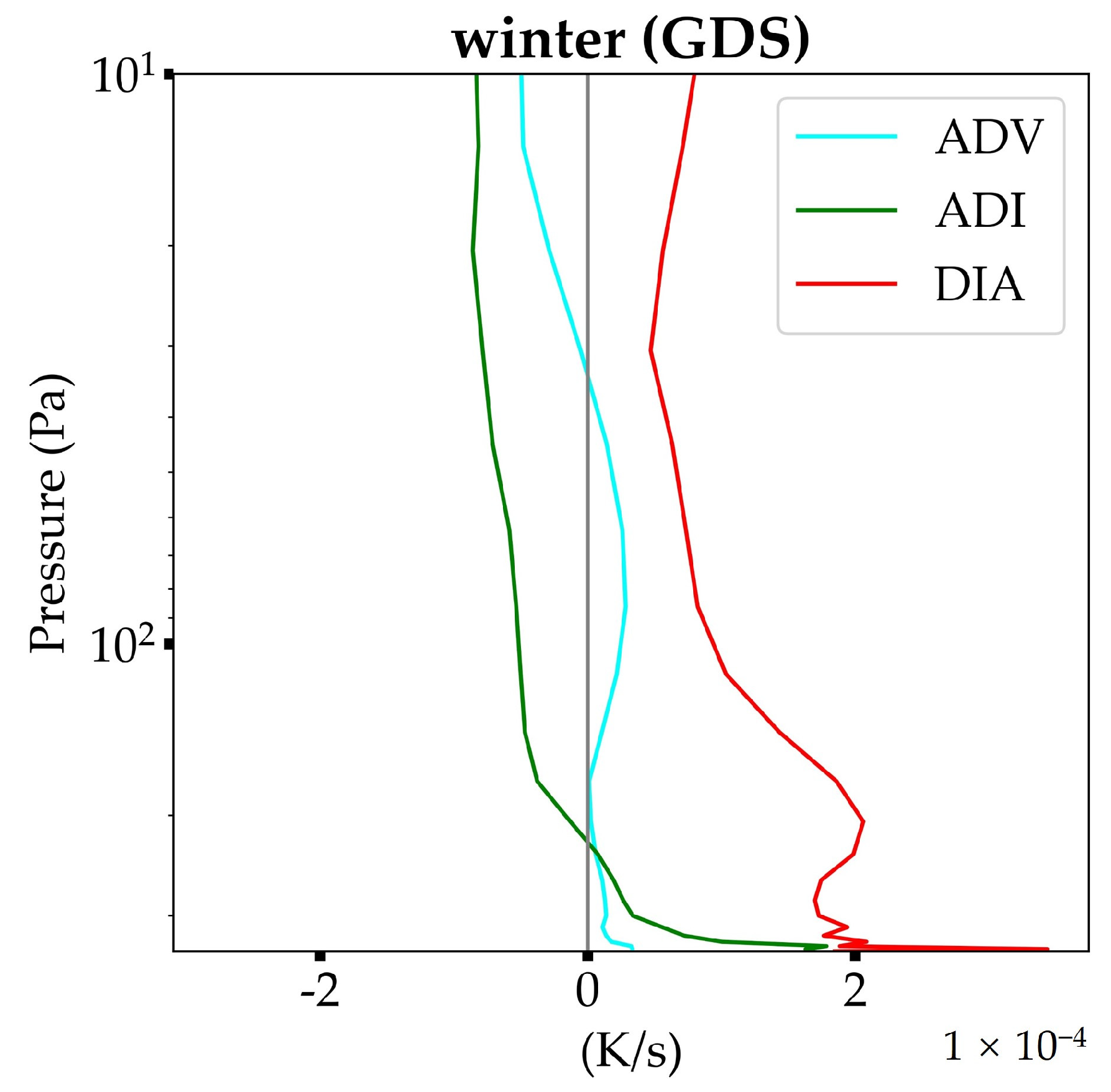
3.4. The Impact of GDSs

In the final section of our investigation, we sought to understand the unique impact of Martian GDSs on the plateau heating dynamics within the CH region. Our study focused on the GDSs that occurred during the 28th Martian year, specifically between Ls = 270° and 300°. Figure 12a and Figure 13b display the vertically integrated mean diabatic heating rates and DOD over the CH region during the Northern Hemisphere’s winter season of that year. It is evident that the dust distribution within Ls = 270°–300°—represented by DOD—almost entirely controlled the radiative heating within the CH region. During this period, radiative heating dominated the diabatic processes, with the peak values aligning closely. The surface sensible heat flux over the plateau was markedly weak during this interval, only beginning to recover around Ls = 300°, as the GDSs abated. Our findings indicate that the radiative heating component (h rad) is influenced by the dust content, with an increase in heating corresponding to the rising dust levels, exceeding 60 W/m² during the GDS period, as depicted in Figure 9 and Figure 12. It is noteworthy that, during GDSs, atmospheric components (e.g., water ice clouds) may be higher beyond the integration pressure region but also makes a difference in the energy budget through mechanisms (e.g., radiative effect), which merits further study.

While correlation does not imply causation, the exceptionally high correlation observed likely indicates a physical relationship. This is demonstrated by the near-identical curves for the h rad and DOD in Figure 9a,c, as well as Figure 12a,b. The correlation decreases when the dust heating and sensible heat flux are similar, as shown in Figure 9b,d. This pronounced correlation between h rad and DOD, evident only at high DOD levels, suggests that dust’s radiative effects predominantly influence h rad variations when they are strong enough.

We presented a time series of daily mean surface temperatures, near-surface air temperatures (the closest atmospheric pressure level to the surface), and the temperature difference between the ground and air over the CH region during the Northern Hemisphere’s winter season of the 28th Martian year in order to corroborate the evidence for changes in the surface sensible heat flux during the GDS (Figure 13). Figure 13 reveals that, during the GDS, the ground–air temperature difference significantly decreased to around 5 K (as shown in the Ls = 270–300° of Figure 13b), substantially lower than the approximate climatological state of 17 K (as shown in Figure 10b and the end of Figure 13b). After the cessation of the GDS, this temperature difference gradually recovered. The aforementioned temperature variation pattern corresponded to the reduction in surface sensible heat flux during the GDS period due to the blocking of solar radiation reaching the surface by dust and the subsequent recovery of the surface sensible heat flux following the dust reduction.

We then examined the average vertical profiles of each term in the thermodynamic energy equation over the CH region during the Northern Hemisphere’s winter, as illustrated in Figure 14. This would help to gain deeper insight into the boundary layer structure during the GDS. As anticipated, due to the substantial enhancement in radiative terms, the overall diabatic heating increased by at least $0.5\times {10}^{-4}\mathrm{K}/\mathrm{s}$ across all tropospheric pressure levels compared to that without a GDS (Figure 11b), governing the atmospheric temperature changes across most of the troposphere. Diabatic heating in the mid-to-lower troposphere significantly intensifies during the GDS period (270–300 Ls) (Figure S9) and gradually returns to levels comparable to the winter of MY30 as the GDS concludes (Figure 11b). However, it is noteworthy that adiabatic cooling induced by vertical motion in the mid-to-upper troposphere is also significantly enhanced during the GDS period, dominating the atmospheric heating there. The intensified adiabatic cooling rapidly subsided after the GDS, returning to levels comparable to the winter of MY30 (Figure 11b) around ~320 Ls (Figure S9).

4. Conclusions

This study marks a significant advancement in our understanding of Martian atmospheric dynamics by documenting the specific thermal and dynamic processes over the Tharsis region. By offering detailed analyses of the convective activity, temperature variations, and the distinct roles of sensible and radiative heating influenced by topographical features and dust storms, our findings contribute to refining the predictive models of Martian atmospheric behavior. This enhanced understanding is crucial for the planning and execution of future Martian missions and may influence the strategic management of exploration activities under varying atmospheric conditions. Further research should integrate these localized insights into global atmospheric models to improve their efficacy in predicting and managing the environmental challenges of Mars exploration.

• Our work embarked on an in-depth investigation of the atmospheric characteristics, boundary layer structure, and heating mechanisms over the CH region of Tharsis on Mars. We also discussed the significant GDS impacts on the atmospheric heating mechanisms. Through a series of combination of diurnal and seasonal analyses of dynamics and thermodynamics, we characterized the planetary boundary layer properties, large-scale wind patterns, pressure and temperature fields, and dust distribution.
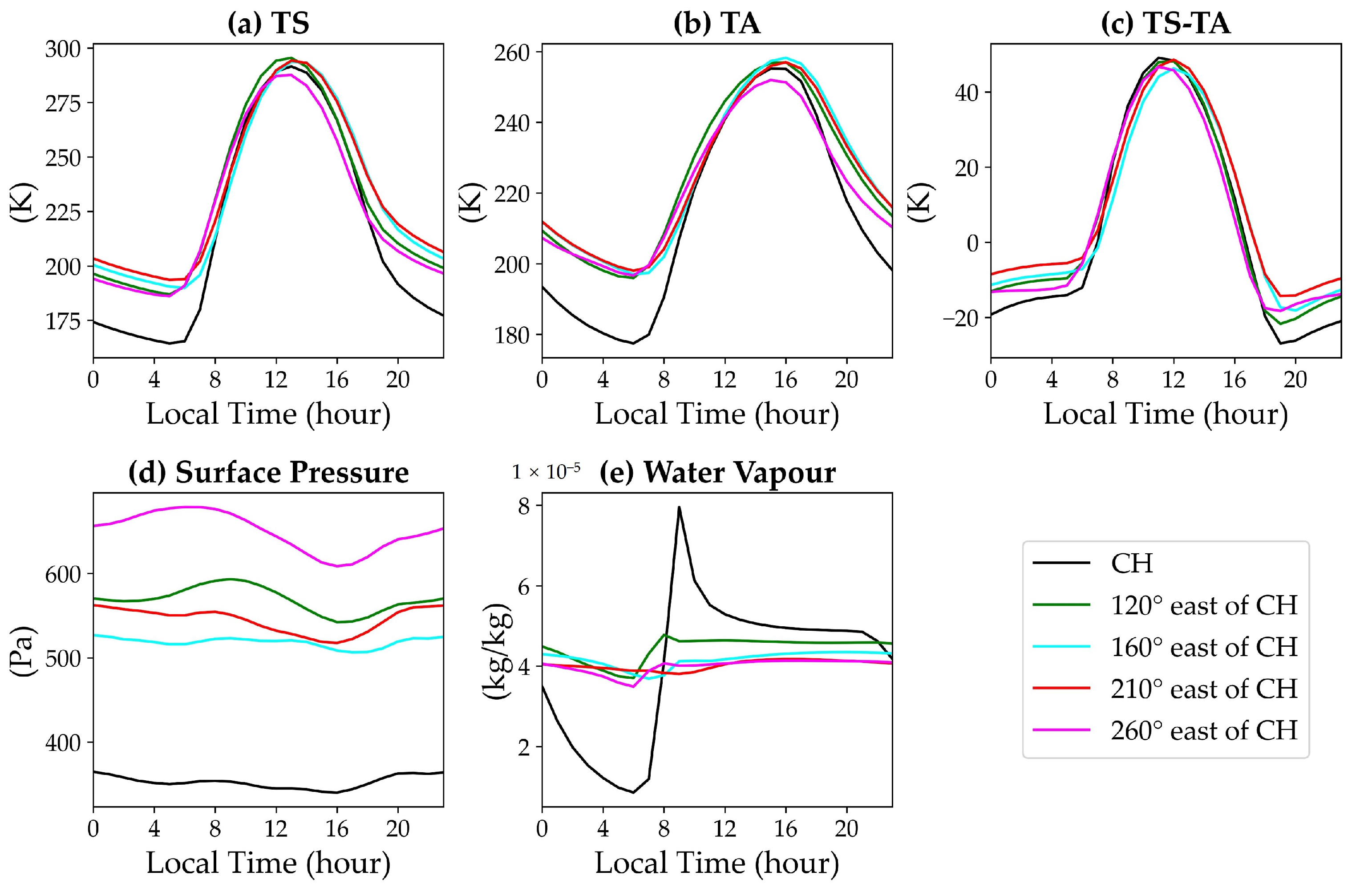
• Extreme Diurnal Temperature Variability: Our research quantified extreme diurnal surface temperature fluctuations, which reached up to 130 K, and the diurnal cycle showed surface pressure swings of approximately 12.5 Pa, dwarfing the Earth’s Tibetan Plateau’s range by a factor of 3 to 4. We also showed that the Tharsis Plateau experiences diurnal surface temperature variations ~25 K higher than the areas at the same latitude, along with diurnal near-surface air temperature fluctuations of ~20 K higher. The water vapor mixing ratio reached its lowest value in the early morning, then rapidly peaked at the local time of 9, showing a different diurnal pattern compared to the Tibetan Plateau on Earth. The boundary layer showed strong convective activity during the day, leading to well-mixed conditions, with a super-adiabatic lapse rate layer indicating strong instability during midday. These characteristics highlight the Tharsis region’s susceptibility to significant thermal extremes compared to previously studied Martian plains or Earth’s high-altitude regions like the Tibetan Plateau, where diurnal temperature variations are considerably less.
• Convective Dynamics and Atmospheric Stability: The pronounced convective activity during daylight, characterized by a super-adiabatic lapse rate indicating strong thermal instability around noon, transitions to a more stabilized atmospheric state by dusk. At the 150 Pa level, there is a massive cold high-pressure system above the plateau, while the CH region’s northwest corner exhibits an average diurnal temperature difference of up to 16 K at nearly the same altitude. This is the first quantification of such dynamic atmospheric behavior over Tharsis, detailing transitions from a noontime instability with a super-adiabatic lapse rate to homogenized conditions by dusk.
• Seasonal Heating Mechanisms: We delineate the seasonal dominance of sensible and radiative heating. Sensible heat predominantly controls the atmospheric heating in the local summer (10 W/m²), whereas radiative heating prevails during the local winter, which contrasts with earlier assumptions that did not account for such distinct seasonal shifts. The Martian dry state and dusty conditions significantly affected the heating dynamics, with latent heat being negligible, a stark contrast to Earth’s atmospheric dynamics.
• Impact of Global Dust Storms (GDS): The influence of GDSs significantly alters the local atmospheric dynamics, reducing the temperature differential between the ground and air from an average of 17 K to about 5 K during storm events. The dust-driven radiative heating dominated, altering the typical heating pattern and revealing the critical role of dust in local processes. The overall diabatic heating below 10 Pa increased by $3.4\times {10}^{-5}\mathrm{K}/\mathrm{s}$ and by at least $5\times {10}^{-5}\mathrm{K}/\mathrm{s}$ above 200 Pa. This change in temperature disparity underscores the profound impact of dust aerosols on radiative heating processes.
• Implications for Martian General Circulation Mode Ls: These findings are pivotal for revising Martian climatological models to better incorporate localized topographical effects and extreme diurnal thermal variations. The evidence suggests that Martian atmospheric models, especially those used in simulations and planning for missions, must account for these localized and seasonal dynamics to enhance prediction accuracy and operational reliability during Martian explorations.