Abstract
Modeling forest structure using multi-source satellite data is beneficial to understanding the relationship between vertical and horizontal structure and image features to provide more comprehensive and abundant information for the study of forest structural complexity. This study investigates and models forest structure as a multivariate structure based on sample data and active-passive remote sensing data (Landsat8, Sentinel-2A, and ALOS-2 PALSAR) from the Saihanba Forest in Hebei Province, Northern China, to measure forest structural complexity, relying on a relationship-driven model between field and satellite data. In this study, we considered the effects of the role of satellite variables in different vertical structure types and horizontal structure ranges, used two methods to stepwise select significant variables (stepwise forward selection and Pearson correlation coefficient), and employed a multivariate modeling technique (redundancy analysis) to derive a forest composite structure index (FSI), combining both horizontal and vertical structure attributes. The results show that optical texture can better represent forest structure characteristics, polarization interferometric radar information can represent the vertical structure information of forests, and combining the two can represent 77% of the variance of multiple forest structural attributes. The new FSI can explain 93% of the relationship between stand structure and satellite variables, and the linear fit R2 to the measured data reaches 0.91, which largely shows the situation of the measured data. The generated forest structure map more accurately reflects the complexity of the forest structure in the Saihanba Forest, achieving a supplementary explanation of the measured data.
1. Introduction
Forests are the most structurally complex and functionally rich of terrestrial ecosystems and one of the richest natural resources in the world [1]. The structural characteristics of forests can be useful indicators of forest conditions and have the potential to be assessed using satellite images, which can provide quantitative information on forest ecosystems at a high spatial and temporal resolution [2]. The forest structure consists of a three-dimensional pattern that is described in both the horizontal and vertical directions. The horizontal structure can be defined as the arrangement of canopy closure or expressed through the distribution of trees, while the vertical structure reflects the diversity of tree heights [3].
The indicators of forest structure differ based on whether they are derived from field or remote sensing data. Field-based forest structure descriptors are obtained from measurements of individual tree sizes, while remote sensing descriptors are often based on the heterogeneous canopy structure of a specific area. Structural indices based on measured data are commonly used to quantify and describe local tree size variation and interactions between neighboring trees of different species [4]. The forest structure can be represented by one-dimensional structural variables, such as the number of forest stand density (S), diameter at breast height (DBH), canopy closure (CC), number of canopy layers, coefficient of variation, and Gini coefficient. This traditional stand description primarily quantifies individual attributes and does not combine the vertical and horizontal spatial layout of the forest, largely ignoring the spatial characteristics of forest structure [5]. FSI is typically used to analyze horizontal and vertical structures based on sample data, which is a composite variable widely used in forest ecology to summarize several measures of vegetation structure, such as stand height, S, CC, and DBH. It is an overall estimate of the structural characteristics in the vertical and horizontal directions. Studies have shown that FSI correlates better with forest parameters than individual structural measurements [6]. Whereas existing FSI analyses forest structure using only optical data, this study uses both optical and synthetic aperture radar (SAR) data as well as new horizontal and vertical structure indices to better estimate the composite structure of forests. The acquisition of measured data is time-consuming, with difficulty obtaining complex plots, slow data updating, and other problems. So, it is challenging to analyze forest complex structure, which cannot continuously provide spatial and temporal information about forest structural variables at various scales. The analysis of forest structure changes based on radar or optical data are typically built indices to capture the complexity of the forest structure in terms of both horizontal and vertical structure. For instance, multi-angle remote sensing was used to obtain bidirectional reflectance distribution function (BRDF) model parameters to analyze vegetation structure information [7]. The optical vegetation index has been used as a horizontal structure to examine changes in canopy cover [8,9]. The profiles obtained by the tomographic reflect certain changes in the vertical and horizontal directions of the forest stand and the variability of the reflectivity is regarded as the forest structure [3,10,11,12]. However, the majority of current remote sensing-based research on forest structure ignores the impact that the overall complexity of the forest structure has on vegetation characteristics in favor of modeling individual horizontal or vertical structures [13].
The definition of stand structural complexity focuses on the structure and composition of forests and necessarily involves the interaction between many different attributes (variables), so many attributes that can represent the stand structure need to be considered simultaneously [14]. In terms of complex multivariate analysis, or using an overall index to summarize interactions between individual attributes [15], there are three primary methods to determine the complex structure of a forest: (1) standardize the variables and create a structural complexity index (SCI) to analyze the degree of complexity; (2) the complexity index is defined a priori by principal component analysis (PCA) based on measured data; (3) the multivariate linear relationship between the image parameters and the forest structural parameters is represented by canonical correlation analysis (CCA) or redundancy analysis (RDA) to determine the FSI. Indeed, in addition to PCA and RDA, emerging machine learning techniques can be used to decorrelate and reduce dimensionality, providing promising avenues for enhancing our understanding of vegetation type characterization and structural analysis [16]. However, fewer studies have combined machine learning with forest parameters to analyze forest structural complexity.
McElhinny et al. established an additivity index to rate the complexity of the forest structure, selecting weights based on the relative importance of each attribute weighted and combining the attributes [17]. Wunderle et al. performed PCA using DBH, DBH standard deviation, basal area, S standard deviation, crown diameter mean, and crown diameter standard deviation, utilizing only the first principal component as the SCI, representing 79% of the total variance [18]. Olthof et al. used airborne image variables to simulate forest structure by CCA, using the first component as FSI to define significant multivariate relationships between structure and variables [19]. Cosmopoulos et al. improved the FSI through RDA and evaluated the potential of applying it to structural change. Due to the use of PCA and CCA for dimensionality reduction, in each method, there is some loss of the original data variance, resulting in a final model that explains only 26% of the variance of the original data [20]. Jon Pasher et al. used multispectral airborne data (spectral and textural information) and topographic information to simulate the multivariate structure of temperate broadleaf forests, using forward stepwise selection to build an RDA model [21]. The first axis was used as a complexity index, explaining 35% of the variance of the measured data and representing a general multivariate gradient in structural complexity [21]. Valerie Torontow et al. established three methods to derive complexity models using topographic data and spectral information obtained from Quickbird [22]. The results showed that indices built using RDA are more objective and provide a more complete characterization of structural compositional complexity than those defined a priori using simplified variable sets (additive indices and PCA) [22]. Because additive and PCA methods approximate the initial variables in a priori definitions, the resulting principal components can only represent a fraction of the total data variance, while individual components do not represent the full complexity of the forest [22]. Thus, RDA is expected to provide a more comprehensive index based on more parameters and differences in forest structure composition.
Existing studies have generally been limited to the prediction of individual measured variables from spectral and spatial data. While these methods are useful and extensive, the structural relationship between sample plots and remote sensing data has not been adequately explored because of the focus on only one single measured variable. Regarding single remote sensing data, optical data contains rich horizontal canopy information, which can be used to estimate parameters such as CC and S, and SAR has a penetration capability that makes it more sensitive to detecting the vertical structure of forests and can be used to estimate parameters such as tree height. Combining multi-source remote sensing information can make full use of the advantages of different remote sensing techniques, help to understand the relationship between vertical and horizontal structure and extracted features, and benefit from their complementary responses to forest features for forest structure complexity estimation in the study area [21,23].
In this context, this study used variables extracted from Landsat8, Sentinel-2A, and ALOS-2 PALSAR data to evaluate forest parameters (DBH, CC, S, basal area, forest height, and canopy thickness) and fully explored the potential structural relationship between measured and satellite data (canopy spectral and three-dimensional volume information) to measure the comprehensive forest structure of Saihanba Forest in Hebei Province. This study considered the effects of remote sensing variables within different vertical structure ranges and horizontal structure types, selecting significant variables using stepwise forward selection and the Pearson correlation coefficient. Then, we performed an RDA of all sample plots to establish the FSI and made an overall estimation of the vertical and horizontal characteristics of forests. The paper is structured as follows: Section 2 describes the basics of the measured data and the processing of the remote sensing data. Section 3 describes the extracted and newly created variables based on the satellite data. The methodology and theory proposed in this paper are explained in Section 4. Section 5 describes the results. Section 6 is the discussion section, which explains and analyzes the results of RDA in detail under different structures and ranges by the two variable selection methods. Section 7 is the conclusion.
2. Study Area and Data
2.1. Study Area and Sample Data
The study area is the Saihanba Mechanical Forest (42°02′N–42°36′N, 116°51′E–117°39′E) in Hebei Province, the largest area of plantation forest in the northern hemisphere, which belongs to the typical semi-arid and semi-humid cold-temperate continental monsoon climate, with 85% forest coverage. The tree species are mainly Larix principis-rupprechtii Mayr, Pinus sylvestris var. mongholica Litv, and Picea asperata Mast., of which Larix principis-rupprechtii Mayr is the most dominant forest type in the forest.
To ensure that the sample plots were as representative as possible of the actual state of the surrounding forest, forest boundaries, and huge openings were avoided for collecting samples, and central locations were instead chosen in preference. Due to thinning and conservation, most forests gradually lose density as they develop and expand. During the sampling process, several sample plots were chosen from forest stands with low, sparse, tall, and dense trees to better represent the general condition of the forest region and restore the genuine forest condition. All of the study objects were artificial coniferous forests, with the primary tree species being Larix gmelinii (Rupr.) Kuzen and Pinus sylvestris var. mongholica Litv. A total of 65 temporary sample plots totaling 0.06 ha were established (Figure 1). The species composition, DBH, CC, forest height, and height of the first living branch were all measured during the field survey. The CC was measured using the method of systematic sample point head-up observation, and the number of trees per hectare was used as the S. Basal area (BA) was the cross-sectional area of the trunk measured at 1.3 m above the ground, estimated according to Equation (1). The canopy thickness was calculated as the difference between the height of the first living branch and the height of the forest.
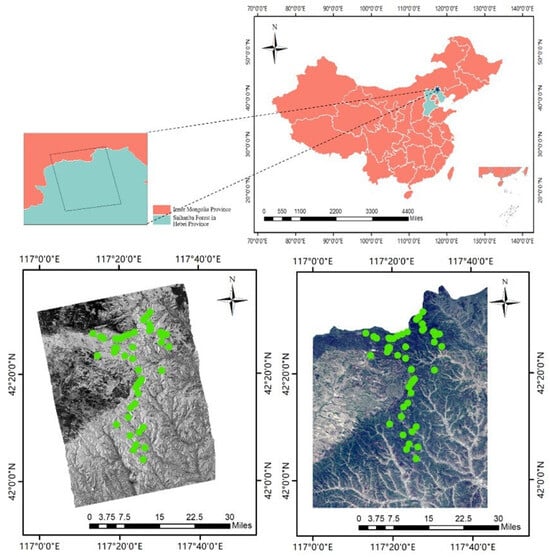
Figure 1.
Location map of the study area, with the actual sample locations indicated by green dots. The detail on the upper right is the spatial location of ALOS-2 PALSAR data, the image on the left is the HV polarization data of the 11 July 2020 view image of the study area, and the right image is the true color image of Sentinel-2A of the 21 June 2020.
Table 1 shows detailed information about the measured data in the sample plots, including the maximum, minimum, mean, and standard deviation of the CC, mean forest height (H), mean canopy thickness (CT), mean DBH, BA, and S. Figure 2 expresses the scatter plot distribution of the sample data in which the DBH and S had a strong inverse relationship; S declined exponentially as DBH grew. However, when DBH was close to 10 cm, the range of S fluctuated significantly. Although there was not much of a positive association between CC and BA, BA was overall still progressively rising as CC did. There was a substantial positive association between DBH and H. Although there was not much of a positive association between H and CT, CT was overall still progressively rising as H rose.

Table 1.
Summary of sample data.
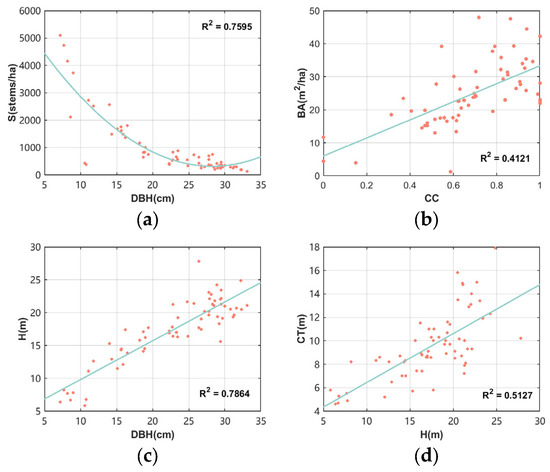
Figure 2.
Relationships between forest structural parameters across sample plots: (a) DBH vs. S; (b) CC vs. BA; (c) DBH vs. H; (d) H vs. CT.
2.2. Remote Sensing Data
2.2.1. Optical Data
Sentinel-2 and Landsat8 provide essential data sources for the long-term monitoring of forest carbon dynamics due to their free availability, global coverage, regular updates, and long-term cover [24]. With nine bands that cover visible, near-infrared (NIR), short-wave infrared (SWIR), and panchromatic band data, the Landsat8 (L8) OLI sensor passively detects solar radiation reflected from the surface and thermal radiation emitted. This results in multispectral data with a spatial resolution of 30 m. In June 2015, Sentinel-2A (S2A) was launched as the second satellite of the European Space Agency, which has a higher resolution (10 m and 20 m) and more spectral bands (red-edge bands) than L8, providing better detail of forest spectral features. This study uses class 2A data from Sentinel-2, which has been corrected for atmosphere and geometry. Therefore, only radiometric calibration, atmospheric correction, and topographic correction were performed for L8. The nearest-neighbor interpolation technique was used to resample the bands of S2A at various spatial resolutions to 30 m to guarantee that the pixel size of the S2 image matches the L8. This study obtained L8 data for 16 June 2020 and S2A data for 21 June 2020.
2.2.2. SAR Data
ALOS-2 PALSAR (ALOS-2) data are L-band, high-resolution airborne synthetic aperture radar, which are ultra-fine full-polarization 1.1-level single-view multiplexed products capable of acquiring observations independent of climatic conditions and time of day. In this study, the five-view fully polarization data were acquired from July to September 2020, during the growing season in the study area, with a range resolution of 5.66 m and an azimuth resolution of 2.86 m. GAMMA (http://www.gamma-rs.ch) and PolSARPro v6.0.2 software were used to conduct geometric decorrelation preprocessing, such as radiometric calibration, multilooking, filtering and denoising, and the removal of ionospheric effects [25], and terrain correction and geocoding for variable extraction were performed using 30 m resolution SRTM DEM data (Table 2).

Table 2.
Table of ALOS-2 data acquisition information.
3. Extraction of Variables
3.1. Extracting Information Based on Optical Data
3.1.1. Band
The structural characteristics of the forest canopy are enhanced using the spectral properties captured with optical remote sensing. From the perspective of the spectral characteristics, of different types of vegetation, different absorption and reflectance can be observed in each band. Furthermore, the grey values of pixels generated in the image are different, which is not the same as that contained in the information. Therefore, it is necessary to extract as much information as possible from the signals reflecting the vegetation data in each band. Six bands of L8 were selected, excluding the coastal, panchromatic, and cirrus bands. Ten bands were chosen from the Sentinel-2A MSI, except for bands 1, 9, and 10, which were mostly associated with atmospheric and water elements.
3.1.2. Texture
Texture information refers to the intensity change regulations of remote sensing images, and the texture based on a greyscale covariance matrix has a better portrayal of the forest spatial distribution and structural information, which can then provide image information about the horizontal structure, spatial variation, and greyscale value correlation [26,27]. In the selection of texture features, the size of the window, band, direction, and other factors need to be comprehensively considered. The optimal window size depends on image spatial resolution and vegetation cover [28,29]. In this study, texture features were extracted from different windows (, , , , , ) in each band, and the offset was set to 1 pixel. Texture features were computed in four directions (, , , ) and then averaged to obtain a single texture directionless metric (Table S1) [30,31,32,33].
3.1.3. Biophysical Parameter (BP)
A biophysical processor based on the PROSAIL radiative transfer model in SNAP’s Sentinel-2 toolbox produced biophysical products utilizing the S2A and L8 data. In the biophysical processor algorithm, an extensive database including top-of-canopy reflectance and associated vegetation features was created, which was used to train a neural network to estimate canopy features from the top-of-canopy reflectance with observed configuration (Table S2) [34,35].
3.1.4. Horizontal Structure Index (HSI)
In this study, we combined the significant differences in vegetation surface reflectance and spectral sensitivity exhibited by various sensors, analyzed the spectral coupling and complementary effects of the S2A and L8 sensors based on common horizontal structural information (CC, S, and BA), and established the horizontal structural indices to help extend the linear relationship between remote sensing variables and vegetation parameters [36]. We considered the differences in response between the bands obtained by L8 and S2A sensors, combined the exhaustive combination of spectral indices with the ratio technique, analyzed the sensitivity of the weights occupied by the bands in the vegetation index to the differences in each vegetation parameter using the relative sensitivities [37] and noise equivalents [38,39], and determined the optimal weights occupied by the bands to establish the ratio vegetation index (RVI) (Equation (2)). The established optimal index bands and their weights are shown in Table S3.
Integrating texture information for forested areas is challenging because textures vary greatly depending on the landscape, texture measurements, and associated parameters (e.g., window size, direction, offset) [40]. Therefore, this study established the ratio texture index (RTI) based on the same window in three ways (Equation (3)): ratio texture indices containing weights using the original texture features (corresponding texture index (CTI), a summary of the optimal indices established for each parameter is shown in Table S4); the average of the features in each direction (mean texture index (MTI), a summary of the optimal indices established for each parameter is shown in Table S5; and the features after PCA (principal component texture index (PTI), a summary of the optimal indices established for each parameter is shown in Table S6. This study used the information advantage of different vegetation parameters contained in different textures, combined with the noise equivalent, to analyze the effect of texture features of different windows and directions on vegetation parameters and determine the optimal weights to establish the optimal texture index. The details of the establishment process and the results of the analysis are shown in [36].
where is a weight value set from 0.1 to 1 with an interval of 0.1, is each band of the sensor, and is a band other than . and denote the same GLCM texture extracted from different bands ( and ) in the same window with the same direction (texture feature ).
3.2. Extracting Information Based on SAR Data
3.2.1. Backscattering Coefficient (BC)
The radar backscatter coefficient () is the signal reflected back to the sensor via the scattering elements of the illuminated scene, which can provide parameter information such as dielectric properties and roughness but is affected by radar parameters such as incidence angle and polarization [41]. Different polarization types have different responses of the radar to scattering mechanisms within the trunk and canopy [42]. HH polarization mainly comes from trunk-ground scattering, VV polarization is influenced by both volume and ground scattering, and HV (VH) polarization mainly comes from volume scattering [43,44].
3.2.2. Polarization Decomposition Variable (PDV)
PolSAR is a polarization intensity and phase-based technique that contains complete target scattering information [45]. Polarization decomposition is the decomposition of the polarization scattering matrix or coherence matrix and covariance matrix into different scattering mechanisms, each corresponding to a certain physical meaning. Since polarization is very sensitive to the shape and direction of scatters, the mechanism of polarization scattering is very important for the acquisition of forest structure information [46]. Currently, coherent target decomposition based on scattering matrix and incoherent target decomposition based on covariance matrix or coherence matrix are the two main types of scattering decomposition [47]. Coherent decomposition can only be used to study coherent or point targets, and incoherent decomposition is used to distribute targets. Considering these factors, in this study, only incoherent decomposition methods established with forest as the object were selected (Table S7), including model-based decomposition (Freeman-Durden three-component decomposition (F) [48,49], Yamaguchi three-component decomposition (Y) [50]), and eigenvalue-eigenvector based decomposition (Van Zyl decomposition (V) [51]), and two polarization decomposition indices were established using different combinations of the three scatterings (Equations (4) and (5)).
where S represents odd scattering, D represents double scattering, and V represents volume scattering.
3.2.3. Polarization Decomposition Parameter (PDP)
In the incoherent decomposition, the covariance matrix and the coherence matrix are interconvertible and are both matrices [52]; thus, only the parameters of were extracted in this study. The is used as an example to illustrate the nine parameters, from which the real and imag parts are extracted separately (Equation (6)).
, , , , , , , , and are Huynen parameters identified as phenomenological target parameters that directly respond to the physical origin of the effects of interest in the target in an interrelated manner, and each contains real physical target information [53]. is the target emitter, which can be viewed as the total return power from the smooth convex part of the regular scatterer, which behaves as an odd scattering; is the target structure generator, which is considered to be a measure of the total power of the unraised rough part of the irregular scatterer; is the target irregularity generator, denoted as double scattering, for sparse regions; is the target asymmetric generator, represented by volume scattering; is the shape factor; is the measurement of the local curvature difference; and are related to the depolarization component of the symmetric target; represents the target asymmetry; is the target helicity; and are related to the depolarization caused by the asymmetric target, which can be regarded as the sum of double and volume scattering and can be used to distinguish between targets with low odd scattering and those with strong double and volume scattering; is the coupling between symmetric and asymmetric targets; is a measure of the component coupling due to target orientation bias; and is the sum of odd and volume scattering.
3.2.4. SAR Index (SI)
SAR index [45] is a series of vegetation polarization characteristic parameters based on the optical vegetation index and established using backscattering coefficients (Table S8) [54,55,56].
3.2.5. Vertical Structure Index (H-VSI)
This study used ALOS-2 data to establish six interference pairs with different spatial and temporal baselines (Table 3) and used the improved forest height inversion model to obtain vertical structure indices [57]. The RVoG semi-empirical improved inversion model adopted in this study overcomes the difficulties in accurately quantifying the coherence and phase errors due to the small vertical wave number of the space-borne data, as well as the temporal decoherence generated by the long temporal baseline, through the introduction of a correction factor to reduce the coherence and phase errors caused by factors such as temporal decoherence and the realization of high-precision forest height inversions using empirical iterations (Equation (7)) [58]. Normalized extinction coefficient curve fitting using phase histograms and Gaussian functions were also used to eliminate extinction coefficient errors caused by heterogeneous vertical structures in the forest volume layer (Equation (8)) [59,60]. The polarimetric decomposition technique of the physical model was introduced to consider the surface scattering as the ground contribution, as well as the double and volume scattering as the contribution from the vegetation layer. The ground and volume contributions were modeled separately, avoiding the model estimation error caused by excessively large ground scattering in many cases and obtaining a better separation of the ground and volume phases, which makes it more suitable for the inversion of forest heights for the complex forest structure (Equation (9)) [61,62].
where is the volume scattering complex coherence, which is a function of the vegetation layer thickness and the average extinction coefficient ; is the vertical wave number; is the ground phase; and is the radar wave incidence angle. , , and are three correction terms introduced on the basis of the RVoG model. is a correction for temporal decoherence on the overall coherence, and and are utilized to implement the correction for the phase effect of temporal decoherence on . is the influence factor of , is the position of maximum extinction in the forest canopy, is the standard deviation represented by the canopy shape, and and reflect the vertical heterogeneity of the forest. represents the ground-volume scattering ratio, and , , and represent the contribution of the odd, double, and volume scattering components, respectively. and are used as the volume layer scattering , and is used as the ground layer scattering .

Table 3.
Information for six pairs of interferometric pairs.
4. Proposed Method of the Research
4.1. Research Methods
Figure 3 shows the flow chart of the proposed method.
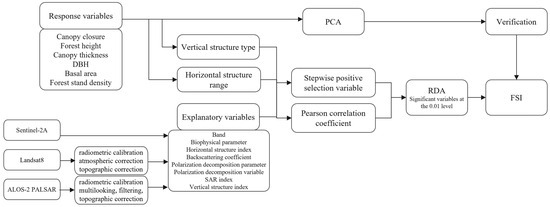
Figure 3.
Flow chart of the method used in this study.
The integrated structure of the forest based on DBH, CC, S, BA, H, and CT was considered when exploring and modeling the multivariate structure of the forest in this study. The RDA was used to analyze the effects of remote sensing variables (spectral bands, biophysical parameters, horizontal structural indices, backscattering coefficients, polarization decomposition parameters, polarization decomposition variables, SAR indices, and vertical structural indices) on the sample data. Since the stand structure is a complex combination of several parameters that depend on the sample structure, and the reflectance of the sample plots mainly depends on the density and distribution, this study combines the relative number of different DBH and H of the trees within each plot to establish three vertical structure types: SC1, SC2, and SC3 (Figure 4) [63]. The different ranges of S and CC were also considered to be divided into six horizontal structural ranges (Table 4). Significant variables were selected stepwise using both stepwise forward selection and the Pearson correlation coefficient in different structures and ranges. Forward selection methods rank explanatory variables according to their importance to the response variable and select those that contribute more than 1% [64]. Variables significantly correlated with vegetation parameters at the 0.05 level were selected for RDA using Pearson correlation coefficients, and variables contributing more than 1% were summarized. Finally, RDA is carried out on variables that contribute significantly under the two methods to all plots to establish the FSI [65].
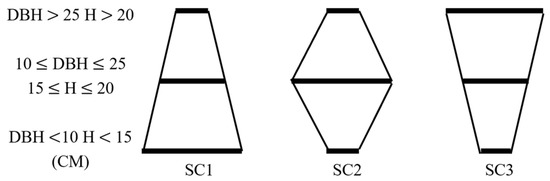
Figure 4.
Map of vertical structure types. The length of the thick line in the figure represents the relative number of trees of this size in the sample plot. Small trees (DBH 10, H 15) are most abundant in the SC1 structure, medium size trees (10 DBH 25, 15 H 20) are most abundant in the SC2 structure, and large trees (DBH 25, H 20) are most abundant in the SC3 structure.

Table 4.
Horizontal structure range.
4.2. Redundancy Analysis (RDA)
RDA is a constrained ordering multivariate statistical technique proposed by Rao, which can be used to explore the linear relationship between two variable sets and maximize the variance considered by response variables [14,64]. As a direct gradient analysis, the amount of variation among the response variables of the RDA can be directly described by a set of explanatory variables. The RDA method was chosen for this study because it allows for the input of raw variables without dimensionality reduction, constrains the sorting axes to a linear combination of the explanatory variable sets, and preserves all data variance to explore the most useful variable types for predicting multivariate forest structure [21,22]. Standardized explanatory variables are usually used in RDA because, in many cases, explanatory variables have different scales. The significance of standardized explanatory variables is that the absolute value of the canonical coefficients (which is the regression coefficient of the model) measures the contribution of the explanatory variables to the constraint axes, which cannot change the fitted value of the regression or the result of the constraint ordering.
RDA provides graphical output showing a comprehensive view of the relationship between the response and explanatory datasets by ranking the response variables according to their importance to the explanatory variables [65]. In this study, correlation biplots were selected to evaluate the relationship between forest attributes and remote sensing information to visualize the correlation between these two sets of variables. In the RDA biplot, the approximation of the correlation between the variables is given by the cosine of the angle between the two vectors, providing a qualitative impression of a positive (or negative) correlation between variables by the direction of the arrows (vectors) pointing in the same (or opposite) direction, indicating a high positive (or negative) correlation. The vector at the right angle indicates that the correlation is close to zero [66,67]. The correlation between any two variables or between the variables and the RDA axis increases as the angle between them decreases, and the arrow length indicates the strength of the variable’s contribution to the model [14]. A biplot can reveal natural groupings or potential structures in data, which is of practical significance in exploring the inherent variability of remote sensing data to other vegetation parameters [66].
5. Results
5.1. Selection Variables
This study estimated a total of 207 variables, including 16 spectral bands (bands), 8 biophysical parameters (BPs), 12 horizontal structural indices (HSIs), 20 backscattering coefficients (BCs), 75 polarization decomposition variables (PDVs), 45 polarization decomposition parameters (PDPs), 25 SAR indices (SIs), and 6 vertical structural indices (H-VSIs), obtained from L8, S2A, and ALOS-2. Due to the excessive number of input variables, a comprehensive RDA was performed by selecting the variables using both stepwise forward selection and the Pearson correlation coefficient under different structures and ranges. Each model consisted of a combination of predictor variables that help to explain the variance in the sample data, so the 18-model structure was summarized to focus on the chosen final output model.
As shown by a summary of the number and significance (significant at the 0.01 level) times of introducing various variables into the model in Table 5, many HSIs and H-VSIs were introduced into the model. The HSIs more significantly contributed to the model and were significantly stronger for the model than H-VSIs. The remaining variables only played some explanatory role in some of the models, and their contribution to the response variable was not stable. The individual variables that were introduced into the model more frequently are also summarized in this study (Table 5). For individual variables, PTI_BA was included in 83% of the models and was significant in 87% of the introduced models, because textures can better distinguish the vegetation structural details and exploration of different forest canopy structural features [68]. PTI_CC, 0808-0919H, and 0905-0919H were shown to be significant in over 50% of the introduced models, with respective inclusion rates of 67%, 56%, and 44% of the models. While FM1 contributed moderately to the model, its significant contribution times were lower, with a 61% lower number of significant contributions in the introduced model compared to PTI_S. 0725-0905H and 0711-0725H contributed less to the model. Therefore, the five variables that contributed significantly to most models were selected for this study: the PTI_BA, PTI_CC, 0808-0919H, 0905-0919H, and PTI_S to build the FSI.

Table 5.
Summary of introduction times and significance (p < 0.01) times of different types of variables (band, BP, HSI, BC, PDP, PDV, SI, and H-VSI). Summary of individual variables that were introduced into the model more often, with the number of times they were introduced into the model and the number of times they contributed significantly to the model.
5.2. Establishment of the FSI Index
This study used the five significant variables selected in the previous section, PTI_CC (V1), PTI_S (V2), PTI_BA (V3), 0808-0919H (V4), and 0905-0919H (V5), to establish the FSI. RDA was performed with the above variables, and a fragmentation plot was created (Figure 5a). From Figure 5a and Table 6, it can be seen that the first two axes cumulatively explained 93% of the relationship between stand structure and remote sensing variables and 77% of the stand structural characteristics, which indicates that the first two axes can well illustrate the relationship between stand structure and remote sensing variables. Therefore, the first and second axes were modeled as RDA, defined as the FSI, which represents the gradient of structural complexity defined by the field measurements.
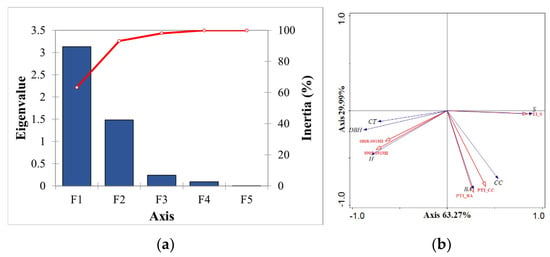
Figure 5.
(a) Gravel plot, where eigenvalue is shown in blue and explained fitted variation is shown in red line. (b) 2D ordination plot for redundancy analysis of relationships between stand structural characteristics and remote sensing variables. RDA biplots with lines for explanatory (red) and response (blue) variables.

Table 6.
Redundancy analysis of explanatory variables for changes in stand structural characteristics.
RDA biplot was established with sample data as the response variable and remote sensing data as the explanatory variable. The RDA biplot for the first two axes was established to determine the relationships between the variables and explanatory quantities (Figure 5b). Table 7 shows the explained amount and significance test of remote sensing variables in the order of V2, V3, V4, V1, and V5, which were all significant at the 0.01 level in their effect on stand structure. As can be seen from Figure 5b and Table 7, both the HSIs and H-VSIs had a high positive correlation with the vegetation parameters, and their vector lengths indicated a high contribution to each attribute. While the vector lengths of V1 and CC were the same, the angle was relatively large, indicating a weak positive correlation. The vectors of V2 and V3 with S and BA had similar lengths and smaller angles, indicating a strong positive correlation. V2 had a strong negative correlation with both CT and DBH because of its angle over . The angle between V3 and CT was , suggesting that there is no relationship between the two. The angle between V4 and V5 and H, DBH, and CT was small, and the positive correlation was strong. The contribution of V4 was higher than that of V5 because of its high positive correlation not only with H but also with DBH and CT.

Table 7.
Explained quantities and significance tests for remote sensing variables; the two columns on the right are the variable scores for the variables in RDA1 and RDA2.
Based on the RDA biplot scores, the relative contribution of each variable to RDA1 and RDA2 was analyzed, with the absolute magnitude of the scores showing the relative importance of each variable to RDA1 and RDA2, and the symbols of the scores showing the relative direction for RDA1 and RDA2. According to the variable scores (Table 7), the major explanatory variable that contributed to the RDA1 was V2, and the RDA2 was V1 and V3. The variables V1, V2, and V3 all showed variations in texture measures and had positive correlations with the RDA1. All variables were negatively correlated with RDA2, with the main correlation being V3. It was shown that increased spatial heterogeneity within the canopy was mainly caused by branches, crowns, and small forest gaps, leading to increased textural variability within the canopy [21]. V1, V2, and V3 were effective in detecting changes within the canopy and shadow in response to increased shading within the canopy. When the tree height changes, the upper canopy may be shaded by neighboring trees, and the lower canopy is shaded by the upper canopy, resulting in hidden information about the lower trees, which is not conducive to the determination of the underlying vegetation and the analysis of the forest structure, which may be the reason for the negative correlation between the two H-VSIs (V4, V5) and RDA1.
In summary, forest parameters are influenced by a combination of several satellite variables, but each forest parameter indicator has a primary influencing component of its own. The correlation between remote sensing variables and forest parameters, as well as the extent to which the remote sensing variables explain the forest parameters, can be visualized through the application of RDA.
5.3. Validation of the FSI
PCA was performed on the sample data for FSI validation. The sample data was tested using Kaiser–Meyer–Olkin (KMO) and Bartlett’s tests. The applicability of KMO and Bartlett’s tests varied from 0 to 1, with bigger values indicating that the set of variables is more appropriate for PCA (Table 8). The result obtained in this study was 0.699, indicating that it is appropriate for PCA. The p < 0.05 for Bartlett’s test indicates that there is a significant correlation between the parameters, which is appropriate for PCA.

Table 8.
KMO and Bartlett test.
PCA of the forest parameters revealed (Figure 6 and Table 9) that the contribution of the first two principal components was 84% and the eigenvalues were greater than 1, indicating that the first two factors contributed more. As shown in Table 9 and Table 10, PC1 accounted for 57% of the variance and was significantly correlated with S, H, DBH, and CT, while PC2 accounted for 27% of the variance and was significantly correlated with CC and BA. The loadings of S, H, DBH, and CT of the first principal component were relatively large; the loadings of CC and BA of the second principal component were relatively large; and the load coefficients above all exceeded 0.5. Therefore, to ensure the overall variance was explained, the first two principal components were chosen as FSI and fitted to the FSI established in the previous section based on remote sensing data (Figure 7). The of the two was as high as 0.91, showing a highly linear relationship overall, indicating that the method of establishing the FSI by RDA of remote sensing variables is feasible and that the FSI can reflect both vertical and horizontal information about the structure of the sample plots.
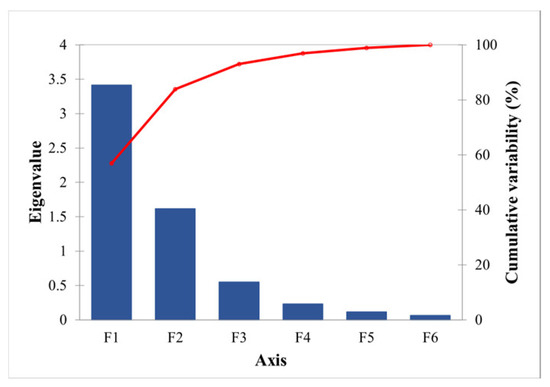
Figure 6.
Gravel diagram, where eigenvalue is shown in blue and cumulative is shown in red line.

Table 9.
Explanation of variance.

Table 10.
Eigenvalues and loading coefficients are associated with the first two principal components.
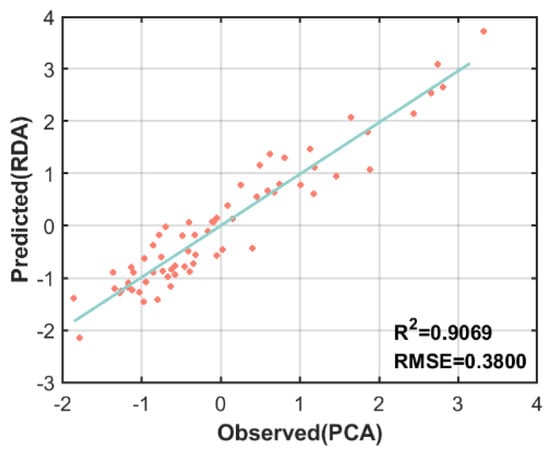
Figure 7.
Scatterplot of linear fit of FSI to measured data. The x-axis is the result obtained by PCA for the sample data, and the y-axis is the FSI created from the satellite data.
The simple forest structure is characterized by a homogeneous upper layer with less vegetation in the lower layers. The complex structure consists of varying upper tree sizes and diverse understory vegetation [21]. All predicted layers were normalized to generate predicted forest structure maps (Figure 8). The size of the resultant value was used to determine the simplicity and complexity of the forest structure. As can be seen from the figure, the light-yellow color indicates the simple forest structure area, and the dark-blue color represents the complex forest structure area, which corresponds to the result of the actual remote sensing image.
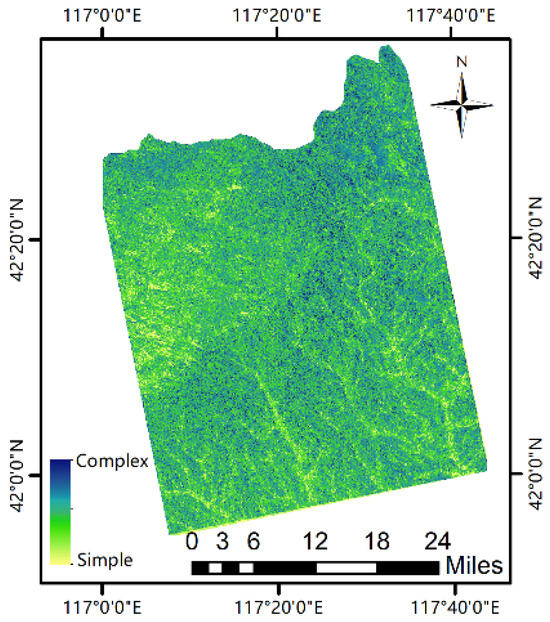
Figure 8.
Forest structure image of the Saihanba research area.
6. Discussion
6.1. Stepwise Forward Selection of Variables
Stepwise forward selection was used in this study to include variables under different types and ranges, and the variables contributing more than 1% were selected for RDA modeling (Figure 9 and Table S9). The various vertical structure graphs show that BPs and RTIs had higher positive correlations with S, BA, CC, and DBH, while H-VSIs, PDVs, and PDPs had stronger correlations with H and CT. Based on the different S plots, more S2A bands were introduced in the model, with smaller angles to S and DBH, which were the main explanatory variables for both. Both HSIs and H-VSIs contributed significantly to the model and could express the sample information better. In different CC ranges, more bands and PDVs were introduced, but the explanation of the model was not adequate because of the short vectors. Individual HSIs or H-VSIs were more capable of interpreting sample data information and had high positive (or negative) correlations with the measured data.
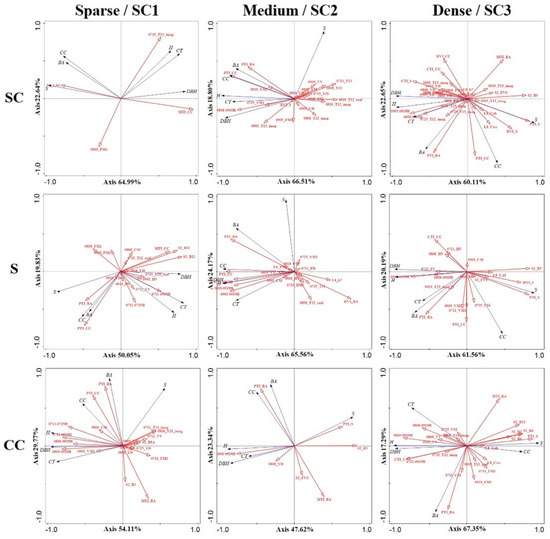
Figure 9.
Using stepwise forward selection of variables on different types and ranges, variables with more than 1% contribution were selected to enter the model for RDA. From left to right, the different SC1, SC2, SC3, and sparse, medium, and dense structure types, and from top to bottom are SC, S, and CC. RDA biplots with lines for explanatory (red) and response (blue) variables.
Table 11 demonstrates that the model introduced a larger number of HSIs, PDVs, PDPs, and H-VSIs. Among them, HSIs and H-VSIs contributed more to the model and had greater correlations with the response variables; the contribution degree of PTIs was more stable across cases, with 84% of the introduced variables being significant. Although a large amount of polarization decomposition information was introduced into the model, and the angle with S was small, due to the short length of the vector, the contributions to the model and explanations were lower than other variables, so there were fewer significant variables at the 0.1 level. Compared to the L8, the S2A sensor introduced more bands to the model, correlated more strongly with forest parameters, and contributed to the model to a higher degree. BPs can represent the vegetation growth trend to some extent and were introduced more in the model, but the correlation with the response variables was low compared to the other variables and cannot be regarded as a significant variable [69].

Table 11.
Summary of introduction times and significance times of different types of variables and individual variables.
6.2. Pearson Correlation Coefficient Selection Variables
In this study, variables were selected using Pearson correlation coefficients under different structures and ranges, and RDA was carried out using variables that were significantly correlated at the 0.05 level with each forest parameter (Figure 10 and Table S10). It can be shown from the various vertical structure plots that the optical variables were related to the information of S, BA, and CC, while the SAR variables were strongly positively correlated with DBH, H, and CT, and the optical variables showed a high degree of negative correlation with these three vegetation parameters. Based on the different S plots, it can be seen that more BPs and SAR variables were introduced into the model and mainly explained S. CC, BA, and DBH were mostly related to optical variables, while H and CT were explained by SAR variables. At different CC ranges, bands and PDVs were introduced into the model, and their limited vector length made them less helpful in explaining the model. Sample plot information relied heavily on the interpretation of HSIs and H-VSIs.
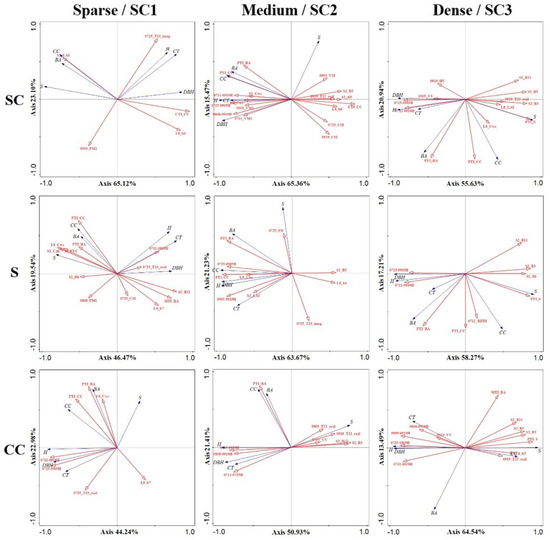
Figure 10.
Selection of variables using the Pearson correlation coefficient on different structure types and ranges, and the selection of variables that were significantly correlated at the 0.05 level to be introduced into the model for RDA. From left to right, the different SC1, SC2, and SC3 and sparse, medium, and dense structure types, and from top to bottom are SC, S, and CC. RDA biplots with lines for explanatory (red) and response (blue) variables.
Table 12 shows that most of the spectral bands were strongly correlated with forest parameters, but the interpretive effects were not stable under different types and ranges. The variables extracted by the S2 sensor were significantly better correlated with forest parameters than the L8 sensor, with 73% of the introduction. The HSIs and H-VSIs correlated well with the measured data. PTIs explained the model significantly better than other HSIs, with 88% of PTIs significant in the introduced model, a 35% increase over the remaining RTIs. The introduction of H-VSIs was high, but they were less able to explain the response variables information. Most BPs were introduced into the model with longer vectors but remained insignificant in the model. This may be because most BPs can only interpret one sample data with an angle close to 90° to the other measured data, so the correlation was weak. Although PDPs were introduced less frequently, they were significantly more frequent, and the percentage of significant explanations (33%) even exceeded H-VSIs (32%). The remaining significant variables (T23_real, Cwc, and M1) showed the same results as the stepwise forward selection, but the proportion of significant times was lower. This was related to the different methods of selecting input variables; the variables selected by the two methods came from different images, so the existing effective information was different, and the contribution degree to the model was different.

Table 12.
Summary of introduction times and significance times of different types of variables and individual variables.
6.3. RDA for All Sample Plots
Figure 9 and Figure 10 show that different structures and ranges result in different correlations between remote sensing variables and sample data. The results show that, compared with the stepwise forward selection method, using the Pearson correlation coefficient to select variables can avoid a large number of PDVs with short vector lengths being input into the model, and bands and BPs with some correlation with forest parameters were introduced into the model to ensure that all variables in the model had a strong explanatory ability. The bands selected by the S2A and L8 sensors included the green, red-edge, and SWIR bands, all of which were more sensitive to changes in the growth of vegetation, less affected by the surrounding environment, and had a strong ability to reflect the complexity of stand structure [70,71]. HSIs combine the ratio techniques with bands and textures and add weights to enhance the sensitivity of the indices, eliminating sensor and terrain effects and better expressing vegetation parameter information (S, BA, and CC). Compared to spectral bands, texture features can better distinguish vegetation structural details and detect different forest canopy structural features [68]. The results show that the most suitable texture window size was , and the PTI_S built using this window had the highest explanation in the model. PTI combines PCA with texture-ratio techniques to reduce the data dimensions while retaining valid information. H-VSIs had a strong correlation with H, while DBH and CT were positively correlated with H to a certain extent (Section 2.1), so H-VSIs better expressed DBH, CT, and H information and contributed more to each structure and type. Some BPs and PDVs related to double and volume scattering can represent canopy structure information to a significant extent because of the high CC and complicated upper canopy structure of the measured data. The remaining variables did not have a significant effect on the model and had a negligible role in explaining the forest structure.
As can be seen in Figure 11, under different structures and ranges, HSIs and H-VSIs correlated with forest parameters to varying degrees, contributed more to the model than other variables, and had a stronger relationship with the response variables. Optical data (bands or BPs) played a major role compared to SAR original variables (BCs, PDPs, PDVs, and SIs) in the low S, medium, and high CC ranges. This is because the trees were taller, the CT was greater, the upper canopy structure of the forest was rich in this type of area, and because all the subjects of this study were artificial coniferous forests, there were more branches and the canopy structure was complex, and optical sensors that can capture biochemical information in the upper canopy can provide two-dimensional distributional information in the horizontal range of the canopy. In the remaining horizontal ranges, the SAR original variables (BCs, PDPs, PDVs, and SIs) contributed more effectively to the model compared to optical original variables (bands or BPs) because SAR interacted with scatterers at different heights, capturing information about stems, branches, and understories, providing more information about the vertical structure of the stand [3].
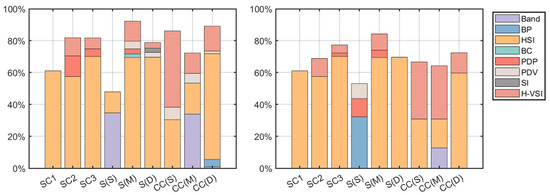
Figure 11.
The proportion of the degree of contribution of significant variables in the model. The two figures show the proportion of the degree of contribution to the RDA model of the significant variables obtained by stepwise forward selection and Pearson correlation coefficient selection of variables on the nine structures and ranges. The S, M, and D in parentheses represent sparse, medium, and dense. The selected variables were plotted according to eight parts: band, BP, HSI, BC, PDP, PDV, SI, and H-VSI.
Optical and SAR variables were used to model the RDA of all plots, respectively, and only the variables that contributed more than 1% to the model were introduced. Figure 12a illustrates that the S2 bands and PTIs contributed more to the model. Spectral bands showed mainly negative correlations with DBH, H, and CT, and the remaining variables had minor correlations with these three vegetation parameters at angles close to 90°. H-VSIs and PDVs provide a stronger explanation for the model, as seen in Figure 12b. H-VSIs had a strong positive connection with H, DBH, and CT and contributed to the model to a high degree. However, the vector length of other variables except H-VSIs was short, and the correlation with vegetation parameters was low, which cannot express the forest structure information well. Relative to the SAR variables, the number of variables introduced in the optical model was smaller, but the explained variance in the first two axes was larger. This indicates that the optical variables contained more information about the measured data and had a stronger role in explaining forest structure compared to the SAR variables.
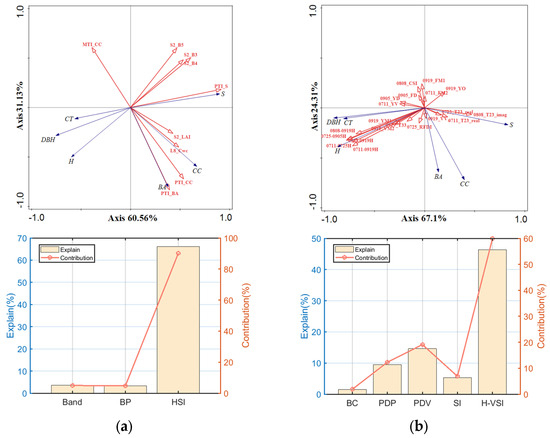
Figure 12.
(a,b) show the results of RDA for optical and SAR variables, respectively. From top to bottom, they are RDA biplots and plots of the contribution of each type of variable (the left y-axis is the amount explained (%), the right y-axis is the contribution (%), and the x-axis is each type of variable). RDA biplots with lines for explanatory (red) and response (blue) variables.
The significant variables (at the level of 0.01) obtained from Section 6.1 and Section 6.2 were summarized, and RDA was performed on all the sample data as input variables (called F1 and F2 for short) (Figure 13). All sample data were subjected to stepwise forward selection, and the variables with contribution degree more than 1% were selected for the RDA model (called F3) (Figure 13). It was discovered that the significant variables of these three methods all included V1, V2, V3, V4, V5, and 0711-0725H (Figure 14 and Table S11). Combined with the angle and length analysis between vectors, it was found that V1, V2, and V3 were highly correlated with CC, S, and BA, respectively, which adequately represent the horizontal structural information. For the H-VSIs, V4 was correlated with CT and DBH, V5 was correlated with H, and 0711-0725H had a weak contribution to these three vegetation parameters. Among the three models, the explanatory value of 0711-0725H was significantly smaller than other variables, with a lower degree of contribution, so this variable was discarded, and the remaining five variables were selected as the final input variables for the RDA to establish the FSI for all sample plots.
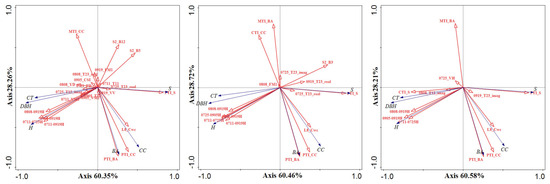
Figure 13.
The results of RDA performed by F1, F2, and F3 are shown from left to right. RDA biplots with lines for explanatory (red) and response (blue) variables.
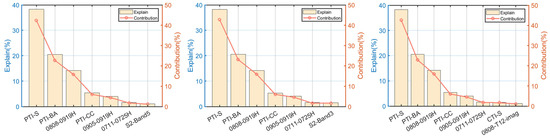
Figure 14.
From left to right are the significant variables obtained by performing RDA for F1, F2, and F3. Where PTI_CC is V1, PTI_S is V2, PTI_BA is V3, 0808-0919H is V4, and 0905-0919H is V5. The x-axis is the significant variable, the left y-axis is the amount of explanation of the variable, and the right y-axis is the contribution of the variable to the model.
Due to the high number of optical and SAR variables used in this study, there may be some correlation between the variables, so there may be overfitting of the results. Moreover, the subjects of this study are artificial coniferous forests, and the main tree species are pine and larch. Since most stand features are spatial- and temporal-dependent, the empirical relationship will vary depending on location, time, and tree species type. The results of this study are not directly applicable to large-scale operations, and the analysis of complex forest structures in other heterogeneous forests needs further research and analysis. This study did not consider the effects of environmental factors such as topography and climate on forest structure, which can cause errors in model estimates. It is expected that combining environmental factors with horizontal and vertical structures can further improve the exploration of the complex forest structure.
7. Conclusions
In this paper, we considered the different response relationships between satellite variables in horizontal and vertical structures and analyzed the degree of contribution of optical and multi-dimensional SAR variables to forest parameters in different vertical structure types and horizontal structure ranges. The results showed that optical and SAR variables contributed to the model to varying degrees at different structures and ranges, and the spectral bands of the S2A sensor had a stronger relationship with the forest parameters than L8. The horizontal texture indices and vertical structure indices enhanced the influence of forest parameters more than the original variables. The composite forest structure index established by RDA can represent 77% of the variance of multiple forest structure attributes, and the cumulative explanation of the relationship between the stand structure and remote sensing variables can reach 93%. The validation showed that the FSI can well represent the situation of the measured sample data and has a strong linear relationship with the measured data ( 0.91), which can accurately estimate the complexity of the regional forest structure in the Saihanba Forest.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16111844/s1. Table S1. Equation of the GLCM texture metric. Table S2. Table of biophysical parameters. Table S3. Summary of the results of the optimal vegetation index obtained through the screening of different sensors and weighting the bands. Table S4. Summary of the optimal CTI results. Table S5. Summary of the optimal MTI results. Table S6. Summary of the optimal PTI results. Table S7. Table of polarization decomposition variables. Table S8. SAR index. Table S9. Summary of variable significance obtained by performing stepwise forward selection of variables for modeling under different structures and ranges. Table S10. Summary of significance of variables obtained by selecting variables for modeling with Pearson correlation coefficients under different structures and ranges. Table S11. Summary of significance of RDA model variables.
Author Contributions
Conceptualization, W.F. and R.S.; methodology, R.S.; software, R.S.; validation, R.S.; formal analysis, R.S.; investigation, R.S.; resources, W.F.; data curation, R.S.; writing—original draft preparation, R.S.; writing—review and editing, R.S.; visualization, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (contract no. 31971654) and the Civil Aerospace Technology Advance Research Project (contract no. D040114).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| Full Name | Abbreviation |
| ALOS-2 PALSAR | ALOS-2 |
| Basal area | BA |
| Backscattering coefficient | BC |
| Biomass index | BMI |
| Biophysical parameter | BP |
| Chlorophyll content in the leaf | Cab |
| Canopy closure | CC |
| Canonical correlation analysis | CCA |
| Canopy structure index | CSI |
| Mean canopy thickness | CT |
| corresponding texture index | CTI |
| Canopy water content | Cwc |
| Diameter at breast height | DBH |
| Freeman-Durden three-component decomposition | F |
| Forest structure index | FSI |
| Fractional Vegetation Cover | FVC |
| Mean forest height | H |
| Horizontal structure index | HSI |
| Vertical structure index | H-VSI |
| Landsat8 | L8 |
| Leaf Area Index | LAI |
| mean texture index | MTI |
| near-infrared | NIR |
| Principal component analysis | PCA |
| Polarization decomposition parameter | PDP |
| Polarization decomposition variable | PDV |
| Principal component texture index | PTI |
| Redundancy analysis | RDA |
| Radar forest degradation index | RFDI |
| Ratio texture index | RTI |
| Ratio vegetation index | RVI |
| Forest stand density | S |
| Sentinel-2A | S2A |
| Synthetic aperture radar | SAR |
| Structural complexity index | SCI |
| SAR Index | SI |
| Sehort-wave infrared | SWIR |
| Van Zyl decomposition | V |
| PTI_CC | V1 |
| PTI_S | V2 |
| PTI_BA | V3 |
| 0808-0919H | V4 |
| 0905-0919H | V5 |
| Volume scattering index | VSI |
| Yamaguchi three-component decomposition | Y |
References
- Chen, W.; Zheng, Q.; Xiang, H.; Chen, X.; Sakai, T. Forest Canopy Height Estimation Using Polarimetric Interferometric Synthetic Aperture Radar (PolInSAR) Technology Based on Full-Polarized ALOS/PALSAR Data. Remote Sens. 2021, 13, 174. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Pelt, R.V.; Carey, A.B.; Thornburgh, D.A.; Berg, D.R.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; et al. Disturbances and structural development of natural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Cazcarra-Bes, V.; Tello-Alonso, M.; Fischer, R.; Heym, M.; Papathanassiou, K. Monitoring of Forest Structure Dynamics by Means of L-Band SAR Tomography. Remote Sens. 2017, 9, 1229. [Google Scholar] [CrossRef]
- Keren, S.; Svoboda, M.; Janda, P.; Nagel, T. Relationships between Structural Indices and Conventional Stand Attributes in an Old-Growth Forest in Southeast Europe. Forests 2020, 11, 4. [Google Scholar] [CrossRef]
- Zenner, E.K.; Hibbs, D.E. A new method for modeling the heterogeneity of forest structure. For. Ecol. Manag. 2000, 129, 75–87. [Google Scholar] [CrossRef]
- Estes, L.D.; Reillo, P.R.; Mwangi, A.G.; Okin, G.S.; Shugart, H.H. Remote sensing of structural complexity indices for habitat and species distribution modeling. Remote Sens. Environ. 2010, 114, 792–804. [Google Scholar] [CrossRef]
- Sharma, R.C. Vegetation Structure Index (VSI): Retrieving Vegetation Structural Information from Multi-Angular Satellite Remote Sensing. J. Imaging 2021, 7, 84. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Spangenberg, G.; Kant, S. Fusion of Spectral and Structural Information from Aerial Images for Improved Biomass Estimation. Remote Sens. 2020, 12, 3164. [Google Scholar] [CrossRef]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Wan, X.; Li, Z.; Chen, E.; Zhao, L.; Zhang, W.; Xu, K. Forest Aboveground Biomass Estimation Using Multi-Features Extracted by Fitting Vertical Backscattered Power Profile of Tomographic SAR. Remote Sens. 2021, 13, 186. [Google Scholar] [CrossRef]
- Tello, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Structural classification of forest by means of L-band tomographic SAR. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5288–5291. [Google Scholar]
- Cazcarra-Bes, T.; Papathanassiou, P. Assessment of forest structure estimation by means of SAR tomography: Potential and limitations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Pasher, J.; King, D.J. Development of a forest structural complexity index based on multispectral airborne remote sensing and topographic data. This article is one of a selection of papers from Extending Forest Inventory and Monitoring over Space and Time. Can. J. For. Res. 2011, 41, 44–58. [Google Scholar] [CrossRef]
- Lee, S.K.; Fatoyinbo, T.; Qi, W.; Hancock, S.; Armston, J.; Dubayah, R. Gedi and Tandem-X Fusion for 3D Forest Structure Parameter Retrieval. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 380–382. [Google Scholar]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Sharma, R.C.; Hara, K. Self-Supervised Learning of Satellite-Derived Vegetation Indices for Clustering and Visualization of Vegetation Types. J. Imaging 2021, 7, 30. [Google Scholar] [CrossRef] [PubMed]
- McElhinny, C.; Gibbons, P.; Brack, C. An objective and quantitative methodology for constructing an index of stand structural complexity. For. Ecol. Manag. 2006, 235, 54–71. [Google Scholar] [CrossRef]
- Wunderle, A.L.; Franklin, S.E.; Guo, X.G. Regenerating boreal forest structure estimation using SPOT-5 pan-sharpened imagery. Int. J. Remote Sens. 2007, 28, 4351–4364. [Google Scholar] [CrossRef]
- Olthof, I.; King, D. Development of a Forest Health Index Using Multispectral Airborne Digital Camera Imagery. Can. J. Remote Sens. 2000, 26, 166–176. [Google Scholar] [CrossRef]
- Cosmopoulos, P.; King, D.J. Temporal analysis of forest structural condition at an acid mine site using multispectral digital camera imagery. Int. J. Remote Sens. 2010, 25, 2259–2275. [Google Scholar] [CrossRef]
- Pasher, J.; King, D.J. Multivariate forest structure modelling and mapping using high resolution airborne imagery and topographic information. Remote Sens. Environ. 2010, 114, 1718–1732. [Google Scholar] [CrossRef]
- Torontow, V.; King, D. Forest complexity modelling and mapping with remote sensing and topographic data: A comparison of three methods. Can. J. Remote Sens. 2014, 37, 387–402. [Google Scholar] [CrossRef]
- Fischer, R.; Knapp, N.; Bohn, F.; Shugart, H.H.; Huth, A. The Relevance of Forest Structure for Biomass and Productivity in Temperate Forests: New Perspectives for Remote Sensing. Surv. Geophys. 2019, 40, 709–734. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-ground biomass change estimation using national forest inventory data with Sentinel-2 and Landsat. Remote Sens. Environ. 2021, 265, 112644. [Google Scholar] [CrossRef]
- Chen, A.; Zebker, H. Reducing Ionospheric Effects in InSAR Data Using Accurate Coregistration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 60–70. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Li, M. Improving Forest Aboveground Biomass (AGB) Estimation by Incorporating Crown Density and Using Landsat 8 OLI Images of a Subtropical Forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef]
- Eckert, S. Improved Forest Biomass and Carbon Estimations Using Texture Measures from WorldView-2 Satellite Data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef]
- Li, C.; Zhou, L.; Xu, W. Estimating Aboveground Biomass Using Sentinel-2 MSI Data and Ensemble Algorithms for Grassland in the Shengjin Lake Wetland, China. Remote Sens. 2021, 13, 1595. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
- Solórzano, J.V.; Meave, J.A.; Gallardo-Cruz, J.A.; González, E.J.; Hernández-Stefanoni, J.L. Predicting old-growth tropical forest attributes from very high resolution (VHR)-derived surface metrics. Int. J. Remote Sens. 2017, 38, 492–513. [Google Scholar] [CrossRef]
- Gini, R.; Sona, G.; Ronchetti, G.; Passoni, D.; Pinto, L. Improving Tree Species Classification Using UAS Multispectral Images and Texture Measures. ISPRS Int. J. Geo-Inf. 2018, 7, 315. [Google Scholar] [CrossRef]
- Sharma, R.C. An Ultra-Resolution Features Extraction Suite for Community-Level Vegetation Differentiation and Mapping at a Sub-Meter Resolution. Remote Sens. 2022, 14, 3145. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Jay, S. S2ToolBox Level 2 Products LAI, FAPAR, FCOVER. [Research Report] EMMAH-CAPTE, INRAe Avignon. ⟨hal-03584016⟩. 2020. Available online: https://step.esa.int/docs/extra/ATBD_S2ToolBox_V2.0.pdf (accessed on 7 April 2024).
- Sa, R.; Fan, W. Estimation of Forest Parameters in Boreal Artificial Coniferous Forests Using Landsat 8 and Sentinel-2A. Remote Sens. 2023, 15, 3605. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Nguy-Robertson, A.; Gitelson, A.; Peng, Y.; Viña, A.; Arkebauer, T.; Rundquist, D. Green Leaf Area Index Estimation in Maize and Soybean: Combining Vegetation Indices to Achieve Maximal Sensitivity. Agron. J. 2012, 104, 1336–1347. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A. New developments in the remote estimation of the fraction of absorbed photosynthtically active radiation in crops. Geophys. Res. Lett. 2005, 32, L17403. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Tsakiri, M.; Patias, P. Evaluation of single-date and multi-seasonal spatial and spectral information of Sentinel-2 imagery to assess growing stock volume of a Mediterranean forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 1–14. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical forest canopy height estimation from combined polarimetric SAR and LiDAR using machine-learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]
- Alappat, V.O.; Joshi, A.K.; Krishnamurthy, Y.V.N. Tropical Dry Deciduous Forest Stand Variable Estimation Using SAR Data. J. Indian Soc. Remote Sens. 2011, 39, 583–589. [Google Scholar] [CrossRef]
- Khati, U.; Lavalle, M.; Singh, G. Spaceborne tomography of multi-species Indian tropical forests. Remote Sens. Environ. 2019, 229, 193–212. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Kuplich, T.M.; da Costa Freitas Yanasse, C.; Frery, A.C. A study of the relationship between radar backscatter and regenerating tropical forest biomass for spaceborne SAR instruments. Remote Sens. Environ. 1997, 60, 1–13. [Google Scholar] [CrossRef]
- Cat, T.; Tani, H.; Wang, X.; Nguyen, T.; Bui, H. Combination of SAR Polarimetric Parameters for Estimating Tropical Forest Aboveground Biomass. Pol. J. Environ. Stud. 2020, 29, 3353–3365. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, W.; Ji, Y.; Marino, A.; Xu, K.; Zhao, L.; Shi, J.; Zhao, H. Aboveground Biomass Retrieval in Tropical and Boreal Forests Using L-Band Airborne Polarimetric Observations. Forests 2023, 14, 887. [Google Scholar] [CrossRef]
- Xu, L.; Li, S.; Deng, Y.; Wang, R. Adaptive model-based scattering decomposition of Polarimetric SAR Interferometry. J. Electron. 2013, 30, 463–468. [Google Scholar] [CrossRef]
- Latrache, H.; Ouarzeddine, M.; Souissi, B. Improved model-based polarimetric decomposition using the polinsar similarity parameter. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 847–850. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, J.; Liao, C.; Shang, J.; Lopez-Sanchez, J.; Fu, H.; Liu, X. On the Use of Neumann Decomposition for Crop Classification Using Multi-Temporal RADARSAT-2 Polarimetric SAR Data. Remote Sens. 2019, 11, 776. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-Component Power Decomposition for Polarimetric SAR Data Based on Adaptive Volume Scatter Modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Varghese, A.O.; Suryavanshi, A.; Joshi, A.K. Analysis of different polarimetric target decomposition methods in forest density classification using C band SAR data. Int. J. Remote Sens. 2016, 37, 694–709. [Google Scholar] [CrossRef]
- Golshani, P.; Maghsoudi, Y.; Sohrabi, H. Relating ALOS-2 PALSAR-2 Parameters to Biomass and Structure of Temperate Broadleaf Hyrcanian Forests. J. Indian Soc. Remote Sens. 2019, 47, 749–761. [Google Scholar] [CrossRef]
- Huynen, J. Phenomenological Theory of Radar Targets. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1970. [Google Scholar]
- Zhu, Y.; Liu, K.; Myint, S.W.; Du, Z.; Li, Y.; Cao, J.; Liu, L.; Wu, Z. Integration of GF2 Optical, GF3 SAR, and UAV Data for Estimating Aboveground Biomass of China’s Largest Artificially Planted Mangroves. Remote Sens. 2020, 12, 2039. [Google Scholar] [CrossRef]
- Pope, K.O.; Rey-Benayas, J.M.; Paris, J.F. Radar remote sensing of forest and wetland ecosystems in the Central American tropics. Remote Sens. Environ. 1994, 48, 205–219. [Google Scholar] [CrossRef]
- Mitchard, E.; Saatchi, S.; White, L.; Abernethy, K.; Jeffery, K.; Lewis, S.; Collins, M.; Lefsky, M.A.; Leal, M.; Woodhouse, I.; et al. Mapping tropical forest biomass with radar and spaceborne LiDAR: Overcoming problems of high biomass and persistent cloud. Biogeosciences Discuss. 2011, 8, 179–191. [Google Scholar] [CrossRef]
- Sa, R.; Nei, Y.; Fan, W. Combining Multi-Dimensional SAR Parameters to Improve RVoG Model for Coniferous Forest Height Inversion Using ALOS-2 Data. Remote Sens. 2023, 15, 1272. [Google Scholar] [CrossRef]
- Mao, Y.; Michel, O.; Yu, Y.; Fan, W.; Sui, A.; Liu, Z.; Wu, G. Retrieval of Boreal Forest Heights Using an Improved Random Volume over Ground (RVoG) Model Based on Repeat-Pass Spaceborne Polarimetric SAR Interferometry: The Case Study of Saihanba, China. Remote Sens. 2021, 13, 4306. [Google Scholar] [CrossRef]
- Choi, C.; Pardini, M.; Heym, M.; Papathanassiou, K. Improving Forest Height-to-Biomass Allometry with Structure Information: A TanDEM-X Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10415–10427. [Google Scholar] [CrossRef]
- Fu, W.; Guo, H.; Song, P.; Tian, B.; Li, X.; Sun, Z. Combination of PolInSAR and LiDAR techniques for forest height estimation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1218–1222. [Google Scholar] [CrossRef]
- Aghabalaei, A.; Ebadi, H.; Maghsoudi, Y. Forest height estimation based on the RVoG inversion model and the PolInSAR decomposition technique. Int. J. Remote Sens. 2019, 41, 2684–2703. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics From Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar] [CrossRef]
- Deng, S.; Katoh, M.; Guan, Q.; Yin, N.; Li, M. Estimating Forest Aboveground Biomass by Combining ALOS PALSAR and WorldView-2 Data: A Case Study at Purple Mountain National Park, Nanjing, China. Remote Sens. 2014, 6, 7878–7910. [Google Scholar] [CrossRef]
- Pasher, J. Forest Structural Complexity in a Temperate Hardwood Forest: A Geomatics Approach to Modelling and Mapping Indicators of Habitat and Biodiversity. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2009. [Google Scholar]
- de la Cueva, A.V. Structural attributes of three forest types in central Spain and Landsat ETM+ information evaluated with redundancy analysis. Int. J. Remote Sens. 2008, 29, 5657–5676. [Google Scholar] [CrossRef]
- Sampson, P.H.; Treitz, P.M.; Mohammed, G.H. Remote Sensing of Forest Condition in Tolerant Hardwoods: An Examination of Spatial Scale, Structure and Function. Can. J. Remote Sens. 2014, 27, 232–246. [Google Scholar] [CrossRef]
- Dragozi, E.; Gitas, I.; Bajocco, S.; Stavrakoudis, D. Exploring the Relationship between Burn Severity Field Data and Very High Resolution GeoEye Images: The Case of the 2011 Evros Wildfire in Greece. Remote Sens. 2016, 8, 566. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, C.; Li, H.; Liu, Q.; Li, J.; Bridhikitti, A.; Liu, G. Effect of Textural Features in Remote Sensed Data on Rubber Plantation Extraction at Different Levels of Spatial Resolution. Forests 2020, 11, 399. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Fu, Y.; Niu, H.; Yang, Y.; Zhang, B. Fractional Vegetation Cover Estimation of Different Vegetation Types in the Qaidam Basin. Sustainability 2019, 11, 864. [Google Scholar] [CrossRef]
- Yongfeng, J. Estimation of Tree Biomass in Hubei Province by Coupling Optical Image Data and Topographic Factors. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2021. [Google Scholar]
- Wang, Y.; Zhang, X.; Guo, Z. Estimation of tree height and aboveground biomass of coniferous forests in North China using stereo ZY-3, multispectral Sentinel-2, and DEM data. Ecol. Indic. 2021, 126, 107645. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).