KNN Local Linear Regression for Demarcating River Cross-Sections with Point Cloud Data from UAV Photogrammetry URiver-X
Abstract
1. Introduction
2. Mathematical Description
2.1. Distance Measurement of the Point Cloud
2.2. Procedure of the KLR
3. Simulation Study
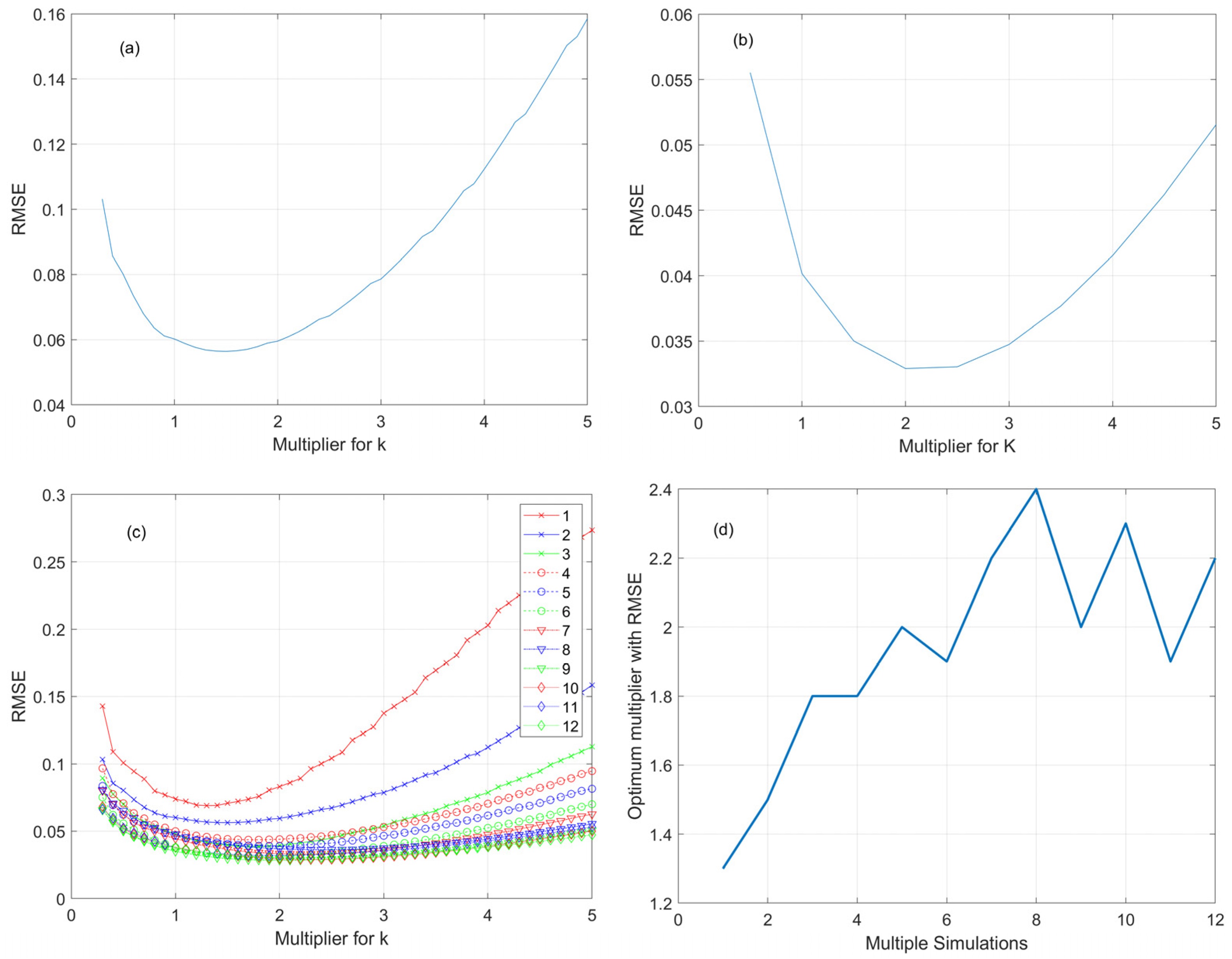
3.1. Model Description and Fitting
3.2. Simulation Results
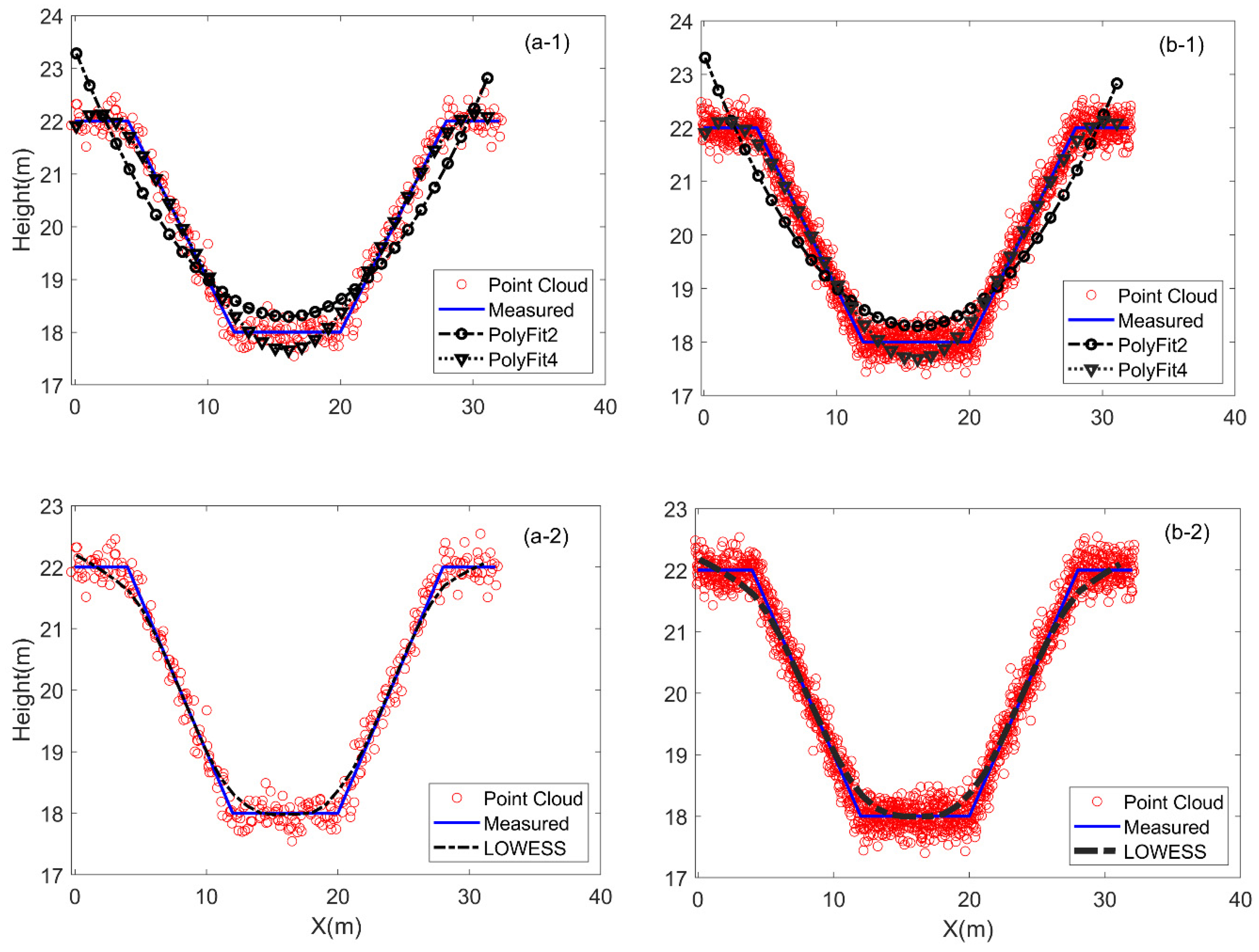
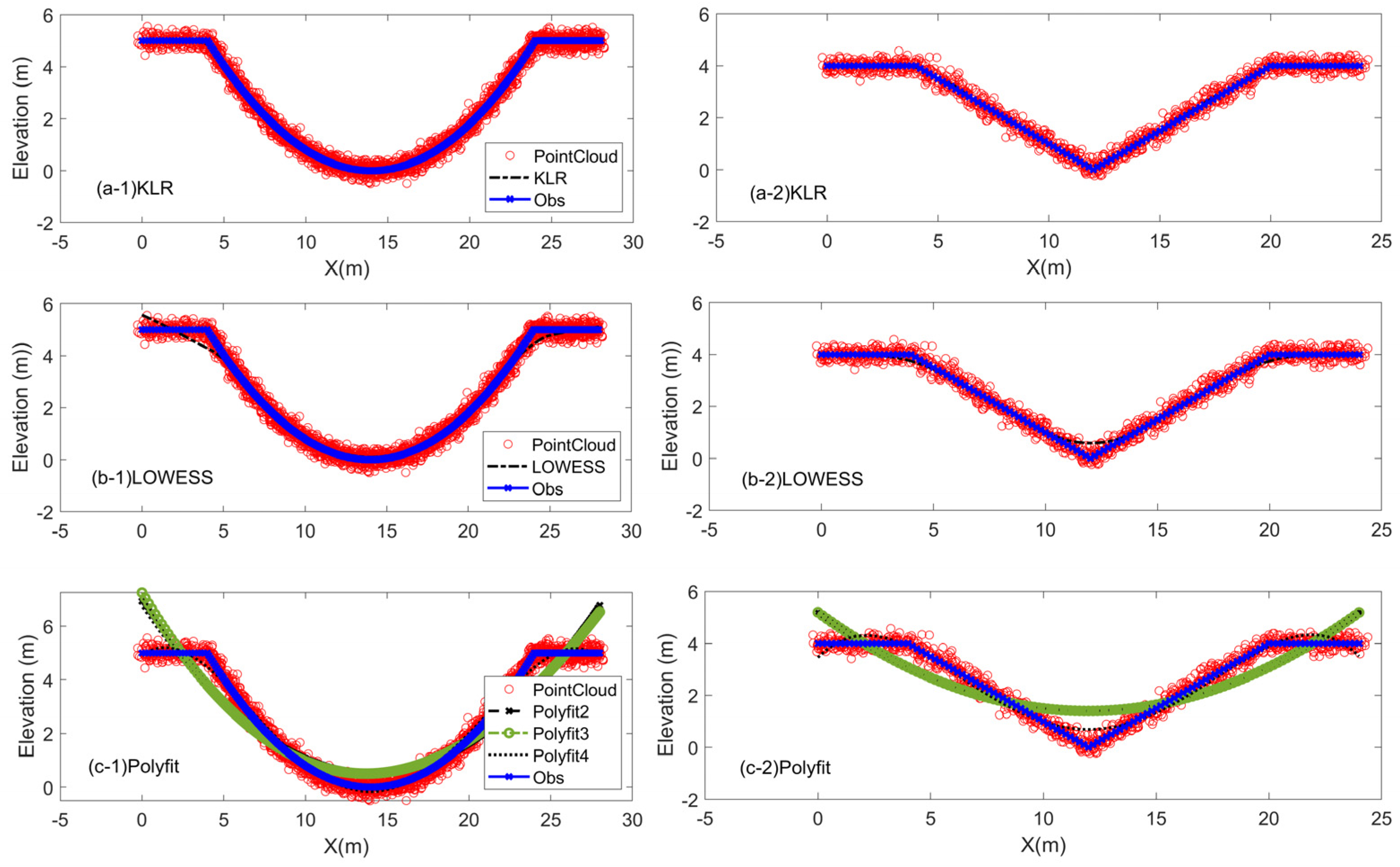
3.3. Simulation Tests with V-Shape and U-Shape Cross-Sections
3.3.1. U-Shape Cross-Section
3.3.2. V-Shape Cross-Section
4. Experimental Study
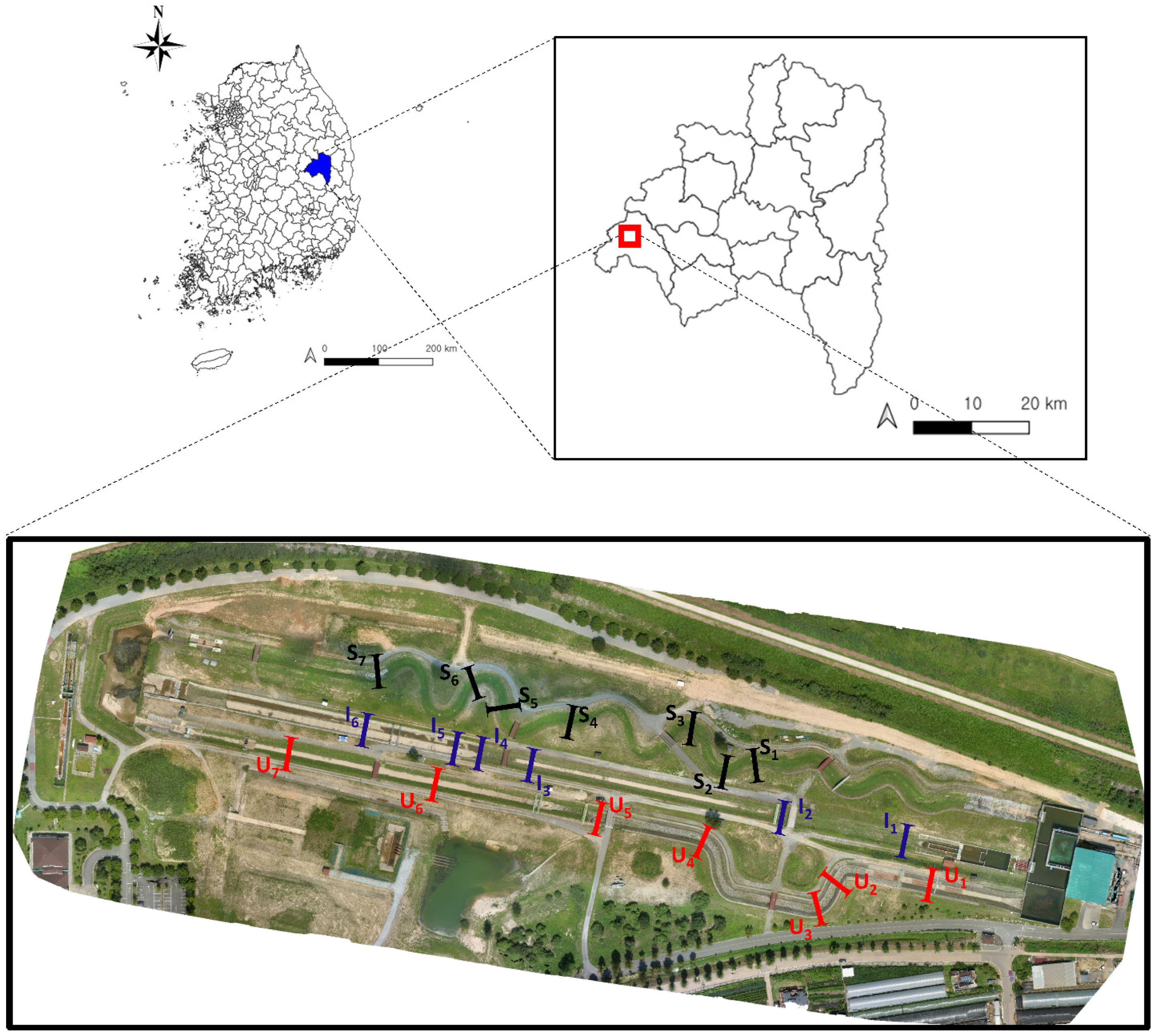
4.1. Experimental Site
4.2. Application Methodology
4.2.1. Ground Surveying
4.2.2. UAV Aerial Surveying
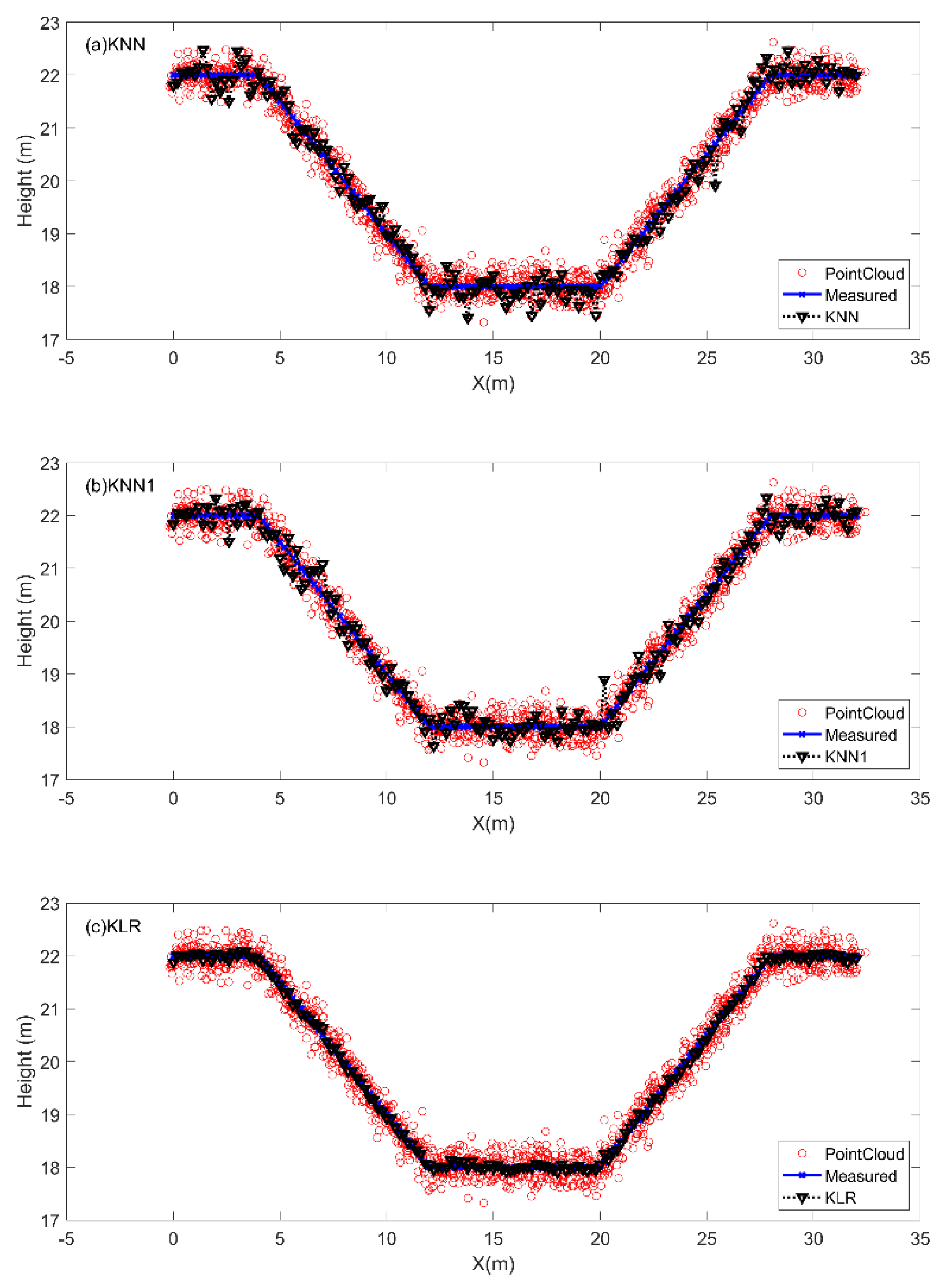
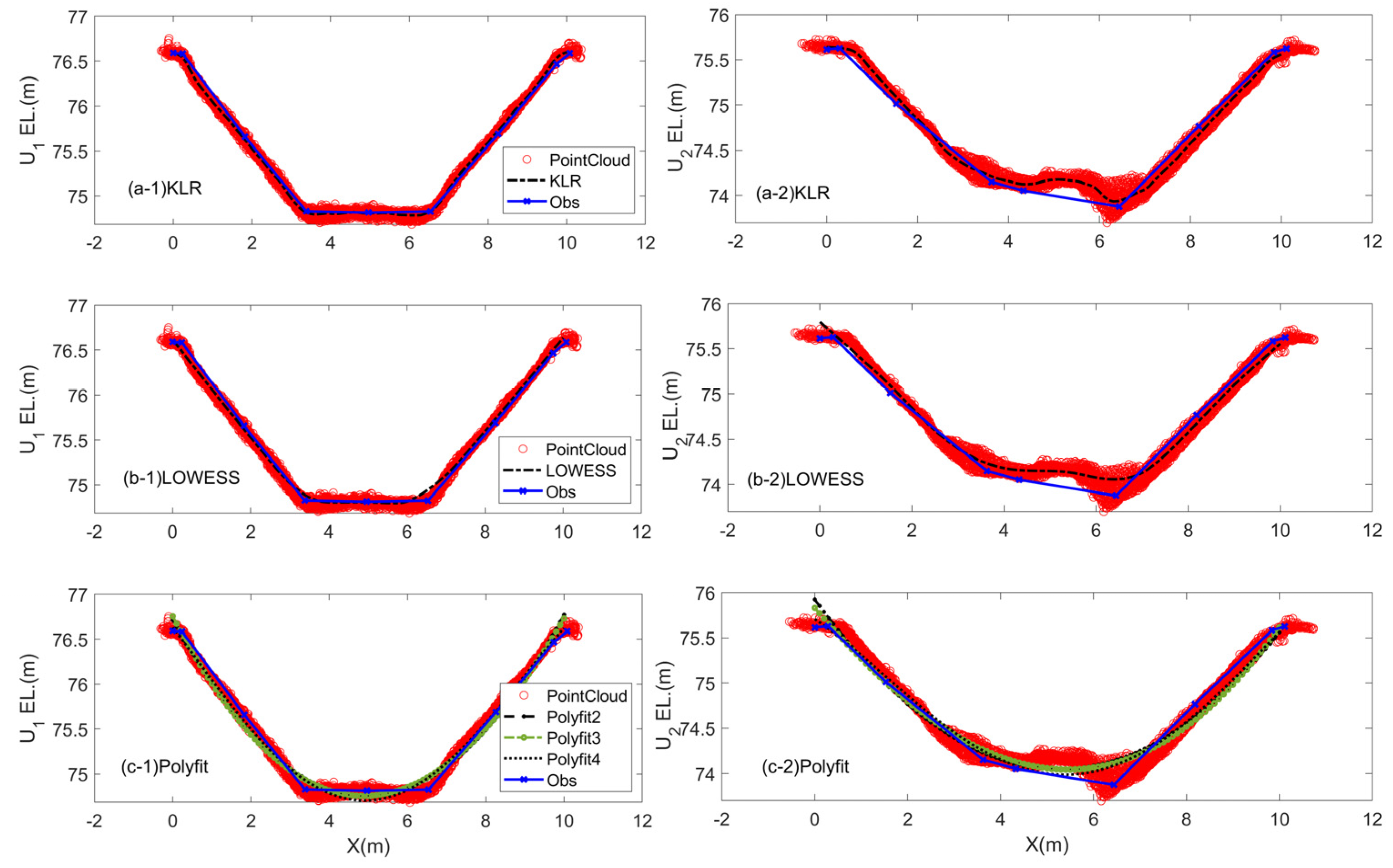
4.3. Experiment Results
5. Case Study of Hapcheon
5.1. Study Area and Data Acquisition
5.1.1. Study Area
5.1.2. Data Acquisition
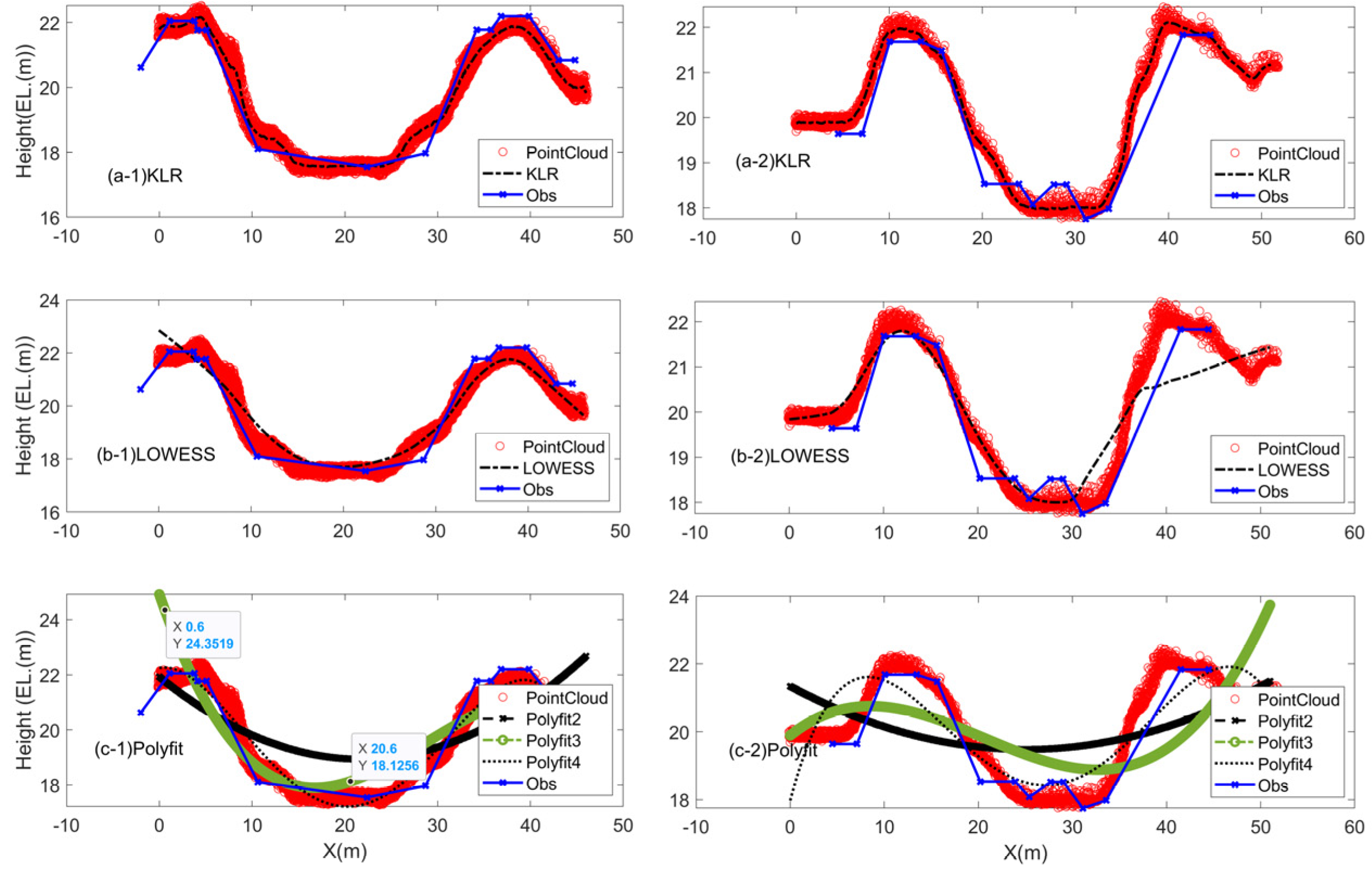
5.2. Results
5.2.1. Selected Sites for Cross-Section Demarcation
5.2.2. Demarcation of Selected Cross-Sections
6. Discussion
7. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watanabe, Y.; Kawahara, Y. UAV Photogrammetry for Monitoring Changes in River Topography and Vegetation. Procedia Eng. 2016, 154, 317–325. [Google Scholar] [CrossRef]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar] [CrossRef]
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV photogrammetry for mapping and 3d modeling—Current status and future perspectives. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, Zurich, Switzerland, 14–16 September 2011; pp. 25–31. [Google Scholar]
- Siebert, S.; Teizer, J. Mobile 3D mapping for surveying earthwork projects using an Unmanned Aerial Vehicle (UAV) system. Autom. Constr. 2014, 41, 1–14. [Google Scholar] [CrossRef]
- Lin, C.; Chen, S.Y.; Chen, C.C.; Tai, C.H. Detecting newly grown tree leaves from unmanned-aerial-vehicle images using hyperspectral target detection techniques. ISPRS J. Photogramm. Remote Sens. 2018, 142, 174–189. [Google Scholar] [CrossRef]
- Marfai, M.A.; Sunarto; Khakim, N.; Fatchurohman, H.; Cahyadi, A.; Wibowo, Y.A.; Rosaji, F.S.C. Tsunami hazard mapping and loss estimation using geographic information system in Drini Beach, Gunungkidul Coastal Area, Yogyakarta, Indonesia. Proc. E3S Web Conf. 2019, 76, 03010. [Google Scholar] [CrossRef]
- Srivastava, K.; Pandey, P.C.; Sharma, J.K. An approach for route optimization in applications of precision agriculture using uavs. Drones 2020, 4, 58. [Google Scholar] [CrossRef]
- Taddia, Y.; Pellegrinelli, A.; Corbau, C.; Franchi, G.; Staver, L.W.; Stevenson, J.C.; Nardin, W. High-resolution monitoring of tidal systems using UAV: A case study on poplar island, MD (USA). Remote Sens. 2021, 13, 1364. [Google Scholar] [CrossRef]
- Wang, S.; Ahmed, Z.; Hashmi, M.Z.; Pengyu, W. Cliff face rock slope stability analysis based on unmanned arial vehicle (UAV) photogrammetry. Geomech. Geophys. Geo-Energy Geo-Resour. 2019, 5, 333–344. [Google Scholar] [CrossRef]
- Yan, Y.; Ma, S.; Yin, S.; Hu, S.; Long, Y.; Xie, C.; Jiang, H. Detection and Numerical Simulation of Potential Hazard in Oil Pipeline Areas Based on UAV Surveys. Front. Earth Sci. 2021, 9, 665478. [Google Scholar] [CrossRef]
- Gracchi, T.; Rossi, G.; Stefanelli, C.T.; Tanteri, L.; Pozzani, R.; Moretti, S. Tracking the evolution of riverbed morphology on the basis of uav photogrammetry. Remote Sens. 2021, 13, 829. [Google Scholar] [CrossRef]
- Langhammer, J. UAV monitoring of stream restorations. Hydrology 2019, 6, 29. [Google Scholar] [CrossRef]
- Lee, G.; Choi, M.; Yu, W.; Jung, K. Creation of river terrain data using region growing method based on point cloud data from UAV photography. Quat. Int. 2019, 519, 255–262. [Google Scholar] [CrossRef]
- Sanhueza, D.; Picco, L.; Ruiz-Villanueva, V.; Iroumé, A.; Ulloa, H.; Barrientos, G. Quantification of fluvial wood using UAVs and structure from motion. Geomorphology 2019, 345, 106837. [Google Scholar] [CrossRef]
- Tomsett, C.; Leyland, J. Remote sensing of river corridors: A review of current trends and future directions. River Res. Appl. 2019, 35, 779–803. [Google Scholar] [CrossRef]
- Anders, N.; Smith, M.; Suomalainen, J.; Cammeraat, E.; Valente, J.; Keesstra, S. Impact of flight altitude and cover orientation on Digital Surface Model (DSM) accuracy for flood damage assessment in Murcia (Spain) using a fixed-wing UAV. Earth Sci. Inform. 2020, 13, 391–404. [Google Scholar] [CrossRef]
- Andreadakis, E.; Diakakis, M.; Vassilakis, E.; Deligiannakis, G.; Antoniadis, A.; Andriopoulos, P.; Spyrou, N.I.; Nikolopoulos, E.I. Unmanned aerial systems-aided post-flood peak discharge estimation in ephemeral streams. Remote Sens. 2020, 12, 4183. [Google Scholar] [CrossRef]
- Zakaria, S.; Mahadi, M.R.; Abdullah, A.F.; Abdan, K. Aerial platform reliability for flood monitoring under various weather conditions: A review. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives; Springer: Cham, Switzerland, 2018; pp. 591–602. [Google Scholar]
- Izumida, A.; Uchiyama, S.; Sugai, T. Application of UAV-SfM photogrammetry and aerial lidar to a disastrous flood: Repeated topographic measurement of a newly formed crevasse splay of the Kinu River, central Japan. Nat. Hazards Earth Syst. Sci. 2017, 17, 1505–1519. [Google Scholar] [CrossRef]
- Kaewwilai, A.J. Analysis of Flood Patterns in Adams County, Pennsylvania Utilizing Drone Technology and Computer Simulations Analysis of Flood Patterns in Adams County. Pa. Util. Drone 2019, 57, 1–20. [Google Scholar]
- Perks, M.T.; Russell, A.J.; Large, A.R.G. Technical note: Advances in flash flood monitoring using unmanned aerial vehicles (UAVs). Hydrol. Earth Syst. Sci. 2016, 20, 4005–4015. [Google Scholar] [CrossRef]
- Tsunetaka, H.; Hotta, N.; Hayakawa, Y.S.; Imaizumi, F. Spatial accuracy assessment of unmanned aerial vehicle-based structures from motion multi-view stereo photogrammetry for geomorphic observations in initiation zones of debris flows, Ohya landslide, Japan. Prog. Earth Planet. Sci. 2020, 7, 24. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Dietrich, J.T. Cost-effective non-metric photogrammetry from consumer-grade sUAS: Implications for direct georeferencing of structure from motion photogrammetry. Earth Surf. Process. Landf. 2017, 42, 473–486. [Google Scholar] [CrossRef]
- Lee, T.; Singh, V.P.S.; Ha, T.H. UAV Photogrammetry-based Flood Early Warning System applied to Migok-cheon Stream, South Korea. J. Hydrol. Eng. 2022. in review. [Google Scholar] [CrossRef]
- Gichamo, T.Z.; Popescu, I.; Jonoski, A.; Solomatine, D. River cross-section extraction from the ASTER global DEM for flood modeling. Environ. Model. Softw. 2012, 31, 37–46. [Google Scholar] [CrossRef]
- Petikas, I.; Keramaris, E.; Kanakoudis, V. Calculation of multiple critical depths in open channels using an adaptive cubic polynomials algorithm. Water 2020, 12, 799. [Google Scholar] [CrossRef]
- Pilotti, M. Extraction of cross sections from digital elevation model for one-dimensional dam-break wave propagation in mountain valleys. Water Resour. Res. 2016, 52, 52–68. [Google Scholar] [CrossRef]
- Petikas, I.; Keramaris, E.; Kanakoudis, V. A novel method for the automatic extraction of quality non-planar river cross-sections from digital elevation models. Water 2020, 12, 3553. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Tarekegn, T.H.; Haile, A.T.; Rientjes, T.; Reggiani, P.; Alkema, D. Assessment of an ASTER-generated DEM for 2D hydrodynamic flood modeling. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 457–465. [Google Scholar] [CrossRef]
- Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H.H.G. Towards an automated SAR-based flood monitoring system: Lessons learned from two case studies. Phys. Chem. Earth 2011, 36, 241–252. [Google Scholar] [CrossRef]
- Azizian, A.; Brocca, L. Determining the best remotely sensed DEM for flood inundation mapping in data sparse regions. Int. J. Remote Sens. 2020, 41, 1884–1906. [Google Scholar] [CrossRef]
- Biswal, S.; Sahoo, B.; Jha, M.K.; Bhuyan, M.K. A hybrid machine learning-based multi-DEM ensemble model of river cross-section extraction: Implications on streamflow routing. J. Hydrol. 2023, 625, 129951. [Google Scholar] [CrossRef]
- Lee, T.; Ouarda, T.B.M.J.; Yoon, S. KNN-based local linear regression for the analysis and simulation of low flow extremes under climatic influence. Clim. Dyn. 2017, 49, 3493–3511. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A nearest neighbor bootstrap for resampling hydrologic time series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Lee, T.; Ouarda, T.B.M.J. Identification of model order and number of neighbors for k-nearest neighbor resampling. J. Hydrol. 2011, 404, 136–145. [Google Scholar] [CrossRef]
- Lee, T.; Salas, J.D.; Prairie, J. An Enhanced Nonparametric Streamflow Disaggregation Model with Genetic Algorithm. Water Resour. Res. 2010, 46, W08545. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; p. 350. [Google Scholar]
- Falkner, E.; Morgan, D. Aerial Mapping: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2001; p. 216. [Google Scholar]
- Weilberg, M. Photogrammetry and Remote Sensing; Syrawood Publishing House: New York, NY, USA, 2016; p. 216. [Google Scholar]
- Neal, J.C.; Odoni, N.A.; Trigg, M.A.; Freer, J.E.; Garcia-Pintado, J.; Mason, D.C.; Wood, M.; Bates, P.D. Efficient incorporation of channel cross-section geometry uncertainty into regional and global scale flood inundation models. J. Hydrol. 2015, 529, 169–183. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Sinclair, C.D.; Werritty, A. Log-logistic flood frequency analysis. J. Hydrol. 1988, 98, 205–224. [Google Scholar] [CrossRef]
- Elek, P.; Márkus, L. A long range dependent model with nonlinear innovations for simulating daily river flows. Nat. Hazards Earth Syst. Sci. 2004, 4, 277–283. [Google Scholar] [CrossRef]
- Orlowsky, B.; Bothe, O.; Fraedrich, K.; Gerstengarbe, F.W.; Zhu, X. Future climates from bias-bootstrapped weather analogs: An application to the Yangtze River basin. J. Clim. 2010, 23, 3509–3524. [Google Scholar] [CrossRef]
- Simonoff, J.S. Smoothing Methods in Statistics; Springer: New York, NY, USA, 1996; p. 353. [Google Scholar]
- Lee, C.; Kim, J.; Kang, W.; Ji, W.; Jung, S. KICT River Experiment Center. Water Future 2022, 55, 91–97. [Google Scholar]
- BRTMA. Reports of Fundamental River Plan for Hwanggang Downstream Rivers. 2019; Volume 1021. Available online: http://www.river.go.kr/ (accessed on 14 May 2024).
- Seong, K.; Lee, S.O.; Jung, H.J.; Lee, T. Safety first? Lessons from the Hapcheon Dam flood in 2020. Nat. Hazards 2020. in review. [Google Scholar]
- Hamdi, D.A.; Iqbal, F.; Alam, S.; Kazim, A.; MacDermott, A. Drone forensics: A case study on DJI phantom 4. In Proceedings of the Proceedings of IEEE/ACS International Conference on Computer Systems and Applications, AICCSA, Abu Dhabi, United Arab Emirates, 3–7 November 2019. [Google Scholar]
- Fernandez-Diaz, J.C.; Glennie, C.L.; Carter, W.E.; Shrestha, R.L.; Sartori, M.P.; Singhania, A.; Legleiter, C.J.; Overstreet, B.T. Early results of simultaneous terrain and shallow water bathymetry mapping using a single-wavelength airborne LiDAR sensor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 623–635. [Google Scholar] [CrossRef]
- Allouis, T.; Bailly, J.; Pastol, Y.; Le Roux, C. Comparison of LiDAR waveform processing methods for very shallow water bathymetry using Raman, near-infrared and green signals. Earth Surf. Process. Landf. 2010, 35, 640–650. [Google Scholar] [CrossRef]
- Lee, C.H.; Liu, L.W.; Wang, Y.M.; Leu, J.M.; Chen, C.L. Drone-Based Bathymetry Modeling for Mountainous Shallow Rivers in Taiwan Using Machine Learning. Remote Sens. 2022, 14, 3343. [Google Scholar] [CrossRef]
- Mandlburger, G.; Kölle, M.; Nübel, H.; Soergel, U. BathyNet: A Deep Neural Network for Water Depth Mapping from Multispectral Aerial Images. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 71–89. [Google Scholar] [CrossRef]





| Shape | KLR | LOWESS | PolyFit4 | |
|---|---|---|---|---|
| RMSE | Trapezoid | 0.0289 | 0.1397 | 0.1565 |
| U-shape | 0.0326 | 0.1868 | 0.1728 | |
| V-shape | 0.0325 | 0.1353 | 0.2299 | |
| MAE | Trapezoid | 0.1549 | 0.3697 | 0.3789 |
| U-shape | 0.1536 | 0.3158 | 0.3518 | |
| V-shape | 0.1558 | 0.2807 | 0.4369 |
| No. | KLR | LOWESS | Polynomial | |||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | ||||
| I-shape | 1 | 0.072 | 0.125 | 0.183 | 0.183 | 0.138 |
| 2 | 0.101 | 0.154 | 0.231 | 0.235 | 0.156 | |
| 3 | 0.074 | 0.192 | 0.281 | 0.284 | 0.148 | |
| 4 | 0.054 | 0.12 | 0.17 | 0.174 | 0.177 | |
| 5 | 0.054 | 0.17 | 0.33 | 0.291 | 0.289 | |
| 6 | 0.062 | 0.127 | 0.359 | 0.287 | 0.205 | |
| U-shape | 1 | 0.029 | 0.074 | 0.134 | 0.13 | 0.088 |
| 2 | 0.066 | 0.118 | 0.182 | 0.155 | 0.119 | |
| 3 | 0.045 | 0.072 | 0.113 | 0.111 | 0.094 | |
| 4 | 0.054 | 0.083 | 0.149 | 0.146 | 0.105 | |
| 5 | 0.170 | 0.183 | 0.196 | 0.183 | 0.219 | |
| 6 | 0.131 | 0.183 | 0.374 | 0.363 | 0.201 | |
| 7 | 0.171 | 0.246 | 0.419 | 0.427 | 0.204 | |
| S-shape | 1 | 0.122 | 0.145 | 0.435 | 0.429 | 0.151 |
| 2 | 0.088 | 0.112 | 0.398 | 0.398 | 0.118 | |
| 3 | 0.204 | 0.216 | 0.428 | 0.416 | 0.203 | |
| 4 | 0.164 | 0.197 | 0.452 | 0.467 | 0.178 | |
| 5 | 0.187 | 0.186 | 0.433 | 0.419 | 0.213 | |
| 6 | 0.123 | 0.146 | 0.402 | 0.404 | 0.136 | |
| 7 | 0.145 | 0.146 | 0.48 | 0.488 | 0.22 | |
| No. | KLR | LOWESS | Polynomial | |||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | ||||
| I-shape | 1 | 0.062 | 0.114 | 0.162 | 0.163 | 0.13 |
| 2 | 0.083 | 0.135 | 0.194 | 0.197 | 0.125 | |
| 3 | 0.06 | 0.146 | 0.183 | 0.184 | 0.123 | |
| 4 | 0.048 | 0.097 | 0.142 | 0.143 | 0.144 | |
| 5 | 0.04 | 0.112 | 0.275 | 0.233 | 0.178 | |
| 6 | 0.05 | 0.098 | 0.299 | 0.224 | 0.139 | |
| U-shape | 1 | 0.021 | 0.061 | 0.117 | 0.112 | 0.08 |
| 2 | 0.059 | 0.104 | 0.141 | 0.132 | 0.105 | |
| 3 | 0.035 | 0.058 | 0.099 | 0.098 | 0.076 | |
| 4 | 0.039 | 0.072 | 0.126 | 0.126 | 0.091 | |
| 5 | 0.117 | 0.14 | 0.173 | 0.142 | 0.177 | |
| 6 | 0.083 | 0.151 | 0.3 | 0.29 | 0.169 | |
| 7 | 0.148 | 0.209 | 0.341 | 0.331 | 0.167 | |
| S-shape | 1 | 0.094 | 0.113 | 0.377 | 0.339 | 0.12 |
| 2 | 0.082 | 0.091 | 0.342 | 0.344 | 0.105 | |
| 3 | 0.167 | 0.173 | 0.36 | 0.33 | 0.162 | |
| 4 | 0.142 | 0.156 | 0.392 | 0.368 | 0.154 | |
| 5 | 0.147 | 0.136 | 0.379 | 0.374 | 0.19 | |
| 6 | 0.101 | 0.117 | 0.372 | 0.371 | 0.1 | |
| 7 | 0.118 | 0.112 | 0.43 | 0.43 | 0.172 | |
| Site No. | KLR | LOWESS | PolyFit2 | PolyFit3 | PolyFit4 | |
|---|---|---|---|---|---|---|
| RMSE | Site-1 | 0.4063 | 0.8389 | 1.8548 | 1.8046 | 1.4218 |
| Site-2 | 0.4010 | 0.6736 | 1.3762 | 1.1252 | 0.8753 | |
| Site-3 | 0.3236 | 0.4514 | 1.4722 | 1.4327 | 0.9753 | |
| Site-4 | 0.4786 | 0.9419 | 1.3834 | 1.9593 | 0.7068 | |
| MAE | Site-1 | 0.5393 | 0.8197 | 1.3034 | 1.2934 | 1.1224 |
| Site-2 | 0.4406 | 0.5764 | 1.1758 | 1.1611 | 0.9482 | |
| Site-3 | 0.5746 | 0.7439 | 1.1536 | 1.0342 | 0.8221 | |
| Site-4 | 0.6422 | 0.8307 | 1.1500 | 1.1057 | 0.7615 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.; Hwang, S.; Singh, V.P. KNN Local Linear Regression for Demarcating River Cross-Sections with Point Cloud Data from UAV Photogrammetry URiver-X. Remote Sens. 2024, 16, 1820. https://doi.org/10.3390/rs16101820
Lee T, Hwang S, Singh VP. KNN Local Linear Regression for Demarcating River Cross-Sections with Point Cloud Data from UAV Photogrammetry URiver-X. Remote Sensing. 2024; 16(10):1820. https://doi.org/10.3390/rs16101820
Chicago/Turabian StyleLee, Taesam, Seonghyeon Hwang, and Vijay P. Singh. 2024. "KNN Local Linear Regression for Demarcating River Cross-Sections with Point Cloud Data from UAV Photogrammetry URiver-X" Remote Sensing 16, no. 10: 1820. https://doi.org/10.3390/rs16101820
APA StyleLee, T., Hwang, S., & Singh, V. P. (2024). KNN Local Linear Regression for Demarcating River Cross-Sections with Point Cloud Data from UAV Photogrammetry URiver-X. Remote Sensing, 16(10), 1820. https://doi.org/10.3390/rs16101820






