UAV Complex-Scene Single-Target Tracking Based on Improved Re-Detection Staple Algorithm
Abstract
1. Introduction
- Based on the improved Staple algorithm, a novel re-detection target-tracking framework is proposed to achieve the long-term tracking of UAVs. In particular, the algorithm adjusts the feature weights adaptively by detecting the response differences between the filter model and the histogram model. Additionally, the improved MFO algorithm is introduced as a re-detection mechanism to enhance the stability of the tracker.
- A refined swarm intelligence algorithm (MFO) employing diverse strategies is proposed to mitigate tracking failures in target tracking. To swiftly correct inaccuracies in unreliable tracking scenarios, a trajectory-driven population initialization method is advocated. Furthermore, the iteration process of the population’s position is enhanced by integrating the influence of sex pheromone concentration on individual moths, thereby optimizing the tracking algorithm’s performance.
- We conducted experiments on well-acknowledged tracking datasets, which demonstrate the outstanding performance of the proposed tracking algorithm. Compared to traditional tracking algorithms, the proposed method exhibits significant improvements in accuracy and robustness, making it effective for tracking aerial photography scenes.
2. Related Works
2.1. Correlation Filtering Tracking Method
2.2. Meta-Heuristic Algorithm Solution
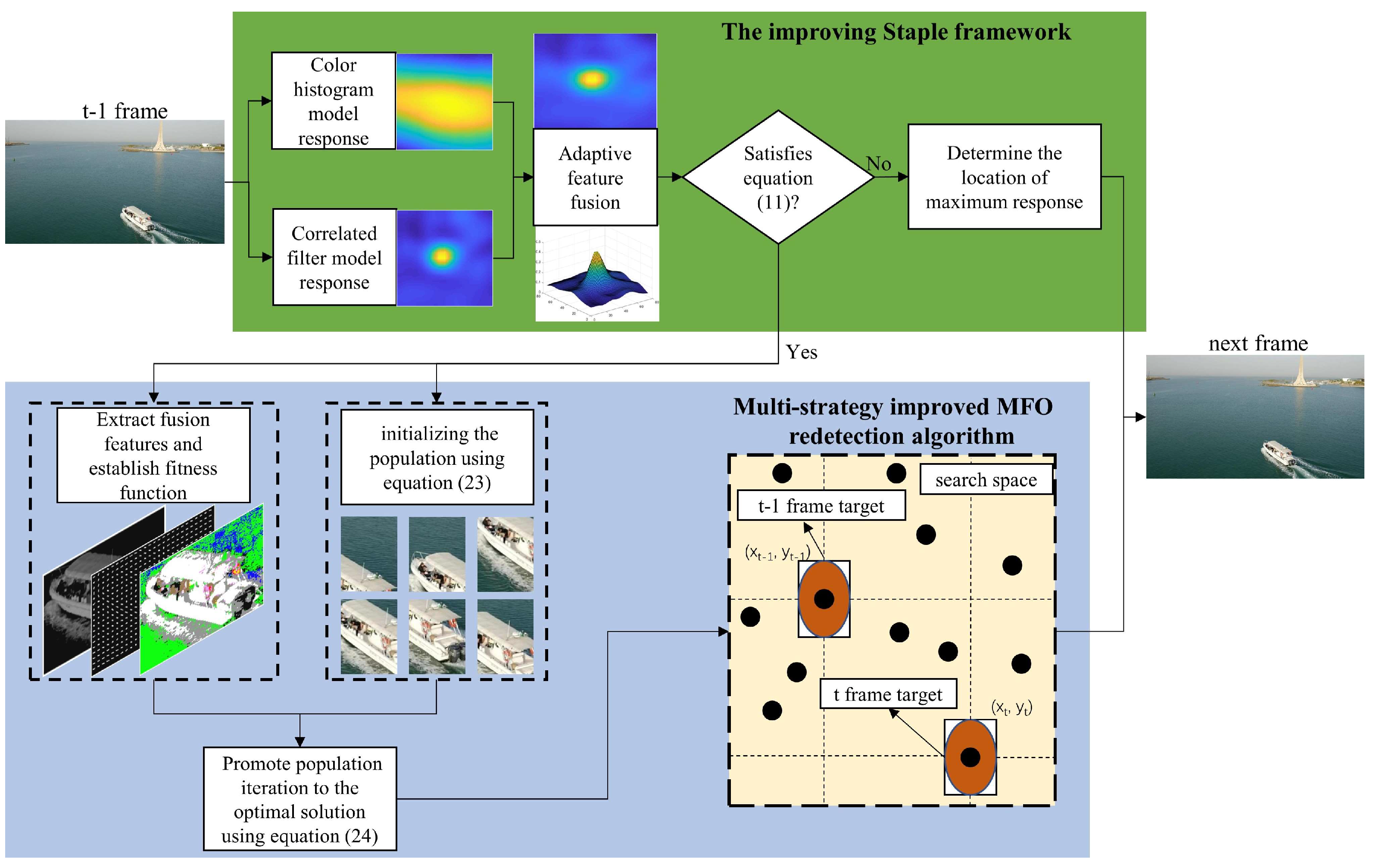
3. Proposed Approach
3.1. Tracking Algorithm and Its Improvement
3.1.1. Staple Filtering Algorithm
- Correlation filter model based on HOG feature
- 2.
- Bayesian classifier model based on color histogram feature
3.1.2. Anomaly Tracking Status Detection
3.1.3. Adaptive Feature Fusion Strategy
3.2. Object Re-Detection Algorithm and Improvement
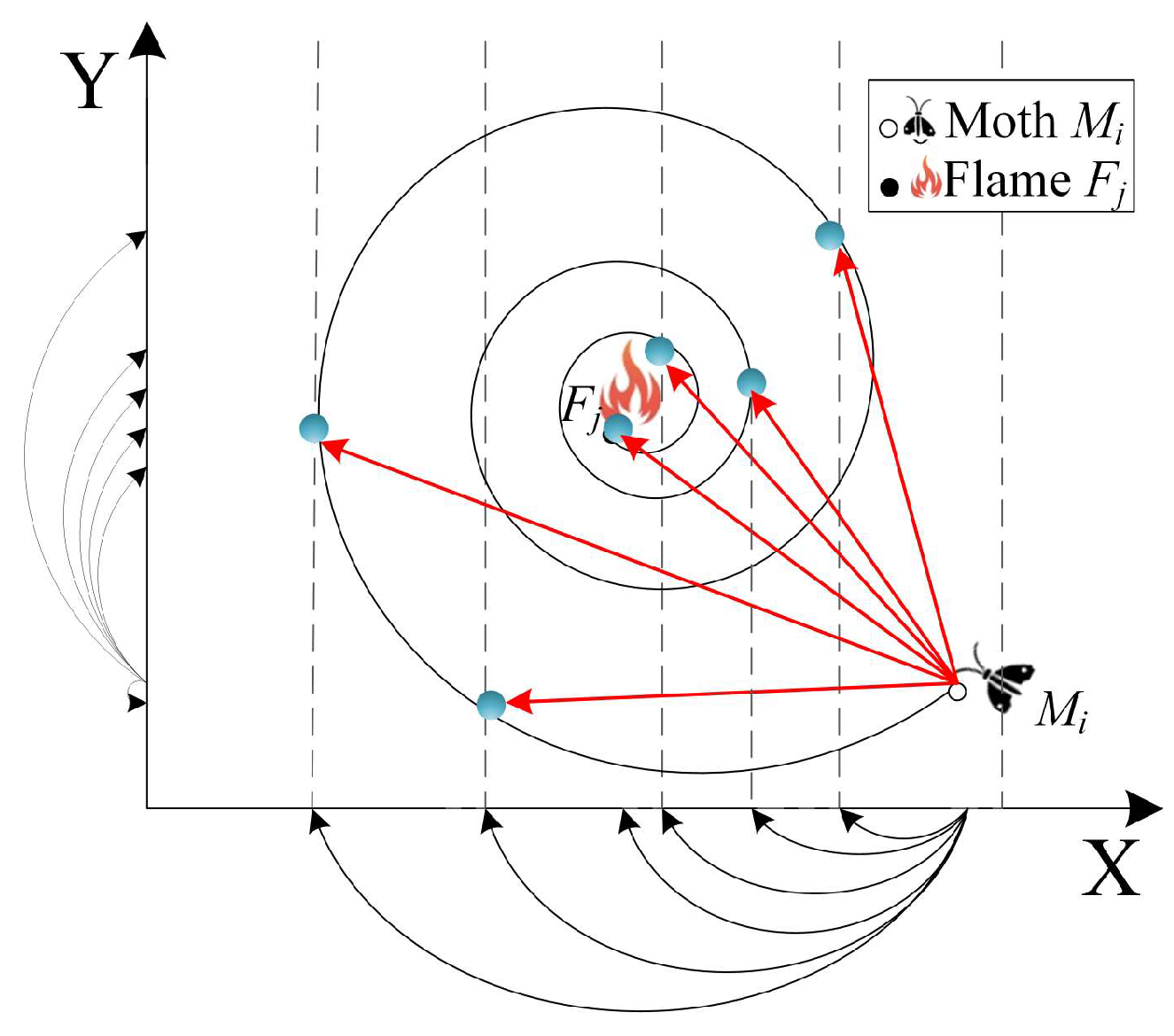
3.2.1. Moth Flame Optimization
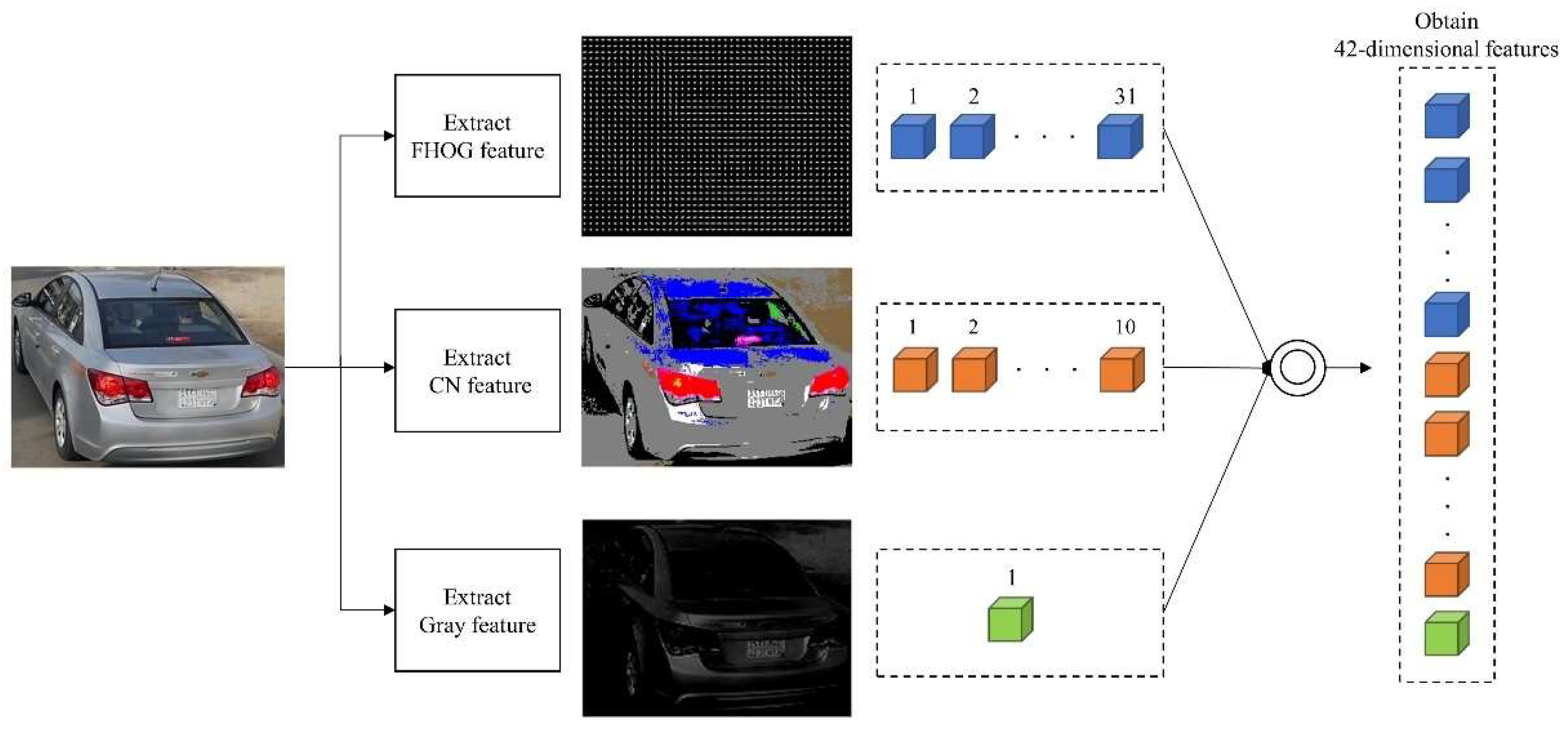
3.2.2. Feature Template Extraction and Update
3.2.3. Establish Fitness Function
3.2.4. Trajectory-Guided Gaussian Initialization
3.2.5. Population Iteration Velocity Dominated by Sex Pheromone Density
| Algorithm 1: The proposed improving re-detection Staple algorithm |
| Input: The initial frame t0 with the corresponding object ground truth bounding box B0 (x0, y0, w0, h0); Output: The predicted bounding box Bt (xt, yt, wt, ht) of the tth frame; 1 Initialize the correlation filter model and histogram model for the Staple algorithm; 2 for i = 1, 2, …, n do 3 Extract features of the current frame image to obtain responses from the relevant filter and histogram classifier; at the current frame moment; then 6 Extract CN, Fhog, and Gray features from the current frame image and merge them into a 42-dimensional feature vector; 7 Build the corresponding feature template at the current frame and establish the fitness function using Equations (19) and (20); 8 Initialize the population in the MFO algorithm using Equation (23); 9 Iterate through the population to obtain the individual with the best fitness as the detected target box; 10 Bt = BtMFO; 11 else 12 Select the position corresponding to the maximum value in the blended response map as the detected target box; 13 Bt = BtStaple; 14 Update the correlation filter model and histogram model. |
4. Experimental Results
4.1. Experiment Setup
- ①
- Precision: Center location error (CLE) represents the ratio of the distance between the algorithm-calibrated coordinates of the target’s center point and the real target center point coordinates in the frame, as calculated by the tracker, and is below a certain threshold. In this paper, the threshold is set to 20. The CLE is defined aswhere (xtrack, ytrack) represents the central point coordinates of the target calculated by the tracker, and (xtruth, ytruth) represents the central point coordinates of the real target area.
- ②
- Success rate: Defining the success rate of the target tracking task as the proportion of frames in which the intersection over union (IoU) value between the predicted bounding box, calculated by the tracker, and the ground truth bounding box exceeds a specified threshold. The IoU per frame is given bywhere Itruth is the actual target region, and Itrack is the target region calculated by the algorithm.
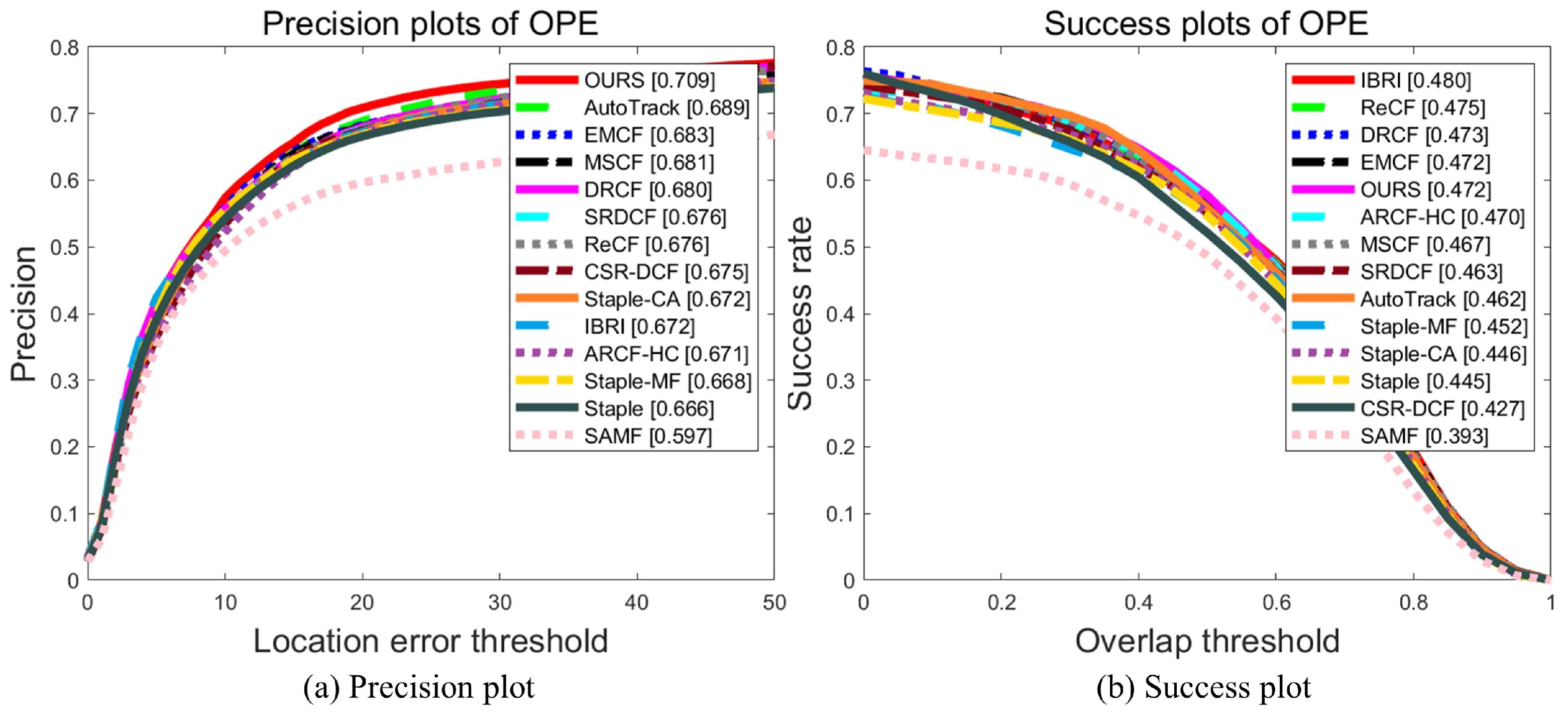
4.2. Quantitative Experimental Results
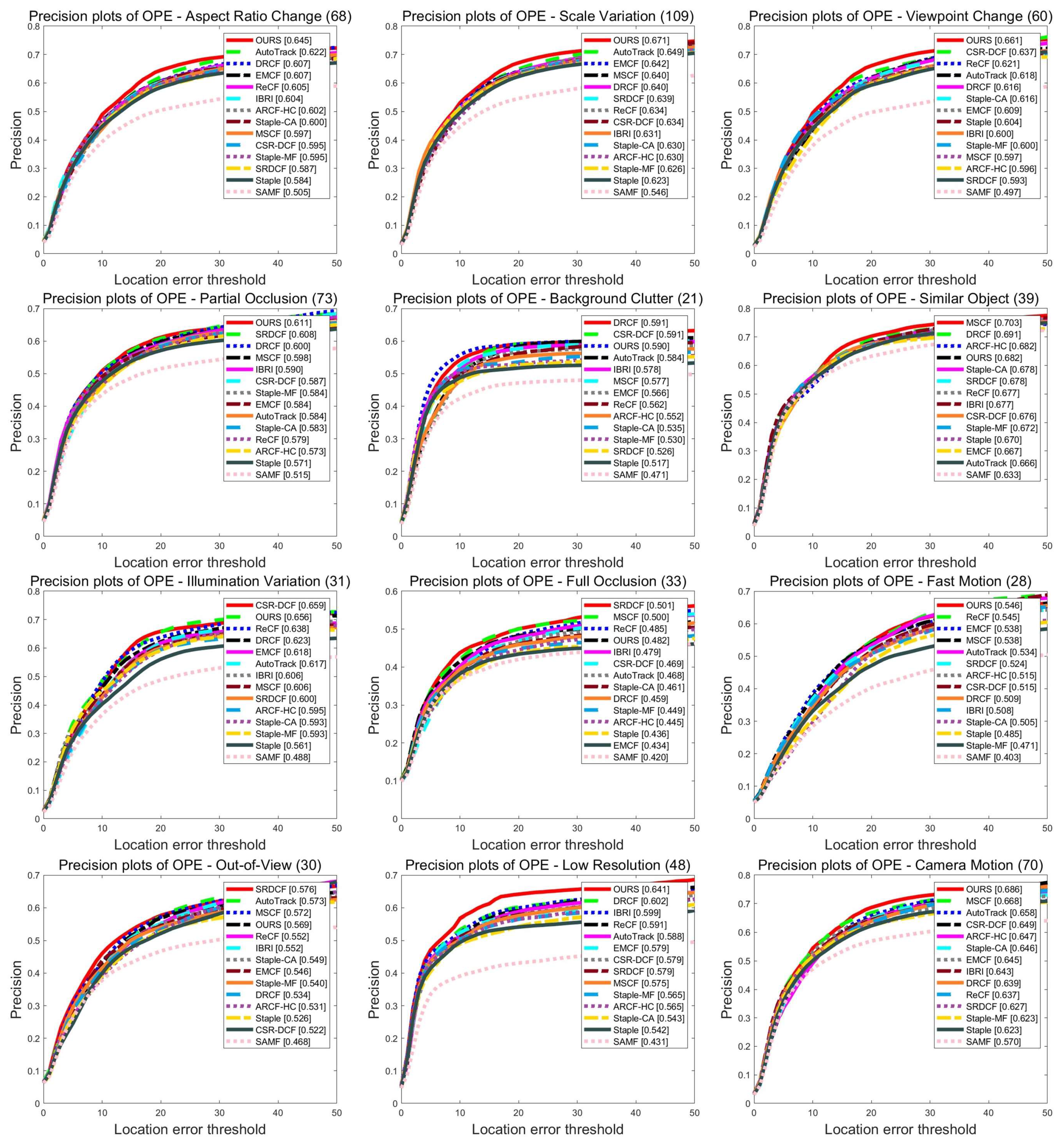
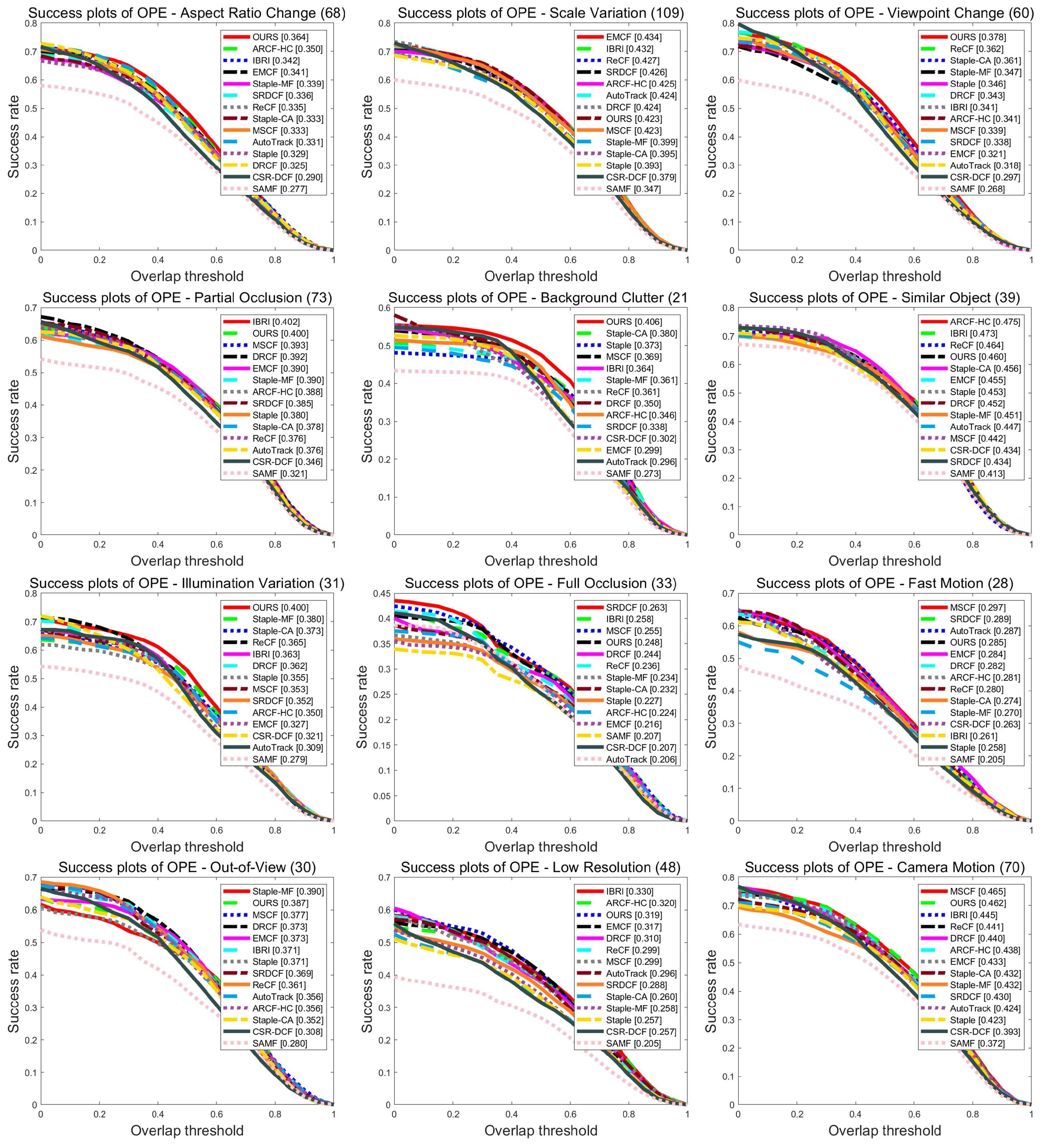
4.2.1. UAV123 Benchmark
- (1)
- Overall evaluation
- (2)
- Attribute evaluation
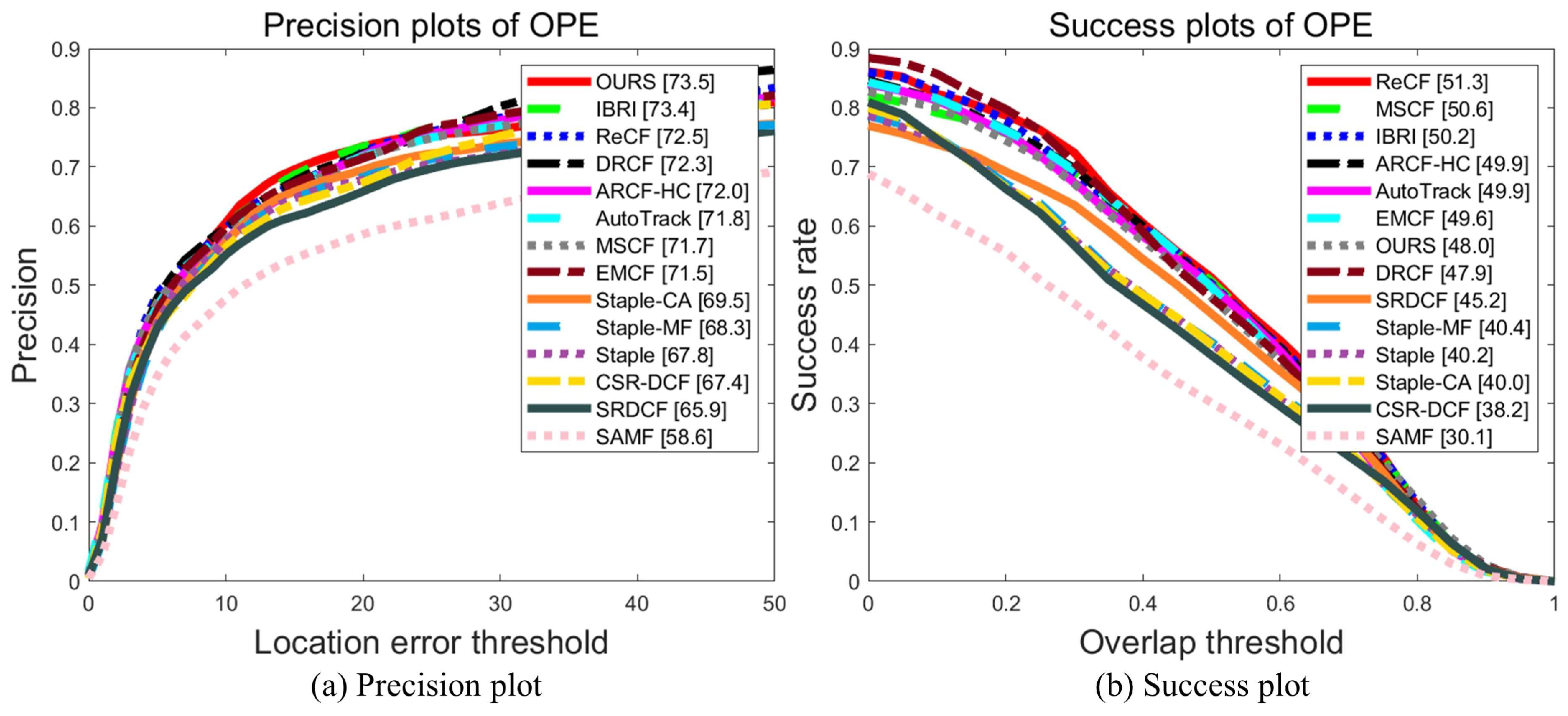
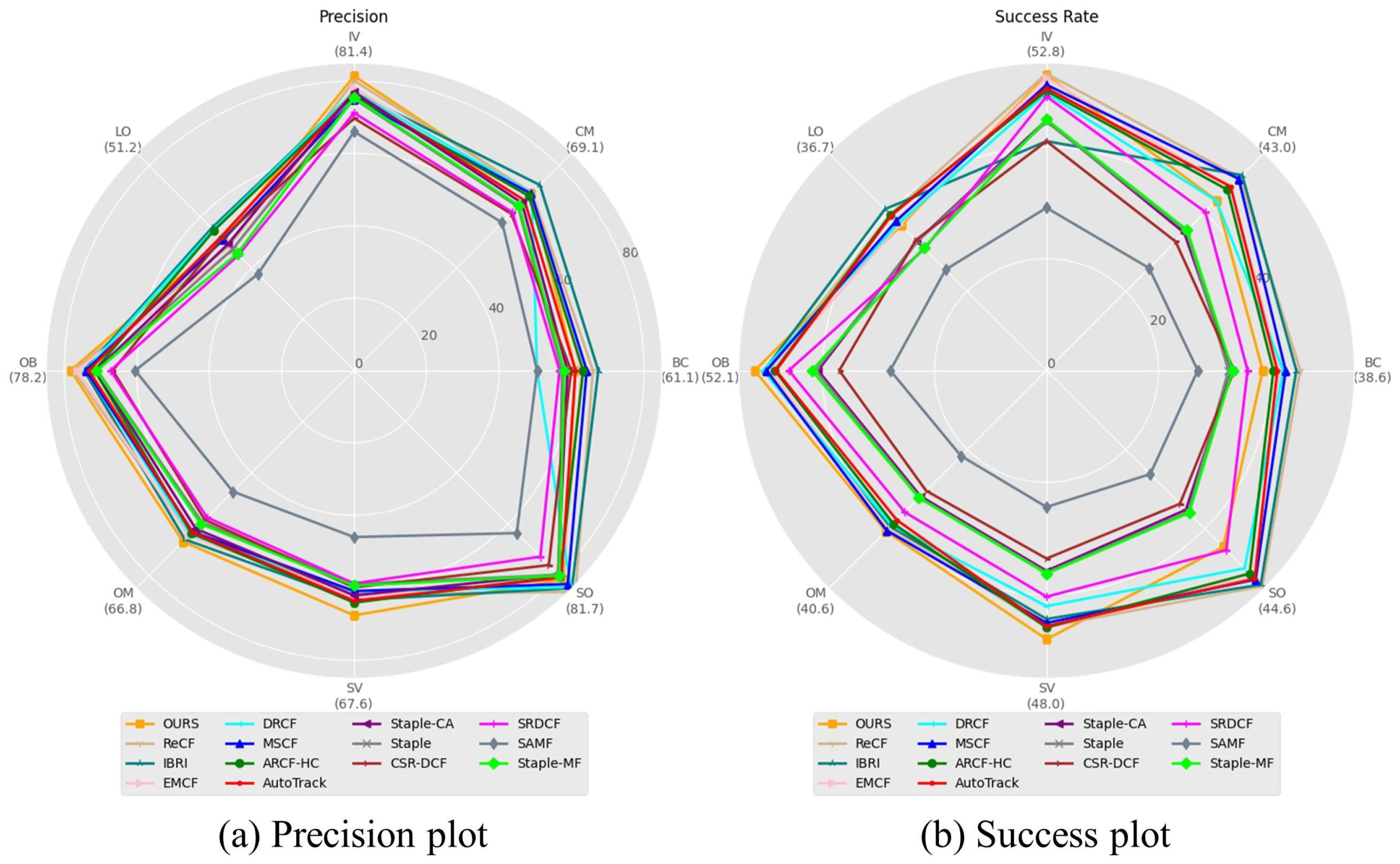
4.2.2. UAVDT Benchmark
- (1)
- Overall evaluation
- (2)
- Overall evaluation
4.3. Qualitative Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruan, W.; Chen, J.; Wu, Y.; Wang, J.; Liang, C.; Hu, R.; Jiang, J. Multi-Correlation Filters with Triangle-Structure Constraints for Object Tracking. IEEE Trans. Multimed. 2019, 21, 1122–1134. [Google Scholar] [CrossRef]
- Rautaray, S.S.; Agrawal, A. Vision Based Hand Gesture Recognition for Human Computer Interaction: A Survey. Artif. Intell. Rev. 2015, 43, 1–54. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Huang, Z.; Cheng, X.; Feng, J.; Jiao, L. Bidirectional Multiple Object Tracking Based on Trajectory Criteria in Satellite Videos. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Yan, H.; Xu, X.; Jin, G.; Hou, Q.; Geng, Z.; Wang, L.; Zhang, J.; Zhu, D. Moving Targets Detection for Video SAR Surveillance using Multilevel Attention Network Based on Shallow Feature Module. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Li, B.; Fu, C.; Ding, F.; Ye, J.; Lin, F. All-Day Object Tracking for Unmanned Aerial Vehicle. IEEE Trans. Mobile Comput. 2023, 22, 4515–4529. [Google Scholar] [CrossRef]
- Hu, S.; Yuan, X.; Ni, W.; Wang, X.; Jamalipour, A. Visual camouflage and online trajectory planning for unmanned aerial vehicle-based disguised video surveillance: Recent advances and a case study. IEEE Veh. Technol. Mag. 2023, 18, 48–57. [Google Scholar] [CrossRef]
- Gao, G.; Yao, L.; Li, W.; Zhang, L.; Zhang, M. Onboard information fusion for multisatellite collaborative observation: Summary, challenges, and perspectives. IEEE Geosc. Remote Sens. Mag. 2023, 11, 40–59. [Google Scholar] [CrossRef]
- Wen, Y.; Gao, T.; Zhang, J.; Li, Z.; Chen, T. Encoder-free Multi-axis Physics-aware Fusion Network for Remote Sensing Image Dehazing. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar]
- Wei, H.; Wan, G.; Ji, S. ParallelTracker: A Transformer Based Object Tracker for UAV Videos. Remote Sens. 2023, 15, 2544. [Google Scholar] [CrossRef]
- Zhang, S.; Zhuo, L.; Zhang, H.; Li, J. Object Tracking in Unmanned Aerial Vehicle Videos via Multifeature Discrimination and Instance-Aware Attention Network. Remote Sens. 2020, 12, 2646. [Google Scholar] [CrossRef]
- Bian, Z.; Xu, T.; Chen, J.; Ma, L.; Cai, W.; Li, J. Auto-Learning Correlation-Filter-Based Target State Estimation for Real-Time UAV Tracking. Remote Sens. 2022, 14, 5299. [Google Scholar] [CrossRef]
- Li, Y.; Fu, C.; Huang, Z.; Zhang, Y.; Pan, J. Intermittent Contextual Learning for Keyfilter-Aware UAV Object Tracking using Deep Convolutional Feature. IEEE Trans. Multimed. 2021, 23, 810–822. [Google Scholar] [CrossRef]
- Zhang, F.; Ma, S.; Yu, L.; Zhang, Y.; Qiu, Z.; Li, Z. Learning Future-Aware Correlation Filters for Efficient UAV Tracking. Remote Sens. 2021, 13, 4111. [Google Scholar] [CrossRef]
- Zhang, F.; Ma, S.; Zhang, Y.; Qiu, Z. Perceiving temporal environment for correlation filters in real-time uav tracking. IEEE Signal Process. Lett. 2021, 29, 6–10. [Google Scholar] [CrossRef]
- Fu, C.; Ye, J.; Xu, J.; He, Y.; Lin, F. Disruptor-aware interval-based response inconsistency for correlation filters in real-time aerial tracking. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6301–6313. [Google Scholar] [CrossRef]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual Object Tracking using Adaptive Correlation Filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the Circulant Structure of Tracking-by-Detection with Kernels. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Häger, G.; Khan, F.; Felsberg, M. Accurate Scale Estimation for Robust Visual Tracking. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014; Bmva Press: Newcastle, UK, 2014. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Golodetz, S.; Miksik, O.; Torr, P.H. Staple: Complementary Learners for Real-time Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1401–1409. [Google Scholar]
- Li, Y.; Zhu, J. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 5–12 September 2014; pp. 254–265. [Google Scholar]
- Kiani Galoogahi, H.; Fagg, A.; Lucey, S. Learning Background-aware Correlation Filters for Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1144–1152. [Google Scholar]
- Deng, C.; He, S.; Han, Y.; Zhao, B. Learning Dynamic Spatial-temporal Regularization for UAV Object Tracking. IEEE Signal Process. Lett. 2021, 28, 1230–1234. [Google Scholar] [CrossRef]
- Kumar, R.; Deb, A.K. Pedestrian Tracking in UAV Images with Kalman Filter Motion Estimator and Correlation Filter. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 4–19. [Google Scholar] [CrossRef]
- Gao, M.-L.; Li, L.-L.; Sun, X.-M.; Yin, L.-J.; Li, H.-T.; Luo, D.-S. Firefly Algorithm (FA) Based Particle Filter Method for Visual Tracking. Optik 2015, 126, 1705–1711. [Google Scholar] [CrossRef]
- Ong, K.M.; Ong, P.; Sia, C.K.; Low, E.S. Effective Moving Object Tracking using Modified Flower Pollination Algorithm for Visible Image Sequences under Complicated Background. Appl. Soft Comput. 2019, 83, 105625. [Google Scholar] [CrossRef]
- Castro, E.C.d.; Salles, E.O.T.; Ciarelli, P.M. A New Approach to Enhanced Swarm Intelligence Applied to Video Target Tracking. Sensors 2021, 21, 1903. [Google Scholar] [CrossRef] [PubMed]
- Sardari, F.; Moghaddam, M.E. A Hybrid Occlusion Free Object Tracking Method using Particle Filter and Modified Galaxy Based Search Meta-heuristic Algorithm. Appl. Soft Comput. 2017, 50, 280–299. [Google Scholar] [CrossRef]
- Kang, K.; Bae, C.; Yeung, H.W.F.; Chung, Y.Y. A Hybrid Gravitational Search Algorithm with Swarm Intelligence and Deep Convolutional Feature for Object Tracking Optimization. Appl. Soft Comput. 2018, 66, 319–329. [Google Scholar] [CrossRef]
- Moghaddasi, S.S.; Faraji, N. A Hybrid Algorithm based on Particle Filter and Genetic Algorithm for Target Tracking. Expert Syst. Appl. 2020, 147, 113188. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Y.; Huang, Z. Large Margin Object Tracking with Circulant Feature Maps. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4021–4029. [Google Scholar]
- Mirjalili, S. Moth-flame Optimization Algorithm: A Novel Nature-inspired Heuristic Paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Abd El Aziz, M.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-flame Optimization for Multilevel Thresholding Image Segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Mueller, M.; Smith, N.; Ghanem, B. A Benchmark and Simulator for uav Tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 445–461. [Google Scholar]
- Du, D.; Qi, Y.; Yu, H.; Yang, Y.; Duan, K.; Li, G.; Zhang, W.; Huang, Q.; Tian, Q. The Unmanned Aerial Vehicle Benchmark: Object Detection and Tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 370–386. [Google Scholar]
- Zheng, G.; Fu, C.; Ye, J.; Lin, F.; Ding, F. Mutation Sensitive Correlation Filter for Real-time UAV Tracking with Adaptive Hybrid Label. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 503–509. [Google Scholar]
- Huang, Z.; Fu, C.; Li, Y.; Lin, F.; Lu, P. Learning Aberrance Repressed Correlation Filters for Real-time UAV Tracking. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2891–2900. [Google Scholar]
- Danelljan, M.; Hager, G.; Shahbaz Khan, F.; Felsberg, M. Learning Spatially Regularized Correlation Filters for Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4310–4318. [Google Scholar]
- Li, Y.; Fu, C.; Ding, F.; Huang, Z.; Lu, G. AutoTrack: Towards High-performance Visual Tracking for UAV with Automatic Spatio-temporal Regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11923–11932. [Google Scholar]
- Lukezic, A.; Vojir, T.; Čehovin Zajc, L.; Matas, J.; Kristan, M. Discriminative Correlation Filter with Channel and Spatial Reliability. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6309–6318. [Google Scholar]
- Mueller, M.; Smith, N.; Ghanem, B. Context-aware Correlation Filter Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1396–1404. [Google Scholar]
- Lin, F.; Fu, C.; He, Y.; Xiong, W.; Li, F. ReCF: Exploiting response reasoning for correlation filters in real-time UAV tracking. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10469–10480. [Google Scholar] [CrossRef]
- Fu, C.; Xu, J.; Lin, F.; Guo, F.; Liu, T.; Zhang, Z. Object saliency-aware dual regularized correlation filter for real-time aerial tracking. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8940–8951. [Google Scholar] [CrossRef]


| Video Sequence | Attributes |
|---|---|
| boat9 | SV, ARC, LR, POC, VC |
| wakeboard5 | SV, ARC, LR, FM, POC, IV, VC, CM |
| S0801 | BC, CM, OM, SV, LO |
| S1201 | BC, CM, OM, SV, LO, IV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Huang, H.; Niu, M.; Miah, M.S.; Wang, H.; Gao, T. UAV Complex-Scene Single-Target Tracking Based on Improved Re-Detection Staple Algorithm. Remote Sens. 2024, 16, 1768. https://doi.org/10.3390/rs16101768
Huang Y, Huang H, Niu M, Miah MS, Wang H, Gao T. UAV Complex-Scene Single-Target Tracking Based on Improved Re-Detection Staple Algorithm. Remote Sensing. 2024; 16(10):1768. https://doi.org/10.3390/rs16101768
Chicago/Turabian StyleHuang, Yiqing, He Huang, Mingbo Niu, Md Sipon Miah, Huifeng Wang, and Tao Gao. 2024. "UAV Complex-Scene Single-Target Tracking Based on Improved Re-Detection Staple Algorithm" Remote Sensing 16, no. 10: 1768. https://doi.org/10.3390/rs16101768
APA StyleHuang, Y., Huang, H., Niu, M., Miah, M. S., Wang, H., & Gao, T. (2024). UAV Complex-Scene Single-Target Tracking Based on Improved Re-Detection Staple Algorithm. Remote Sensing, 16(10), 1768. https://doi.org/10.3390/rs16101768







