Modeling and Locating the Wind Erosion at the Dry Bottom of the Aral Sea Based on an InSAR Temporal Decorrelation Decomposition Model

Abstract

The dust originating from the extinct lake of the Aral Sea poses a considerable threat to the surrounding communities and ecosystems. The accurate location of these wind erosion areas is an essential prerequisite for controlling sand and dust activity. However, few relevant indicators reported in this current study can accurately describe and measure wind erosion intensity. A novel wind erosion intensity (WEI) of a pixel resolution unit was defined in this paper based on deformation due to the wind erosion in this pixel resolution unit. We also derived the relationship between WEI and soil InSAR temporal decorrelation (ITD). ITD is usually caused by the surface change over time, which is very suitable for describing wind erosion. However, within a pixel resolution unit, the ITD signal usually includes soil and vegetation contributions, and extant studies concerning this issue are considerably limited. Therefore, we proposed an ITD decomposition model (ITDDM) to decompose the ITD signal of a pixel resolution unit. The least-square method (LSM) based on singular value decomposition (SVD) is used to estimate the ITD of soil (SITD) within a pixel resolution unit. We verified the results qualitatively by the landscape photos, which can reflect the actual conditions of the soil. At last, the WEI of the Aral Sea from 23 June 2020, to 5 July 2020 was mapped. The results confirmed that (1) based on the ITDDM model, the SITD can be accurately estimated by the LSM; (2) the Aral Sea is experiencing severe wind erosion; and (3) the middle, northeast, and southeast bare areas of the South Aral Sea are where salt dust storms may occur.

1. Introduction

The fine particles produced by wind erosion are essential for wind-blown sand activity. Sand and dust activities, especially salt dust activities, are a disaster for surrounding residents and ecosystems of the Aral Sea [1]. Wind erosion accelerated the desertification process and promoted the formation of the Aralkum Desert. Sufficient fine particles from this new desert provide favorable conditions for sand and dust activities. The salt storms generated by winds caused various diseases among the surrounding residents and resulted in the death of a large area of vegetation, especially that of crops. Accurate localization of these wind erosion areas is necessary for human intervention in salt and dust storms. Scientists have developed numerous models based on traditional experimental physics and remote sensing technology to distinguish different degrees of wind erosion.

Wind erosion research results based on traditional experimental physics provide a solid theoretical foundation for wind erosion research. According to the study of Liu and Zobeck, based on experimental physics methods, wind blowing, impact, and abrasion of moving particles are the three primary forms of particle moving and separation [2,3]. Bagnold derived the threshold of the starting wind speed of a particle fluid according to a moment balance equation [4]. The research results of Lu and Shao show that when the ground particles are mainly dust, the vertical dust flux caused by the impact is proportional to the 3–4 power of the wind speed [5]. Numerous scientists have studied the forms and laws of the movement of sand and dust and provided many physical models of different forms of movement [3,6,7,8,9,10,11,12,13,14,15]. Particles suspended in the air fall to the ground mainly through dry and wet sedimentation. The physical processes involved in dry and wet sedimentation are relatively complex, and there are no effective means to describe the dry and wet sedimentation process [6,16,17,18]. Clarifying the influencing factors of the wind erosion process is the basis for establishing the wind erosion model. Chepil’s classification of wind erosion factors plays an essential role in advancing the research on the wind erosion process [19]. Based on Chepil’s research results, subsequent researchers have proposed many well-known wind erosion models [20,21,22,23,24,25]. The research of wind erosion processes based on traditional experimental physics has essential value and significance for human understanding of the fundamental laws of wind erosion activity. However, the uncertainty of the wind erosion model itself and the difficulty in obtaining high spatial and temporal resolution data greatly limit the wind erosion model in the application of describing large-scale wind erosion scenarios.

InSAR (interferometric synthetic aperture radar) decorrelation can be used to describe random changes in the surface due to wind erosion, expecting to solve the problem of quantitative characterization of wind erosion intensity [26]. Coherence is commonly employed to assess the similarity of InSAR echo signals. It quantifies the correlation between two complex InSAR echo signals by calculating their correlation coefficient. The computation of radar echo signal coherence typically involves the spatial averaging of the radar echo signals within a moving window. Decorrelation, numerically equal to 1 minus the coherence coefficient, denotes the loss of coherence. Various factors contribute to decorrelation, including temporal, thermal, and spatial ones. Estimating temporal decorrelation involves eliminating the impacts of thermal and spatial decorrelation from the total decorrelation [27].

In 1992, Zebker and Villasenor studied the relationship between ITD and the surface erosion of Death Valley in California, and the results showed that ITD and wind erosion degrees have a negative linear correlation. In another study in 2000, Wegmuller confirmed this relationship, and he pointed out that the above relationship is still valid when vegetation coverage is less than 40% [28]. Later, InSAR decorrelation was used to study desertification due to wind erosion, also showing that this technology has the ability to detect ground changes due to wind erosion [29,30,31]. In some other studies related to dune stability, it has been confirmed that temporal decorrelation technology can detect changes in the surface of dunes due to wind erosion [32,33].

Although many indicators in this current study were proposed to describe WEI, few can be used to describe and measure the WEI of a pixel resolution unit accurately. This paper proposed a novel WEI of a pixel resolution unit based on the surface deformation caused by wind erosion. Zebker’s research shows that the ITD in a pixel resolution unit is related to the displacement of scatters in it [26]. Based on the relationship between scatters’ random displacement and the surface random deformation within a pixel resolution unit, we related the WEI with the SITD of a pixel resolution unit. In fact, a pixel resolution unit’s ITD often involves the contribution of soil and vegetation in the bare lands of the Aral Sea. Wegmuller’s study indicates that the ITD of a pixel resolution unit was equal to the sum of the weighted ITD of all scatterers within the pixel resolution unit [28]. However, few studies have been conducted to decompose the ITD contributions of all scatterers within a pixel resolution unit. Therefore, this paper focuses on the following:

• Modeling the WEI of a pixel resolution unit and relate the WEI with the SITD of this pixel resolution unit.
• SITD estimation within a pixel resolution unit.
• Mapping the WEI of the dry lakebed of the Aral Sea.

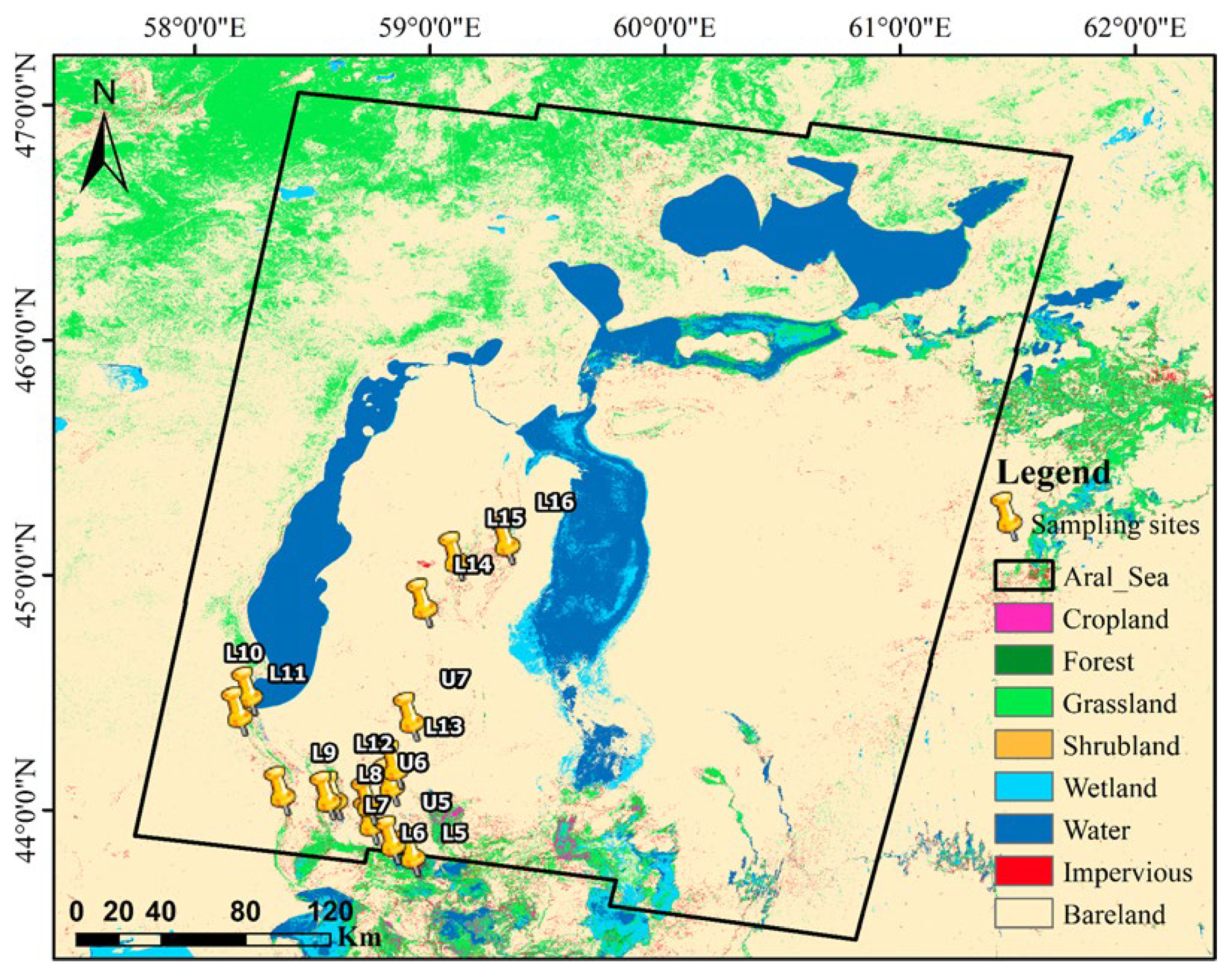
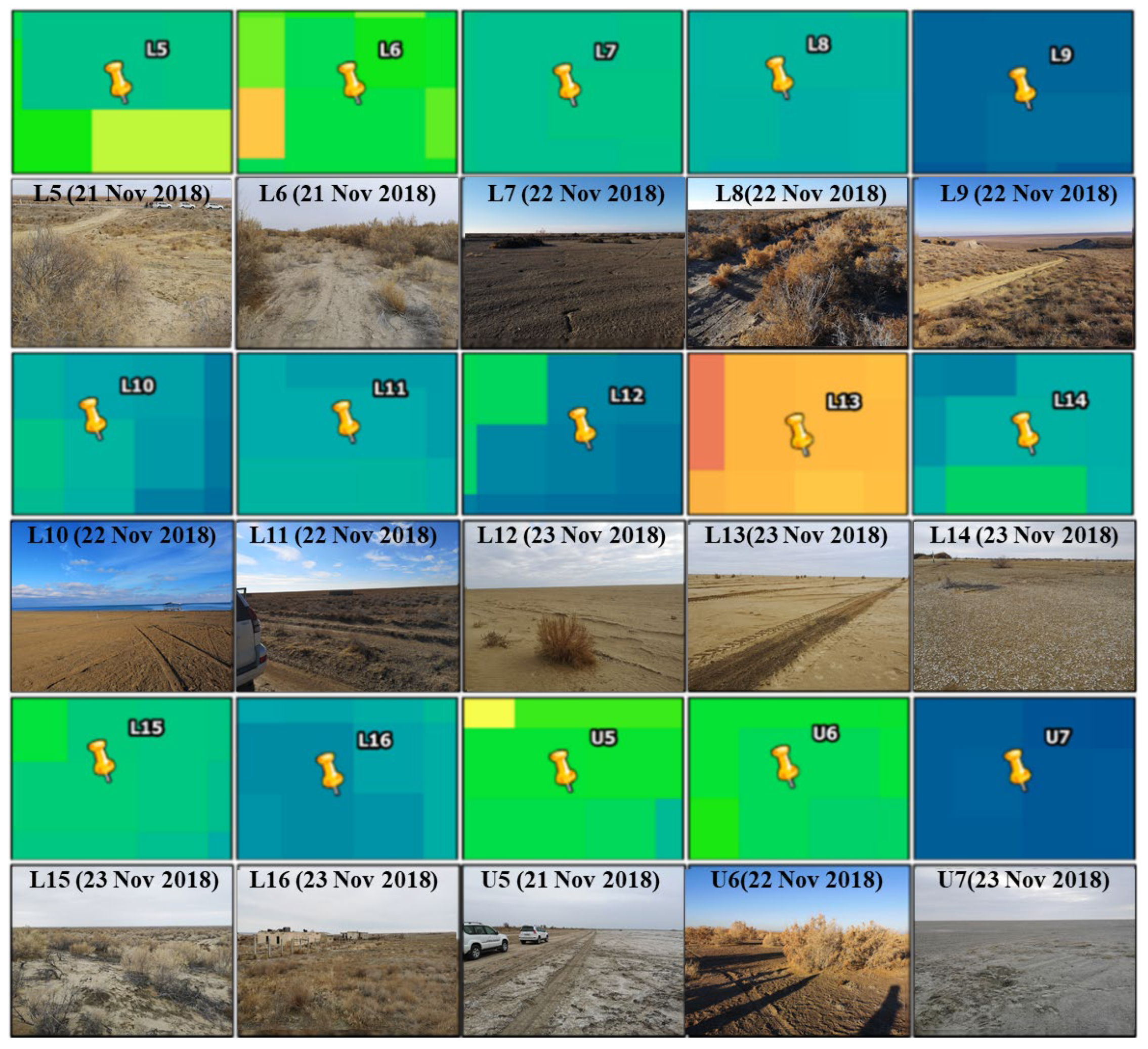
2. Study Area

Part of the Aral Sea is in southern Kazakhstan, and the rest is in northern Uzbekistan. Due to the extended distance from the sea, the Aral Sea has a classical continental dry climate. The study area is shown in Figure 1.

In the Aral Sea, the maximum temperature difference between spring and summer can reach 60 °C, and the average annual precipitation is about 100 mm, which is very rare. The significant temperature difference and scarce rainfall are very conducive to wind erosion. Furthermore, as shown in Figure 1, this area is dominated by bare land. These things considered, the desertification of the dry lakebed is very severe, and the loose soil is vulnerable to erosion. Thus, the dry climate, sparse vegetation coverage, and loose soil properties make this area a potential wind erosion area. Sampling data were from a field survey about the Aral Sea’s desertification in November 2018, and parts of the sampling sites are listed in Figure 1.

Two factors closely associated with wind erosion include the abundance of fine particles on the soil surface and wind conditions. The presence of abundant fine particles on the surface of the Aral Sea and strong wind conditions create highly favorable conditions for wind erosion. Soil particle size analysis results from sampling points U5, U6, and U7 indicate that the majority of soil particles fall within the range of 2 μm to 63 μm, providing a rich source of material for wind erosion activity. Simultaneously, we conducted a simple investigation of wind conditions in the South Aral Sea, which was experiencing severe wind erosion, during the study period (23 June 2020 to 5 July 2020). Wind conditions based on GLDAS-2.1 dataset (https://developers.google.com/earth-engine/datasets/catalog/NASA_GLDAS_V021_NOAH_G025_T3H (accessed on 15 May 2024)) are illustrated in Figure 2 and Figure 3. Results from Figure 2 demonstrate that the daily average wind speeds in the Aral Sea remained relatively high over the two-week period, with 5 days having average wind speeds above 6 m/s, 4 days between 4 and 6 m/s, and only 3 days between 3 and 4 m/s. Results from Figure 3 indicate that there was no significant spatial variation in average wind speeds within the South Aral Sea during the two-week period, ranging from 4.8 m/s to 6 m/s, except for slightly lower wind speeds (below 5 m/s) along the entire southern coastal region of the Aral Sea. Wind speeds in the remaining areas were consistently above 5 m/s.

3. Method and Data

3.1. Soil Sampling and Volumetric Soil Moisture Data

We obtained soil data at the sampling point in this field survey, including soil photos and soil salinity data. The landscape photos can visually indicate whether the soil is vulnerable to wind erosion. Therefore, we can use these data to qualitatively assess the ITDDM model and the estimation results of SITD. The volumetric soil moisture (topsoil from 0 to 7 cm) data comes from the EAR5 dataset on the Google Earth Engine platform and is used to extract potential dust emission areas.

3.2. Vegetation Fraction Coverage Data

Vegetation fraction coverage (VFC) is related to the vegetation and soil’s backscattering weights under the assumption that only these two land types are in this pixel resolution unit [34]. We can use VFC to estimate the soil microwave backscattering coefficient (SMBC) and vegetation microwave backscattering coefficient (VMBC) related to the ITD weights of vegetation and soil. In this paper, we used the NDVI of Landsat 8 to compute VFC based on the Pixel dichotomy [35], and the spatial resolution of NDVI data was 30 m.

3.3. Microwave Backscattering Data

Sentinel-1 dataset C-band synthetic aperture radar (SAR) dataset is used to estimate SMBC and VMBC of a pixel resolution unit. The spatial resolution of this data is about 10 m. Usually, the normalized microwave backscattering coefficient (NMBC) is between 0 and 1. The NMBC and the microwave backscattering coefficient (MBC) described in dB have a relationship as follows [28]:

$${\sigma }_{dB}=10{l\mathrm{o}\mathrm{g}}_{10}{\sigma }_N,$$

(1)

where ${\sigma }_{dB}$ denotes the MBC in dB, and ${\sigma }_N$ is the NMBC. Due to the very sparse vegetation coverage in the arid and semi-arid areas, the volume scattering is very weak. Thus, we use the ITD of VV polarization to characterize wind erosion of topsoil. The ITD weights of vegetation and soil are related to the SMBC and VMBC in the pixel resolution unit. Therefore, the SMBC and VMBC in a pixel resolution unit are estimated firstly by the VFC and the total MBC. The backscattering images with VV polarization taken on 23 June 2020, and 5 July 2020 (https://code.earthengine.google.com/ (accessed on 15 May 2024)) were obtained, and this time interval is the same as that for calculating the VFC.

3.4. Soil Sampling Data

We used the Sentinel-1A satellite C-band single-look complex (SLC) SAR images to calculate the ITD of a pixel resolution unit. In this study, the satellite mode was right-looking, and the orbit cycle was 12 days. We acquired two SLC image pairs with a descending strip-map pattern on 23 June 2020 and 5 July 2020. The incident angle was about 34.23°, and the spatial resolution was 20 m after multi-look processing. Other information on two SLC image pairs is shown in

Table 1. Information and interferometry pattern of two SLC image pairs.

Footprint	Acquisition Date	Obit Number	Combination Mode	Time Baseline	Normal Baseline
North Aral Sea	23 June 2020	33,138	master	12 days	−33.064 m
	5 July 2020	33,313	slaver
South Aral Sea	23 June 2020	33,138	master	12 days	−35.154 m
	5 July 2020	33,313	slave

The Sentinel-1A data are from the Copernicus dataspace (https://dataspace.copernicus.eu/).

.

As is shown in Table 1, the SLC images acquired on 23 June 2020 were set as the master images, and the others were set as slave images. The absolute time baseline of these two SLC image pairs is 12 days, and the normal baseline is about −33.064 m and −33.154 m for the SLC image pairs of the study area, respectively. The relatively short time baseline setup mainly meets the assumption of identical backscattering levels for acquisitions 1 and 2 [28]. The short spatial baseline is much smaller than the critical baseline, indicating that the influence of the spatial baseline on ITD is negligible [26].

3.5. Method

3.5.1. Wind Erosion Intensity Modeling

Generally, the areas where wind erosion occurs within a pixel resolution unit are randomly distributed. Therefore, the degree of wind erosion of the 1D soil profile can help us analyze and define a pixel resolution unit’s degree of wind erosion. Figure 4 shows the deformation of the soil surface in the pixel resolution unit after wind erosion.

The ground surface will sink slightly and randomly after wind erosion for most arid bare lands, except for desert regions. Due to particles’ deposition or surface movement, the ground surface may slightly uplift after wind erosion in desert areas. Fortunately, there are few active deserts in the study area. The deformation of different positions in the pixel resolution unit can be regarded as a random signal $\delta \left(x,y\right)$ at position $\left(x,y\right)$. Since the root mean square can describe the intensity of the random signal, we can use the root mean square of the erosion depth at different locations within the pixel resolution unit to define WEI.

$$WEI=\sqrt{\frac{1}{S}\iint {\delta \left(x,y\right)}^{2}dxdy},$$

(2)

In order to simplify this process, we only consider the discrete case. Assuming that there are N differential elements in a pixel resolution unit, the wind erosion intensity of the pixel resolution unit can be simplified as

$$WEI=\sqrt{\frac{1}{Nds}{\sum }_{i=1}^N{\delta }_i^{2}ds}=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\delta }_i^2},$$

(3)

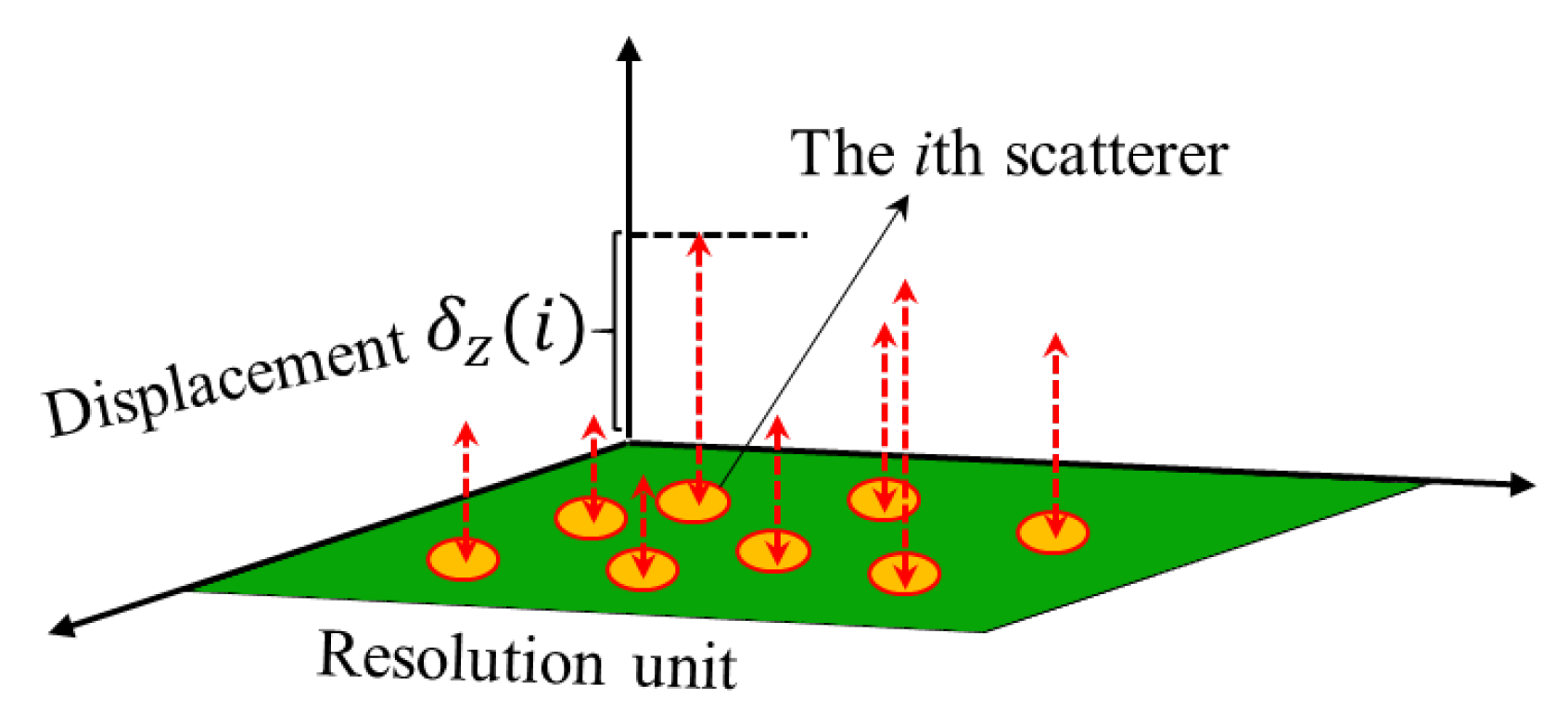
3.5.2. InSAR Temporal Decorrelation

Coherence is used to measure the similarity of the InSAR echoes and is often used to describe different degrees of terrain changes. The coherence between two complex echo signals ($s_1$ and $s_2$) is defined as their correlation coefficient $\gamma$.

$$\gamma =E\left\{s_1·s_2^{*}\right\}/\sqrt{E\left\{{\left|s_1\right|}^2\right\}·E\left\{{\left|s_2\right|}^2\right\}},$$

(4)

Decorrelation $\rho$, which is equal to $1-\gamma$, is usually caused by thermal decorrelation ${\rho }_{thermal}$, spatial decorrelation ${\rho }_{spatial}$, and temporal decorrelation ${\rho }_{temporal}$. Temporal decorrelation due to environmental changes over time can be described by the following formula [26]:

$${\rho }_{temporal}=\rho /{\rho }_{thermal}/{\rho }_{spatial},$$

(5)

3.5.3. The Relationship between InSAR Temporal Decorrelation and Wind Erosion Intensity

According to the microwave backscattering theory, the differential element’s random subsidence in the pixel resolution unit can be equivalent to the random displacement of the scatterers (or scattering differential bins) in a vertical direction (Figure 5).

Zebker derived the relationship between the root mean square (RMS) displacement of scatterers and ITD [26]:

$${\rho }_{temporal}=exp\left\{-\frac{1}{2}{\left(\frac{4\pi }{\lambda }\right)}^2\left({\delta }_y^2{sin}^2\theta +{\delta }_z^2{cos}^2\theta \right)\right\},$$

(6)

where ${\rho }_{temporal}$ is the ITD for scatterers within a pixel resolution unit, ${\delta }_y$ denotes the horizontal displacement of the scatterer, ${\delta }_z$ denotes the vertical displacement of the scatterer, and $\theta$ is the incident angle. Since wind erosion in a pixel resolution unit can be equivalent to the vertical displacement of the scatterers within the pixel resolution unit, Equation (6) can be simplified to the following:

$${\rho }_{temporal}=exp\left\{-\frac{1}{2}{\left(\frac{4\pi }{\lambda }\right)}^2{\delta }_z^2{cos}^2\theta \right\},$$

(7)

However, it must be noted that the vertical displacement of the scatterers may be positive or negative because of the existence of horizontal displacement of the scatterers or the deposition of the soil particles. In fact, except for the more mobile deserts, most of the bare land in the Aral Sea exhibited random subsidence rather than uplift under wind erosion. Furthermore, the ground uplift caused by the particles’ horizontal displacement and the particles’ deposition is so tiny that it can be ignored. We plotted the relationship between the ITD of the C-band and the wind erosion intensity when the incident angle was 34°, and the results are shown in Figure 6.

According to Figure 6 and Formula (7), ITD and WEI have a non-linear negative correlation, which coincides well with Wegmuller’s field survey [28]. However, in the bare land of the Aral Sea, a pixel resolution unit usually contains soil and vegetation. Therefore, we must decompose these contributions and estimate the SITD, which can be used to describe the wind erosion degree of soils.

3.5.4. InSAR Temporal Decorrelation Decomposition Model

Usually, there is sparse vegetation on the arid bare lands. According to Wegmuller, the ITD of a pixel resolution unit can be decomposed into the contributions of soil and vegetation when there is only soil and vegetation within it [28].

$$\mathsf{\gamma }=\frac{{\sigma }_v}{\sigma }{\gamma }_v+\frac{{\sigma }_s}{\sigma }{\gamma }_s,$$

(8)

${\sigma }_v$, ${\sigma }_s$, and $\mathsf{\sigma }$ are the VMBC, SMBC, and total MBC of this pixel resolution unit, respectively. ${\gamma }_s$, ${\gamma }_v$, and $\mathsf{\gamma }$ denote the SITD, vegetation ITD (VITD), and total ITD of this pixel resolution unit, respectively. However, before Formula (8) can be used to estimate the SITD, we must know the backscattering coefficient of soils and vegetation of a pixel resolution unit. Therefore, a backscattering contribution decomposition (MBCD) model within a pixel resolution unit proposed in our previous work is used to unmix the backscattering contributions of vegetation and soil and estimate the VMBC and SMBC within a pixel resolution unit [34].

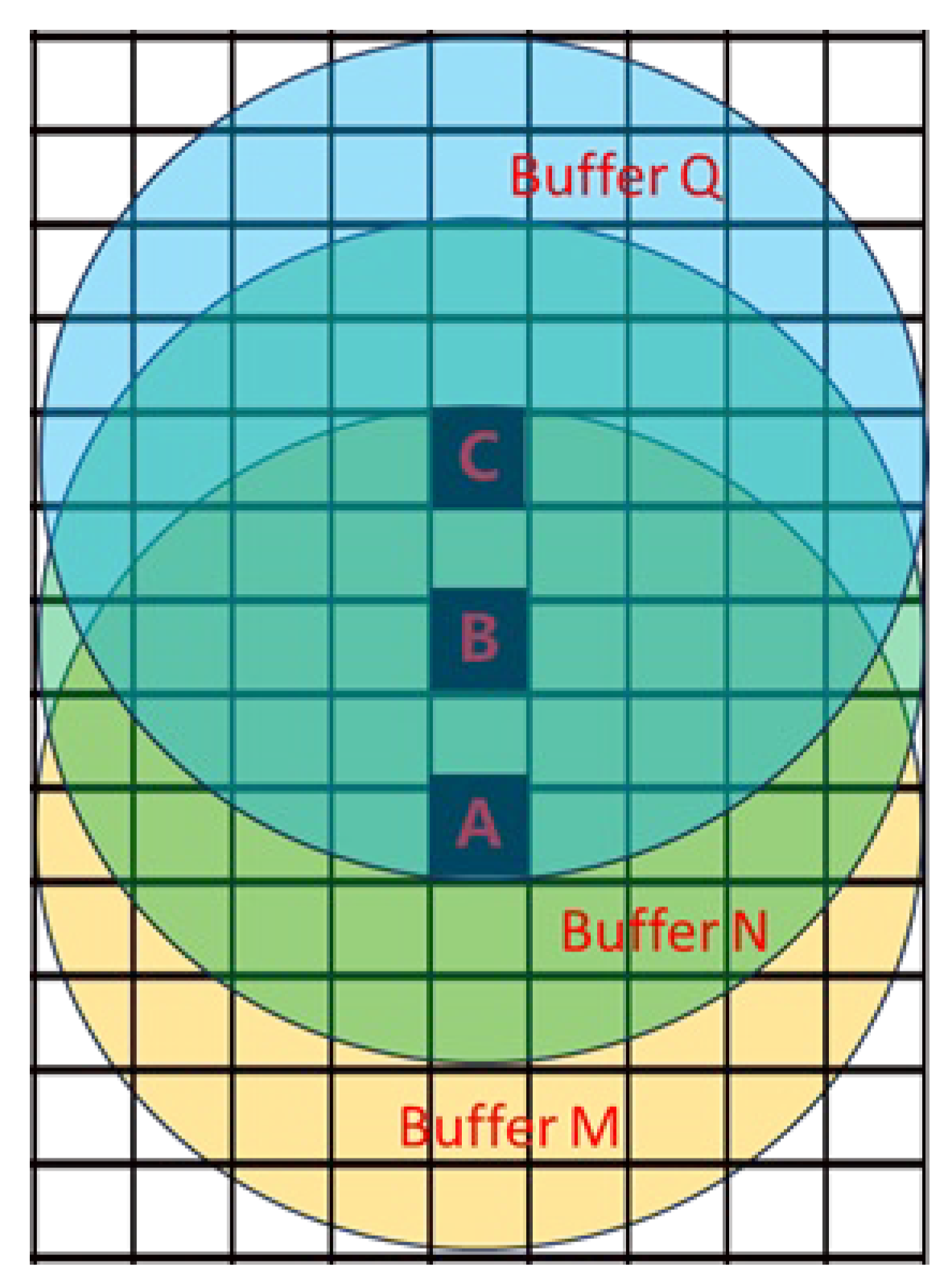
3.5.5. Backscattering Contribution Decomposition and Estimation within a Pixel Resolution Unit

In our previous work about the backscattering contribution decomposition within a pixel resolution unit, we reached an important conclusion: the SMBC, VMBC, and total MBC of a pixel resolution unit satisfy a simple linear relationship. This relationship can be expressed as follows [34]:

$${\sigma }_{veg}{f}_{veg}+{\sigma }_{soil}\left(1-f_{veg}\right)=\sigma ,$$

(9)

${\sigma }_{veg}$, ${\sigma }_{soil}$, and $\sigma$ are the VMBC, SMBC, and total MBC of a pixel resolution unit, respectively. $f_{veg}$ is the VFC of this pixel resolution unit. Our previous work also provided the estimation method of VMBC and SMBC, which will be used to estimate the SITD [34].

3.5.6. SITD Estimation Based on LSM-SVD Method

The continuity of the spatial distribution of soil and vegetation allows them to have nearly the same temporal decorrelation in adjacent pixel resolution units. Thus, the temporal decorrelation of a pixel resolution unit can be estimated by the sample points within the buffer of this pixel resolution unit. If n sample points around the pixel resolution unit (resolution P) were used to estimate the ITD of vegetation and soil of this pixel resolution unit, n linear equations can be written as follows:

$$\begin{gathered} w_v^1{\gamma }_v+w_s^1{\gamma }_s={\gamma }_1 \\ {w}_v^2{\gamma }_v+w_s^2{\gamma }_s={\gamma }_2 \\ ⋮ \\ {w}_v^i{\gamma }_v+w_s^i{\gamma }_s={\gamma }_i \\ ⋮ \\ {w}_v^n{\gamma }_v+w_s^n{\gamma }_s={\gamma }_n, \end{gathered}$$

(10)

where $w_v^i$ and $w_s^i$ are the ITD weights of vegetation and soil of the $ith$ sampling point, ${\gamma }_v$ and ${\gamma }_s$ denote VITD and SITD of the pixel resolution unit P, respectively, and ${\gamma }_i$ is the composite ITD of the $i\mathrm{t}\mathrm{h}$ sampling point. The system equations (Formula (10)) can also be written in the form of a matrix:

$$\left[\begin{array}{cc}\begin{array}{c}{w}_v^1\\ \begin{array}{c}{w}_v^2\\ ⋮\\ \begin{array}{c}{w}_v^i\\ \begin{array}{c}⋮\\ w_v^n\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}{w}_s^1\\ \begin{array}{c}{w}_s^2\\ \begin{array}{c}⋮\\ \begin{array}{c}{w}_s^i\\ \begin{array}{c}⋮\\ w_s^n\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\gamma }_v\\ {\gamma }_s\end{array}\right]=\left[\begin{array}{c}{\gamma }_1\\ \begin{array}{c}{\gamma }_2\\ ⋮\end{array}\\ \begin{array}{c}{\gamma }_i\\ ⋮\\ {\gamma }_n\end{array}\end{array}\right],$$

(11)

Let $\mathrm{w}$ be the ITD weight matrix, ${\mathsf{\gamma }}_{\mathrm{p}}$ be the InSAR temporal decorrelation decomposition matrix of the pixel resolution unit P, $\mathsf{\gamma }$ be the InSAR temporal decorrelation composite matrix, and make the following conventions:

$$\mathrm{w}=\left[\begin{array}{cc}\begin{array}{c}{w}_v^1\\ \begin{array}{c}{w}_v^2\\ ⋮\\ \begin{array}{c}{w}_v^i\\ \begin{array}{c}⋮\\ w_v^n\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}{w}_s^1\\ \begin{array}{c}{w}_s^2\\ \begin{array}{c}⋮\\ \begin{array}{c}{w}_s^i\\ \begin{array}{c}⋮\\ w_s^n\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right], {\mathsf{\gamma }}_{\mathrm{p}}=\left[\begin{array}{c}{\gamma }_v\\ {\gamma }_s\end{array}\right],\mathsf{\gamma }=\left[\begin{array}{c}{\gamma }_1\\ \begin{array}{c}{\gamma }_2\\ ⋮\end{array}\\ \begin{array}{c}{\gamma }_i\\ ⋮\\ {\gamma }_n\end{array}\end{array}\right],$$

(12)

Then, Formula (10) can be simplified as follows:

$$\mathrm{w}{\mathsf{\gamma }}_{\mathrm{p}}=\mathsf{\gamma },$$

(13)

Then, the least-square estimation of ${\mathsf{\gamma }}_{\mathrm{p}}$ can be expressed as follows:

$$\widehat{{\mathsf{\gamma }}_{\mathrm{p}}}={\left({\mathrm{w}}^{\mathrm{T}}\mathrm{w}\right)}^{-1}{\mathrm{w}}^{\mathrm{T}}\mathsf{\gamma },$$

(14)

Considering the huge computational load, we can use the SVD method to estimate SITD. Assume that $\mathrm{w}$ can be decomposed as follows:

$$\mathrm{w}={\mathrm{M}\mathrm{S}\mathrm{E}}^{\mathrm{T}},$$

(15)

The SVD-based least-square estimation of ${\mathsf{\gamma }}_{\mathbf{p}}$ can be expressed as follows:

$$\widehat{{\mathsf{\gamma }}_{\mathrm{p}}}={\mathrm{E}}_{2\times r}{\left({\mathrm{S}}_{r\times r}\right)}^{-1}{\left({\mathrm{M}}_{n\times r}\right)}^{\mathrm{T}}{\mathsf{\gamma }}_{n\times 1},$$

(16)

When the first singular value of $\mathrm{w}$ is greater than or equal to 90% of the sum of all its singular values, the value of $r$ is 1, and $\mathbf{S}$ has the following form:

$$\mathrm{S}={ϵ}_1,$$

(17)

where ${ϵ}_1$ is the first singular value of $\mathbf{w}$. Otherwise, S has the following form:

$$\mathrm{S}=\left[\begin{array}{cc}{ϵ}_1& 0\\ 0& {ϵ}_2\end{array}\right],$$

(18)

where ${ϵ}_2$ is the second singular value of $\mathbf{w}$.

4. Results

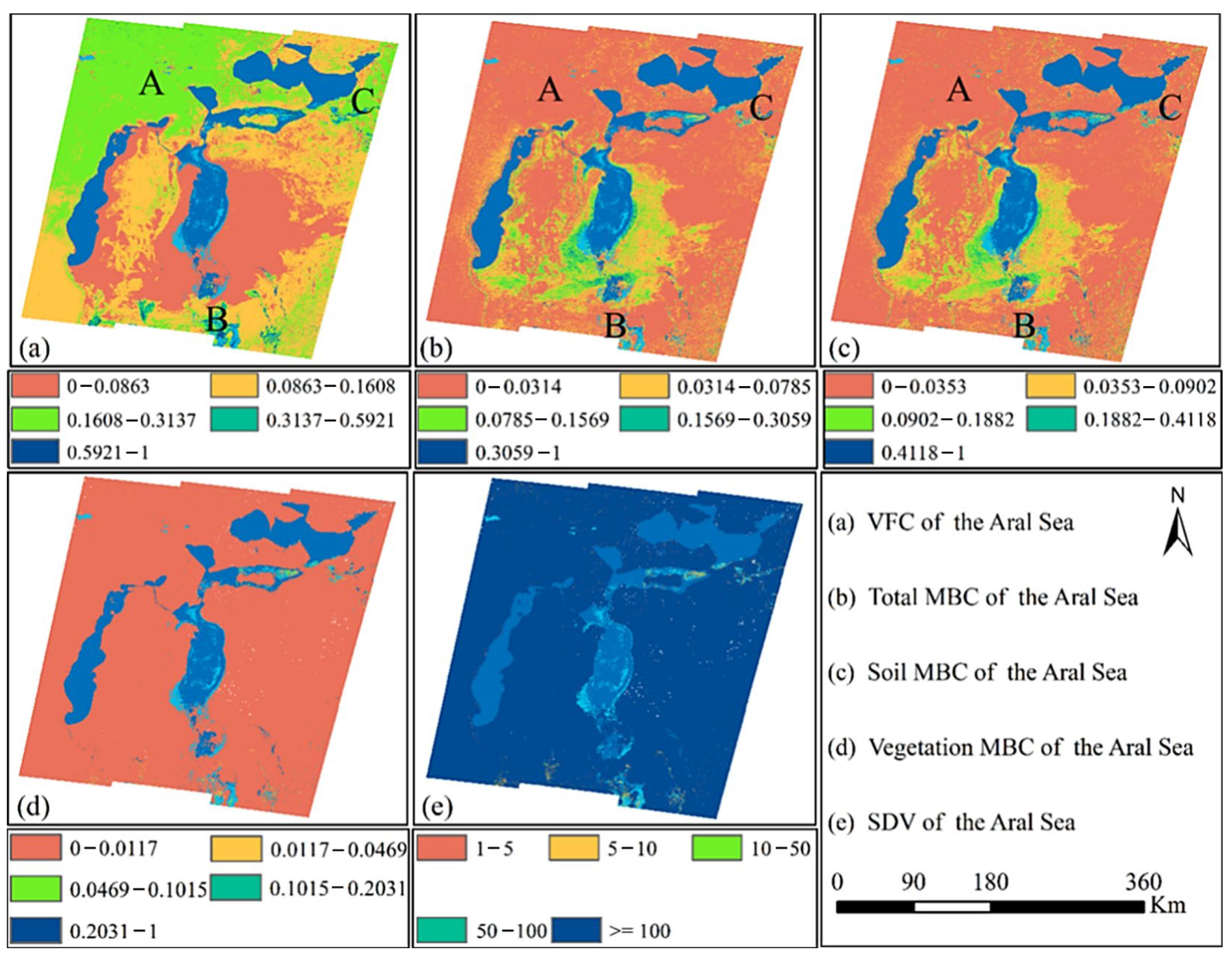
4.1. VFC and MBC of the Study Area

VFC with a resolution of 30 m calculated by Landsat 8 NDVI and the Sentinel-1A C-band microwave backscattering coefficient of VV polarization with a resolution of 10 m from the Google Earth Engine platform was used to estimate the VMBC and SMBC. To evaluate the vegetation’s influence on SITD estimation, we also calculated the SMBC-to-VMBC (SDV) ratio. Suppose the total ITD of the pixel resolution unit replaces the SITD of a pixel resolution unit. In that case, the error mainly depends on the VMBC and SMBC in the pixel resolution unit. The VFC, total MBC, SMBC, VMBC, and SDV are shown in Figure 7. As shown in Figure 7a, vegetation coverage in the Aral Sea and its surrounding areas is very sparse. The vegetation coverage of most of the study areas is between 0 and 0.1608. In comparison, vegetation coverage is relatively high in the northwest and northeast (VFC ranges from 0.1608 to 0.3137) and the southern part of the study area (VFC is between 0.3137 and 1).

It can be seen from Figure 7b that, except for the area around the east branch of the South Aral Sea, the backscattering coefficients in other regions are relatively low. Figure 7c shows that the soil’s backscattering coefficient is very close to the total backscattering coefficient of the pixel resolution unit. However, there are obvious errors in estimating soil backscattering coefficients in the northwest and northeast of the study area, most probably due to the uniform spatial distribution of vegetation [34]. In addition, the results of backscattering coefficient estimation have been fully verified in our previous work, so this paper does not refer to the verification of backscattering coefficient estimation results [34]. Furthermore, the areas with incorrect backscattering coefficient estimation results often have relatively high soil water content or vegetation coverage, so we can remove these places from the study area, which will be discussed in Section 4.2. Figure 7e shows that the backscattering coefficient of soil is much higher for most of the study area than that of vegetation. According to Formula (9) and SDV shown in Figure 7, the influence of vegetation on the SITD in the pixel resolution unit may be negligible. However, when the SMBC in a pixel resolution unit is close to the VMBC (such as in severely desertified areas), the ITD weights of vegetation and soil are almost the same. In this case, the impact of vegetation on the SITD is not negligible. The process of MBC and ITD estimation is badly time-consuming. Extracting the potential wind erosion area can significantly reduce the target area and effectively reduce the amount of calculation. Numerous studies have shown that wind erosion is almost impossible in these areas when the soil moisture exceeds 10%, or VFC is higher than 40% [36,37,38,39,40,41,42]. When vegetation coverage exceeds 40%, the volumetric soil moisture is usually higher than 10%. Our survey results also show that when vegetation coverage exceeds 40%, the soil volumetric water content is usually higher than 10% [34]. Therefore, these areas can be removed from the study area to effectively reduce the calculation amount. In the following section, we obtained soil moisture data. Soil moisture and vegetation coverage data were used to extract potential wind erosion areas.

4.2. Potential Wind Erosion Areas

We used GIS 10.2 software to label the areas with vegetation coverage higher than 0.4 or volumetric soil moisture higher than 0.1 in the study area. Then, we obtained the potential wind erosion area, and the result is shown in Figure 8. It should be noted that since the volumetric soil moisture (VSM) of only one pixel in area B exceeds 10%, we have ignored this area. Figure 8 shows that except for areas B, E, and F, the rest of the lakebed is vulnerable to wind erosion.

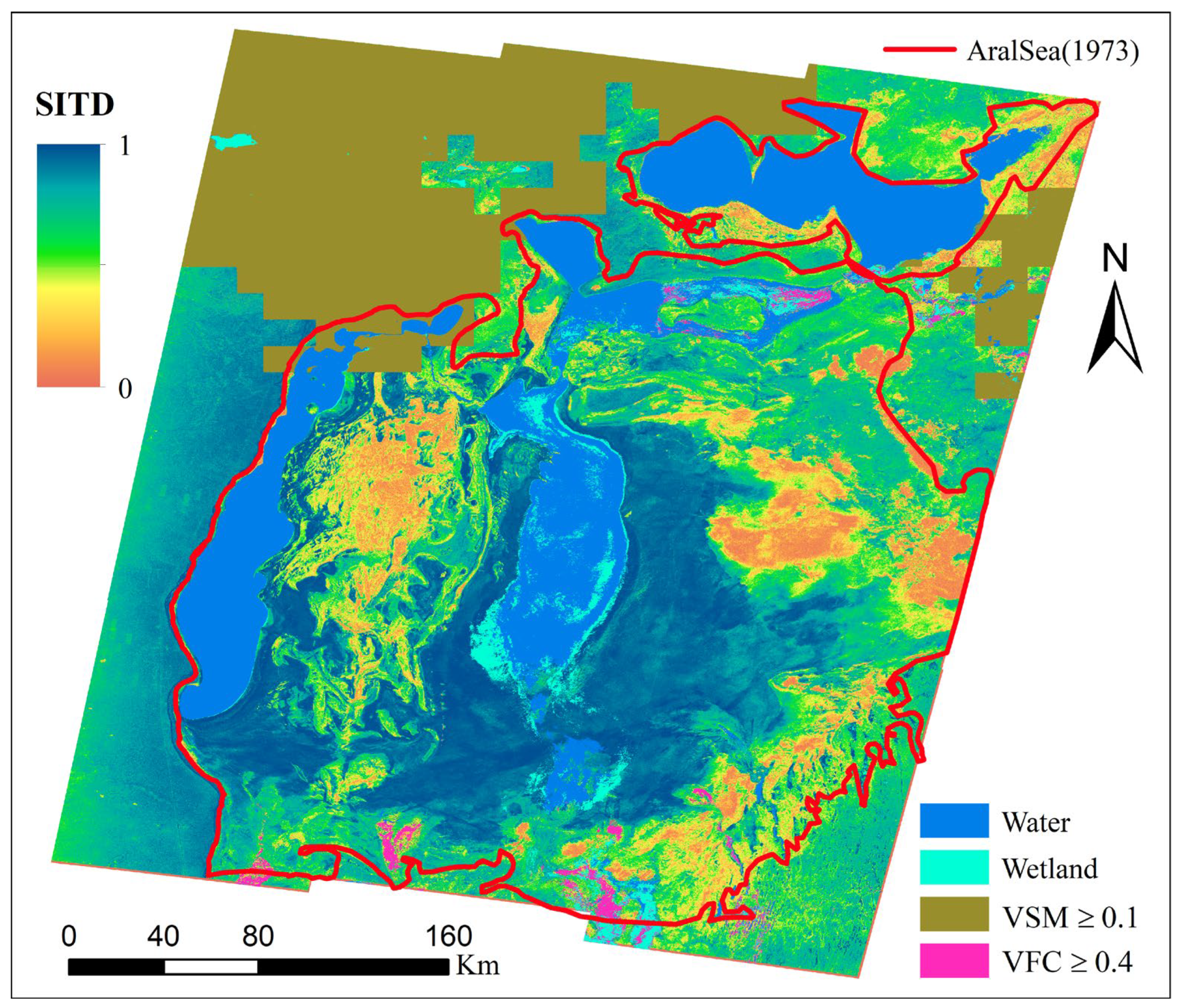
4.3. InSAR Temporal Decorrelation of Soil

We calculated the SITD of all regions except regions A, B, D, E, and F based on Equation (16). According to Equation (8), estimating the SMBC and VMBC is necessary prior to calculating the SITD. However, the estimation of SMBC and VMBC requires constraining the VFC differences between pixels within the buffer zone. This constraint is necessary because such differences are likely to introduce significant errors in the estimation of the SMBC and VMBC, subsequently affecting the estimation of the SITD. Significant changes in vegetation cover are likely to result in notable variations in soil roughness, soil moisture, and soil salinity (which affect backscattering coefficients). This, in turn, leads to the violation of the assumption that “buffer zone pixels have the same backscattering coefficients for soil and vegetation.” Consequently, we are unable to utilize the buffer zone pixels to estimate the backscattering coefficients of soil and vegetation for the target point. Furthermore, when the VFC difference between any two pixels within the buffer zone becomes too small, the computation process encounters singular matrices, resulting in significant computational errors. The upper bound for the VFC difference is derived from our field observations in the Aral Sea region. The upper bound for the VFC difference is determined based on our field observations in the Aral Sea region. By observing the variations in soil surface roughness (which affects soil backscattering coefficients) and soil surface moisture (which also affects soil backscattering coefficients) in relation to changes in vegetation cover, we set the upper bound for VFC at 0.2. The lower bound for the VFC difference is derived from practical computations of soil and vegetation backscattering coefficients. We have determined that when the VFC difference is set above 0.05, there are no further instances of matrix singularity issues during the computation process. Therefore, we set the lower bound for VFC at 0.05. The calculation process is still quite time-consuming. Therefore, we resampled the ITD weights of soil and vegetation and the total ITD to 50 m to further reduce the amount of calculation. The estimated result of the SITD is shown in Figure 9. Figure 9 shows that the areas with severe temporal decorrelation are mainly distributed in the bare lands of the middle, northeast, and southeast of the South Aral Sea. In addition, the coastal areas of the North Aral Sea are also areas with severe soil InSAR temporal decorrelation. Beyond the boundaries of the water body of the Aral Sea in 1973, the soil InSAR temporal decorrelation in most areas is very slight. This significant contrast indicates that the dry lakebed is highly susceptible to wind erosion.

Quantitative validation of the SITD estimation results is extremely challenging because it is nearly impossible to accurately measure the wind erosion intensity of a single pixel of soil during the monitoring period. However, fortunately, we captured landscape photographs of the sampling points during our investigation of desertification in the Aral Sea. These landscape photos provide a means to assess the susceptibility of the soil to wind erosion. Regions that are prone to wind erosion experience more severe erosion during the monitoring period, and, therefore, they should exhibit lower SITD values. Conversely, areas that are less susceptible to wind erosion, such as regions with higher soil moisture content, sparse vegetation cover, or a significant presence of larger particles on the ground, undergo minimal erosion during the monitoring period. Consequently, these areas should have higher SITD values. Based on these observations, we can qualitatively validate the model. Therefore, we magnified the SITD values corresponding to the sampling points in Figure 9 to the pixel scale and combined them with the corresponding landscape photographs, resulting in Figure 10.

The landscape photos in Figure 10 clearly show the soil’s actual condition near the sampling points, which can be used to judge the degree of soil susceptibility to wind erosion visually. The SITD will be used to describe the spatial distribution of wind erosion of different degrees. As in the description in Section 3.3, because the waters and wetland cannot be the potential place where wind erosion will happen, the SITD was not estimated for these two land types. In the next section, the SITD will be used to describe the WEI of the study area.

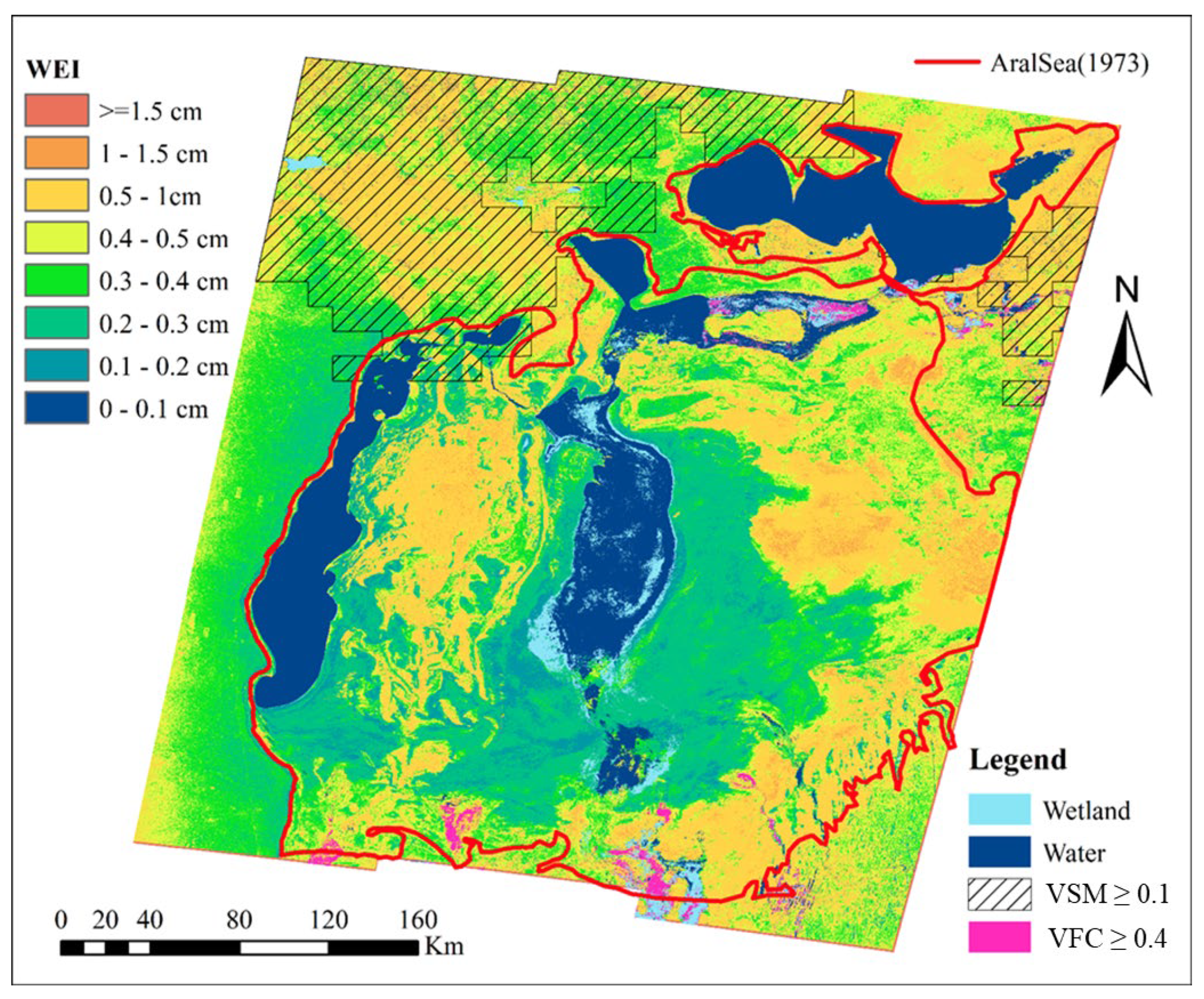
4.4. Wind Erosion at the Dry Bottom of the Aral Sea

4.4.1. The Calculating Process and Results of Wind Erosion Intensity

If we carry out an inverse transform according to Equation (7), then we can convert the SITD to WEI. Furthermore, we divided WEI into eight levels, and the results are shown in Figure 11. Figure 11 shows that the wind erosion in the study area mainly occurs on the lakebed. These things considered, our previous field survey showed that the dry lakebed is rich in salt and toxic substances [34]. Therefore, the fine particles produced in the wind erosion process should also be rich in these materials.

Salt storms that carry fine particles rich in salt and toxic substances will badly threaten the surrounding ecosystems and human health. Therefore, we counted the wind erosion area of the dry lakebed. We used GIS 10.2 software to remove areas with VFC greater than or equal to 0.4, areas with VSM greater than or equal to 0.1, wetlands, and water bodies from the Aral Sea water surface in 1973. Then, we used this vector to extract the WEI map of the potential wind erosion area on the dry bottom of the Aral Sea. At last, we performed simple statistics on the wind erosion intensity, and the results are shown in

Table 2. Sample statistics of the WEI at the dry bottom of the Aral Sea.

Interval Number	SITD Interval	SITD Interval	Percent (%)
1	$0.9832 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le$ 1.0000	$0.0 \le WEI \le 0.1$	0.1736
2	$0.9346 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.9832$	$0.1 \le WEI \le 0.2$	3.7238
3	$0.8589 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.9346$	$0.2 \le WEI \le 0.3$	27.2261
4	$0.7631 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.8589$	$0.3 \le WEI \le 0.4$	15.4784
5	$0.6554 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.7631$	$0.4 \le WEI \le 0.5$	15.3211
6	$0.1846 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.6554$	$0.5 \le WEI \le 1.0$	35.5420
7	$0.0223 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.1846$	$1.0 \le WEI \le 1.5$	2.2560
8	$0.0000 \le \mathrm{S}\mathrm{I}\mathrm{T}\mathrm{D} \le 0.0223$	$WEI \ge 1.5$	0.2790
total			100

.

4.4.2. Overview of Wind Erosion in the Aral Sea

We conducted a simple statistic of different degrees of WEI according to Figure 9, and the results showed that the dry lakebed is suffering from different degrees of wind erosion. The area with wind erosion intensity greater than 1.5 cm accounts for 0.2790% of the lakebed, which is about 176 km². The area with wind erosion intensity ranging from 1 to 1.5 cm accounts for 2.2560%, approximately 1426 km². The site with a wind erosion intensity of 0.5 to 1 cm accounts for 35.5420%, approximately 22,471 km². The area with a wind erosion intensity of 0.4 to 0.5 cm accounts for 15.3211%, approximately 9687 km². The site with wind erosion intensity between 0.3 and 0.4 cm accounts for 15.4784%, about 9786 km². The area with a wind erosion intensity of 0.2 to 0.3 cm accounts for 27.2261%, approximately 17,214 km². The site with wind erosion intensity ranging from 0.1 to 0.2 cm accounts for 3.723%, about 2354 km². The area with wind erosion intensity between 0 and 0.1 cm occupies 0.1736%, approximately 110 km².

4.4.3. Spatial Distribution of Wind Erosion

According to the WEI of the study area, the severe wind erosion areas (WEI ≥ 1 cm) are mainly distributed in bare lands of the middle, northeast, and southeast of the South Aral Sea. The spatial distribution of the moderate wind erosion area (0.3 cm ≤ WEI ≤ 1 cm) is the same as that of the severe wind erosion area. The moderate and severe wind erosion areas coincide well with the area of sand and dust activities, and these areas can be treated as the focus areas for people to intervene in sand and dust activities [43]. The severe wind erosion areas within the dry lakebed are most probably where salt dust storms occur.

5. Discussion

Due to the harsh natural environmental conditions of the Aral Sea, it is a challenge to verify the accuracy of dust activity intensity described by soil temporal decorrelation through the measurement of dust activity intensity. The sampling data for validation is from a joint desertification survey referring to the Aral Sea in 2018 by China and Uzbekistan. However, the survey was not designed specifically for this research, so we can only provide limited validation by analyzing the partial sampling data. Nevertheless, through rigorous theoretical derivation, few sampling points, and the supporting literature, we can still prove the accuracy of the spatiotemporal distribution results of dust activity intensity described in this paper. The accuracy of the spatiotemporal distribution results of dust activity intensity in the Aral Sea depends on three aspects:

• Can soil temporal decorrelation accurately describe dust activity intensity?
• Whether soil temporal decorrelation only depends on the mathematical expectation of phase random variation within the pixel resolution unit and whether other factors, such as variation in soil dielectric constant and soil roughness, will affect soil temporal decorrelation.
• Are the estimation results of soil temporal decorrelation accurate?

For the first question, we have provided a comprehensive argumentation through the proposal of dust activity intensity in Section 3.5.2 and the derivation of the relationship between dust activity intensity and soil temporal decorrelation in Section 3.5.3, which demonstrates the feasibility of using soil temporal decorrelation to describe dust activity intensity. Next, we will discuss the impact of the other two factors.

5.1. The Impact of Non-Phase Factors on Soil Temporal Decorrelation

According to the definition of soil temporal decorrelation, it mainly depends on variations in the backscattering coefficient and the phase during the interferometric period. Significant changes in soil roughness, moisture content, and salinity can all lead to notable variations in backscattering levels. Through an investigation of precipitation during the interferometric period, no significant rainfall was observed in these regions within 1–2 days before the second imaging (in June and July, the temperature in the Aral Sea is high, and any small amount of rainfall occurring a few days before the second imaging would quickly evaporate). This survey indicates that the soil moisture content in most areas is unlikely to undergo significant changes, thus not significantly influencing the backscattering coefficient. The soil salinity of the Aral Sea primarily comes from the evaporated seawater, and after the seawater dries up, the salt deposits in the soil at the bottom of the dried-up lake. Therefore, soil salinity is unlikely to undergo significant changes over a relatively short time interval (12 days), and thus, it cannot cause drastic variations in the backscattering coefficient. The spatial continuity of soil types within the pixel resolution unit and similar wind conditions within the unit ensure slight variation in erosion levels among different regions within the unit. Consequently, the surface roughness variation is relatively minor. Therefore, the soil temporal decorrelation of a pixel resolution unit primarily depends on the mathematical expectation of phase random variations at different locations within this pixel resolution unit, representing dust activity intensity, and these phase variations are mainly caused by wind erosion.

5.2. The Results of SITD Estimation Assessment

The accuracy of soil temporal decorrelation estimation primarily depends on the assumptions made during decomposition and estimation. According to Wegmuller’s research, two assumptions regarding the soil temporal decorrelation decomposition model are often valid for bare soil and sparse low-vegetation regions in arid and semi-arid areas. The estimation was based on the assumption that “spatial adjacent pixel resolution units have the same soil and vegetation temporal decorrelation.” Soil and vegetation’s temporal decorrelation primarily depend on all scatterers’ root mean square displacement within a pixel resolution unit. Spatial adjacent pixel resolution units have similar vegetation types and structures, soil types and structures, and highly similar wind conditions. Therefore, the root mean square of soil random erosion of a pixel resolution unit is almost the same as that of an adjacent pixel resolution unit. Similarly, a pixel resolution unit’s vegetation temporal decorrelation is nearly the same as that of an adjoining pixel resolution unit. Hence, the assumption that a pixel resolution unit’s soil or vegetation temporal decorrelation is almost the same as that of a spatial adjacent pixel resolution unit is reasonable.

The differences in the backscattering coefficients of soil and vegetation among adjacent pixel resolution units are the prerequisite for estimating the soil and vegetation temporal decorrelation. Because of the slight differences in soil dielectric constant (due to spatial variations in soil moisture and salinity), soil roughness (due to the spatial difference in wind erosion depth within pixel resolution units), vegetation dielectric constant (due to spatial variations in vegetation moisture content, vegetation type, vegetation density, health, and condition), and vegetation roughness (due to the spatial distribution variations in leaf structure, branching patterns, vegetation canopy height and density, vegetation growth stage, and environmental factors.), the backscattering coefficients of soil and vegetation in adjacent pixel resolution units often exhibit differences. The statement seems to contradict our previous assumption made during the estimation of the VMBC and SMBC within a pixel, where adjacent pixels are assumed to have the same VMBC and SMBC. However, it is commonly observed that the estimated results for the VMBC and SMBC of adjacent pixels are usually different. In the following, we will illustrate this issue by considering the process of VMBC and SMBC estimation, as shown in Figure 12.

As shown in Figure 12, let us assume that buffer M, consisting of K pixels, is used to estimate the SMBC and VMBC at pixel A. Within these K pixels, the areas of soil and vegetation within each pixel are different, but all pixels have the same SMBC and VMBC. Furthermore, we assume that the backscattering coefficient for soil is denoted as ${\sigma }_s$, the backscattering coefficient for vegetation is denoted as ${\sigma }_v$, the area of soil within the ith pixel is $s_s^i$, the area of vegetation is $s_v^i$, and the total area of soil and vegetation is $s_i$. The soil- and vegetation-weighted average backscattering coefficient is denoted as ${\sigma }_i$ (Equation (9)). Based on the principles of energy conservation and the definition of radar backscattering coefficients, we can derive the following relationship ($p_t$ denotes the radar’s transmit power):

$${\sigma }_s{p}_t{\sum }_{i=1}^K{s}_s^i+{\sigma }_v{p}_t{\sum }_{i=1}^K{s}_v^i={\sum }_{i=1}^K{\sigma }_i{p}_t{s}_i,$$

(19)

Therefore, ${\sigma }_s$ can be regarded as the average scattering power from soil within the buffer, ${\sigma }_v$ can be regarded as the average scattering power from vegetation within the buffer, $\sum _{i=1}^K{s}_s^i$ can be interpreted as the scattering area of soil, and $\sum _{i=1}^K{s}_v^i$ can be interpreted as the scattering area of vegetation. Therefore, the left-hand side of the equation represents the total energy scattered within the entire buffer. Additionally, ${\sigma }_i$ can be regarded as the average scattering power from pixel i, so the right-hand side of the equation represents the sum of the scattered energy from each pixel within the buffer. Thus, the left-hand side and the right-hand side should be equal, which is consistent with the principle of energy conservation. Therefore, the estimated SMBC for pixel A is actually the average scattering power from all the soil within the buffer, while the estimated VMBC for pixel A is the average scattering power from all the vegetation within the buffer. Theoretically, this represents the optimal estimation of the SMBC and VMBC for pixel A. It is evident that the buffer N used for estimating the SMBC and VMBC for pixel B is different from buffer M. Therefore, although we assume that the SMBC and VMBC are the same for the pixels within the buffer in the estimation of the backscattering coefficients, their optimal estimations are typically different.

As described in Section 4.3, we use the SITD maps (SITDMs) and the corresponding landscape photos to verify the estimation results of the SITD. As is shown in landscape photos of L5, L6, and L15, some parts of arid soil are covered by relatively dense vegetation ($\mathrm{V}\mathrm{F}\mathrm{C}\ge 0$.4), while some are covered by very sparse vegetation ($\mathrm{V}\mathrm{F}\mathrm{C}\le 0$.1). These things considered, these landscape photos also showed that the soil is relatively loose here. According to the study by Bagnold, the ground surface wind speed will significantly decrease when vegetation exists, and the degree of wind erosion will also decline [4]. So, the wind erosion of soils around L5, L6, and L15 with little vegetation coverage is severe but is relatively slight for soils around L5, L6, and L15 with relatively dense vegetation coverage, and the wind erosion of soils shown in the SITDMs coincides well with the actual soil property shown in the corresponding landscape photos. Although there is little vegetation at site L7, the soil was very stable according to the ITDM of L7. Precipitation around L7 between 22 June 2020 and 5 July 2020 is a possible cause of the stable status of soils. (The precipitation data from the NASA_GPM_L3_IMERG_V06 dataset, sourced from the Google Earth Engine (GEE) platform, reveals the occurrence of a small amount of precipitation during this period. Specifically, on June 25th, the precipitation exceeded 2 mm.) The relatively stable status of L8, L9, and L11 shown in their corresponding SITDMs is most probably the result of dense vegetation coverage shown in their corresponding landscape photos. The relatively slight wind erosion of L10 (SITDM of L10) may be due to the soil’s high-water content, which is most probably the result of the short distance between L10 and water. As shown in the landscape photos of site L12, the desertification trend is severe. However, the SITDM of L12 indicates the soil here is very stable, and the relatively stable status of the soil is most probably due to the rain between 23 June 2020 and 5 July 2020, which can reduce wind erosion significantly [33]. In Figure 10, the soil property of L13 is just the same as that of L12, and the corresponding SITDM indicates the wind erosion here is very severe, so the actual soil property shown in the landscape photo is also in good agreement with the wind erosion degree shown in the corresponding SITDM. The landscape photos of L14 and U7 show that there is little vegetation in these places, but these places are rich in relatively large stones. The large stones are hard to move by wind; meanwhile, they can reduce the wind speed on the ground surface, which makes these places remarkably stable. For L16, as is shown in the landscape photos of L16, there are many artificial buildings and roads here, the SITD and backscattering coefficient of which are much higher than those of vegetation [32]. Therefore, the SITD should be very high for the pixel resolution unit with buildings in it according to Formula (9). The high SITD of L16, as shown in its SITDM, coincides nicely with the soil property shown in the landscape photo of L16. Large areas of bare soil were found around U5 and U6, and there are few large stones here, so U5 and U6 are very vulnerable to soil erosion. The analysis above is consistent with the severity of wind erosion shown in the SITDMs of U5 and U6. In conclusion, the SITDMs, except for some influenced by precipitation, are all consistent with the actual soil property shown in the corresponding landscape photos, and this result indicates that the SITD can be used to describe the severity of wind erosion.

Based on the aerosol data derived from the MODIS/061/MCD19A2_GRANULES dataset, it is observed that wind erosion is primarily concentrated in the bare land between the two branches of the South Aral Sea and along the eastern coast of the South Aral Sea (Figure 13). These areas spatially coincide well with the results of this study.

These things considered, the aerosol optical thickness in the Aral Sea (from 23 June 2020 to 5 July 2020) also indicates that the northeastern and southeastern parts of the South Aral Sea are the right places where dust storms often occur [43]. Although sandstorm events also happened in the bare land between the two branches of the South Aral Sea, the frequency is much lower than that of the northeast and southeast of the South Aral Sea. Therefore, the locations of dust emission identified in this study, except for the bare land between the two branches of the South Aral Sea, are consistent with the investigation results. A plausible explanation is that desertification had already occurred in the bare land between the two branches of the South Aral Sea in 2008 or even before, but the desertification was mild. After about 12 years of desertification, this region’s desertification became severe.

Furthermore, the dust activity intensity of this region described in this paper is confirmed by the landscape photographs of the three sampling points falling in this area (Figure 14). Therefore, it is highly likely that the bare land between the two branches of the South Aral Sea has developed into a new outbreak area for salt and dust storms.

6. Conclusions

For areas where desertification is not severe, since the backscattering coefficient of rough topsoil is much higher than that of vegetation, the ITD weight of the soil is far higher than that of the vegetation. Therefore, in these areas, the soil ITD can be approximately replaced by the total ITD of the pixel resolution unit. However, for areas with desertification, the backscattering coefficient of smooth topsoil is very close to the backscattering coefficient of vegetation, so the ITD weights of soil and vegetation should also be very close to each other. In this case, the influence of vegetation on the SITD cannot be ignored. The consistency between the SITDM of the sampling points and the actual soil property shown in the corresponding landscape photos indicates that the ITDDM and the corresponding estimation method can accurately estimate the SITD in the pixel resolution unit. The wind erosion areas are mainly distributed in bare lands of the middle, northeast, and southeast of the South Aral Sea. The severe wind erosion areas within the range of the dry lakebed are the most possible places where salt dust storms occur.

InSAR technology can provide technical support for human intervention in salt dust storms in the Aral Sea. The desiccation and desertification of the Aral Sea provide a substantial material foundation for the occurrence of salt dust storms, which are closely associated with surface wind erosion. By InSAR technology, it is possible to promptly and accurately locate areas with severe wind erosion. This, in turn, offers valuable information support for subsequent large-scale vegetation planting endeavors aimed at mitigating wind erosion.