Long-Time Coherent Integration for the Spatial-Based Bistatic Radar Based on Dual-Scale Decomposition and Conditioned CPF
Abstract
1. Introduction
- It inherits the advantage of the DS decomposition framework in that the RM can be fully corrected using the GIFT procedure on the coarse motion parameter space.
- It inherits the advantage of CPF such that joint three-dimensional searching is not required, but instead independent one-dimensional searching takes place.
- The proposed CCPF is designed in a much smaller space, i.e., the fine motion parameter space, conditioned on each coarse motion parameter. With this structure, multiple targets are grouped naturally according to coarse motion parameters, leading to an advantage of suppressing false peaks caused by cross-terms of the CPF.
2. Background
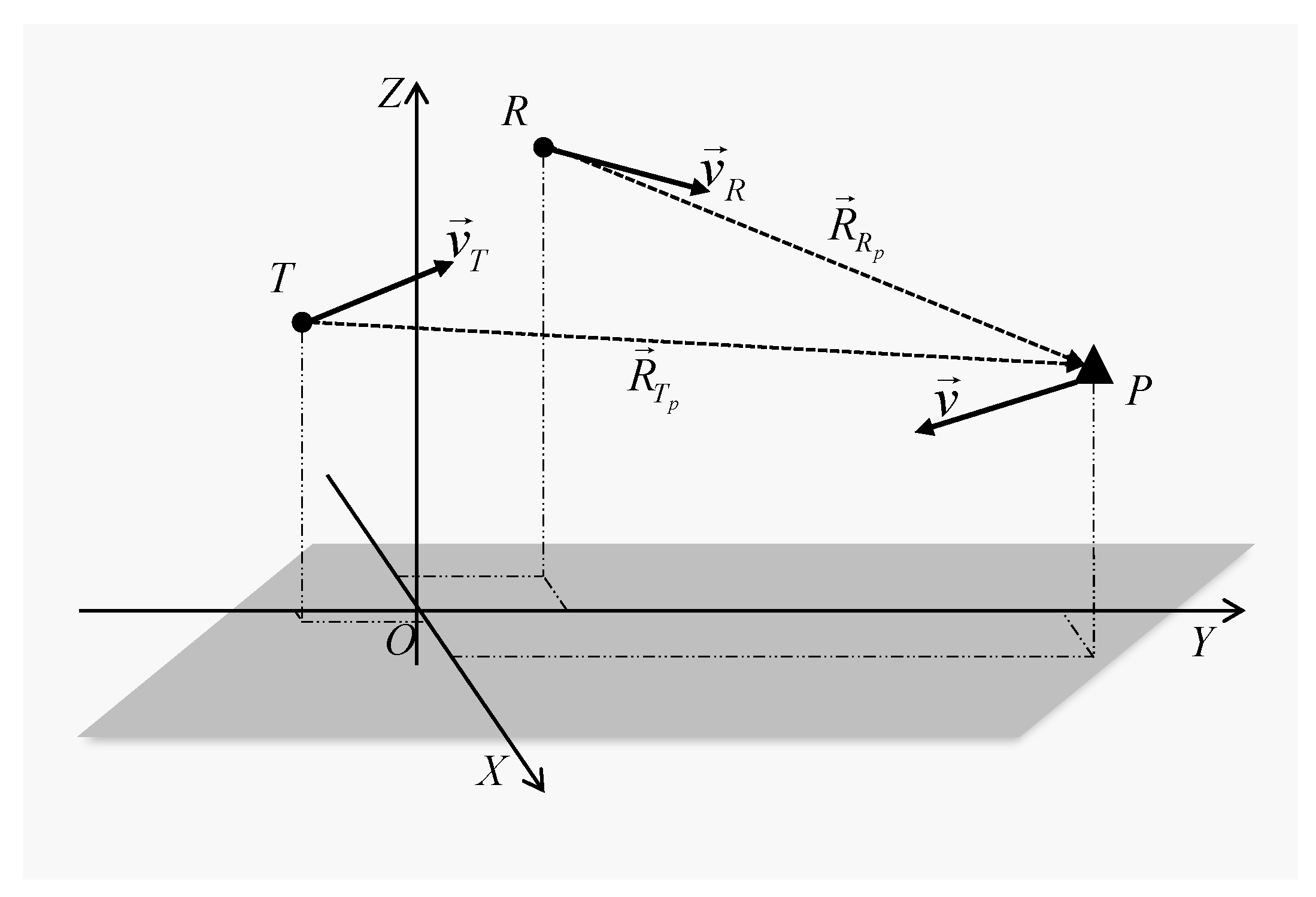
2.1. Signal Model
2.2. RM and DFM Effects
3. Dual-Scale GIFT-CCPF Detector
3.1. Dual-Scale Decomposition of Motion Parameters for the Bistatics Radar
3.2. Dual-Scale GRFT Detector for the Bistatics Radar
3.3. Conditional CPF
3.4. The Single-Target Case
3.5. The Multi-Target Case
3.6. Summary
4. Implementation Issues
4.1. Pseudo-Code of the Proposed DS-GIFT-CCPF Detector
| Algorithm 1: CCPF |
 |
| Algorithm 2: DS-GIFT-CCPF |
 |
4.2. Computational Complexity Analysis
5. Performance Assessment
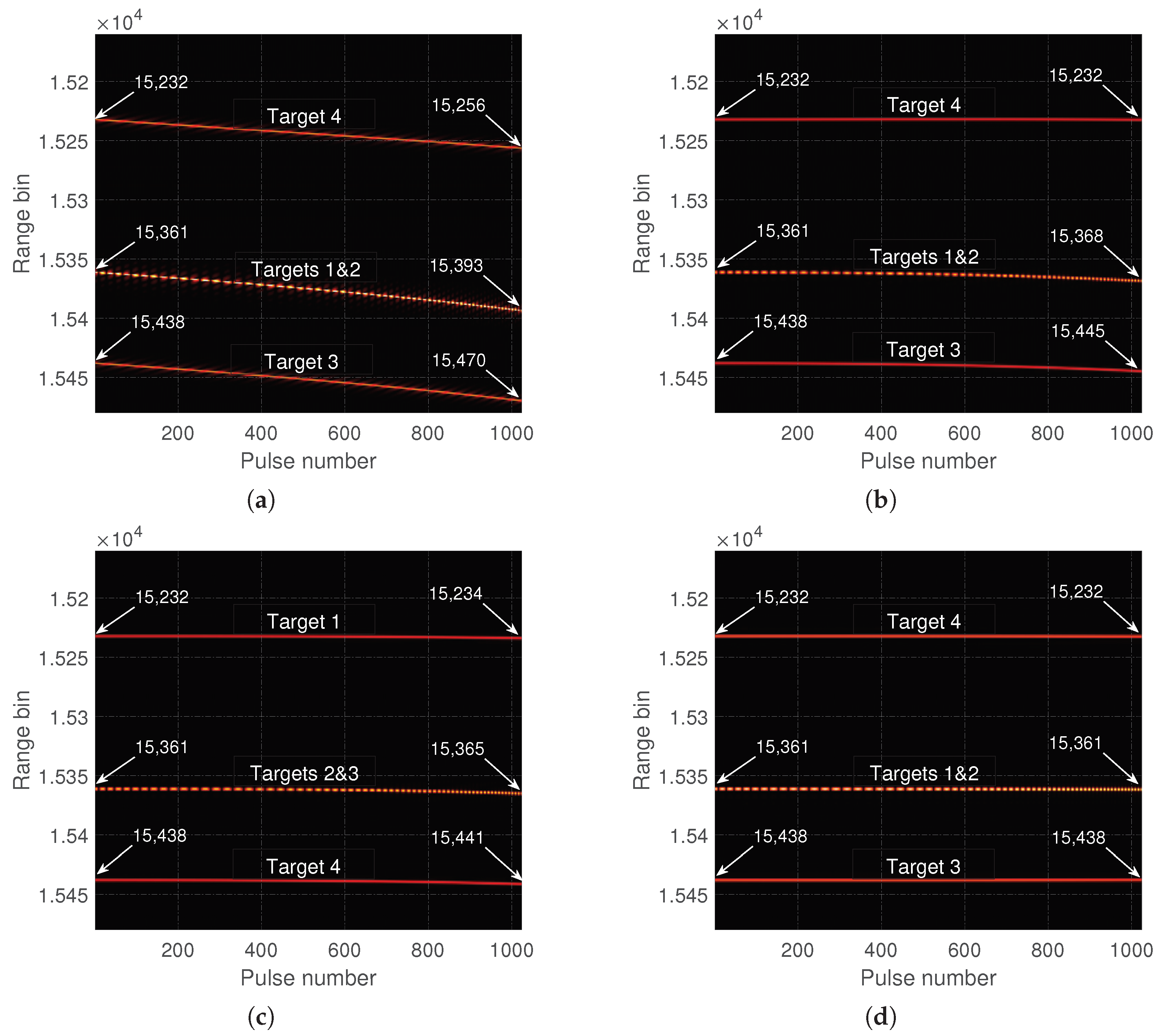
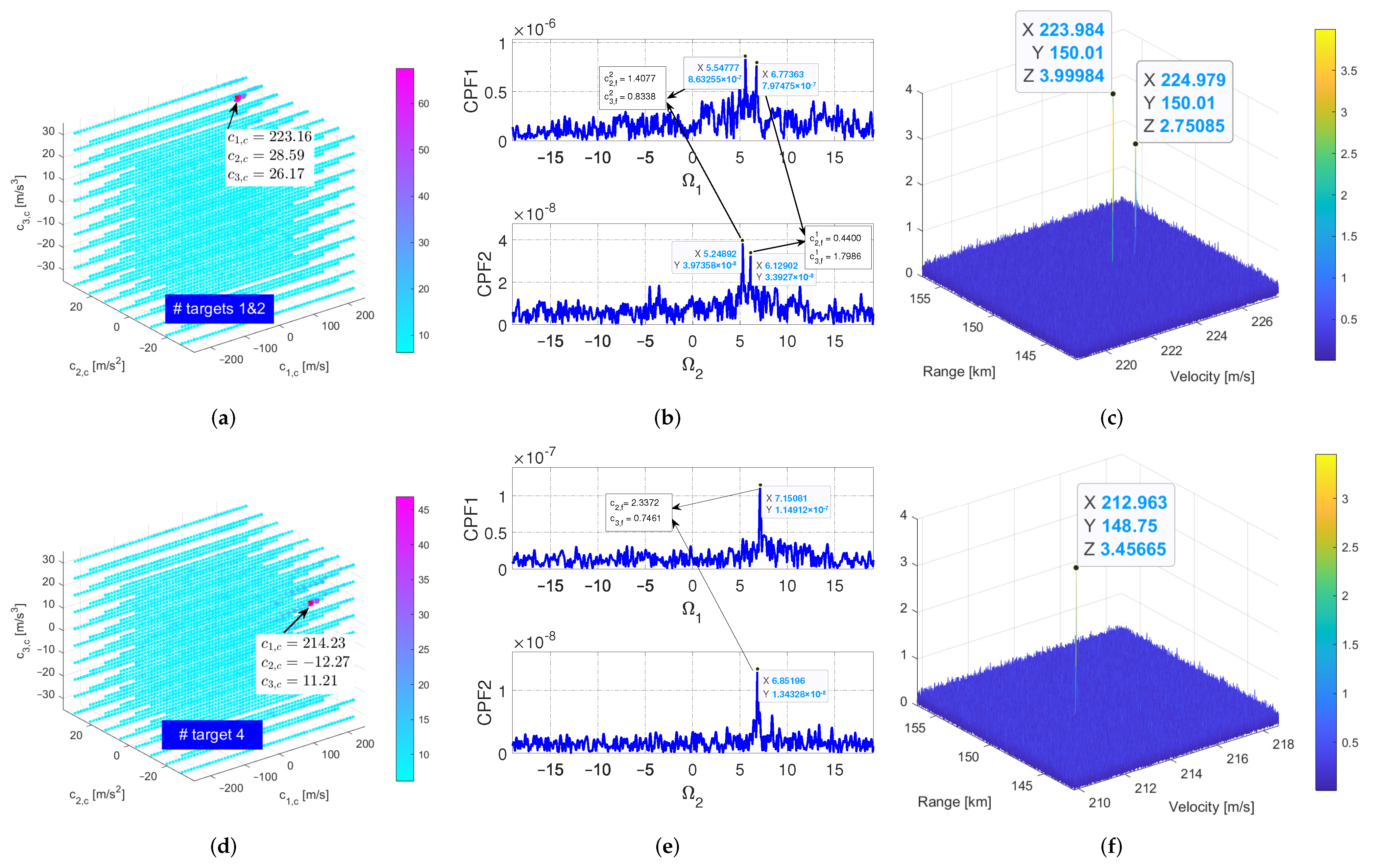
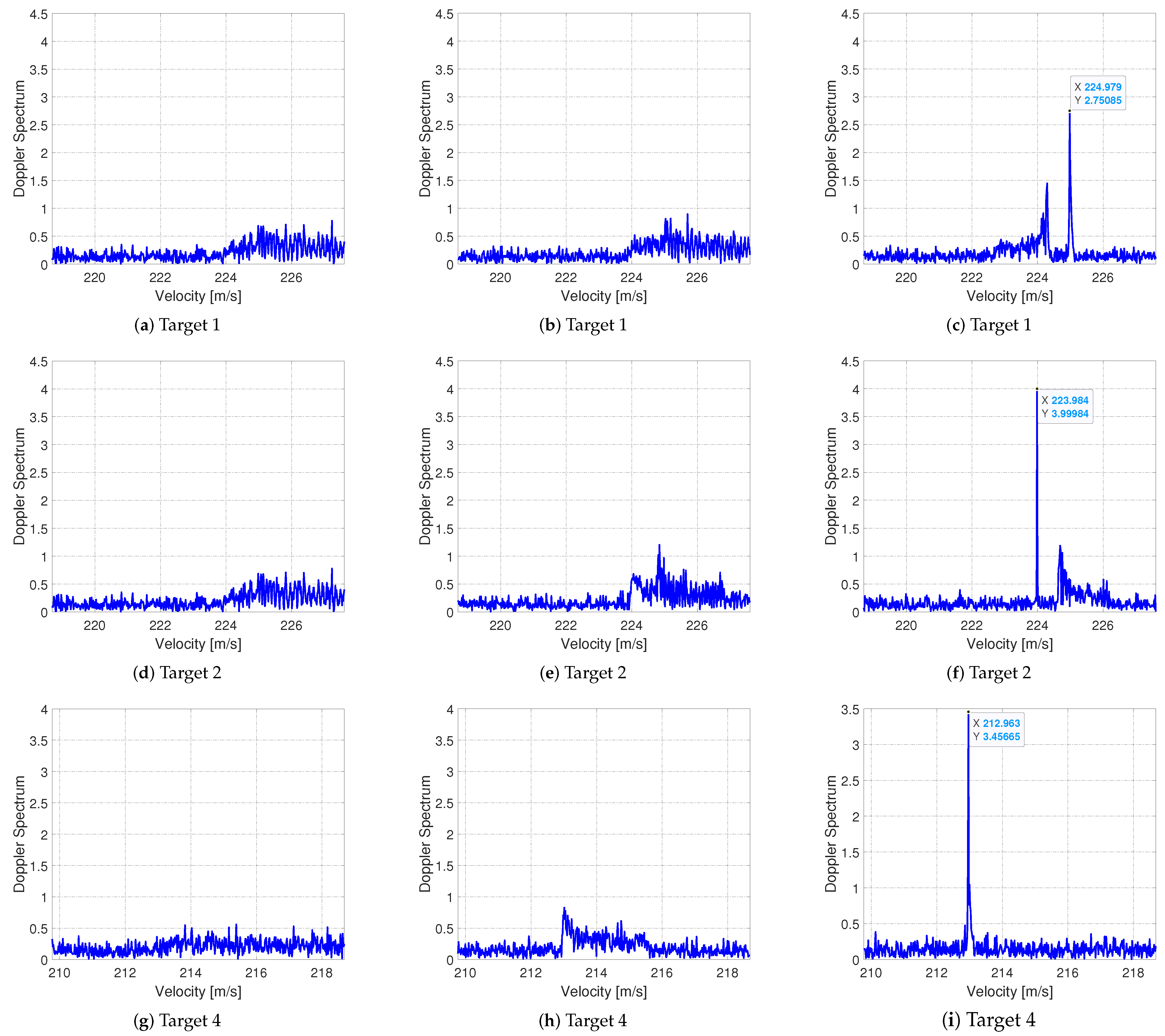
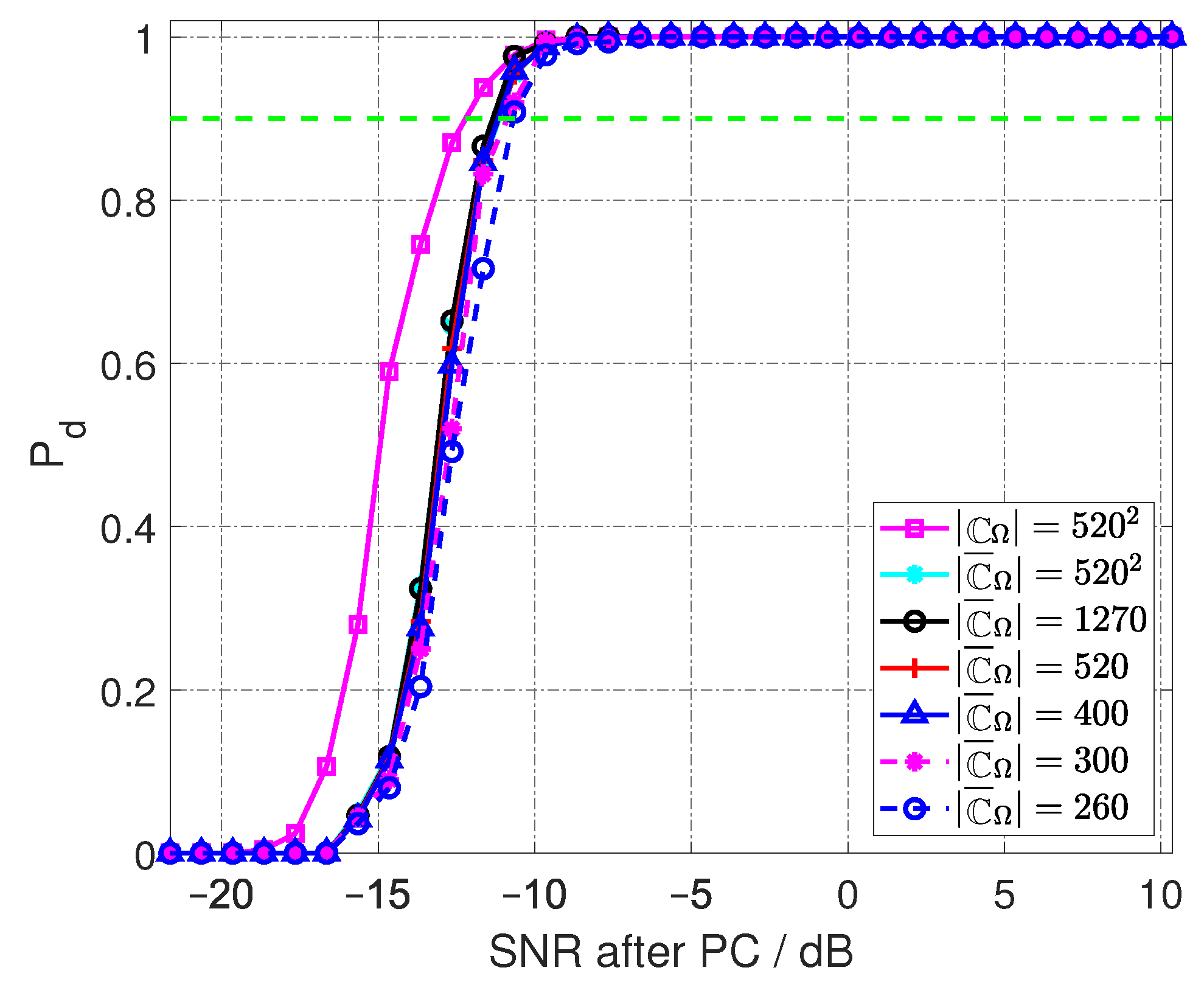
5.1. Experiment 1
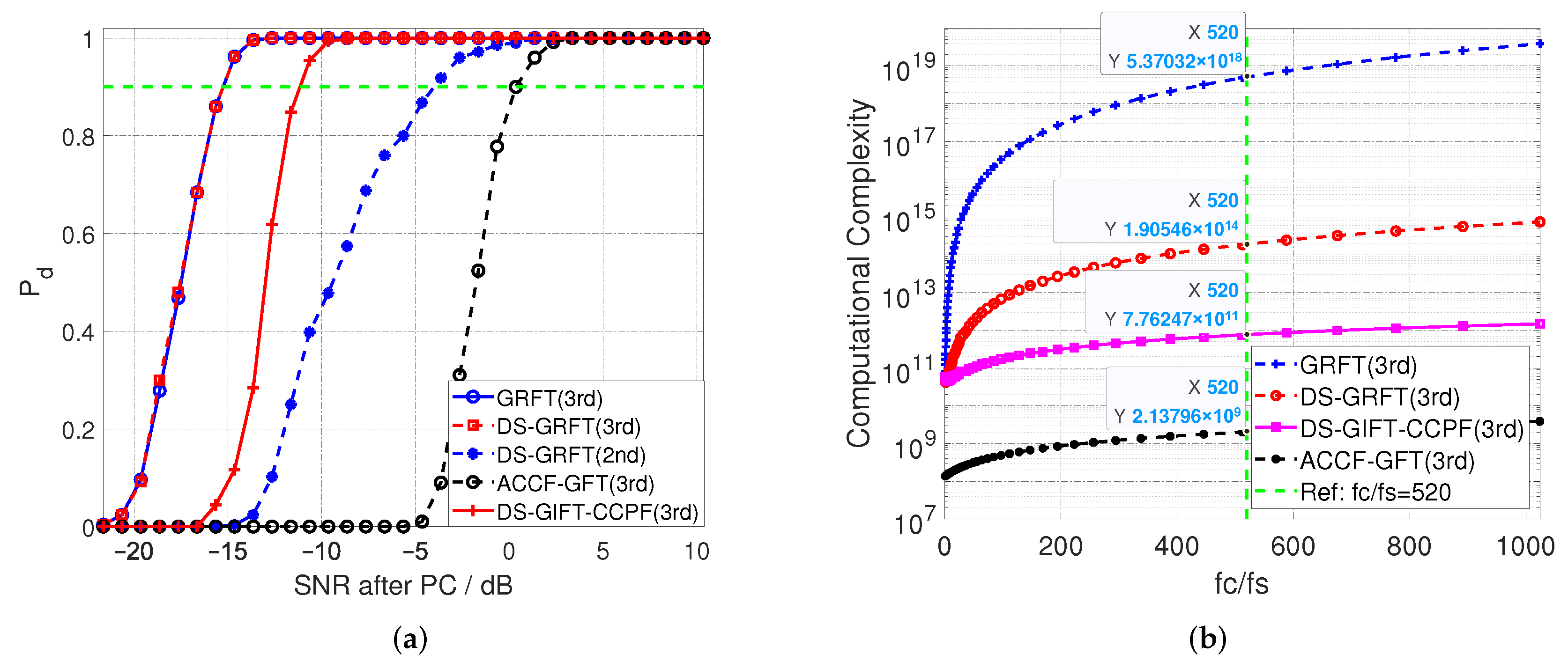
5.2. Experiment 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| the discrete frequency of the signal, | |
| the interval of frequency bins | |
| k | the number of frequency bins, |
| K | the number of frequency bins |
| the slow time (inter-pulse sampling time) | |
| m | the number of pulses, |
| M | the number of pulses |
| the carrier frequency | |
| c | the velocity of light |
| the wave length | |
| the instantaneous slant range between the receiver and the transmitter | |
| the fast time (intra-pulse sampling time), | |
| the sampling interval of fast time, | |
| the sampling rate of frequency | |
| the signal bandwidth, | |
| the valid number of frequency bins | |
| p | the order of the target motion parameters |
| the initial radial distance of the signal from the transmitter to the receiver | |
| the radial components of the target of order p | |
| the motion parameter variable of order p | |
| the minimum value of | |
| the maximum value of | |
| the coarse motion parameter variable of | |
| the fine motion parameter variable of | |
| the folding factor | |
| the fine motion parameter variable of weighted by | |
| the step size of | |
| the step size of | |
| the coarse motion parameter of | |
| the fine motion parameter of | |
| the estimation of | |
| the estimation of | |
| the estimation of | |
| the search space of | |
| the search space of | |
| the search space of | |
| the joint search spaces of the fine part of target motion parameters | |
| the vector consisting of motion parameter variables | |
| the vector consisting of coarse motion parameter variables | |
| the vector consisting of fine motion parameter variables | |
| the vector consisting of fine motion parameter variables weighted by | |
| the vector consisting of real coarse motion parameters | |
| the constructed instantaneous frequency rate variable | |
| the search space of | |
| the i-th time position | |
| the homogeneous search space of | |
| the estimation of | |
| the step size of | |
| the size of the space | |
| the vector consisting of and | |
| the estimation of | |
| the vector consisting of and | |
| the injective function from elements of to those of |
References
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing bistatic SAR data using the nonlinear chirp scaling algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef]
- Ma, H.; Michail, A.; Debora, P.; Fabrizio, S.; Federica, P.; Marta, B.; Mikhail, C. Maritime moving target indication using passive GNSS-based bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 115–130. [Google Scholar] [CrossRef]
- Feng, W.; Wei, W.; Liu, F. Modefied keystone processing algorithm for the space-based bistatic radar systems. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–6. [Google Scholar]
- Simpson, R. Spacecraft studies of planetary surfaces using bistatic radar. IEEE Trans. Geosci. Remote Sens. 1993, 31, 465–482. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, T.; Zhang, L. Long time coherent integration algorithm for high-speed maneuvering target detection using space-based bistatic radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Xu, J.; Xia, X.; Peng, S.; Yu, J.; Peng, Y.; Qian, L. Radar maneuvering target motion estimation based on generalized Radon-Fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.; Xiang, G. Radon-Fourier transform for radar target detection (III): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 60, 6190–6201. [Google Scholar]
- Xu, J. Radon-Fourier transform (RFT) for radar target detection I: Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; Zhou, W.; He, Y. Detection of a low observable sea-surface target with micromotion via Radon-linear canonical transform. IEEE Geosci. Remote Sens. Lett. 2014, 60, 6190–6210. [Google Scholar]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Coherent integration for maneuvering target detection based on Radon-Lv’s distribution. IEEE Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.; Zheng, J. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Yi, W.; Cui, G.; Kong, L. Detection of weak maneuvering target based on keystone transformand matched filtering process. Signal Process. 2017, 140, 127–138. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, T.; Long, T.; Wang, Z. Range migration compensation and Doppler ambiguity resolution by keystone transform. In Proceedings of the 2006 CIE International Conference on Radar (CIE ICR), Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Li, S.; Wang, Y.; Wang, B.; Battistelli, G.; Chisci, L.; Cui, G. Efficient dual-scale generalized Radon-Fourier transform detector family for long time coherent integration. arXiv 2024, arXiv:2403.06788. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A fast maneuvering target motion parameters estimation algorithm based on ACCF. IEEE Signal Process Lett. 2015, 22, 270–274. [Google Scholar] [CrossRef]
- Yu, L.; He, F.; Zhang, Q.; Su, Y.; Zhao, Y. High maneuvering target long-time coherent integration and motion parameters estimation based on Bayesian compressive sensing. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4984–4999. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.; Battistelli, G.; Chisci, L. Dual-scale generalized Radon-Fourier transform family for long time coherent integration. In Proceedings of the 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022; pp. 499–505. [Google Scholar]
- Key, E.L.; Fowle, E.N.; Haggarty, R.D. A method of designing signals of large time-bandwidth product. IRE Int. Conv. Rec. 1961, 4, 146–154. [Google Scholar]
- Smith, J.O. Spectral Audio Signal Processing. Available online: http://books.w3k.org/ (accessed on 12 March 2024).
- Wang, B.; Li, S.; Battistelli, G.; Chisci, L. Fast iterative adaptive approach for indoor localization with distributed 5G small cells. IEEE Wirel. Commun. Lett. 2022, 11, 1980–1984. [Google Scholar] [CrossRef]
- Fessler, J.; Sutton, B. Nonuniform fast Fourier transforms using minmax interpolation. IEEE Trans. Signal Process. 2003, 51, 560–574. [Google Scholar] [CrossRef]
- O’Shea, P. A fast algorithm for estimating the parameters of a quadratic FM signal. IEEE Trans. Signal Process. 2004, 52, 385–393. [Google Scholar] [CrossRef]
- Lv, Y.; Wu, Y.; Wang, H.; Qiu, L.; Jiang, J.; Sun, Y. An inverse synthetic aperture ladar imaging algorithm of maneuvering target based on integral cubic phase function-fractional Fourier transform. Electronics 2018, 7, 148. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J. Multicomponent chirp signals analysis using product cubic phase function. Digit. Signal Process. 2006, 16, 654–669. [Google Scholar] [CrossRef]
- Zhang, J.; Su, T.; Zheng, J.; He, X. Parameter estimation of CFM signals based on MICPF-HAF. Electron. Lett. 2018, 54, 456–458. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled Random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]


| BOs | MF | IFFT | CCPF /ACCF | FFT | Total CC | ||
|---|---|---|---|---|---|---|---|
| Times | |||||||
| Alg.s | |||||||
| GRFT | – | – | |||||
| DS-GRFT | – | ||||||
| DS-GIFT-CCPF | ) | ||||||
| ACCF-GFT | |||||||
| [GHz] | [MHz] | [MHz] | PRF [Hz] | M |
|---|---|---|---|---|
| 8 | 15.36 | 12.5 | 937.5 | 1024 |
| Num. | [km] | [m/s] | ] | ] | SNR after PC [dB] |
|---|---|---|---|---|---|
| target 1 | 150.00 | 225 | 29 | 28 | −1.2 |
| target 2 | 150.00 | 224 | 30 | 27 | −1.8 |
| target 3 | 150.75 | 225 | 27 | 25 | −3.8 |
| target 4 | 148.74 | 213 | −10 | 12 | −2.8 |
| Alg.s | GRFT | DS-GRFT | DS-GIFT-CCPF | ACCF-GFT |
|---|---|---|---|---|
| Execution Time [s] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wang, Y.; Liang, Y.; Wang, B. Long-Time Coherent Integration for the Spatial-Based Bistatic Radar Based on Dual-Scale Decomposition and Conditioned CPF. Remote Sens. 2024, 16, 1798. https://doi.org/10.3390/rs16101798
Li S, Wang Y, Liang Y, Wang B. Long-Time Coherent Integration for the Spatial-Based Bistatic Radar Based on Dual-Scale Decomposition and Conditioned CPF. Remote Sensing. 2024; 16(10):1798. https://doi.org/10.3390/rs16101798
Chicago/Turabian StyleLi, Suqi, Yihan Wang, Yanfeng Liang, and Bailu Wang. 2024. "Long-Time Coherent Integration for the Spatial-Based Bistatic Radar Based on Dual-Scale Decomposition and Conditioned CPF" Remote Sensing 16, no. 10: 1798. https://doi.org/10.3390/rs16101798
APA StyleLi, S., Wang, Y., Liang, Y., & Wang, B. (2024). Long-Time Coherent Integration for the Spatial-Based Bistatic Radar Based on Dual-Scale Decomposition and Conditioned CPF. Remote Sensing, 16(10), 1798. https://doi.org/10.3390/rs16101798







