Small Target Radiometric Performance of Drone-Based Hyperspectral Imaging Systems
Abstract
1. Introduction
2. Background
2.1. Equipment Overview
2.2. Field Irradiance Measurement Theory
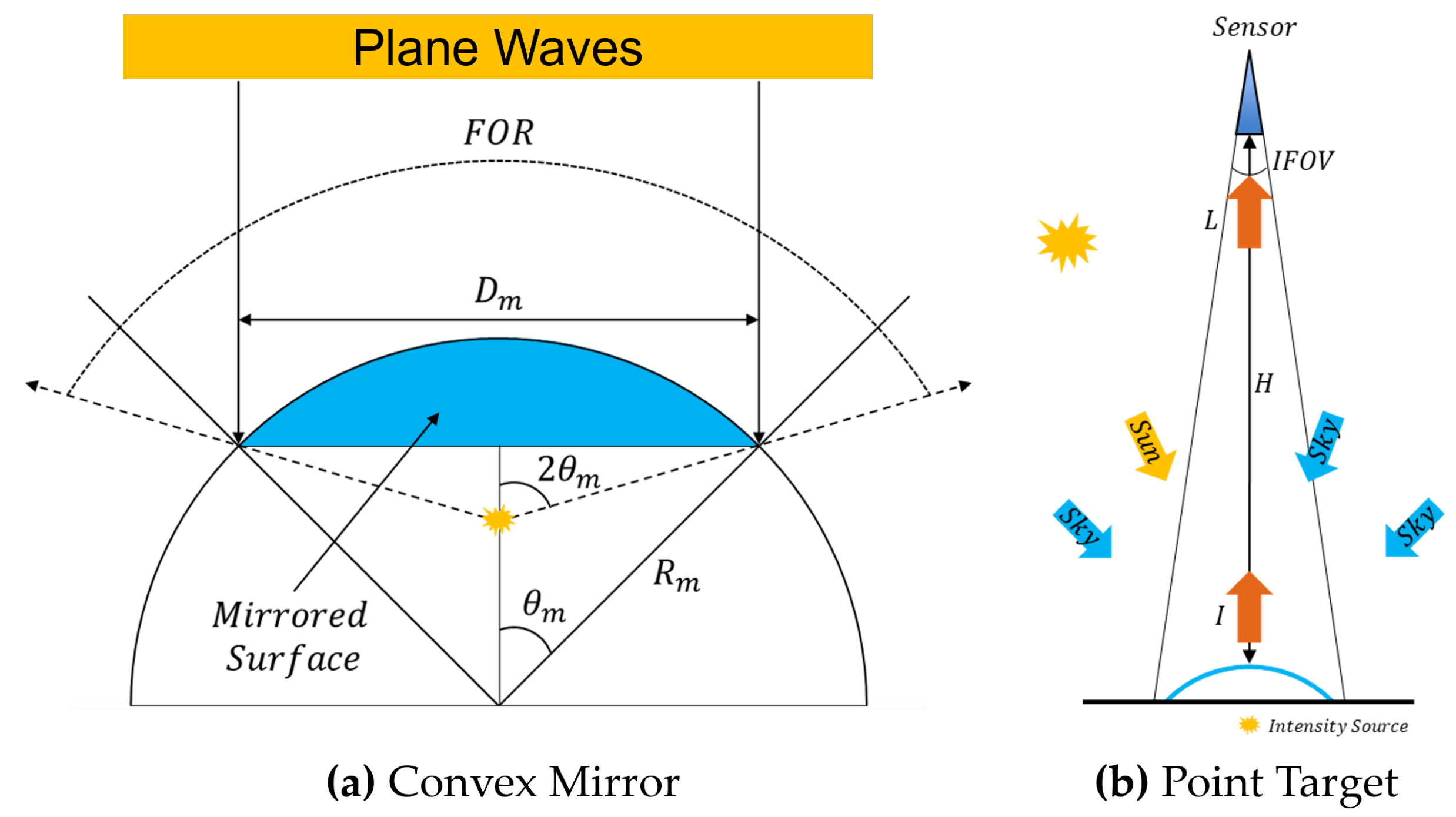
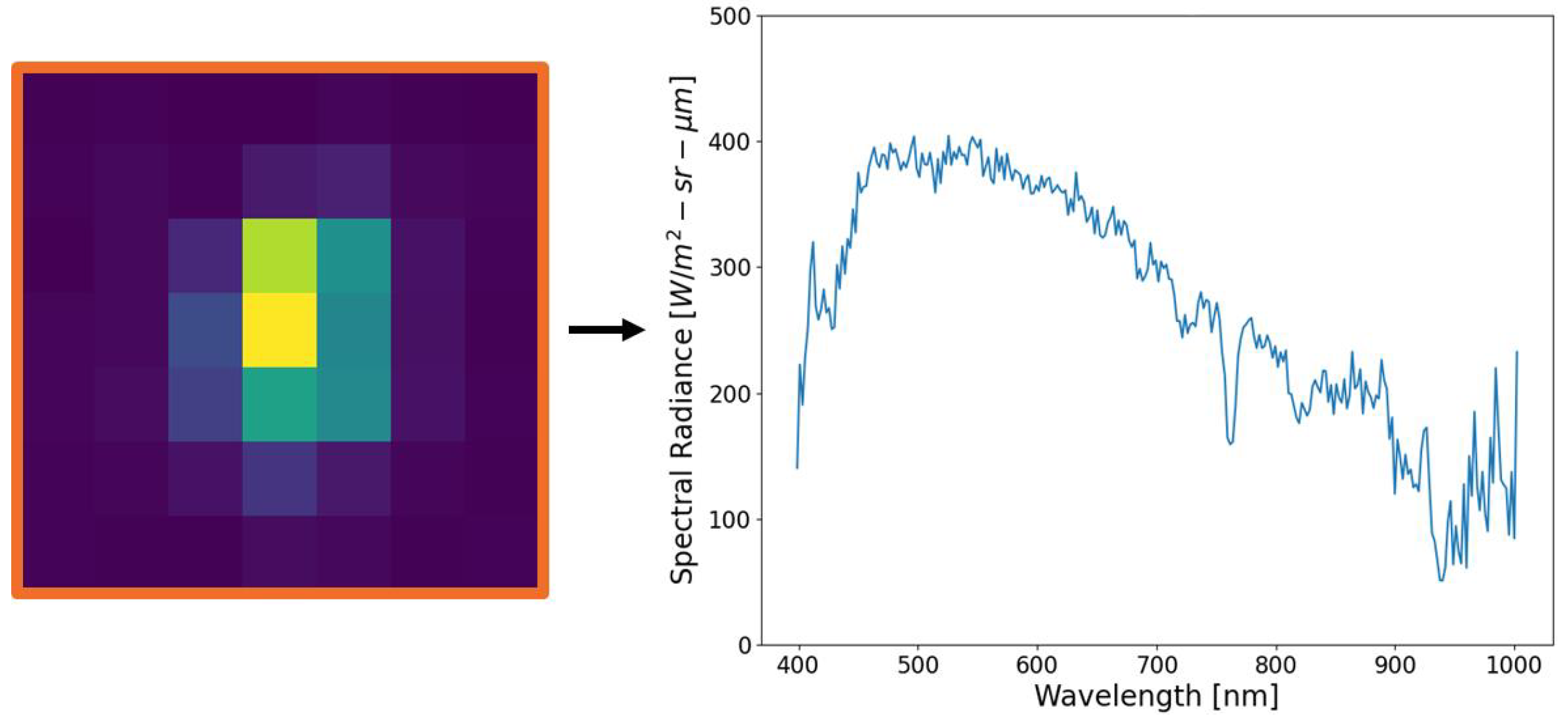
2.3. Imaging Point Targets: Radiometric and Spatial Response
3. Methodology
3.1. Experiment Overview
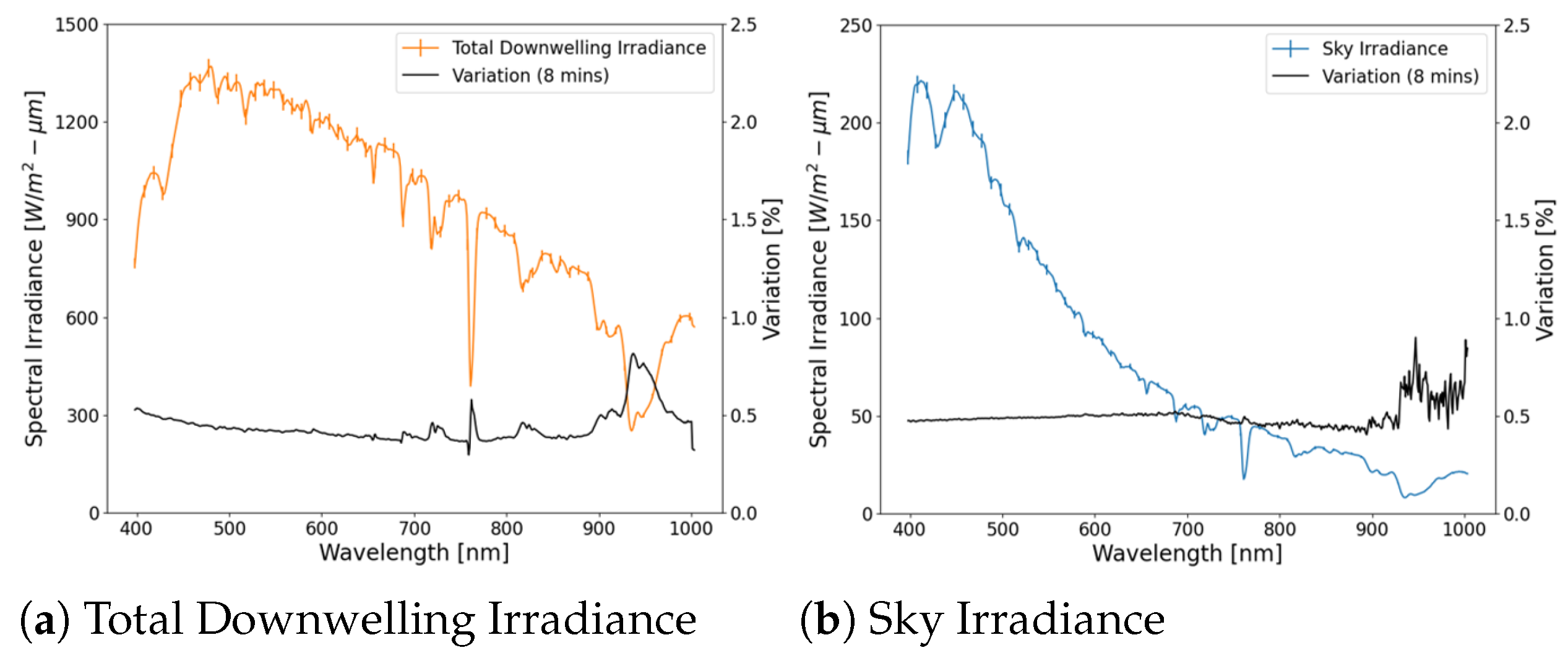
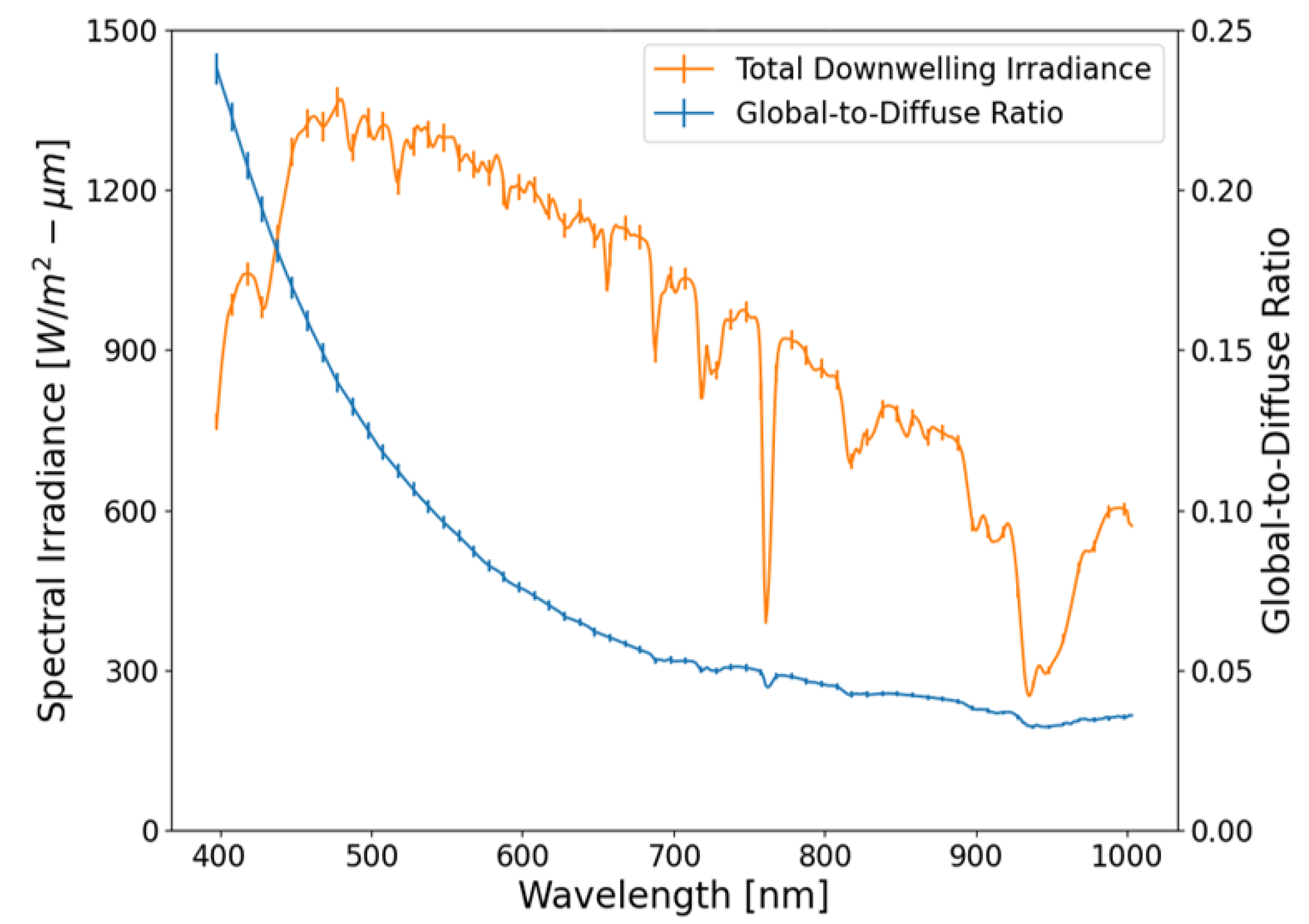
3.2. Field Irradiance Measurements
3.3. Data Processing and Analysis
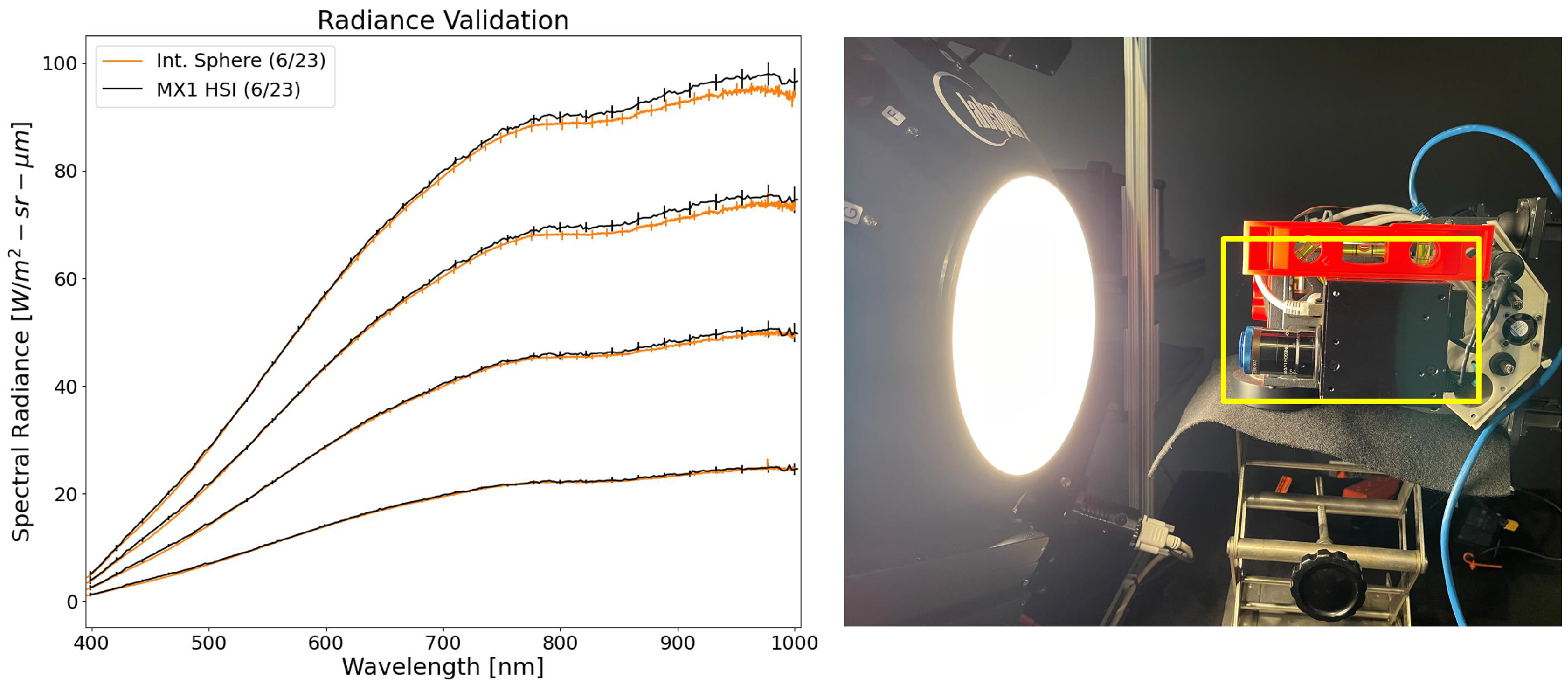
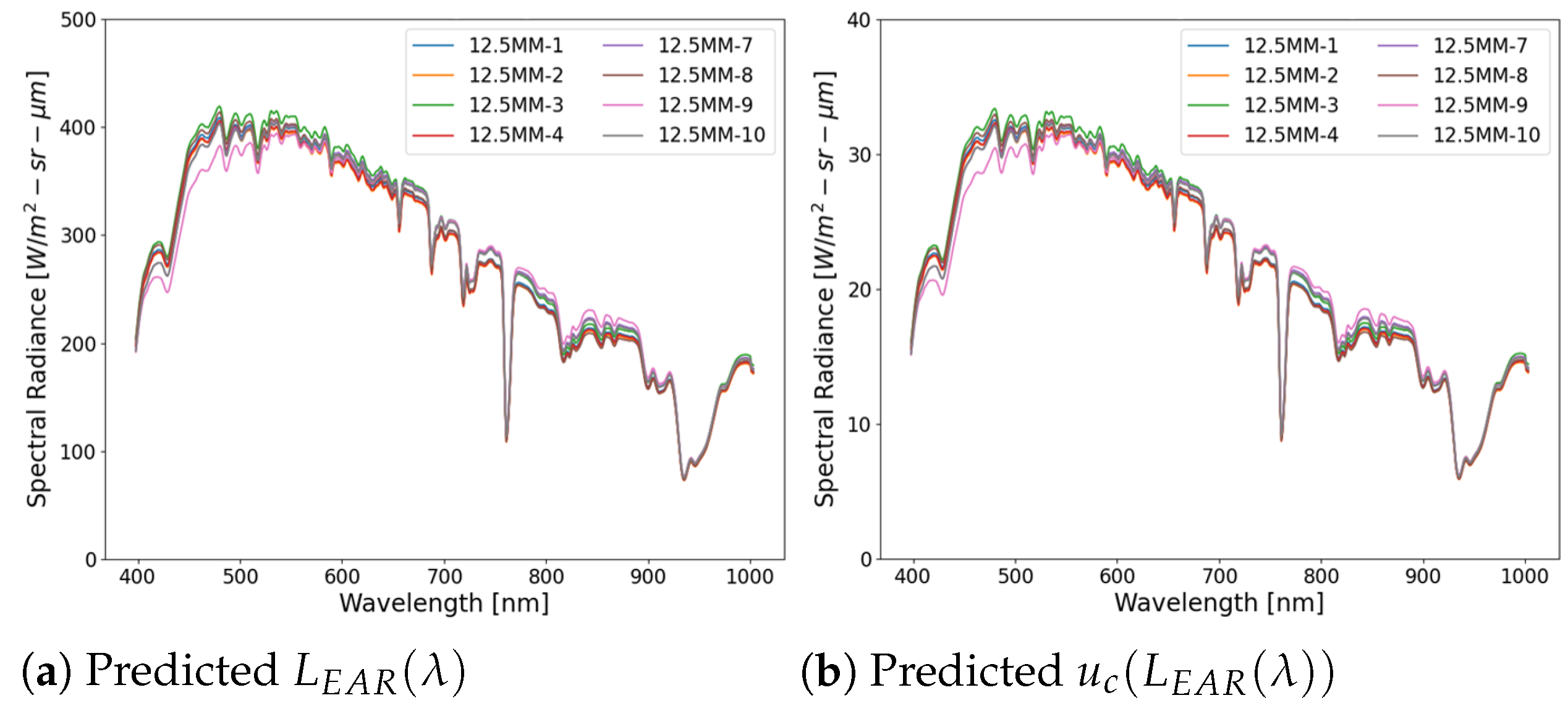
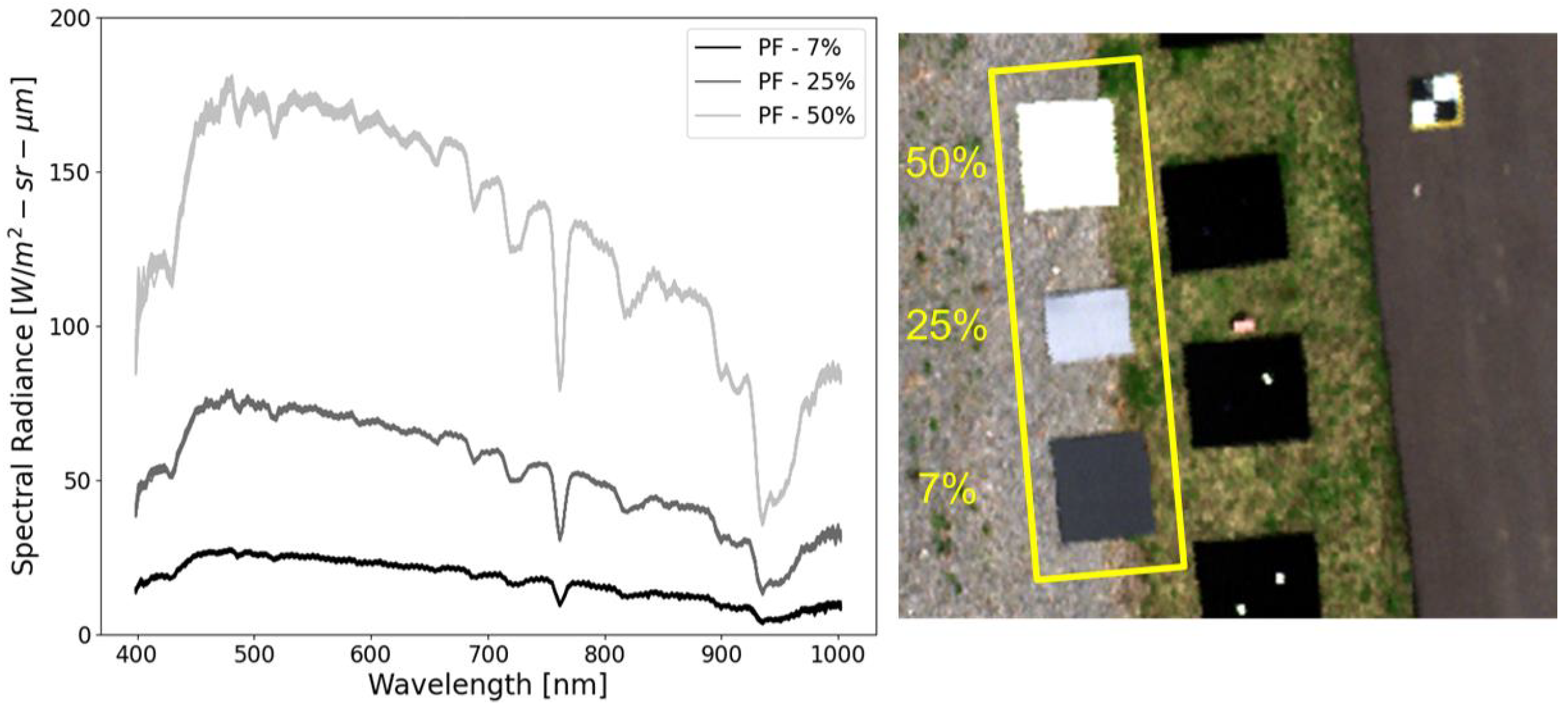
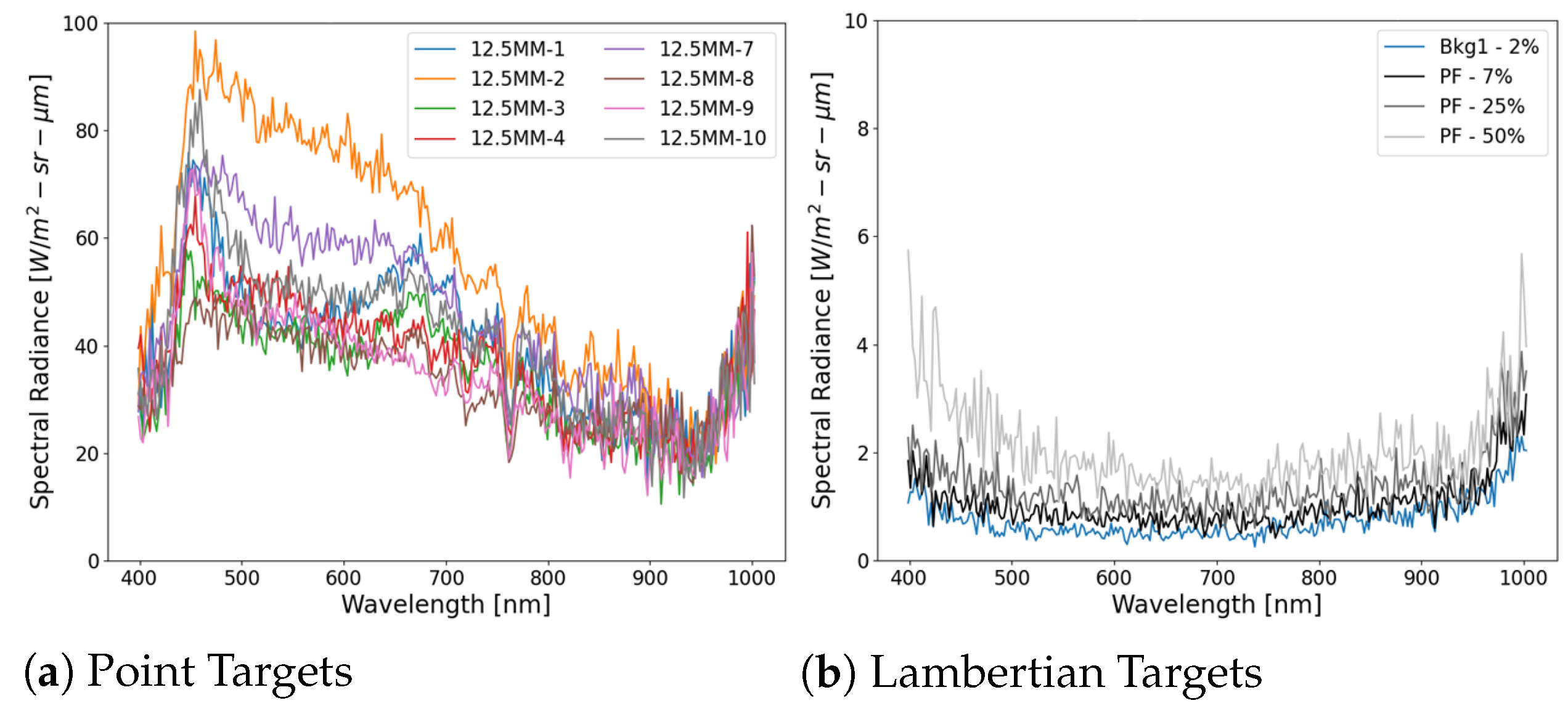
4. Results
5. Discussion
5.1. Overall Point Target Performance
5.2. Radiometric Accuracy Concerns
5.3. Spectral Inconsistencies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DIRS | Digital Imagery and Remote Sensing |
| VNIR | Visible-Near Infrared |
| LWIR | Long-Wave Infrared |
| LIDAR | Light Detection and Ranging |
| HSI | Hyperspectral Imaging |
| GSD | Ground Sampling Distance |
| QTH | Quartz-Tungsten Halogen |
| SPSF | Sampled Point Spread Function |
| NEI | Noise-Equivalent Irradiance |
| FOV | Field-Of-View |
| m | meters |
| cm | centimeter |
| NIR | Near Infrared |
| HS | Hyperspectral |
| SPARC | SPecular Array for Radiometric Calibration |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
Appendix A
Appendix B
References
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Baugh, W.; Groeneveld, D. Empirical proof of the empirical line. Int. J. Remote Sens. 2008, 29, 665–672. [Google Scholar] [CrossRef]
- Mamaghani, B.G.; Sasaki, G.V.; Connal, R.J.; Kha, K.; Knappen, J.S.; Hartzell, R.A.; Marcellus, E.D.; Bauch, T.D.; Raqueño, N.G.; Salvaggio, C. An initial exploration of vicarious and in-scene calibration techniques for small unmanned aircraft systems. In Proceedings of the Autonomous Air and Ground Sensing Systems for Agricultural Optimization and Phenotyping III, Orlando, FL, USA, 15–19 April 2018; Thomasson, J.A., McKee, M., Moorhead, R.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10664. [Google Scholar] [CrossRef]
- DeCoffe, L.J.R.; Conran, D.N.; Bauch, T.D.; Ross, M.G.; Kaputa, D.S.; Salvaggio, C. Initial Performance Analysis of the At-Altitude Radiance Ratio Method for Reflectance Conversion of Hyperspectral Remote Sensing Data. Sensors 2023, 23, 320. [Google Scholar] [CrossRef] [PubMed]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Eismann, M. Hyperspectral Remote Sensing; Press Monographs, Society of Photo Optical: Bellingham, WA, USA, 2012. [Google Scholar]
- Bioucas-Dias, J.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. Geosci. Remote Sens. Mag. IEEE 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Schiller, S.; Silny, J. Using Vicarious Calibration to Evaluate Small Target Radiometry. CALCON. 2016. Available online: https://digitalcommons.usu.edu/calcon/CALCON2016/all2016content/2/ (accessed on 12 April 2021).
- Schiller, S.J. Specular Array for Radiometric Calibration and Method. U.S. Patent 8158929 B2, 17 April 2012. [Google Scholar]
- Inamdar, D.; Kalacska, M.; Arroyo-Mora, J.P.; Leblanc, G. The directly-georeferenced hyperspectral point cloud: Preserving the integrity of hyperspectral imaging data. Front. Remote Sens. 2021, 2, 675323. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R. Geo-atmospheric processing of airborne imaging spectrometry data. Part 1: Parametric orthorectification. Int. J. Remote Sens. 2002, 23, 2609–2630. [Google Scholar] [CrossRef]
- Labsphere Inc. ISO 17025 NVLAP Accreditation. Available online: https://www.labsphere.com/capabilities/calibrated-confidence/ (accessed on 28 January 2024).
- Soffer, R.; Ifimov, G. Experiences Learned in the Acquisition, Processing, and Assessment of In-Situ Point Spectroscopy Measurements Supporting Airborne Hyperspectral Cal/Val Activities. CALCON. 2019. Available online: https://digitalcommons.usu.edu/calcon/CALCON2019/all2019content/11/ (accessed on 12 January 2022).
- Hodges, G.B.; Michalsky, J.J. Multifilter Rotating Shadowband Radiometer (MFRSR) Handbook with subsections for derivative instruments: Multifilter Radiometer (MFR) Normal Incidence Multifilter Radiometer (NIMFR). In DOE ARM Climate Research Facility; DOE’s Office of Scientific and Technical Information (OSTI): Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Schiller, S.J.; Silny, J. The Specular Array Radiometric Calibration (SPARC) method: A new approach for absolute vicarious calibration in the solar reflective spectrum. In Proceedings of the Remote Sensing System Engineering III, San Diego, CA, USA, 1–5 August 2010; Ardanuy, P.E., Puschell, J.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2010; Volume 7813, p. 78130E. [Google Scholar] [CrossRef]
- Silney, J.F.; Schiller, S.J. Method and System for Vicarious Spatial Characterization of a Remote Image Sensor. WO 2013/019180 AL, 7 February 2013. [Google Scholar]
- Durell, C. Top-of-Atmosphere Reflectance Calibration of Satellite and Airborne Sensor Systems Using FLARE Vicarious Calibration Network; Technical Report; Labsphere, Inc.: North Sutton, NH, USA, 2019. [Google Scholar]
- Russell, B.; Scharpf, D.; Holt, J.; Arnold, W.; Durell, C.; Jablonski, J.; Conran, D.; Schiller, S.; Leigh, L.; Aaron, D.; et al. Initial results of the FLARE vicarious calibration network. In Proceedings of the Earth Observing Systems XXV, Online, 24 August–4 September 2020; Butler, J.J., Xiong, X.J., Gu, X., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11501, p. 115010F. [Google Scholar] [CrossRef]
- Pinto, C.T.; de Carvalho e Oliveira, P.V.; Aaron, D.; Holt, J.; Russell, B.; Durell, C.; Leigh, L. Preliminary evaluation of the mirror-based empirical line method using FLARE system. In Proceedings of the Earth Observing Systems XXVII, San Diego, CA, USA, 21–26 August 2022; Butler, J.J., Xiong, X.J., Gu, X., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2022; Volume 12232, p. 1223214. [Google Scholar] [CrossRef]
- Russell, B.J.; Soffer, R.J.; Ientilucci, E.J.; Kuester, M.A.; Conran, D.N.; Arroyo-Mora, J.P.; Ochoa, T.; Durell, C.; Holt, J. The Ground to Space CALibration Experiment (G-SCALE): Simultaneous Validation of UAV, Airborne, and Satellite Imagers for Earth Observation Using Specular Targets. Remote Sens. 2023, 15, 294. [Google Scholar] [CrossRef]
- Hedler, D.; Maddox, E.; Mann, J.; Leigh, L.; Raqueno, N.; Gerace, A.; Rehman, E.; Conran, D.; Bauch, T.; Falcon, L.; et al. Landsat Surface Product Validation Instrumentation: The BigMAC Exercise. Remote Sens. Environ. 2023. in review. [Google Scholar]
- Conran, D.; Ientilucci, E.J. Interrogating UAV Image and Data Quality Using Convex Mirrors. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4525–4528. [Google Scholar]
- Conran, D.N.; Ientilucci, E.J. A Vicarious Technique for Understanding and Diagnosing Hyperspectral Spatial Misregistration. Sensors 2023, 23, 4333. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Sexton, J.O.; Huang, C.; Masek, J.G.; Vermote, E.F.; Gao, F.; Narasimhan, R.; Channan, S.; Wolfe, R.E.; Townshend, J.R. Global surface reflectance products from Landsat: Assessment using coincident MODIS observations. Remote Sens. Environ. 2013, 134, 276–293. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. In Joint Committee for Guides in Metrology, JCGM 100:2008. Available online: https://ncc.nesdis.noaa.gov/documents/documentation/JCGM_100_2008_E.pdf (accessed on 17 November 2019).
- Breckinridge, J.B.; Oppenheimer, B.R. Polarization effects in reflecting coronagraphs for white-light applications in astronomy. Astrophys. J. 2004, 600, 1091. [Google Scholar] [CrossRef]
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]





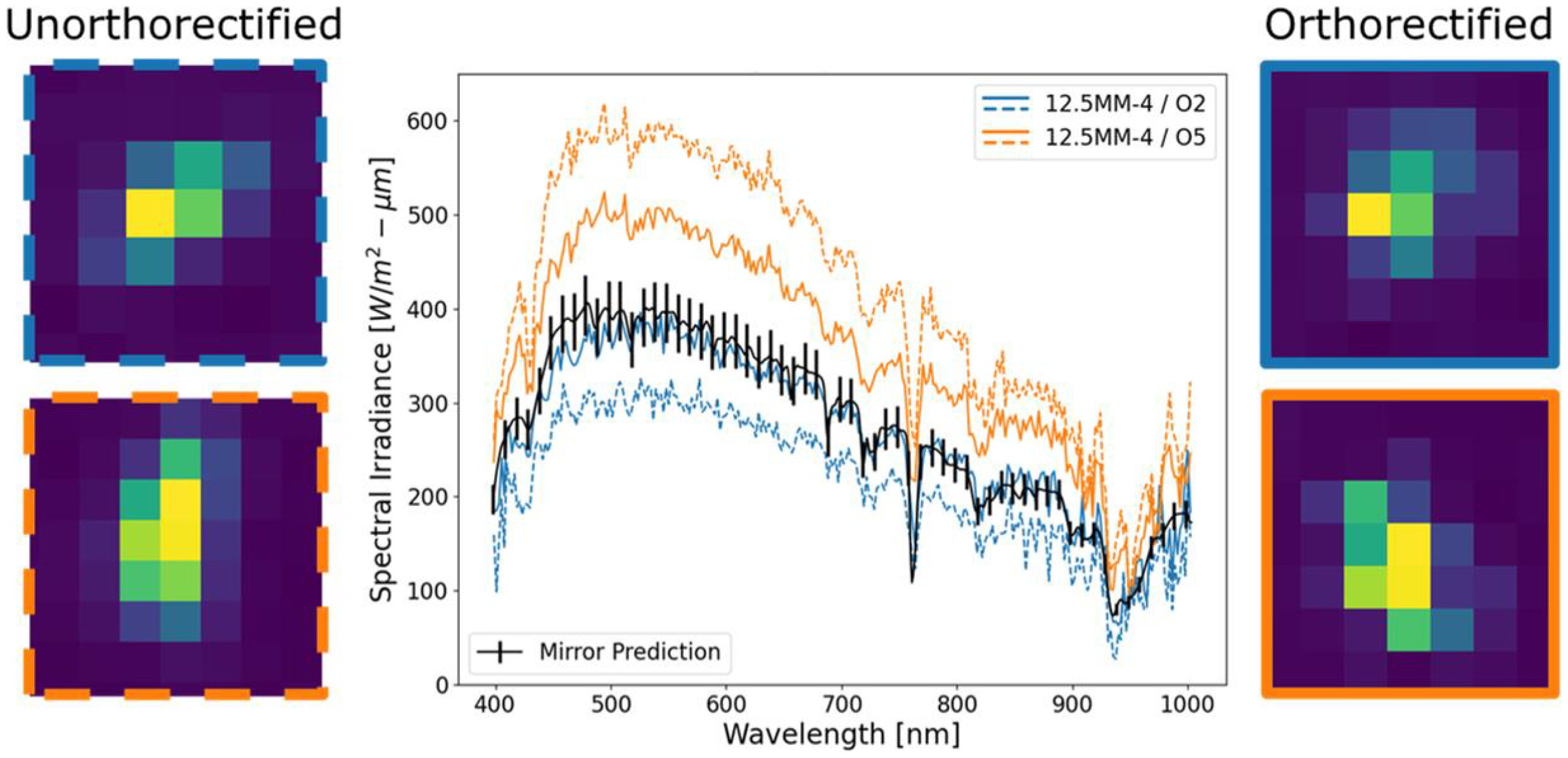
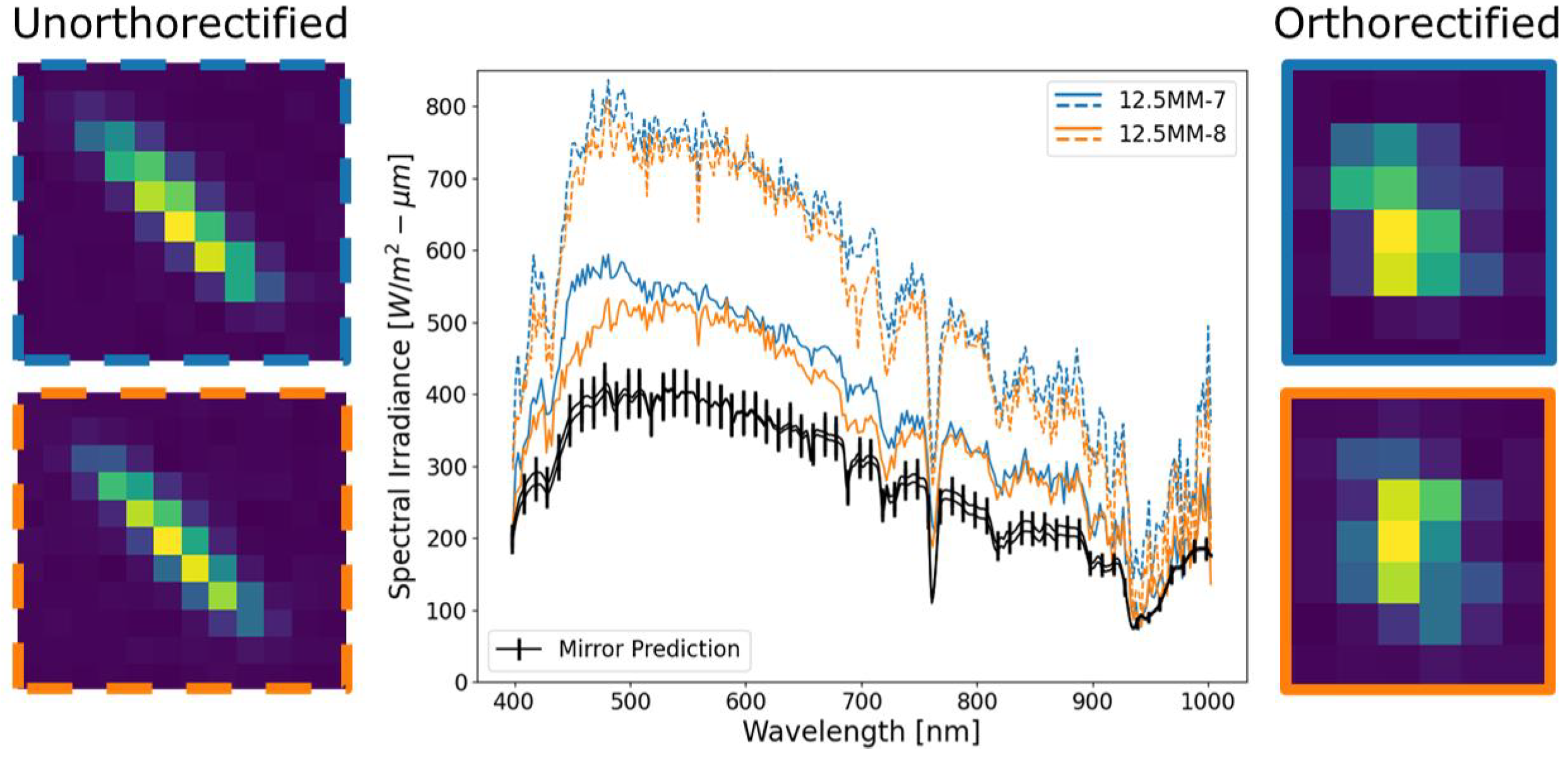
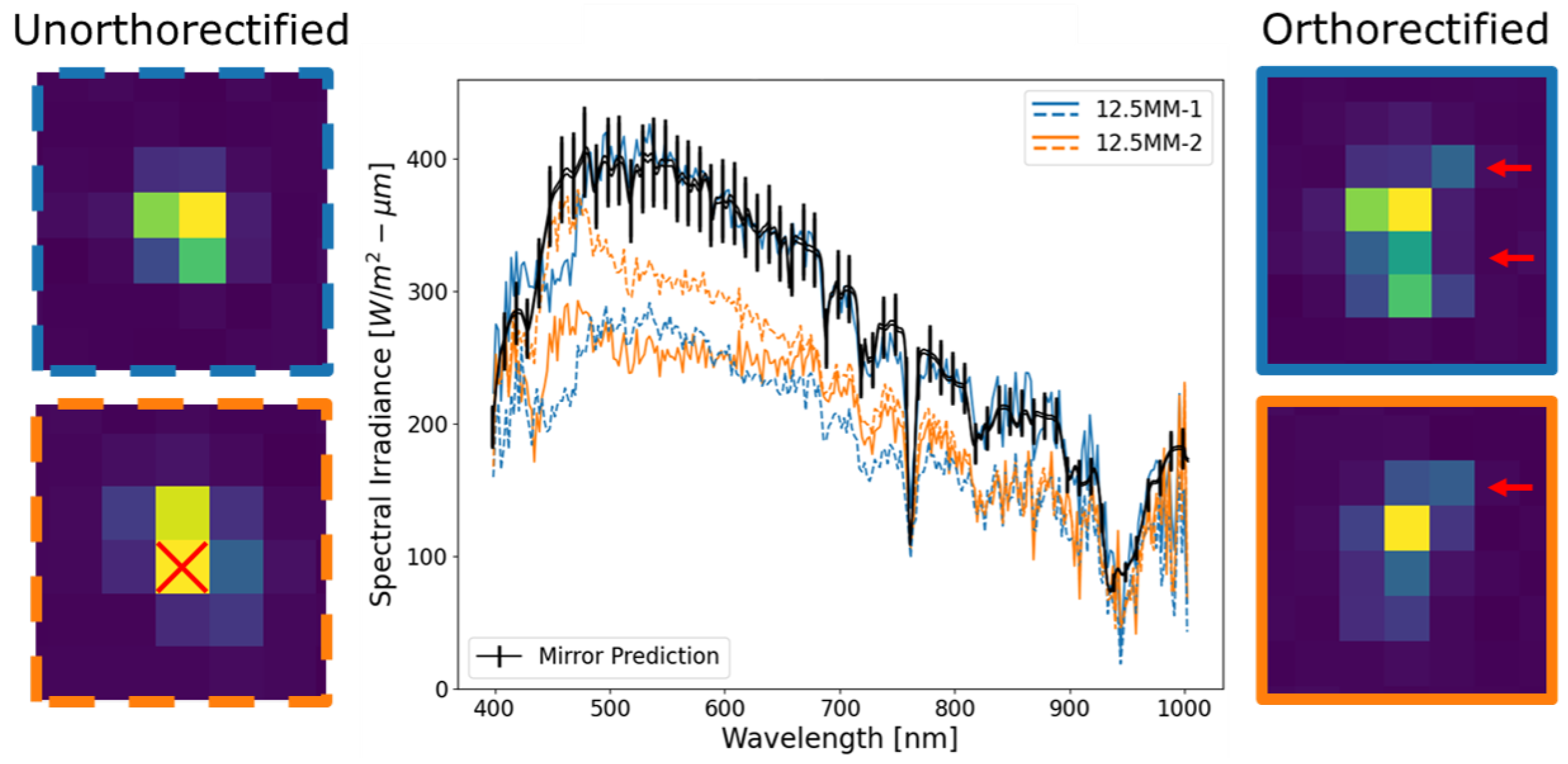

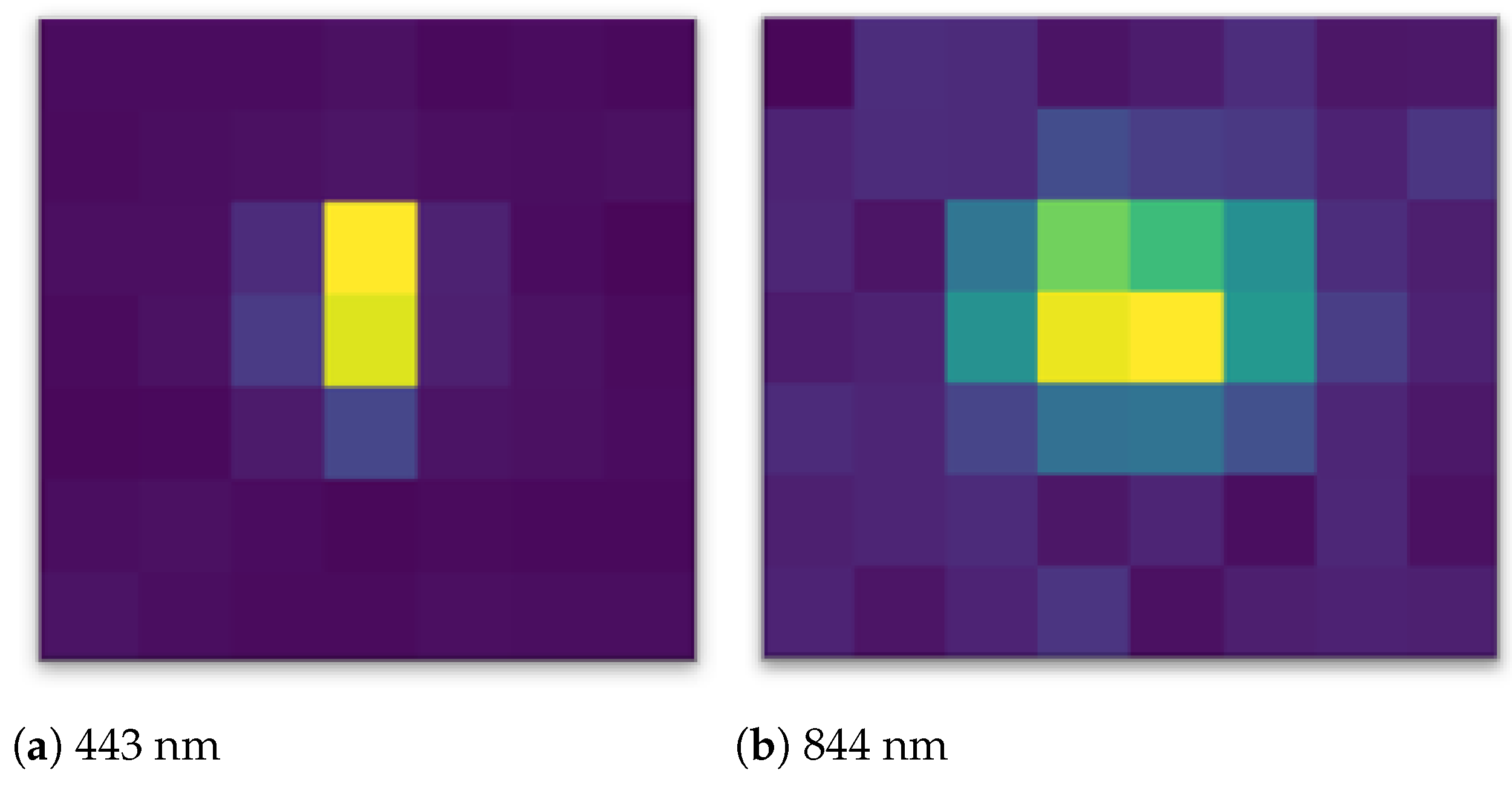
| 3% | 2% | 2% | 2.06% | 2.05% | 3% | 8.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conran, D.N.; Ientilucci, E.J.; Bauch, T.D.; Raqueno, N.G. Small Target Radiometric Performance of Drone-Based Hyperspectral Imaging Systems. Remote Sens. 2024, 16, 1919. https://doi.org/10.3390/rs16111919
Conran DN, Ientilucci EJ, Bauch TD, Raqueno NG. Small Target Radiometric Performance of Drone-Based Hyperspectral Imaging Systems. Remote Sensing. 2024; 16(11):1919. https://doi.org/10.3390/rs16111919
Chicago/Turabian StyleConran, David N., Emmett J. Ientilucci, Timothy D. Bauch, and Nina G. Raqueno. 2024. "Small Target Radiometric Performance of Drone-Based Hyperspectral Imaging Systems" Remote Sensing 16, no. 11: 1919. https://doi.org/10.3390/rs16111919
APA StyleConran, D. N., Ientilucci, E. J., Bauch, T. D., & Raqueno, N. G. (2024). Small Target Radiometric Performance of Drone-Based Hyperspectral Imaging Systems. Remote Sensing, 16(11), 1919. https://doi.org/10.3390/rs16111919








