1. Introduction
With the development of various synthetic aperture radar (SAR) systems [
1,
2], the next generation of spaceborne SAR requires a high resolution and wide swath, especially for maritime surveillance applications. High-spatial-resolution SAR images facilitate the detection and imaging of small-to-medium-sized maritime targets, providing reliable information for subsequent localization, identification, and interpretation [
3,
4]. A wide swath, which is characterized by a short revisit time, proves to be beneficial for discovering and monitoring dynamic targets in a wide maritime area. Compared with traditional SAR systems, the HRWS SAR configuration imposes higher requirements on maritime moving target imaging. In addition to the inherent spatial displacement and defocusing issues caused by target motion, it is essential to address the impact of the HRWS SAR configuration itself, such as multiple beams or a variable pulse repetition interval (PRI), on moving target imaging.
The existing high-resolution and wide swath (HRWS) systems are mainly proposed for imaging stationary scenes, while the application for monitoring moving targets is limited since the complex target motion produces evident image defocusing. A typical HRWS SAR system adopts multiple RX channels arranged along the azimuth. Due to the similar system architecture, this system combines moving target indication (MTI) systems to realize clutter suppression and moving target imaging [
5]. However, operating with a low pulse repetition frequency (PRF) exaggerates the azimuth ambiguities of the moving targets, along with the long antenna and the expense of high system complexity.
Without the necessity to lengthen the antenna, a staggered SAR has greatly advanced the HRWS system by combining multiple elevation beam (MEB) technology and a variable PRI, which has been adopted in Tandem-L [
6,
7] and NISAR satellites [
8]. The technology of multiple elevation beams (MEBs) provides an attractive solution for mapping an ultra-wide swath with a high resolution. The entire wide swath is illuminated by a wide beam on transmit, and the multiple elevation beams sweep following the directions of echo arrival to simultaneously map multiple subswaths. In a conventional MEB SAR system [
9] with a constant PRI, there will be constant blind areas due to the coincidence of transmitting and receiving events, resulting in gaps in the whole swath.
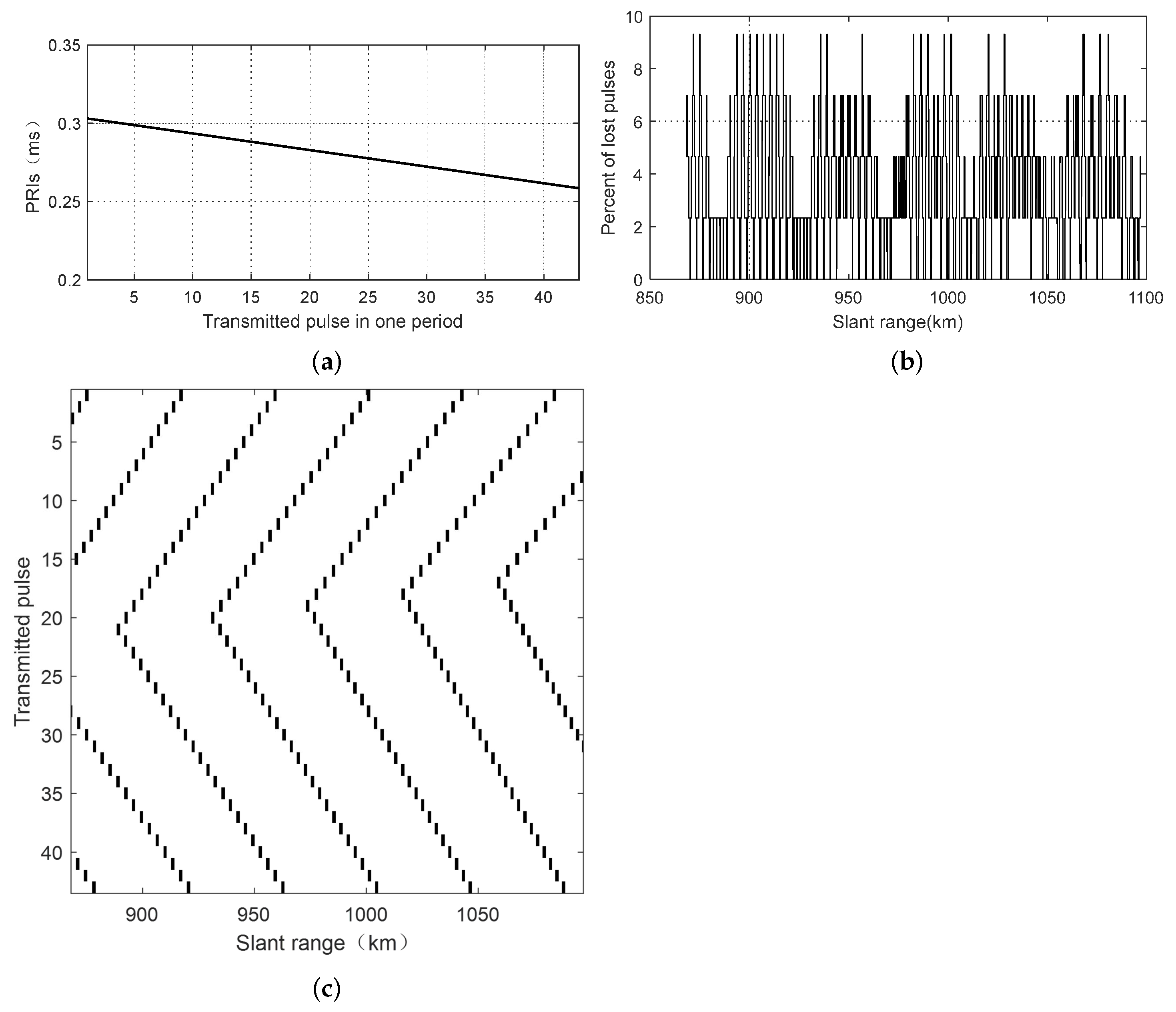
When operated with a variable PRI, a staggered SAR can address the problems of the constant blind areas to achieve gapless observation [
10,
11]. Meanwhile, the cost is that the variable PRI leads to lost pulses and nonuniformly sampled signals along the azimuth. To enable subsequent SAR processing, it is essential to reconstruct the nonuniform echo signal into the uniformly sampled signal. A number of reconstruction algorithms have been proposed, including the best linear unbiased (BLU) interpolation [
12], missing data iterative adaptive algorithm (MIAA) [
13], and other methods [
14,
15,
16].
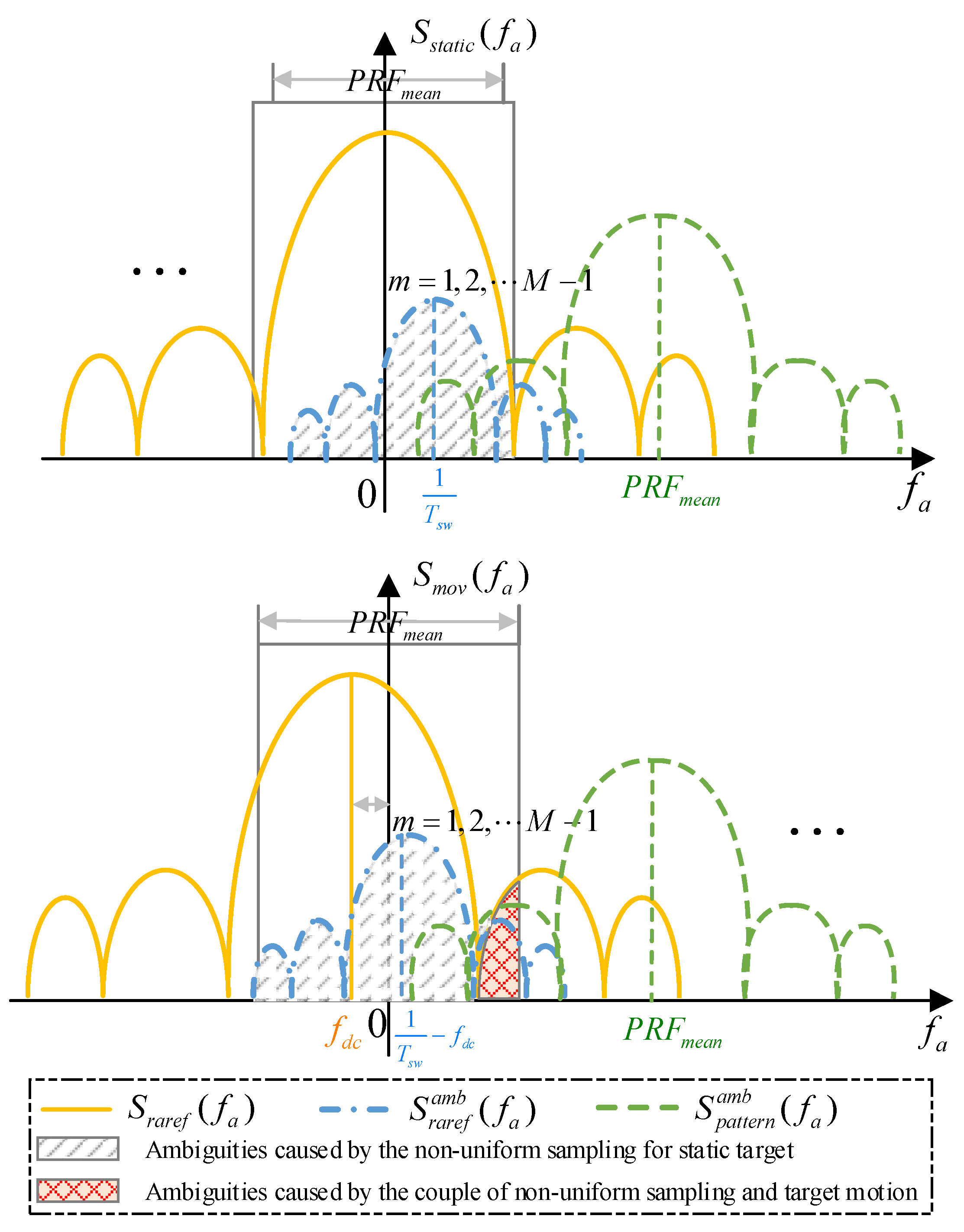
These existing reconstruction methods achieve good performance for a stationary scene. However, reconstructing the echoes of moving targets will produce evident image defocusing caused by complex target motion. Recently, scholars have turned their attention to the investigation of a staggered SAR for motion target detection, primarily emphasizing system design and detection methodologies, which have achieved impressive results [
17,
18]. However, little can be found in the literature about imaging the moving targets in a staggered SAR system. Actually, the complex target motion and the nonuniform azimuth sampling are two main issues that affect the focusing performance of moving targets in a staggered SAR. The maritime target motion includes translational movement and three-dimensional rotation accompanied with roll–pitch–yaw movement. Both of these can lead to blurred and displaced images. The nonuniform sampling causes spectrum aliasing along the azimuth, which is aggravated by the Doppler center due to target translational motion. These two issues interact, causing inevitable ambiguity and degrading the reconstruction performance. To solve this problem, this paper proposes a reconstruction algorithm for moving target imaging in a staggered SAR system.
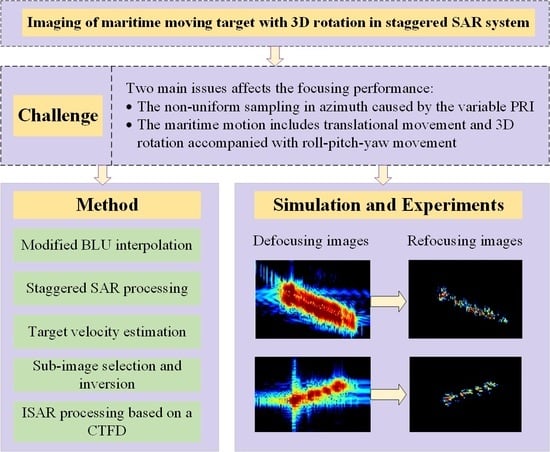
Overall, motivated by the BLU and hybrid SAR/ISAR techniques, our contributions in this paper are summarized as follows:
(1) The spectrum of maritime moving targets was derived in staggered mode. The derivation indicates that the complex target motion coupled with nonuniform sampling greatly aggravates image defocusing.
(2) Inspired by hybrid SAR/ISAR technology [
19], a novel reconstruction algorithm named MBLCFD is proposed to image the maritime targets with three-dimensional rotation in staggered mode. The BLU algorithm was modified after roughly estimating the target translational velocity. An accurate SAR processing method was used based on the method of inverse reversion to counteract the range and Doppler migration caused by the curved orbit, the wide swath, and the target motion. The complex-lag time-frequency distribution (CTFD) was carried out to refocus the maritime moving target images.
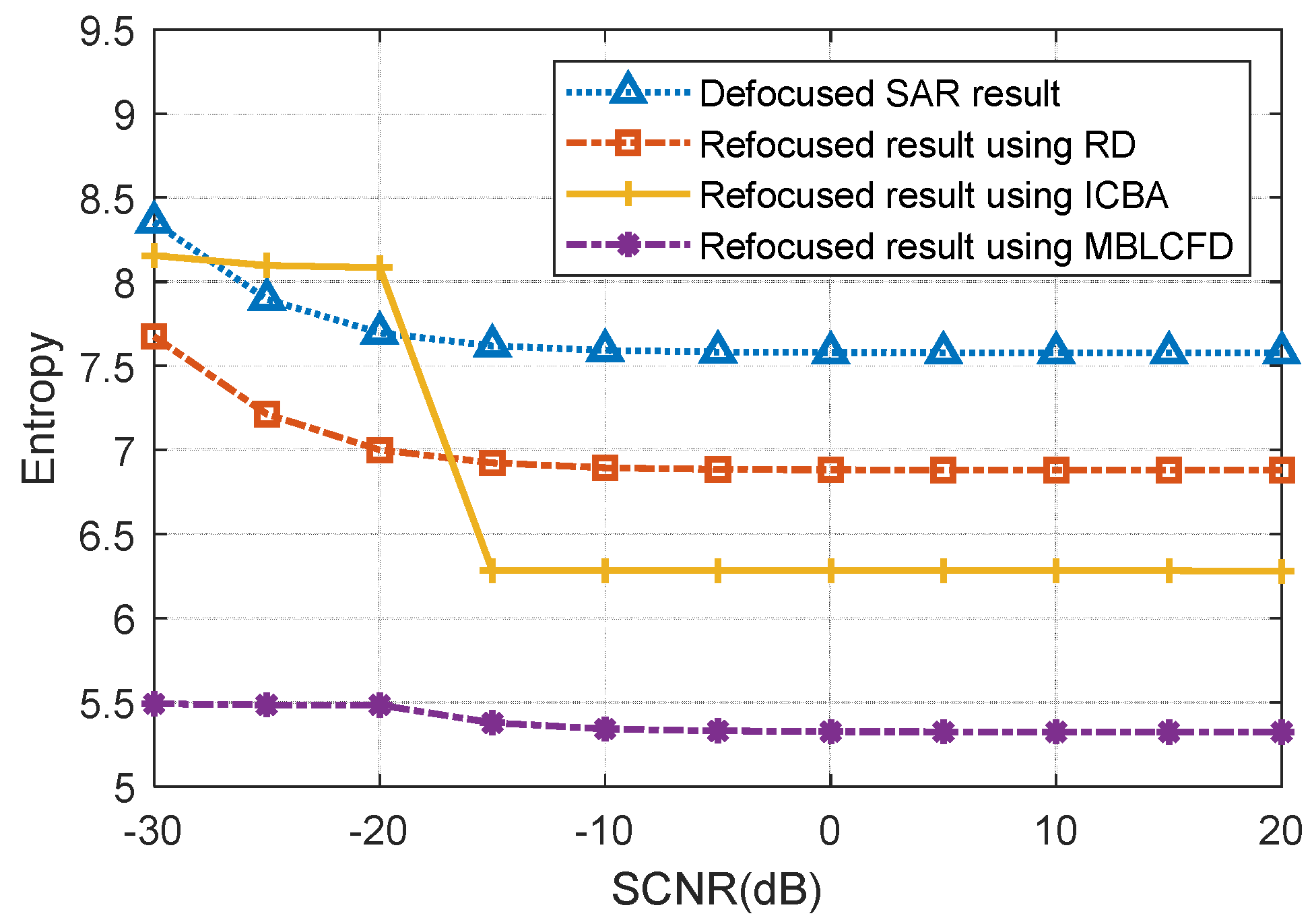
(3) In addition, compared with its rivals, the proposed algorithm provided superior refocusing performance in terms of the main lobe width (MW), peak-to-sidelobe ratio (PSLR), and integration sidelobe ratio (ISLR) for maritime moving targets in a staggered SAR system.
The remainder of this paper is organized as follows:
Section 2 establishes the geometric configuration and signal model in a staggered SAR mode. The spectrum of echo signal for maritime moving targets is derived in
Section 3. Derivations show that the complex motion of the maritime target, coupled with nonuniform sampling, aggravates the spectrum aliasing and the azimuth ambiguity. To address this issue, the proposed MBLCFD reconstruction is presented in
Section 4. In
Section 5, simulated data and equivalent raw data are employed to verify the feasibility and effectiveness of the proposed algorithm. A brief conclusion is given in
Section 6.
2. Geometric Configuration and Signal Model
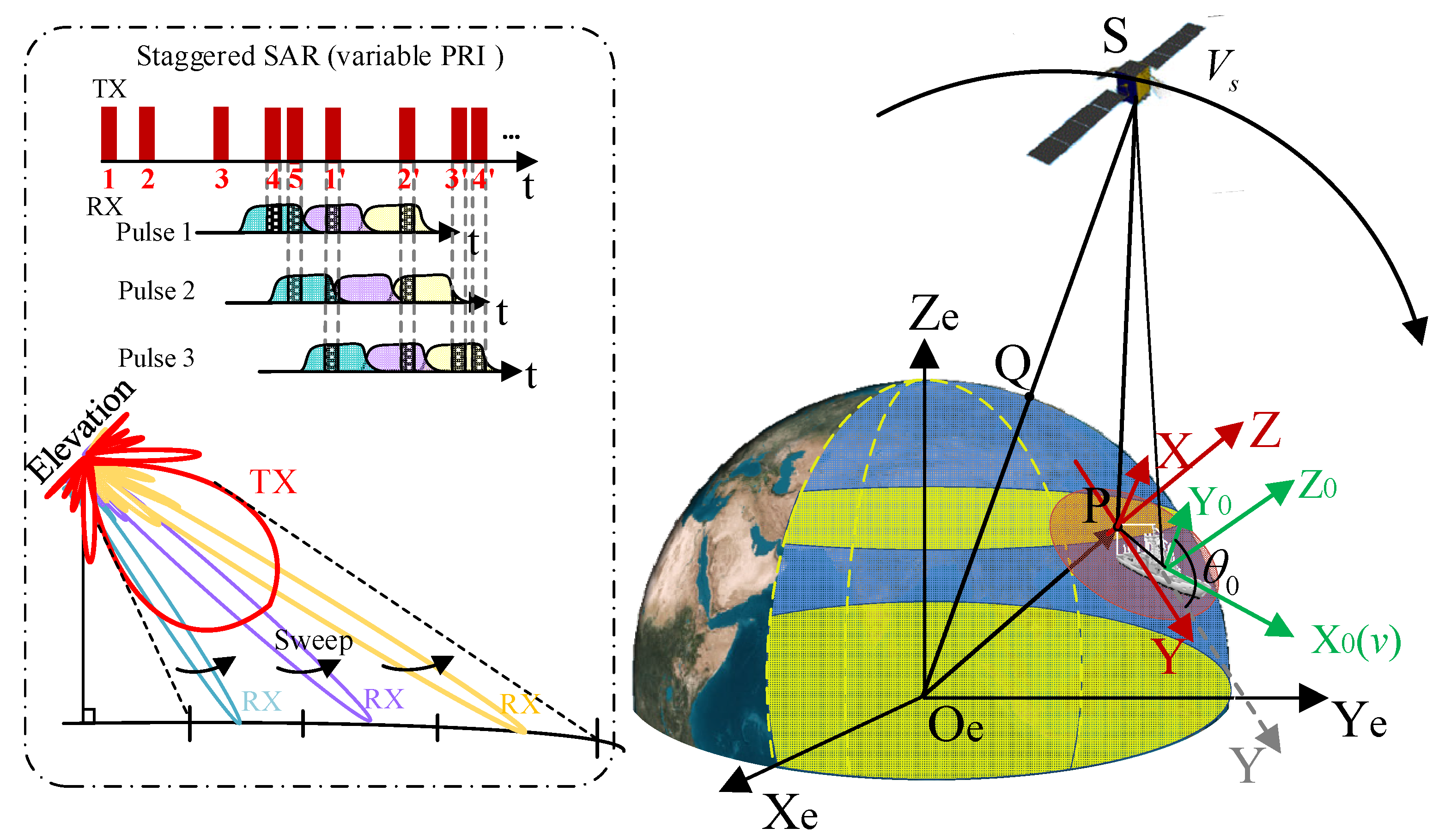
The geometry of the staggered SAR for maritime targets is depicted in
Figure 1. In the Earth rectangular coordinates (ERCs)
,
denotes the Earth’s center. The
-axis follows the Greenwich meridian direction, and the
-axis follows the Earth’s angular momentum direction. The beam-pointing direction and the Earth’s surface intersect at
P. Assume that
P is the origin of the imaging scene coordinate
. The
-axis is oriented toward the Earth’s center. The
-axis is located within
and is perpendicular to the
-axis.
denotes the radar look angle. Considering the Earth’s angular velocity and the curved orbit, the radar’s position
in the
coordinate is obtained in [
20].
The target coordinate is established by rotating clockwise along the Z-axis with . is along the direction of the ship’s bow. denotes the vector from the point P to the target. Thus, the position of the satellite in the target coordinates is . is the rotation matrix. The ship target has a translational motion along with a velocity of v, which is denoted as in . The position of a scatter point i on the ship target is at the initial moment.
After the hull has been constructed in three dimensions, the location of the point
i in the target coordinate
is given by
where
is the rotation matrix is the superposition of the effects of pitch, yaw, and roll directions. The rotation matrices
,
, and
can be expressed as
The rotation follows sinusoidal motion [
21]:
where
denotes the amplitude of the rotation,
represents the rotation period, and
is the initial phase of the rotation. These parameters are related to the sea state, the maritime target types, the velocities, and so on.
The slant range between the satellite and the scatterer
i can be expressed as
where
,
,
, and
are the terms of Taylor series caused by the satellite motion [
22], and
,
,
, and
denote the terms induced in the target motion. The
,
,
, and
can be obtained by
where
,
, and
represent the velocity vector, acceleration vector, and second-order acceleration vector of the satellite.
In a staggered SAR, the entire wide swath is illuminated by a wide beam on transmit as shown in
Figure 1, and the multiple elevation beams sweep following the directions of echo arrival to simultaneously map multiple subswaths. When operated with the variable PRIs, the blind areas appear at varying slant ranges for different echo pulses, allowing for mapping a wide continuous swath. The pulses are transmitted with different PRIs denoted as
. After this, the
M pulses repeat periodically. Thus, the
ath pulse is transmitted at the slow time
:
where the period
. The echo signal after demodulation is represented as follows:
where
is the fast time.
is the scattering coefficient of the
ith scatter point. The wavelength and chirp rate are expressed as
and
, respectively.
refers to the azimuth envelope. The blind range matrix
equals 0 when the pulse is lost and equals 1 when the pulse is fully received.
4. Image Reconstruction of Maritime Targets for Staggered SAR System
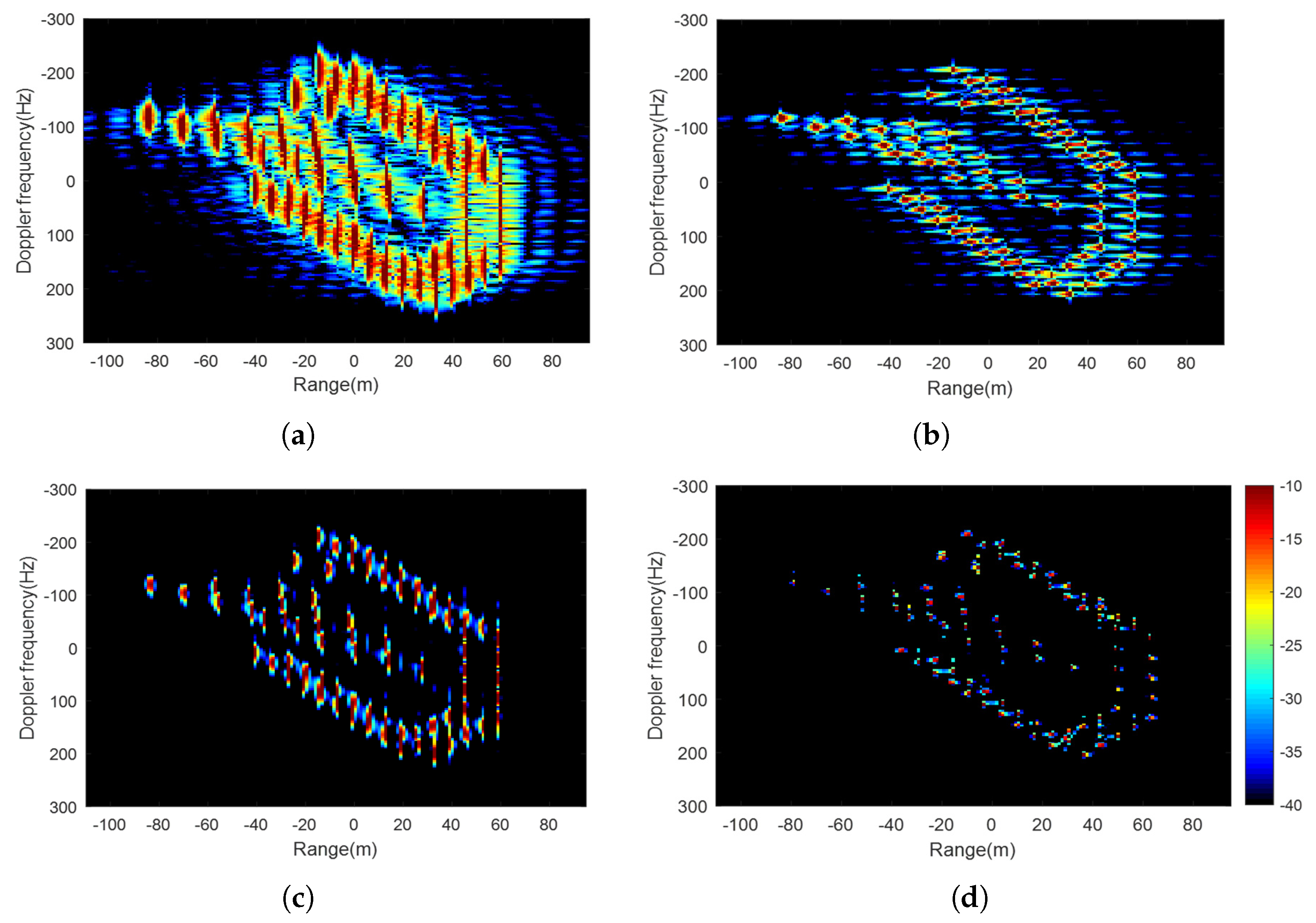
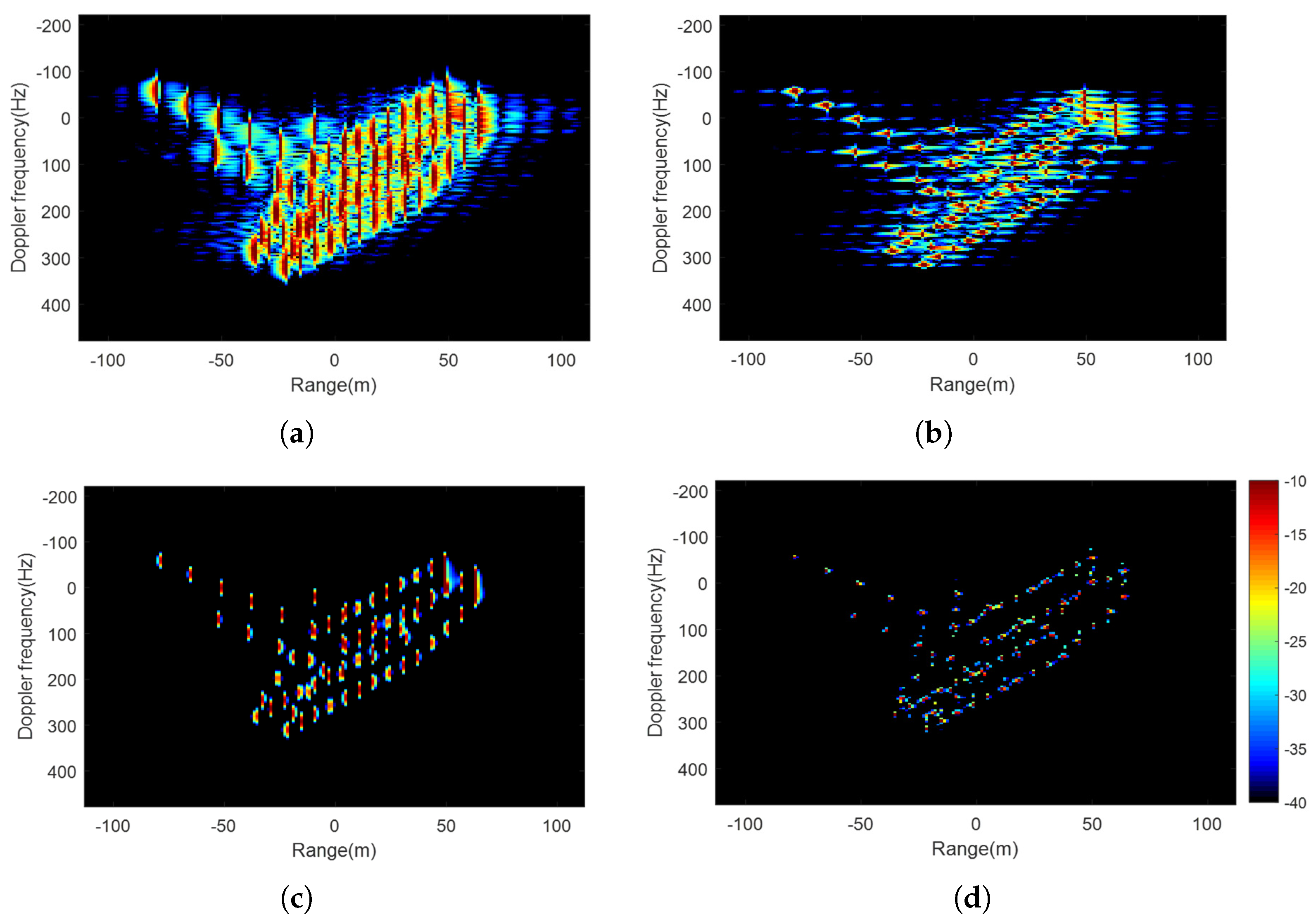
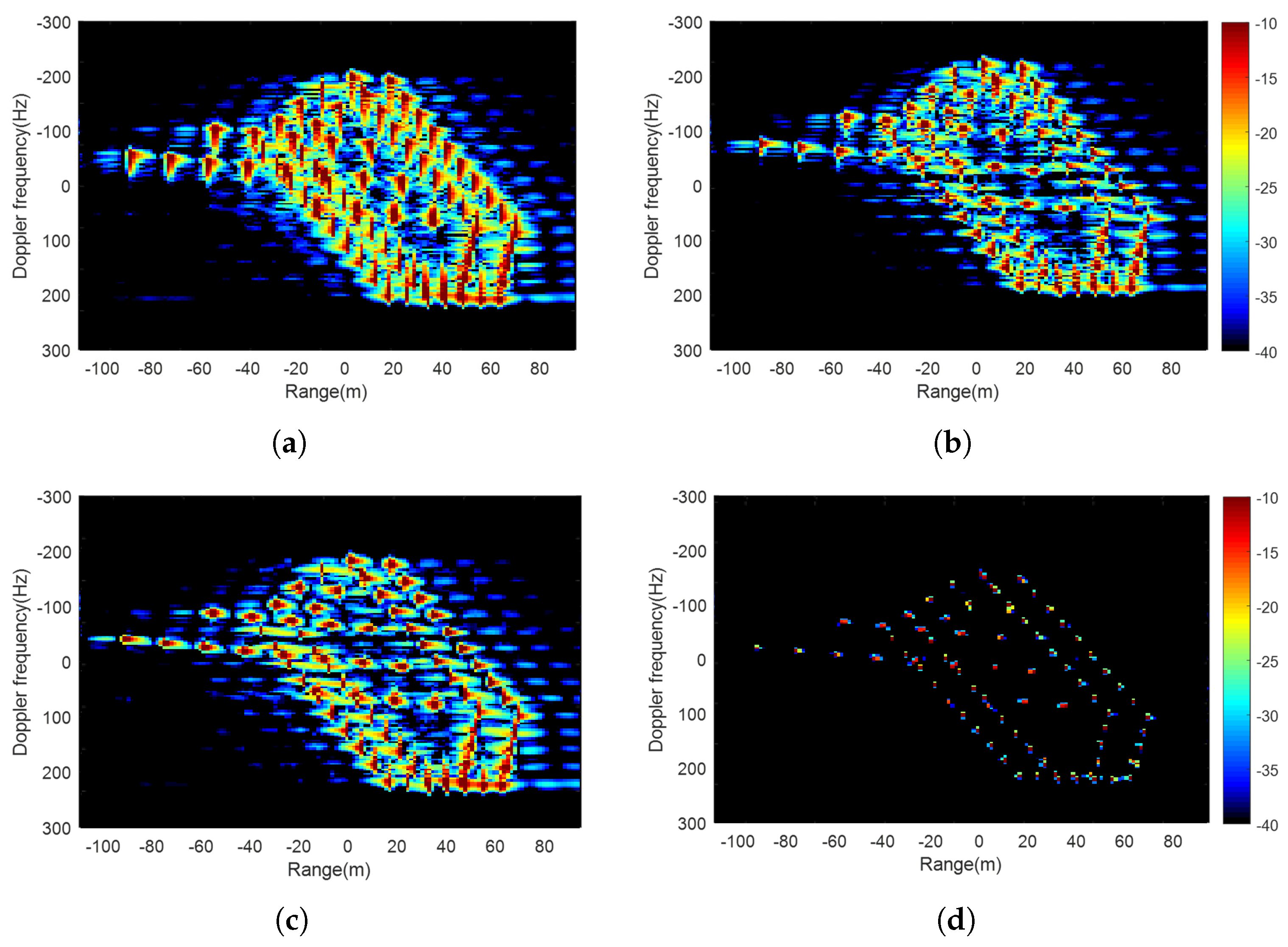
Figure 3 depicts the flowchart of the proposed MBLCFD algorithm, which is summarized as follows.
Step 1 (modified BLU interpolation): The BLU interpolation is operated with the power spectral density (PSD). The PSD is proportional to the antenna power pattern [
12]. Considering the translational target velocity, the modified PSD of the raw azimuth signal
for the moving target can be expressed as
where
and
denote the translational velocities of the satellite and the target along the track.
denotes the synthetic aperture length. The autocorrelation function
of the complex-valued stochastic process
is obtained through the inverse Fourier transform of its PSD:
The PSD can also be considered as the convolution of two square functions of the sinc function. Given that the square of the sinc function corresponds to the Fourier transform of the triangular function,
can thus be regarded as the convolution of two triangular functions. Additionally, considering the illumination time at the azimuth,
should satisfy
In the presence of the additive white Gaussian random noise, the correlation function can be expressed as
where SNR represents the signal-to-noise ratio, and
is the Kronecker delta function.
The nonuniform sampling
is used to estimate the uniform sampling
. The uniformly sampled azimuth signal is reconstructed by the optimal linear unbiased estimation interpolation [
12] using
where
is the nonuniform sampling at the azimuth.
is a column vector. The
qth element in
equals
, where
. The
th element in
G equals
for
and
.
is the correlation function of the signal and noise.
Remark 1: Using the information about the target velocity, the modified BLU can alleviate the coupling of the nonuniform sampling and the target motion. The target velocity is roughly obtained by the estimation of the Doppler center and Doppler rate. The former is estimated by the correlation function, and the latter is estimated by the minimum entropy method. The accuracy of the estimation of the target translational velocity is limited, as the 3D rotation exists and the satellite ephemeris data used would be slightly different from the actual satellite motion.
Remark 2: Compared with the traditional BLU interpolation, the modified BLU interpolation can effectively reconstruct the nonuniform azimuth sampling into a uniform grid. However, the modified BLU interpolation still achieves the rough reconstruction, and the reconstruction performance is limited. As is apparent from (
21) and (
22), the translational target velocity along the track is considered in the PSD and the autocorrelation function. Actually, the radial velocity and the 3D rotation of the target also have an influence on the reconstruction performance. The Doppler shift caused by the radial velocity does not change the shape of the PSD and the amplitude of the autocorrelation function, which indicates a slight influence on the reconstruction performance. The influence of the radial velocity is alleviated in the subsequent step 3. After this, due to the limited accuracy of target velocity estimation, there is still residual translational motion that requires further fine compensation in subsequent processing. The residual translational motion and the 3D rotation are accurately compensated in step 5.
Step 2 (staggered SAR processing): Using the estimation of the target velocity, SAR image processing is performed to compensate for the movement of the radar platform and the translational motion of the target. Exploiting the method of series reversion, the 2D Fourier transform (FT) is used to obtain a 2D spectrum of echo signal after range compression. The details are described as follows:
Performing the Fourier transform in Equation (
12), it can be obtained that
Combining Equations (
12) and (
26), the phase within the integral can be expressed as
where
c is the speed of light. Taking the derivative of Equation (
27), we can obtain
Assuming that
, the relationship between the fast time frequency
and the fast time
is
According to the principle of the stationary phase, Equation (
26) can be expressed as
Similarly, performing an azimuthal Fourier transform on (
30), the following can be derived:
Combining Equations (
30) and (
31), the phase within the integral can be expressed as
Assuming that
, it can be obtained that
Applying the method of series reversion, the slow time can be rewritten as
where
Using Equation (
34) and the principle of stationary phase, the 2D spectrum of the echo signal after range compression can be obtained as
where
is the blind area matrix.
is the range envelope in the frequency domain.
represents the azimuthal spectral envelope with
as the Doppler center frequency.
is the phase term, which can be expressed as
Utilizing a Taylor series expansion of
, the above expression can be further rewritten as
The
,
,
,
, and
are given as
The compensation functions defined in (
43)–(
45) provide a range migration compensation, residual range compensation, and higher order phase compensation, respectively. These compensation functions are used to multiply the received signals, and then the inverse Fourier transform in range is performed. The azimuth compression is carried out by convolving the signals with (
41).
Step 3 (target velocity estimation): Estimating the Doppler center and Doppler rate after the range compression. The Doppler center is estimated by the correlation function method, where is obtained by the peak of the power spectrum. The Doppler rate is estimated by an iterative search to minimize the image entropy.
Subsequently, the translational velocity of the target
is estimated from
and
. The theoretical values
and
. Thus, the difference between the theoretical value
and the estimation
can be expressed as
where
is the slant range from the beam center to the radar platform. The
and
can be ignored in the linear Doppler phase. The radial velocity of the target can be estimated as
The Doppler rate
can be estimated by the minimum entropy method, which can also be expressed as
where
is the satellite velocity.
is the acceleration of the satellite. Based on Equation (
48), the target velocity
along the track can be obtained with
Assuming that
, the translational velocity estimation of the target
can be obtained.
Remark 3: After estimating the target velocity
, the satellite velocity
is replaced with the relative velocity
to update the parameters
,
,
, and
to
where
is the reference slant range, and the second and third order accelerations are expressed as
and
. Note that the compensation of the target translational motion is rough. Due to the limited accuracy of the target velocity estimation, there is still residual translational motion that requires further fine compensation in subsequent processing.
Remark 4: The target velocity needs to be estimated after a rough target detection, which provides an approximate target position. It is difficult to obtain target information solely from the low SNR with sea clutter in the echo domain. The range compression and azimuth compression can improve the SNR via coherent integration. After a rough target detection, the target position can be roughly obtained, and the velocity estimation can be performed. The roughly estimated velocity serves two purposes within the proposed algorithm: (i) modifying the BLU algorithm to mitigate the coupling of the nonuniform sampling and the target motion, reducing the azimuth ambiguity caused by the reconstruction, and (ii) compensating for the translational target motion in SAR processing to the greatest possible extent. In this way, the subsequent ISAR processing can focus more on dealing with the target rotation, improving the performance of target refocusing. The rough target detection, the sea clutter, and the 3D rotation indeed affect the accuracy of the target translational velocity estimation, resulting in residual translational target motion. The residual target motion can be compensated for by the ISAR processor using the hybrid SAR/ISAR technique in the proposed method.
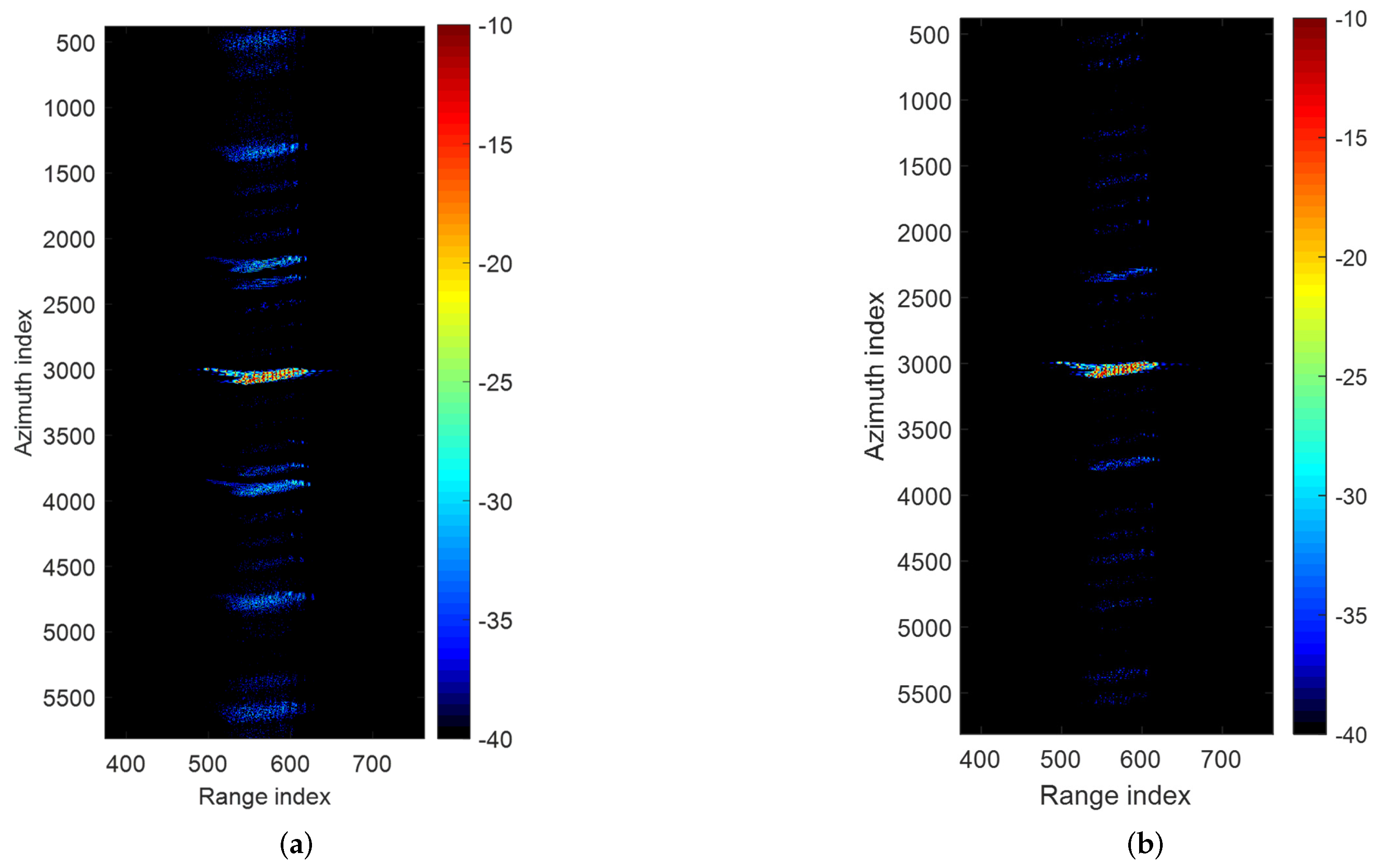
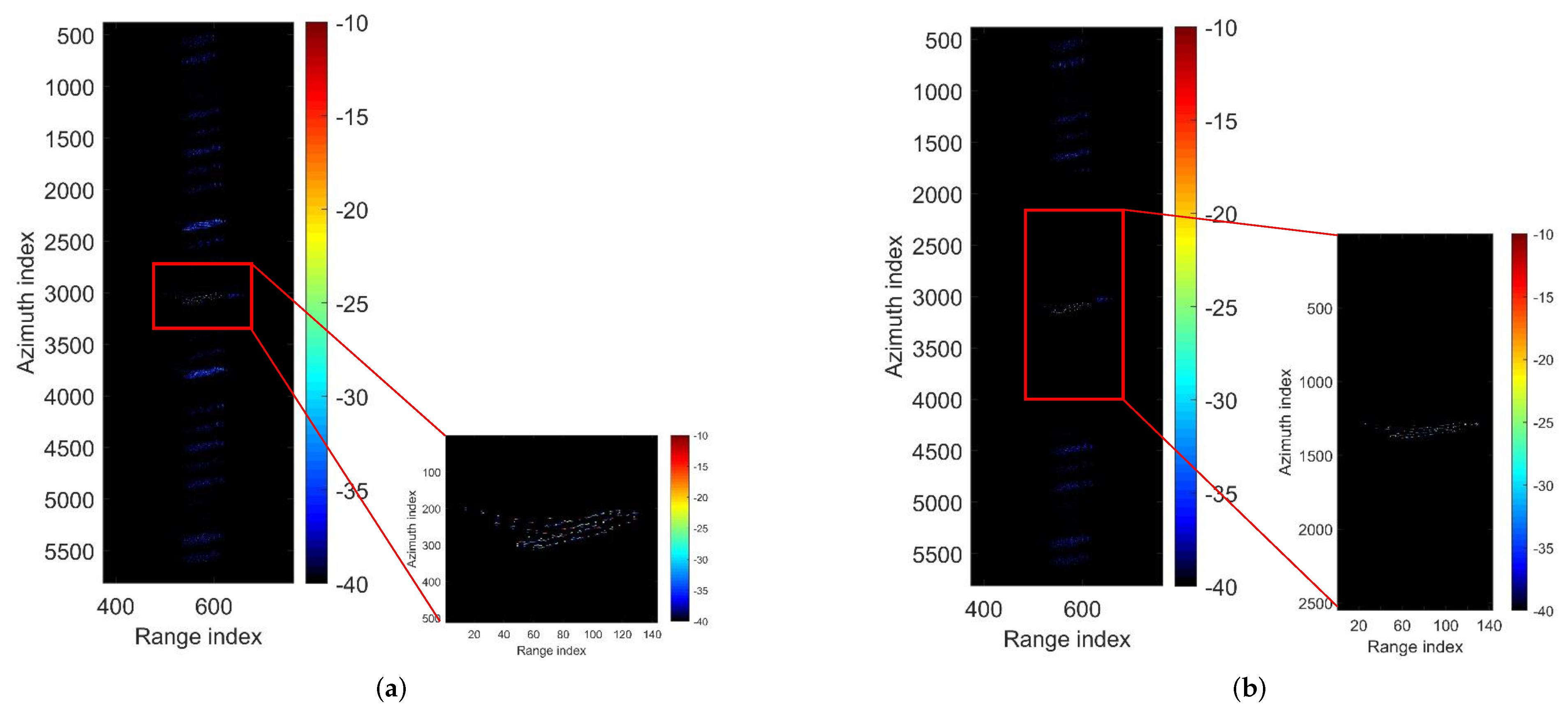
Step 4 (sub-image selection and inversion): The target detection we adopted is a simple detector that compares the intensity of the focused SAR image with a threshold. The threshold varies with the range to account for variations in the noise equivalent sigma zero (NESZ) and resolution cell inside the swath [
17]. The sub-image selection and inversion is processed to obtain the input data for the ISAR processing. Since the SAR image contains several targets with different motions with a large amount of data, the SAR raw data cannot be directly used as the input data. After detecting the moving targets, the sub-image selection is achieved by cropping a small area around a defocused target, containing only the target and some background noise. After that, we invert the sub-image to the equivalent raw data via a two-dimensional inverse fast Fourier transform. The uniformly sampled equivalent raw data are the input of the ISAR processor that aims at forming well-focused ISAR images.
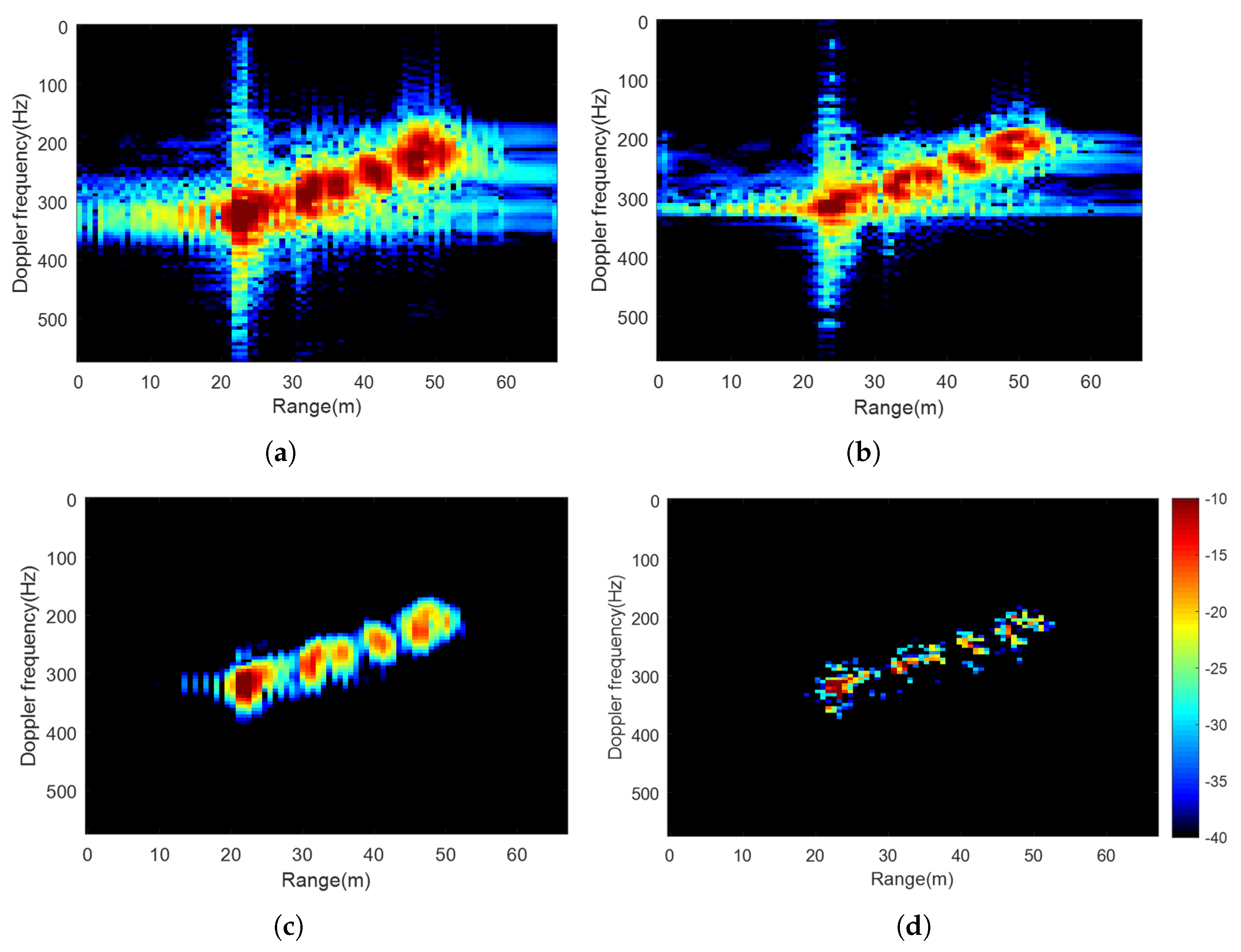
Step 5 (ISAR processing based on a CTFD): The ISAR technology is exploited, as it does not require prior knowledge of the motion parameters of the moving targets and does not impose any restrictions on the motion model. The maritime targets typically undergo translation and complex 3D rotation. The motion is divided into the identical translational component along the radar line of sight (LOS) for all scatterers and the individual rotational component perpendicular to the LOS for each scatterer. To compensate for the former, the phase gradient autofocus (PGA) is adopted. The latter generates the time-varying Doppler frequency, which can be solved for by the range instantaneous Doppler technology with a CTFD [
23,
24]. When operated in the complex domain, a four-order CTFD for the signal
after motion compensation can be expressed as
The echoes of the maritime target can be well approximated as a multi-component cubic phase signal. It should be mentioned that the order of the LFM could be even higher, especially when the rotation of the target is intense under a high sea state and the target is maneuvering. For dealing with polynomial phase signals of fourth order and below,
has no self-crossing term and has excellent aggregation. For higher-order polynomial phase signals,
is still effective. This is due to the fact that the phase derivative coefficients of signals of all orders in the spread factor (SF) decay very quickly. The narrow-band filtering and the CLEAN technique are used to filter out each component of the signal, which can deal with a high-order phase signal, providing good time–frequency aggregation (high resolution) and suppressing the cross-terms effectively.
Remark 5: The algorithm can be applicable for scenarios containing multiple moving targets and stationary scenes. However, the limitation is that the distance between the multiple moving targets or between the targets and the stationary scenes cannot be too close. The multiple moving targets located in different ranges can be distinguished through range compression, while for targets located in different azimuth indexes, their translational velocities need to be estimated separately. When the distance between the targets is too close along the azimuth, the estimation accuracy of the target velocity would be affected, resulting in residual translational motion and degrade the refocusing performance. Step 5 can compensate for the residual translational motion caused by the inaccuracy of the target velocity estimation to some extent. Furthermore, the separation of multiple moving targets is achieved in the image domain in step 4 of the sub-image selection and inversion. Each target is selected by a rectangle and the sub-image is selected to capture most of the target’s signal energy. The size of the rectangle should be appropriate. If the rectangle is too large, there will be more than one target in the sub-image, especially if the distance between the targets is too close. Conversely, if the rectangle is too small, it may degrade the performance of suppressing high sidelobes at the azimuth.