Abstract
A space-time variational method is developed for retrieving upper-level vortex winds from geostationary satellite rapid infrared scans over hurricanes. In this method, new vortex-flow-dependent correlation functions are formulated for the radial and tangential components of the vortex wind. These correlation functions are used to construct the background error covariance matrix and its square root matrix. The resulting square root matrix is then employed to precondition the cost function, constrained by an advection equation formulated for rapidly scanned infrared image movements. This newly formulated and preconditioned cost function is more suitable for deriving upper-level vortex winds from GOES-16 rapid infrared scans over hurricanes than the cost function in the recently adopted optical flow technique. The new method was applied to band-13 (10.3 µm) brightness temperature images scanned every min from GOES-16 over Hurricanes Laura on 27 August 2020 and Hurricanes Ida on 29 August 2021. The retrieved vortex winds were shown to not only be much denser than operationally produced atmospheric motion vectors (AMVs) but also more rotational and better organized around the eyewall than the super-high-resolution AMVs derived from optical-flow technique. By comparing their component velocities (projected along radar beams) with limited radar velocity observations available near the cloud top, the vortex winds retrieved using the new method were also shown to be more accurate than the super-high-resolution AMVs derived from the optical-flow technique. The new method is computationally efficient for real-time applications and potentially useful for hurricane wind nowcasts. Furthermore, the combined use of VF-dependent covariance functions and imagery advection equation is not only novel but was also found to be critically important for the improved performance of the method. This finding implies that similar combined approaches can be developed with improved performance for retrieving vortex flows rapidly scanned using other types of remote sensing on different scales, such as tornadic mesocyclones rapidly scanned by phased-array radars.
1. Introduction
Remote sensing from geostationary satellites has long been recognized and utilized as an important and critical source of information for monitoring atmospheric motions, especially over oceans, where in situ observations are scarce. Beyond qualitative applications provided by geostationary satellite imagery, atmospheric motion vectors (AMVs) derived from sequential geostationary satellite images by tracking coherent cloud and water vapor targets have benefited global model analyses and predictions [1,2], especially tropical cyclone (TC) track predictions [3,4,5]. With the advent of increased resolutions, rapid-scan AMVs were also used to improve reginal model data assimilation and subsequent TC track and intensity predictions in [6,7,8,9]. The findings from these referenced studies indicated that the direct assimilation of high-resolution AMVs has an overall modest positive impact on TC predictions. However, the magnitude of this impact depends on several factors, including (1) the availability of rapid-scan imagery used to produce the AMVs, (2) the AMV derivation approach, (3) the level of quality control employed in the assimilation, and (4) the vortex initialization procedure. Despite the advancements made, further improvement of TC predictions remains difficult (especially for intensity predictions) and requires AMVs produced with a further increased resolution and accuracy by using advanced high-resolution imagers from new-generation geostationary satellites, along with increased computing capacities.
To fully exploit the information provided by advanced high-resolution imagers from new-generation geostationary satellites and thereby improve the resolution and accuracy of operationally produced AMVs for TC applications, optimal AMV processing strategies were explored in [10]. These strategies included (1) adjusting the target selection, spacing and search box criteria to allow denser AMV coverage to better capture smaller-scale hurricane flow fields; and (2) relaxing the QC post-processing steps in the vicinity of a targeted hurricane to accommodate the highly convergent/divergent flow fields associated with hurricane circulations. Furthermore, a “classical variational optical flow” technique [11] was also adopted and employed in [10] to derive super-high-resolution AMVs from GOES-16 rapid infrared scans (every min) over hurricanes. Specifically, it was shown that the derived super-high-resolution AMVs can provide single-pixel spatial resolution, filling gaps not addressed by the aforementioned strategies in upper-levels over the central dense overcast region outside the hurricane eye. While [10] indicated that the derived super-high-resolution AMV field can qualitatively match other cloud-tracked vectors quite well in most areas and depict the conceptual model of hurricane flow near the core, the adopted optical flow technique remains experimental and requires quantitative validation. Given this adopted optical flow technique was not originally developed for TC applications, it exhibits shortcomings for TC applications, as revealed below.
As reviewed in the introduction section of [11], various optical flow techniques have been developed for broad applications. Although optical flow techniques have also been applied to fluid mechanics (see for example [12]), they were not specifically tailored for meteorological applications. In particular, the variational formulation used in the optical flow technique [11] is neither exactly suitable nor optimal for retrieving vortex winds over hurricanes. As shown in Equations (4)–(7) in [11], the cost function consists of three terms. The first term imposes a weak constraint based on the assumed conservation of the imagery grey value. This conservation is essentially the same as that formulated in the imagery advection equation, successfully used as either a strong constraint in [13,14,15] or a weak constraint in [16,17,18], for retrieving vector wind fields from single-Doppler radar scanned images. The second term imposes a weak constraint based on the assumed conservation of the gradient of imagery value. This constraint aids in tracking solid-body motion but proves not suitable for tracking fluid flows. The third term is a penalty term constructed using squared gradients of estimated velocity components, which is similar to the background term in meteorological data assimilation. However, it differs from the conventional approach as it uses the inverse of background wind error covariance, formulated independently for each velocity component by a highly-truncated differential operator to retain only the first order. Consequently, the background wind error covariance is modeled much more crudely than that commonly used in variational data assimilations for meteorological applications [19,20,21,22,23,24,25] and also much less accurately than those formulated for vortex flow analyses and retrievals [26,27] in which the primary feature of the vortex flow is known.
To overcome the shortcomings revealed above, it is necessary not only to eliminate the assumed conservation of the gradient of imagery value but also to construct a background error covariance matrix in the cost function with proper vortex flow (VF) dependent structures tailored specifically for hurricane vortex wind analyses. This can be achieved by modifying the VF-dependent covariance functions [26,27] adaptively for the radial and tangential components of hurricane vortex wind, to construct the background error covariance matrix in the cost function. In this way, the square root of the covariance matrix can be also easily constructed to precondition the cost function, making the preconditioned cost function more efficient and more suitable for hurricane vortex wind analyses compared to the cost function used in the optical flow technique. In this case, the advection equation, previously formulated for radar scanned image pattern movements and used as a strong constraint in the simple adjoint method [13,14,15], can also be modified for infrared image pattern movements scanned from geostationary satellites. As shown in Equation (3.4) of [15], the cost function in the simple adjoint method contains two penalty terms constructed using squared horizontal divergence and squared vertical vorticity, respectively. As these two penalty terms are computed from the retrieved wind field, their imposed weak constraints on the retrieved wind field mimic the background term in meteorological data assimilation, but the background wind error covariance is still modeled crudely (using the inverses of highly-truncated differential operators according to [25]) without any flow dependence. Using the adaptively modified VF-dependent covariance functions in combination with the modified advection-equation constraint to construct the cost function, a novel space-time variational method can be devised for retrieving upper-level vortex winds from geostationary satellite rapid scans over hurricanes. This innovative approach is anticipated to be more effective and more accurate than the optical flow technique for retrieving vortex winds above hurricanes.
By implementing the aforementioned modifications, this paper aims to develop a new space-time variational method and apply the new method to GOES-16 rapid scans over hurricanes. By comparing the new-method retrieved vortex winds with the operationally produced AMVs and the super-high-resolution AMVs derived by the optical flow technique, we intend to demonstrate that the vortex winds retrieved using the new method are not only much denser than operationally produced AMVs but also more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs. Furthermore, by projecting the retrieved vortex winds along the radar beams and verifying the projected components against available radar velocity observations in narrow arc-shape areas on radar scanned conic surfaces near the cloud top, we aim to illustrate that the vortex winds retrieved with the new method are more accurate than the optical-flow technique derived super-high-resolution AMVs, at least for their projected component velocities in areas where radar velocity observations are available near the cloud top.
In this paper, the new method is applied to band-13 (10.3 µm) brightness temperature images scanned every min from GOES-16 over Hurricanes Laura on 27 August 2020 and Hurricanes Ida on 29 August 2021. The selection of these hurricanes was based on their proximity to coastal areas, with radar velocity observations available near the cloud top for comparison with the satellite-based technique. The paths of these two hurricanes are shown in Figure 1 in the following reports from the NOAA National Hurricane Center: https://www.nhc.noaa.gov/data/tcr/AL132020_Laura.pdf (accessed on 6 December 2023), https://www.nhc.noaa.gov/data/tcr/AL092021_Ida.pdf (accessed on 6 December 2023).
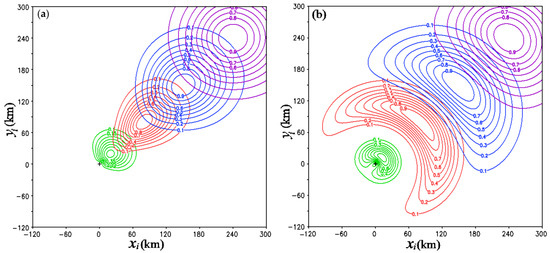
Figure 1.
(a) Correlation function constructed using G0(ri, rj)C(βi, βj) for the radial-component velocity vr plotted as functions of (xi, yi), with green, orange, blue, and purple contours corresponding to four different locations where (xj, yj) is fixed at radial distances of R = 14.1, 113.1, 212.1, and 339.4 km, respectively, along the diagonal line northeastward away from the vortex center marked by red + sign. (b) As in (a) but for correlation function constructed for the tangential-component velocity vt. Here, (xi, yi) and (xj, yj) are the same two paired correlation points as (ri, βi) and (rj, βj), respectively, but transformed and expressed in the original physical space. In each panel, the correlation function is plotted as a function of (xi, yi) for each fixed (xj, yj) using nine contours of the same color, with the contour values labeled every 0.1 from 0.1 to 0.9.
This paper is organized as follows. The new method is introduced with the modified VF-dependent covariance functions and modified cost function in Section 2. The results from Hurricanes Laura and Ida are presented in Section 3 and Section 4, respectively, where the new-method retrieved vortex winds are compared with the operationally produced AMVs and optical-flow technique derived super-high-resolution AMVs and partially verified against available radar velocity observations near the cloud top. The merits and limitations of the new method are discussed in Section 5. The conclusions follow in Section 6.
2. Space-Time Variational Method
2.1. VF-Dependent Covariance Functions
To facilitate the formulation of VF-dependent covariance functions, the vortex-following Cartesian coordinate system, (x, y), co-centered with the vortex at a given vertical level needs to be transformed into a polar coordinate system, (R, β), where R ≡ (x2 + y2)1/2 and (x, y) = R(cosβ, sinβ). As shown in Equation (3.6) of [27], by transforming R further into r ≡ arcsinh(R/Rc)]/l, where Rc is a scale factor for R and l is the decorrelation length factored into r, VF-dependent covariance functions can be conveniently formulated in (r, β) with a properly specified decorrelation arc angle Φ. In this way, as shown in Section 4b of [27], the decorrelation arc length ΦR and the decorrelation radial-length, denoted by L, in the original physical space both approach Rsinh(l/2) as R increases beyond Rc. This increase in L and ΦR with R is desirable for velocity error correlations near and around the vortex core, because it reflects the increased scales of turbulent eddies in true VFs away from the vortex center, while the background error is essentially the true VF, given that the background VF is zero.
However, as R increases far away from the vortex core, L and ΦR should approach the same constant value, so the correlation functions can become isotropic and homogeneous for the large-scale environmental flow as commonly assumed in variational data assimilation [19,20,21,22]. To have this property, r and Φ are reformulated into
where a (>1) and b (>0) are adjustable parameters, and Φ0 is the decorrelation angle in the limit of R → 0. The VF-dependent covariance functions can be then formulated in this new (r, β)-coordinate system using the correlation functions G0(ri, rj) in Equation (3.8a) and C(βi, βj) in Equation (4.9) from [27], where (ri, βi) and (rj, βj) denote the two paired correlated points in the (r, β)-coordinate system. In the limit of R → 0, the reformulated r in Equation (1) approaches the same limit, that is, r → R/(Rcl), as r defined in Equation (3.6) of [27] and the reformulated Φ in Equation (2) approaches the same limit, that is, Φ → Φ0, as Φ defined in Equation (4.9) of [27]. Thus, the correlation functions G0(ri, rj) and G0(ri, rj) continue to have the same (or nearly the same) structures at the vortex center (or in the vortex core) as those shown and explained in [27]. However, for the reformulated r in Equation (1), when R > or >> Rc, the decorrelation radial length in R is given by L ≈ dR/dr = alRc/[1 + (a − 1)ch−2(R/Rc)] and this gives L → alRc as R → ∞. In this case, for the reformulated Φ in Equation (2), it is easy to see that ΦR → alRc as R → ∞. Thus, L and ΦR approach the same constant value of alRc and the correlation functions become not only isotropic but also homogeneous as R → ∞.
r ≡ [R/Rc + (a − 1)tanh(R/Rc)]/(al),
Φ ≡ al(Rc/R)tanh [Φ0R/(alRcb)] [1 + (b − 1) exp (−0.5R2/Rc2)]
Using G0(ri, rj)C(βi, βj) with the reformulated r and ΦR, the background error correlation functions are constructed for the radial-component velocity, denoted by vr, by setting Rc = 150 km, l = 0.2, a = 2, b = 0.2, and Φ0 = 2 (in arc), and for the tangential-component velocity, denoted by vt, by setting Rc = 150 km, l = 0.1, a = 4, b = 2, and Φ0 = 1.5. The correlation function constructed by G0(ri, rj)C(βi, βj) for vr (or vt) is plotted in Figure 1a (or Figure 1b) as functions of one correlated point (xi, yi) in the original physical space using contours of four different colors corresponding to the four different locations where the other correlated point (xj, yj) is fixed at four different radial distances along the diagonal line northeastward away from the vortex center.
As shown in Figure 1a, the correlation function for vr exhibits a slightly curved structure around the vortex center within the vortex core (that covers the hurricane eye and eyewall), particularly when the reference point (i.e., the other correlated point (xj, yj)) is very close to the vortex center. However, as the reference point moves away from the vortex core, the correlation structure becomes radially elongated. Subsequently, with increasing distance from the vortex core, it asymptotically becomes isotropic and homogeneous. The radially elongated structure, observed when the reference point is outside (but not too far away from) the vortex core, manifests that the spatial correlation of background vr error is predominantly aligned with the radial direction. This alignment is expected because the background vr error is essentially the true vr for zero background VF and the spatial variations of true vr are correlated dominantly in the radial direction for upper-level divergent VFs over hurricanes.
As illustrated in Figure 1b, the correlation function for vt displays a highly curved structure around the vortex center within the vortex core when the reference point is very close to the vortex center. The correlation structure is stretched and curved along the azimuthal direction. With an increasing distance from the vortex core, it asymptotically becomes isotropic and homogeneous. This azimuthally stretched structure, observed when the reference point is outside (but not too far away from) the vortex core, indicates that the spatial correlation of background vt error predominantly aligns with the azimuthal direction, as expected. This alignment arises because the background vt error is essentially the true vt for zero background VF and the spatial variations of true vt are correlated dominantly in the azimuthal direction for upper-level VFs over hurricanes.
The background error covariance matrix and its root square for the state vector of (vr, vt) can be derived in the following decomposed form:
where B1/2 ≡ (σrPr, σtPt)diag is the root square of B, ( )T denotes the transpose of ( ), σr2 (or σt2) is the background error variance for vr (or vt), and Pr (or Pt) is the square root of correlation matrix derived from the correlation function for vr (or vt), essentially in the same way as shown in Section 4c of [27].
B = B1/2BT/2 = (σrPr, σtPt)diag(σrPrT, σtPtT)diag,
2.2. Cost Function
The advection equation for radar scanned reflectivity (or velocity) image pattern movements, originally formulated as a strong constraint in the simple adjoint method [13,14,15], has been adopted and reformulated for the applications considered in this paper. The reformulated advection equation is in a moving (x, y) coordinate system co-centered with the hurricane, and it has the following form:
where Tb is the brightness temperature from GOES infrared (IR) image scans over the retrieval domain that is moving and co-centered with the hurricane, v ≡ (u, v) is the time-averaged horizontal velocity in and relative to the moving retrieval domain, k is a constant diffusion coefficient, and s is a time-averaged source term. The time average is taken over the retrieval time period τ, during which multiple consecutively scanned Tb are used for the retrieval. Here, v (or s) is a unknow vector (or scalar) field of (x, y) to be retrieved and k is a unknow constant to be retrieved. The radial (or tangential) component of v is still denoted by vr (or vt). The state vectors of (vr, vt, s) are denoted by (vr, vt, s) and transformed into control vectors (cr, ct, cs) defined by (σrPrcr, σtPtct, σsPscs) ≡ (vr, vt, s) to precondition the background term in the cost function, where σrPr and σtPt are as in (3), σsPs is the root square of the background error covariance matrix for s, σs2 is the background error variance for s, and the background errors are assumed to be uncorrelated between vr, vt, and s. Ps is constructed by using the same parameter setting as Pr, except that l is reduced from 0.2 to 0.1 by considering that s tends to have errors in smaller scales and correlated in shorter distances than vr. In this paper, we set σr = σt = 30 m/s and set σs to the averaged value of |∂tTbob| over the retrieval domain and time period τ, where Tbob denotes the observed Tb. The retrieval domain D covers a 600 × 600 km2 area that is moving and co-centered with the hurricane, τ (= 2 min) covers three consecutive Tbob scans, and the time step is ∆t = τ/4 for integrating (4) on a 2 km grid.
∂tTb + v·∇Tb − k∇2Tb = s,
The preconditioned cost function has the following form:
where ∑n denotes the summation over integer n from 1 to N (=4), fn (or yn) is the state vector of Tbf (or Tbob) at t = n∆t, Tbf is the Tb computed by integrating (4) forward in time with the initial and boundary conditions given by Tbob, σn2 ≡ σo2(n + 1)1/2, and σo2 is the error variance of Tbob. Here, σn2 is the sum of error variances of Tbob and Tbf, so σn2 − σo2 = σo2 [(n + 1)1/2 − 1] is the error variance of Tbf and is estimated as an increasing function of n by considering that the error of Tbf increases with t as it is computed by integrating (4) forward in time. This consideration is similar to that explained in Section 3b of [13] and its implement is similar to that shown in Section 4a of [15].
J = |cr|2 + |ct|2 + |cs|2 + ∑n|fn − yn|2/σn2,
The cost function J is minimized in the space of (cr, ct, cs, k) using the standard conjugate-gradient descending algorithm with the initial guess of (cr, ct, cs, k) given by zero (cr, ct, cs) and k = 200 m2/s, while the gradients of J with respect to the controls (cr, ct, cs, k) are derived in the same way as shown in Appendix B of [14]. From the value of cr (or ct) at the minimum of J, the retrieved vr (or vt) is computed in terms of its state vector using vr = σrPrcr (or vt = σtPtct).
3. Applications to Hurricane Laura on 27 August 2020
3.1. Retrieved Vortex Winds at 06:00 UTC
The new space-time variational method was applied to three consecutive band-13 (10.3 µm) brightness temperature images (for Tbob < 280 °K) scanned every min around 06:00 UTC on 27 August 2020 from GOES-16 over Hurricane Laura, capturing the period shortly before Hurricane Laura made landfall near the Texas–Louisiana border. The vortex wind retrieval was performed in a 600 × 600 km2 domain that was moving and co-centered with the hurricane. The hurricane center moving velocity was (uc, vc) = (−0.74, 6.85) m/s, and this moving velocity was added back to the domain-relative vortex winds (retrieved within the 600 × 600 km2 moving domain) to derive the ground-relative vortex winds. The retrieved ground-relative vortex winds are plotted in Figure 2a using black arrows superimposed on the GOES-16 band-13 brightness temperature image (shown by color shades for Tbob < 280 °K at 06:00 UTC). These retrieved vortex winds are much denser than the operationally produced AMVs from GOES-16 IR image movements shown in Figure 2b. To further illustrate their assigned heights (at the cloud top), the retrieved vortex winds in Figure 2a are replotted in Figure 2c, but atop the color shades of cloud top height (estimated operationally from GOES-16 observations). The comparison of Figure 2c,d reveals that the (ground-relative) vortex winds retrieved using the new method are more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs.
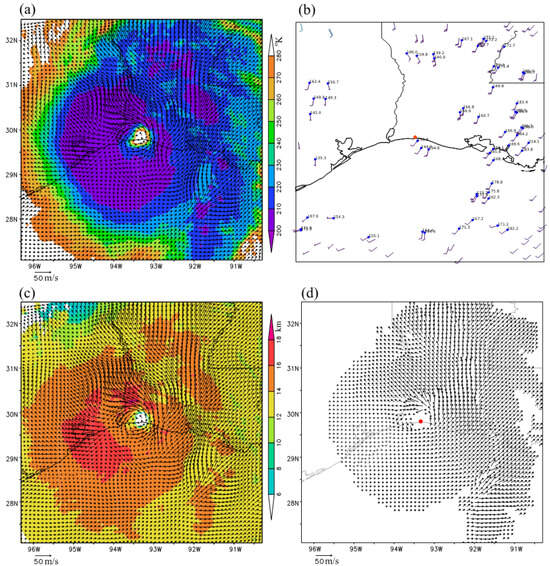
Figure 2.
(a) Retrieved (ground-relative) vortex winds (plotted using black arrows atop the color shades of GOES-16 band-13 brightness temperature image for Tbob < 280 °K) obtained by applying the new method to GOES-16 band-13 brightness temperature images scanned (every minute) over Hurricane Laura around 06:00 UTC on 27 August 2020. (b) Operational products of AMVs derived from GOES-16 band-14 (10.3 µm) brightness temperature image displacements around 06:00 UTC on 27 August 2020 (with the AMVs shown using wind bars and the assigned pressure levels shown in mb). (c) As in (a) but atop the color shades of cloud top height. (d) Super-high-resolution AMVs (plotted by black arrows) derived by applying the optical flow technique to GOES-16 band-13 brightness temperature images scanned at 05:59 and 06:00 UTC. In each panel, the coastline and state lines are plotted in thin solid black. The hurricane vortex center is shown by the red dot in (b,d).
Direct and comprehensive verifications of retrieved vortex winds are challenging due to the shortage of ground-truth upper-level wind data. Fortunately, dealiased radar velocity observations are available near the cloud top from the operational KHGX radar in several narrow arc-shape areas (see Figure 3a,b). Note that these arc-shape areas are not only far away (>100 km) from the radar but also on the conical surfaces of radar scans at relatively high elevation angles (that is, primarily 4.0°, 5.1°, 6.4° and 8.0°), so these arc-shape areas are scanned at heights near the cloud top (within 3 km below the cloud top as shown in Figure 3a). The total number of velocity observations within 3 (2 or 1) km below the cloud top is 1321 (733 or 229), with mean and RMS values of −14.4 (−20.6 or −20.7) and 19.5 (22.9 or 22.7) m/s, respectively. These observations served as ground truths to assess the accuracies of the retrieved vortex winds, as described below.
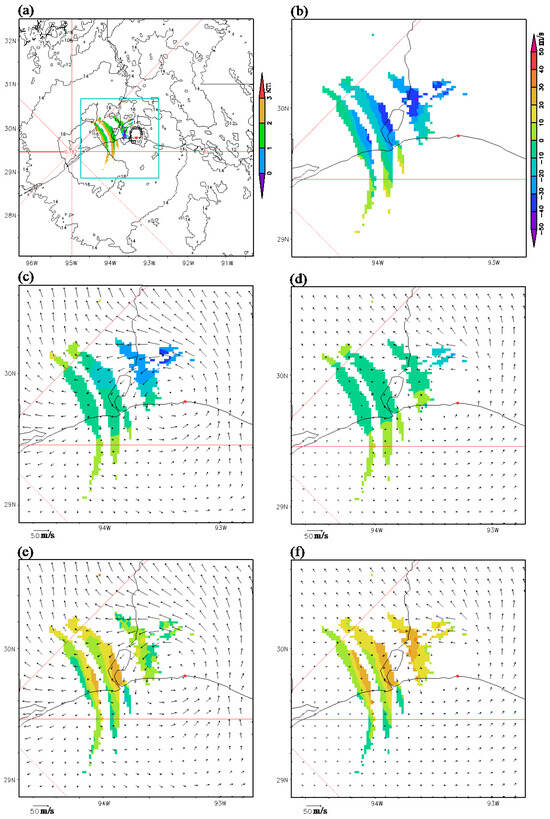
Figure 3.
(a) Depths (shown by color shades) of available radar velocity observations (from the operational KHGX radar in narrow arc-shape areas) within 3 km from the cloud top (with the cloud top height plotted using black contours) over Hurricane Laura. (b) Values of available radar velocity observations (shown with color shades in narrow arc-shape areas within 3 km below the cloud top) within the magnified area enclosed by cyan boundary lines in (a). (c) As in (b) but for projected components (along the radar beams) of the new-method retrieved vortex winds (shown using the black arrows from Figure 2a). (d) As in (b) but for projected components of the optical-flow technique derived super-high-resolution AMVs (shown using the black arrows from Figure 2d). (e) As in (c) but the color shades show the differences of projected component velocities in (c) from the radar observed in (b). (f) As in (d) but the color shades show the differences of projected component velocities in (d) from the radar observed in (b). In each panel, the red lines show the cardinal and intercardinal directions from the radar, and the red dot marks the hurricane vortex center. The color scale for radar observed velocities shown on the right side of panel (b) also applies to the color shades in panels (c–f).
The new-method retrieved (ground-relative) vortex winds are projected along the radar beams and the projected component velocities are shown in Figure 3c using color shades in the same arc-shape areas as those shown for the radar velocity observations in Figure 3b, while the black arrows in Figure 3c duplicate those in Figure 2c. The optical-flow technique derived super-high-resolution AMVs are also projected along the radar beams and the projected component velocities are shown in Figure 3d using color shades in the same arc-shape areas as those shown in Figure 3b, while the black arrows in Figure 3d duplicate those in Figure 2d. Clearly, the projected component velocities shown with the color shades in Figure 3c are mostly negative and more negative than those in Figure 3d, although less negative than the observed velocities in Figure 3b. Thus, the projected component velocities of the new-method retrieved vortex winds are closer to the observed velocities in Figure 3b than the projected component velocities of optical-flow technique derived super-high-resolution AMVs. Specifically, averaged over the narrow arc-shape areas where the radar velocity observations are available within 3 (2 or 1) km below the cloud top, the mean value of projected component velocities of new-method retrieved vortex winds in Figure 3c is −8.1 (−11.8 or −13.9) m/s, which is much closer to the mean value of radar observations (that is, −14.4 (−20.6 or −20.7) m/s as mentioned earlier) than the mean value of the projected component velocities of the optical-flow technique derived super-high-resolution AMVs in Figure 3d; that is, −3.2 (−4.5 or −5.1) m/s.
The color shades in Figure 3e represent the differences between the projected component velocities shown by color shades in Figure 3c (for the new-method) and the radar-observed velocities in Figure 3b. Meanwhile, the color shades in Figure 3f plot the differences between the projected component velocities shown by color shades in Figure 3d (for the optical-flow technique) and the radar observed velocities in Figure 3b. Clearly, the differences shown by the color shades in Figure 3e are much closer to zero that those shown by color shades in Figure 3f. In particular, computed over the narrow arc-shape areas where radar velocity observations are available within 3 (2 or 1) km below the cloud top, the computed mean and RMS values of color-shaded difference field in Figure 3e for the new method are −6.2 (−8.8 or −6.8) and 11.1 (12.6 or 12.0) m/s, respectively. In contrast, the computed mean and RMS values of the color-shaded difference field in Figure 3f for the optical-flow technique are −11.1 (−16.1 or −15.6) and 15.0 (17.8 or 17.4) m/s, respectively. These results and comparisons indicate that the new-method retrieved vortex winds are more accurate than the optical-flow technique derived super-high-resolution AMVs, at least for their projected component velocities in the narrow arc-shape areas (shown in Figure 3a).
3.2. Retrieved Vortex Winds at 03:00 UTC
The new method was also applied to three consecutive band-13 brightness temperature images (for Tbob < 280 °K) scanned at 02:59, 03:00, and 03:01 UTC on 27 August 2020 from GOES-16 over Hurricane Laura. The vortex wind retrieval was again performed in a 600 × 600 km2 domain that was moving and co-centered with the hurricane. During this time, the hurricane center moving velocity was (uc, vc) = (−1.35, 6.67) m/s. Adding this moving velocity to the retrieved domain-relative vortex winds resulted in the ground-relative vortex winds. These retrieved (ground-relative) vortex winds are plotted using black arrows in Figure 4a atop the brightness temperature image (for Tbob < 280 °K at 03:00 UTC) and in Figure 4c atop the color shades of cloud top height. Again, these retrieved vortex winds are not only much denser than the operationally produced AMVs shown in Figure 4b but also more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs, as illustrated in Figure 4d.
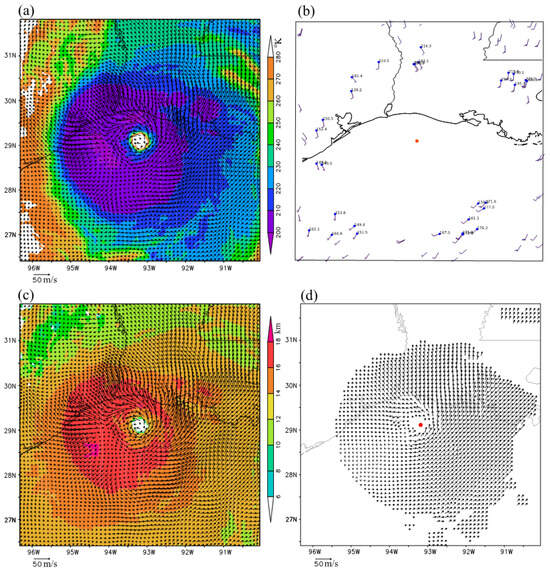
Figure 4.
As in Figure 2 but around 03:00 UTC on 27 August 2020.
At 03:00 UTC, the hurricane was offshore and exhibited greater intensity with taller clouds than at 06:00 UTC shortly before the hurricane landfall. Although dealiased radar velocity observations are still available for 03:00 UTC within 3 km below the cloud top in narrow arc-shape areas (as shown in Figure 5a,b), these narrow arc-shape areas are on the conical surfaces of radar scans at only three elevation angles (that is, 4.0°, 5.1°, and 6.4°). Thus, in comparison with the observations available at 06:00 UTC, the total number of observations available at 03:00 UTC within 3 (2 or 1) km below the cloud top was reduced to 728 (327 or 116). The mean value of these observations negatively increased to −22.1 (−27.6 or −27.5) m/s, and their RMS value increased to 26.4 (29.4 or 28.5) m/s.
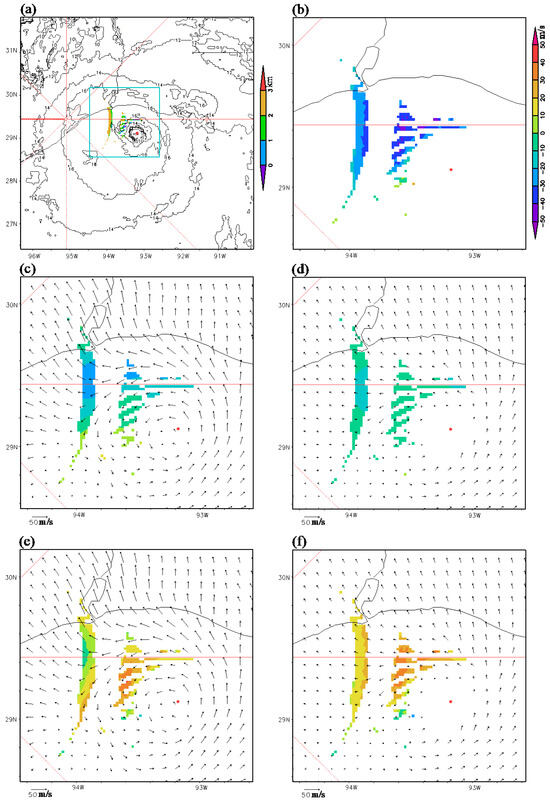
Figure 5.
As in Figure 3 but around 03:00 UTC on 27 August 2020.
In this case, the new-method retrieved vortex winds (or the optical-flow technique derived super-high-resolution AMVs) are plotted in Figure 5c (or Figure 5d) using black arrows that duplicate those in Figure 4c (or Figure 4d). Additionally, the projected component velocities (along the radar beams) are shown in Figure 5c (or Figure 5d) using color shades in the same arc-shape areas as those shown for the velocity observations in Figure 5b. Again, the projected component velocities shown with the color shades in Figure 5c for the new method are closer to those observed in Figure 5b than those in Figure 5d for the optical-flow technique. To provide specific values, when averaged over the narrow arc-shape areas where the velocity observations are available within 3 (2 or 1) km below the cloud top, the mean value of projected component velocities in Figure 5c is −9.0 (−10.3 or −9.9) m/s for the new method. This value is notably closer to the mean value of the radar-observed velocities (that is, −22.1 (−27.6 or −27.5) m/s as mentioned earlier) than the mean value of the projected component velocities in Figure 5d; that is, −6.0 (−7.0 or −7.3) m/s for the optical-flow technique.
The color shades in Figure 5e illustrate the differences in the projected component velocities in Figure 5c (for the new method) from the radar-observed velocities in Figure 5b. In contrast, the color shades in Figure 5f show the differences of the projected component velocities in Figure 5d (for the optical-flow technique) from the radar-observed velocities in Figure 5b. Again, the color-shaded differences in Figure 5e are closer to zero than those seen in Figure 5f. Computed over the narrow arc-shape areas where the velocity observations are available within 3 (2 or 1) km below the cloud top, the computed mean and RMS values of the color-shaded difference field in Figure 5e are −13.1 (−17.3 or −17.6) and 17.0 (19.4 or 18.6) m/s, respectively. In contrast, the computed mean and RMS values of the color-shaded difference field in Figure 3f are −16.1 (−20.6 or −20.3) and 19.9 (22.2 or 21.0) m/s, respectively. These results reaffirm that the new method was more accurate than the optical-flow technique, at least for their projected component velocities in the narrow arc-shape areas (shown in Figure 5a).
4. Applications to Hurricane Ida on 29 August 2021
4.1. Retrieved Vortex Winds at 16:00 UTC
The new method was next applied to three consecutive band-13 brightness temperature images (for Tbob < 280 °K) scanned at 15:59, 16:00, and 16:01 UTC on 26 August 2021 from GOES-16, capturing Hurricane Ida shortly before its landfall in Port Fourchon, Louisiana. The vortex wind retrieval was still performed in a 600 × 600 km2 moving domain co-centered with the hurricane. The hurricane center moving velocity was (uc, vc) = (−3.29, 3.49) m/s. With this moving velocity added to the retrieved domain-relative vortex winds, the resulting ground-relative vortex winds were as plotted using black arrows in Figure 6a atop the brightness temperature image (for Tbob < 280 °K at 16:00 UTC) and replotted in Figure 6c but atop the color shades of the cloud top height. Again, these retrieved vortex winds are not only much denser than the operationally produced AMVs from GOES-16 IR image movements shown in Figure 6b but also more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs shown in Figure 6d. It is worth noting that the optical-flow technique derived super-high-resolution AMVs in Figure 6d became very noisy and contained some unrealistically large values in the periphery of the hurricane vortex where the cloud top height drops below 12 km (see the color shades in Figure 6c).
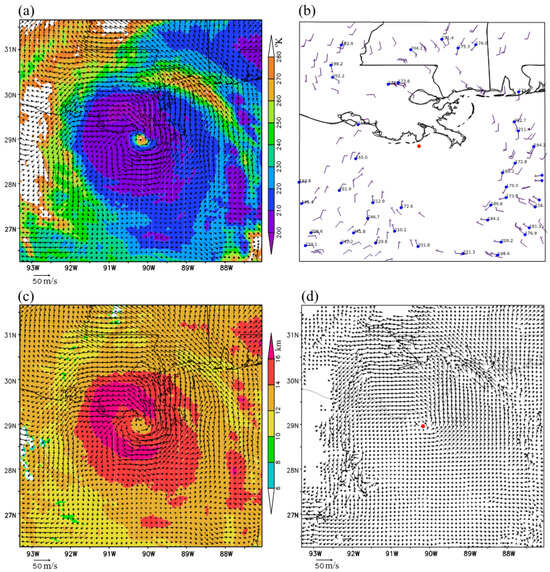
Figure 6.
As in Figure 2 but for Hurricane Ida around 16:00 UTC on 29 August 2021.
In this case, as illustrated in Figure 7a,b, dealiased radar velocity observations are available from the operational KLIX radar within 3 km below the cloud top in many narrow arc-shape areas, not only south of the radar site (between the hurricane center and radar site) but also north of the radar site (far away from the hurricane center). These narrow arc-shape areas are on the conical surfaces of radar scans, spanning a range of 11 elevation angles, from 1.8° to 19.5°. Thus, in comparison with the situations described in Section 3 for Hurricane Laura, the total number of dealiased radar velocity observations within 3 (2 or 1) km below the cloud top increased substantially to 4128 (1739 or 511) with their RMS value reduced to 17.5 (17.3 or 18.0) m/s. Additionally, their mean value shifted toward zero to −4.5 (−2.5 or 0.32) m/s. In this case, as shown in Figure 7b, the observed velocities were no longer dominantly negative (as those shown in Figure 3b and Figure 5b), so their positive and negative values largely offset each other, resulting in a mean value close to zero.
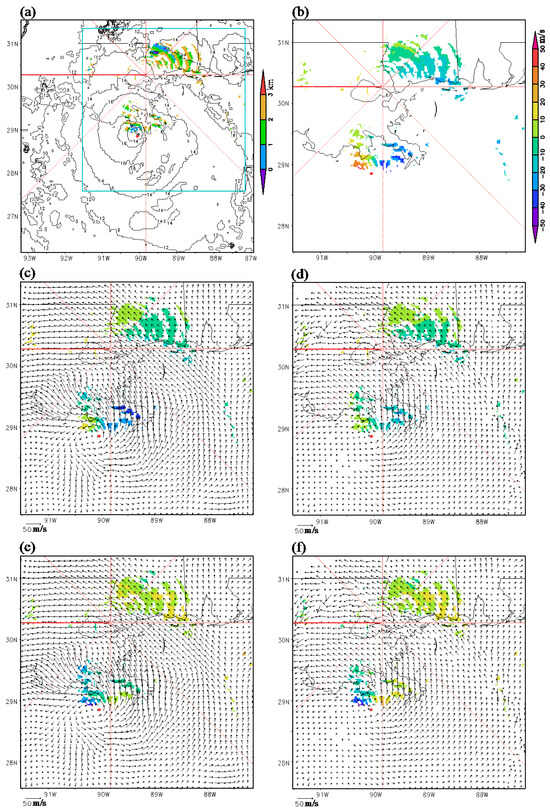
Figure 7.
As in Figure 3 but for Hurricane Ida around 16:00 UTC on 29 August 2021 with available radial-velocity observations (within 3 km below the cloud top) from the operational KLIX radar.
The new-method retrieved vortex winds (or optical-flow technique derived superhigh-resolution AMVs) are plotted in Figure 7c (or Figure 7d) using black arrows that duplicate those in Figure 6c (or Figure 6d), while their projected component velocities (along the radar beams) are shown in Figure 7c (or Figure 7d) using color shades in the same narrow arc-shape areas as those shown for the radar velocity observations in Figure 7b. Evidently, the color shades in Figure 7c more closely resemble those in Figure 7b than those in Figure 7d. As explained earlier for Figure 7b, the positive and negative values in the observations largely cancelled out each other in their mean. Similar cancelations are also seen for the projected component velocities shown by the color shades in Figure 7c,d. It is thus neither informative nor meaningful to compare their mean values with the mean value of the observed radial velocities, but the differences of the projected component velocities from radar observed velocities can still be properly measured and overall effectively quantified through their RMS value.
The differences between the projected component velocities shown by color shades in Figure 7c (or Figure 7d) and the radar observed velocities shown using color shades in Figure 7b are shown using color shades in Figure 7e for the new method (or in Figure 7f for the optical-flow technique). It is evident that the color-shaded differences in Figure 7e are closer to zero than those in Figure 7f. Computed over all the narrow arc-shape areas where the radar velocity observations were available within 3 (2 or 1) km below the cloud top, the computed RMS value of the color-shaded difference field in Figure 7e was 17.0 (19.4 or 18.6) m/s for the new method but increased to 19.9 (22.2 or 21.0) m/s for the color-shaded difference field shown in Figure 7f for the optical-flow technique. Thus, the new-method retrieved vortex winds were still more accurate than the optical-flow technique derived super-high-resolution AMVs, at least for their projected component velocities in the narrow arc-shape areas (Figure 7a).
4.2. Retrieved Vortex Winds at 15:00 UTC
The new method was also applied to three consecutive band-13 brightness temperature images (for Tbob < 280 °K) scanned at 14:59, 15:00, and 15:01 UTC on 26 August 2021 from GOES-16 over Hurricane Ida. With the hurricane center moving velocity, (uc, vc) = (−3.61, 3.59) m/s at 15:00 UTC, added to the retrieved domain-relative vortex winds, the resulting ground-relative vortex winds are plotted using black arrows in Figure 8a atop the brightness temperature image and in Figure 8c atop the color shades of cloud top height. Again, the retrieved vortex winds are, not only much denser than operationally derived AMVs shown in Figure 8b, but also more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs shown in Figure 8d. At this time, as shown in Figure 8d, the super-high-resolution AMVs were still very noisy and contained some unrealistically large values in the periphery of hurricane vortex where the cloud top height drops below 12 km (see the color shades in Figure 8c).
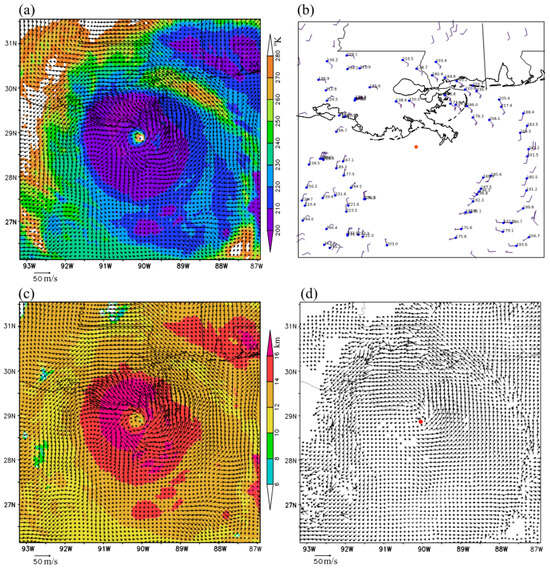
Figure 8.
As in Figure 6 but around 15:00 UTC on 29 August 2021.
At 15:00 UTC, the hurricane was slightly more off-shore and more intense, with slightly taller clouds than at 16:00 UTC. At this time, as shown in Figure 9a,b, dealiased radar velocity observations were still available from the operational KLIX radar within 3 km below the cloud top in many narrow arc-shape areas to the northeast of the radar site (far away from the hurricane center) but in fewer narrow arc-shape areas to the south of the radar site (between the hurricane center and radar site) compared to those at 16:00 UTC in Figure 7a,b. Thus, in comparison with the observations available at 16:00 UTC, the total number of radar velocity observations within 3 (2 or 1) km below the cloud top reduced slightly to 3541 (1408, 450). The corresponding RMS value reduced slightly to 16.1 (15.3 or 16.0) m/s. The mean value shifted to −6.8 (−4.8 or −0.61) m/s, which was slightly more negative than the mean value of −4.5 (−2.5 or 0.32) m/s at 16:00 UTC, because the radar velocity observations were mostly negative at this time in many narrow arc-shape areas to the northeast of radar site. Nevertheless, this shifted mean value was still close to zero.
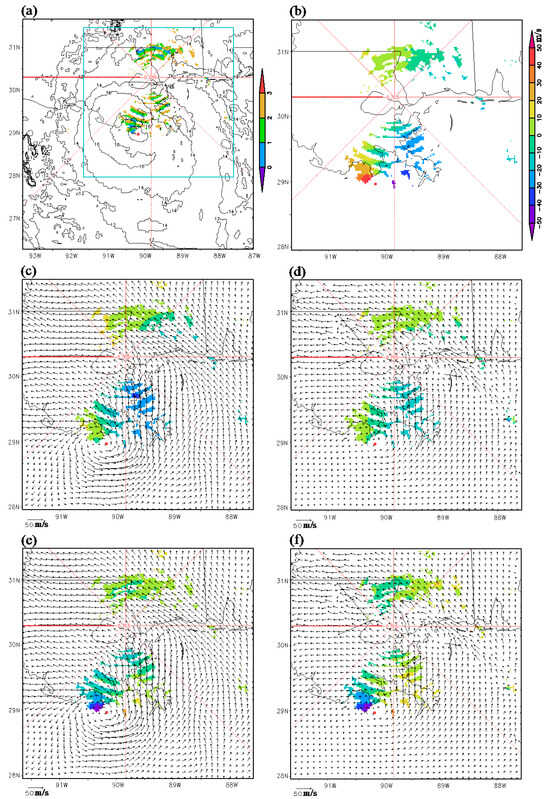
Figure 9.
As in Figure 7 but around 15:00 UTC on 29 August 2021.
The new-method retrieved vortex winds (or optical-flow technique derived superhigh-resolution AMVs) are replotted using black arrows in Figure 9c (or Figure 9d), in which their projected component velocities (along the radar beams) are illustrated by color shades in the same narrow arc-shape areas as those shown for the radar velocity observations in Figure 8b. Again, the color shades in Figure 9c are clearly closer to those in Figure 9b than those in Figure 9d, and the positive and negative values of the radar observed velocities in Figure 9b are still largely cancelled each other in their mean value, and similar cancelations are seen for the projected component velocities depicted by the color shades in Figure 9c,d. Thus, as explained earlier, only the RMS difference between the observed and projected component velocities is used below to qualify their overall differences.
The color shades in Figure 9e (or Figure 9f) illustrate the differences between the projected component velocities shown by color shades in Figure 9c (or Figure 9d) and the radar observed velocities in Figure 9b. Clearly, the color-shaded differences in Figure 9e are closer to zero than those in Figure 9f. Computed over all the narrow arc-shape areas where the radar velocity observations were available within 3 (2 or 1) km below the cloud top, the computed RMS value of color-shaded difference field in Figure 9e was 10.6 (11.0 or 12.5) m/s for the new method but increased to 11.3 (11.5 or 13.1) m/s for the color-shades difference field shown in Figure 9f for the optical-flow technique. Thus, all the results obtained so far consistently demonstrate that the new method is more accurate than the optical-flow technique, at least for the projected component velocities in the narrow arc-shape areas (shown in Figure 3a, Figure 5a, Figure 7a and Figure 9a).
5. Discussions
The new method presented in this paper is much simpler and more straightforward to implement than the optimization strategies explored in [10] for enhancing the resolution and accuracy of operationally produced AMVs for TC applications. This simplicity arises because the new method does not require the use increasingly sophisticated algorithms to adjust the target selection, spacing, and search box criteria for better tracking cloud motions and capturing smaller-scale hurricane flow fields. In addition to the aforementioned merits, the new method is also more accurate and suitable for hurricane applications than the optical flow technique [11]. Furthermore, as the new-method retrieved vortex wind field is expressed using the square root matrices that are derived analytically from VF-dependent covariance functions, essentially as continuous vector functions, the retrieved wind field is also essentially continuous. Rigorous proof of this can be given by constructing J as a functional in the space of continuous functions similar to those presented in Appendix A of [25]. Thus, as an additional advantage, the spatial resolution of new-method retrieved vortex wind field can be higher than for the optical-flow technique derived super-high-resolution AMVs.
Although the new-method retrieved vortex wind field is essentially continuous, its intrinsic spatial resolution is limited by the de-correlation lengths of VF-dependent correlation functions. Additionally, as an approximation, the correction reduction caused by the height difference between the two correlated points (within the horizontal de-correlation distance) is neglected, so the correlation between the two points only depends on their horizontal distance. With this approximation, the VF-dependent covariance functions constructed in Section 2.1 (also see Figure 1) can be applied to a horizontally variable smooth surface. Thus, by only applying the new method to brightness temperature images in areas of Tbob < 280 °K (as stated at the beginning of Section 3.1), the vortex wind field is actually retrieved on a horizontally variable smooth surface (at/around the cloud top). In this paper, the height assigned to the retrieved wind field was simply taken from an operationally estimated cloud top height based on GOES-16 observations. It is not yet clear whether or how this simplified height assignment should be improved. However, it is possible to relax the above explained approximation by extending the VF-dependent covariance functions in the vertical direction in three-dimensional space. This can be done in a manner similar to the three-dimensional VF-dependent covariance functions constructed in [27], while the control variable space can be reduced adaptively in the vertical direction, to cover only the range of cloud-top height variations for efficient computations. This approach needs to be investigated in future studies.
For each case, vortex wind retrieval was performed in a moving coordinate system co-centered with the hurricane. It has long been recognized that using a moving coordinate system can reduce advection-caused errors, not only in analyzing radar observed moving storm systems, but also in retrieving unobserved advection velocities from observed tracer movements. The techniques involved and their related merits have been studied by many investigators [28,29,30,31,32,33,34]. When retrieving the wind field in a moving storm system, an optimal moving frame needs to be searched and used to improve the wind retrieval. In the vortex wind retrievals considered in this paper, the moving coordinate system was simply co-centered with the hurricane, while the hurricane upper-level vortex center location and moving velocity were estimated from the best hurricane track in each case. Note that the hurricane vortex was nearly vertical in each case considered in this paper, so the estimated vortex center location should have been very close (at least, well within a half of the vortex core radius) to the true upper-level vortex center. The estimated vortex center location was thus sufficiently accurate for using VF-dependent covariance functions to analyze vortex winds in a vortex-following coordinate system, according to the recent sensitivity study [35]. However, for real-time applications, the upper-level hurricane vortex center location and moving velocity often cannot be accurately estimated from an operationally issued (every 6 h) hurricane center location. In this case, the new method faces a challenging issue of how to accurately estimate the upper-level hurricane vortex center location and moving velocity. This issue deserves further exploration and continued studies.
6. Conclusions
In this paper, we presented a space-time variational method for retrieving upper-level winds from infrared image pattern movements rapidly scanned from geostationary satellites over hurricanes. In this method, the recently formulated VF-dependent covariance functions [26,27] are modified adaptively for the radial and tangential components of hurricane vortex winds and used to construct the background error covariance matrix and its square root matrix for preconditioning the cost function. The advection equation constraint, formulated for radar-scanned reflectivity (or radial-velocity) pattern movements in the simple adjoint method [13,14,15], is adapted for infrared image pattern movements captured by geostationary satellites. The preconditioned cost function newly formulated in this method is more efficient and more suitable for deriving upper-level vortex winds from GOES-16 rapid infrared scans over hurricanes than the cost function in the recently adopted optical flow technique. The method is novel due to its adaptive modifications of the VF-dependent covariance functions in [26,27] and the imagery advection equation in [13,14,15] and, most importantly, due to its combined use of the modified VF-dependent covariance functions and advection equation. The utility and effectiveness of this new method were demonstrated by its application to band-13 (10.3 µm) brightness temperature images scanned every minute from GOES-16 around 03:00 and 06:00 UTC on 27 August 2020 over Hurricane Laura and around 15:00 and 16:00 UTC on 29 August 2021 over Hurricane Ida.
For the aforementioned hurricane cases, the new-method retrieved vortex winds were demonstrated to be, not only much denser than operationally produced AMVs from GOES-16 IR image movements, but also more rotational and better organized around the eyewall than the optical-flow technique derived super-high-resolution AMVs. When verified against radar velocity observations only available in narrow arc-shape areas (on radar scanned conic surfaces) near the cloud top, the new-method retrieved vortex winds were shown to be more accurate than the optical-flow technique derived super-high-resolution AMVs, at least for their projected component velocities (along the radar beams) in those narrow arc-shape areas near the cloud top. The new method is expected to be tested with more validation cases in future studies. Furthermore, as the combined use of VF-dependent covariance functions and imagery advection equation is novel and found to be critically important for the improved performance of the method, we expect that similar combined approaches can be developed with improved performance for retrieving vortex flows rapidly scanned using other types of remote sensing on different scales. In particular, the recently developed variational method for analyzing vortex flows in radar-scanned tornadic mesocyclones [27] can be further improved by incorporating the radar reflectivity imagery advection equation as a strong constraint, to take advantage of the phased-array radar capability in rapid image scanning. Future research is required and deserved in this direction.
In addition to the merits and limitations discussed in Section 5, the new method is computationally efficient and suitable for real-time applications, as it takes only about 2 min of CPU time (without parallel computation) to retrieve each vortex wind field on a 300 × 300 grid with a 2 km horizontal resolution over a 600 × 600 km2 domain (that is moving and co-centered with the hurricane). Further studies and applications of this method should be conducted to explore its potential usefulness for hurricane wind nowcasts and for assimilating the retrieved vortex winds into numerical models to improve hurricane track and intensity predictions, which are of paramount importance for disaster preparedness and response.
Author Contributions
New method formulations, experiment design, manuscript writing, and funding acquisition: Q.X. New method algorithm development and coding, experiment execution, and visualization: L.W. Radar velocity data preparation and dealiasing: K.N. GOES-16 rapid-scan data preparation and operational AMV acquisition: H.Z. Use of the optical-flow technique in deriving super-high-resolution AMVs: R.R. All authors have read and agreed to the published version of the manuscript.
Funding
The research work was supported by the Warn-on-Forecast project at NSSL and the ONR Grant N000142012449 to University of Oklahoma (OU). Funding was also provided by NOAA/Office of Oceanic and Atmospheric Research under NOAA-OU Cooperative Agreement #NA21OAR4320204, U.S. Department of Commerce.
Data Availability Statement
Data produced in this study for vortex winds retrieved by using the new method are archived at https://drive.google.com/drive/folders/1zfEpoNqZxuBZCsNvfWt2xO5AgO5yDUiG, which are accessible for users within NOAA. For users outside NOAA, please contact the corresponding author Qin Xu for permission to access the data.
Acknowledgments
The authors are thankful to Jidong Gao at NSSL for his internal review of the original manuscript and to the five anonymous reviewers for their constructive comments and suggestions that improved the presentation of the results. The numerical experiments were performed at the OU Supercomputing Center for Education and Research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Velden, C.S.; Hayden, C.; Nieman, S.; Menzel, W.; Wanzong, S.; Goerss, J. Upper-Tropospheric Winds Derived from Geostationary Satellite Water Vapor Observations. Bull. Am. Meteorol. Soc. 1997, 78, 173–195. [Google Scholar] [CrossRef]
- Velden, C.; Daniels, J.; Stettner, D.; Santek, D.; Key, J.; Dunion, J.; Holmlund, K.; Dengel, G.; Bresky, W.; Menzel, P. Recent Innovations in Deriving Tropospheric Winds from Meteorological Satellites. Bull. Am. Meteorol. Soc. 2005, 86, 205–223. [Google Scholar] [CrossRef]
- Velden, C.S.; Olander, T.; Wanzong, S. The Impact of Multispectral GOES-8 Wind Information on Atlantic Tropical Cyclone Track Forecasts in 1995. Part 1: Dataset Methodology, Description and Case Analysis. Mon. Weather Rev. 1998, 126, 1202–1218. [Google Scholar] [CrossRef]
- Goerss, J.S.; Velden, C.S.; Hawkins, J.D. The Impact of Multispectral GOES-8 Wind Information on Atlantic Tropical Cyclone Track Forecasts in 1995. Part II: NOGAPS Forecasts. Mon. Weather Rev. 1998, 126, 1219–1227. [Google Scholar] [CrossRef]
- Goerss, J.S. Impact of satellite observations on the tropical cyclone track forecasts of the Navy Operational Global Atmospheric Prediction System. Mon. Weather Rev. 2009, 137, 41–50. [Google Scholar] [CrossRef]
- Pu, Z.; Li, X.; Velden, C.; Aberson, S.; Liu, W. The Impact of Aircraft Dropsonde and Satellite Wind Data on Numerical Simulations of Two Landfalling Tropical Storms during the Tropical Cloud Systems and Processes Experiment. Weather Forecast. 2008, 23, 62–79. [Google Scholar] [CrossRef]
- Wu, T.; Liu, H.; Majumdar, S.; Velden, C.; Anderson, J. Influence of Assimilating Satellite-Derived Atmospheric Motion Vector Observations on Numerical Analyses and Forecasts of Tropical Cyclone Track and Intensity. Mon. Weather Rev. 2014, 142, 49–71. [Google Scholar] [CrossRef]
- Wu, T.; Velden, C.; Majumdar, S.; Liu, H.; Anderson, J. Understanding the Influence of Assimilating Subsets of Enhanced Atmospheric Motion Vectors on Numerical Analyses and Forecasts of Tropical Cyclone Track and Intensity with an Ensemble Kalman Filter. Mon. Weather Rev. 2015, 143, 2506–2531. [Google Scholar] [CrossRef]
- Velden, C.; Lewis, W.; Bresky, W.; Stettner, D.; Daniels, J.; Wanzong, S. Assimilation of High-Resolution Satellite-Derived Atmospheric Motion Vectors: Impact on HWRF Forecasts of Tropical Cyclone Track and Intensity. Mon. Weather Rev. 2017, 145, 1107–1125. [Google Scholar] [CrossRef]
- Stettner, D.; Velden, C.; Rabin, R.; Wanzong, S.; Daniels, J.; Bresky, W. Development of enhanced vortex-scale atmospheric motion vectors for hurricane applications. Remote Sens. 2019, 11, 1981. [Google Scholar] [CrossRef]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High accuracy optical flow estimation based on a theory for warping. In Proceedings of the European Conference on Computer Vision (ECCV), Prague, Czech Republic, 11–14 May 2004; Pajdla, T., Matas, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3024, pp. 25–36. [Google Scholar]
- Mendes, L.P.N.; Ricardo, A.M.C.; Bernardino, A.J.M.; Rui, L. A Comparative Study of Optical Flow Methods for Fluid Mechanics. Exp. Fluids 2022, 63, 7. [Google Scholar] [CrossRef]
- Qiu, C.; Xu, Q. A Simple Adjoint Method of Wind Analysis for Single-Doppler Data. J. Atmos. Ocean. Technol. 1992, 9, 588–598. [Google Scholar] [CrossRef]
- Xu, Q.; Qiu, C.; Yu, J. Adjoint-Method Retrievals of Low-Altitude Wind Fields from Single-Doppler Reflectivity Measured during Phoenix II. J. Atmos. Ocean. Technol. 1994, 11, 275–288. [Google Scholar] [CrossRef]
- Xu, Q.; Qiu, C.; Gu, H.; Yu, J. Simple Adjoint Retrievals of Microburst Winds from Single-Doppler Radar Data. Mon. Weather Rev. 1995, 123, 1822–1833. [Google Scholar] [CrossRef]
- Laroche, S.; Zawadzki, I. A Variational Analysis Method for Retrieval of Three-Dimensional Wind Field from Single-Doppler Radar Data. J. Atmos. Sci. 1994, 51, 2664–2682. [Google Scholar] [CrossRef]
- Shapiro, A.; Ellis, S.; Shaw, J. Single-Doppler Velocity Retrievals with Phoenix II Data: Clear Air and Microburst Wind Retrievals in the Planetary Boundary Layer. J. Atmos. Sci. 1994, 52, 1265–1287. [Google Scholar] [CrossRef]
- Qiu, C.; Xu, Q. Least Squares Retrieval of Microburst Winds from Single-Doppler Radar Data. Mon. Weather Rev. 1996, 124, 1132–1144. [Google Scholar] [CrossRef]
- Daley, R. Atmospheric Data Analysis; Cambridge University Press: New York, NY, USA, 1991; pp. 1–457. [Google Scholar]
- Gaspari, G.; Cohn, S.E. Construction of Correlation Functions in Two and Three Dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Purser, R.J.; Wu, W.S.; Parrish, D.F.; Roberts, N.M. Numerical Aspects of the Application of Recursive Filters to Variational Statistical Analysis. Part I: Spatially Homogeneous and Isotropic Gaussian Covariances. Mon. Weather Rev. 2003, 131, 1524–1535. [Google Scholar] [CrossRef]
- Wu, W.-S.; Purser, R.J.; Parrish, D.F. Three-Dimensional Variational Analysis with Spatially Inhomogeneous Covariances. Mon. Weather Rev. 2002, 130, 2905–2916. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Brewster, K.; Droegemeier, K.K. A Three-Dimensional Variational Data Assimilation Method with Recursive Filter for Doppler Radars. J. Atmos. Ocean. Technol. 2004, 21, 457–469. [Google Scholar] [CrossRef]
- Xu, Q. Representations of Inverse Covariances by Differential Operators. Adv. Atmos. Sci. 2005, 22, 181–198. [Google Scholar] [CrossRef]
- Xu, Q. On the Choice of Momentum Control Variables and Covariance Modeling for Mesoscale Data Assimilation. J. Atmos. Sci. 2019, 76, 89–111. [Google Scholar] [CrossRef]
- Xu, Q.; Wei, L.; Nai, K. Analyzing Vortex Winds in Radar Observed Tornadic Mesocyclones for Nowcast Applications. Weather Forecast. 2015, 30, 1140–1157. [Google Scholar] [CrossRef]
- Xu, Q. A Variational Method for Analyzing Vortex Flows in Radar-Scanned Tornadic Mesocyclones. Part I: Formulations and Theoretical Considerations. J. Atmos. Sci. 2021, 78, 825–841. [Google Scholar] [CrossRef]
- Gal-Chen, T. Errors in Fixed and Moving Frame of References: Applications for Conventional and Doppler Radar Analysis. J. Atmos. Sci. 1982, 39, 2279–2300. [Google Scholar] [CrossRef]
- Chong, M.; Testud, J.; Roux, F. Three-Dimensional Wind Field Analysis from Dual-Doppler Radar Data. Part II: Minimizing the Error due to Temporal Variation. J. Clim. Appl. Meteorol. 1983, 22, 1216–1226. [Google Scholar] [CrossRef]
- Zhang, J.; Gal-Chen, T. Single-Doppler Wind Retrieval in the Moving Frame of Reference. J. Atmos. Sci. 1996, 53, 2609–2623. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Q. Statistical Errors in Variational Data Assimilation—A Theoretical One-Dimensional Analysis Applied to Doppler Wind Retrieval. J. Atmos. Sci. 1996, 53, 2563–2577. [Google Scholar] [CrossRef]
- Liou, Y. Single Radar Recovery of Cross-Beam Wind Components Using a Modified Moving Frame of Reference Technique. J. Atmos. Ocean. Technol. 1999, 16, 1003–1016. [Google Scholar] [CrossRef]
- Liou, Y. An Explanation of the Wind Speed Underestimation Obtained from a Least Squares Type of Single-Doppler Radar Velocity Retrieval Method. J. Appl. Meteorol. 2002, 41, 1216–1226. [Google Scholar] [CrossRef]
- Liou, Y. Single-Doppler Retrieval of the Three-Dimensional Wind in a Deep Convective System Based on an Optimal Moving Frame of Reference. J. Meteorol. Soc. Jpn. 2007, 85, 559–582. [Google Scholar] [CrossRef][Green Version]
- Xu, Q.; Wei, L. A Variational Method for Analyzing Vortex Flows in Radar-Scanned Tornadic Mesocyclones. Part III: Sensitivities to Vortex Center Location Errors. J. Atmos. Sci. 2022, 79, 1515–1530. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).