Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision
Abstract
:1. Introduction
2. Datasets Used in This Study
2.1. Evapotranspiration (E) Estimates
2.2. Other Water Cycle Components
2.3. Environmental Indices (EIs)
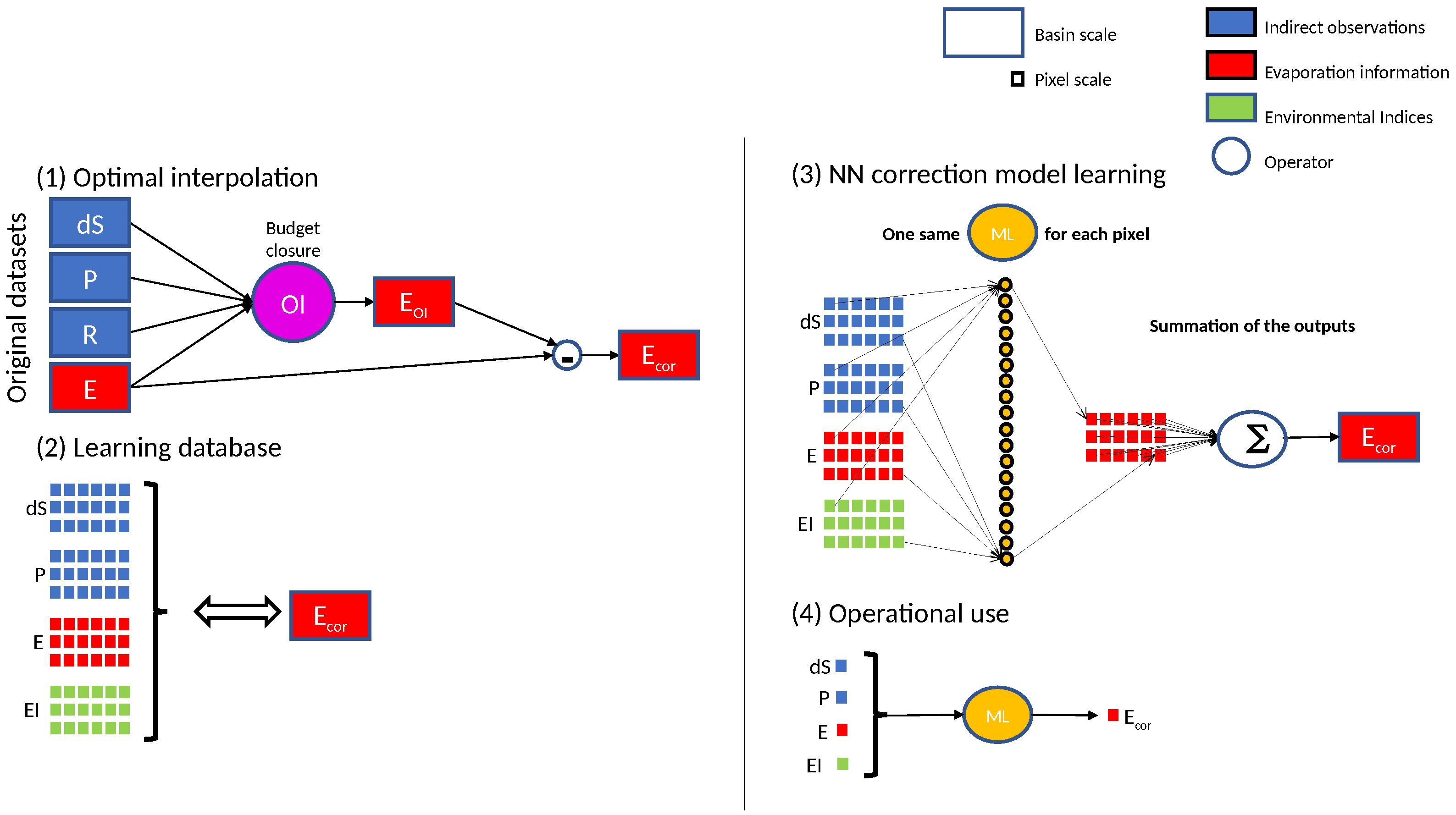
3. Obtaining E Correction at Catchment Scale
3.1. A Set of Basins around the World
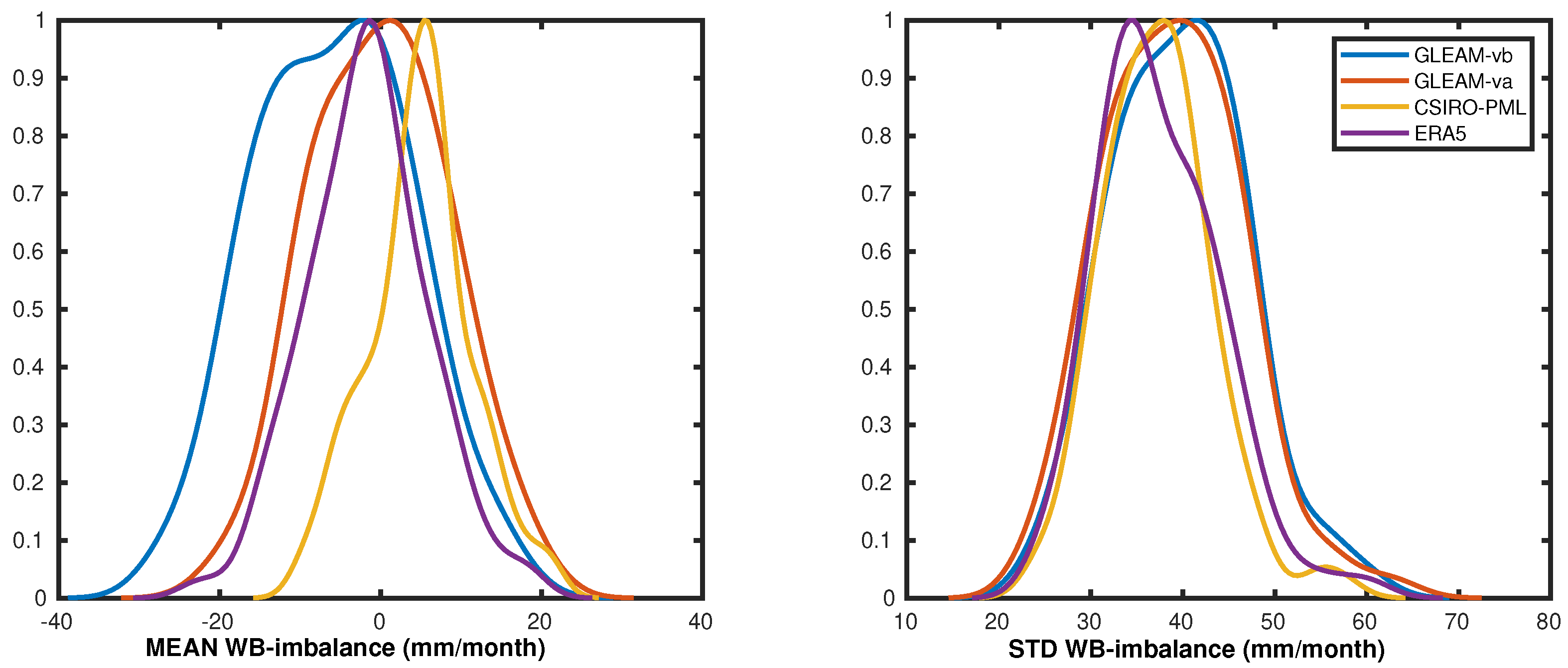
3.2. Non-Closure of the Water Budget
3.3. Optimal Interpolation (OI)
4. Propagating E Corrections from Catchment to Pixel Scale
4.1. Notations
4.2. A probabilistic Formulation
4.3. Catchment-Level Supervision
4.4. Experiment Details
5. E-Correction Modeling Results
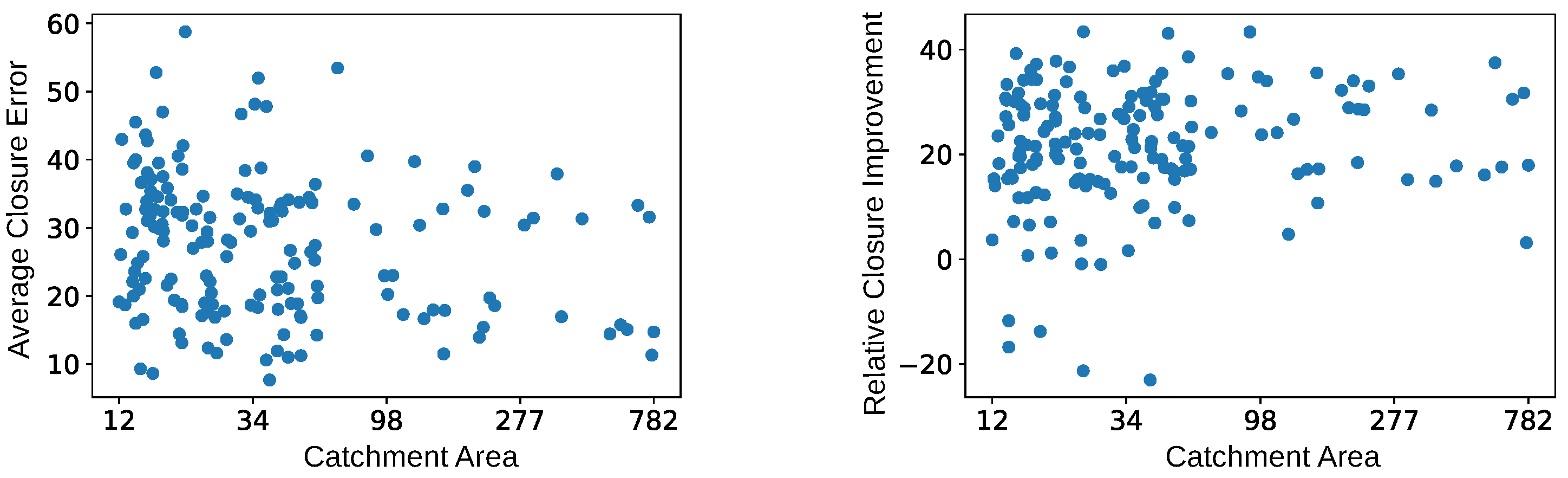
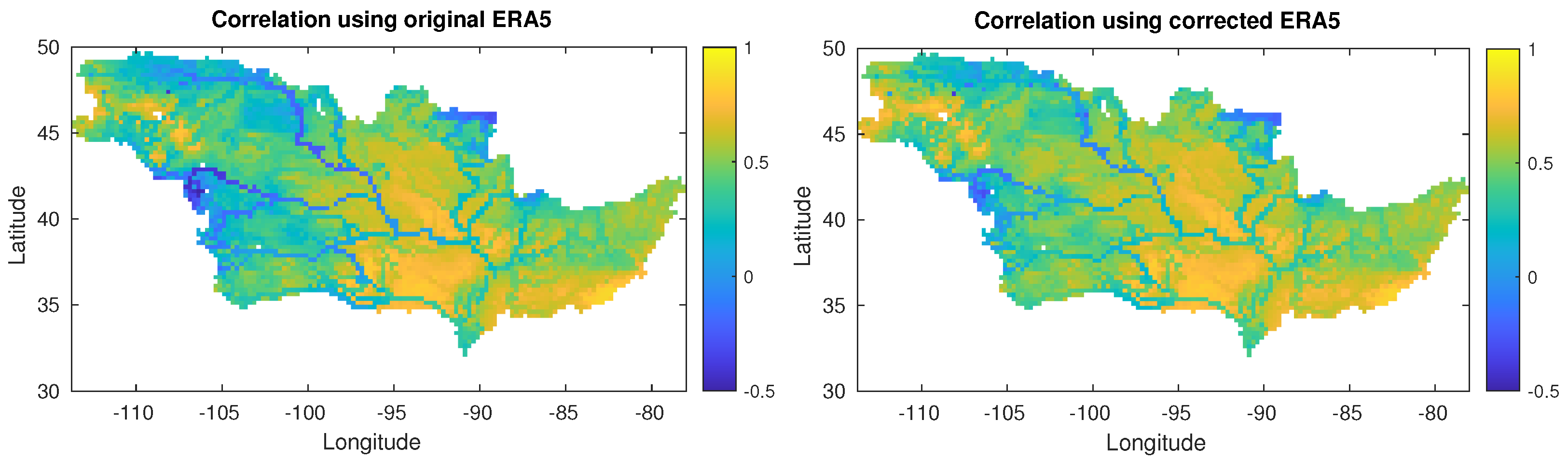
5.1. Spatial Analysis of the Bias Corrections
5.2. Seasonal Analysis of the Corrections
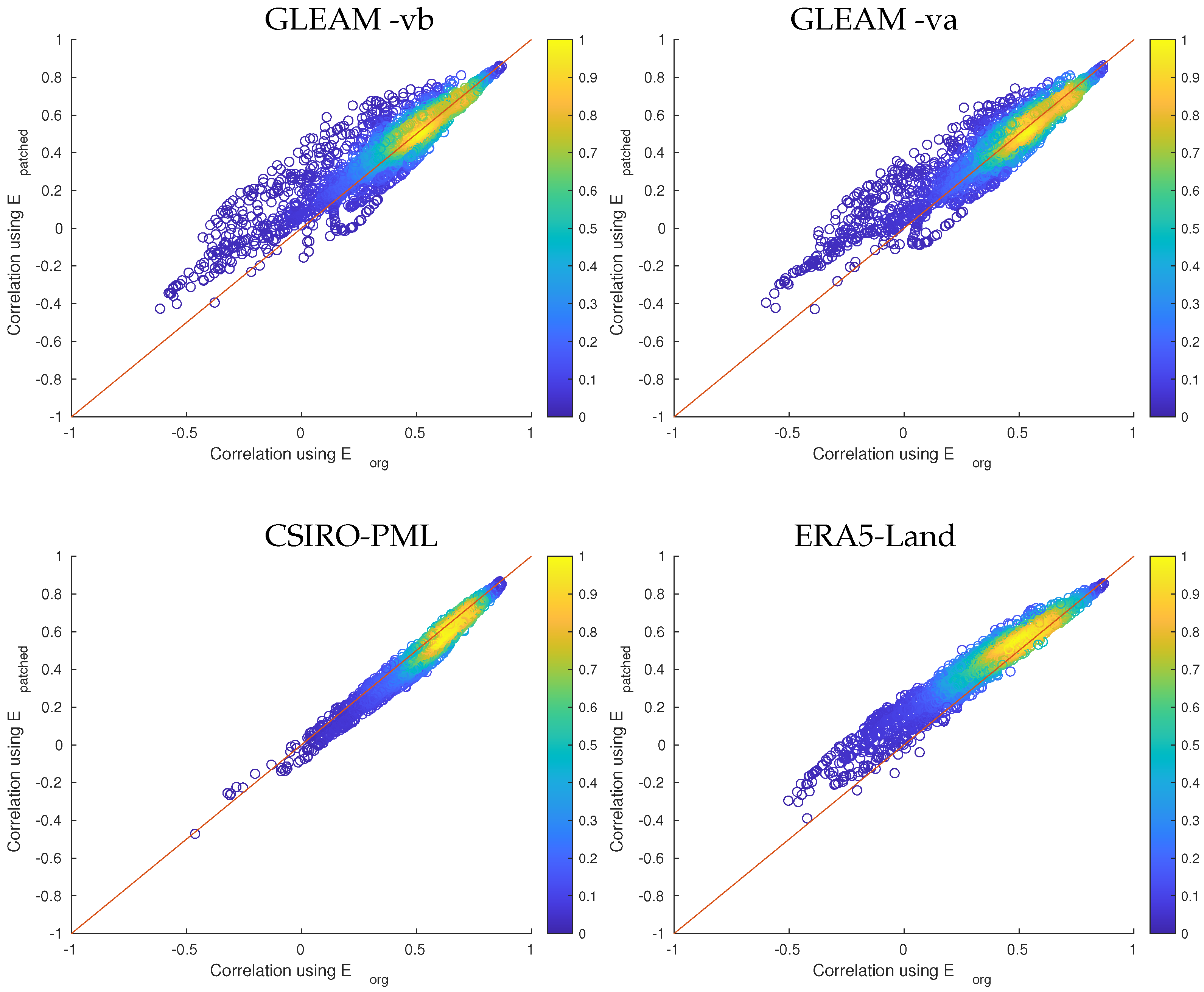
5.3. Water Cycle Closure Results
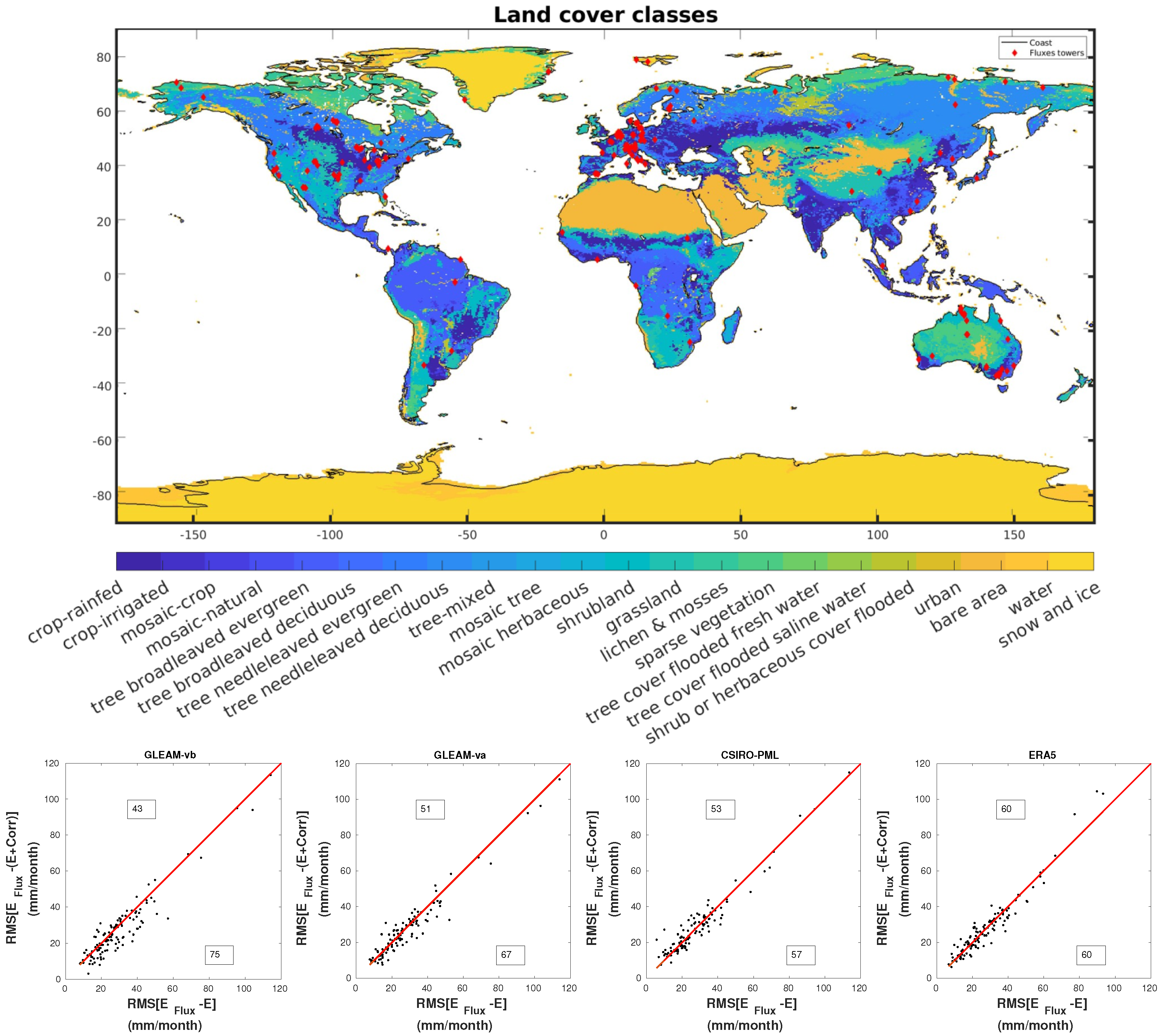
5.4. Land Cover-Based Correction Analysis
5.5. Quality Assessment Index
6. Evaluation Using Auxiliary Observations
6.1. Validation Using Flux Tower Evaporation
6.2. Indirect Evaluation Based on River Discharge Reconstruction over the Mississippi
7. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Falge, E.; Aubinett, M.; Bakwin, P.; Baldocchi, D.; Berbigier, P.; Hernhofer, C.; Black, T.; Ceulemans, R.; Davis, K.; Dolman, A.; et al. Fluxnet Research Network Site Characteristics, Investigators, and Bibliography, 2016; ORNL DAAC: Oak Ridge, TN, USA, 2017. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. In Proceedings of the Royal Society of London; Series A, Mathematical and Physical Sciences; The Royal Society: London, UK, 1948; Volume 193, pp. 120–145. [Google Scholar]
- Monteith, J. Evaporation and the Environment in the State and Movement of Water in Living Organisms. In Proceedings of the Society for Experimental Biology; Cambridge University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Shuttleworth, W.J. Terrestrial Hydrometeorology, 1st ed.; John Wiley & Sons, Ltd.: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. RASPOTION—A New Global PET Dataset by Means of Remote Monthly Temperature Data and Parametric Modelling. Hydrology 2022, 9, 32. [Google Scholar] [CrossRef]
- Jensen, M.; Haise, H. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar] [CrossRef]
- Priestley, C.; Taylor, R. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Leuning, R.; Kriedemann, P.E.; McMurtrie, R.E. Simulation of evapotranspiration by trees. Agric. Water Manag. 1991, 19, 205–221. [Google Scholar] [CrossRef]
- Fassoni-Andrade, A.C.; Fleischmann, A.S.; Papa, F.; de Paiva, R.C.D.; Wongchuig, S.; Melack, J.M.; Moreira, A.A.; Paris, A.; Ruhoff, A.; Barbosa, C.C.F.; et al. Amazon hydrology from space: Scientific advances and future challenges. Rev. Geophys. 2021, 59, e2020RG000728. [Google Scholar] [CrossRef]
- Martens, B.; Schumacher, J.; Wouters, H.; Muñoz-Sabater, J.; Verhoest, N.E.C.; Miralles, D.G. Evaluating the land-surface energy partitioning in ERA5. Geosci. Model Dev. 2020, 13, 4159–4181. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Tran, B.N.; van der Kwast, J.; Seyoum, S.; Uijlenhoet, R.; Jewitt, G.; Mul, M. Uncertainty Assessment of Satellite Remote Sensing-based Evapotranspiration Estimates: A Systematic Review of Methods and Gaps. EGUsphere 2023, 27, 4505–4528. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, M.; Sheffield, J.; Siemann, A.; Fisher, C.; Liang, M.; Beck, H.; Wanders, N.; MacCracken, R.; Houser, P.R.; et al. A Climate Data Record (CDR) for the global terrestrial water budget: 1984–2010. Hydrol. Earth Syst. Sci. Discuss. 2017, 22, 241–263. [Google Scholar] [CrossRef]
- Dorigo, W.; Dietrich, S.; Aires, F.; Brocca, L.; Carter, S.; Cretaux, J.-F.; Dunkerley, D.; Enomoto, H.; Forsberg, R.; üntner, A.G.; et al. Closing the water cycle from observations across scales: Where do we stand? Bull. Am. Meteorol. Soc. 2021, 102, 1–95. [Google Scholar] [CrossRef]
- Van Dijk, A.I.; Schellekens, J.; Yebra, M.; Beck, H.E.; Renzullo, L.J.; Weerts, A.; Donchyts, G. Global 5 km resolution estimates of secondary evaporation including irrigation through satellite data assimilation. Hydrol. Earth Syst. Sci. 2018, 22, 4959–4980. [Google Scholar] [CrossRef]
- Aires, F. Combining Datasets of Satellite-Retrieved Products. Part I: Methodology and Water Budget Closure. J. Hydrometeorol. 2014, 15, 1677–1691. [Google Scholar] [CrossRef]
- Pellet, V.; Aires, F.; Munier, S.; Fernández Prieto, D.; Jordá, G.; Arnoud Dorigo, W.; Polcher, J.; Brocca, L. Integrating multiple satellite observations into a coherent dataset to monitor the full water cycle - Application to the Mediterranean region. Hydrol. Earth Syst. Sci. 2019, 23, 465–491. [Google Scholar] [CrossRef]
- Rodell, M.; Beaudoing, H.; L’Ecuyer, T.; Olson, W.; Famiglietti, J.; Houser, P.; Adler, R.; Bosilovich, M.; Clayson, C.; Chambers, D.; et al. The Observed State of the Water Cycle in the Early 21st Century. J. Clim. 2015, 28, 8289–8318. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Pan, M.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Reconciling the global terrestrial water budget using satellite remote sensing. Remote Sens. Environ. 2011, 115, 1850–1865. [Google Scholar] [CrossRef]
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Multisource estimation of long-term terrestrial water budget for major global river basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Munier, S.; Aires, F. A new global method of satellite dataset merging and quality characterization constrained by the terrestrial water cycle budget. Remote. Sens. Environ. 2017, 205, 119–203. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; McVicar, T.R.; Zambrano-Bigiarini, M.; Alvarez-Garreton, C.; Baez-Villanueva, O.M.; Sheffield, J.; Karger, D.N. Bias Correction of Global High-Resolution Precipitation Climatologies Using Streamflow Observations from 9372 Catchments. J. Clim. 2020, 33, 1299–1315. [Google Scholar] [CrossRef]
- Koppa, A.; Rains, D.; Hulsman, P.; Poyatos, R.; Miralles, D.G. A deep learning-based hybrid model of global terrestrial evaporation. Nat. Commun. 2022, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; érnandez-Prieto, D.F.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. Discuss. 2016, 10, 1903–1925. [Google Scholar] [CrossRef]
- Zhang, Y.; Pena Arancibia, J.; McVicar, T.; Chiew, F.; Vaze, J.; Zheng, H.; Wang, Y.P. Monthly global observation-driven Penman-Monteith-Leuning (PML) evapotranspiration and components. CSIRO Data Collect. 2016. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J.; Huffman, G.J.; Adler, R.F.; et al. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25deg; global gridded precipitation by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Watkins, M.M.; Yuan, D.-N. GRACE Gravity Recovery and Climate Experiment JPL Level-2 Processing Standards Document For Level-2 Product Release 05.1; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar]
- Bettadpur, S. GRACE 327-742 (CSR-GR-12-xx) GRAVITY RECOVERY AND CLIMATE EXPERIMENT UTCSR Level-2 Processing Standards Document) (For Level-2 Product Release 0005), GRACE 327–742, Center for Space Research Publ. GR-12-xx, Rev. 4.0, University of Texas at Austin, 16 pp. 2012. Available online: http://icgem.gfz-potsdam.de/L2-CSR0005_ProcStd_v4.0.pdf (accessed on 29 October 2023).
- Dahle, C.; Flechtner, F.; Gruber, C.; König, D.; König, R.; Michalak, G.; Neumayer, K.-H. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005. 2013. Available online: http://icgem.gfz-potsdam.de/L2-GFZ_ProcStds_0005_v1.1-1.pdf (accessed on 29 October 2023).
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- Do, H.X.; Gudmundsson, L.; Leonard, M.; Westra, S. The Global Streamflow Indices and Metadata Archive (GSIM)-Part 1: The production of a daily streamflow archive and metadata. Earth Syst. Sci. Data 2018, 10, 765–785. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Didan, K. MOD13C2 MODIS/Terra Vegetation Indices Monthly L3 Global 0.05Deg CMG V006 [Data Set]. 2015. Distributed by NASA EOSDIS Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/products/mod13c2v006/ (accessed on 29 October 2023).
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Munøz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Balsamo, G.; Beljaars, A.; Scipal, K.; Viterbo, P.; van den Hurk, B.; Hirschi, M.; Betts, A.K. A Revised Hydrology for the ECMWF Model: Verification from Field Site to Terrestrial Water Storage and Impact in the Integrated Forecast System. J. Hydrometeorol. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- Albergel, C.; Balsamo, G.; De Rosnay, P.; Muñoz-Sabater, J.; Boussetta, S. A bare ground evaporation revision in the ECMWF land-surface scheme: Evaluation of its impact using ground soil moisture and satellite microwave data. Hydrol. Earth Syst. Sci. 2012, 16, 3607–3620. [Google Scholar] [CrossRef]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; Mccabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; Mccabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project - Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef]
- Yu, X.; Quian, L.; Wang, W.; Hu, X.; Dong, J.; Pi, Y.; Fan, K. Comprehensive evaluation of terrestrial evapotranspiration from different models under extreme condition over conterminous United States. Agric. Water Manag. 2023, 289, 108555. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.; Chen, T.; Li, S.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B.; Jung, M. A harmonized global land evaporation dataset from model-based products covering 1980–2017. Earth Syst. Sci. Data 2021, 13, 5879–5898. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Leuning, R.; Chiew, F.H.S.; Wang, E.L.; Zhang, L.; Liu, C.M.; Sun, F.B.; Peel, L.M.C.; She, Y.J.; Jung, M. Decadal Trends in Evaporation from Global Energy and Water Balances. J. Hydrometeor. 2012, 13, 379–391. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Kong, D.; Gan, F.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 3165–3182. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Schneider, U.; Rudolf, B.; Becker, A.; Ziese, M.; Finger, P.; Meyer-Christoffer, A.; Schneider, U. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2011, 115, 15–40. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Ziese, M.; Rudolf, B. Global Precipitation Analysis Products of the GPCC. Internet Publ. 2014, 1–13. [Google Scholar]
- Pellet, V.; Aires, F.; Yamazaki, D.; Papa, F. Satellite monitoring of the water cycle over the Amazon using upstream/downstream dependency. Part 1: Methodology and initial evaluation. Water Resour. Res. 2021, 2020, 1–26. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, 9. [Google Scholar] [CrossRef]
- Rodriguez-Vazquez, J.; Fernandez-Cortizas, J.M.; Perez-Saura, D.; Molina, M.; Campoy, P. Overcoming Domain Shift in Neural Networks for Accurate Plant Counting in Aerial Images. Remote Sens. 2023, 15, 1700. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. 2017. Available online: https://note.wcoder.com/files/ml/automatic_differentiation_in_pytorch.pdf (accessed on 29 October 2023).
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-j.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Rodell, M.; Mcwilliam, E.B.S.; Famiglietti, J.S.; Beaudoing, H.K.; Nigro, J. Estimating evapotranspiration using an observation based terrestrial water budget. Hydrol. Process. 2011, 25, 4082–4092. [Google Scholar] [CrossRef]
- Pellet, V.; Aires, F.; Yamazaki, D.; Zhou, X.; Paris, A. A first continuous and distributed satellite-based mapping of river discharge over the Amazon. J. Hydrol. 2022, 614, 128481. [Google Scholar] [CrossRef]
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47, 4. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, W.; Echizenya, W.; Yamazaki, D. The uncertainty of flood frequency analyses in hydrodynamic model simulations. Nat. Hazards Earth Syst. Sci. 2021, 21, 1071–1085. [Google Scholar] [CrossRef]







| Dataset | Coverage | Spatial Resolution () | Temporal Resolution | Reference |
|---|---|---|---|---|
| Evapotranspiration | ||||
| GLEAM v3.3b | 2003–2017 | 0.25 | daily | [29] |
| GLEAM v3.3a | 1980–2017 | 0.25 | daily | [29] |
| CSIRO-PML | 1980–2012 | 0.5 | monthly | [30] |
| ERA-5 | 1980–2017 | 0.25 | 6 h | [31] |
| Precipitation | ||||
| GPCP | 1979–2015 | 1 | monthly | [32] |
| TMPA | 2002–2015 | 0.25 | daily | [33] |
| MSWEP | 1979–2015 | 0.5 | daily | [34] |
| ERA-5 | 1980–2015 | 0.25 | 6 h | [31] |
| Water storage | ||||
| JPL | 2002–2017 | 1 | monthly | [35] |
| CSR | 2002–2017 | 1 | monthly | [36] |
| GFZ | 2002–2017 | 1 | monthly | [37] |
| River network and discharge | ||||
| Flow direction | static | 0.25 | NA | [38] |
| Discharge | 1980–2015 | NA | monthly | [39] |
| Auxiliary information used in the ML-correction model | ||||
| Soil moisture | 1980–2015 | 0.25 | 6 h | [40] |
| Surface temperature | 1980–2015 | 0.25 | 6 h | [40] |
| LAI | 1980–2015 | 0.25 | 6 h | [40] |
| NDVI | 1980–2015 | 0.25 | daily | [41] |
| P-E | 1980–2015 | 0.25 | 6 h | [31] |
| Dataset | Org. | Org. + Bias | Org. + Season | Org. + Monthly |
|---|---|---|---|---|
| GLEAM vb | 41.4 | 39.0 | 36.5 | 32.6 |
| GLEAM va | 40.2 | 38.7 | 36.5 | 32.5 |
| CSIRO-PML | 38.5 | 38.3 | 36.6 | 32.2 |
| ERA5-Land | 38.5 | 38.5 | 37.1 | 32.4 |
| Dataset | Org. | Org. + Bias | Org. + Season | Org. + Monthly |
|---|---|---|---|---|
| GLEAM vb | 29.2 | 28.1 | 26.6 | 27.5 |
| GLEAM va | 27.7 | 27.3 | 26.8 | 27.7 |
| CSIRO-PML | 27.8 | 27.5 | 28.1 | 28.7 |
| ERA5-Land | 27.6 | 27.3 | 27.5 | 28.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hascoet, T.; Pellet, V.; Aires, F.; Takiguchi, T. Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision. Remote Sens. 2024, 16, 170. https://doi.org/10.3390/rs16010170
Hascoet T, Pellet V, Aires F, Takiguchi T. Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision. Remote Sensing. 2024; 16(1):170. https://doi.org/10.3390/rs16010170
Chicago/Turabian StyleHascoet, Tristan, Victor Pellet, Filipe Aires, and Tetsuya Takiguchi. 2024. "Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision" Remote Sensing 16, no. 1: 170. https://doi.org/10.3390/rs16010170
APA StyleHascoet, T., Pellet, V., Aires, F., & Takiguchi, T. (2024). Learning Global Evapotranspiration Dataset Corrections from a Water Cycle Closure Supervision. Remote Sensing, 16(1), 170. https://doi.org/10.3390/rs16010170








