Abstract
The pursuit of higher-resolution and more reliable spatial distribution simulation results for air pollutants is important to human health and environmental safety. However, the lack of high-resolution remote sensing retrieval parameters for gaseous pollutants (sulfur dioxide and ozone) limits the simulation effect to a 1 km resolution. To address this issue, we sequentially generated and optimized the spatial distributions of near-surface PM2.5, SO2, and ozone at a 1 km resolution in China through two approaches. First, we employed spatial sampling, random ID, and parameter convolution methods to jointly optimize a tree-based machine-learning gradient-boosting framework, LightGBM, and improve the performance of spatial air pollutant simulations. Second, we simulated PM2.5, used the simulated PM2.5 result to simulate SO2, and then used the simulated SO2 to simulate ozone. We improved the stability of 1 km-resolution SO2 and ozone products through the proposed sequence of multiple-pollutant simulations. The cross-validation (CV) of the random sample yielded an R2 of 0.90 and an RMSE of 9.62 µg∙m−3 for PM2.5, an R2 of 0.92 and an RMSE of 3.9 µg∙m−3 for SO2, and an R2 of 0.94 and an RMSE of 5.9 µg∙m−3 for ozone, which are values better than those in previous related studies. In addition, we tested the reliability of PM2.5, SO2, and ozone products in China through spatial distribution reliability analysis and parameter importance reliability analysis. The PM2.5, SO2, and ozone simulation models and multiple-air-pollutant (MuAP) products generated by the two optimization methods proposed in this study are of great value for long-term, large-scale, and regional-scale air pollution monitoring and predictions, as well as population health assessments.
1. Introduction
The grid-based reconstruction of the spatial distribution of air pollutants is important [1,2,3]. At present, there are various spatial distribution datasets for air pollutants available, such as China High Air Pollutants (CHAP) and Tracking Air Pollution (TAP) in China [4]. However, the resolution and reliability of key elements such as sulfur dioxide (SO2) and ozone (O3) still need to be improved [5,6]. Therefore, it is very important to optimize and establish a set of near-surface air pollution spatial distribution products with a resolution of 1 km.
Studies in recent years have shown that the aerosol optical depth (AOD) retrieved by satellites is correlated with near-surface PM2.5 (particulate matter with an aerodynamic diameter ≤ 2.5 μm) [7,8]. Therefore, it is acceptable to simulate PM2.5 with a 1 km resolution in combination with the Multiangle Implementation of Atmospheric Correction (MAIAC) AOD [9]. The resolution of the column data from remote sensing products corresponding to SO2 and ozone is relatively low (lower than 5 km), and it is difficult to generate reliable spatially distributed air pollution datasets with a resolution of 1 km from only column data, such as ozone monitoring instrument (OMI) or Sentinel 5P data [10,11]. Furthermore, the use of meteorological interpolation or reanalysis data to simulate 1 km-resolution SO2 or ozone is an approach that has been explored in many studies [12,13]. However, when the number of meteorological sites is small or a large 1 km atmospheric pollutant region is simulated, the uncertainty of the atmospheric pollutants simulated significantly increases [14,15]. In addition to meteorological elements, there is also a certain degree of correlation among air pollutants. For example, many cities are characterized by heavy air pollution, and many remote rural areas have relatively mild air pollution [16]. Therefore, considering the spatial distribution of PM2.5 with a 1 km resolution can potentially improve the resolution and reliability of SO2 and ozone estimates.
The spatial distribution of air pollutants simulated based on site-monitoring data requires strict verification of the accuracy of the simulation results. Therefore, it is also crucial to check the accuracy of the simulations. The mainstream method of assessing simulation results is cross-validation (CV), such as global CV, local (time, space) CV, and continuous CV. These methods are necessary in many cases, but CV also has disadvantages. For example, results in regions without site observations cannot be verified by CV. Many studies have shown that using large-scale remote sensing data to simulate near-surface atmospheric pollutants is prone to “banding” or “patchy” phenomena that do not conform to natural laws (Supplementary Figure S4) [12,17]. Therefore, it is equally important to confirm that the spatial distribution of air pollutants near the surface does not conform to natural laws.
Since 2013, China has gradually improved the establishment of an air pollutant monitoring network and generated massive amounts of air pollutant monitoring data [18,19,20]. Aided by massive multisource heterogeneous datasets, many studies have produced a variety of spatial distribution products for atmospheric pollutants (such as the CHAP and TAP) [21]. Random forest, XGBoost, LightGBM, and other machine-learning methods have achieved good stability and reliability in the process of generating spatial distribution products for atmospheric pollutants [22]. LightGBM implements gradient-based one-sided sampling and exclusive feature bundling on the basis of the GBM. In the process of fitting and predicting large datasets, this approach is extremely efficient and provides a stable accuracy guarantee [23]. Further optimizing the simulation accuracy of the LightGBM model for PM2.5, SO2, and ozone can provide more stable spatial distribution products for these atmospheric pollutants. This optimization process mainly includes spatial sampling and the use of a random ID for each pixel (RID). Notably, an RID is a means of randomly labeling pixels to effectively suppress the phenomenon of “banding” or “patchiness”. In addition, the convolution operation for samples or parameters can effectively increase the data dimension and the number of features, enhance learning, and improve the accuracy of the model training and fitting process. The introduction of these methods to optimize LightGBM is expected to further improve the simulation effect of air pollutants.
Trace gases such as SO2 and ozone are affected by the resolution of key corresponding remote sensing products, resulting in serious constraints on the resolution and accuracy of near-surface spatial simulations [24]. Fortunately, PM2.5 can be used to help optimize such simulations. Therefore, in this study, LightGBM is optimized using spatial sampling and parameter convolution to simulate the levels of atmospheric pollutants. Using site observations, remote sensing products, meteorological parameters, RIDs, and sequential simulations of multiple air pollutants, the spatially distributed multiple air pollutant (MuAP) dataset, including PM2.5, SO2, and ozone, is generated at a resolution of 1 km and at the daily scale in most of China (excluding some islands) from 2015 to 2020. We interpret the output of the model using the SHapley Additive exPlanations (SHAP) method. The air pollutant trends in China before and after the outbreak of COVID-19 are assessed using the Air Pollution Index (API). This paper is organized as follows: in Section 2, the dataset is described; Section 3 presents the methodology of the model; Section 4 presents the results of the model; Section 5 focuses on the model and its application; Section 6 presents the conclusions.
2. Datasets
The data used in this study include daily site observation data for PM2.5, SO2, and ozone in China. Additionally, remote sensing data, meteorological data, and auxiliary data are used.
2.1. Air Pollution and Meteorological Site Observation Data
In this study, hourly observation data from 2108 air pollutant sites were obtained from 1 January 2015 to 31 December 2020. Notably, the National Environmental Monitoring Center of China operates 2020 sites (air.cnemc.cn (accessed on 28 November 2023)), the Hong Kong Environment Department operates 18 sites (www.epd.gov.hk (accessed on 28 November 2023)), and the Taiwan Environment Agency operates 70 sites (data.moenv.gov.tw (accessed on 28 November 2023)). Figure 1 shows that the spatial distribution of the air pollutant monitoring sites is heterogeneous, with a higher density of sites along the east coast and a lower density in the western plateau region. In addition, we collected daily site observation data from 760 meteorological sites (Supplementary Figure S7) in mainland China from 1 January 2015 to 31 December 2020, with a focus on four parameters: wind speed (Ws), humidity (Hum), air pressure (Pr), and temperature (Tem).
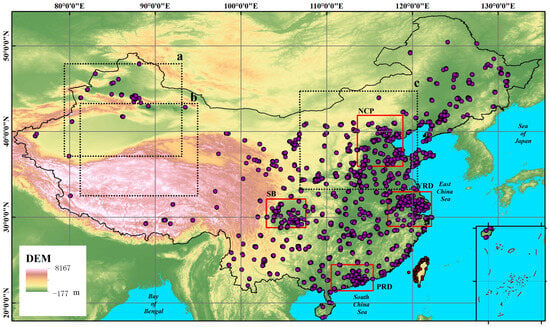
Figure 1.
Map of the study region and distribution of air pollutant monitoring sites. The purple dots denote the atmospheric pollutant monitoring sites. The four red boxes represent the North China Plain (NCP), the Yangtze River Delta (YRD), the Pearl River Delta (PRD), and the Sichuan Basin (SB), areas considered in the CV process. The three black boxes (a, b, and c) are used for visual assessment.
2.2. Remote Sensing Data
The remote sensing datasets used included (1) AOD data, (2) SO2 and ozone column data, and (3) other data. (1) The MAIAC AOD and Himawari-8 AOD datasets included 470 nm AOD and 550 nm AOD. Notably, the MAIAC AOD dataset (search.earthdata.nasa.gov (accessed on 28 November 2023)) has a spatial resolution of 1 km and a temporal resolution of 1 day [25], and the L3 daily product of the Himawari-8 AOD dataset (ftp.ptree.jaxa.jp (accessed on 28 November 2023)) has a spatial resolution of 5 km. The above attributes are the same for AOD550 and AOD470 [26]. (2) The SO2 and ozone column data included OMI and Sentinel 5P data. The OMI is an L3 product, the resolution is approximately 0.25°, the temporal resolution is 1 day, and the time range is 1 January 2015–31 December 2020. Sentinel 5P is a Level-2 product, the resolution is approximately 5.5~7 km, and the time range is 1 January 2019–31 December 2020. The above attributes are the same for COLSO2 and COLO3. (3) Other data include NDVI, topography, population distribution, road, and land use datasets. The NDVI was calculated from MODIS data (search.earthdata.nasa.gov (accessed on 28 November 2023)) at a temporal resolution of 16 days and a spatial resolution of 1 km [27]. Topographic data, including elevation and slope, were extracted from SRTM data (search.earthdata.nasa.gov (accessed on 28 November 2023)), with a spatial resolution of 90 m [28]. These data were used to obtain Ele and SLOP. Population data were obtained from LandScan (landscan.ornl.gov (accessed on 28 November 2023)) at a spatial resolution of approximately 1 km [29]. The 2018 road data were obtained from OpenStreetMap (www.openstreetmap.org (accessed on 28 November 2023)) in the format of an ESRI shapefile [30]. Land use data were obtained from the Copernicus Climate Change Service (C3S) 2018, with a spatial resolution of 300 m (cds.climate.copernicus.eu (accessed on 28 November 2023)) [31]. The planetary boundary layer height and PBLH were obtained from the Modern-Era Retrospective Analysis for Research and Applications version 2 (MERRA2) dataset (search.earthdata.nasa.gov (accessed on 28 November 2023)) [32].
2.3. Auxiliary Data
We constructed a WGS84 coordinate grid covering China (the spatial extent is shown in Figure 1), with a longitudinal resolution of 0.01° and a latitudinal resolution of 0.008° (1 km). The year (Year), day of the year (DOY), weekday/nonweekday (WOND; where nonweekdays included statutory holidays), and the independent pixel space ID parameter (RID) were considered. We generated PM2.5, SO2, and ozone rankings for different provinces. In different provinces, the daily concentration of pollutants at all sites was ranked in reverse order (for example, the province with the highest concentration was ranked first), and this ranking was divided into PrPM2.5, PrSO2, and PrO3. According to this rule, we generated CtPM2.5, CtSO2, CtO3 and CoPM2.5, CoSO2, and CoO3 results for the rankings of PM2.5, SO2, and ozone at the city and county levels. In addition, we constructed the parameter space (Ps) (Supplementary Section S1.2) according to the research of Wei et al. [33]. The data preprocessing steps are described in Supplementary Section S1. The data description is given in Supplementary Section S2.
3. Method
We use spatial sampling, RIDs, parameter convolution, and multiple pollutant simulation sequentialization to optimize LightGBM and jointly simulate the spatial distribution of multiple atmospheric pollutants. Finally, MuAP products were generated. We evaluated the model results using CV and visual qualitative analysis (Figure 2). LightGBM, LSTM, and RF-Ps (Supplementary Section S1.2) were compared to MuAP to assess its performance. Finally, SHAP was used to interpret the output of the model.
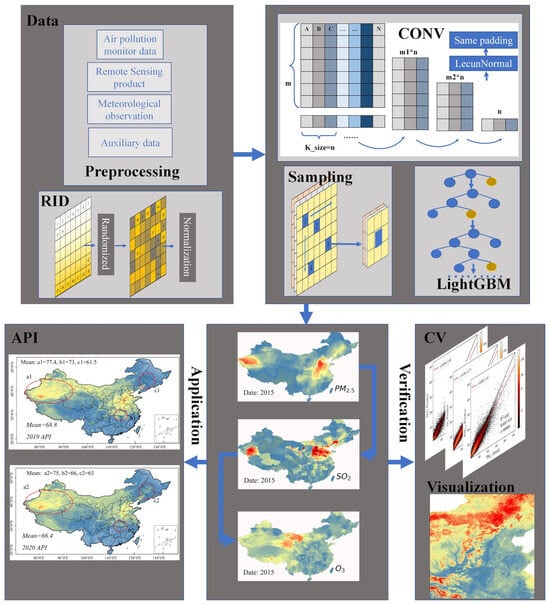
Figure 2.
Technical flow chart. The diagram at the upper left shows the data collection and RID creation process. The model at the upper right includes parameter convolution, spatial sampling, and the application of LightGBM. The data are transferred to the model, and the spatial distributions of atmospheric pollutants are obtained. Then, SHAP is used to analyze the model results and generate an API for secondary analysis.
3.1. Multipollutant LightGBM Combining Spatial Sampling, Random IDs, and Parameter Convolution
LightGBM improves upon the gradient-boosting decision tree (GBDT). LightGBM mainly implements gradient-based one-sided sampling (GOSS) and exclusive feature bundling (EFB). Compared with the GBDT model, LightGBM improves the calculation speed, ensures high accuracy, and can better cope with large amounts of data. At present, LightGBM has been applied in many fields. However, applications in atmospheric remote sensing are limited and have significant potential. When developing LightGBM, we created new mechanisms for spatial sampling, parameter convolution, random ID generation, and the sequential simulation of multiple pollutants.
3.1.1. Spatial Sampling
The spatial distribution of air pollutants is significantly affected by the locations and characteristics of monitoring sites and the surrounding environment, and many studies have considered the spatial correlations between different factors and air pollutants. We thoroughly explored the spatial information associated with remote sensing data and considered the environmental factors near air pollutant monitoring sites. For a given pixel (), the feature group of surrounding elements in a 3 × 3 neighborhood can be expressed as
where represents an array of 9 pixel values around a given pixel () and the pixel itself.
3.1.2. Random IDs
Parameter randomization is a key method of model optimization. Based on this approach, the derived RIDs were used to optimize the spatial distribution of atmospheric pollutants. We denoted the positions of all pixels with independent IDs, shuffled these IDs with a random algorithm, and introduced the RIDs into a random forest model. The specific steps are as follows.
- Randomize the position parameters, scramble the position IDs with a random algorithm, and assign a random ID to each pixel.
- Apply a 0–1 normalization algorithm to normalize the location parameters and random location IDs.
3.1.3. Parameter Convolution
The spatial distribution of air pollutants is affected by various factors, the relationships among factors are complex, and the correlation coefficients among factors are low (Supplementary Figure S3). Generally, independent remote sensing data cannot fully explain the various properties of atmospheric pollutants. Therefore, it is very important to deeply explore the relationships between datasets. To provide more features for model training, we implement random 1D convolution operations for various factors. The specific process is as follows:
- Normalize all features.
- Select a 1 × 3 convolution window.
- Set the number of features considered for the two convolution boosting parameters, where m1 = 64 and m2 = 16.
- Input random features into the convolution window.
- Initialize the random convolution kernel (LecunNormal) [34,35].
- Apply the ‘same padding’ method to obtain a set of results.
3.1.4. Sequential Multiple-Pollutant Simulation
PM2.5, SO2, and ozone interact with each other, and there is a synergistic relationship among the corresponding trends in space and time. To effectively predict the spatial distribution of multiple pollutants, it is necessary to introduce different pollutants into the prediction model. We set the sequential simulation prediction order as PM2.5 > SO2> ozone.
3.2. Other Models
The LightGBM, LSTM, and RF-Ps models were used to independently simulate the spatial distributions of PM2.5, SO2, and ozone. Only RF-Ps included an additional parameter, Ps (Supplementary Section S1.2), and the other parameters remained the same. The details of the models are given in Table 1.

Table 1.
Details of the other models.
3.3. CV and Visualization Assessment
CV is divided into random CV and regular CV. Random CV was used to randomly select 90% of the data for modeling and the rest for testing. This process was repeated ten times, and the average result was used. In regular CV, data from a specific time and space are used for testing, and the rest are used for training. The CV result in this study was evaluated using the coefficient of determination (R2) and root mean square error (RMSE).
Combined with atmospheric convection and regional transport theories, we qualitatively determined whether there were significant anomalies (patches and bands) in the visualization results.
3.4. Model Explanation
SHAP is a game theory approach for calculating the importance of features in a model by comparing model estimates with and without features [36]. A variety of parameter measurement methods can be used, and we selected the bee swarm approach to calculate the influence of each input parameter and each feature on the output [37]. The main parameters that affect the model were identified, and the effect of each parameter on the simulation results was constrained [23].
4. Results and Analysis
4.1. CV Results
4.1.1. Total Random Sampling CV
The sequential training and verification process of the models for multiple air pollutants included training and verification using ground observation data and secondary training and verification using simulated data. Among them, training and verification were randomly performed in CV, and we illustrate the CV results for these two steps in Figure 3.
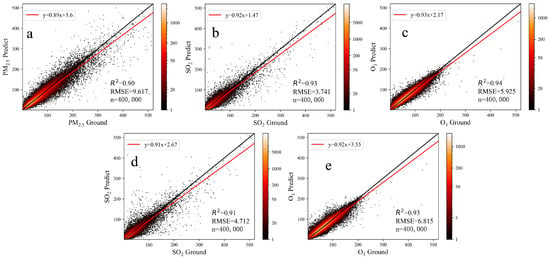
Figure 3.
Model construction results considering various air pollutants and the CV of the spatial distributions of pollutants. (a) CV of PM2.5 in the model. (b) CV of the SO2 model trained with PM2.5 ground observations. (c) CV of the ozone model trained with SO2 ground observations. (d) CV of the SO2 model trained with PM2.5 simulations. (e) CV of the ozone model trained with SO2 simulations. In the figure, n represents the number of samples, and the color bar on the right represents the density of the samples. The black line represents the 1:1 reference. The red line represents the results of sample fitting.
Simulating the spatial distribution of atmospheric pollutants requires a complete spatial distribution dataset. Before constructing the spatial distribution dataset, only site observation data were available. However, due to the lack of complete spatial information on air pollutants, this process could not be used for the further spatial modeling of multiple air pollutant products. Therefore, in the spatial distribution model, the predicted spatial air pollutant levels were used as the model inputs. This was also the reason why there are two types of ground observations (b and c in Figure 3) and training data (d and e in Figure 3). For example, the estimation model of SO2 uses the simulated spatial distribution of PM2.5. Figure 3 shows that as the number of parameters increases, the R2 values of PM2.5, SO2, and ozone increase sequentially. In addition, the estimates of the models based on simulation results are slightly lower than the site observations by approximately 1% (SO2 and ozone). Finally, we explored the sequence of PM2.5, ozone, and SO2. The results showed that the CV result obtained in this case was slightly worse than that for the order of PM2.5, SO2, and ozone (Supplementary Figure S5).
We randomly sampled one-tenth of the site data for CV (Figure 4). The R2 values of PM2.5, SO2, and ozone varied from 0.84–0.95, 0.85–0.96, and 0.85–0.96, respectively.
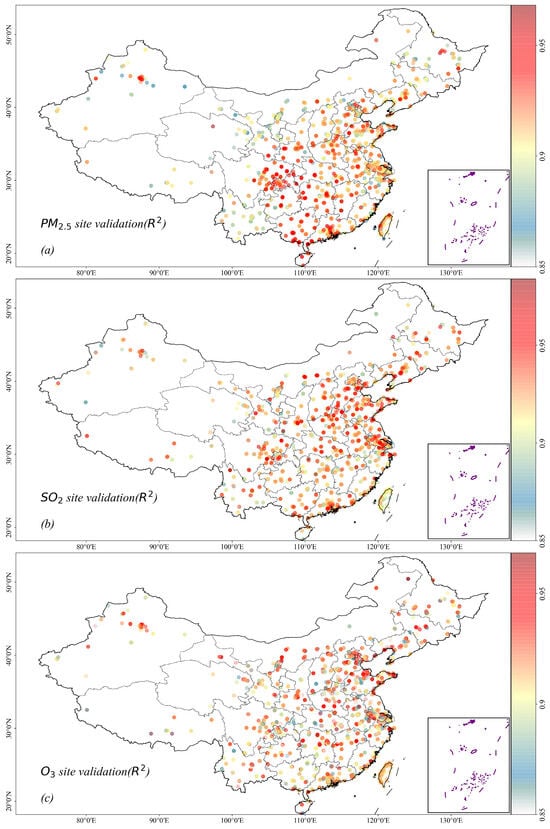
Figure 4.
Random site sampling verification results for PM2.5, SO2, and ozone. (a) represents the CV (R2) distribution of each site of PM2.5. (b) represents the CV (R2) distribution of each site of SO2. (c) represents the CV (R2) distribution of each site of O3. The dots represent the spatial locations of the monitoring sites, and the colored column denotes the R2 value.
4.1.2. Regular Sampling CV
The NCP (113.6–118.8°E, 36–41.9°N), YRD (117–122.2°E, 29–32.9°N), PRD (110.4–115.3°E, 21.5–24.6°N), and SB (102.9–107.5°E, 28.8–32.2°N) regions were selected for CV analysis. A verification based on air pollution data obtained at monitoring sites in the NCP, YRD, PRD, and SB areas was performed, and the training data were not used for verification. The CV verifications of the PM2.5, SO2, and ozone simulation models in different regions were performed separately (Figure 5).
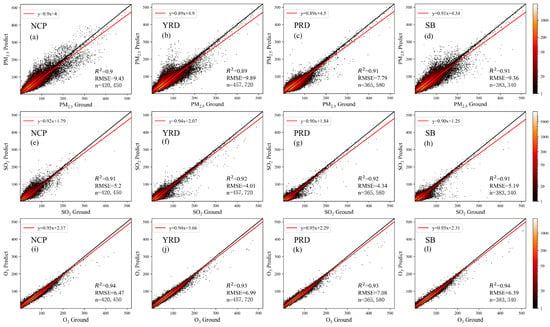
Figure 5.
CV results for PM2.5, SO2, and ozone in different regions. The simulation mode refers to the simulation data used. (a–d) show the results of the PM2.5 CV in the four regions. (e–h) show the results of the SO2 CV in the four regions. (i–l) show the results of the ozone CV in the four regions. NCP, YRD, PRD, and SB denote the North China Plain, Yangtze River Delta, Pearl River Delta, and Sichuan Basin, respectively.
Figure 5 shows that satisfactory RMSE and R2 values are obtained for the sampling results in the four regions. The results verify the stability of the MuAP data in regional validation (regular spatial sampling). Next, monthly or annual air pollution site-monitoring data were extracted for verification, and the remaining data were used for training. The model was retrained, and the CV process was repeated. The corresponding CV statistics are shown in Figure 6.
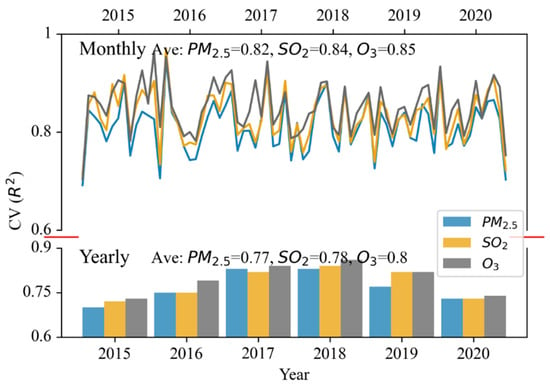
Figure 6.
Annual and monthly CV results for samples from 2015–2020. The upper part of the figure shows the mean of the resulting curve and CV for monthly sampling, and the lower part of the figure illustrates the bar plots and means for annual sampling. The three colors of the curves and columns denote PM2.5, SO2, and ozone.
In Figure 6, the R2 of monthly sampling for PM2.5, SO2, and ozone is not as high as that for random sampling but is similar (0.78–0.83). The R2 values for PM2.5, SO2, and ozone based on monthly sampling are all higher than those for annual sampling (0.71–0.76); this result is related to the number of samples considered for training and validation. Regardless of whether the three pollutants were sampled monthly or annually, the average R2 displayed the following order: PM2.5 < SO2 < ozone. Compared to random and regular spatial validation, regular temporal sampling validation was associated with a lower R2, especially for CV at the annual scale. However, the model still displayed strong stability.
4.1.3. CV of LSTM, RF-Ps, and LightGBM
Figure 7 shows the results of random sampling-based CV for the LSTM, RF-Ps, and LightGBM models. In this case, training and verification data were randomly divided for CV.
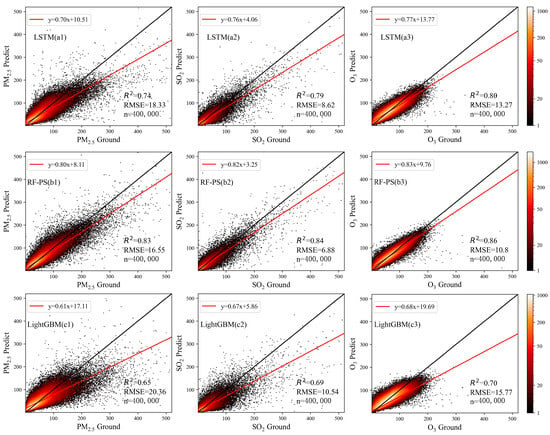
Figure 7.
CV of the LSTM, RF-Ps, and LightGBM models. LSTM (a1)–LSTM (a3) illustrate the CV results for PM2.5, SO2, and ozone simulations using the LSTM model, RF-Ps (b1)–RF-Ps (b3) show the CV results for PM2.5, SO2, and ozone simulations using the RF-Ps model, and LightGBM (c1)–LightGBM (c3) illustrate the CV results for PM2.5, SO2, and ozone simulations using the LightGBM model.
In Figure 7, the CVs of the LSTM and RF-Ps models are similar to those of the proposed model for PM2.5, SO2, and ozone, with R2 (PM2.5) < R2 (SO2) < R2 (ozone). This result suggests that air pollutant output data can be input into different models to improve the prediction of other pollutants. However, the R2 and RMSE values obtained with the LSTM and RF-Ps models are quite different from those of MuAP. Among the three models, the best CVs are obtained for RF-Ps. However, MuAP still yields the highest R2 and RMSE. Notably, the R2 value of the proposed model is 6–8% higher than that of the RF-Ps model. Additionally, the RMSEs of MuAP are 6 µg∙m−3, 2 µg∙m−3, and 4 µg∙m−3, which are lower than those of the RF-Ps model for PM2.5, SO2, and ozone, respectively. The LightGBM model performs poorly based on both the R2 and RMSE values, possibly due to the lack of auxiliary parameters and optimization. Comparatively, the MuAP and RF-Ps models use more auxiliary parameters than LightGBM, indicating that artificial auxiliary parameters enhance model training. Compared with the RF-Ps model, our model mainly improves the parameter convolution process and uses parameter convolution to further explore the relationships among features and parameters (Supplementary Section S4.2). Although the LSTM model does not perform as well as MuAP based on various verification parameters, it displays excellent development potential.
In addition, we performed CV assessments of the random sampling approach after adding RID, Ps, and RID+Ps parameters to LightGBM (Supplementary Figure S5). The results indicated that RID inclusion increased the performance of LightGBM more than the addition of Ps and RID+Ps. Additionally, we confirmed that RIDs can effectively improve the reliability of visualization and mitigate “banding” or “patchiness” (Supplementary Section S4.1).
Next, we measured the time needed to run the four models, as shown in Table 2 (for the PM2.5 case).

Table 2.
Time efficiency of the four models.
In terms of efficiency, LightGBM runs the fastest, followed by MuAP, with the LSTM and RF-Ps models requiring much more time to run. Among them, LightGBM, the LSTM model, and our model all support GPU computing. However, RF-Ps is not yet supported on GPUs [38]. In addition, we selected 16 models from the relevant literature to compare with MuAP based on the CV, RMSE, and spatial resolution results, and the findings are presented in Table 3.

Table 3.
Comparison of multiple models in the simulation of different air pollutants.
In Table 3, compared with recent machine-learning models, the proposed model yields better results for PM2.5, SO2, and ozone, especially for SO2 and ozone.
In addition, we identified and compared the differences and advantages between the MuAP results and the CHAP and TAP products (details in Supplementary Figure S3). Based on a comparison of the reanalysis products considering the product resolution, whether the visualization conforms to natural laws, and product ease of use, it was found that MuAP is the most advanced among these datasets.
4.2. Visual Comparison of the Spatial Distribution of Air Pollutants
We randomly sampled the spatial distributions of PM2.5, SO2, and ozone on January 26, 2015, and performed corresponding simulations with the LSTM, RF-Ps, and LightGBM models.
In a2–a4, b2–b4, and c2–c4 of Figure 8, there are “bands” or “patchiness” (a2, a4) in the simulation results, and the high or low values of the simulated air pollutants do not match the site observations (e.g., in the upper part of a3, in the areas of high values on the left and right sides of b2, in the lower parts of b3 and b4, and near the arrows in c2–c4). In contrast, the visualization of the MuAP results for these three regions is more in line with natural laws, and the local simulation results are closer to the site observations. This suggests that MuAP provides good stability in local simulation.
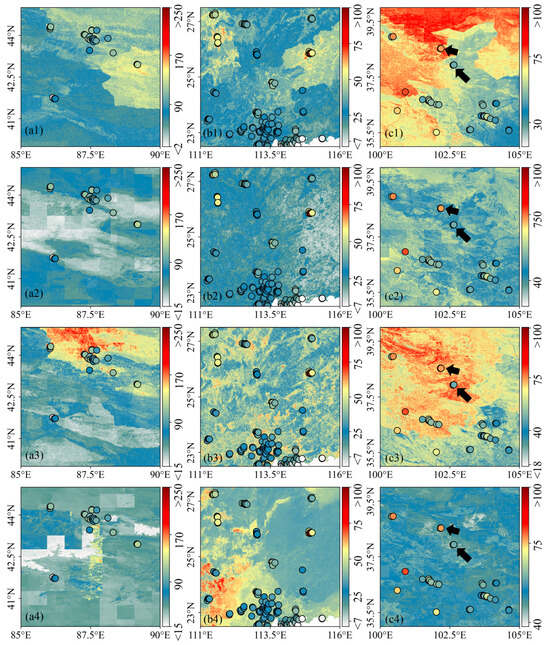
Figure 8.
Local comparison of different methods. (a1–a4) illustrate the PM2.5 results of MuAP, LSTM, RF-Ps, and LightGBM, respectively. (b1–b4) illustrate the SO2 results of MuAP, LSTM, RF-Ps, and LightGBM, respectively. (c1–c4) illustrate the ozone results of MuAP, LSTM, RF-Ps, and LightGBM, respectively. The black arrow highlights the differences between simulations and site monitoring. The red bars represent atmospheric pollutant concentrations. The range of column A is 85°–90°E, 40°–45°N, the range of column B is 111°–116°E, 22.5°–27.5°N, and the range of column C is 100°–105°E, 35°–40°N. The dots represent the positions of air pollutant monitoring sites and the corresponding daily monitoring values.
4.3. SHAP Results
Figure 9 shows the results of the SHAP approach with the bee swarm method, which was used to assess the impact of each sample and parameter on the model results. Moreover, SHAP was used to analyze the influence of parameter convolution on the model results (Figure 10).
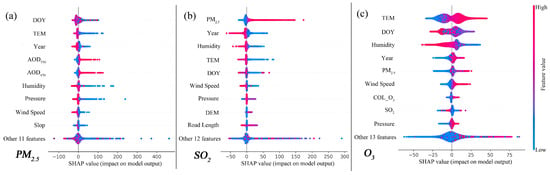
Figure 9.
SHAP bee swarm results. (a–c) show the SHAP results for PM2.5, SO2, and ozone, respectively. The color bar on the right represents the relative magnitude of the variable value, and the abscissa represents the SHAP value.
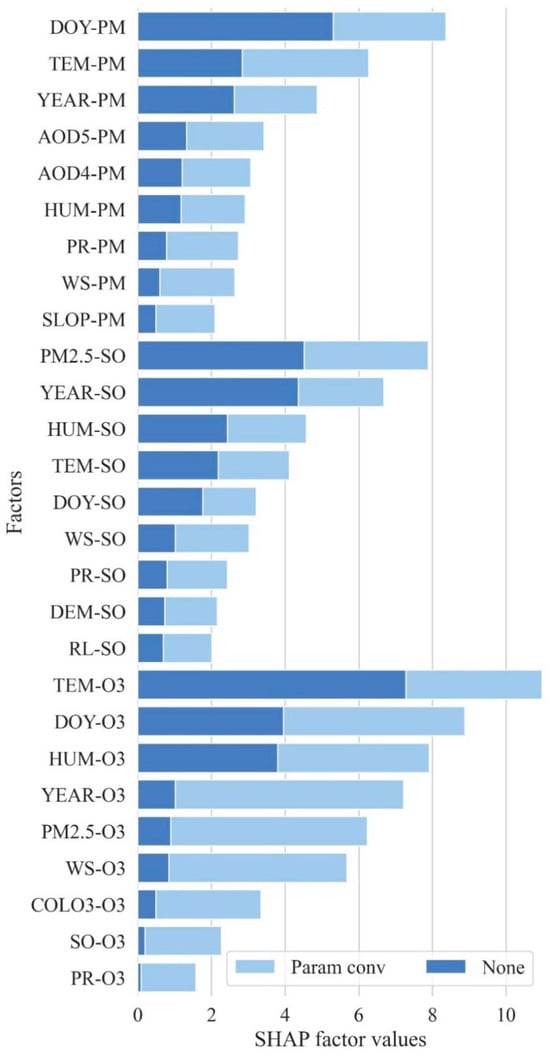
Figure 10.
Comparison of the SHAP values with and without applying parameter convolution. PM represents the main parameters used to simulate PM2.5, SO represents the main parameters used to simulate SO2, ozone represents the main parameters used to simulate ozone, Param conv represents the use of parameter convolution, and None indicates the absence of parameter convolution.
Figure 9 shows the SHAP summary for the proposed model, and the ranking of features from top to bottom reflects the importance of each feature in the model. The results show that different variables have different effects on the simulation of PM2.5, SO2, and ozone. We note that in our model, DOY and Year are crucial for the prediction of air pollutant trends. In fact, physical quantities such as TEM and AOD have a close and important relationship in air pollutant modeling. Empirical auxiliary parameters such as DOY and Year also play an important role in the model. These parameters have been introduced in many related studies but are rarely explained in depth. As also shown in Supplementary Figure S2, PM2.5, SO2, and ozone display obvious fluctuations in China at the daily and annual scales. Thus, DOY and Year can be used to effectively improve the fitting accuracy of the model to the data (see the detailed explanation in Supplementary Section S6). In addition, in sequential multiple-pollutant simulation, the explicit and implicit relationships among atmospheric pollutants are quantified by SHAP. For example, in Supplementary Figure S3, there is a strong positive correlation between PM2.5 and SO2, which is consistent with the SHAP results. Of course, this phenomenon is intuitive. SO2 and ozone are equally important in the SHAP results. However, the relationship between SO2 and ozone is not obvious in most studies. In this study, the simulated SO2 displays an obvious relationship with ozone, and it is possible that this relation enhanced their influence in SHAP. Although the mechanism remains to be studied, this result shows, to a certain extent, that the sequential simulation method for the spatial distribution of various atmospheric pollutants is effective.
In Figure 10, the SHAP value is the mean absolute value of the SHAP value of each sample, and the larger the value is, the stronger the contribution of the parameter to estimates of the concentrations of atmospheric pollutants. Notably, parameter convolution significantly contributes to improvements in the predictions of atmospheric pollutants.
4.4. Long-Term Spatial Distribution Characteristics of Various Air Pollutants
Figure 11 shows the average annual distributions of PM2.5, SO2, and ozone in China from 2015 to 2020 simulated with the proposed method.
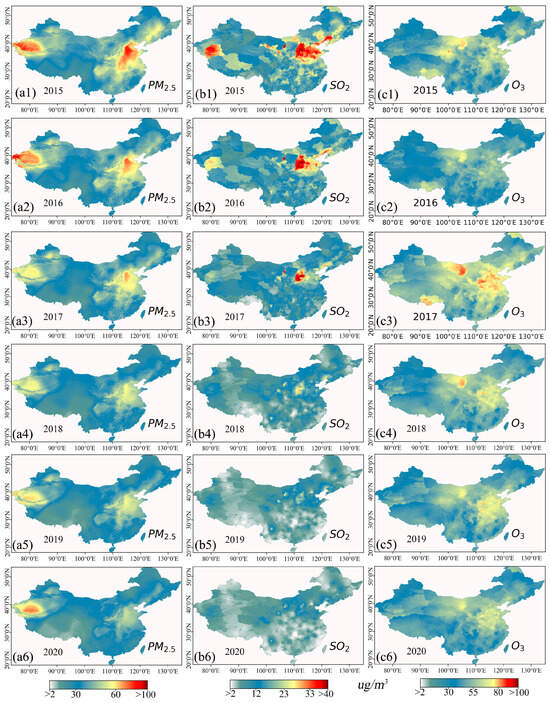
Figure 11.
Maps of the annual average spatial distributions of PM2.5, SO2, and ozone in China from 2015–2020. (a1–a6) show the annual average PM2.5 values from 2015–2020. (b1–b6) show the annual average SO2 values from 2015–2020. (c1–c6) illustrate the annual average ozone values from 2015–2020. The bars at the bottom give the concentrations of pollutants in the study area.
The high-risk areas of PM2.5 and SO2 are mainly located in the northern and northwestern parts of China. Although ozone is also high in these two regions, there are two high-value areas in northern and northwestern China and on the Qinghai–Tibet Plateau. This phenomenon is consistent with the site observations and the research of Gao et al. [23,42,55]. Although this result is not quite consistent with the CHAP and TAP results, it does verify the stability and reliability of MuAP in ozone simulation. Moreover, due to the addition of meteorological parameters and the ranking of provinces, cities, and counties based on the concentrations of SO2 and ozone, significant regional boundary differences can be identified.
4.5. Impact of COVID-19 on Air Pollution in China in 2019 and 2020
Changes in air pollution before and after the COVID-19 pandemic can be effectively assessed using the API. Based on the calculation method reported in the National Environmental Protection Standard of the People’s Republic of China–Ambient Air Quality Index (AQI), we calculated the daily API values of PM2.5, SO2, and ozone in 2019 and 2020. Figure 12 shows the average annual spatial distribution of the API in 2019 and 2020. If the API exceeds 100 on a given day, the secondary standard of the ambient air pollution concentration limit is exceeded.
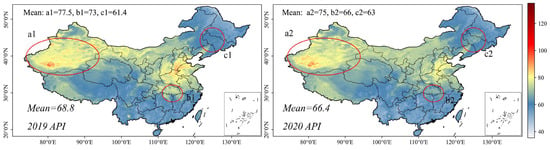
Figure 12.
Spatial distribution of the API in China in 2019 and 2020. (a1 and a2) shows the results for the Xinjiang region of China, with an API of 77.5 in 2019 and 75 in 2020. (b1 and b2) shows the results for Hubei, China. Wuhan was on lockdown for the first time due to COVID-19 from 23 January to 8 April 2020. The API was 73 in 2019 and 66 in 2020. (c1 and c2) shows the results for the Jilin region in Northeast China, with an API of 61.4 in 2019 and 63 in 2020. The color bar on the right shows the magnitude of the API values.
The results in Figure 12 are consistent with the trend of decreasing concentrations of major air pollutants in China. The API in China in 2019 and 2020 displayed a downward trend, decreasing from 68.8 in 2019 to 66.4 in 2020. The percentage of areas with API values greater than 100 decreased from 85.2% in 2019 to 75.6% in 2020. The influence of the main pollutant, PM2.5, gradually decreased, and the range of influence of ozone increased. In addition, the API in central China declined in 2020, the API in the northwest nonsignificantly decreased (Figure 12(a1,a2)), and the API in the northeast increased (Figure 12(c1,c2)) [56].
In the obtained histogram and the API results (Supplementary Figure S6), both the maximum value and the average value of the API decreased from 2019 to 2020, but the API values generally remained high. Since 2015, PM2.5 and SO2 have displayed significant downward trends, but the downward trend of ozone is not apparent (Figure 9 and Figure 10). As shown in Figure 11 and Figure 12, the epidemic in 2020 had a significant impact on air pollution in local areas (such as Figure 12(b1,b2) Wuhan and Hubei). However, the impact on the entire region of China was not particularly obvious. Due to the closure of Wuhan and other effective control measures in the early stage of the epidemic in 2020, the restriction of human activities significantly reduced air pollution in some areas. However, these measures in specific cities did not influence trends in the rest of China. In the second half of 2020, with the global spread of the epidemic, the industrial chains in other parts of the world were severely impacted, which in turn led to an increase in the industrial production capacity in areas of China not affected by the epidemic, thus increasing the emission of air pollutants to a certain extent. Local lockdowns associated with epidemics led to the return of urban workers to their hometowns, increased straw burning (remote sensing observations suggest that the number of fires in 2020 increased by 20% over the number in 2019) [57,58], increased domestic heating and other phenomena that exacerbated air pollution in Northeast China and other regions (Figure 12(c1,c2)). Nevertheless, under the governance of policies such as the “Blue Sky Protection Campaign”, the air pollution conditions in China have generally improved since 2020 [59].
5. Discussion
5.1. Model Overview
This study introduces a variety of optimization rules based on LightGBM, ground air pollutant observations, and remote sensing, meteorological, and auxiliary data. Following sequential model training, gap-free PM2.5, SO2, and ozone products were obtained at a 1 km daily resolution near the ground in China. Good results were achieved for PM2.5 (R2 = 0.9, RMSE = 9.62 µg∙m−3), SO2 (R2 = 0.91, RMSE = 4.71 µg∙m−3), and ozone (R2 = 0.93, RMSE = 6.81 µg∙m−3). MuAP mitigates the phenomena of patches and bands and strengthens the consistency of atmospheric pollutant concentrations at the regional scale, such as in county-level administrative districts. Additionally, the optimization processes applied did not seriously hinder the efficiency of the model.
5.2. The Efficacy of the Model
We verified the improvements achieved through spatial sampling, RID generation, and parameter convolution for CV and visualization. Using the sequential PM2.5, SO2, and ozone simulation results, we stably generated the spatial distributions of SO2 and ozone at a 1 km resolution. Compared with the models in related research, MuAP yields the highest CV results and more stable and accurate visualization effects in the verification of PM2.5, SO2, and ozone. In addition, for most SO2 and ozone products, there is a strong effect associated with county-level administrative boundaries, which we believe may be associated with the air pollution ranking inputs of provinces, cities, and counties. Additionally, this phenomenon can limit the simulated anomalies to a small area (county level). Compared with CHAP and TAP, MuAP yields results in the standard GeoTIFF format and provides a better product resolution and enhanced CV results. Consequently, data gaps are avoided.
Based on the SHAP method, we obtained a detailed understanding of how the input samples affect the model, including positive and negative effects. For example, the important factor with the greatest influence on ozone is TEM (a high temperature promotes the formation of ozone), and a key factor that influences PM2.5 is SO2 (logically, sulfate generated by SO2 should affect the PM2.5 concentration). However, areas with high concentrations of PM2.5 also have high concentrations of SO2. This rather far-fetched explanation happens to be conducive to using machine-learning models to assist in explaining empirically strong logical relationships. The impact of these parameters on air pollutants is consistent with intuition. However, MuAP includes empirical auxiliary parameters. For example, the crucial factor related to the PM2.5 trend is DOY. Notably, the changes in PM2.5 concentrations coincide with DOY over time. Although these empirical auxiliary parameters do not affect factors such as temperature and AOD, the introduction of these auxiliary parameters can improve the performance of the model without notably increasing the cost of data collection. Therefore, it is useful to introduce these empirical auxiliary parameters. In addition, the SHAP approach can be used to not only determine the contributions of these parameters but also guide the optimization of the model. For example, SHAP can be used to quantify the effect of parameter convolution on model improvement, and the results can be used to further explore the relationships between datasets and improve the effectiveness of atmospheric pollutant simulations.
Advances in technology will lead to more high-resolution and high-precision remote sensing products in the future, which will significantly improve the performance of air pollutant products. Therefore, continuously assessing updates to remote sensing datasets will be crucial. However, as noted above, due to the limitations of existing technologies, parameters must be further created or optimized. The auxiliary parameters introduced in this study are important for the construction of MuAP. However, the parameter introduction process should be cautiously explored, and blind selection may reduce the overall performance of the model (Supplementary Figure S4). In addition, as with many reanalysis products, the PM2.5 data used in the simulations of SO2 and ozone with MuAP are important and can provide a direct or indirect contribution to the simulation of the spatial distributions of other atmospheric pollutants. In this study, both the CV result and the resolution of the SO2 and ozone models were enhanced with the addition of atmospheric pollutant parameters. However, the repeated use of simulated atmospheric pollutants increases uncertainty to some extent. Therefore, the proposed model was only used to simulate three air pollutants. In the future, we will explore the quantification and resolution of uncertainties in atmospheric pollutant simulation results and simulate other major atmospheric pollutants.
Finally, we added an LSTM model to our study for comparison. Although the LSTM does not display excellent CV performance, it exhibits great development potential. Shwartz et al. and Grinsztajn et al. [60,61] noted that when performing classification or regression tasks with tabular data, machine-learning methods, such as LightGBM and random forests, are often superior to deep-learning methods, as demonstrated by the unsatisfactory performance of the LSTM model in this study. However, the simulation of the spatial distribution of atmospheric pollutants involves not only tabular data but also the key features of graphical data. LSTM also exhibits strong spatial simulation capabilities. We have shown that spatial sampling and parameter convolution are effective LightGBM optimization methods, and they are both closely related to convolution methods in deep learning. In the future, we will further explore the spatial distribution of air pollutants by combining time series and convolutional neural networks.
6. Conclusions
We introduce spatial sampling, RIDs, and parameter convolution to jointly optimize LightGBM. Sequential multiple-pollutant simulation is performed with MuAP. The spatial resolution of the results is 1 km, and gap-free PM2.5, SO2, and O3 products are obtained (from 1 January 2015–31 December 2020). Based on random sampling CV for the proposed model, we obtained an R2 of 0.9 and an RMSE of 9.62 µg∙m−3 for PM2.5, an R2 of 0.91 and an RMSE of 4.71 µg∙m−3 for SO2, and an R2 of 0.93 and an RMSE of 6.81 µg∙m−3 for ozone. In addition, we demonstrated the stability and excellent generalization ability of MuAP by utilizing random sampling site validation, rule validation, and side-by-side comparison. It was confirmed that MuAP reduced the insufficient visualization of patches and bands, even when simulating the spatial distributions of multiple pollutants in the large-scale study area. Our results indicate that the potential of deep-learning models is enormous. In the future, we will further optimize various deep-learning models and simulate the spatial distributions of additional atmospheric pollutants. In addition, we have published MuAP at https://github.com/pingyinforbidden/China_air_pollutions [62,63,64] (accessed on 10 December 2023).
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs15245705/s1, Figure S1: Factor histogram. Where the one with the highest LandUse represents the urban area. It shows that most air pollutant monitoring sites are mainly located in urban areas; Figure S2: Monthly average of ground monitoring of air pollution in China; Figure S3: Correlation coefficients of PM2.5, SO2, and ozone and other elements at the level of ground observation sites; Figure S4: Schematic diagram of the “banding” or “patchy” phenomenon simulated in the spatial distribution of air pollutants. The black marks clearly show this phenomenons; Figure S5: LightGBM added RID, Ps and RID+Ps parameters to the CV evaluation difference of PM2.5, SO2, and ozone. The R2 of RID is the highest and the RMSE is the lowest. Among them, the unit of RMSE is µg/m3; Figure S6: Histogram of API statistics for 2019 and 2020. The 2020 API results are more concentrated than 2019, while having smaller values; Figure S7: Spatial distribution of meteorological data sites. Combined with Figure 1, we found that the distribution of the meteorological sites we collected is not completely consistent with that of atmospheric pollutant sites; Figure S8: Comparison of spatial features of CHAP, TAP, and MuAP; Figure S9: Comparison of one day simulation of PM2.5 with and without RID addition. The black arrow in A shows that there are more obvious display abnormalities (“banding” or “patchy”), and the same area in B has been significantly optimized. A. PM2.5 simulation without RID added. B. PM2.5 simulation with RID added; Figure S10: Comparison of the effect of parametric convolution on model CV. A is the CV without parameter convolution, and B is the CV with parameter convolution. With the addition of parameter convolution, R2 has been significantly improved, and RMSE has also decreased significantly. A. Without parameter convolution. B. With parameter convolution; Figure S11: The effect of parametric convolutions on the visualization of ozone simulations. A. is the result of no parameter convolution. B. is the result of parameter convolution. Parameter convolution significantly improves the visual rationality of ozone. A. Without parameter convolution. B. With parameter convolution; Figure S12: The interception of the manuscript Figure 3; Figure S13: The CV after replacing the air pollutant simulation sequence. (b) Combined with simulated PM2.5, the resulting CV of ozone. (a) Combining simulated PM2.5 and ozone, the CV of SO2 is further simulated; Table S1: The annual average of air pollution ground monitoring in China; Table S2: Site revalidation R2 for air pollutants; Table S3: Comparison of different products with Taiwan region observed averages; Table S4: Part key parameters of remote sensing datasets; Table S5: Key parameters of Auxiliary data.
Author Contributions
Y.C. collected and processed the data, designed the model and wrote the manuscript. Y.Z., K.W. and H.Y. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 42271299), the International Partnership Program of the Chinese Academy of Sciences (grant no. 132c35kysb2020007), the Ningbo Commonweal Science and Technology Planning Project (grant no. 2021S081), the Science Foundation of Fujian Province (grant no. 2023J011027), the Fujian Province Young and Middle-Aged Teacher Education Research Project (grant no. JAT220350) and the Introduction of High-Level Talents at Sanming University (grant nos. RD21006P, KC22020P, and KD22028P).
Data Availability Statement
The spatial distribution of various air pollutants in China at 1 km (MuAP) reported in this manuscript can be accessed at the following repositories via different data DOIs: 1. https://doi.org/10.5281/zenodo.8093749 [62], 2. https://doi.org/10.5281/zenodo.8093719 [63], and 3. https://doi.org/10.5281/zenodo.8180923 [64].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Abbreviate | Explanation | Abbreviate | Explanation |
| Hum | Humidity | Ele | Elevation |
| Ws | Wind speed | SLOP | Slope |
| Pr | Atmospheric pressure | POP | Population |
| Tem | Temperature | NDVI | Normalized difference vegetation index |
| RL | Road length | DOY | Day of year |
| LUCC | Land use cover change | YEAR | Specific year |
| WOND | Weekday/nonweekday | PBLH | Planetary boundary layer height |
| AOD550 | AOD at 550 nm | AOD470 | AOD at 470 nm |
| COLSO | SO2 column concentration | COLO3 | Ozone column concentration |
| PM2.5 | Particulate matter with an aerodynamic diameter ≤ 2.5 μm | SO2 | Sulfur dioxide |
| MuAP | The spatially distributed multiple-air-pollutant model | SHAP | SHapley Additive exPlanations |
| CHAP | China high air pollutants | TAP | Tracking air pollution in China |
| AOD | Aerosol optical depth | MAIAC | Multiangle implementation of atmospheric correction |
| OMI | Ozone monitoring instrument | CV | Cross-validation |
| LightGBM | Tree-based machine-learning gradient-boosting model | RID | Random ID for each pixel |
| RF-Ps | Random forest with spatial weights | API | Air pollution index |
| LSTM | Long short-term memory network | NPC | The North China Plain |
| YRD | Yangtze River Delta | PRD | Pearl River Delta |
| SB | Sichuan Basin |
References
- Dedoussi, I.C.; Eastham, S.D.; Monier, E.; Barrett, S.R.H. Premature mortality related to United States cross-state air pollution. Nature 2020, 578, 261–265. [Google Scholar] [CrossRef] [PubMed]
- Landrigan, P.J. Air pollution and health. Lancet Public Health 2016, 2, e4–e5. [Google Scholar] [CrossRef]
- Shen, G.; Ru, M.; Du, W.; Zhu, X.; Zhong, Q.; Chen, Y.; Shen, H.; Yun, X.; Meng, W.; Liu, J.; et al. Impacts of air pollutants from rural Chinese households under the rapid residential energy transition. Nat. Commun. 2019, 10, 3405. [Google Scholar] [CrossRef]
- Zhang, A.L.; Balmes, J.R.; Lutzker, L.; Mann, J.K.; Margolis, H.G.; Tyner, T.; Holland, N.; Noth, E.M.; Lurmann, F.; Hammond, S.K.; et al. Traffic-related air pollution, biomarkers of metabolic dysfunction, oxidative stress, and CC16 in children. J. Expo. Sci. Environ. Epidemiol. 2021, 32, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Li, Z.; Li, K.; Dickerson, R.R.; Pinker, R.T.; Wang, J.; Liu, X.; Sun, L.; Xue, W.; Cribb, M. Full-coverage mapping and spatiotemporal variations of ground-level ozone (O3) pollution from 2013 to 2020 across China. Remote Sens. Environ. 2021, 270, 112775. Available online: https://www.sciencedirect.com/science/article/pii/S0034425721004958 (accessed on 10 December 2023). [CrossRef]
- Geng, G.; Xiao, Q.; Liu, S.; Liu, X.; Cheng, J.; Zheng, Y.; Xue, T.; Tong, D.; Zheng, B.; Peng, Y.; et al. Tracking Air Pollution in China: Near Real-Time PM2.5 Retrievals from Multisource Data Fusion. Environ. Sci. Technol. 2021, 55, 12106–12115. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Presto, A.A.; Zimmerman, N. Spatial Modeling of Daily PM2.5, NO2, and CO Concentrations Measured by a Low-Cost Sensor Network: Comparison of Linear, Machine Learning, and Hybrid Land Use Models. Environ. Sci. Technol. 2021, 55, 8631–8641. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Zheng, Y.; Zhang, Q.; Xue, T.; Zhao, H.; Tong, D.; Zheng, B.; Li, M.; Liu, F.; Hong, C.; et al. Drivers of PM2.5 air pollution deaths in China 2002–2017. Nat. Geosci. 2021, 14, 645–650. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Gupta, P.; Wang, K.; Jena, C.; Zhang, Y.; Lu, Z.; Streets, D.G. Using gap-filled MAIAC AOD and WRF-Chem to estimate daily PM2.5 concentrations at 1 km resolution in the Eastern United States. Atmos. Environ. 2018, 199, 443–452. Available online: https://www.sciencedirect.com/science/article/pii/S135223101830829X (accessed on 10 December 2023). [CrossRef]
- Kang, Y.; Choi, H.; Im, J.; Park, S.; Shin, M.; Song, C.-K.; Kim, S. Estimation of surface-level NO2 and O3 concentrations using TROPOMI data and machine learning over East Asia. Environ. Pollut. 2021, 288, 117711. Available online: https://www.sciencedirect.com/science/article/pii/S0269749121012938 (accessed on 10 December 2023). [CrossRef]
- Verhoelst, T.; Compernolle, S.; Pinardi, G.; Lambert, J.-C.; Eskes, H.J.; Eichmann, K.-U.; Fjæraa, A.M.; Granville, J.; Niemeijer, S.; Cede, A.; et al. Ground-based validation of the Copernicus Sentinel-5P TROPOMI NO2 measurements with the NDACC ZSL-DOAS, MAX-DOAS and Pandonia global networks. Atmos. Meas. Tech. 2021, 14, 481–510. Available online: https://amt.copernicus.org/articles/14/481/2021/ (accessed on 10 December 2023). [CrossRef]
- Chi, Y.; Zhan, Y. A Simple and Effective Random Forest Refit to Map the Spatial Distribution of NO2 Concentrations. Atmosphere 2022, 13, 1832. [Google Scholar] [CrossRef]
- Wang, C.; Guan, K.; Peng, B.; Chen, M.; Jiang, C.; Zeng, Y.; Wu, G.; Wang, S.; Wu, J.; Yang, X.; et al. Satellite footprint data from OCO-2 and TROPOMI reveal significant spatio-temporal and inter-vegetation type variabilities of solar-induced fluorescence yield in the U.S. Midwest. Remote. Sens. Environ. 2020, 241, 111728. Available online: http://www.sciencedirect.com/science/article/pii/S0034425720300985 (accessed on 10 December 2023). [CrossRef]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.-Y.; Künzli, N.; Schikowski, T.; Marcon, A.; et al. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe—The ESCAPE project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- Lin, C.-A.; Chen, Y.-C.; Liu, C.-Y.; Chen, W.-T.; Seinfeld, J.H.; Chou, C.C.-K. Satellite-Derived Correlation of SO2, NO2, and Aerosol Optical Depth with Meteorological Conditions over East Asia from 2005 to 2015. Remote Sens. 2019, 11, 1738. [Google Scholar] [CrossRef]
- Womack, C.C.; Manfred, K.M.; Wagner, N.L.; Adler, G.; Franchin, A.; Lamb, K.D.; Middlebrook, A.M.; Schwarz, J.P.; Brock, C.A.; Brown, S.S.; et al. Complex refractive indices in the ultraviolet and visible spectral region for highly absorbing non-spherical biomass burning aerosol. Atmos. Meas. Tech. 2021, 21, 7235–7252. Available online: https://acp.copernicus.org/articles/21/7235/2021/ (accessed on 10 December 2023). [CrossRef]
- Zhan, Y.; Luo, Y.; Deng, X.; Chen, H.; Grieneisen, M.L.; Shen, X.; Zhu, L.; Zhang, M. Spatiotemporal prediction of continuous daily PM2.5 concentrations across China using a spatially explicit machine learning algorithm. Atmos. Environ. 2017, 155, 129–139. Available online: http://www.sciencedirect.com/science/article/pii/S1352231017300936 (accessed on 10 December 2023). [CrossRef]
- Hu, H.; Hu, Z.; Zhong, K.; Xu, J.; Zhang, F.; Zhao, Y.; Wu, P. Satellite-based high-resolution mapping of ground-level PM2.5 concentrations over East China using a spatiotemporal regression kriging model. Sci. Total. Environ. 2019, 672, 479–490. Available online: https://www.ncbi.nlm.nih.gov/pubmed/30965262 (accessed on 10 December 2023). [CrossRef]
- Semlali, B.-E.B.; El Amrani, C.; Ortiz, G.; Boubeta-Puig, J.; Garcia-De-Prado, A. SAT-CEP-monitor: An air quality monitoring software architecture combining complex event processing with satellite remote sensing. Comput. Electr. Eng. 2021, 93, 107257. Available online: https://www.sciencedirect.com/science/article/pii/S0045790621002421 (accessed on 10 December 2023). [CrossRef]
- Semlali, B.-E.B.; Amrani, C.E. A stream processing software for air quality satellite datasets. In Proceedings of the International Conference on Advanced Intelligent Systems for Sustainable Development, Athens, Greece, 30 July 2020–2 August 2020; Springer: New York, NY, USA, 2020; pp. 839–853. [Google Scholar]
- Yu, M.; Masrur, A.; Blaszczak-Boxe, C. Predicting hourly PM2.5 concentrations in wildfire-prone areas using a SpatioTemporal Transformer model. Sci. Total. Environ. 2023, 860, 160446. Available online: https://www.sciencedirect.com/science/article/pii/S0048969722075489 (accessed on 10 December 2023). [CrossRef]
- Karimi, A.; Shirmardi, M.; Hadei, M.; Birgani, Y.T.; Neisi, A.; Takdastan, A.; Goudarzi, G. Concentrations and health effects of short- and long-term exposure to PM2.5, NO2, and O3 in ambient air of Ahvaz city, Iran (2014–2017). Ecotoxicol. Environ. Saf. 2019, 180, 542–548. Available online: https://www.sciencedirect.com/science/article/pii/S0147651319305676 (accessed on 10 December 2023). [CrossRef] [PubMed]
- Zhong, J.; Zhang, X.; Gui, K.; Wang, Y.; Che, H.; Shen, X.; Zhang, L.; Zhang, Y.; Sun, J.; Zhang, W. Robust prediction of hourly PM2.5 from meteorological data using LightGBM. Natl. Sci. Rev. 2021, 8, nwaa307. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Liu, X.; Bi, J.; Liu, Y. A machine learning model to estimate ground-level ozone concentrations in California using TROPOMI data and high-resolution meteorology. Environ. Int. 2021, 158, 106917. Available online: https://www.sciencedirect.com/science/article/pii/S0160412021005420 (accessed on 10 December 2023). [CrossRef]
- Feng, Z.; Wang, X.; Yuan, J.; Zhang, Y.; Yu, M. Changes in air pollution, land surface temperature, and urban heat islands during the COVID-19 lockdown in three Chinese urban agglomerations. Sci. Total. Environ. 2023, 892, 164496. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, W.; Fan, M.; Tao, M.; Wei, J.; Jin, J.; Wang, Q. Validation of Himawari-8 aerosol optical depth retrievals over China. Atmos. Environ. 2019, 199, 32–44. [Google Scholar] [CrossRef]
- Beck, P.S.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote. Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Cowan, D.; Cooper, G. The Shuttle Radar Topography Mission—A New Source of Near-Global Digital Elevation Data. Explor. Geophys. 2005, 36, 334–340. [Google Scholar] [CrossRef]
- Rose, A.; McKee, J.; Sims, K.; Bright, E.; Reith, A.; Urban, M. Landscan Global 2020; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2021. [Google Scholar]
- Mooney, P.; Minghini, M. A review of openstreetmap data. Mapp. Citiz. Sens. 2017, 37–59. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service Climate Data Store. Land Cover Classification Gridded Maps from 1992 to Present Derived from Satellite Observation; Copernicus Climate Change Service Climate Data Store: Reading, UK, 2019. [Google Scholar] [CrossRef]
- Merra, G. Tavgu_2d_lnd_nx: 2d, Diurnal, Time-Averaged, Single-Level, Assimilation, Land Surface Diagnostics v5. 12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015.
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. Available online: http://www.sciencedirect.com/science/article/pii/S0034425719302408019 (accessed on 10 December 2023). [CrossRef]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. Adv. Neural Inf. Process. Syst. 2017, 1, 30. [Google Scholar]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.-R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: New York, NY, USA, 2012; pp. 9–48. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.-W.; Newman, S.-F.; Kim, J.; et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2018, 2, 749–760. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Brunner, D.; Kuhlmann, G. Importance of satellite observations for high-resolution mapping of near-surface NO2 by machine learning. Remote. Sens. Environ. 2021, 264, 112573. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Pan, X.; Wang, W. National-Scale Estimates of Ground-Level PM2.5 Concentration in China Using Geographically Weighted Regression Based on 3 km Resolution MODIS AOD. Remote. Sens. 2016, 8, 184. [Google Scholar] [CrossRef]
- Li, R.; Cui, L.; Meng, Y.; Zhao, Y.; Fu, H. Satellite-based prediction of daily SO2 exposure across China using a high-quality random forest-spatiotemporal Kriging (RF-STK) model for health risk assessment. Atmos. Environ. 2019, 208, 10–19. Available online: https://www.sciencedirect.com/science/article/pii/S1352231019302006 (accessed on 10 December 2023). [CrossRef]
- Xiao, Q.; Chang, H.H.; Geng, G.; Liu, Y. An Ensemble Machine-Learning Model To Predict Historical PM2.5 Concentrations in China from Satellite Data. Environ. Sci. Technol. 2018, 52, 13260–13269. [Google Scholar] [CrossRef]
- Zhang, H.; Di, B.; Liu, D.; Li, J.; Zhan, Y. Spatiotemporal distributions of ambient SO2 across China based on satellite retrievals and ground observations: Substantial decrease in human exposure during 2013–2016. Environ. Res. 2019, 179, 108795. Available online: https://www.sciencedirect.com/science/article/pii/S0013935119305924 (accessed on 10 December 2023). [CrossRef]
- Zhu, S.; Xu, J.; Yu, C.; Wang, Y.; Zeng, Q.; Wang, H.; Shi, J. Learning Surface Ozone from Satellite Columns (LESO): A Regional Daily Estimation Framework for Surface Ozone Monitoring in China. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Yu, X.; Xi, M.; Wu, L.; Zheng, H. Spatiotemporal Weighted for Improving the Satellite-Based High-Resolution Ground PM2.5 Estimation Using the Light Gradient Boosting Machine. Remote Sens. 2023, 15, 4104. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Cheng, M.; Wu, X.; Zhan, N.; Xu, J. Long-term ambient SO2 concentration and its exposure risk across China inferred from OMI observations from 2005 to 2018. Atmos. Res. 2020, 247, 105150. Available online: https://www.sciencedirect.com/science/article/pii/S0169809520310863 (accessed on 10 December 2023). [CrossRef]
- Zhu, S.; Xu, J.; Fan, M.; Yu, C.; Letu, H.; Zeng, Q.; Zhu, H.; Wang, H.; Wang, Y.; Shi, J. Estimating Near-Surface Concentrations of Major Air Pollutants from Space: A Universal Estimation Framework LAPSO. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Song, Z.; Chen, B.; Zhang, P.; Guan, X.; Wang, X.; Ge, J.; Hu, X.; Zhang, X.; Wang, Y. High temporal and spatial resolution PM2.5 dataset acquisition and pollution assessment based on FY-4A TOAR data and deep forest model in China. Atmos. Res. 2022, 274, 106199. Available online: https://www.sciencedirect.com/science/article/pii/S0169809522001855 (accessed on 10 December 2023). [CrossRef]
- Devi, S.; Esmaeilbeiki, F.; Karimi, S.M.; Sihag, P. Prediction of sulphur dioxide (SO2) in air by using bagging, ANN and M5P: A case study, Gaya and Tirupati, India. Arab. J. Geosci. 2022, 15, 631. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Q.; Li, T.; Zhu, L.; Zhang, L. Estimating daily full-coverage near surface O3, CO, and NO2 concentrations at a high spatial resolution over China based on S5P-TROPOMI and GEOS-FP. ISPRS J. Photogramm. Remote Sens. 2021, 175, 311–325. Available online: https://www.sciencedirect.com/science/article/pii/S0924271621000897 (accessed on 10 December 2023). [CrossRef]
- He, W.; Meng, H.; Han, J.; Zhou, G.; Zheng, H.; Zhang, S. Spatiotemporal PM2.5 estimations in China from 2015 to 2020 using an improved gradient boosting decision tree. Chemosphere 2022, 296, 134003. Available online: https://www.sciencedirect.com/science/article/pii/S0045653522004969 (accessed on 10 December 2023). [CrossRef] [PubMed]
- Wei, J.; Li, Z.; Wang, J.; Li, C.; Gupta, P.; Cribb, M. Ground-level gaseous pollutants (NO2, SO2, and CO) in China: Daily seamless mapping and spatiotemporal variations. Atmos. Meas. Tech. 2023, 23, 1511–1532. Available online: https://acp.copernicus.org/articles/23/1511/2023/ (accessed on 10 December 2023). [CrossRef]
- Silibello, C.; Carlino, G.; Stafoggia, M.; Gariazzo, C.; Finardi, S.; Pepe, N.; Radice, P.; Forastiere, F.; Viegi, G. Spatial-temporal prediction of ambient nitrogen dioxide and ozone levels over Italy using a Random Forest model for population exposure assessment. Air Qual. Atmos. Health 2021, 14, 817–829. [Google Scholar] [CrossRef]
- Ma, M.; Liu, M.; Liu, M.; Li, K.; Xing, H.; Meng, F. Resolving contributions of NO2 and SO2 to PM2.5 and O3 pollutions in the North China Plain via multi-task learning. J. Appl. Remote Sens. 2023, 18, 012004. [Google Scholar] [CrossRef]
- Li, T.; Cheng, X. Estimating daily full-coverage surface ozone concentration using satellite observations and a spatiotemporally embedded deep learning approach. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102356. Available online: https://www.sciencedirect.com/science/article/pii/S0303243421000635 (accessed on 10 December 2023). [CrossRef]
- Gao, M.; Gao, J.; Zhu, B.; Kumar, R.; Lu, X.; Song, S.; Zhang, Y.; Jia, B.; Wang, P.; Beig, G.; et al. Ozone pollution over China and India: Seasonality and sources. Atmos. Meas. Tech. 2020, 20, 4399–4414. Available online: https://acp.copernicus.org/articles/20/4399/2020/ (accessed on 10 December 2023). [CrossRef]
- Wen, X.; Chen, W.; Chen, B.; Yang, C.; Tu, G.; Cheng, T. Does the prohibition on open burning of straw mitigate air pollution? An empirical study in Jilin Province of China in the post-harvest season. J. Environ. Manag. 2020, 264, 110451. Available online: https://www.sciencedirect.com/science/article/pii/S0301479720303856 (accessed on 10 December 2023). [CrossRef] [PubMed]
- MEEPRC. Bulletin on China’s Ecological Environment (2019); MEEPRC: Beijing, China, 2020.
- MEEPRC. Bulletin on China’s Ecological Environment (2020); MEEPRC: Beijing, China, 2021.
- de Leeuw, G.; van der, A.R.; Bai, J.; Xue, Y.; Varotsos, C.; Li, Z.; Fan, C.; Chen, X.; Christodoulakis, I.; Ding, J.; et al. Air quality over China. Remote Sens. 2021, 13, 3542. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on tabular data? arXiv 2022, arXiv:2207.08815. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. Available online: https://www.sciencedirect.com/science/article/pii/S1566253521002360 (accessed on 10 December 2023). [CrossRef]
- Chi, Y.; Zhan, Y.; Wang, K.; Ye, H. MuAP Spatial Distribution of Various Air Pollutants in China at 1 km (SO2 2015-01-01:2020-12-31) (Version1.1); Zenodo: Genève, Switzerland, 2023. [Google Scholar] [CrossRef]
- Chi, Y.; Zhan, Y.; Wang, K.; Ye, H. MuAP Spatial Distribution of Various Air Pollutants in China at 1 km (PM2.5 2015-01-01:2020-12-31) (Version1.1); Zenodo: Genève, Switzerland, 2023. [Google Scholar] [CrossRef]
- Chi, Y.; Zhan, Y.; Wang, K.; Ye, H. MuAP Spatial Distribution of Various Air Pollutants in China at 1 km (O3 2015-01-01:2020-12-31) (Version1.1); Zenodo: Genève, Switzerland, 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).